Аннотация
Предложены неотражающие граничные условия для уравнений Максвелла с финитной плотностью
электрического тока. Условия формулируются на границе, расположенной в области однородности
уравнений, вблизи носителя плотности тока. Представлен алгоритм вычисления решения на границе,
основанный на методе разностных потенциалов. Эффективность алгоритма определяется свойствами
лакун разностного волнового уравнения. Доказана теорема, позволяющая свести вычисление
электромагнитного поля на границе к решению трех независимых волновых уравнений.
Abstract
The non-reflecting boundary conditions for the Maxwell's equations with the compact density of
the electrical current are offered. The conditions are formulated on border located in the
field of uniformity of the equations, near to density of the current. The algorithm based on a
difference potentials method is suggested for the calculation of the decision on the border.
The efficiency of algorithm is determined by properties of lacunas of the difference wave
equation. The theorem, which allows to reduce calculation of an electromagnetic field on
border to the decision of three independent wave equations, is proved.
Рассмотрим следующую задачу для системы Максвелла
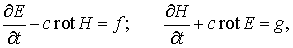 (1) (1)
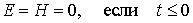 , (2) , (2)
причем 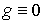 , а f(t,x,y,z) удовлетворяет условию , а f(t,x,y,z) удовлетворяет условию
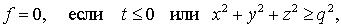 (3) (3)
где q<1
заданное положительное число. Пусть решение (E, H) задачи (1-3) нужно вычислить только в области
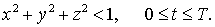 (4) (4)
Вычисление решения задачи (1-4) по
употребительным разностным схемам на сетках с шагами O(h) требует  арифметических
операций и с ростом T быстро становится непосильным. Здесь
будет построен алгоритм, требующий неуменьшаемого по порядку арифметических
операций и с ростом T быстро становится непосильным. Здесь
будет построен алгоритм, требующий неуменьшаемого по порядку 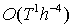 количества
арифметических операций. количества
арифметических операций.
Для
вычисления решения воспользуемся сеткой M точек m=(t, x, y, z)
с координатами
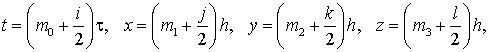 (5) (5)
где t и h, 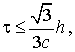 постоянные шаги сетки; постоянные шаги сетки;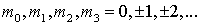 ; i, j, k, l=0,1. Сетка M введена в [1]. Обозначим ; i, j, k, l=0,1. Сетка M введена в [1]. Обозначим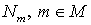 , совокупность семи точек , совокупность семи точек
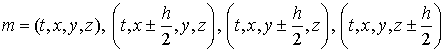 . .
Обозначим
 совокупность точек совокупность точек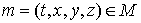 , для которых , для которых 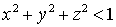 ; ; 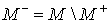 ; ; 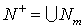 , , 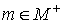 ; ; 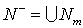 , , 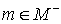 ; ; 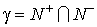 . Для любого множества Z в
пространстве (t, x, y, z) обозначим . Для любого множества Z в
пространстве (t, x, y, z) обозначим 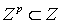 совокупность точек Z, лежащих в гиперплоскости совокупность точек Z, лежащих в гиперплоскости
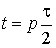 . .
Обозначим 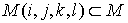 ту подсетку сетки M, координаты точек которой задаются формулами (5) при
фиксированном наборе i, j, k, l.
ту подсетку сетки M, координаты точек которой задаются формулами (5) при
фиксированном наборе i, j, k, l.
Обозначим:
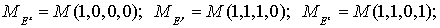
 (6) (6)

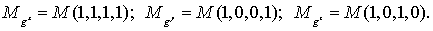
Искомые скалярные компоненты 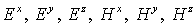 заменим искомыми
скалярными функциями заменим искомыми
скалярными функциями 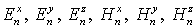 на сетках на сетках 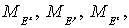 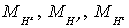 соответственно, для
вычисления которых воспользуемся следующей схемой [2]: соответственно, для
вычисления которых воспользуемся следующей схемой [2]:
 (7) (7)
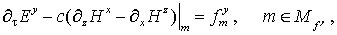 (8) (8)
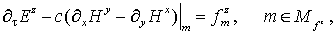 (9) (9)
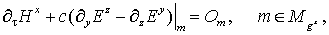 (10) (10)
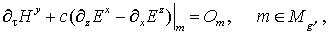 (11) (11)
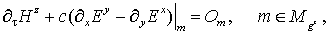 (12) (12)
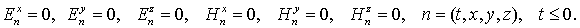 (13) (13)
Через 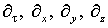 обозначены операции
симметричных разделенных разностей с шагами t, h, h и h соответственно.
Заметим, что в
соответствии с (6) точки обозначены операции
симметричных разделенных разностей с шагами t, h, h и h соответственно.
Заметим, что в
соответствии с (6) точки 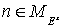 , , 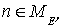 и и 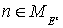 , где определены , где определены 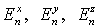 , все лежат на нечетных слоях , все лежат на нечетных слоях
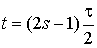 , , 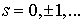 ,
а точки ,
а точки 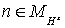 , , 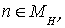 , ,  на четных слоях на четных слоях 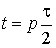 , , 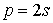 , по времени. , по времени.
Поставим задачу вычислить
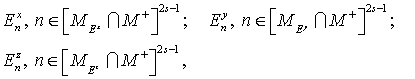 (14) (14)
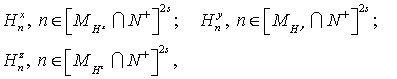 (15) (15)
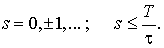
Таблицы (14), (15) представляют собой
таблицы значений компонент 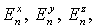 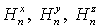 решения задачи (7-13)
в сеточных расчетных подобластях, указанных в (14-15) и соответствующих области
(4). решения задачи (7-13)
в сеточных расчетных подобластях, указанных в (14-15) и соответствующих области
(4).
Вычисление
таблиц (14-15) путем непосредственного решения по явной разностной схеме (7-13)
вовлекает в расчет  точек сетки M, и требует точек сетки M, и требует  арифметических
операций. арифметических
операций.
Построение
неулучшаемого по порядку 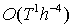 числа арифметических
действий алгоритма для получения таблиц (14-15) с высокой точностью начнем с
того, что разобьем таблицу (15) на следующие две таблицы числа арифметических
действий алгоритма для получения таблиц (14-15) с высокой точностью начнем с
того, что разобьем таблицу (15) на следующие две таблицы
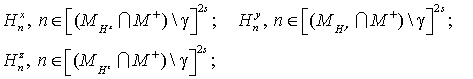 (16) (16)
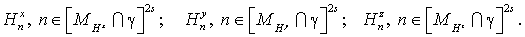 (17) (17)
Рассмотрим теперь следующую
разностную систему уравнений
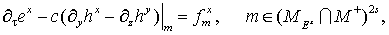 (18) (18)
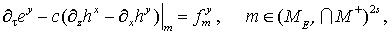 (19) (19)
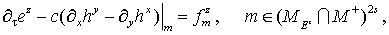 (20) (20)
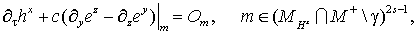 (21) (21)
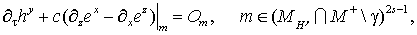 (22) (22)
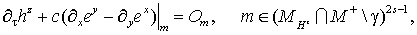 (23) (23)
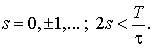
Дополним систему (18-23) начальными
условиями
 , если , если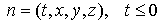 (24) (24)
и следующими искусственными
граничными условиями:
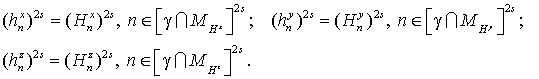 (25) (25)
Величины 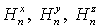 в правых частях
условий (25) суть значения решений задачи (7-13) в соответствующих точках n. в правых частях
условий (25) суть значения решений задачи (7-13) в соответствующих точках n.
Лемма. Решение 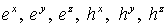 задачи (18-25) существует,
единственно и совпадает с решением задачи (18-25) существует,
единственно и совпадает с решением 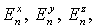 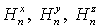 задачи (7-13) в тех точках, где решение задачи (18-25) определено,
т.е. в точках расчетной подобласти. задачи (7-13) в тех точках, где решение задачи (18-25) определено,
т.е. в точках расчетной подобласти.
Из леммы следует, что
условия (25) равносильно заменяют разностную систему (7-13) вне расчетной
подобласти, т.е. являются неотражающими искусственными граничными условиями.
Таблицы
(14) и (15) при s£0 являются тождественно нулевыми в
силу (13). Допустим, что таблицы уже вычислены при 2s£p, где p некоторое четное число. Тогда в силу
леммы можно вычислить таблицу (14) при p+1=2s+1, используя явные разностные уравнения (18-20),
выписанные при 2s=p. После того
как таблица (14) вычислена на слое p+1=2s+1, можно
вычислить также часть таблицы (15), а именно таблицу (16) на слое p+2=2(s+1), воспользовавшись для этого
разностными уравнениями (21-23), выписанными на (p+1)-ом слое,
т.е при  . .
Для завершения вычисления таблицы (15) на слое
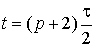 осталось вычислить
таблицу (16) на (p+2)-ом слое, т.е. правые части искусственных граничных условий (25) при 2s=p+2.
осталось вычислить
таблицу (16) на (p+2)-ом слое, т.е. правые части искусственных граничных условий (25) при 2s=p+2.
Введем обозначение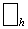 , полагая для каждой функции v(t, x, y, z) , полагая для каждой функции v(t, x, y, z)
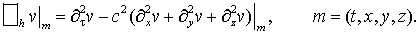
Теорема. Числа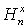 , , 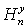 , ,  , составляющие таблицу
(16) при , составляющие таблицу
(16) при 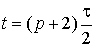 , совпадают со
значениями , совпадают со
значениями 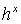 , , 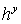 , , 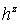 в соответствующих точках решений
следующих трех разностных вспомогательных волновых задач в соответствующих точках решений
следующих трех разностных вспомогательных волновых задач
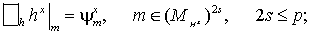 (26) (26)
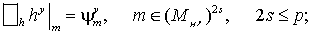 (27) (27)
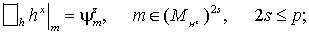 (28) (28)
 (29) (29)
Правые части этих задач задаются
формулами
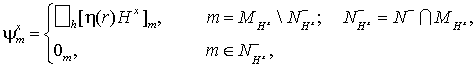 (30) (30)
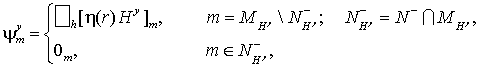 (31) (31)
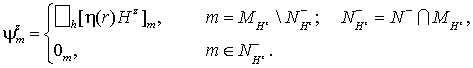 (32) (32)
В формулы (30-32) входит функция h(r), определенная равенствами
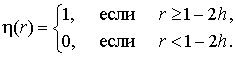 (33) (33)
Для точки 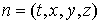 число число 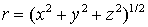 . Решения задач (26-32) имеют смысл на слоях . Решения задач (26-32) имеют смысл на слоях 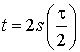 , 2s£p+2, так как правые части , 2s£p+2, так как правые части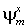 , , 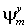 , , 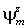 определены формулами
(30-33), в которые входят уже вычисленные значения определены формулами
(30-33), в которые входят уже вычисленные значения 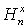 , , 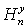 , ,  из таблицы (15) при из таблицы (15) при 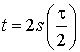 , 2s£p, а также значения уже вычисленных величин, входящих в
таблицу (16) на слое , 2s£p, а также значения уже вычисленных величин, входящих в
таблицу (16) на слое 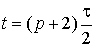 . .
Сформулированная
теорема, сводящая вычисление правых частей неотражающих искусственных граничных
условий (25) к решению трех скалярных волновых задач, и составляет результат
настоящей работы.
Значение
этого результата состоит в том, что мы получили возможность вычислять таблицы
(14-15) за 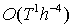 арифметических
операций, поскольку ранее [6-10] нами уже разработан алгоритм вычисления с
высокой точностью решения разностных волновых задач вида (26-33) также за арифметических
операций, поскольку ранее [6-10] нами уже разработан алгоритм вычисления с
высокой точностью решения разностных волновых задач вида (26-33) также за 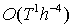 операций. Заметим, что
не существует алгоритма точного или приближенного вычисления таблиц (14-15),
требующего меньшего по порядку числа арифметических операций, так как порядок
числа элементов таблиц (14-15) также есть операций. Заметим, что
не существует алгоритма точного или приближенного вычисления таблиц (14-15),
требующего меньшего по порядку числа арифметических операций, так как порядок
числа элементов таблиц (14-15) также есть 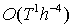 . .
Построенные
неотражающие граничные условия и алгоритм их вычисления не изменятся, если
изменить сетки и разностные уравнения внутри сферы 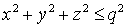 . Поэтому наши конструкции и алгоритмы можно использовать при
решении произвольных, имеющих единственное решение, электродинамических задач
на больших временах. Например, электромагнитное поле внутри сферы может быть
самосогласованным или (и) развиваться в среде со сложным распределением
электрофизических параметров. . Поэтому наши конструкции и алгоритмы можно использовать при
решении произвольных, имеющих единственное решение, электродинамических задач
на больших временах. Например, электромагнитное поле внутри сферы может быть
самосогласованным или (и) развиваться в среде со сложным распределением
электрофизических параметров.
Переход
от исходной задачи (7-15) к задаче в расчетной подобласти с удобными для
вычислений неотражающими граничными условиями на ее сеточной границе (18-25)
осуществлен с использование подходов и конструкций метода разностных
потенциалов [3-6]. Экономный алгоритм вычисления правых частей условий (25)
опирается на фундаментальное свойство решений волнового уравнения иметь лакуны.
Идея использования этого свойства для экономного вычисления неотражающих
искусственных граничных условий была впервые высказана в [4], а затем развита и
программно реализована в [7-14], см. также [6].
Список литературы
[1] Лебедев В.Н. О методе сеток для одной
системы уравнений в частных производных. Изв. АН СССР, серия математ., т.22, 1958, с.717-734.
[2] Yee K.S. Numerical solution
of initial boundary value problem involving Maxwell’s equations in isotropic
media, IEEE Trans. Antennas Propagat, v.14, 1966, p.302-307.
[3] Рябенький В.С. Точный перенос разностных
краевых условий. Функц. анализ и его приложения, т.24, в.3, 1990, с.90-91.
[4] Рябенький В.С. Точный перенос краевых
условий. Вычислит. механика твердого тела, 1990, с.129-145.
[5] Ryaben’kii V.S.
Nonreflecting time dependent boundary conditions on artificial boundaries of
varying location and chape. Applied Numerical Mathematics, V.33, 2000, p.481-492.
[6] Рябенький В.С. Метод разностных потенциалов
и его приложения. Физматлит, 2002, с.1-492.
[7] Рябенький В.С., Турчанинов В.И., Цынков
С.В. Использование лакун решений 3D–волнового уравнения для вычисления
решения задачи Коши на больших временах. Математическое моделирование, 1999,
т.11, №12, с.113-126.
[8] Турчанинов В.И. Свойство лакун решений
разностного аналога пространственного волнового уравнения. Доклады РАН, т.375,
№4, 2000.
[9] Рябенький В.С., Турчанинов В.И., Цынков
С.В. Неотражающие искусственные граничные условия для замены отбрасываемых уравнений
с лакунами. Математическое моделирование, т.12, №12, 2000.
[10] Ryaben’kii V.S., Tsynkov
S.V., Turchaninov V.I. Long-time numerical computation of wave type solutions
driven by moving sources. Applied Numerical Mathematics, 2001, V.38, p-187-222.
[11] Ryaben’kii V.S., Tsynkov
S.V., Turchaninov V.I. Global discrete artificial boundary conditions for
time-dependent wave propagation. J. Comput. Physics, 2001, v.174, p.712-758.
[12] Tsynkov S.V. Artificial
boundary conditions for the numerical simulation of anstady accoustic waves. J.Comput. Physics, 2003, V.189(2), p.626-650.
[13] Цынков С.В. Нелокальные искусственные
граничные условия для численного решения задач в неограниченных областях.
Дисс.докт. физ.-мат. наук, М., Институт математического моделирования РАН,
2003.
[14] Tsynkov S.V. On the
application of lacunae-based methods to Maxwell’s equations, J. Comput.
Physics, 2004, v.199, p.126-149.
|