Задача доставки реликтового вещества к Земле.

Исследования космического пространства, полеты к планетам Солнечной системы начатые запуском первого советского спутника в 1957 году, ставят одной из важнейших целей получение данных для решения фундаментальной задачи о происхождении Солнечной системы. Задача эта имеет не только большое теоретическое, но и важное практическое применение. В 1990 году, открывая Международный геологический конгресс в Москве, наш министр геологии говорил о важности новых геологических концепций строения Земли, необходимых для обоснования стратегии поиска полезных ископаемых. Необходимые для проверки и уточнения теорий экспериментальные данные о земных глубинах могут быть получены со дна океана, сверхглубоким бурением и исследованием космоса, планет Солнечной системы. Все три способа сравнимы по сложности и дороговизне, но они необходимы для уточнения и отбора моделей, получаемых из теории и данных геофизики и геологии. Многочисленные модели формирования Земли и особенно верхней части мантии, известные в настоящее время, требуют для сравнения, уточнения и проверки использования новых фактических данных. Космохимия является одним из источников получения необходимых данных, путем сравнения химии и минерального состава тел Солнечной системы и аппроксимация по ним состава вещества Земли.

Новая теория происхождения Солнечной системы, полученная путем численного моделирования в ИПМ им. М.В. Келдыша в 1970-х годах [1] предлагает некоторые подходы, имеющие соответствия в других данных современной космохимии. Различные области Солнечной системы – кольцевые зоны пояса формирования планет из протопланетного диска – на первоначальной стадии имели слабое перемешивание и могли заметно отличаться по своему химическому составу, входящим в этот состав изотопам, а также по образовавшимся в них минералам.

Для оценки химического состава Протоземли важно было бы получить образцы вещества из нескольких различных поясов Солнечной системы, чтобы по ним составить представление о веществе Земли. При этом следует иметь в виду два обстоятельства.

Во-первых, желательно, чтобы эти образцы относились к «реликтовому» веществу, сохранившему минералогический, химический и изотопный состав со времен формирования Солнечной системы в возможно неизмененном виде. Вещество больших планет этому условию не удовлетворяет, так как оно прошло через многочисленные геологические процессы метаморфизма и стратификации. Считается, что в неизмененном виде может сохраниться вещество небесных тел размерами около 100-200 км в диаметре. Образцы вещества метеоритов, например (которые являются осколками таких тел), отличаются большой примитивностью минералов, в них входящих, и заметным отличием химического и изотопного состава от вещества Земли (так, в метеоритах содержится во много раз больше, чем в земных породах, элемента иридия).

Во-вторых, необходимо знать, из какой области Солнечной системы происходят полученные образцы вещества. Доставленные с Луны образцы грунта показали, в основном, близость с веществом Земли. Кроме земного вещества, в нашем распоряжении имеются многочисленные образцы вещества метеоритов. Однако, по современным представлениям, метеориты, как и порождающие их астероиды, сближающиеся с Землей (АСЗ), образующие группы Амура, Аполлона и Атона, являются мигрантами из отдаленных областей Солнечной системы. Первые соображения о приходе АСЗ не из Главного астероидного пояса, а из далеких областей, были высказаны еще в 60-х годах Андерсом и Эпиком. Механизм миграции малых тел из удаленных областей в окрестность Земли был тогда же исследован, на примере комет, Е.И.Казимирчак-Полонской.

Согласно теории, основанной на моделировании формирования Солнечной системы, процесс формирования планет из кольцевых зон происходил в состоянии вещества в виде газо-полевых сгущений, облаков больших размеров (в тысячи и десятки тысяч км в диаметре). Причем, первоначальные орбиты движения сгущений вокруг Солнца были близки к круговым и лежали в плоскости эклиптики. Поддержание этих облаков в газообразном состоянии, обеспечивалось подогревом и ионизацией со стороны коротко живущих радиоактивных изотопов (прежде всего, ²⁶Al с периодом полураспада ~ 0.75 млн. лет) образовавшихся при взрыве сверхновой, который послужил зарождению Протосолнца и протопланетного диска из межзвездного вещества.

Процесс объединения газо-полевых сгущений в планету в разных областях, кольцевых зонах происходил с разной скоростью пропорциональной периодам обращения их по своим орбитам. Так, согласно указанной модели, планеты земной группы образовывались за времена в десятки тысяч лет, Юпитер – за 100 тысяч лет, Сатурн – за 300 тысяч. Время образования Нептуна оказывается близким к полураспаду ²⁶Al и уменьшению потока энергии, препятствовавшему коллапсированию газо-пылевых сгущений в твердые тела, планетезимали. В кольцевой зоне, области (или областях) за Нептуном подогрев газо-пылевых сгущений за счет ²⁶Al прекратился до формирования единой в планеты и вместо нее образовался астероидный пояс из множества планетезималей.

Соображения, изложенные выше, были высказаны, как одно из следствий теории моделирования образования Солнечной системы, в 1980 году Т.М. Энеевым [2]. Было предсказано существование астероидного пояса за Неп-туном (и даже нескольких поясов), предполагалось, что Плутон является одним из тел такого пояса, и предлагалось организовать их наблюдение. Было организовано наблюдение этих тел, одно из них удалось обнаружить, однако на пределе погрешности, и подтвердить его наблюдение не удалось. С тех пор открыто большое число астероидов занептунного пояса, размеры которых составляют, как правило, 200-300 км в диаметре, но есть и большие. Тела такого размера, содержащие вещество в неизмененном состоянии, могут иметь каменно-металлические ядра и льдистые мантии. Предполагалось [2], что из осколков этих тел, получившиеся в результате их столкновений, могли образоваться астероиды, в том числе АСЗ, – из их ядер, и кометы – из их мантий.

Исследования последнего времени по миграции малых тел в Солнечной системе показали достаточно подробно, как может происходить «раскачка» орбит астероидов в занептунном поясе, изменение их эксцентриситетов и больших полуосей [3], понижающая перигелии их орбит и делающая их подверженными сильным возмущениям больших планет, в первую очередь Нептуна. Тогда начинает действовать механизм воздействия на орбиты возмущений от больших планет, опускания перигелием их орбит внутрь Солнечной системы, в области воздействия Урана, Сатурна и Юпитера, приводящие часть из них в зону планет земной группы. Другая часть, большая в процентном отношении, теми же возмущениями больших планет выбрасывается в отдаленные области Солнечной системы или за ее пределы. Таким образом, в настоящее время можно уверенно считать (и это признается все большим числом исследователей), что основная часть АСЗ и метеоритов, происходящих из них, являются мигрантами из удаленной занептунной области, называемой также «поясом Койпера».

Образцы реликтового вещества можно получить, причем с привязкой к известной области, с некоторых спутников планет и из Главного пояса астероидов. Чтобы содержать реликтовое вещество, спутники должны быть относительно небольшими и близко расположенными к планете. У Юпитера, например, этим требованиям удовлетворяет спутник Амальтея, в то время как дальние спутники (особенно, обнаруженные в последние годы), с большой вероятностью являются захваченными. Удовлетворяют этим требованиям также спутники Марса Фобос и Деймос. В связи с их свойством в Российскую космическую программу, в проект исследования Марса «Фобос-Грунт» была включена задача доставки реликтового вещества с Фобоса [4].

Астероиды Главного пояса образовались в кольцевой зоне, лежащей между Марсом и Юпитером. Формированию единой планеты, видимо, помешал Юпитер, «оттянувший» к себе большую часть вещества соседней зоны или выбросивший другую часть, попавшую в резонанс с его движением. В образовавшемся Главном астероидном поясе известны в настоящее время десятки тысяч астероидов диаметром от нескольких сотен км до нескольких км. Астероиды по спектральным свойствам и отражательной способности относят к нескольким классам, среди которых наиболее многочисленными (и достаточно загадочными из-за непохожести на земные минералы и вещество метеоритов) являются классы С и S, названные «углистыми хондритами» и «силикатными». Доставка вещества астероидов этих двух классов к Земле является задачей первостепенной важности. Быть может, представляет интерес получение образцов вещества из ближней и дальней части Главного пояса – так как он достаточно протяженный: большие полуоси основной его части лежат в диапазоне 2.3-3.5 а.е.

Астероиды группы S расположены, в основном, в ближней части Главного пояса, астероиды группы С, наоборот, – в более удаленной части. С точки зрения достижимости и реализуемости экспедиции по доставке образцов вещества, естественно, астероиды в ближней части пояса имеют преимущество, они легче достижимы. Еще удобнее, в смысле достижимости, астероиды группы Апполона и Амура, АСЗ, как, например, Эрос, к которому успешно была осуществлена американская экспедиция. Однако, с точки зрения доставки реликтового вещества, АСЗ, как и кометы, представляют гораздо меньший интерес ввиду их происхождения из далеких (и неопределимых точно) областей Солнечной системы. Образцы вещества астероидов группы Аполлона мы имеем в виде метеоритов.

Задаче доставки вещества с астероида спектрального класса С Фортуны (d ~ 150 км, 19 – номер по каталогу астероидов) был посвящен Российско-Евро-пейский проект «Fortuna», выполненный объединенной рабочей группой в 1992-95 годах [5,6]. Он предполагал полет с помощью электроракетных ионных или плазменных двигателей (ЭРД) с энергетикой от бортового ядерного реак-тора типа «ТОПАЗ», с выводом на межпланетную орбиту ракетой-носителем «Протон». Этот проект и его отдельные части неоднократно докладывался на международных научных форумах и, с большой вероятностью, повлиял на осознание необходимости доставки реликтового вещества с малых тел к Земле [7,8]. Задача доставки реликтового вещества, впервые сформулированная в отечественной науке, постепенно получает все большее признание в мире. Слова о реликтовом веществе, о его доставке и исследовании, начинают звучать в космических проектах разных стран.

Последующие отечественные исследования доставки реликтового вещества, включая проект «Фобос-Грунт», предполагали использование ракетоносителя среднего класса «Союз», электроракетных двигателей СПД с энергетикой от современных солнечных батарей [9]. Исследовались экспедиции по доставке реликтового вещества с астероидов Главного пояса, комет группы Юпитера,

Возможность осуществления экспедиций по доставке реликтового вещества с астероидов Главного пояса и комет группы Юпитера с помощью КА с ЭРД, разрабатываемого в рамках проекта «Фобос-Грунт», рассматривается ниже.

ЭКСПЕДИЦИИ В АСТЕРОИДНЫЙ ПОЯС КА с МАЛОЙ ТЯГОЙ

Рассматривается возможность использования космического аппарата, разрабатываемого в настоящее время в рамках проекта «Фобос-Грунт», для экспедиций к малым планетам Главного астероидного пояса. Научной целью таких экспедиций является доставка реликтового вещества с астероидов на Землю, что может дать ответы на многие вопросы о процессах формирования Солнечной системы, и дать ценную информацию для наук о Земле. Эти ожидания проистекают из космогонической концепции, базирующейся на компьютерном моделировании образования Солнечной системы [1]. В соответствии с этой концепцией, дифференциация вещества в протопланетном диске обусловила дифференциацию вещества планет. Обнаружение такой дифференциации с помощью изотопного и минерало­гического анализа является одной из целей космических экспедиций. Поэтому задача полетов в различные области Солнечной системы, и в том числе в Главный астероидный пояс, для получения образцов реликтового вещества, имеет большое научное значение.

Лет 10 назад Объединенная группа российских и немецких ученых и инженеров разработала проект новой универсальной космической системы [5,6], предназначенной для решения многочисленных задач исследования Солнечной системы, которые не могут быть решены с использованием традиционных космических технологий. Проект предполагал использовать ракетоноситель «Протон» и космический аппарат с электроракетными двигателями и бортовой ядерной энергетической установкой. В качестве первоочередной была предложена экспедиция к астероиду Фортуна, с доставкой с него образца грунта на Землю. Была рассмотрена следующая схема полета. Космический аппарат должен был быть выведен на межпланетный участок полета с помощью большой тяги (разгонным блоком «Д»), а последующий перелет к астероиду с выравниванием скоростей КА и астероида – с использованием малой тяги (электроракетных двигателей); по достижении астероида специальный посадочный модуль должен обеспечить забор грунта, старт с астероида и возврат к Земле с помощью большой тяги.

Характеристики КА и траектории полета следующие. Начальная масса КА (на межпланетном участке полета) – 6 тонн, из которых половину составляет масса ядерной энергети­ческой установки; ее электрическая мощность – 30 киловатт; геоцентрический гиперболический избыток скорости – 3 км/с; продолжительность перелета к астероиду – 2 года, обратного полета к Земле – полгода, полная продолжи­тельность экспедиции – 4 г. Положительным свойством ядерной электро­установки является относительно большая электрическая мощность, которая практически не зависит от расстояния до Солнца и от времени полета. Отрицательным – необходимость защиты оборудования и научных приборов от ядерного излучения, как следствие – большая масса КА и необходимость использования довольно дорогого ракетоносителя «Протон».

Технические характеристики космической системы, разрабатываемой в рамках проекта «Фобос-Грунт» [4], более скромны. Предполагается использовать более легкий и дешевый ракетоноситель типа «Союз» (вместо «Протона») и легкие солнечные панели (вместо ядерной энергоустановки). Начальная масса КА на межпланетном участке полета – 2 т. (т.е. в три раза меньше по сравнению с проектом [5,6]); номинальная электрическая мощность солнечных панелей (на расстоянии одной астрономической единицы от Солнца) – 7.5 Квт (в четыре раза меньше); гиперболический избыток скорости – 1.75 км/с; масса транспортного блока, электроракетных движителей и солнечных батарей M_БЛ – 0.3 тонны. Полезная масса, доставляемая на «Фобос» – около 0.9 тонны:

M_П = M_К – M_Б – M_БЛ ,

– это конечная масса КА за вычетом массы баков M_Б = 0.2M_РВ (M_РВ – масса рабочего вещества) и вышеупомянутой массы M_БЛ .

Положительным свойством солнечных батарей является их малая масса; отрицательным – малая номинальная электрическая мощность и ее уменьшение с удалением от Солнца (около Фортуны электрическая мощность в пять раз меньше, чем у Земли). Неудивительно, что экспедиция к Фортуне, так же, как и экспедиции к другим астероидам Главного пояса, становятся невозможными (этот вывод исходит из предположения, что полезная масса у астероида должна быть не меньше той, что доставляется к Фобосу, т.е. 0.9 т.). Даже с увеличением продолжительности перелета к астероиду с 2 лет до 3 полезная масса у Фортуны не превышает 0.7 т. (см. табл.1, [10]). В таблице 1 индекс «ид» относится к модели идеальной малой тяги (когда скорость истечения струи V_С может принимать любые положительные значения), индекс «ст» – к модели ступенчатой тяги (V_С = 16.5 км/с на активных участках траектории); T – продолжительность перелета, φ – его угловая дальность; M_К и M_П – соответственно конечная масса КА и полезная масса у астероида.

Таблица 1.

Экспедиции к астероидам Главного пояса с гравитационным

маневром в сфере действия Марса.

Есть два способа заметного увеличения полезной массы. Первый – использовать гравитационный маневр у Марса. Второй – увеличить номиналь­ную мощность солнечных панелей.

Использование гравитационного маневра в сфере действия Марса может значительно – иногда в полтора и более раз по сравнению с прямым перелетом от Земли к астероиду – увеличить полезную массу. Некоторые параметры комбинированного перелета к Фортуне представлены в табл.2. Название астероида, его геохимический тип и номер по каталогу даны в первом столбце. Характеристики КА и оптимальной траектории (участка перелета к астероиду) – те же, что и в табл.1 – приведены во втором столбце. Импульс DV большой тяги, прикладываемый у астероида для возврата к Земле, дата начала экспедиции t_З (старта с Земли), и ее продолжительность T_Э – в третьем столбце. Продолжительность T_Э экспедиции включает в себя время сопровождения астероида космическим аппаратом в ожидании оптимального момента старта к Земле.

В дополнение к ступенчатой программе малой тяги со скоростью истечения V_C = 16.5 км/с рассмотрен вариант программы с двумя уровнями скорости истечения: 16.5 км/с и 25 км/с. Дело в том, что ступенчатая модель тяги с одним уровнем скорости истечения может иногда заметно отличаться (в данном случае на 214 кг) по полезной нагрузке от идеальной модели (которая дает верхнюю оценку для возможного значения полезной нагрузки). В то время как модель с двумя уровнями скорости истечения обычно дает очень близкое к идеальному значение доставляемой полезной массы. В рассматриваемом случае разница между двумя программами ступенчатой тяги довольно значительна и составляет 131 кг. Но последний вариант предполагает использование двух типов электроракетных движителей (а проект «Фобос-Грунт» – только одного.)

Таблица  2.

Пример оптимального перелета от Земли к Марсу и последующего полета к Фортуне дан на рис. 1. Орбита Земли и траектория КА изображены сплошной линией, орбиты Марса и астероида – пунктиром. Оскулирующая орбита, по которой двигался бы КА без тяги после выхода из сферы действия Марса – жирным пунктиром. Символом α отмечены афелии орбит; Ñ ­– точки старта с Земли и финиша у Фортуны, Æ – пролета Марса.

Две программы ступенчатой тяги, точнее, величины w = 1/ V_C обратной скорости истечения струи, приведены на рис. 2 (а) и (б) сплошными линиями, на них же программа идеальной малой тяги показана пунктиром. Хорошо видно, что ступенчатая программа с двумя уровнями скорости истечения струи гораздо лучше аппроксимирует идеальную программу, чем ступенчатая тяга с одним уровнем V_C. И потому дает лучшее значение полезной массы.

Отметим, что данный расчет был выполнен без привязки к конкретному движению планет по их орбитам, что позволяет выявить некоторые качественные характеристики оптимального перелета. Во-первых, видно, что встреча КА с Марсом происходит в окрестности перигелия его орбиты, т.е. в области наибольшего сближения Марса с Землей. Во-вторых, встреча с астероидом происходит практически точно в афелии его орбиты. Оскулирующая орбита после выхода КА из сферы действия Марса занимает промежуточное положение между орбитами Марса и астероида – и по положению линии апсид в пространстве, и по величине средней полуоси.

Попытки привязки оптимальной траектории перелета (между орбитами планет) к реальному движению планет обычно, в случае двух планет, не вызывает больших проблем, так как в случае малой тяги окна старта и финиша шире, чем в случае большой тяги. И потому на отрезке в несколько лет (для даты старта T_З) удается подобрать параметры T_З, T_А так, что проигрыш в функционале оказывается не слишком большим (при той же примерно продолжительности перелета). Однако в случае трех планет их удачное взаимное положение случается гораздо реже. Так, отношение периодов Фортуны и Марса равно » 2.03, поэтому схожее положение этих двух планет случается раз в 125 лет. Хотя иногда возможен еще один «хороший» вариант расположения трех планет – с перелетом в перигелий астероида, а также возможно повторение старта через 1-2 периода Марса, если астероид при этом еще не сильно сместится от наилучшего положения, в целом возможность перелета к конкретному астероиду случается редко.

Рис. 1. Перелет к астероиду Фортуна космического аппарата с идеальной малой тягой с гравитационным маневром в сфере действия Марса. Сплошная линия – орбита Земли и траектория перелета, пунктир – орбиты Марса и астероида, жирный пунктир – оскулирующая орбита в момент выхода из сферы действия Марса. Через a обозначены апогеи орбит. Параметры гравитационного поворота: V_BX = 2.8 км/с, g = 75^o, w = 9.5 ^o, минимальная высота пролета над поверхностью Марса 100 км, t_M – через 3 недели после прохождения Марсом перигея. Угловые дальности участков траектории до и после гравитационного маневра соответственно 269^o и 221^o, продолжительности перелета – 386 и 675 суток, суммарная продолжительность полета 2.9 года. Начальная масса КА 1947 кг, масса у Марса 1810 кг, конечная масса у астероида 1520 кг. Гиперболический избыток скорости при выходе из сферы действия Земли V_¥ = 1.75 км/с.

     w = 1/V_C [ с/км ]

(а)

     w = 1/V_C [ с/км ]

Рис. 2. Оптимальные программы малой тяги для перелета к астероиду Фортуна с гравитационным маневром в сфере действия Марса. Сплошная линия – ступенчатая тяга, пунктир – идеальная тяга. Идеальная программа тяги имеет разрыв при пересечении (точечной) сферы действия Марса. Начальная масса КА у Земли m_З = 1947 кг. Конечная масса у астероида m_А^ид  = 1520 кг – для идеальной модели тяги, m_А^ст = 1363 кг – для (а) двухступенчатой программы тяги ( w₁ = 0, w₂ = 0.0606, что соответствует V_C = 16.5 км/с ) и m_А^ст = 1472 кг – для (б) трехступенчатой программы тяги (w₁ = 0, w₂ = 0.4, w₃ = 0.0606, что соответствует V_C = 16.5 и 25 км/с ).

Поэтому актуальной становится задача поиска других астероидов Главного пояса в качестве целей для космических полетов. Поскольку имеются сотни астероидов с диаметром ³ 50 – 100 км и тысячи более мелких астероидов с достаточно хорошо известными орбитами, удается найти немало интересных вариантов экспедиций. Примеры таких экспедиций приведены в табл. 3,4,5.

Так как великое противостояние Земли и Марса случается раз в 15-17 лет, даты старта этих экспедиций, как видно из таблицы 4, образуют группы с примерно таким же периодом. Было найдено 16 вариантов экспедиций к астероидам (главным образом из первых двух сотен по каталогу, и следовательно, больших по размерам) со стартом в 21 веке. Важно, что этот список включает экспедиции к астероидам всех основных геохимических типов: C,E,I,M,O,S.

В табл. 3 приведены: N – номер астероида по каталогу; тип ( C, E, I, M, O, S, U ) – классификация по составу; D – диаметр планеты;

Таблица 3.

a, e, i, w, W – параметры орбиты (большая полуось, эксцентриситет, наклонение, угловое расстояние перицентра от узла, долгота восходящего узла); D – разность долготы перицентра планеты и Марса ( » углу между направлениями на перицентр планеты и Марса);

R_p , R_a – расстояния до перицентра и апоцентра орбиты планеты; T/T_З , T/T_М – отношение периода обращения планеты вокруг Солнца соответственно к периоду Земли и к периоду Марса.

В таблице 4 приведены следующие характеристики перелетов к астероидам с гравитационным маневром у Марса КА с идеальной МТ:

t_З – старт с Земли, R_M, R_A – расстояния до Солнца [в млн. км] в моменты t _М, t _А пролета СД Марса и встречи с астероидом; DT₁, DT₂, j₁, j₂ – продолжительности [в сутках] и угловые дальности участков перелета соответственно от Земли к Марсу и от Марса к астероиду; DT_S , j_S – продолжительность [в годах] и угловая дальность [в оборотах вокруг Солнца] всего перелета к астероиду; V_BX, g , w – величина вектора скорости входа в СД Марса и угол его поворота, а также угол отклонения его от плоскости входа в СД (образованной векторами скорости КА и Марса);  M_К, M_П – конечная масса КА и «полезная» масса M_П = M_К – 0.3 – 0.2*(M₀ – M_К ) [в тоннах] у астероида.

Таблица 4.

В таблице 5 даны характеристики возвратного участка экспедиций к астероидам Главного пояса (перелет к астероиду – с идеальной малой тягой на солнечных батареях, возврат к Земле – с большой тягой):

t _З – начало экспедиции (год старта с Земли), M_П  –  полезная масса у астероида; DТ_П –  пауза (время ожидания старта с астероида), DТ_О  –  продолжительность обратного перелета,

Т_Э –  продолжительность экспедиции; DV – импульс скорости у астероида для возврата к Земле;

** – нулевое время ожидания; необходимое время для маневров у астероида и забора грунта может быть получено за счет уменьшения продолжительности перелета к астероиду (с уменьшением на 2 недели полезная масса уменьшается на несколько кг);

·        –  имеется в виду более короткий перелет к астероиду – соответственно меньше полезная масса у астероида M_П = 1.004 т).

Таблица 5.

В большинстве случаев приведены два варианта возврата – с разным временем ожидания у астероида удобного момента старта к Земле. Вторые варианты (обычно с большим временем ожидания и соответственно с большей суммарной продолжительностью экспедиции) приведены в том случае, если для них возвратный импульс заметно меньше. Как видно из таблицы, возвратный импульс в «хороших» случаях порядка 4 км/с, в «плохих» – 5 км/с и более. Общая продолжительность экспедиции – от 4 до 6 с половиной лет.

Наконец, в табл. 6 приведены уточненные данные для двух ближайших экспедиций к астероидам Ангелина (№ 64,Е) и Помона (№ 32,S) – и для модели с идеальной малой тягой, и для модели со ступенчатой тягой.

Таблица 6.

Экспедиции к Фортуне без гравитационного маневра у Марса.

В последнее время, благодаря прогрессу в космических технологиях и созданию новых материалов, появляется возможность значительно увеличить мощность солнечных батарей без увеличения их размеров и массы. Представляется реалистичным, что в обозримом будущем удастся увеличить мощность батарей почти в полтора раза – с нынешних 7-7.5 Квт до 10 Квт, а возможно, и вдвое – до 14 Квт. Большая электрическая мощность позволит заметно увеличить полезную нагрузку, доставляемую к астероидам. Так, при мощности батарей в 10 Квт и использовании двух типов электроракетных движителей удается получить дополнительно 150 кг полезной массы в сравнении с мощностью в 7.5 Квт и увеличить ее до почти приемлемой величины в 845 кг (сравни табл.7 и 1).

Увеличение номинальной мощности батарей до 14 Квт позволит значительно расширить возможности новой космический системы и сделает возможными прямые перелеты от Земли ко многим астероидам Главного пояса. В отличие от комбинированной схемы (с гравитационным маневром у Марса), возможность старта для прямого перелета к определенной цели будет повторяться через несколько лет. И поэтому каждый год можно будет найти различные варианты экспедиций к интересным с научной точки зрения астероидам Главного пояса. Два типа астероидов – C и S – представляют особенный интерес для исследований. Астероиды типа C расположены в основном в дальней, более труднодостижимой области Главного пояса. Тем не менее и в ближней части пояса имеется много таких астероидов (так же как и астероидов типа S), приемлемых размеров и с «хорошими» параметрами орбит (эксцентриситетом e < 0.15, наклонением i < 15⁰ и большой полуосью a < 2.5 а.е.). Энергозатраты на перелет к этим астероидам того же порядка, что и к астероиду Фортуна.

Параметры экспедиции к астероиду Фортуна космического аппарата с электрической мощностью солнечных батарей в 14 Квт и датой старта в 2006 году представлены в табл.8. Приведены два варианта обратного перелета к Земле с большой тягой. Один – со стартом от Фортуны в 2010 году, с импульсом большой тяги DV= 4.6 км/с и общей продолжительностью экспедиции Т_Э = 5 лет. Второй – со стартом от Фортуны в 2011 году, с DV= 3.5 км/с и Т_Э = 6.12 лет. Рассмотрены две программы ступенчатой малой тяги. Первая – со скоростью истечения струи V_C = 25 км/с. Вторая – с двумя уровнями скорости истечения струи в 25 и 48.3 км/с, дает большее значение полезной массы, но она предполагает использование двух типов электроракетных движителей – российского СПД и немецкого RIT-XX, и могла бы быть предложена для совместного Российско-Европейского проекта.

Таблица 7.

Таблица 8.

Заключение

Использование гравитационного маневра в сфере действия Марса или солнечных батарей большой электрической мощности » 14 Квт позволит осуществить экспедиции (с доставкой на Землю образца грунта) ко многим астероидам Главного пояса с помощью космической системы, разрабатываемой в настоящее время в рамках пректа «Фобос-Грунт».

Приложение.      Оптимизация  перелетов  Земля-Марс-астероид  с гравитационным маневром в сфере действия Марса.

Схема полета.

Сферы действия Земли и Марса считаем точечными «извне», то есть их размерами пренебрегаем при расчетах межпланетных участков, а «изнутри» – бесконечными, то есть оценки скорости выхода из сферы действия делаем для расстояния r = ¥ . Предполагается, что из сферы действия Земли КА выводится с помощью традиционного двигателя большой тяги, и имеет в начале межпланетного перелета гиперболический избыток скорости V_¥ = 1.75 км /с при начальной массе КА m _Н = 1.947 т. Гравитационным влиянием астероида пренебрегаем.

В результате имеем следующие терминальные условия для траектории: 1) в начальный момент времени t = t _З :

 = _З,   = _З + V_¥× _¥,

где _З, _З – радиус-вектор и вектор скорости Земли; величина V_¥ задана, а ее направление _¥ должно быть выбрано оптимальным образом;

2) в конечный момент времени t = t _А:

 = _А,   = _А,

где _А, _А – радиус-вектор и вектор скорости астероида; это есть условие сопровождения астероида.

В схеме полета с гравитационным маневром добавляются условия оптимального пролета сферы действия Марса в момент времени t = t _М. Выведем эти условия.

Рис.3.

                                                                Рис.4.

Рис.5.

Гравитационный поворот.

Будем исходить из того, что в сфере действия Марса большая тяга не используется. Далее, поскольку пролет сферы действия Марса происходит относительно быстро, то влиянием малой тяги на этом участке можно пренебречь. Будем считать, что малая тяга равна нулю и, следовательно, движение происходит по гиперболической траектории (см. рис. 3). Марсоцентрическая скорость входа в сферу действия равна

_ВХ = ^– – _М ,

где _М и ^– – соответственно скорость Марса и скорость подлета КА к сфере действия – в гелиоцентрической системе координат. Марсоцентрическая скорость выхода по величине равна скорости входа: V_ВЫХ = V_ВХ, гелиоцентрическая скорость КА после прохождения сферы действия:

⁺ = _ВЫХ  + _М .

Угол поворота g зависит как от скорости входа V_ВХ , так и от параметра q (рис. 3), который ограничен снизу:

q ³ q _min .

Фокальный параметр p гиперболы, ее большая полуось a, эксцентриситет e и постоянная энергии h связаны соотношениями

p = a× ( e² – 1 ) ,  h = m_M / a ,

в которых m_M – гравитационный параметр Марса. Из этих формул и интеграла энергии

V² – 2×m_M / r = h

имеем при r  =  ¥ :

a  =  m_M / h  =  m_M / V_¥²  =  m_M / V_ВХ² .

Используя формулу для расстояния

r  =   ,

при q = 0 получим параметр

q = r _min =  = a× = a×( e – 1 ) = ( e – 1 )×m_M / V_ВХ² ,

а полагая в ней  r  =  ¥ , получим условие  1 + e×cosq  =  0  для максимального угла q. С учетом  g + p = 2q (см. рис. 4) для угла g получаем

sin (g/2) = sin (q – p/2) = – sin ( p/2 – q ) = – cos q  = 1 / e ,

g = 2× arcsin (1/e) = 2× arcsin () .                              (1)

Отметим, что в плоском случае КА может пролететь также по симметрично расположенной относительно притягивающего центра гиперболе (рис. 3), поэтому  угол g может быть как положительным, так и отрицательным.

В пространственном случае множество векторов _ВЫХ  образует конус (рис. 5), для описания которого введем дополнительный угол w . Проектируя вектор _ВЫХ  на тройку ортов { _v , _n , _b }, связанную с вектором _ВХ  и плоскостью { _ВХ ,  } формулами

_v = _ВХ / V_ВХ , _n =  , _b = _n ´ _n ,

получим

_ВЫХ  =  V_ВХ × ( _v × cos g  + _n × sin g × sin w + _b × sin g × cos w ),

или

⁺ = _М + V_ВХ × ( _v × cos g  + _n × sin g × sin w + _b × sin g × cos w ),     (2)

Углы g, w должны быть выбраны оптимальным образом.

Уравнения движения.

 = ;    =   +  ;   =  – β  .

Здесь , , m –  радиус-вектор, вектор скорости и масса КА;

 = – m_С / R³

–  гравитационное ускорение Солнца;

 =  P× / m

– вектор ускорения малой тяги; P, –  величина и направление тяги; тяга P и секундный расход массы β связаны со скоростью струи V_C и мощностью в струе N_C соотношениями

P = β ×V_C ;  N_C = β ×V_C² / 2 .

Для солнечных батарей мощность в струе N_C зависит от электрической мощности батарей N_Э (на расстоянии одной астрономической единицы I  » R _З ) и от расстояния КА до Солнца R. Используем приближенную формулу

N_C =  k× N_Э / ( R / I ) ^S ,

где k = const –  к.п.д. двигательной установки, показатель степени s » 2 (в расчетах принято k = 0.5, s = 1.7).

Обозначая через w º 1/ V_C величину, обратную скорости истечения струи, а через N º 2× k× N_Э / a ^S , получим уравнения движения в виде

 = ;    =   + Nw × / (m ×R ^S ) ;  =  – Nw² / R ^S .                 (3)

Обозначая через

 = {, , m }

вектор фазовых переменных, через

 = { , N ,w }

вектор управления, через

(, )

правые части уравнений (3), а через

G( , g, w )

– правую часть формулы (2), получим задачу максимизации функционала

L₀ = m_A

при дифференциальных связях

  = (, ),

фазовом ограничении

q ³ q _min                                                     (4)

при пролете сферы действия Марса,

терминальных условиях:

1) в начальный момент времени t = t _З :

 = _З,   = _З + V_¥ × _¥,

2) в конечный момент времени t = t _А:

 = _А, 

3) в момент пролета сферы действия Марса t = t _М:

^– = _М,  ⁺ = _М,   ⁺ = G( , g, w ),                     (5)

и ограничениях на управляющие функции:

 Î U,

где U:

0 ≤ N ≤ N_max,

w > 0 – для модели идеальной малой тяги,

w Î { w₁} или w Î { w₁, w₂ }, ( все w_i > 0 ) – для модели ступенчатой тяги;

на направление тяги  никаких ограничений не накладывается.

Условия оптимального движения

Для определения оптимальных программ управляющих функций и значений параметров сформируем Лагранжиан задачи L. Обозначим через  вектор сопряженных переменных:

 =  {_R, _V,  l_m }  .

L = l₀×m_A +  (– , ) dt + (– , ) dt  ®  max,

где l₀ > 0.

Проварьируем Лагранжиан в предположении, что все три момента времени фиксированы:

dL = l₀×dm_A + (d– d, ) dt + (d– d, ) dt .

Используя формулу интегрирования по частям:

( – d, ) dt = ( – (d)dt, ) = ( – d (d), ) =

= (d, )  + (d, ) dt ,

получим:

dL = l₀×dm_A + (d, )   + (d, )  +

+ (d_u, ) dt + (()^*× + , d) dt.

Из условия максимума Лагранжиана

dL = 0

( в более общем виде dL £ 0 ) получим дифференциальные уравнения для сопряженных переменных

 = – ()^*×,

или, в развернутом виде:

 _R = – _V + ( (, _V) – l_m×w );   _V = –_R;  _m = (, _V) . (6)

Рассмотрим различные группы слагаемых, которые входят в первые три члена в выражении для dL. Объединяя слагаемые с одинаковыми значениями вариаций, получим терминальные условия и условия стыковки для сопряженных переменных.

1.                 (l_m, dm)ú – (l_m, dm)   + (l_m, dm)  – (l_m, dm) + l₀×dm_A ;

учитывая, что dm ( t_З ) = 0, а dm ( t_M + 0) = dm ( t_M – 0) (как указывалось выше, мы исходим из того, что сферу действия Марса КА проходит с нулевой тягой), получим

l_m ( t_M + 0) = l_m ( t_M – 0),  l_m ( t_A ) = l₀ > 0;  l_m ( t_З )  – ",            (7)

(т.е. l_m ( t_З )  – произвольно).

2.                 (_R, d)ú – (_R, d)   + (_R, d)  – (_R, d) ;

поскольку все радиус-векторы фиксированы, то

d( t_З ) = d( t_M – 0) = d( t_M + 0) = d( t_A ) = 0

(здесь имеется в виду, что равны нулю все три компоненты векторов d), и, следовательно,

_R ( t_З ), _R ( t_M – 0), _R ( t_M + 0), _R ( t_A )   – ".

Аналогичным образом получим терминальные условия для _V.

3.                 (_V, d)ú – (_V, d)   + (_V, d)  – (_V, d) .

В конечный момент времени                   _V ( t_A )   – ",

поскольку d( t_A ) = 0.

В начальный момент времени

d = V_¥ × d_¥ .

Условие (_V, V_¥ × d_¥ ) = 0 есть условие максимума по _¥ выражения

(_V, V_¥ × _¥ ) .

Максимум достигается, когда единичный вектор _¥ параллелен вектору _V, т.е. _¥ = _V /ú _Vú .                                                (8)

Оптимальный пролет сферы действия Марса.

При пролете сферы действия Марса

d⁺ = d^– + dg + dw .

Вариация dg зависит от того, является ли g: а) независимой переменной, или б) она связана условием q º q _min . Рассмотрим первый случай.

Этот случай имеет место либо когда ограничение q ³ q _min вообще не накладывается, либо оно оказывается несущественным. В этом случае вариации  d^–, dg и dw являются независимыми.

Полагая d^– = 0 и dg = 0, получим условие оптимальности параметра w в виде

(_V ⁺ , ) = 0 ,

которое фактически означает требование

( _V ⁺ , G ) .

В предположении sin g > 0 оно сведется к

( sin w × (_V ⁺, _n ) + cos w × (_V ⁺, _b ) ) .

Последнее выражение достигает максимума, когда вектор < sin w , cos w > параллелен вектору < (_V ⁺, _n ) , (_V ⁺, _b ) >, т.е. при

sin w = (_V ⁺, _n ) ¤ l_w ,  cos w = (_V ⁺, _b ) ¤ l_w ,           (9)

где через l_w обозначено

l_w  = ( (_V ⁺, _n )² + (_V ⁺, _n ) ² )^0.5 .

Аналогичным образом, полагая d^– = 0 и dw = 0, получим условие оптимальности параметра g в виде

(_V ⁺ , ) = 0 ,

или

( _V ⁺ , G ) ,

т.е.

 ( sin g ×l_w + cos g × (_V ⁺, _v ) ) .

Þ      sin g = l_w ¤ l_g ,  cos g = (_V ⁺, _v ) ¤ l_g ,                   (10)

где через l_g обозначено

l_g  = ( l_w² + (_V ⁺, _v )² )^0.5 .

Отметим, что полученные значения (w, g) доставляют ( _V ⁺ , G ),  по­скольку sin g ³ 0. Если предположить sin g < 0, то получим другое решение (w,g), которому соответствует движение по симметричной относительно гравитационного центра гиперболе, причем сама гипербола будет повернута на 180⁰ по углу w, так что фактически будет реализовано то же самое прохождение сферы действия Марса, что и в первом случае.

Наконец, полагая dg = 0, dw = 0, получим условие скачка для _V :

_V ^–  = (_V ⁺ , ) ,                                            (11)

или

_V ^–  = _V ⁺ cos g + sin g sin w [ (_V ⁺, _n ) _v + V_ВХ ×(_М ×_V ⁺) / d] +

+ [ sin g sin w V_ВХ ×(_V ⁺, _n ) + sin g cos w V_ВХ ×(_V ⁺, _b )] ×

×[ (^–,_ВХ ) × (^– + _ВХ) – ^–×V_ВХ² – _ВХ×(^–)²] / d² +

+ [ _V ⁺ (V_ВХ² – (^–,_ВХ) ) + 2(_V ⁺,^– ) ×_ВХ  – (_V ⁺,_ВХ ) × (^– + ×_ВХ) ]×

×sin g cos w / d ,                                              (12)

где обозначено d = |_ВХ ×^–| – модуль векторного произведения.

Рассмотрим второй случай – когда g не может рассматриваться в качестве независимой переменной, поскольку связана условием q º q _min, и зависит от ^–.

В этом случае в условии скачка для _V появляются дополнительные слагаемые:

_V ^–  = _V ⁺ cos g + sin g sin w [ (_V ⁺, _n ) _v + V_ВХ ×(_М ×_V ⁺) / d] +

+ [ sin g sin w V_ВХ ×(_V ⁺, _n ) + sin g cos w V_ВХ ×(_V ⁺, _b )] ×

×[ (^–,_ВХ ) × (^– + _ВХ) – ^–×V_ВХ² – _ВХ×(^–)²] / d² +

+ [ _V ⁺ (V_ВХ² – (^–,_ВХ) ) + 2(_V ⁺,^– ) ×_ВХ  – (_V ⁺,_ВХ ) × (^– + ×_ВХ) ]×

×sin g cos w / d +                                            (12’)

+ [ cos g ×_ВХ×( sin w ×(_V ⁺, _n ) + cos w ×(_V ⁺, _b ) ) –  sin g (_V ⁺,_ВХ)] × ,

где из (1):                      = – sin( g/2 ) ×tg( g/2 ) ×4q_min×V_ВХ/m_M .

Оптимальное управление.

В результате условие максимума лагранжиана сводится к

dL = (d_u, ) dt = 0 ( £0 ),

которое фактически есть хорошо знакомое условие максимума гамильтониана

H º (, )  max ,

или

N [ (,_V) ×w/m – l_m×w² ] ® max .                               (13)

Сначала рассмотрим случай |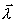_V | ¹ 0.

Из (13) следует, что оптимальное направление тяги должно быть параллельно вектору 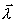_V :

 = _V / |_V | .                                                    (14)

Оптимальные значения N, w для модели ступенчатой малой тяги определяются непосредственно из условия (13).

Для модели идеальной малой тяги необходимо выяснить, каков знак величины l_m, и как она изменяется на траектории. На правом конце l_m( t_A ) = l₀ > 0 (7), и, соответственно, оптимальное w :

w = |_V | / (2m×l_m)                                               (15)

(если только |_V | ¹ 0).

Из уравнений оптимального движения имеем:

(m²×l_m) = 2m×l_m×m + m²×l_m =

= – 2m×l_m×Nw² / R ^S + m²×(, _V) = 0.                          (16)

Отсюда следует, что во все время движения величина l_m остается положительной, а потому формула (15) верна на всей траектории, где |_V | ¹ 0. Тогда в (13)

[ (,_V) ×w/m – l_m×w² ] = |_V |² / (4m×l_m) > 0 .

При этом оптимальное N :

N = N_max .                                                   (17)

Если в какой-либо момент станет |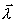_V | = 0, и, значит 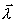_V = 0, то, поскольку w > 0, из

N [ – l_m×w² ] ® max

следует                                            N = 0 .

Причем |_V | = 0 возможно лишь в отдельных точках траектории, в которых _R ¹ 0. Если одновременно _V = 0 и _R = 0 в какой-либо точке траектории, то, как следует из уравнений движения, тождественно будет выполняться _V º 0, _R º 0, N º 0 на всем отрезке непрерывности вектора _V. Это случай движения без малой тяги, который если и возможен, то лишь для отдельных наборов значений параметров { t _З , t _M , t _A }, т.е. при особом расположении планет (в дальнейшем такие случаи рассматривать не будем).

Отметим, что с точки зрения простоты математической модели удобно расширить множество значений w, добавив к ним нулевое значение. Т.е. в случае идеальной тяги считать w ³ 0, а в случае ступенчатой вместо w Î { w₁} или w Î { w₁, w₂ } соответственно w Î { 0, w₁ } или w Î { 0, w₁, w₂ }. Тогда можно положить N º N_max . Пассивному полету будет соответствовать N = N_max, w = 0.

Задача оптимизации.

Задачу оптимизации  будем решать в два этапа.

Сначала, с использованием модели идеальной малой тяги, рассмотрим задачу оптимизации перелетов Земля – Марс – астероид в целом, а затем, используя модель ступенчатой тяги, уточним параметры траектории для конкретного перелета.

Основную оптимизационную задачу разделим на две: внутреннюю – решение краевой задачи для заданных значений параметров { t _З , t _M , t _A }, и внешнюю – поиск оптимальных значений этих параметров. Организовать итерационный поиск оптимальных параметров возможно только в тех областях пространства параметров, в которых существует решение краевой задачи. Для модели ступенчатой тяги это очень затруднительно, поскольку из-за ограниченности ступенчатой тяги такие области, если и существуют (для конкретного астероида), то очень ограниченны. А для большинства астероидов Главного пояса их просто не существует. В отличие от ступенчатой тяги идеальная малая тяга – неограниченна, и поэтому решение, в принципе, должно существовать для любых наборов параметров { t _З , t _M , t _A }. Хотя, конечно, и в этом случае решение краевой задачи представляет немалые трудности, и практически ее удается решать только в случае «удачного» взаимного расположения трех планет, и при наличии «хорошего» начального приближения для краевой задачи – обычно какого-либо уже найденного решения для астероида с близкими значениями параметров орбиты.

Краевая задача.

Для идеальной малой тяги уравнения движения (3), (6) с учетом (14), (15), (17) приводятся к виду:

 = ;    =   + N_max×_V / (2m² ×l_m ×R ^S) ;  =  – N_max×|_V|² /(4m² ×l_m²×R ^S);

_R = – _V + N_max×|_V|² /(4m²×l_m); _V = –_R; _m = N_max×|_V|² /(2m³ ×l_m×R ^S).

Эту систему можно упростить, если учесть, что m²×l_m = const (16), и что сопряженные переменные определены с точностью до произвольного положительного множителя, который можно выбрать так, чтобы выполнялось условие m²×l_m = N_max/2. В результате система уравнений преобразуется к виду:

 = ;   =  + _V / R ^S ;   _R = – _V + ×s×|_V|² /(2R^S+2);   _V = –_R ;   (18)

 =  – |_V|² ×m² /(N_max×R^S) .                                           (19)

Таким образом, мы получили хорошо известное для модели идеальной малой тяги разделение оптимизационной задачи на траекторную и массовую, что позволяет понизить размерность краевой задачи. При ее формировании будем рассматривать только уравнения (18) (без уравнения (19) для массы m).

Краевая задача в рассматриваемом случае является трехточечной, и может быть сформирована различными способами. Причем обычный вариант, при котором траектория интегрируется от начала и до конца с требованием обеспечить выполнение условий в моменты времени t _M , t _A , неудобен тем, что малые вариации переменных в начальный момент времени из-за наличия гравитационного маневра приводят к очень большим вариациям в конечный момент времени.

Менее капризная краевая задача получается, если разбить траекторию полета на два участка: перелет от Земли к Марсу, и перелет «в обратном времени» от астероида к Марсу, со сшивкой их на сфере действия (рис. 6). Тем более, что в конечный момент времени t_A полностью определены фазовые переменные ,, а опыт решения двухточечной краевой задачи [4] позволяет получить приемлемое начальное приближение для организации итерационного процесса решения трехточечной краевой задачи.

Итак, необходимо найти значения 12 сопряженных переменных

_R (t_З), _V (t_З), и _R (t_M), _V (t_M),

которые при

(t_З) = _З,  (t_З) = _З + V_¥ × _V /ú _Vú , (t_A) = _A,  (t_A) = _A

обеспечили ли бы выполнение условий (5,11):

^– = _М,  ⁺ = _М,   ⁺ = G( , g, w ),  _V ^–  = (_V ⁺ , ) ,

где w удовлетворяет (9).

Остается только определиться с g и ограничением (4). Отметим, что для конкретных значений параметров { t _З , t _M , t _A } это ограничение может быть несущественным. Поэтому после интегрирования обеих частей траектории необходимо определить два значения угла g: одно – из условия (1) с q=q_max, второе – из (10), и использовать меньшее значение в формулах (1) и (11). Соответственно выбрать (12) или (12’) для сопряжения _V ^–  и _V ⁺ .

Поскольку мы рассматриваем оптимизационную задачу шире – варьируем также параметры { t _З , t _M , t _A }, логично предположить, что в таком случае оптимальное решение должно в максимальной степени использовать возможности гравитационного маневра. А т.к. гравитационное поле Марса относительно слабое, то почти наверняка оптимальная траектория выйдет на ограничение (4). Раз так, можно ограничиться выбором g из (1), тем самым упростив вычислительный процесс. И лишь после нахождения «оптимального решения» осуществлять проверку того, действительно ли для него выполнено условие оптимальности по g.

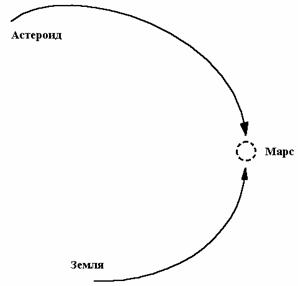Рис. 6.

Полеты к астероидам и кометам с идеально регулируемой малой тягой.

Оценка достижимости при различной мощности солнечных батарей.

Известно, что в случае идеально регулируемой малой тяги (МТ) с постоянной мощностью N_C [6] возможен пересчет массовых характеристик полета КА с МТ на другие параметры аппарата и энергетической установки. По известной величине затрат J*, его начальной массе M₀ и эффективной мощности энергоустановки «в струе» N_C величина M_K в конце полета вычисляется по формуле

M_K = M_O / (1+n),  n = J* M_O /2 N_C , M_П = M_K – M_Б – M_БЛ ,            (20)

где M_PT – масса затрат рабочего тела на полет, M_Б – масса баков, M_БЛ – масса блока с ЭРД вместе с СБ. Используя это свойство полетов КА с МТ, удается получить оценки для возможностей полетов к астероидам с центральной части Главного пояса. Для досчетов были взяты полеты КА с МТ и СБ к ряду астеро­идов [9] с разнообразными параметрами орбит, представленными в табл. 9.

             Таблица 9. Характеристики орбит целей полета.

Параметры КА с МТ при досчете принимались близкими к параметрам КА, разрабатываемого в рамках проекта «Фобос-Грунт»: масса в начале межпланет­ной траектории M₀ = 2000 кг при V_¥ = 1 км/с (1800 кг при V_¥  = 3 км/с), M_БЛ = 320 кг, M_Б = 0.2 M_PT . Рассмотрены варианты мощности СБ – эффективной «в струе» N_C = 5,7,10 Квт при электрической N_Э = 10, 14, 20 Квт, – в полтора, два и три раза выше, чем стандартная мощность КА в проекте «Фобос-Грунт». Результаты расчетов собраны в таблице 10.