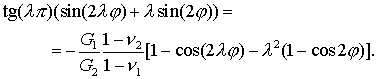Численное моделирование процесса деформации
элементов электродинамического ускорителя в двумерном случае
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
в якоре: |
в рельсе: |
В уравнениях учтена сила инерции. Конфигурация пространственной области и краевые
условия сохраняются.
Далее мы часто будем рассматривать уравнения , , с помощью т.н. смешанного
эйлерово - лагранжева подхода [3] в локальных перемещениях точек подвижного
объема, движущегося со скоростью якоря ![]() . При этом производная по времени величины
. При этом производная по времени величины ![]() равна
равна
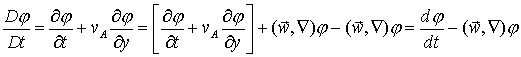 .
.
Переход к квазистационарному приближению
В качестве начального приближения в данной работе будем далее использовать квазистационарное приближение уравнений термоупругости, то есть откажемся от использования в модели всей левой части уравнений движения в рельсе (производные по времени и конвективные слагаемые), а, следовательно, и в якоре. Аналогично и в уравнениях , .
Это возможно по следующим причинам. Время движения якоря в установке
составляет примерно ![]() , скорость продольной (звуковой) упругой волны, например, для
алюминия
, скорость продольной (звуковой) упругой волны, например, для
алюминия ![]() . Тогда время её пробега характерного для рассматриваемой
области расстояния (
. Тогда время её пробега характерного для рассматриваемой
области расстояния (![]() ) составляет
) составляет ![]() . Таким образом, волна успевает за время движения якоря
отразиться порядка 300 раз. При этом влияющие на поле перемещений параметры
системы (температура, сила Лоренца и др.) незначительно изменяются даже за
несколько
. Таким образом, волна успевает за время движения якоря
отразиться порядка 300 раз. При этом влияющие на поле перемещений параметры
системы (температура, сила Лоренца и др.) незначительно изменяются даже за
несколько ![]() . Поэтому на каждом временном слое процессы, связанные с
деформацией, можно считать установившимися.
. Поэтому на каждом временном слое процессы, связанные с
деформацией, можно считать установившимися.
Данное приближение достаточно часто используется при решении задач рассматриваемого класса – см. [14, 15].
Условия на контакте
В [11] получены соотношения в точках поверхности разрыва, которые являются следствием балансовых соотношений, записанных для этой области в интегральной формулировке. В нашем случае имеет место тангенциальный разрыв, так как материалы якоря и рельса друг в друга не проникают.
В результате в точках контакта имеем условия:
При скольжении с трением из третьего закона Ньютона для касательных напряжений в зоне контакта получим
Проинтегрировав второе уравнение по якорю и применив теорему
Остроградского-Гаусса [12], получим формулу для вычисления ускорения ![]() и скорости якоря:
и скорости якоря:
3. Алгоритм решения
Дискретизация пространственной области
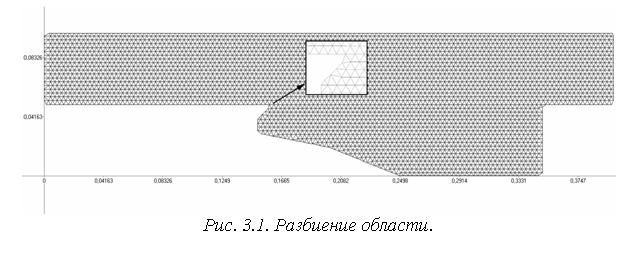
Для дискретизации
пространственной области будем использовать треугольную сетку (рис 3.1). Она
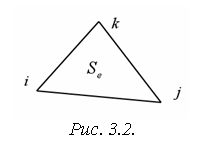
построена так, чтобы любой треугольник (рис. 3.2) содержал только один
материал. В результате разбиения получим ![]() узлов и
узлов и ![]() треугольников [16].
треугольников [16].
Конечномерная аппроксимация задачи
Введем систему функций:
![]() – кусочно-линейные функции, равные 1 в
– кусочно-линейные функции, равные 1 в ![]() -й вершине треугольника (рис. 3.2) и 0 во всех остальных и
называемые функциями формы [4, 5].
-й вершине треугольника (рис. 3.2) и 0 во всех остальных и
называемые функциями формы [4, 5].
В литературе [4] для функции ![]() обычно используют
представление:
обычно используют
представление:
![]() ,
,
где ![]() – площадь треугольника
– площадь треугольника
![]() (рис. 3.2).
(рис. 3.2).
Введем аппроксимацию функции ![]() , определенной в области
, определенной в области ![]() :
:
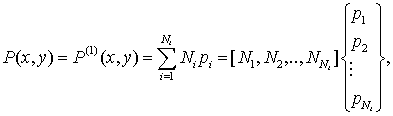
где ![]() – значения
– значения ![]() в i-м узле сетки.
в i-м узле сетки.
На отдельном элементе можно определить «локальную» аппроксимацию
скалярной функции ![]() :
:
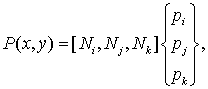
где ![]() – номера узлов
элемента.
– номера узлов
элемента.
В соответствии с введенными обозначениями вектор перемещений ![]() представим на элементе
в виде:
представим на элементе
в виде:
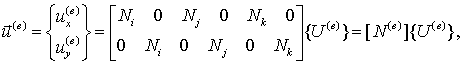
где ![]() , нечетные номера соответствуют значениям компонент
, нечетные номера соответствуют значениям компонент ![]() в узлах с
соответствующими индексами, четные –
в узлах с
соответствующими индексами, четные – ![]() .
.
Подставляя представление в соотношения для ![]() , получим формулу для
, получим формулу для ![]() на элементе [4] через
матрицу градиентов
на элементе [4] через
матрицу градиентов ![]() :
:
Подставив выражение в , получим формулу для вычисления узловых компонент тензора напряжений:
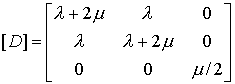
– матрица упругих характеристик материала ячейки.
Аппроксимация правой части уравнений движения
Запишем решаемую задачу , в виде
где
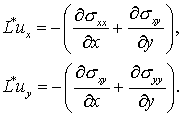
Применим метод Галеркина-Бубнова к уравнению , умножив скалярно обе его части на функцию формы. В результате получим
где ![]() ,
,
Используем далее для треугольника (рис. 3.2) формулу интегрирования по частям и теорему Остроградского-Гаусса. Например,
Члены вида ![]() в этих выкладках
сокращаются или равны нулю: 1. при суммировании по всей области, так как для
смежных треугольников обход контура осуществляется в противоположных
направлениях при равенстве подынтегральных функций; 2. вследствие заделки , так как соответствующие
строки в матрице заменяются главными граничными условиями; 3. из-за свободной
от напряжений границы и равенства нулю на границе
функции формы или соответствующей компоненты нормали.
в этих выкладках
сокращаются или равны нулю: 1. при суммировании по всей области, так как для
смежных треугольников обход контура осуществляется в противоположных
направлениях при равенстве подынтегральных функций; 2. вследствие заделки , так как соответствующие
строки в матрице заменяются главными граничными условиями; 3. из-за свободной
от напряжений границы и равенства нулю на границе
функции формы или соответствующей компоненты нормали.
Вследствие граничных условий на линии симметрии ![]() выполнено:
выполнено:
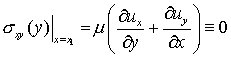 .
.
Выражение для 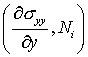 аналогично . Член
аналогично . Член ![]() на части контура,
совпадающей с линией симметрии, равен нулю, так как для неё
на части контура,
совпадающей с линией симметрии, равен нулю, так как для неё ![]() .
.
Применяя полученные выше соотношения и введенные обозначения,
получим выражение для вклада величины ![]() [4] на элементе в
матрицу системы:
[4] на элементе в
матрицу системы:
Для случая плоских деформаций [10] получаем
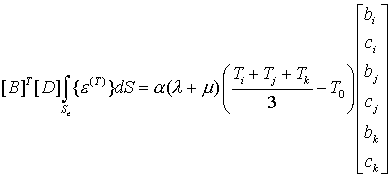 .
.
Интеграл от объёмных сил в вычисляется следующим образом [4]:
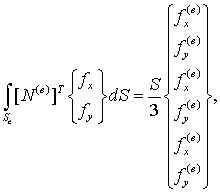
где ![]() – средние значения
компонент объёмных сил на элементе
– средние значения
компонент объёмных сил на элементе ![]() .
.
Моделирование контакта
Подробный обзор способов решения контактных задач теории упругости, поиска формы контакта приведен в работе [17].
Особенностью решаемой задачи является наличие контактного разрыва
искомого решения на линии разрыва скорости движения – контакте якоря и рельса
[3, 11]. Для его описания необходимо запасти два различных значения скорости
для узлов на контакте. Поэтому при разбиении области линия контакта содержит
пары узлов сетки, координаты которых совпадают, но один из них относится к
элементу рельса (![]() ), другой – к элементу якоря (
), другой – к элементу якоря (![]() ).
).
На граничные узлы накладываются кинематические условия
непроникновения и статические условия , . Компоненты ![]() неизвестны на границе
и требуют доопределения, для
неизвестны на границе
и требуют доопределения, для ![]() – это выражения , задающие скольжение с
трением, для
– это выражения , задающие скольжение с
трением, для ![]() – условия на контакте .
– условия на контакте .
Криволинейные интегралы, возникающие при конечномерной аппроксимации уравнений вида на треугольниках со сторонами, попадающими на контакт, можно сократить, сложив попарно выражения из :
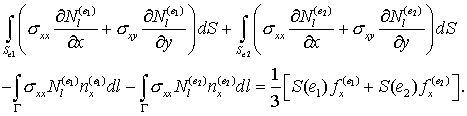
где ![]() – общая граница
контактирующих элементов
– общая граница
контактирующих элементов ![]() и
и ![]() , а
, а ![]() и
и ![]() – их площади. Так как
– их площади. Так как ![]() ,
, ![]() , то, следовательно, интегралы вида
, то, следовательно, интегралы вида ![]() сокращаются.
сокращаются.
Таким образом, для контактных узлов рельса вместо аппроксимации используется соотношение , а в соответствующих узлах
якоря используются контактные условия на перемещения ![]() :
:
![]()
где ![]() – узловые перемещения
– узловые перемещения ![]() в контактирующих узлах
в контактирующих узлах
![]() и
и ![]() рельса и якоря
соответственно.
рельса и якоря
соответственно.
При аппроксимации определяющих соотношений ![]() в контактных узлах
матрица системы формируется как обычно, а в правую часть дополнительно войдут
слагаемые, связанные с интегрированием по поверхности контакта силы трения. В
результате вектор правой части отличается на величину
в контактных узлах
матрица системы формируется как обычно, а в правую часть дополнительно войдут
слагаемые, связанные с интегрированием по поверхности контакта силы трения. В
результате вектор правой части отличается на величину 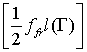 для строки с номером
для строки с номером ![]() , где
, где ![]() – номер узла на
контактной поверхности со стороны рельса, и на величину
– номер узла на
контактной поверхности со стороны рельса, и на величину 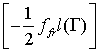 для строки с номером
для строки с номером ![]() , где
, где ![]() – номер узла на
контактной поверхности со стороны якоря,
– номер узла на
контактной поверхности со стороны якоря, ![]() – вычисленный на
данном элементе модуль силы трения.
– вычисленный на
данном элементе модуль силы трения.
Итерационный процесс
При численном решении полной системы алгебраических уравнений наличие трения, необходимость расчета скорости и ускорения якоря, участие упругих деформаций в энергетическом балансе системы требуют внедрения внешнего итерационного процесса, связанного с расчетом упругости.
Как это традиционно происходит [18], такой итерационный процесс устроен по блокам: электромагнитный, тепловой, кинематический (упругий). Процесс считался сошедшимся при выполнении условия:
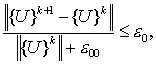
где ![]() ,
, ![]() – векторы, например,
узловых перемещений, вычисленные на
– векторы, например,
узловых перемещений, вычисленные на ![]() -ой и
-ой и ![]() -ой итерациях соответственно. В расчетах принято
-ой итерациях соответственно. В расчетах принято ![]() ,
, ![]() , а
, а ![]() – равномерная норма
вектора
– равномерная норма
вектора ![]() .
.
Вычисленный на новой итерации вектор узловых перемещений используется для расчета скорости якоря, узловых значений силы трения, её мощности и других величин, зависящих от перемещений. Далее вновь рассчитываются температура и напряженность магнитного поля до сходимости.
Вклад энергии деформации в уравнение энергии
Рассмотрим конечноэлементную аппроксимацию уравнения энергии. Оно содержит член, связанный с энергией деформации [13]. Такая модификация ведет в конечном итоге к добавлению в правую часть соответствующих линейных уравнений слагаемого, вычисляемого на каждом КЭ:
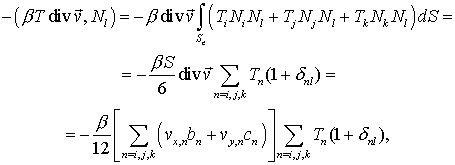
где ![]() – узловые
значения температуры и компонент скорости
на элементе соответственно,
– узловые
значения температуры и компонент скорости
на элементе соответственно, ![]() – номер
рассматриваемого узла (соответствует элементу вектора правой части системы).
Далее будем их брать с предыдущей внешней итерации или предыдущего временного
слоя.
– номер
рассматриваемого узла (соответствует элементу вектора правой части системы).
Далее будем их брать с предыдущей внешней итерации или предыдущего временного
слоя.
Умножим уравнения движения на скорость ![]() . В результате преобразований получим следующее выражение:
. В результате преобразований получим следующее выражение:
где ![]() – скорость работы
внешних сил [13].
– скорость работы
внешних сил [13].
После умножения скалярно на функцию формы ![]() получим:
получим:
Левая часть содержит слагаемое, связанное с температурной деформацией, которое после преобразований имеет тот же вид, что и выражение :
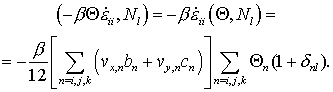
Это слагаемое обеспечивает связь уравнений движения и уравнения
теплопроводности, а также консервативность [18, 19] всего конечноэлементного
алгоритма.
4. Результаты расчётов
Разработанная программа тестировалась на известных
точных решениях, полученных путем подбора правой части под заданное решение.
Тесты показали относительную точность вектора смещения (в равномерной норме)
порядка ![]() на 2601-й точке сетки
и
на 2601-й точке сетки
и ![]() на 961-й.
на 961-й.
В качестве примеров ниже приведем результаты расчётов, проведённых для медного рельса и алюминиевого якоря.
Характерный размер
исследуемого участка рельса составляет около
Значения параметров
материалов, используемых в расчёте, приведены в таблице 4.2. В ней, в
частности, приведены значения плотности ![]() и предела текучести
материала
и предела текучести
материала ![]() .
.
Таблица 4.2. Параметры материалов
|
Параметр\Материал |
Алюминий |
Медь |
Сталь |
|
|
|
г/см3 |
2,54 |
8,93 |
7,80 |
|
|
ГПа |
80,3 |
74,7 |
115,4 |
|
|
ГПа |
25,4 |
45,8 |
77,0 |
|
|
ГПа |
70 |
120 |
200 |
|
|
Безразмер. |
0,31 |
0,38 |
0,30 |
|
|
|
20 |
17 |
14 |
|
|
|
4,2 |
4,1 |
5,4 |
|
|
МПа |
80 |
215 |
500 |
В работе проведены расчеты
для вариантов геометрии якоря, отличающихся величиной угла ![]() в месте стыка рельса и
якоря (
в месте стыка рельса и
якоря (![]() , рис. 2.2). Примеры параметров геометрии, разбиения области
и характеристики материалов подобластей [16] приведены в таблице 4.3.
, рис. 2.2). Примеры параметров геометрии, разбиения области
и характеристики материалов подобластей [16] приведены в таблице 4.3.
Таблица 4.3. Параметры областей.
|
Вариант |
|
|
|
Материал рельса |
Материал якоря |
|
V11 |
0,38 |
3716 |
6970 |
Медь |
Алюминий |
|
V29 |
0,62 |
3709 |
6958 |
Медь |
Алюминий |
|
V30 |
0,66 |
3676 |
6893 |
Медь |
Алюминий |
|
V31 |
0,25 |
3724 |
6982 |
Медь |
Алюминий |
Счёт прекращался при наступлении «кризиса» контакта [3], то есть резкого роста сопротивления контакта и потери эффективности ускорения (с точки зрения физики процесса). Одной из причин «кризиса» контакта является достижение температуры кипения [3, 20]. Скорость, при которой происходит вскипание, называют критической.
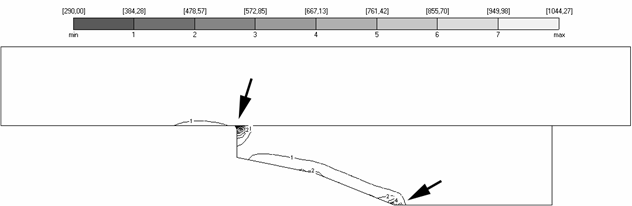
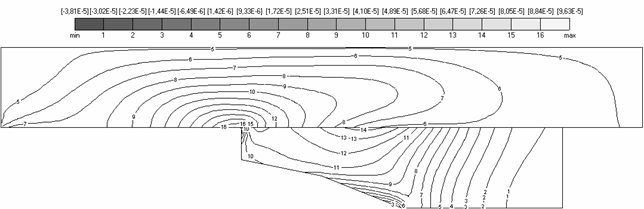
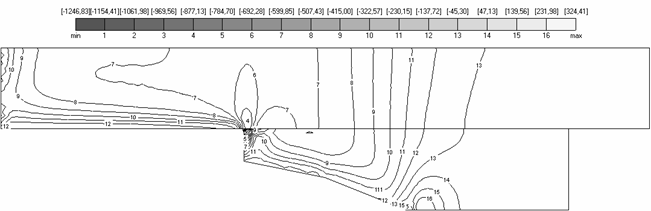
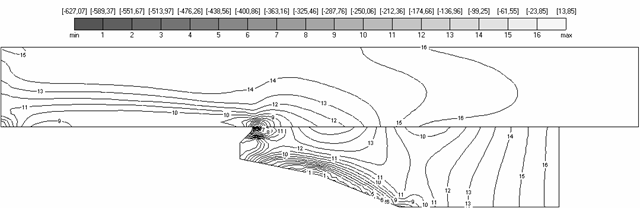
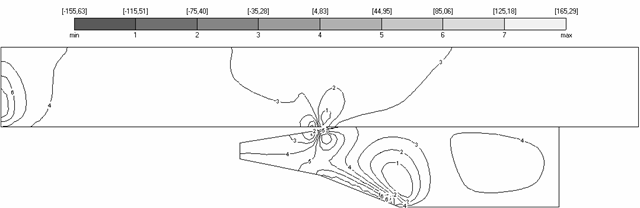
Углы областей, разные материалы рельса и якоря являются источником появления особенностей, которые проявляются в неограниченности значений исследуемых величин в окрестности угловых точек [3, 21]. Один из примеров подобной ситуации представлен на рис. 4.1, где в угловых точках температура возрастает на величину около 740 K, что приводит в дальнейшем к плавлению материала.
Стрелками на рис. 4.1
показаны зоны области рельса и якоря, а именно окрестности угловых точек якоря,
в которых решение имеет особенность. Как следствие этого, в данных окрестностях
имеет место резкое возрастание тепловых и силовых нагрузок. Здесь (рис. 4.1) и
далее на графиках построены линии уровня соответствующих полей (температура T на рис. 4.1),
промаркированные в соответствии с легендой в верхней части каждого рисунка.
Целое значение обозначает индекс линии уровня (например, линия уровня №1
соответствует значению ![]() ), кроме того, на легенде выведены минимальное (min) и максимальное (max) значения.
), кроме того, на легенде выведены минимальное (min) и максимальное (max) значения.
|
Временной слой M=100, расчёт V11 (табл. 4.2, 4.3) |
|
|
|
|
|
Рис. 4.1. Температурное поле. Расчет V11, M=100 |
Расчеты показали, что
максимумы плотности силы Лоренца ![]() также расположены в
окрестности угловых точек (показаны стрелками на рис. 4.1), в частности, в
угловой точке стыка рельса и якоря, то есть там, где ток втекает практически в
одну точку [3], вследствие чего его плотность резко возрастает.
также расположены в
окрестности угловых точек (показаны стрелками на рис. 4.1), в частности, в
угловой точке стыка рельса и якоря, то есть там, где ток втекает практически в
одну точку [3], вследствие чего его плотность резко возрастает.
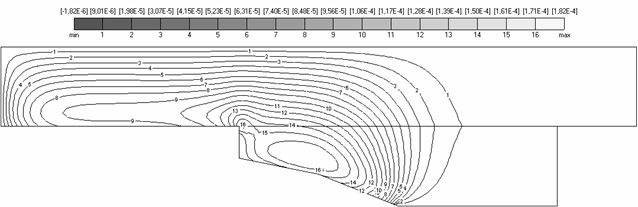
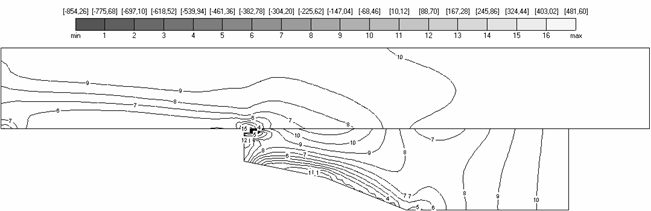
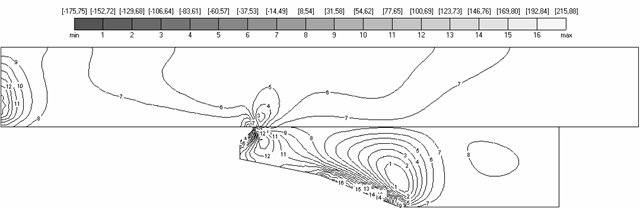
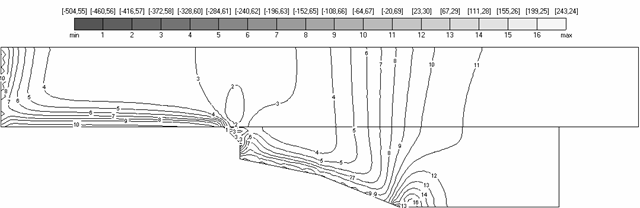
Рис. 4.2 (а,б), на которых
изображены поля компонент перемещений, свидетельствуют о выполнении главных
граничных условий , . В точках заделки ![]() (рис. 2.2) поле
перемещений имеет нулевые значения компонент, что определяется ближайшей к нулю
линией уровня №1 (
(рис. 2.2) поле
перемещений имеет нулевые значения компонент, что определяется ближайшей к нулю
линией уровня №1 (![]() ) на рис. 4.2(а), на рис. 4.2(б) – линией уровня №5 (
) на рис. 4.2(а), на рис. 4.2(б) – линией уровня №5 (![]() ).
).
Также выполнено второе
граничное условие на линии симметрии ![]() , так как соответствующие линии уровня (рис. 4.2, б)
ортогональны линии симметрии
, так как соответствующие линии уровня (рис. 4.2, б)
ортогональны линии симметрии ![]() (рис. 2.2).
(рис. 2.2).
Кроме того, поле перемещений (рис. 4.2) качественно соответствует представленному выше графику распределения температуры, то есть имеет максимумы вблизи угловых точек (рис. 4.1), а также вдоль линии контакта и левой кромки якоря.
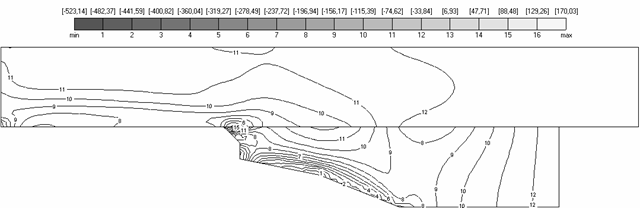
Рис. 4.2(б) свидетельствует
о том, что якорь постоянно находится в сжатом состоянии вдоль оси ![]() (линии уровня №1-4
соответствуют отрицательным значениям
(линии уровня №1-4
соответствуют отрицательным значениям ![]() , №5-16 – положительным). Это обусловлено тем, что вблизи
левой грани якоря
, №5-16 – положительным). Это обусловлено тем, что вблизи
левой грани якоря ![]() преимущественно
действует положительная сила Лоренца
преимущественно
действует положительная сила Лоренца ![]() , а в остальной части якоря – отрицательная сила инерции, так
как плотность силы Лоренца здесь близка к нулю ввиду отсутствия тока в данной
области.
, а в остальной части якоря – отрицательная сила инерции, так
как плотность силы Лоренца здесь близка к нулю ввиду отсутствия тока в данной
области.
Представленные на рис. 4.2
результаты качественно соответствуют условиям контактной задачи: в зоне
контакта перемещение ![]() является непрерывным в
контактных точках (рис. 4.2, а), так как это задано явно при аппроксимации
уравнений движения. При этом возможен слабый разрыв
является непрерывным в
контактных точках (рис. 4.2, а), так как это задано явно при аппроксимации
уравнений движения. При этом возможен слабый разрыв ![]() (линии уровня №1-3).
Перемещение
(линии уровня №1-3).
Перемещение ![]() терпит сильный разрыв
в точках контакта (рис. 4.2, б), так как действующие внешние силы испытывают
скачок при переходе через линию контакта на величину силы инерции. О
правильности вычисления силы инерции свидетельствует то, что локальные перемещения
точек якоря
терпит сильный разрыв
в точках контакта (рис. 4.2, б), так как действующие внешние силы испытывают
скачок при переходе через линию контакта на величину силы инерции. О
правильности вычисления силы инерции свидетельствует то, что локальные перемещения
точек якоря ![]() в среднем равны нулю
(рис. 4.2, б).
в среднем равны нулю
(рис. 4.2, б).
|
Временной слой M=100, расчёт V11 (табл. 4.2, 4.3) |
|
|
|
|
|
Рис. 4.2. Компонента |
|
Временной слой M=100, расчёт V11 (табл. 4.2, 4.3) |
|
|
|
|
|
Рис. 4.2. Компонента |
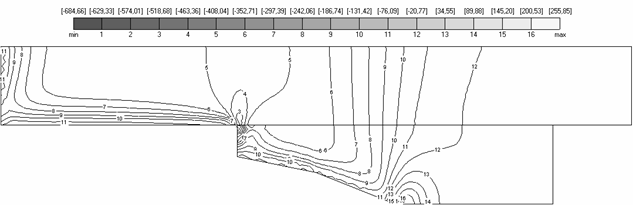
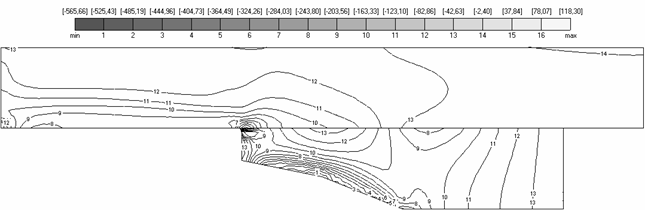
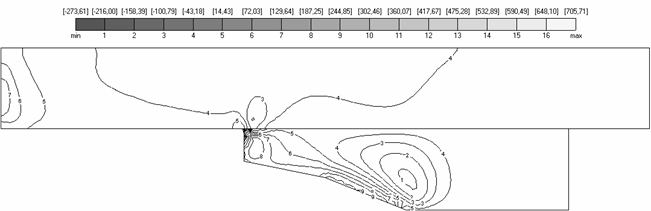
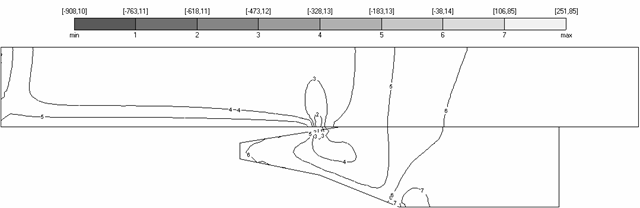
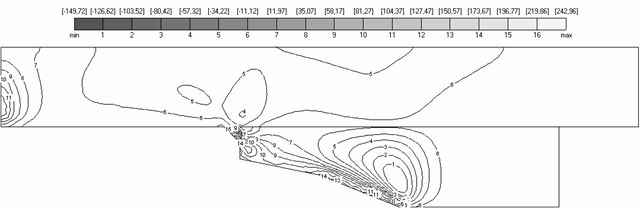
Аналогично рис. 4.3-4.4 свидетельствуют о выполнении естественных граничных условий , то есть значения соответствующих полей напряжений близки к нулю на свободной границе области. Нулевые значения находятся на рис. 4.3(а) между линиями уровня №12 и №13, на рис. 4.3(б) – вблизи линии уровня №14, на рис. 4.3(в) – между №6 и №7.
Рис. 4.3 (б) - 4.7 (б) также
свидетельствуют о сжатом состоянии якоря вдоль оси ![]() , так как
, так как ![]() во всей области якоря
[12].
во всей области якоря
[12].
|
Временной
слой M=100, расчёт V11 (табл. 4.2, 4.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.
4.3. Поля напряжений |
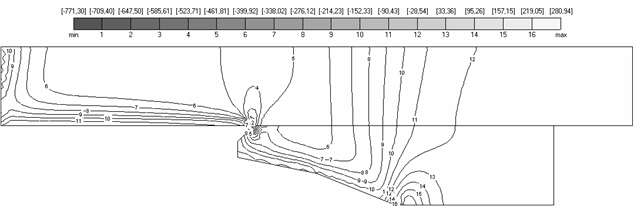
Также на рисунках можно
видеть выполнение условий контактной задачи. В частности, на рис. 4.4-4.7
видно, что поле ![]() непрерывно на
контакте, но не везде является гладким, то есть имеется слабый разрыв;
непрерывно на
контакте, но не везде является гладким, то есть имеется слабый разрыв; ![]() имеет близкое к нулю
значение (например, между линиями уровня №6 и №7 на рис. 4.3(в) и между линиями
уровня №4 и №5 на рис. 4.4(в)), что качественно соответствует использованному в
расчете нулевому коэффициенту трения
имеет близкое к нулю
значение (например, между линиями уровня №6 и №7 на рис. 4.3(в) и между линиями
уровня №4 и №5 на рис. 4.4(в)), что качественно соответствует использованному в
расчете нулевому коэффициенту трения ![]() . При этом
. При этом ![]() терпит сильный разрыв
при переходе через линию контакта, как и должно быть при касательном разрыве
(разрыв линий уровня на рис. 4.3(б)-4.7(б)).
терпит сильный разрыв
при переходе через линию контакта, как и должно быть при касательном разрыве
(разрыв линий уровня на рис. 4.3(б)-4.7(б)).
|
Временной слой M=290 (Конец счета), расчёт V11 (табл. 4.2, 4.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
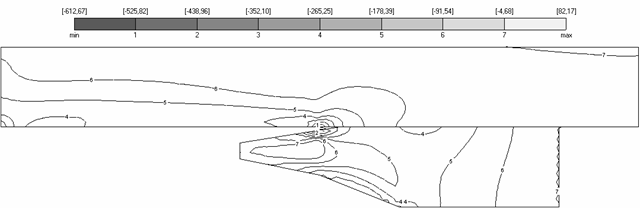
Рис.
4.4. Поля напряжений |
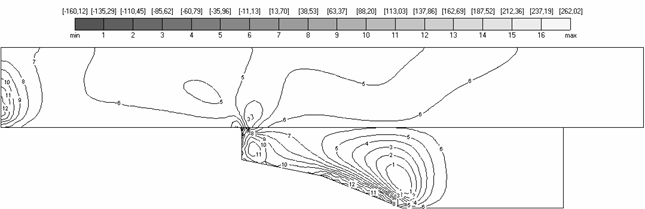
Для вариантов V29, V30, V31 характерные поля напряжений (временной слой M=100) показаны на рис. 4.5-4.7.
Анализ вычисленных полей
напряжений позволяет сделать следующие выводы. В соответствии с проведенными
расчетами якорь, имеющий представленные геометрические конфигурации, еще до
достижения критической скорости (примерно временной слой ![]() ) практически полностью разрушается, так как условие
) практически полностью разрушается, так как условие ![]() (см. табл. 4.2 и рис.
4.5-4.7) выполняется в значительной части якоря и рельса, а не только локально
в угловых точках, где сконцентрированы основные виды воздействий (температура и
сила Лоренца).
(см. табл. 4.2 и рис.
4.5-4.7) выполняется в значительной части якоря и рельса, а не только локально
в угловых точках, где сконцентрированы основные виды воздействий (температура и
сила Лоренца).
Полученные результаты свидетельствуют о том, что применение изотропных однородных материалов при конструировании ускорителей нередко ведет к разрушению рельса и якоря, что вызвано характером течения тока. Можно предположить, что применение анизотропных и слоистых материалов с улучшенными электрофизическими свойствами [20] позволит повысить прочностные характеристики устройства и значительно повысить величину критической скорости. Кроме того, представленные в работе геометрические конфигурации не являются оптимальными.
Отметим, что в данной работе не использовалась адаптивная сетка (см. рис. 3.1), сгущающаяся в зонах особенностей и резкого изменения исследуемых величин: вблизи областей с высокой концентрацией тепловых и силовых нагрузок, а также в точках свободной границы, близких к точкам заделки, то есть в точках, где упругие напряжения резко возрастают по модулю. Это вызвало связанную с усреднением вычисленных значений потерю точности при вычислении полей напряжений в окрестностях особых точек. При этом вычисленные значения компонент тензора напряжений являются усредненными внутри соответствующих элементов сетки (см. выражение для вычисления компонент тензора напряжений).
|
Временной слой M=100, расчёт V29 (табл. 4.2, 4.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.5. Поля напряжений |
|
Временной слой M=100, расчёт V30 (табл. 4.2, 4.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.
4.6. Поля напряжений |
|
Временной слой M=100, расчёт V31 (табл. 4.2, 4.3) |
|
|
|
|
|
|
|
|
|
|
|
|
Рис.
4.7. Поля напряжений |
5. Особенность напряжений в вершине сложного
клина
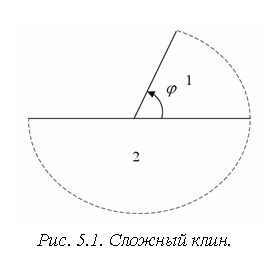 Важным участком рассматриваемой в задаче
области является вершина образованного якорем и рельсом сложного клина,
состоящего в данном случае из двух изотропных упругих клиньев (см. рис. 5.1). В
вершине возникает особенность напряжений, порядок которой определяется
параметрами материалов и геометрией клиньев. Асимптотическое поведение полей
напряжений и деформаций в окрестности многогранной вершины композитного тела
исследовалось в работах [6 – 9, 21] и др.
Важным участком рассматриваемой в задаче
области является вершина образованного якорем и рельсом сложного клина,
состоящего в данном случае из двух изотропных упругих клиньев (см. рис. 5.1). В
вершине возникает особенность напряжений, порядок которой определяется
параметрами материалов и геометрией клиньев. Асимптотическое поведение полей
напряжений и деформаций в окрестности многогранной вершины композитного тела
исследовалось в работах [6 – 9, 21] и др.
Рассмотрим вопрос более подробно.
В полярных координатах ![]() (начало в вершине
клина) уравнения равновесия принимают вид [12]
(начало в вершине
клина) уравнения равновесия принимают вид [12]
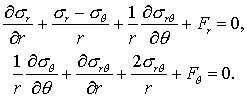
В работе [7] используется
формулировка Мусхелишвили для задачи расчёта плоского
напряженно-деформированного состояния, в которой функция напряжений Эри
выражается через комплексные функции ![]() [12]. Тогда компоненты
напряжений и перемещений в полярных координатах для случая плоского
деформированного состояния выражаются следующим образом [7]:
[12]. Тогда компоненты
напряжений и перемещений в полярных координатах для случая плоского
деформированного состояния выражаются следующим образом [7]:
![]()
где ![]() – модуль сдвига,
– модуль сдвига, ![]() – коэффициент
Пуассона.
– коэффициент
Пуассона.
Подставим граничные и контактные условия, включая соотношения для
трения , в полученные соотношения. При этом считаем
[7], что функции ![]() в близкой к особой
вершине окрестности имеют вид:
в близкой к особой
вершине окрестности имеют вид:
Подставляя в -, замечаем, что исследуемая особенность имеет
порядок ![]() , то есть чем ближе
, то есть чем ближе ![]() к единице, тем
медленнее рост напряжений при
к единице, тем
медленнее рост напряжений при ![]() .
.
В результате некоторых преобразований
получим систему однородных линейных алгебраических уравнений относительно
неизвестных ![]() . Исключив из этой системы неизвестные
. Исключив из этой системы неизвестные ![]() , приравняем нулю детерминант матрицы коэффициентов.
, приравняем нулю детерминант матрицы коэффициентов.
В результате получим
уравнение для определения ![]() для случая
для случая ![]() [7]:
[7]:
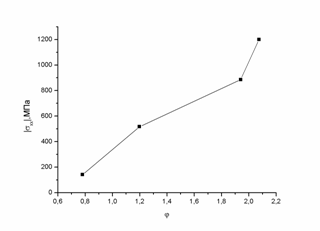
На рис. 5.2 показана
зависимость ![]() от величины угла клина
от величины угла клина
![]() для случая медного
рельса и алюминиевого якоря, полученная в результате численных расчетов,
описанных в §4. Особенность решения подразумевает бесконечные значения
напряжений в вершине клина, но численный расчет напряженного состояние даёт
возможность только приблизительно оценить поведение решения по величине
напряжений вблизи особой вершины.
для случая медного
рельса и алюминиевого якоря, полученная в результате численных расчетов,
описанных в §4. Особенность решения подразумевает бесконечные значения
напряжений в вершине клина, но численный расчет напряженного состояние даёт
возможность только приблизительно оценить поведение решения по величине
напряжений вблизи особой вершины.
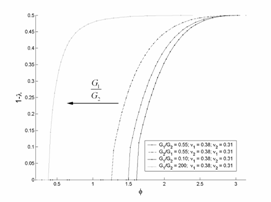
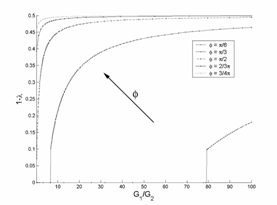
С помощью пакета программ Maple найдены
действительные корни уравнения . Графики зависимостей величины ![]() от угла клина
от угла клина ![]() и отношения
и отношения 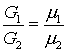 изображены на рис. 5.4
и 5.5 соответственно. Стрелками на рисунках показано направление увеличения
параметров, указанных в легенде,
изображены на рис. 5.4
и 5.5 соответственно. Стрелками на рисунках показано направление увеличения
параметров, указанных в легенде, ![]() и
и ![]() соответственно. В
расчетах использовались значения
соответственно. В
расчетах использовались значения ![]() (медь),
(медь), ![]() (алюминий). Графики показывают, что порядок особенности, то
есть величина
(алюминий). Графики показывают, что порядок особенности, то
есть величина ![]() , возрастает с ростом величин
, возрастает с ростом величин ![]() и
и ![]() соответственно, а при
малых углах равен нулю (граничные значения отчетливо видны на рис. 5.4, 5.5).
Поведение графика (см. рис. 5.4) согласуется с ростом значений
соответственно, а при
малых углах равен нулю (граничные значения отчетливо видны на рис. 5.4, 5.5).
Поведение графика (см. рис. 5.4) согласуется с ростом значений ![]() вблизи вершины якоря
(см. рис. 5.2) при
вблизи вершины якоря
(см. рис. 5.2) при ![]() .
.
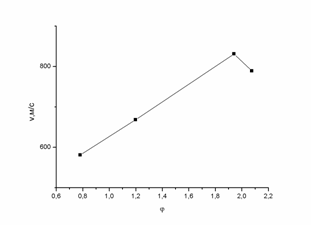
На рис. 5.3 показана
зависимость величины критической скорости ![]() от угла
от угла ![]() . Видно, что, начиная с некоторого угла, значение критической
скорости падает. Здесь следует отметить, что в модели не учитывается влияние
деформации и разрушения материала на величину критической скорости.
. Видно, что, начиная с некоторого угла, значение критической
скорости падает. Здесь следует отметить, что в модели не учитывается влияние
деформации и разрушения материала на величину критической скорости.
|
|
|
|
Рис. 5.2. Зависимость |
Рис. 5.3. Зависимость критической скорости от угла. |
|
|
|
|
Рис. 5.4. Зависимость |
Рис. 5.5. Зависимость |
6. Литература
1. "Материалы I Всесоюзного семинара по динамике сильноточного дугового разряда в магнитном поле" (Новосибирск, 10-13 апреля 1990 г.), под ред. М.Ф. Жукова, Новосибирск, изд. Инст. Теплофизики СО АН СССР, 1990. 350 с.
2. "Материалы II Всесоюзного семинара по динамике сильноточного дугового разряда в магнитном поле" (Новосибирск, 4-6 декабря 1991г.), под ред. В.Е. Накорякова, Новосибирск, изд. Инст. Теплофизики СО РАН, 1992. 367 с.
3. Галанин М.П., Попов Ю.П. Квазистационарные электромагнитные поля в неоднородных средах: Математическое моделирование. – М.: Наука, Физматлит, 1995. 320 с.
4. Сегерлинд Л. Применение метода конечных элементов.– М.: Мир, 1979. 392 с.
5. Зенкевич О. Метод
конечных элементов в технике. – М.: Мир, 1975. 543 с.
6. Bogy D.B. Two edge-bonded elastic wedges of
different materials and wedge angles under surface tractions. J. Appl. Mech., 1971. Vol. 38. pp. 377-386.
7. Theocaris P.S., Gdoutos E.E. Stress
singularities at vertices of composite plates with smooth and rough interfaces
// Archives of Mechanics, Archiwum Mechaniki Stosowanej, Warszawa, 1976. Vol.
28, 4. pp. 693-704.
8. Theocaris P.S. The Order of singularity at a
multi-wedge corner of a composite plate // Int. J. Engng Sci., 1974. Vol. 12.
P.p. 107-120.
9.
Hein V.L., Erdogan F. Stress singularities in a two-material wedge //
International Journal of Fracture
Mechanics, Wolters-Noordhoff Publishing-Groningen, Vol. 7, No. 3, 1971.
10. Тимошенко С.П., Гудьер Дж. Теория упругости. – М.: Наука, 1975. 576 с.
11. Седов Л.И. Механика сплошной среды. Т.1. – М.: Наука, 1994. 528 с.
12. Лурье А.И. Теория упругости. – М.: Наука, 1970. 940 с.
13. Галанин М.П. Построение и исследование разностной схемы для одномерной динамической связанной задачи термоупругости. // Препр. Ин. прикл. матем. им. М.В. Келдыша РАН, 1990. №39. 37 с.
14. А.В. Плеханов, А.Н. Терещенко, Д.В. Хандрыга. Численное
и экспериментальное исследование электромагнитного ускорения макротел с
использованием металлического якоря. // Прикладная механика и техническая
физика. 1996.
Т. 37. № 1. С. 21 – 27.
15. D.V. Khandryga, A.V.
Plekhanov, A.N. Tereschenko. Numerical Simulation and Experimental Results of
the Metal Armature Acceleration. // IEEE Transactions on Magnetics. 1995. V.
31. N. 1. P. 193 – 197.
16. Галанин М.П., Миляев К.К. Организация расчёта двумерных квазистационарных электромагнитных полей со сложной геометрией и различными физическими свойствами. // Препр. Ин. прикл. матем. им. М.В. Келдыша РАН, 2001. № 55. 29 с.
17. Бураго Н.Г. Численное решение задач МСС с подвижными границами раздела. Диссертация на соискание ученой степени доктора физико-математических наук. М.: Институт проблем механики РАН, 2003. 222 с.
18. А.А. Самарский, Ю.П. Попов. Разностные методы решения задач газовой динамики. М.: Наука, 1980, 352 с.
19. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. М.: Наука, 1978. 592 с.
20. М.П. Галанин, А.Д. Лебедев, А.П. Лотоцкий, К.К. Миляев. Тепловые и электромагнитные процессы на контактах электродинамического ускорителя // Препр. ИПМ им. М.В. Келдыша РАН. 2000. № 42. 32 с.
21. Галанин М.П., Миляев К.К. Об особенностях физических характеристик в окрестности электрического контакта. // Препр. Ин. прикл. матем. им. М.В. Келдыша РАН. 1997, № 57. 33 с.

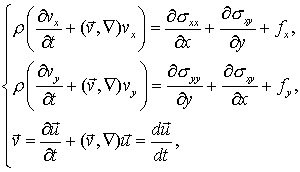
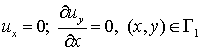 .
.  , получим:
, получим: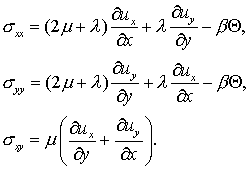
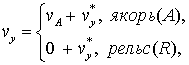
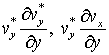 , которые малы по сравнению со слагаемыми
, которые малы по сравнению со слагаемыми 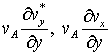
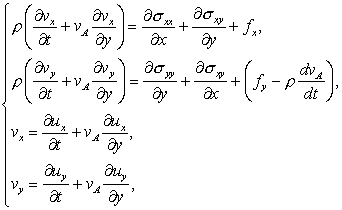
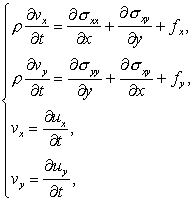
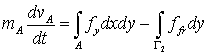 .
.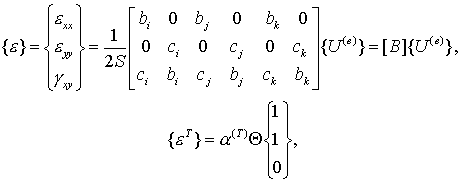
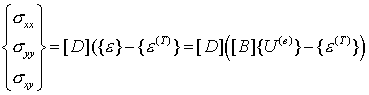 ,
,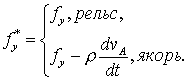
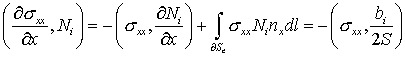 .
.