Алгоритмы распознавания штриховых кодов
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Код PDF-417. Является многострочной символикой.
Информация |
|
|
|
|
Рис. 6. Примеры символик, распознаваемых видеосканерами. Эти символики плохо или совсем не распознаются лазерными сканерами. |
|
Обобщённая схема работы видеосканера штрих-кодов
показана на рис. 7. Задачами сигнального процессора являются: локализация
штриховых символик, выделение структурных элементов и декодирование.
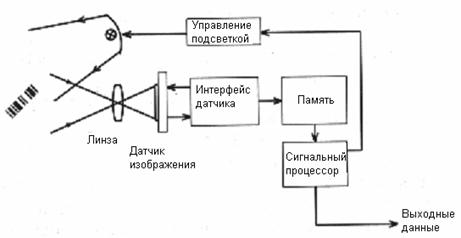
Рис. 7. Обобщенная структурная схема видеосканера.
Для видеосканера требуется разработка алгоритмов и
методов обнаружения штриховых символик кардинально отличных от других сканеров.
Это связанно с большим потоком неструктурированной входной видео информации.
Используются как последовательные, так и параллельные алгоритмы обработки
изображений. Параллельные алгоритмы более эффективны, но требуют специальных
схемотехнических решений при создании оборудования сканера. Ниже описывается
разработанный алгоритм для обнаружения и декодирования штрих-кодов.
Алгоритм работы видеосканера штрих-кодов.
Разработанный алгоритм можно разделить на три большие части, как показано на рис. 8.

Рис. 8. Блок схема алгоритма работы видеосканера штрих-кодов.
Алгоритм локализации штрих-кодов содержит часть,
которая определяет участок изображения, содержащий штриховую символику. Внутри
выделенного участка ищется прямая, пересекающая все штрихи символики, и
формирует вектор яркостей вдоль этой прямой.
Полученный вектор яркостей передаётся на алгоритм
выделения структурных элементов, где осуществляется перевод нечетких значений
ширины элементов символики (штрихов и пробелов) в числа, кратные модулю
(элементу минимальной ширины) штрихового кода. На выходе алгоритма получается
целочисленный вектор значений ширины элементов.
Алгоритм декодирования разбирает структуру
целочисленного вектора и декодирует закодированные символы в соответствии с
кодовыми таблицами.
При разработке алгоритма учитывались такие параметры,
как надёжность, быстродействие, экономичность аппаратного решения. Параметр
надёжности является наиболее сложным для определения. Большая доля нагрузки при
его оценке ложится на эксперимент.
Для достижения высокого быстродействия при анализе
изображений необходимо использовать различные формы одновременности и
параллельности процессов [2]. В разработанном алгоритме локализации штрих-кодов
самой часто используемой операцией является фильтрация при помощи матриц
размером 2х2 и 3х3. Эта операция использует данные только из локальной и
заранее известной области обработки, требует значительно меньшего объёма
памяти, чем те операции, исходные данные для которых разбросаны по всему
изображению или расположение которых существенно зависит от результатов
предыдущих вычислений. Учитывая также объём входных данных
1600х1200х5=9.6МБ/сек, эта часть алгоритма была адаптирована для выполнения
одновременно нескольких фильтраций на ряде элементов жёсткой логики.
При разработке алгоритма выделения структурных
элементов штрих-кода предполагались неопределёнными размер и положение входных
данных. В алгоритме также применяются итерационные методы для определения
расположения штрихов и пробелов. Следовательно, объём используемой памяти, и
режим работы алгоритма изменяются в зависимости от входных данных. Этот
алгоритм полностью реализуется программно.
Алгоритм декодирования штрих-кода – алгоритм верхнего
уровня. Он получает на вход значительно меньший объём информации, имеет большое
множество вариантов работы в зависимости от типа декодируемого кода. Поэтому он
может быть реализован только программно.
Быстродействие и экономичность аппаратных решений
определяются количеством используемых в алгоритме элементарных операций.
Преимущественно использовались операции сложения, изменения знака и сдвига,
реализованные на жёсткой логике.
Локализация штрихового кода в изображении сцены.
Постановка задачи.
На вход алгоритма подается монохромное 256
градационное изображение сцены размером 1600х1200 элементов. Необходимо
обеспечить поиск символик с минимальной высотой штрихов
Алгоритм локализации линейного штрих-кода должен
работать в масштабе реального времени (для этого он должен обеспечивать
обработку не менее 5 кадров в секунду) и при этом себестоимость изделия должна
быть невысокой (сравнимой с аналогами). Учитывая, что объём входной информации
(9,6МБ/сек) существенен, последовательная реализация алгоритма будет стоить
достаточно дорого, вследствие высоких цен на сигнальные процессоры с высокой тактовой
частотой (около 1 GHz). Должна быть возможность
параллелизации алгоритма и при этом паралеллизуемые операции должны быть
достаточно простыми или их количество должно быть небольшим.
В первой части алгоритма определяются границы
участков, занимаемых штрих-кодом, а во второй ищется отрезок прямой,
пресекающей все штрихи и пробелы данной символики. Значения яркости вдоль
отрезка передаются на алгоритм выделения структурных элементов.
Алгоритм определения границ участков занимаемых штрих-кодом.
Следует заметить, что штрих-код, также как и текст,
имеет довольно резкое, многократно изменяющееся на небольших площадях, значение
яркости. Но, в отличие от текста, это изменение имеет определенную
пространственную монотонность вдоль штрихов. Таким образом, локально анализируя
свойства текстуры изображения, можно различать штрих-код по однонаправленности
градиентов яркости на некоторой площади. В алгоритме использовались простейшие
локальные дифференцирующие фильтры. Осуществлялась двухмерная фильтрация (1)
исходного монохромного изображения, с приведёнными в таблице фильтрующими
матрицами (см. табл. 1).
![]() (1)
(1)
a – исходное изображение.
b – фильтрующая матрица.
k1 ,k2 – индексы,
пробегающие по всем элементам фильтрующей матрицы.
Таблица 1. Фильтрующие матрицы.
|
1 |
2 |
3 |
4 |
||||||||
|
Горизонтально дифференцирующая матрица |
Вертикально дифференцирующая матрица |
Диагонально (45˚) дифференцирующая матрица |
Диагонально (135˚) дифференцирующая матрица |
||||||||
|
-¼ |
-¼ |
|
¼ |
-¼ |
|
0 |
-¼ |
0 |
0 |
¼ |
0 |
|
¼ |
¼ |
|
¼ |
-¼ |
|
¼ |
0 |
-¼ |
¼ |
0 |
-¼ |
|
|
|
|
|
|
|
0 |
¼ |
0 |
0 |
-¼ |
0 |
Две пары фильтрующих матриц 1 и 2, 3 и 4 являются
линейно независимыми и ортогональными. Каждая пара находит максимальный отклик
значений компонент градиента яркости в двух взаимно перпендикулярных
направлениях. Линейный штрих-код имеет определённое направление штрихов. Таким
образом, осреднённое по некоторой площади значение модуля компонент градиента
вдоль двух перпендикулярных направлений, имеющих различные углы с линиями
штрих-кода, будет существенно отличаться. Это свойство используется для
предварительной оценки мест возможного расположения линейного штрих-кода, а
также грубого определения направлений штрихов.
Для уменьшения
объёмов вычислений, связанных с оценкой углов поворота градиента, решено было
разбить всевозможные направления (360˚) на 4 дискретных направления (см.
рис. 9), отстоящих друг от друга на 45˚. Этот факт объясняет необходимость
использования двух диагонально дифференцирующих матриц.
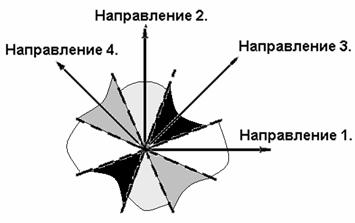
Рис. 9. Дискретность направлений при анализе свойств текстуры.
Для проверки достаточности выделения лишь 4 дискретных
направлений, при обнаружении линейного штрих-кода, был реализован следующий
алгоритм:
- выполняется
операция фильтрации с фильтрами 1-4.
- для каждого, полученного продукта фильтрации,
находится сумма модулей элементов его составляющих.
- вычисляется модуль отношений в децибелах результатов
для двух пар ортогональных матриц 1, 2 и 3, 4.
На вход этого алгоритма подавались изображения
постоянного размера 110х110 элементов, содержащие отрезок длиной 100 элементов. Угол отрезка с горизонтальной
осью изображения изменялся. В результате была получена зависимость отношений
отклика в двух взаимно-перпендикулярных направлениях от угла наклона отрезка
(см. рис. 11).
В то же время были получены аналитические выражения
для отношений сумм модулей откликов на фильтрации в перпендикулярных
направлениях, в зависимости от угла наклона отрезка, определяемых в алгоритме
(см. рис. 11).
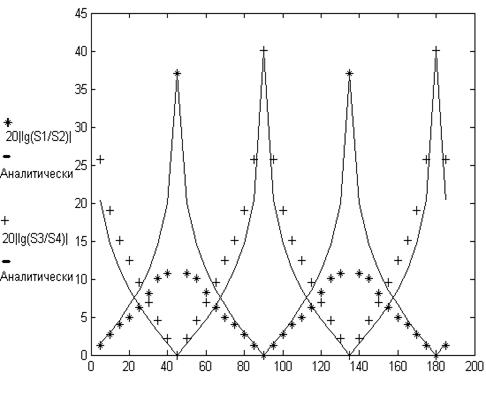
Рис. 11. Графики отношений сумм абсолютных значений откликов на фильтрацию с фильтрами, в двух парах взаимно перпендикулярных направлениях в зависимости от угла поворота отрезка прямой линии в фиксированном квадратном окне.
S1 - сумма модулей откликов, при использовании дифференцирующей матрицы в горизонтальном направлении (№1).
S2 - сумма модулей откликов, при использовании дифференцирующей матрицы в вертикальном направлении (№2).
S3 - сумма модулей откликов, при использовании дифференцирующей матрицы в диагональном направлении (№3).
S4 - сумма модулей откликов, при использовании дифференцирующей матрицы в диагональном направлении (№4).
Если при обнаружении линейного штрих-кода, опираться
на максимальное значение из этих двух отношений для каждого угла наклона (см.
рис. 11), то минимальное значение будет превышать 6 дБ. Т. о. данную символику можно обнаружить по ослаблению
значений отклика в одном из двух взаимно-перпендикулярных направлениях
фильтрации более чем в два раза.
Продукт фильтрации исходного изображения с
фильтрующими матрицами представляет собой контурный рисунок с контурными
линиями, перпендикулярными направлению дифференцирования. Этот рисунок является
довольно прерывистым и не может дать информацию о размере области, занимаемой
штрих-кодом. Возникает необходимость в осреднении значений градиентов по
некоторой площади, значительно меньшей размеров штрих-кода и большей размеров
его элементов. Кроме того, задачей данного осреднения является низкочастотная
фильтрация изображений с целью уменьшения пространственного разрешения картины
градиентов. Уменьшение разрешения позволит уменьшить вычислительные нагрузки
при поиске интересующих областей изображения.
Идеальным решением для низкочастотной фильтрации
является фильтрация двумерной Гауссовой поверхностью (5), далее называемым
двумерным гауссианом (см. рис. 12). Во-первых, эта поверхность имеет
спектральную характеристику той же формы, что и сам гауссиан, т.е. монотонно
убывающую (см. рис.15). Во-вторых, спектральная характеристика одинакова во
всех направлениях. В-третьих, для нахождения продукта фильтрации нет
необходимости в фильтрации исходного рисунка с квадратной матрицей, т. к. эту
операцию можно заменить двумя одномерными фильтрациями вдоль строк и вдоль
столбцов (см. рис. 13).
![]() (5)
(5)
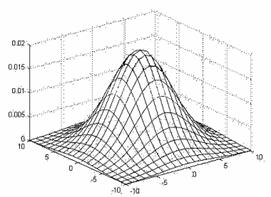
Рис. 12. Двухмерный гауссиан.
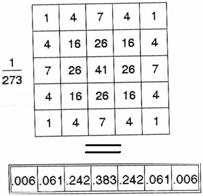
Рис. 13. Эквивалентная замена двумерного фильтра в форме гауссиана двумя одномерными массивами, предназначенными для фильтрации вдоль строк и вдоль столбцов.
Вместе с тем, фильтрация при помощи двумерного
гауссиана уступает по вычислительным затратам двумерному единичному окну (см.
рис. 14), которое так же рассматривалось при разработке алгоритма. Фильтрации
квадратным единичным окном - простое суммирование яркостей точек по площади
осреднения. В случае фильтрации квадратным единичным окном можно наблюдать
колебания спектра и неоднородность полученной картины по направлениям (см. рис.
15), но это даёт незначительную ошибку в определении расположения границ
области, занимаемой штрих-кодом. Поэтому в описываемом алгоритме решено было
использовать единичное окно, из-за требований возможности использования
аппаратуры с невысокой производительностью.
Информация о минимальной высоте штрихов (
|
|
1/25 |
|
|
|||||||||||||||||||||||||
|
Рис. 14. Двумерное единичное окно 5x5 элементов. |
||||||||||||||||||||||||||||
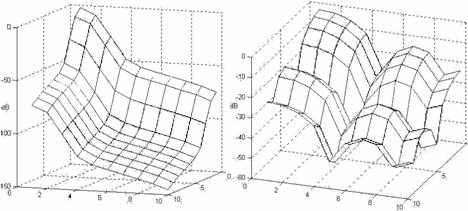
Рис. 15. Спектральная характеристика фильтра Гаусса (слева) и простого квадратного единичного двухмерного окна (справа).
Ниже приведён пример работы алгоритма, на вход
которого было подано изображение, содержащее линейные штрих-коды,
ориентированные под различными углами (см. рис. 16).

Рис. 16. Исходное изображение сцены.
Результаты
работы описанного алгоритма можно увидеть на рис. 17. Здесь показаны
осреднённые при помощи единичного окна продукты фильтрации четырьмя
приведёнными в таблице 1 матрицами. Более яркие области соответствуют
наибольшему отклику на фильтрацию с дифференцирующими матрицами. Можно
заметить, например, что изображения штрих-кодов с штрихами параллельными
горизонтальному направлению имеют максимальный отклик при фильтрации
вертикально дифференцирующей матрицей №2, тогда как при фильтрации горизонтально
дифференцирующей матрицей №1 их отклик незначителен и практически не отличается
от 0, отклик на фильтрацию с диагонально дифференцирующими матрицами двух типов
различается не значительно (пример обработки такого штрих-кода обведён кружком
на всех этапах (см. рис. 16, 17¸ 18)).
Такая же ситуация при фильтрации с диагонально
дифференцирующими матрицами №3 и №4 наблюдается в месте изображения штрих-кода
наклонённого под углом, близким к 45° с горизонтальным направлением картинной
плоскости.

Рис. 17. Осреднённые единичным квадратным окном продукты фильтрации исходного монохроматизированого изображения с четырьмя видами дифференцирующих матриц.
Тот факт, что при фильтрации с матрицами двух
ортогональных направлений, область изображения, содержащая линейный штрих-код,
будет иметь отклик, различающийся более чем в два раза, хотя бы для одной пары
ортогональных матриц, позволяет определять области, содержащие штрих-код
простым вычитанием пар изображений. Алгоритм заключается в следующем.
Находится поэлементная разность продуктов фильтрации и
осреднения матриц №1 и №2, а также матриц №3 и №4. Результат проведённой
операции изображён на рис. 18. Вычитание
двух изображений сцен помогает избавиться, от таких похожих по контрастности на штрих-код
объектов, как текст. Оно требует количество операций равное количеству точек
изображения.
Можно заметить, что после проведения операции поэлементной разницы, кроме областей,
занимаемых штрих-кодами, значительной яркостью обладают элементы, имеющие
определённую пространственную направленность. Такими элементами могут являться,
например, одиноко расположенные контурные линии объектов. Осреднение их отклика
по площади имеет малые, по сравнению с результатами штрих-кодов, значения,
следовательно, от них можно избавиться, сравнивая каждое значение с некоторым
порогом[1]. Это
также требует числа операций равного числу точек сцены.
Опишем процедуру выбора порога. Введём для
распознаваемых штрих-кодов следующие параметры:
Strength=”Среднее количество перепадов яркости на каждые 10 точек”,
Brigtness_Difference=”Среднее значение разностей яркости между пробелами и
штрихами”.
Осреднённая яркость области размером 10x10 точек,
после операции фильтрации может быть рассчитана:
Window_Brightness=(2*(1/4)*Strength*Brightness_Difference*10)/(10х10) (6)
Необходимо
учесть, что в перпендикулярном направлению с максимальным откликом это же
значение будет, как минимум, в два раза меньше (на 6дБ, (см. рис. 11)),
следовательно ограничение порога сверху может быть заданно:
![]() (7)
(7)
В рассматриваемом примере изображения штрих-кодов
имеют следующие характеристики: Strength≈2;
Brightness_Difference>0.5; подставив эти значения в формулы 4 получим,
что максимальный порог будет равен 0.025.

Рис. 18. Абсолютные значения поэлементной разницы между осреднёнными продуктами матриц №1, №2 слева и №3, №4 справа.
Из гистограммы распределения яркостей на рисунках изображающих результат
абсолютных значений поэлементной разницы, можно заметить, что большинство
значений яркостей точек лежит ниже порога 0.02 (см. рис.19) Для продолжения
примера сравним значение яркостей на рис. 18 с порогом равным 0.02.
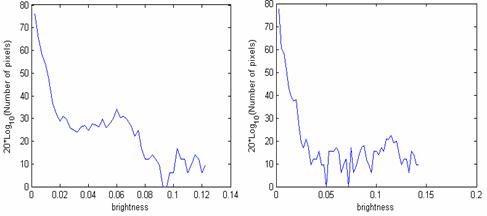
Рис. 19. Гистограмма распределения яркостей на изображениях абсолютных значений поэлементной разницы между осреднёнными продуктами матриц №1, №2 слева и №3, №4 справа.
Применение операции сравнения с порогом даст единицы в
местах предположительного расположения штрих-кода и нули во всех остальных (см.
рис.20).
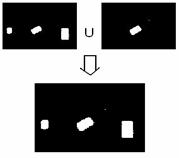
Рис. 20. Применение операции порог и объединение результатов для двух пар матриц.
Имея такую бинарную картину для уменьшения вычислительных нагрузок можно
определить зоны изображения, с которыми будут работать последующие алгоритмы.
Для начала необходимо сосчитать полученные объекты. Осуществляется нумерация 8-связных объектов
[1]. На выходе имеем рисунок, значения точек которого либо равны 0 – фон, либо
равны номеру объекта.
Вокруг каждого объекта выделяется прямоугольная область, содержащая все
точки, принадлежащие конкретному штрих-коду. Далее, если площадь этой области
меньше некоторой константы, она исключается из рассмотрения. Полученный
прообраз окна выделяется и на исходном изображении с высоким разрешением. На
этой операции считается законченным этап определения участков изображения
занимаемых штрих-кодом.
Алгоритм определение ориентации штрих-кодов.
Дальнейшие операции проводятся
отдельно для каждой области, занимаемой штрих-кодом. Задача состоит в
нахождении уравнения прямой пересекающей все элементы символики. В данном
алгоритме решено было строить прямую, опираясь на скелет фигуры, образованной штрих-кодом.
Операция нахождения скелета фигуры называется скелетизацией [1]. Суть
операции скелетизации заключается в управляемой последовательной равномерной
эрозии объекта. Эрозия продолжается до тех пор, пока не останутся линии шириной
в одну точку. Эти линии в силу алгоритма и эрозии являются равноудалёнными от
двух ближних к ним сторон объекта, и их ширина составляет одну точку.

Рис. 21. Скелетизация фигур, образованных штрих-кодами.
Ввиду того, что скелет состоит из серединных линии, прямая, проходящая через узлы скелета,
пересечёт все элементы штрихового кода. Полученное уравнение прямой внутри
области необходимо преобразовать к уравнению в исходной картинной:
![]() =>
=> ![]()
![]() =>
=> ![]() , (8)
, (8)
,
где kx, ky, x0
и y0 – коэффициенты
параметрического уравнения внутри прямоугольной области; xB, yB – координаты начала области в
изображении с низким разрешение; SCALE
– линейный коэффициент преобразования между системой координат исходного
изображения и полученных меньшего разрешения.
Пример выделения отрезка прямой, пересекающей все элементы штрих-кода,
показан на рис. 22, а на рис. 23 изображены яркости вдоль нескольких отрезков
параллельных выделенному.

Рис. 22. Найденный отрезок, пересекающий все элементы символики.
![]()
Рис. 23. Значения яркостей вдоль нескольких близлежащих отрезков, параллельных найденному.
На этом этапе заканчивается работа алгоритма
локализации штрих-кода.
В отличие от всенаправленных лазерных сканеров,
описанный алгоритм позволяет работать с узкими штрих-кодами. Алгоритм является
легко параллелизуемым, так как имеет значительный объём локальных однотипных
операций (типа фильтраций, осреднений, поэлементной разницы матриц и т. п.).
Описанный алгоритм изначально задумывался для
обнаружения линейных одномерных штрих-кодов. Но он может быть с успехом
применён для локализации многострочных и модулированных по высоте символик,
описанных в [3], так как в них опять же существует пространственная
монотонность в одном направлении. Далее, небольшая модификация алгоритма,
направленная именно на поиск наиболее интенсивных, с точки зрения изменения
контраста областей, позволяет обнаруживать 2-х мерные символики, также
описанные в [3]. Повидимому, операция фильтрации с представленными в таблице 1
фильтрами может являться базовой при обнаружении многих типов символик.
Экспериментальные исследования алгоритма локализации штрих-кода.
Экспериментальные исследования проводились с целью
определения диапазонов изменения входных величин, при которых обеспечивается
надёжная работа алгоритма. А также проверялась правильность выбора константных
величин алгоритма (таких как порог яркости).
Эксперимент состоял в следующем: на вход алгоритма
подавались штрих-коды с разными значениями ширины самого узкого элемента
(модуля), а также с различной амплитудой изменения яркости вдоль всей
символики. Один и тот же штрих-код подавался под разными углами, равномерно
изменяющимися (с шагом 10º) в плоскости изображения. Бралось максимальное
значение яркости одной и той же точки штрих-кода из двух картин полученных после операции поэлементной
разницы изображений. Были построены зависимости яркостей точек (расположенных в
пределах изображения штрих-кода) от угла поворота символики.
Для эксперимента использовались изображения четырёх
штрих-кодов и текста (см. рис. 24):
Штрих-код с шириной модуля 2,5 точки изображения и
амплитудой изменения яркости 0,5 от динамического диапазона (кривая 1).
Штрих-код с шириной модуля 5 точек изображения и
амплитудой изменения яркости 0,5 от динамического диапазона (кривая 2).
Штрих-код с шириной модуля 2,5 точки изображения и
амплитудой изменения яркости 0,25 от динамического диапазона (кривая 3).
Текст с толщиной линий около 2,5 точек изображения и
амплитудой изменения яркости 0,5 от динамического диапазона (кривая 5).
Порог бинаризации изображения после операции
вычисления поэлементной разницы, выбранный при разработке алгоритма локализации
штрих-кода, равен 0,02 и изображен на рисунке (прямая 4).
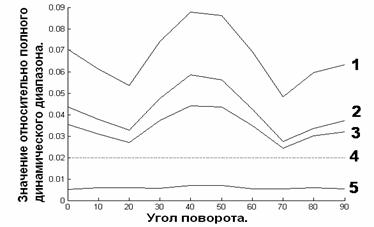
Рис. 24. Зависимость яркости точки объекта после операции поэлементной разницы в зависимости от угла поворота в плоскости изображения.
Как видно из графиков описываемый алгоритм позволяет
успешно справится с поставленной задачей. Все кривые, относящиеся к изображению
штрих-кода оказались выше порогового значения, в то время, как такой
контрастный объект, как текст, тем не менее, оказался ниже порога и выпал из
рассмотрения.
Операции, идущие после операции поэлементной разницы
алгоритма локализации штрих-кода, не нуждаются в экспериментальных
исследованиях, так как их действия вполне детерминированы. Скелет прямоугольной
фигуры (символики штрих-кода) имеет два узла (в случае, если он не повреждён и
не загорожен другими объектами), и прямая проходящая через них определяется
однозначно. Остальные операции и весь алгоритм нуждаются в тестировании
работоспособности в реальных условиях, направленном на выявление ошибок в
реализации алгоритма.
Алгоритм выделения структурных элементов в изображении штрихового кода.
Постановка задачи.
На вход алгоритма поступают векторы значений яркости
элементов изображения (пикселов) вдоль прямых пересекающих все штрихи и пробелы
штрихового кода.
Алгоритм должен позволять определить ширину
минимального элемента штрих-кода – его модуля. Опираясь на ширину модуля и
местоположение элементов изображения необходимо определить толщины штрихов и
пробелов. В алгоритме также должно быть предусмотрено взаимодействие с
алгоритмом декодирования для исправления возможных ошибок.
Алгоритм выделения структурных элементов.
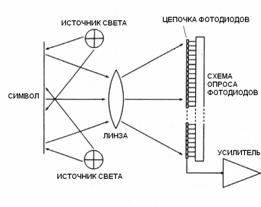
Технология автоматического считывания линейного
штрих-кода была разработана более десяти лет назад. Для этих целей применяется
датчик в виде линейки светочувствительных элементов (ПЗС линейка). Разрешение
линейки значительно превосходит ширину модуля считываемого штрих-кода, т. е. на
границу раздела штрихов и пробелов попадает незначительное количество точек.
Кроме этого для увеличения диапазона воспринимаемых яркостей осуществляется
искусственное освещение сканируемой поверхности.
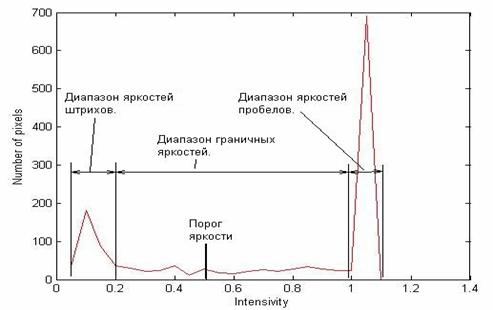
Рис. 25. Гистограмма распределения значений яркостей.
Порог яркости, по которому точка в линейке отождествляется
либо со штрихом, либо с пробелом обычно является константой. (см. рис. 25),
Полученную цепочку нулей и единиц можно отмасштабировать (привести к
представлению с точностью до модуля) и декодировать.
Такой подход к решению задачи невозможен в описываемом
устройстве, использующем не ПЗС линейку, а ПЗС матрицу, т. к. высокое двумерное
разрешение ПЗС матрицы во-первых
приведёт к высокой цене датчика изображения, а во-вторых к огромным
вычислительным нагрузкам алгоритма локализации штрих-кода Количество
обрабатываемых точек будет расти как вторая степень от линейного разрешения.
В соответствии с теоремой Котельникова, зададимся низким минимальным разрешением – 2 точки на модуль и, следовательно, позволим большему количеству точек находиться в диапазоне граничных яркостей. Точка, находящаяся в граничном диапазоне может отождествиться как с пробелом, так и со штрихом, в зависимости от положения значения яркости в граничной области, и от выбора порогового значения (см. рис. 26). Это, в свою очередь, может повлечь неверное определение границ штрихов и пробелов и привести к ошибке декодирования штрих-кода. Следовательно, для поставленной задачи применение одного порогового значения недостаточно. Информация о точном положении границы (более точном, нежели пространственное разрешение изображения) так же содержится в яркости граничной точки. Поэтому необходимо использовать методы, позволяющие опираться на пространственное положение и значение яркости граничной точки для уточнения границы между штрихом и пробелом.
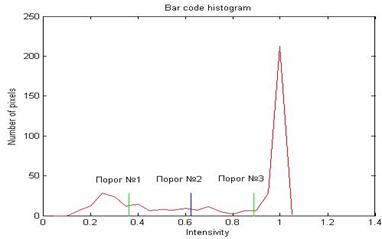

Рис. 26. Применение операции порог с тремя различными значениями порога к исходному изображению штрих-кода с его низким пространственным разрешением
Учитывая сделанный вывод, что для более точной
локализации границы раздела штриха и пробела необходимо использовать информацию
о яркости точки в пределах которой эта граница проходит, а также зная, что
граница между штрихом и пробелом, в идеальном случае – ступенька функции
яркости, можно попробовать увеличить пространственное разрешение изображения за
счёт бинаризации его яркости.
На рис. 27 показана типичная картина проекции границы
между штрихом и пробелом на светочувствительные элементы датчика изображения.
Видно, что точки (1,3), (2,3), (2,2), (2,1) и (3,1) попали на границу раздела
яркости между штрихом и пробелом. Эти точки за период экспозиции ПЗС накопят
некоторое среднее значение яркости и попадут в диапазон граничных яркостей
гистограммы распределения значений яркости.
Пусть в диапазоне граничных яркостей некоторым образом
выбрано три порога яркости, причём:
Порог №1 < Порог №2 < Порог №3
После
применения 3-х операций сравнения в зависимости от яркости пиксела, ему для
каждого значения порога будет присвоена либо 1 либо 0.
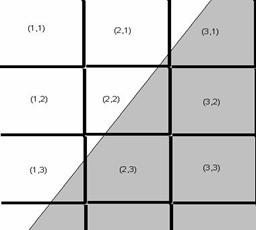
Рис. 27. Засветка элементов светочувствительной матрицы при прохождение по их площади границы раздела освещенностей штриха и пробела.
Для каждой точки исходного, серого изображения
(назовём её материнской) в соответствие поставим 3 точки получаемого
изображения (назовём их потомками). Потомки содержат набор яркостей (единиц и нулей),
полученных, после операций сравнения с порогами материнской точки. При этом одинаковые значения сгруппированы по
расположению, например 001 или 011, в то время, как 010 или 101 - невозможны.
Правила преобразования наглядно изображены на рис. 28.
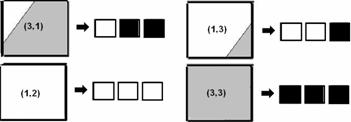
Рис. 28. Правила преобразования яркостей точек в бинарное изображение.

Рис. 29. Пример повышения разрешения на границе раздела штрихов и пробелов.
На рис. 29 показан пример работы этого метода трёх
порогов. Гистограмма анализируемого изображения, а так же результаты его
преобразования с тремя значениями порогов, приведены на рис. 26.
Следующий этап распознавания штрих-кода заключается в
сборе статистики по ширинам штрихов и пробелов. Операция состоит в построении
гистограммы количества штрихов и пробелов в зависимости от их ширины (см. рис.
30). Для уменьшения ошибок, связанных с дискретностью изображения, а также
дефектами нанесения штрих-кода, используется суммирование (накапливание)
значений ширины одних и тех же элементов на разных строчках изображения. При
правильном выборе порогов на такой гистограмме будет наблюдаться совокупность
кривых, напоминающих кривые нормального закона распределения. Математические
ожидания этих центров отстоят друг от друга на величину равную ширине модуля.
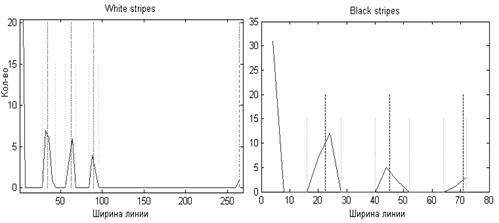
Рис. 30. Гистограмма распределения ширин пробелов (справа) и штрихов (слева).
Таким образом, гистограммы ширины штрихов и пробелов
оказываются полезными для оценки правильности выбора порогов. Кроме того, их
использование позволяет определить
диапазоны ширины штрихов и пробелов, которым необходимо приписать одно и
тоже количество модулей ширины.
Полученные диапазоны ширины можно перевести в единицы
измерения, кратные целому количеству ширин модуля (элемента штрих-кода
минимальной ширины). Вектор таких значений передаётся далее для использования в
алгоритме декодирования штрих-кода.
Алгоритм декодирования штрихового кода.
Постановка задачи.
Алгоритм получает значения ширины элементов штрих-кода
(пробелов и штрихов) в модулях ширины.
Алгоритм должен декодировать символы, закодированные
шириной штрихов и пробелов.
Рекомендуемые алгоритмы декодирования описаны в ГОСТах
для соответствующих типов символик:
- ЕАН/ЮПиСи - ГОСТ Р 51201-98.
- 2 из 5 чередующийся” - ГОСТ Р 51001-96.
- Код 39 - ГОСТ 30742-2001 (ИСО/МЭК 16388-99)
- Код 128 - ГОСТ 30743-2001 (ИСО/МЭК 15417-2000).
Далее приведено подробное описание алгоритма
декодирования для символики «ЕАН/ЮПиСи», как наиболее часто используемой в
предприятиях розничной торговли (основной области применения разработанного
сканера). Описание для остальных символик опущено вследствие их схожести.
Отличие алгоритмов состоит лишь в различии таблиц перекодировки символов.
Символика ЕАН/ЮПиСи.
Определения.
Знак-разделитель — вспомогательный знак, используемый
для отделения информационных знаков и дополнительного
символа.
Четный паритет — характеристика кодирования знака
символа, указывающая, содержит ли он четное число темных модулей — штрихов
(сумма модулей штрихов знака четного паритета является четным числом).
Нечетный паритет—характеристика кодирования знака
символа, указывающая, содержит ли он нечетное число темных модулей — штрихов
(сумма модулей штрихов знака нечетного паритета является
нечетным числом).
Знак-ограничитель - комбинация штрихов/пробелов,
которая либо соответствует знаку СТАРТ и
СТОП в других символиках, либо служит для разделения основного
символа на две половины.
Коэффициент увеличения — постоянный множитель для
номинальных размеров символа «ЕАН/ЮПиСи».
Набор знаков — серия комбинаций штрихов и пробелов с четным или
нечетным паритетом, кодирующая цифры от 0
до 9.
Кодирование с переменным паритетом — процесс
кодирования дополнительной информации в последовательности знаков символа, при
котором на основе заданной комбинации знаков с четным или нечетным паритетом
представлены в неявном виде знак или контрольный знак
Сегмент символа — группа информационных знаков символа
заданной длины и комбинации
паритета, из которых образуются блоки в
символе «ЮПиСи» версии Д.
Требования к символике
·
«ЕАН/ЮПиСи» имеет
следующие показатели:
·
набор кодируемых
знаков: цифровой (от 0 до 9), т.
о. символы версии КОИ-7 но по ГОСТ 27463 с целочисленными значениями от 48 до
57:
·
тип кода:
непрерывный;
·
элементы в знаке
символа: 4, включая 2 штриха и 2 пробела, состоящие каждый из 1, 2, 3 или 4 модулей
по ширине (знаки-ограничители и
вспомогательные знаки имеют другое количество элементов);
·
самоконтролируемость
знака: присутствует;
·
длина
закодированной строки данных: фиксированная (различная длина — от 2 до 13
знаков, в зависимости от конкретного типа
символов):
·
многонаправленное
декодирование: присутствует;
·
контрольный знак
символа: один, обязательный:
·
плотность знака
символа: 7 модулей в знаке символа:
·
незначащая часть
кода: равна 11 модулям для символов «.ЕАН-13», «ЕАН-8» и «ЮПиСи-Л», 9 модулям для
символов «ЮПиСи-Е» и различному количеству модулей для других символов.
Структура символа включает в себя:
·
начальную
свободную зону (начальное свободное поле);
·
вспомогательные
знаки и информационные знаки символа, кодирующие данные и контрольный знак;
·
конечную
свободную зону (конечное свободное поле).
Кодирование знаков
Информационные знаки символа составляются из 7 модулей
и кодируются в наборах знаков A, B и C. (см. табл. 2).
Таблица 2. Наборы знаков A, B и C.
|
Знак данных |
Представление знаков и ширина элементов в модулях в наборе |
|||||||||||
|
А |
В |
С |
||||||||||
|
П |
Ш |
П |
Ш |
П |
Ш |
П |
Ш |
Ш |
П |
Ш |
П |
|
|
0 |
3 |
2 |
1 |
1 |
1 |
1 |
2 |
3 |
3 |
2 |
1 |
1 |
|
1 |
2 |
2 |
2 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
|
2 |
2 |
1 |
2 |
2 |
2 |
2 |
1 |
2 |
2 |
1 |
2 |
2 |
|
3 |
1 |
4 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
4 |
1 |
1 |
|
4 |
1 |
1 |
3 |
2 |
2 |
3 |
1 |
1 |
1 |
1 |
3 |
2 |
|
5 |
1 |
2 |
3 |
1 |
1 |
3 |
2 |
1 |
1 |
2 |
3 |
1 |
|
6 |
1 |
1 |
1 |
4 |
4 |
1 |
1 |
1 |
1 |
1 |
1 |
4 |
|
7 |
1 |
3 |
1 |
2 |
2 |
1 |
3 |
1 |
1 |
3 |
1 |
2 |
|
8 |
1 |
2 |
1 |
3 |
3 |
1 |
2 |
1 |
1 |
2 |
1 |
3 |
|
9 |
3 |
1 |
1 |
2 |
2 |
1 |
1 |
3 |
3 |
1 |
1 |
2 |
|
Примечание — Обозначения: П - пробел (светлый элемент), Ш - штрих (темный элемент), цифры — ширина каждого элемента в модулях. |
||||||||||||
Сумма модулей в штрихах знака
символа определяет его паритет. Знаки символа в наборе A являются знаками нечетного паритета, наборах В и С — четного паритета. Знаки символа
в наборе С представляют собой зеркальные изображения знаков набора В.
Знаки символа в наборах А и В всегда начинаются слева
со светлого модуля и заканчиваются справа темным модулем. Знаки символа в
наборе С начинаются слева с темного модуля и заканчиваются справа светлым
модулем.
Каждый знак данных обычно представлен определенным
знаком символа. Но в некоторых случаях сочетание знаков различных наборов в
символе может кодировать в неявном виде данные или контрольный знак. Такой способ является кодированием с переменным
паритетом.
Кодирование
вспомогательных знаков
Вспомогательные знаки составлены в соответствии с таблицей 3.
Таблица 3. Вспомогательные знаки.
|
Вспомогательный знак |
Количество модулей |
Представление знака и ширина элемента в модулях |
|||||
|
|
|
П |
Ш |
П |
Ш |
П |
Ш |
|
Типовой знак-ограничитель |
3 |
|
1 |
1 |
1 |
|
|
|
Центральный знак-ограничитель |
5 |
1 |
1 |
1 |
1 |
1 |
|
|
Специальный знак-ограничитель |
6 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Знак-ограничитель дополнительного символа |
4 |
|
1 |
1 |
2 |
|
|
|
Знак-разделитель
дополнительного символа |
2 |
1 |
1 |
|
|
|
|
|
Обозначения: П — пробел (светлый элемент), Ш—штрих (темный элемент), цифры — ширина каждого элемента в модулях. |
|||||||
Типовой знак-ограничитель соответствует знакам СТАРТ и СТОП в других символиках,
а специальный знак-ограничитель используют
как знак СТОП в символиках
«ЮПиСи-Е».
Символ «ЕАН-13».
Символ «ЕАН-13» составлен следующим образом (при
считывании слева направо):
- типовой знак-ограничитель;
- 6 информационных знаков символа из наборов знаков А
и В;
- центральный знак-ограничитель;
- 6 информационных знаков символа из набора знаков С;
- типовой знак-ограничитель.
- Последний информационный знак символа кодирует
контрольный знак.
Так как символ «ЕАН-13» содержит только 12
информационных знаков символа, но кодирует 13 цифр данных (включая контрольный
знак), значение дополнительной цифры — крайнего левого знака в представлении для визуального чтения —
представляется изменением паритета между знаками наборов А и В для 6
информационных знаков символа в левой половине символа. Кодирование начальной
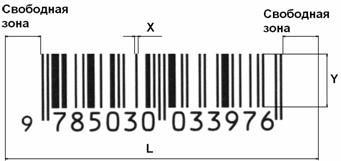
цифры должно соответствовать таблице 4. Пример символа штрихового кода «ЕАН-13»
приведен на рис. 31.
Таблица 4. Левая половина символа ЕАН-13.
|
Неявно закодированная |
Наборы знаков, кодирующие левую половину символа «ЕАН13» (номера позиций информационных знаков) |
|||
|
|
1 3 4 5 |
|||
|
0 |
A |
A |
A |
A |
|
1 |
A |
B |
A |
B |
|
2 |
A |
B |
B |
A |
|
3 |
A |
B |
B |
B |
|
4 |
A |
A |
A |
B |
|
5 |
A |
B |
A |
A |
|
6 |
A |
B |
B |
A |
|
7 |
A |
A |
B |
A |
|
8 |
A |
A |
B |
B |
|
9 |
A |
B |
A |
B |

Рис. 31. Символ штрихового кода «ЕАН-13»
Символ «ЮПиСи-А»
Символ «ЮПиСи-А» составлен следующим образом (при
чтении слева направо):
- типовой знак-ограничитель;
- 6 информационных знаков символа из набора А;
- центральный знак-ограничитель;
- 6 информационных знаков символа из набора С;
- типовой знак-ограничитель.
- Последний информационный знак символа кодирует
контрольный знак.
Алгоритм декодирования
На рис. 32 представлена блок-схема реализованного
алгоритма декодирования символик «ЕАН/ЮпиСи».
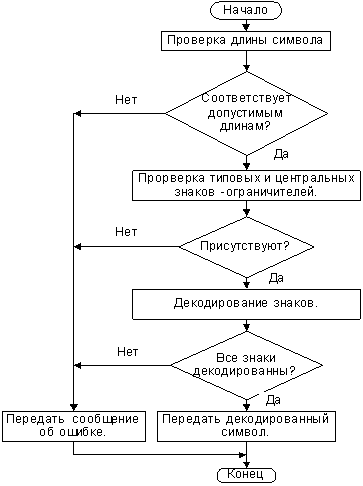
Рис. 32. Блок схема алгоритма декодирования символик «ЕАН/ЮпиСи».
Заключение.
Описанный алгоритм был внедрён и опробован в
экспериментальном образце видеосканера (см. рис. 33). В ходе испытаний сканер
показал высокую надёжность работы при различных условиях освещения и приемлемую
скорость обработки видео информации (от 6 до 12 кадров в секунду).
Автор выражает благодарность А. К. Платонову за ценные
советы при разработке алгоритмов работы видеосканера и за помощь при подготовке
этой публикации. Также хочется поблагодарить М. Маматова за помощь в реализации
устройства.

Рис. 33. Экспериментальный образец видеосканера штрих-кодов.
Список использованной литературы.
1. E. R. Davies, Machine Vision
2.
Кинсун Фу и др.
СБИС для распознавания образов и обработки изображений. –М.: МИР, 1988. - 247с.
3.
Roger C. Palmer, The bar code book. Helmers
Publishing, Inc. Formerly North American Technology, Inc., 1995.
[1] Операцию сравнения с порогом подразумевает присваивание 1 точкам, значение яркости которых больше или равным порогу, и присвоение 0 точкам, значение яркостей которых меньше порога.

 кодируется
шириной элементов в каждой строке.
кодируется
шириной элементов в каждой строке.  Код
Код