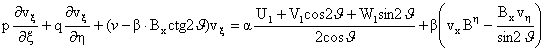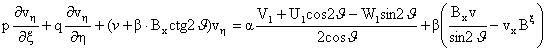Расчет отражения электромагнитного излучения молнии от ионосферы в плоском приближении с учетом нелинейного разогрева

( The Calculation of the reflection of the electromagnetic radiation of lightning from ionosphere in flat approach with provision for nonlinear heating
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Содержание

     Введение                                                                                 4

1.  Описательная постановка задачи                                         5

2. Математическая формулировка задачи                                7

3. Основы вычислительной методики                                     11

4. Пример расчета                                                                      14

5. Расчет модифицированной задачи                                       20

Введение

Настоящая публикация продолжает развитие тематики /1 – 4/  по расчетам отражения электромагнитных волн от ионосферной плазмы. В отличие от упомянутых работ, рассматриваются нестационарные процессы распространения излучения от источников типа молниевых разрядов, описание которых может выходить за рамки линейных моделей. Наиболее важным процессом такого типа является  нелинейный разогрев электронного газа, учет которого основан на использовании теоретической и экспериментальной информации (см., напр., /5/). В работе используется естественная для задач такого типа вычислительная технология, основанная на временном и характеристическом представлении задачи, что также отличает ее от публикаций /1 – 4/. Рассчитанные задачи отражения ЭМИ молниевого разряда дают основание рассматривать предложенную методику, как работоспособную во всем диапазоне параметров ионосферы. На основе анализа решений задач сформулированы тактические принципы организации расчетов, один из которых предусматривает эксплуатацию высокопроизводительных многопроцессорных ЭВМ. Исследовательская направленность проведенных расчетов заключается в определении механизма возникновения  высокочастотных осцилляций незначительной амплитуды, содержащихся в волне отражения. Параметры этих колебаний могут быть использованы как дополнительный инструмент исследования свойств ионосферной плазмы, поскольку существующий арсенал методов расчета отражения не полностью соответствует запросам геофизики (см. /6/).

Трудности решения нестационарной нелинейной задачи, и, тем более, выделения колебательных фрагментов малой амплитуды, заключаются для реальных начальных данных в разномасштабности характерных размеров в задаче, достигающих девяти десятичных порядков. Этот же факт может быть сформулирован указанием диапазона собственных чисел линеаризованной матрицы задачи, меняющихся от нуля до 10⁹.

1.  Описательная постановка задачи

     Описательная постановка задачи состоит в следующем. На плоский слой плазмы с заданными распределениями по высоте плотности свободных электронов, начальной частоты электронных соударений   и температуры, моделирующими распределение соответствующих характеристик в ионосфере Земли, при наличии внешнего геомагнитного поля B падает плоская, произвольно поляризованная электромагнитная волна под заданным углом J между нормалью к слою и направлением распространения фронта. Задача заключается в определении временной зависимости электрического и магнитного полей в отраженной волне при учете теплового разогрева плазмы.     Для решения задачи выбирается система  x,y,z декартовых координат, в которой плоский слой плазма толщиной Z_max расположен при z>0, а его нижняя граница лежит в плоскости x,y. Расчеты физических величин проводятся в системе единиц CGSE. Результаты представлены в других, более удобных системных, или внесистемных, единицах.

                              Рисунок 1. Схема геометрии задачи.

Рисунок 1 поясняет смысл и геометрию решаемой задачи.

Нормаль к фазовому фронту плоского электромагнитного импульса, падающего снизу на ионосферный слой, ортогональна оси x и расположена в плоскости (y,z). Она составляет угол J с вертикалью z. Должны быть рассмотрены процессы, развивающиеся в слое ионосферной плазмы и рассчитаны параметры отраженной волны при учете возможного наличия обеих поляризаций в падающей и отраженной волнах.

     В невозмущенной плазме задаются:

N_e(z) – начальное распределение электронной концентрации,

n₀(z) – начальная частота электронных столкновений,

T₀(z) – начальное распределение электронной температуры.

 Учет независимости распределений N_e, n₀, T₀ от координаты y, в условиях вышеприведенного описания постановки позволяет утверждать существование в задаче трансляционной симметрии, что означает возможность уменьшения на единицу размерности пространства аргументов. Начальные электрическое поле и токи отсутствуют. Учитывается постоянное поле В земного магнетизма. В начальный момент времени t=0 передний фронт падающей снизу волны проходит через начало пространственной системы координат. Решение не зависит от координаты x, что позволяет свести задачу к двумерной (включая время). Амплитудные характеристики компоненты излучения, соответствующей вертикальной поляризации, задаются проекцией магнитного поля волны на ось x, как функция времени. Аналогичные характеристики горизонтально поляризованной компоненты поля задаются независимой функцией времени для проекции электрического поля на ту же ось.

2. Математическая формулировка задачи

     Уравнения Максвелла:

              (1)

     Уравнения Лоренца для скоростей движения электронов в геомагнитном поле :

               (2)

     Уравнение локального баланса энергии, описывающее изменение T электронной температуры T_e :

            ,                     (3)

K=1.38×10^-16 – постоянная Больцмана.

     Параметр    характеризует средние потери электронной энергии при одном акте столкновения электрона с молекулами воздуха (при упругом характере этих столкновений  ~ 10^-3 , где m и M - массы электрона и молекулы, соответственно).

     В уравнении связи тока  со скоростью :

                        (4)

используется односкоростная аппроксимация функции распределения электронов по скоростям.

При анализе нелинейных эффектов используется предложенная в /5/  аппроксимационная  формула для температурной зависимости частоты электронных соударений:

                      (5)

Зависимости напряженности поля падающей волны от времени устанавливаются функциями f₁(t) и f₂(t):

                     H_x =f₁(t);   E_x =f₂ (t);                        (6)

Описание конкретной формы этих функций опускается. Следует отметить только возможность их произвольного задания на временной сетке или (и) в виде формульной комбинации полиномов, экспонент и синусоид.

   Особенностью методики является характеристическая форма определения задачи. В качестве  аргументов используются переменные, определяющие систему характеристик:

   (7)

      Вводятся новые неизвестные функции поля:

                                     (8)

      Для вектора тока вводятся новые компоненты:

                              (9)

                   .

Компонента по оси  x  остается неизменной.

      Для скорости электронов и вектора напряженности геомагнитного поля используются преобразования, аналогичные преобразованиям (9). Нижние и верхние индексы с точностью до нормировки соответствуют определениям ко- и контравариантных компонент векторов.

      Смысл введения координат (7) заключается в учете координатно-временной сдвиговой инвариантности решения и переходу к характеристическим направлениям. Введенные в (8) функции образуют независимую систему переменных на характеристиках.

      Координатная форма уравнений приводится ниже.

;

;

;

J_x = e×N_e ×v_x ;  J_x = e×N_e ×v_x ;  J_h = e×N_e ×v_h ;                            (10)

;

;;;

;

.

     В рассматриваемом нерелятивистском случае в уравнениях (10) далее будет использовано приближение  p=q=1. Поэтому сумма производных в 5 – 8 уравнениях системы (10) заменяется производной по t.

Вследствие того, что производная по t линейно выражается через производные по x и h, следует справедливость анонсированного предложения о двумерности задачи, подтверждаемая конкретной реализацией системы.

Решение системы уравнений (1) – (6) разыскивается в пределах Z_beg<z<Z_max   0<t<t_max.

       Область интегрирования  ОАВС системы (10) указана на рисунке 2.

       Начальные условия для искомых функций в ОАВС - нулевые.

      Граничные условия :

- на отрезке прямой ОА  U₁=U₂=0, а также все компоненты скорости и температура суть нули;

- на отрезке АВ  U₁=U₂=0, что свидетельствует об отсутствии волны, падающей  сверху на ионосферу;

- на отрезке ОС V₁=-2f₁(x)cosJ, V₂=2f₂(x)cosJ - выполняются условия (6) для напряженностей поля в падающей волне;

- нa отрезке ВС дополнительные граничные условия не требуются.

			B

 

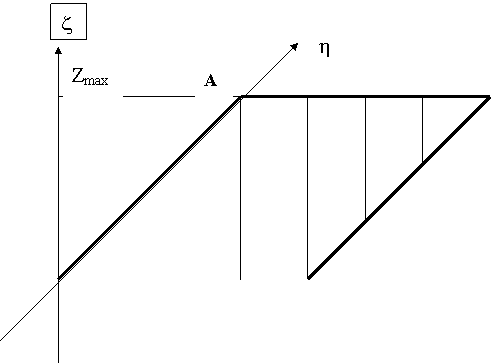
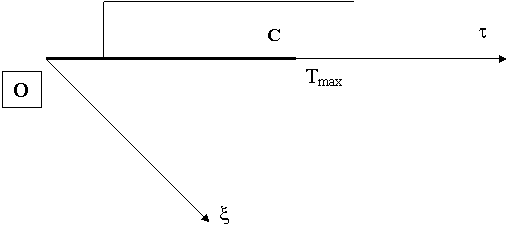
Рисунок 2. Область интегрирования и разностная сетка при Z_beg = 0.

3. Основы вычислительной методики

Характеристическая форма (10) двумерной задачи с девятью неизвестными (W₂ не учитывается вследствие тривиальности) позволяет легко конструировать различные аппроксимации второго порядка точности, три из которых излагаются ниже. Для унификации описания этих схем удобно записать систему (10) в матричной форме. Вводятся векторы , соответствующие характеристическим направлениям x, h, t:

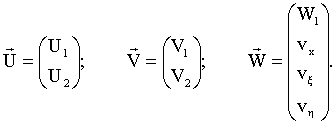          .                   (11)

Уравнение для температуры будет записано далее.

Вводятся матрицы:

;       ;

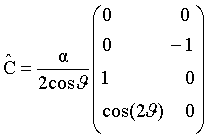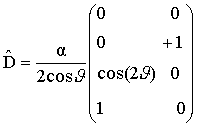    ;     ;     (12)

.

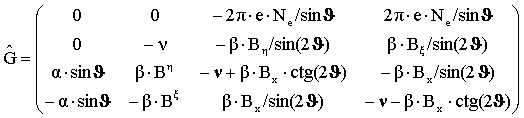В обозначениях (11), (12) система (10) приобретает вид:

;    ;    ;

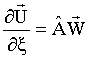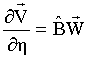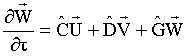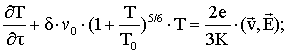                                           (13)

.

Далее, для упрощения индексации, матричные символы будут опущены.

 На рисунке 2 представлена квадратная сетка с шагами по сторонам, параллельным осям t, z, составляющим: Dt, Dz = h. Шаги по диагоналям, соответствующим осям x и h: Dx, Dh =2h. Ее узлы по горизонтали и вертикали нумеруются целочисленными парами (_k^j), соответственно. Середины сторон ячеек имеют полуцелую индексацию по обоим индексам.

Схема №1.

;      

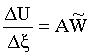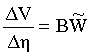                                 ;                                     (14)

; 

 .

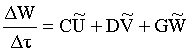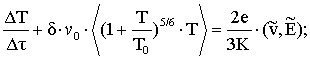
Знак D означает приращение функции на расчетном шаге по направлению соответствующей характеристики. Знак тильды означает усреднение функции, свое для каждого уравнения. Так, если для первого и второго уравнений разумно положить  , то для третьего естественным представлением среднего является . Угловые скобки также обозначают усреднение, удобное для вычислений.  Стрелками  указана трансформация значений величин при выполнении перехода (один шаг) от индекса k к индексу k+1. В формулах со стрелками содержится вся информация о пространственной локализации переменных и о тактике вычислений. Для последующих схем достаточно ограничиться формулами  перехода. Из рассматриваемых схем является наиболее дешевой. Частично неявная, требует решения линейной алгебраической системы четвертого порядка. Использовалась для сравнений при разработке производственной методики.

Схема № 2.

   ;   ;   ;         (15)

Неявная по электродинамическим уравнениям схема. Требует решения линейной алгебраической системы восьмого порядка. Достоинство: существует точка (_k+1/2^j+1/2), в которой со вторым порядком точности аппроксимируется сразу вся система. Схема использовалась для построения частотного анализатора, что будет изложено позже.

Схема № 3.

      ;   ;   ;             (16)

 Неявная по электродинамическим уравнениям схема. Требует решения линейной алгебраической системы восьмого порядка. Аппроксимация отдельных подсистем системы (13) со вторым порядком точности осуществляется в различных точках плоскости tz.

Для аппроксимации со вторым порядком полной системы в каждой из всех трех схем могут потребоваться дополнительные операции для нелинейного теплового уравнения (например, итерации).

4. Пример расчета

Распределения по высоте плотности электронов N_e(z) и частоты электронных соударений (z) с молекулами для дневных условий заимствованы из книги /7/ с последующим сглаживанием данных. Рисунки 3-а,  3-б  иллюстрируют зависимости от высоты ионосферного слоя (отсчитываемого от земли) десятичных логарифмов соответственно электронной концентрации N_e и частоты электронных соударений.

Рассчитана задача для следующих начальных данных:

- нижний слой ионосферы Zbeg = 50 км (отсчет от поверхности Земли);

- глубина ионосферного слоя Zmax = 300 км;

шаги расчетов, излагаемых в настоящем разделе, Dt = 1000; 100;  10 нс;

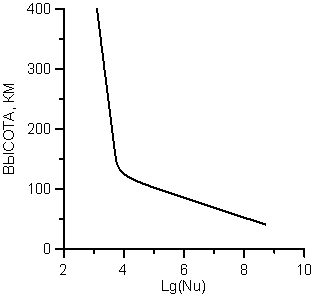
              а)                                                              б)

Рисунок 3. Зависимости от высоты z:

а) концентрации электронов N_e, б) частоты электронных соударений .

- конечные моменты расчетов tmax = 600; 600; 1000 мкс (соответственно шагам);

- угол падения волны J = 60^о;

- геомагнитное поле  (B_X = 0.16, B_Y = 0, B_Z = -0.46) Э;

Константа dlt = 0.005 (см. формулу (4)).

Начальное распределение температуры постоянно: T₀(z) = 250 ^oK.

Введенная в расчет зависимость напряженности поля в падающей волне от времени, согласно книге /8/, соответствует таковой в типичной картине разряда молнии при регистрации на больших расстояниях.  Приведенная на рисунке 4 временная зависимость напряженности поля падающей волны в В/м соответствует расстоянию  100 км от молниевого разряда. В выбранной  системе координат горизонтальная компонента геомагнитного поля ориентирована вдоль оси x, то есть перпендикулярно плоскости распространения.

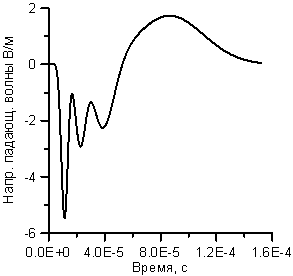
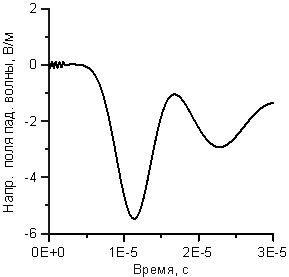
         а)                                                           б)

Рисунок 4.  Зависимость напряженности поля падающей волны

от времени: а)– основной вариант, б) – модифицированный.

Для рассчитываемой задачи выбрана вертикальная поляризация поля падающей волны, т. е. та, в которой направление магнитного поля совпадает с осью x (или направлением горизонтальной компоненты магнитного поля Земли). Для удобства восприятия в дальнейшем такая поляризация электромагнитного поля будет именоваться первичной, в то время как горизонтальная поляризация – вторичной. Временная зависимость волны первичной поляризации, использованная для расчетов настоящего раздела, изображена на рисунке 4-а Этот вариант рассматривается как основной. Модифицированный вариант представлен на рисунке 4-б. От основного варианта отличается зависимостью поля на коротком интервале в начале процесса импульса. Будет обсуждаться в следующем разделе.

На рисунке 5-а приведен результат расчета инвариантной компоненты  U₁ = E_Y + H_X×cosJ  первичной поляризации поля отраженной волны в В/м в зависимости от времени. Компонента поля U₂ =H_Y + E_X×cosJ вторичной поляризации, существующая только при ненулевом внешнем магнитном поле, представлена на рисунке 5-б. Расчеты проводились с тремя шагами: 1000, 100 и 10 нс. На рисунке 5 изображены крайние расчеты, поскольку промежуточный , с шагом 100 нс, на графиках неотличим от расчета  с шагом 10 нс. Слабое расхождение линий графиков для различных шагов позволяет  сделать заключение о наличии внутренней сходимости. Выводы о количественной закономерности скорости сходимости можно сделать по данным таблицы 1. Ее содержанием является информация о расположении и значении максимума в основной отраженной волне. Максимум определялся по трем последовательным значениям программной выдачи результатов в окрестности момента t @ 1.55×10^-4 с последующей квадратичной интерполяцией. В таблице приведены также данные о длительности расчета на ЭВМ PC-800 МГц.

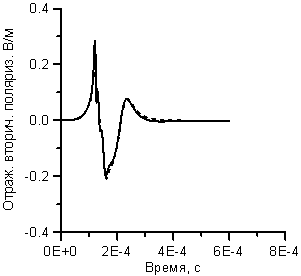
Отличием волны вторичной поляризации является более заметная зависимость результатов расчетов от длительности шага .

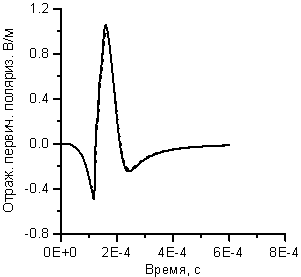
    a)                                                                    б)

Рисунок 5.  Зависимость поля отраженной волны от времени

 в расчетах до момента t=0.6×10^-3 cек. с шагами

 Dt = 10 нс (сплошная линия) и Dt=1000 нс (пунктир) для:

а) - компоненты U1 первичной поляризации

б) - компоненты U2 вторичной поляризации

Таблица 1 

    Для исследования ионосферных процессов, помимо параметров отраженных волн, может оказаться полезной и другая информация, получаемая при расчетах данной задачи.

а                                                              б

                                          в

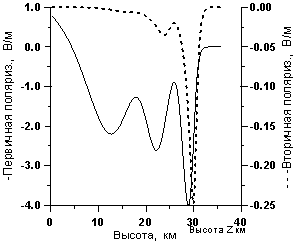
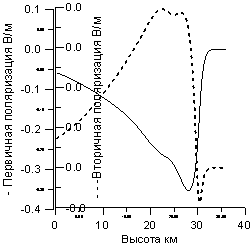
Рисунок 6. Разрез по высоте значений компонент решения:

а) по направлению волны падения сплошная линия -V₁-первичная,

пунктирная - V₂.-вторичная поляризация;

б) по направлению волны отражения сплошная линия - U₁-первичная,

пунктирная  - U₂-вторичная поляризация;

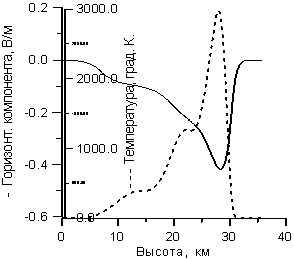
в) сплошная, - значения W₁ компонент поля вдоль характеристики t,

пунктир- график приращения T температуры, рассчитанной по формуле /3/.

На рисунке 6 представлено распределение основных расчетных величин по высоте ионосферы на момент времени t = 60 мкс.  Отсчет высот ведется от нижнего ионосферного слоя, расположенного на расстояние 50 км от поверхности Земли.   На  рисунке 6а приведены графики распределения по высоте ионосферного слоя V₁- первичной и V₂ – вторичной характеристических компонент электромагнитного поля, распространяющихся вдоль координатной оси h, т.е. по направлению падающей волны. Напряженности для обеих поляризаций  представлены раздельно: сплошной линией – первичная поляризация, пунктиром – вторичная.    На  рисунке 6-б приведены графики распределения по высоте ионосферного слоя U₁ - первичной и U₂ – вторичной характеристических компонент электромагнитного поля, распространяющихся вдоль координатной оси x, т.е. по направлению отраженной волны. Напряженности для обеих поляризаций также представлены раздельно. На графиках волн отражения (типа изображенных на рисунке 5) информация по температуре не приведена, как не представляющая особого практического интереса. Но так как высотное ее распределение носит немонотонный характер, то положение и значение максимума может оказаться полезным, например, в качестве одной из характеристик развивающихся в ионосфере физических процессов или для апостериорной оценки пределов применимости использованной модели теплового разогрева плазмы. Построение замкнутой системы уравнений задачи проведено в рамках “элементарной” теории нелинейного взаимодействия электромагнитного импульса с ионосферной плазмой, развитой в монографии /5/, с использованием аппроксимационной формулы (5), справедливой для сравнительно несильного разогрева электронной компоненты плазмы при Т<10^{4 o}K. На рисунке 6-в приведен график распределения по высоте электронной температуры, позволяющий установить области в ионосфере с максимальным разогревом ионосферной плазмы.

Использование выполненных в настоящей работе расчетов позволяет осуществить апостериорную оценку о значениях размеров областей применимости использованных допущений, а также оценить влияние нелинейности в данной модели. Результаты одной из серий таких расчетов приводятся ниже, в таблице 2, и заключаются в информации о значениях приращения максимальной температуры Tmax и ее локализации в ионосферной плазме при подобных вариациях напряженностей поля в падающей волне. В таблице 2 значения основного варианта, повсеместно приводимые выше, помечены жирным шрифтом.

Таблица 2.

5. Расчет модифицированной задачи

В докладе /9/, посвященном начальному этапу разработки методики решения и анализу первых результатов излагаемой задачи, отмечались колебания в пятом-шестом знаках напряженности поля волны отражения. Факт их наличия был установлен и подтвержден прецизионными расчетами на вычислительном комплексе МВС-1000. В настоящем разделе, на базе проведенных расчетов, излагаются эвристические соображения о причинах возникновения этих явлений. Интерес к исследованию колебаний в решении связан с возможностью уточнения состояния ионосферы по параметрам колебаний в отраженной волне электромагнитного излучения. Ради удобства изложения предварительно будут указаны некоторые технические детали расчетной методики, определяемые свойствами рассматриваемой задачи. Вначале будет рассмотрен линейный случай задачи без теплового нагрева электронного газа. Его реализация осуществляется либо в расчетах с малыми (<< 1 В/м) значениями максимума модуля напряженности поля падающей волны, либо простым обнулением рассчитанных значений приращения температуры. Нелинейный случай будет рассмотрен последним.

Основой последующих выводов является оценка высотного распределения мгновенных значений спектра разностной задачи. Она осуществляется следующим образом. Пусть, в расчетной ячейке OABC, приведенной на рисунке 7, вертикальная  сторона с номером k является носителем начальных данных. Пусть, далее, ее размер составляет h, т.е. Dt=h, Dz=h. Тогда, в этой ячейке Dx=2h, Dh=2h. Запись формул (14) с центрированием усреднения в точке М приводит к разностной схеме № 2 (см. формулы (15)) с аппроксимацией второго порядка точности. Переобозначение переменных схемы малыми литерами  ; ;  с последующими заменами приращений вдоль характеристик их значениями через размер h, а их, в свою очередь, через  Dt приводит после предельного перехода Dt®0 к линейной системе обыкновенных дифференциальных уравнений. Введение вектора q, объединяющего векторы u, v, w и матрицы R, объединяющей A, B, C, D, G, позволяет записать систему в стандартной форме:

                                       dq/dt=Rq.                                          (17)

Эта система справедлива в пределах рассматриваемой сеточной ячейки и ее решение позволяет продлить значение вектора q из точки D задания начальных данных в точку E завершения сеточного шага: q(D) Þ q(E). Последующее расслоение q(E) на векторы , ,  и обратное переобозначение , , ,

Рисунок 7. Схема построения системы обыкновенных д.у.

носящее, так же как и прямое, смысл операторов сдвига векторной информации, завершают перенос начальных значений искомых функций на один сеточный шаг. Совокупность этих операций означает аппроксимацию системы (13). Очевидно, ее порядок равен порядку аппроксимации системы (13) промежуточной разностной схемой (14), т.е. двум. Отличие от схемы (14) состоит, во-первых в трассе перемещения информации. Так, трасса по отрезку характеристики АС для вектора v (штрих) заменяется ломаной ADEC (точки) для вектора V. Во-вторых, вместо точечных носителей классических разностных схем (14) представление (17) позволяет получить решение в виде суммы взвешенных экспонент от аргументов (), k=1,..8. Восемь слагаемых соответствуют порядку системы (17) или системы (13) без температуры. 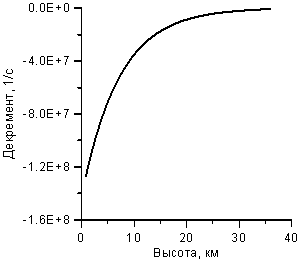Система (17) в проводимых расчетах ограничена ролью анализатора собственных значений Но ее правомочность, как расчетной схемы на сеточном квадрате рисунка 7, контролируется по результатам перевода начальных данных с одного временного шага на последующий: 1)ее аналитическим решением и 2) используемой классической разностной схемой, не являющейся источником этой системы. Совокупность , k=1,…8 составляет мгновенный локальный спектр оператора R. В качестве примера, полезного для дальнейшего, на рисунке 8 приводится высотное распределение l_1,2 (z) – наибольших по модулю собственных чисел.

    а                                                                  б

Рисунок 8.  Распределение по высоте

наибольших по модулю собственных чисел:

а) – мнимая часть;   б) – вещественная

В качестве примера полного набора собственных чисел приводится их комплект для высоты 28,52 км: l_1,2 = -0.2619E+07 ± i×0.8659E+07;

l_3,4 = -0.3149E+05 ± i× 0.8073E+05;  l₅ = -0.1759E+07;   l₆ -0.8915E+06;

  l₇ = 0.0;   l₈ = 0.0; Этот пример позволяет сделать вывод о том, что система (17) является жесткой. Действительно, разбиение спектра на два подмножества, в одно из которых входят нулевые собственные значения, а во второе все остальные, позволяет применить классификационный признак жесткости с положительным результатом (см., например, /10/).Причинами появления знаков << в указанном признаке, или, что то же, разномасштабности длин переходных режимов (пограничных слоев) являются большие критериальные параметры в правых частях системы (13). Обезразмеривание в этой системе всех переменных, кроме времени, приводит к двум характерным параметрам задачи: b = a×||||/c @ 0.9×10⁷ [1/c] и .Например, для высот от нуля до z = 300 км этот параметр меняется в пределах от нуля до  w @ 1.4×10⁸ [1/c]. Аналитические оценки собственных чисел утверждают наличие в них множителей w либо b для различных ситуаций. Таким образом, именно их значения ответственны за необходимость применения неявных вычислительных схем с большими весами для окончания расчетного шага, что формально означает падение порядка точности до первого. Восстановление второго порядка точности достигалось приемами пересчета первичных результатов шага. В некоторых случаях, но не всегда, применение таких приемов приводило к повышению эффективности расчета. Для унификации условий все данные по скорости прохождения задач относятся к расчетам по схемам первого порядка точности.

Обращаясь к основной теме настоящего раздела, изложим ряд расчетных результатов, из которых будут извлечены главные выводы.

1. Положим, что предметом изучения являются колебания с частотой 2 МГц. Рассчитывалась модифицированная задача с напряженностью поля падающей волны f(t) = f₀ + Df, где f₀ – напряженность основного варианта, изображенная на рисунке 4-а. Добавка определяется формулой:

     Df = 0.1×sin(2pt×2×10⁶),  t Î [0; 2×10^-6];   Df = 0,  t Ï [0; 2×10^-6],         (18)

т.е. это есть четыре периода синусоиды с частотой 2 МГц.

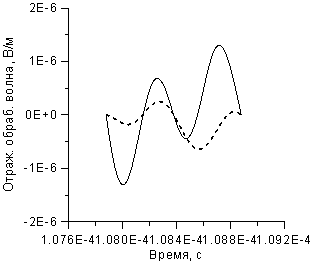
Модифицированная функция f(t), включающая добавку Df, изображена при начальных значениях времени на рисунке 4-б. Рассчитанная отраженная волна обеих поляризаций представлена на рисунке 9-а. Расчет проводился с 16-изначными числами и шагом Dt = 2 нс. На рисунке 90-б представлен фрагмент волны отражения первичной поляризации в окрестности момента 108 мкс. Этот график представляет собой периодическую структуру с частотой, близкой к 2 МГц. Для наглядности машинный результат обработан введением локальных приращений напряженности, удалением тренда и средней кривизны. В более ранние моменты обнаружены колебания той же частоты, но с амплитудами порядка 10^-7, 10^-8 и 10^-10 В/м. В модифицированном варианте задачи результат рисунка 9-б означает колебания в пятом, шестом знаке.

2. В основном варианте задачи подобные формы отсутствуют.

  а                                                                   б

Рисунок 9. Отражение модифицированной волны.

а):  Сплошная линия – первичная поляризация, пунктир – вторичная.

б):  Обработанный фрагмент волн отражения .

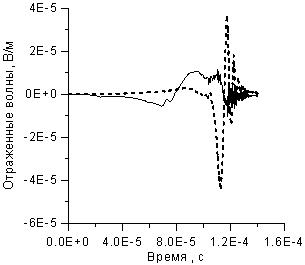
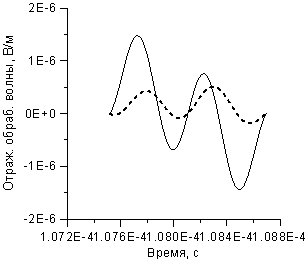
3. На рисунке 10, приводятся результаты по задаче, решенной только для возмущения Df напряженности поля падающей волны. Графики рисунка 10-а дают общую картину отражения. Из нее видно, где происходят колебания на отражении первичной поляризации. В картине фрагмента на рисунке 10-б видна аналогия с изображением 9-б, несмотря на разницу (варьируемого) тренда.

  а                                                                 б

Рисунок 10. Отражение волны возмущения.

Сплошная линия – первичная поляризация, пунктир – вторичная.

a) Общая картина отражения.  б) Фрагмент отражения.

4. При решении задачи предыдущего, третьего, пункта была сделана выдача по отрезку трассы отраженного сигнала, т.е. вдоль линии h = const, от максимума по вертикали в 35.4 км до точки приема на нижнем слое ионосферы в момент 118 мкс. В выдачу вошли компоненты поля U₁, U₂ первичной и вторичной поляризаций, распространяющиеся вдоль оси h (x=const), т.е. по направлению падающей волны и компоненты V₁,V₂ отраженной волны, распространяющиеся вдоль оси x. Графики представлены на рисунке 11. Из него видно, что все характеристические проекции напряженности поля испытывают резкий подъем на 36-м километре высоты ионосферного слоя. Начало подъема можно отнести  к 28 – 30-му километру.

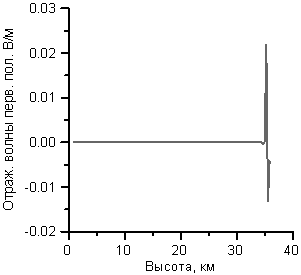
5. Обращаясь к рисунку 9, отметим, что собственная функция частоты 2 МГц (круговая частота 1.26×10⁷ 1/с) достигается на высоте  35-36 км. На этих же высотах декремент затухания имеет сравнительно небольшие значения.

   а                                                                б

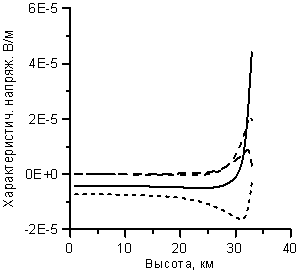
Рисунок 11. Характеристические напряженности поля на нисходящем отрезке трассы распространения отраженного сигнала. Сплошная линия – первичная поляризация, пунктир – вторичная. а) Компоненты поля вдоль направления оси h падения волны, б) –  компоненты поля

вдоль направления оси x отражения.волны

6. Нелинейная задача, учитывающая тепловой разогрев,  решалась до момента t = 140 мкс в двух вариантах- с шагами Dt = 2  и 0.25 нс. Она содержит ряд специфических особенностей, подлежащих учету при вычислении осцилляций. Высотное распределение собственных чисел, типа приведенного на рисунке 8, становится зависимым от решения. Замечание в конце предыдущего раздела о приближенной линейности электродинамических результатов вне зависимости от температуры относится только к низкочастотной составляющей решения, но не к малым высокочастотным элементам вообще. 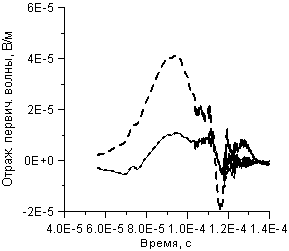Решение имеет общую (низкочастотную) картину отражения мало отличающуюся от изображенной на рисунке 5. На рисунке (12) приводятся результаты расчетов отражения при напряженности поля в падающей волне только от возмущения Df, определенном формулой (18), но в различных температурных полях.. Из данных расчетов следует, что при слабых суммарных полях падающих волн порядка десятых долей В/м линейная модель успешно описывает высокочастотные колебания. На рисунке 12 это выражается в совпадении сплошной линии и линии с мелким штрихом.  Но на разрядах молний, типа изображенного на рисунке 4, выделение высокочастотных осцилляций независимым расчетом элементов разложения поля падающей волны может привести к принципиальным погрешностям. Этому заключению на рисунке 12 соответствует отличие линии с крупным штрихом от остальных. Раздельный расчет малых добавок может производиться только в суммарном тепловом поле.

а                                                                б

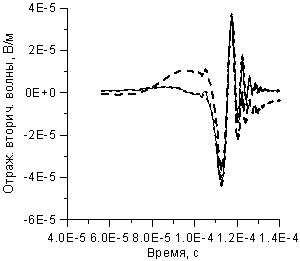
Рисунок 12.  Отражение малого возмущения Df в температурных полях:

сплошная линия – при нулевой температуре,

мелкий штрих – в собственном температурном поле,

крупный штрих – в поле суммарной волны f+Df;

а) – первичная поляризация;  б) – вторичная поляризация

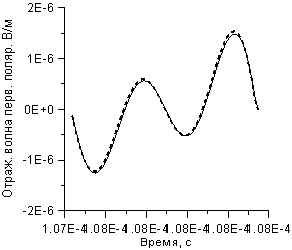
На рисунке 13 приведены отдельные результаты расчетов нелинейной задачи с возмущением, относящиеся к вопросу об осцилляциях. Рисунок 13-а представляет собой сопоставление идентичных фрагментов грубого (шаг 2 нс) и точного расчетов. Из предыдущего опыта решения аналогичных задач использован тот факт, что расчеты с шагами 0.25 и 0.5 нс приводят к одинаковым параметрам осцилляций. На этом основании расчет с шагом 0.25 нс будет именоваться «точным». Впечатление совпадения расчетов на рисунке 13–а объясняется обработкой результатов расчетов, состоящей из устранения смещений, тренда и кривизны. В действительности разница напряженностей демонстрируемого фрагмента составляет 1.4×10^-5 В/м, т.е. на порядок больше значения анализируемой амплитуды осцилляций.

             a                                                             б

Рисунок 13. Расчеты с учетом теплового разогрева:

а) - фрагмент отражения волны первичной поляризации;

штрих – шаг расчета Dt = 2 нс, сплошная линия Dt = 0.25 нс;

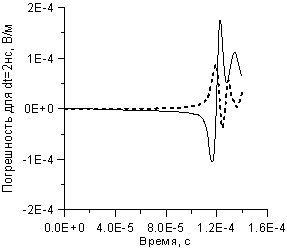
 б) – разность значений волн отражения при шагах 0.25 и 2 нс

сплошная линия – первичная поляризация, штрих – вторичная.

.

Полностью разница расчетов на интервале (0; 140) мкс, т.е. погрешность расчета с шагом 2 нс, показана на рисунке 13-б. Вывод из данных рисунка 13 состоит в необходимости «точного» расчета при анализе осцилляций с малой амплитудой в нелинейной задаче. Разница с линейной задачей состоит в том, что в последней точный расчет не более, чем желателен. Однако, в групповых вариациях нелинейной задачи достаточно проведение единственного опорного точного расчета для оценки значений возможных смещений, а полный анализ осцилляций достаточно проводить на грубых режимах. Основой этой концепции являются слабая нелинейность (см. таблицу 2), малости слагаемых в падающем импульсе, инициирующем осцилляции, совпадение частот и амплитуд на рисунке 13-а.

Из изложенного материала следуют два вывода.

В качестве эвристической гипотезы, согласующейся с пунктами 1 – 5, выдвигается утверждение: высокочастотные колебания в отраженной волне формируются в результате резонансного взаимодействия пакетов осцилляций падающей волны с ионосферными зонами, обладающими соответствующими собственными частотами. Возникающая амплитуда зависит от частоты через соответствующие значения декремента затухания.

Пункты 1 – 6 позволяют оценить экономические особенности двух тактик проведения расчетов, допускаемых рассматриваемой методикой.

I. В случае затруднений с ресурсами ЭВМ рациональная тактика для определения осциллирующих компонент малой амплитуды заключается в следующей организации. Напряженность поля падающей волны должна быть априорно разложена на гладкую и осциллирующие составляющие. В линейном случае расчету подлежат независимо как элементы разложения, так и задача с полной напряженностью (для контроля). При малых порядках амплитуд осциллирующих компонент различимость осцилляций возрастает на эти порядки. Такая тактика позволяет проводить расчеты на грубой сетке, избегать использования двойной точности в численных расчетах и использования многопроцессорной техники. Роль последней в этом случае ограничивается исследованиями во внештатных ситуациях и проведением контрольных расчетов.

II. Наличие многопроцессорной техники позволяет решать задачи единым действием, что сокращает сроки исполнения и экономит ресурс времени исследователей. В качестве примеров времени работы ЭВМ, затрачиваемого на решение рассматриваемых задач до момента t= 140 мкс, и шагом 0.25 нс приведем следующие данные. ЭВМ МВС-1000 М для программы на «Фортране», обработанной системой DVM (см. /11, 12/), при 100 процессорах и коэффициенте их использования от 0.31 до 0.38. затрачивает от 4411 до 3552 секунд работы, а при 200 процессорах и коэффициенте 0.249 – 2700 сек.  Время для расчета одного варианта , затрачиваемое машиной PC/800 МГц при шаге 2 нс, составляет 3.5 часа.

Литература

1. В.Я. Арсенин,   В.А. Горячев,   В.П. Загонов,   М.Н. Нечаев,                   В.Н. Приставко,  Р. А. Трахониотовская.   Расчет импульсных функций отражения радиосигналов от ионосферы в плоской модели для произвольного состояния ионосферного слоя. .  Препринт ИПМ АН № 114, М., 1974 г.

2. В.Я. Арсенин,   В.А. Горячев,   В.П. Загонов,   М.Н. Нечаев,                   В.Н. Приставко,  Р. А. Трахониотовская.   О влиянии состояния ионосферы на форму импульсной функции ионосферного отражения.  Препринт ИПМ АН № 2 М., 1975 г.

3. В.Я. Арсенин,   В.А. Горячев,   В.П. Загонов,   М.Н. Нечаев,                   В.Н. Приставко,  Р. А. Трахониотовская.   О влиянии геомагнитного поля на распространение волн СДВ и ДВ диапазонов в ближней зоне волновода Земля – ионосфера.  Препринт ИПМ АН № 20, М., 1976 г.

4. В.Я. Арсенин,   В.А. Горячев,   В.П. Загонов,   М.Н. Нечаев,                   В.Н. Приставко,  Р. А. Трахониотовская.   О методе расчета коэффициентов отражения радиоволн СВ и КВ диапазонов от ионосферы.  Препринт ИПМ АН № 134, М., 1978 г.

5. А.В. Гуревич, А.В. Шварцбург. Нелинейная теория распространения радиоволн в ионосфере. М., «Наука», 1973 г.

6. Магнитосферно-ионосферная физика. Краткий справочник под ред. Ю.П. Малышева. СПБ, «Наука», 1993 г., стр.163.

7. Я.Л. Альперт. Распространение электромагнитных волн и ионосфера. «Наука», 1972 г.

8. Э.М. Базелян , Ю.П. Райзер.  Физика молнии и молниезащиты. Физматлит, М., 2001 г.

9. Брылев Ю.Н., Поддерюгина Н.В., Подливаев И.Ф. Эффективность использования мощных ЭВМ в конструировании вычислительных методов и трактовке результатов расчета ионосферного отражения электромагнитной волны с учетом нелинейного разогрева. Международный семинар «Супервычисления и математическое моделирование». Тезисы докладов. РФЯЦ, Всероссийский НИИ экспериментальной физики, Саров, июнь 2002 г.

10.  Математическая энциклопедия. Том 2, стр. 411, «Советская энциклопедия», М., 1979 г., стр. 411

11.  Система DVM. http://www.keldysh.ru/dvm/

12.  Коновалов Н., Крюков В. Параллельные программы для вычислительных кластеров и сетей. Открытые системы, март, 2002 г., стр. 12–18.