МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

РАСПРОСТРАНЕНИЯ ФЕМТОСЕКУНДНОГО ИМПУЛЬСА

А.Д. Балашов, А.Х. Пергамент

Институт прикладной математики им. М.В. Келдыша РАН

Работа посвящена исследованию численными методами распространения фемтосекундных лазерных импульсов в атмосфере. Характер явления определяется соотношением между процессами многофотонной ионизации и множественной мелкомасштабной самофокусировки (филаментации). Резкое уменьшение актуального размера задачи в процессе самофокусировки, а также необходимость обеспечить точность аппроксимации при расчете неустойчивости, каковой является филаментация, приводит к тому, что используются сетки с мелким шагом, общий объем которых достигает 10¹² ячеек. Расчеты такого объема выполнены на кластере с применением технологии параллельного программирования. Установлен ступенчатый характер развития процесса, при котором до достижения пороговых значений интенсивности происходит развитие филаментации без потери энергии импульса. При достижении пороговых значений интенсивности начинается потеря энергии на ионизацию, сопровождаемая дефокусирующим воздействием электронной плазмы, что приводит к потере интенсивности. При падении интенсивности ниже порогового значения могут создаться условия для повторного зарождения самофокусировки.

MATHEMATICAL MODELING

OF FEMTOSECOND PULSE PROPAGATION

A.D. Balashov, A.Kh. Pergament

Keldysh Institute for Applied Mathematics Russia Academy of Science

This paper is devoted to the investigation of the femtosecond pulse propagation in the air by means of numerical methods. The phenomenon behavior is determined by the relation between the multiphoton ionization and small-scale self-focusing (filamentation). A sharp decrease of the problem actual size during self-focusing and necessity need of the accuracy for the approximation of calculations result in the numerical meshes of small-scale with number of steps about of 10¹². These calculations were made by means of the cluster with using of parallel programming algorithms. The step-by-step behaviour of this process was established, where the evolution of filamentation takes place without energy losses till the intensity reaches the threshold value. Then the dissipation for ionization comes into play and the intensity starts to decrease under defocusing influence of electron plasma. The conditions for repeated self-focusing can be formed after the intensity is below the ionization threshold.

Введение

Среди всевозможных режимов распространения лазерного излучения в нелинейной среде, распространение мощного фемтосекундного импульса представляет в настоящий момент особый научный интерес. Области применения таких знаний: дистанционное зондирование, микрофотоника, дистанционное управлении электрическим разрядом [1]. Впервые эксперименты по дальнему распространению фемтосекундных лазерных импульсов были выполнены в середине 1990-ых [2-4]. В этих экспериментах использовался инфракрасный лазер с продолжительностью импульса около 100 фс и мощностью превышающей , т.е. мощностью, достаточной для самофокусировки импульса [5]. В экспериментах наблюдался распад начального пучка на узкие нити длиной несколько метров. Количество возникающих нитей зависело от мощности импульса. В каждой из них была сконцентрирована доля мощности импульса.

В результате самофокусировки растет интенсивность импульса и уменьшается его ширина, но «схлопывания» не происходит из-за дефокусирующего воздействия электронной плазмы, созданной многофотонной ионизацией молекул воздуха. В результате, максимальная интенсивность в филаменте не превышает для инфракрасных импульсов. В зоне максимальной интенсивности регистрируется движущийся вдоль оси распространения импульса фокус, след которого принято называть филаментом (от англ. filament – нить), а процесс образования таких структур - филаментация. Возникновение нескольких фокусов при наличии достаточной мощности импульса обычно объясняется мелкомасштабной самофокусировкой шумовых возмущений начального профиля импульса [6] либо отсутствием его аксиальной симметрии [7].

Два процесса формируют характерные особенности явления, рассмотренного в этой работе: неустойчивость Беспалова-Таланова, которая порождает мелкомасштабную самофокусировку, и дефокусирующее влияние электронной плазмы, созданной за счет многофотонной ионизации. Данное исследование показало, что до тех пор, пока максимальная интенсивность импульса не достигнет пороговых значений, не наблюдается потери энергии – мощность импульса не меняется. Только после достижения порогового значения интенсивности начинается процесс многофотонной ионизации, и падают как мощность, так и интенсивность импульса, после чего многофотонная ионизация прекращается.

В настоящее время четырьмя институтами Франции и Германии выполняется проект «Teramobile» по экспериментальному и численному исследованию распространения мощных фемтосекундных импульсов. В результате этих экспериментов по распространению терраватных импульсов наблюдалось несколько десятков филаментов, которые упорядочивались в группы (кластеры) протяженностью более десяти метров.

Существует значительное количество работ различных авторов, посвященных математическому моделированию процесса филаментации [7;8;14;16]. Рассматриваемая для данного явления система уравнений для медленно меняющейся амплитуды светового поля является нестационарной 3-х мерной задачей. Для того, чтобы иметь возможность сравнить экспериментальные данные с расчетами при условии учета мелкомасштабных возмущений, требуется порядка ~10¹⁶ счетных ячеек. Такое большое количество делает счет уравнений при больших расстояниях слишком долгим. Для качественного исследования образования филамент и их упорядочивания в кластеры применяется упрощенная физическая модель, которая в совокупности с использованием технологий параллельных вычислений позволяет в обозримое время провести счет задачи.

Как известно, для всех естественных пластов характерна развитая в той или иной степени трещиноватость. С помощью модели с двойной пористостью и двойной проницаемостью, возможно, описать трещиновато-пористую среду. Поскольку проницаемость в трещинах очень велика, то давление в них устанавливается гораздо быстрее, чем в порах, так что для описания таких процессов можно использовать квазистатическое уравнение. Кроме того, можно предположить, что объем трещин пренебрежимо мал, и, как следствие можно пренебречь величиной флюидосодержания в трещинах. В результате получается модель, отличающаяся от модели Био для пористых сред дополнительным уравнением.

Физическая модель и ее усреднение

Для описания процесса распространения коротких импульсов в среде с кубической нелинейностью обычно используется следующая система уравнений [8]: нелинейное уравнение Шредингера (НУШ) для огибающей электрического поля , движущейся с групповой скоростью vg (здесь , z – переменная, вдоль которой распространяется импульс, – поперечная направлению распространения импульса плоскость):

, (1.a)

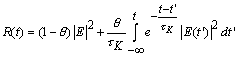где (1.б)

и модель Друда [19] для локальной плотности плазмы :

, (1.в)

где l₀ = 800 нм - длина волны; – центральное волновое число; n₂ = 3.1·10 ^-19 см²/Ватт - индекс преломления эффекта Керра; k″ = 0.2 фс²/см - коэффициент дисперсии групповой скорости; – время релаксации; r_c = 1.8·10 ²¹ см^-3 - критическая плазменная плотность; b ^(K) = 4.25·10 ^-98 см¹³/Ватт⁷ - коэффициент многофотонного поглощения; - число фотонов, которое требуется для ионизации; s  = 5.44·10 ^-20 см² - коэффициент каскадной ионизации и плазменного поглощения в поперечном сечении для обратного тормозного излучения; s _K = 2.88·10 ^-99 см¹⁶/с·Ватт⁸ - коэффициент многофотонной ионизации; U_i = 12.1e Вольт - промежуточный потенциал ионизации молекул кислорода; r_nt = 5.4·10 ¹⁸ см^-3 - эффективная плотность нейтральных молекул, равная 20% от стандартной r_at = 2.7·10 ¹⁹ см^-3.

В целях сокращения времени счета для качественного исследования задачи можно применить следующий алгоритм упрощения данной модели. Во-первых, пренебрежимо мало действие обратного тормозного излучения при продолжительностях импульса менее пикосекунды, поэтому положим . Также не будем учитывать изменение второй производной по времени , т.к. комплексная амплитуда световой волны медленно меняется со временем. Во-вторых, в предположении, что в области высокой интенсивности излучения световые поля имеют Гауссов профиль по временной координате и могут быть представлены в виде произведения. Будем искать решение системы в виде:

,

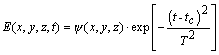где - временной слой, где формируется максимальный по интенсивности пик с полушириной , сохраняющейся все время распространения [8].

Применяя сделанные выше предположения, сначала найдем из уравнения (1.в):

,

где . Далее в уравнение 1(a) подставим найденное и уравнение (1.б), затем умножим получившееся уравнение на и проинтегрируем по всему временному домену, т.е. (-∞;+∞). Распишем все подробно:

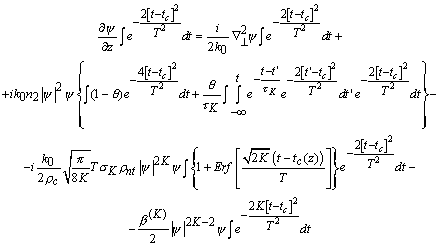
Далее, учитывая значение интеграла , упростим получившееся выражение:

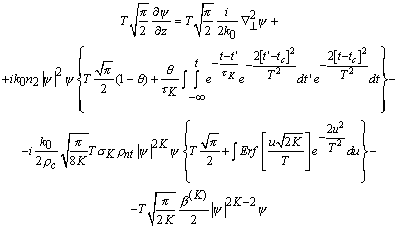(2)

Рассмотрим первый из двух оставшихся интегралов уравнения (2):

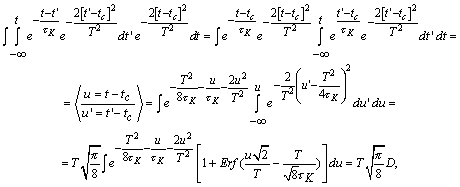
где .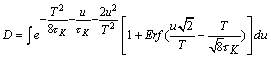

Второй интеграл , т.к. подынтегральное выражение – нечетная функция. Введя в уравнении (2) обозначения

и ,

окончательно получим:

. (3)

В работе [18] было показано влияние комбинационного рассеяния на нелинейный отклик в воздухе при . Также положим значение ( – длительность импульса) для изучения процесса филаментации при наличии многофотонной ионизации, которая укорачивает длительность импульса. Чтобы обезразмерить уравнение (3), вводим

переменные: , , ,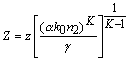

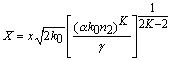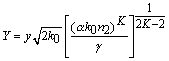поле: 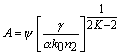и параметр: . После подстановки получим:

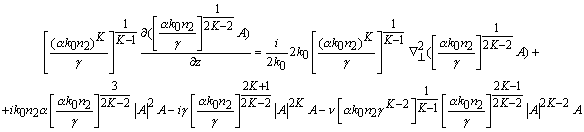
Упростив выражение и сократив его на множитель , получим:

, (4)

где параметр примет значение при выбранных выше параметрах и .

Численное решение

Для численного моделирования уравнений данного типа (НУШ) применяются разные методы, призванные уменьшить требуемое для счета процессорное время и сохранить требуемую точность счета.

Спектральный метод позволяет эффективно использовать алгоритм быстрого преобразования Фурье, но реализуется только на равномерных сетках. Преимущество спектрального подхода бесспорно только для простых решений типа движущегося солитона.

Расщепление по процессам - решение уравнения (4) на шаге заменяется последовательным решением двумерных задач дифракции в линейной среде сначала в плоскостях, параллельных XZ, затем в плоскостях, параллельных YZ, после чего вычисляется нелинейный набег фазы светового поля на том же интервале в отсутствие дифракции. Для схем расщепления по процессам существенна проблема консервативности, которая требует отдельного обсуждения.

В данной работе использован прямой метод решения уравнения (4) с использованием симметричной разностной схем, консервативность которых установлена.

Решаемая задача представляет собой нелинейное уравнение параболического типа, на границе задаются условия равенства нулю потока . Уравнение можно считать двумерным (относительно переменных x, y) и нестационарным относительно переменной z, которая в данном случае принимает роль времени. Для решения задачи составим для квадратной области в координатах равномерную (в общем случае) сетку с шагом с общим количеством ячеек . Составим неявную разностную схему (значение функции будем брать в середине j-ой ячейки составленной сетки):

, (5)

,

где приняты стандартные обозначения: - значение на нижнем слое, - значение на верхнем слое, - среднее арифметическое. Для предложенной разностной схемы в случае отсутствия многофотонного поглощения () выполняются разностные аналоги интегральных законов сохранения мощности

и гамильтониана

.

Решим задачу методом Ньютона. Мы имеем , тогда для нахождения составим итерационный процесс (значения для нулевой итерации берем с предыдущего по времени слоя):

, , (6)

где - совокупность номеров всех соседних ячеек для рассматриваемой. Представим комплекснозначную функцию , тогда из (4) получим два уравнения для каждой ячейки сетки:

;

.

К каждому из полученных уравнений применим метод Ньютона. Окончательно получим (чтобы не загромождать уравнения, далее положим и )

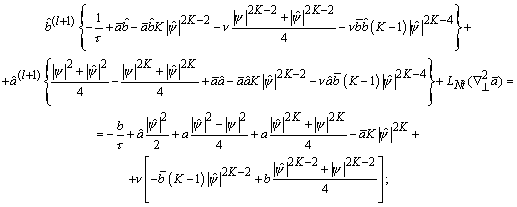
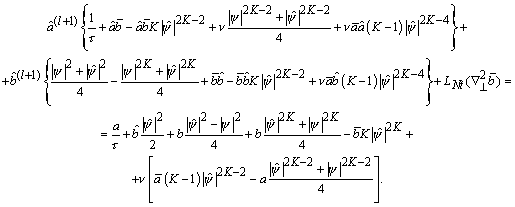
Здесь использовано обозначение , которое подразумевает оператор описанного выше процесса линеаризации Ньютона. Распишем, к примеру, значение на правой границе квадратной области (в случае рассматриваемой равномерной сетки). В случае применения 5-точечного шаблона

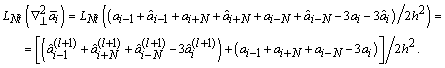
В ходе решения линейной системы с помощью итерационного метода (сравнение производительности различных методов для данной задачи обсуждается ниже) получим вектор решения длины . Критерием для завершения итерационного процесса по нелинейности служит выполнение следующего неравенства:

, где .

Как правило, для достижения критерия сходимости метода Ньютона хватает 2-6 итераций по нелинейности.

В качестве начальных условий выбирается профиль:

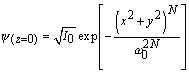, (7)

где – начальная ширина импульса; - начальная амплитуда.

Чтобы оценить необходимые размеры расчетной сетки, воспользуемся следующими условиями и результатами экспериментов [Teramobile]:

• для изучения процесса филаментации используется мощный (от 100GW до 3TW) лазерный импульс, начальная ширина которого может достигать 2 см;
• ширина образующейся филаменты, как мелкомасштабного эффекта, постоянна и достигает 100-150 мкм, а интенсивность в фокусе филаменты может превышать интенсивность фона в десятки раз;
• наблюдаемая длина распространения импульса составляет от десятков до сотен метров.

Таким образом, длина ребра квадрата расчетной сетки может достигать 10 см, чтобы избежать влияния границ. Длина же ребра одной ячейки должна быть не более 10-15 мкм для удовлетворительной передачи характера мелкомасштабных эффектов. Таким образом, количество ячеек в расчетной области может достигать. Шаг по z выбирается ~, и уменьшается обратно пропорционально максимальной интенсивности . Тем самым обеспечена не только устойчивость, но и точность.

Параллельный алгоритм

Ввиду большой размерности решаемой системы линейных уравнений и необходимости численного моделирования процесса распространения фемтосекундного импульса на длинные дистанции использовался параллельный вычислительный комплекс.

Для анализа эффективности параллельных алгоритмов обычно используются такие понятия, как эффективность и ускорение. Ускорением параллельного алгоритма () называют отношение времени выполнения алгоритма на одном процессоре () ко времени выполнения на системе из процессоров (). Эффективностью параллельного алгоритма () называют отношение его ускорения к числу процессоров, на котором это ускорение получено.

, .

Максимальное значение эффективности , но на практике это значение меньше из-за затрат на обмен данными между процессорами. В рассматриваемой задаче получается 6-ти диагональная матрица, поэтому эффективность распараллеливания высокая. На диаграмме (рис.1) приведены значения для одной итерации по Ньютону () и всего шага по времени (), включающего в себя 2 итерации по Ньютону по 2 и 6 итераций решения линейной системы в каждой.

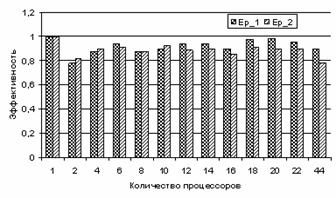
Рис.1 Эффективность параллельного алгоритма

В сформулированной выше постановке задачи основным ресурсоемким процессом является решение систем линейных уравнений. Из-за процесса линеаризации за один шаг по координате требуется несколько раз выполнять решение системы. При реализации программного кода было принято решение использовать пакет Aztec [11], разработанный в исследовательской лаборатории параллельных вычислений Сандии (США), как достаточно эффективный и удобный в использовании пакет для решения итерационными методами системы уравнений. Предоставляемые средства трансформации данных позволяют легко создавать разреженные неструктурированные матрицы для решения как на однопроцессорных, так и на многопроцессорных системах [12]. Aztec включает в себя процедуры, реализующие ряд итерационных методов:

· метод сопряженных градиентов (CG),

· обобщенный метод минимальных невязок (GMRES),

· квадратичный метод сопряженных градиентов (CGS),

· метод квазиминимальных невязок (TFQMR),

· метод бисопряженного градиента (BiCGSTAB) со стабилизацией.

Все методы используются совместно с различными предобуславливателями (полиномиальный метод и метод декомпозиции областей, использующий как прямой метод LU, так и неполное LU разложение в подобластях). Хотя матрица может быть общего вида, пакет ориентирован на матрицы, возникающие при конечно-разностной аппроксимации дифференциальных уравнений в частных производных (Partial Differential Equations - PDE). Наконец, Aztec может использовать одно из двух представлений разреженных матриц:

· поэлементный формат модифицированной разреженной строки (MSR),

· блочный формат переменной блочной строки (VBR).

Стандартные функции пакета, тем не менее, не позволяют достаточно эффективно решать нелинейные системы, требующие многократного решения матриц одинаковой структуры, но с изменяющимися коэффициентами. Для этой цели был написан программный модуль, сохраняющий массивы преобразования глобальной индексации матрицы в локальную для каждого процессора, что существенно ускорило выполнение процедуры решения системы.

В процессе моделирования подбиралась наиболее эффективная по производительности пара итерационного метода и предобуславливателя. В таблице представлены значения времени, затраченные на счет одного шага по при выборе соответствующего итерационного метода (столбцы таблицы) и предобуславливателя (строки таблицы).

	CGS	TFQMR	BiCGSTAB
Нет	0.77 (2)	0.76 (2)	1.37 (6)
LS	0.68 (2)	0.71 (2)	1.35 (6)
LU	0.82 (2)	0.81 (2)	1.41 (6)
ILU	0.68 (2)	0.78 (2)	0.78 (2)
Sym_GS	0.77 (2)	0.75 (2)	1.52 (6)

Таблица 1. Таблица сравнения результатов счета для разных сочетаний итерационных методов и предобуславливателей.

В итоге был выбран метод сопряженных градиентов со стабилизацией (CGS) и предобуславливатель ILU (incomplete LU).

Результаты для одиночного Гауссова импульса

При численном моделировании распространения лазерных импульсов во многих работах зачастую ориентируются лишь на мощность импульса, как определяющий параметр. Иногда этого бывает недостаточно для определения тех или иных тенденций с необходимой полнотой. Во внимание следует принимать значение таких начальных параметров, как полуширина и максимальная интенсивность профиля. Сочетание этих параметров при одном и том же значении критической мощности может существенно повлиять на характер распространения лазерного импульса.

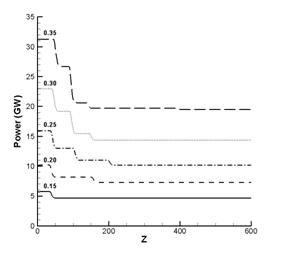
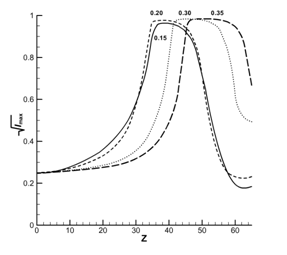
На графиках приведены зависимости по координате распространения значений мощности и максимальной амплитуды для Гауссовых профилей с одинаковой амплитудой и разными полуширинами . Хорошо видно (рис.2-б), что на скорость возрастания пиковой интенсивности влияет не только мощность импульса (при мощности меньше пороговой имеет место дефокусировка), но и его ширина. Ранее в работе [9] рассматривался критерий Беспалова-Таланова для условия неустойчивости периодического возмущения на фоне. Было показано, что в зависимости от уровня фона существует пороговое значение для частоты возмущения. Частоты ниже пороговой являются неустойчивыми. Также найдено значение частоты, при котором инкремент неустойчивости принимает максимальное значение, следовательно, достигается наискорейший рост пиковой интенсивности. При этом было отмечено первоначальное увеличение полуширины импульса в том случае, если в начальном профиле она мала. С точки зрения анализа спектра такого возмущения, при первоначальном уширении (и, соответственно, падении амплитуды) увеличивается доля низкочастотных составляющих спектра, отвечающих за неустойчивость.

Рост интенсивности в рассматриваемой задаче ограничен плазменными эффектами и, как видно из рисунка, максимальное значение интенсивности не превышает 1.                       В физических   величинах   максимальная    величина   интенсивности   составляет I _max ^∼= 7·10 ¹³Ватт/см² , что согласуется с экспериментальными данными. При возрастании интенсивности все большую роль начинает играть последний член в уравнении, ответственный за многофотонное поглощение, таким образом, как видно на рис.2-а, наблюдается резкое уменьшение мощности импульса. В то же время усиливается влияние другого члена уравнения, ответственного за многофотонную ионизацию, благодаря которому уменьшается действие эффекта Керра. В результате поглощения излучения в процессе многофотонной ионизации и дефокусировки падает пиковая интенсивность импульса, что приводит к прекращению многофотонной ионизации и постоянству интеграла мощности вплоть до следующего момента возрастания интенсивности.

Рис.2–а. Динамика мощности	Рис.2–б. Динамика пиковой интенсивности

Значение гамильтониана к моменту установления постоянного уровня мощности (рис.2–а) меняет знак на положительный, что, как известно [13], является необходимым условием расходимости пучка в среднем. Однако факт расходимости пучка в среднем не противоречит тому, что некоторая его внутренняя часть может сфокусироваться.

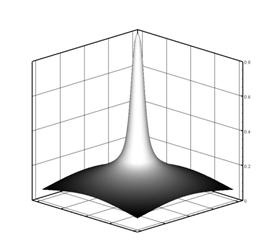
Чтобы объяснить ступенчатый характер падения мощности, рассмотрим подробнее этапы самофокусировки Гауссова импульса, описанные в [9]. Для самофокусировки Гауссова импульса необходима концентрация малых частот спектра. Если ширина пучка велика, то также велика доля низкочастотных компонент и происходит самофокусировка без начального уширения импульса в отличие от того, как это бывает с менее широкими импульсами. 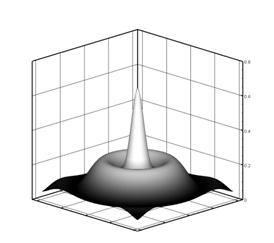В итоге образуется довольно крутой «столб» интенсивности с наличием вокруг фона из дефокусирующейся части начального импульса (рис.4-а). Но при достижении пиковым значением интенсивности порогового значения начинается падение интенсивности как за счет потери энергии на ионизацию, так и дефокусирующего воздействия электронной плазмы, возникшей в результате многофотонной ионизации. Первые участки, на которые оказывается воздействие, являются зонами больших градиентов. В рассматриваемом случае интенсивность падает быстрее на краю «столба» (рис.4-б).

Рис. 4-а. Распределение амплитуды при	Рис. 4-б. Распределение амплитуды при
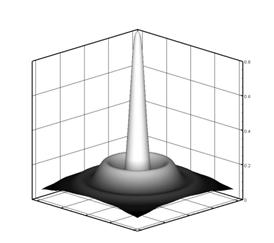
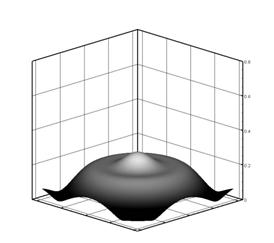
Рис. 4-в. Распределение амплитуды при	Рис. 4-г. Распределение амплитуды при

При дальнейшем падении интенсивности отток мощности от центра встречается с областями подпитки и образуется квазистационарная кольцевая структура (рис.4-в). На рис.5 (который соответствует рис.4-б) показаны потоки мощности, определяемые градиентом фазы . На рисунке можно выделить 3 структуры: центральный приосевой профиль и 2 кольцевых структуры. Внутри этих колец поток мощности направлен к центру. Эти структуры можно отделить друг от друга областями с минимальной интенсивностью, где поток мощности направлен «от центра» (заштрихованы на рисунке).

Рис.5 Градиент фазы распределения комплекснозначной величины .

При концентрации определенной мощности в кольцевой структуре после падения всего «столба» создаются условия для повторного роста интенсивности (рис.4-г). Такими условиями в рассмотренном случае являются форма распределения (рис.4-г) - Гауссов профиль с мощностью, большей критической, и достаточной для развития самофокусировки полушириной. Таким образом, происходит первоначальный рост интенсивности, образование кольцевой структуры и после падения интенсивности формирование такого профиля, который вновь самофокусируется. В итоге получается ступенчатое падение мощности импульса (рис.4-а).

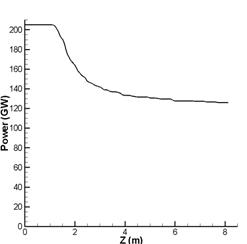
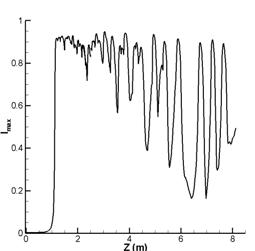
На рис.6 одновременно представлены зависимости падения мощности импульса (Power) и возрастания его пиковой интенсивности (Intensity) на протяжении распространения импульса (z). Можно заметить, что уровень, при котором начинается поглощение, равен . Известна оценка [17] , что ионизация воздуха становится существенной при интенсивности 4.5·10 ¹³ Ватт/см² , что и соответствует найденному пороговому значению. По мере уменьшения мощности импульса уменьшается величина теряемой мощности и длина, на которой наблюдается поглощение.

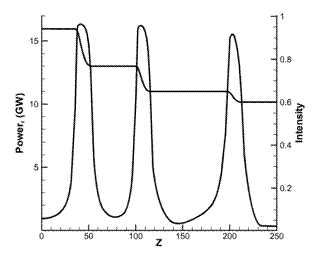
Рис.6 Сопоставление интенсивности и мощности

Напишем уравнение для изменения мощности по . Для этого умножим уравнение (4) на и сложим с комплексно-сопряженным уравнением для (4), умноженным на . Проинтегрировав по всей поперечной плоскости , получим

;

;

.

Для получения равенства по порядку величины было использовано выражение для формы начального профиля импульса. Таким образом, можно оценить длину диссипативного участка

,

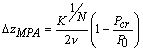которая при и при стремится к максимальной величине , что и подтверждается приведенными выше результатами вычислений. В физических величинах .

При использовании начального Гауссова профиля с высокой, близкой к пороговой (или максимальной) интенсивностью и мощностью, не на много превышающей , не наблюдается ступенчатого характера изменения интенсивности при распространении импульса (рис.7).

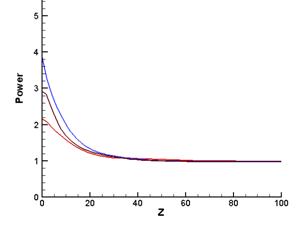
Рис.7 Изменение мощности

Это можно объяснить отсутствием вокруг импульса «фона» низкочастотных компонент спектра. Поэтому моделирование распространения импульсов необходимо начинать с момента входа лазерного импульса в нелинейную среду, а не со стадии развитой самофокусировки.

Результаты для двух Гауссовых импульсов

В работе [9] нами уже было рассмотрено взаимное влияние друг на друга двух Гауссовых импульсов. При наличии многофотонной ионизации влияние становится более заметным. Работы по моделированию влияния двух импульсов проводились группой исследователей под руководством В.П. Кандидова и описаны в [10].

Приведем два показательных примера расчета двух Гауссовых профилей, демонстрирующих, как наличие диссипации влияет на характер развития областей высокой интенсивности. Были рассмотрены два равных Гауссовых возмущений с полушириной и амплитудой интенсивности на расстоянии . Распространение импульса моделировалось на расстояние .

Рис.8-а. Области высокой интенсивности для двух равных Гауссовых возмущений с и на расстоянии без наличия диссипации.	Рис.8-б. Области высокой интенсивности для двух равных Гауссовых возмущений с и на расстоянии при наличии диссипации .

Как видно из рисунков, в консервативном случае (рис.8-а), т.е. при в формуле (3), мощность импульса концентрируется в середине между двух возмущений и сохраняется в области, подвергаясь колебаниям. При наличии диссипации (, рис.8-б), каждый из двух импульсов начинает терять мощность, сужаясь при этом, а момент слияния находится намного дальше по , чем в консервативном случае.

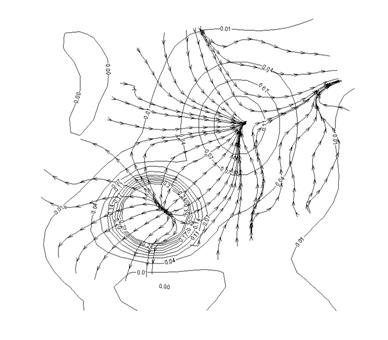
Рис.9 Переток мощности в широком пучке.

Взаимодействие между филаментами в широком импульсе с мощностью, на много превышающей критическую более сложно. Пример перетока мощности из развитой филаменты с максимальной интенсивностью в область, где зарождается новая филамента, представлен на рис.9.

Результаты расчета мощного лазерного импульса

Развитие параллельных вычислительных методов, как правило, ведет к возможности расчета реальных физических систем. В случае рассмотрения распространения на дальние дистанции лазерного импульса применение параллельных технологий также обосновано. Целью данной работы является доказать возможность такого расчета.

Мощность реального лазерного импульса достигает нескольких терраватт, ширина импульса может достигать нескольких сантиметров. Профиль импульса реальных лазерных систем обычно задают в форме функции супер-гаусса, т.е. показатель степени в формуле (7). Особенностью реального лазерного пучка также является наличие шума во входном профиле. Для воспроизведения случайного поля флуктуаций амплитуды использовался спектральный метод [15]. Этот метод основывается на суммировании Фурье-гармоник пространственного спектра. Алгоритм задания спектральным методом случайной реализации комплексного поля флуктуаций входного сигнала состоит в следующем. Сначала получаем комплексную случайную величину для каждой точки спектрального пространства , где и - независимые равномерно распределенные на отрезке [-1,1] случайные величины. Затем строится функция

, где

- амплитуда шума (например, 0.1), - радиус корреляции (например, 1/0.1мм). Для получения амплитудного шума выполняется преобразование Фурье:

Окончательно, накладываем функцию шума на входной профиль по следующему закону

.

Развитие мелкомасштабной самофокусировки [6], приводящей к распаду симметрии профиля, классически объясняется наличием амплитудных флуктуаций начального распределения. Вследствие процесса мелкомасштабной самофокусировки и достижения амплитудами отдельных флуктуаций порога многофотонной ионизации в мощном лазерном импульсе начинает развиваться множественная филаментация. При наблюдении этого процесса вырисовывается картина множественных связей отдельных филамент между собой, вследствие чего происходят поглощение и зарождение новых филамент. В процессе такого хаотического развития в лазерных импульсах можно выделить области, где процесс филаментации продолжается непрерывно за счет поглощения энергии соседних участков. Такие области называют кластерами [1] и именно их наличие объясняет характер экспериментальных данных (рис.10).

Рис.10 Эксперимент по распространению лазерного луча

В качестве примера расчета приводим расчет для среднего по мощности () импульса с полушириной w₀ = 3 мм. Расчетная область представляет собой квадрат с длиной стороны 2 см. На начальном профиле задан Гауссов шум по описанному выше алгоритму. Расчет проводился на сетке ячеек.

Рис.11–а. Распределение интенсивности при z = 31.6	Рис.11–б. Распределение интенсивности при z = 92.1
Рис.11–в. Распределение интенсивности при z = 110.7	Рис.11–г. Распределение интенсивности при z = 156.8

Рис.12 Линии уровня распространения импульса

с мощностью на расстояние около 9м.

Рис.13-а Мощность	Рис.13-б Максимальная интенсивность

Заключение

Целью настоящей работы была разработка эффективных алгоритмов для расчета явлений филаментации, позволяющих произвести математическое моделирование процесса филаментации в различных лазерных системах. Были использованы симметричные разностные схемы, обладающие свойством консервативности, созданы распараллеленные программы для расчета таких задач.

Показан  ступенчатый характер развития нелинейности,   который определяется пороговым значением  интенсивности  5·10 ¹³ Ватт/см² , при котором ионизация воздуха становится существенной. Характер процесса определяется соотношением между процессом многофотонной ионизации и мелкомасштабной самофокусировки. До тех пор, пока интенсивность не достигает пороговых значений, световой пучок не теряет энергию и происходит самофокусировка. При достижении пороговых значений интенсивности начинается потеря энергии на ионизацию и дефокусирующее воздействие электронной плазмы, что приводит к потере интенсивности. Когда интенсивность падает ниже порогового значения, вновь начинается самофокусировка. Таким образом, процесс носит ступенчатый характер (рис. 2-а). Процесс прекращается, когда спектральный состав становится таким, что дальнейшее развитие неустойчивости невозможно, т.к. выполняется условие устойчивости согласно критерию Беспалова-Таланова.

При использовании начального Гауссова профиля с высокой, близкой к пороговой (или максимальной) интенсивностью и мощностью не намного превышающей , не наблюдается ступенчатый характер изменения интенсивности при распространении импульса.

Литература.

1. J.Kasparian, M.Rodrigues, G.Mejean, J.Yu, E.Salmon, H.Wille, R.Bourayou, S.Frey, Y.-B.Andre, A.Mysyrowicz, R.Souerbrey, J.-P.Wolf, L.Woste, Science, 301, 61 (2003).

2. A. Braun et al., Opt. Lett. 20, 73 (1995); E.T.J. Nibber-ing et al., Opt. Lett. 21, 62 (1996).

3. A. Brodeur et al., Opt. Lett. 22, 304 (1997).

4. B.LaFontaine et al., Phys. Plasmas, 1999, №6, p.1615.

5. R.Y.Chiao, Phys.Rev.Lett, 1964, V13, N5.

6. В.И.Беспалов, В.И.Таланов. О нитевидной структуре пучков света в нелинейных жидкостях // Письма в ЖЭТФ,1966, Т.3, с.471.

7. G.Fibich, B.Ilan. Vectorial and random effects in self-focusing and in multiple filamentation // Phisica D, 2001, 157: 113-147.

8. S.Skupin, L.Berge et al., Phys. Rev. E, 70, 046602, 2004.

9. А.Д.Балашов, А.Х.Пергамент. Математическое моделирование процессов филаментации в средах с кубической нелинейностью. – М.: ИПМ им. М.В.Келдыша РАН, 2004, препринт №40.

10. В.П.Кандидов, О.Г.Косарева, С.А.Шленов и др. Динамическая мелкомасштабная самофокусировка фемтосекундного импульса // Квантовая электроника, 2005, Т.35, №1.

11. Aztec. A Massively Parallel Iterative Solver Library for Solving Sparse Linear Systems. -
http://www.cs.sandia.gov/CRF/aztec1.html

12. В.Н. Дацюк, А.А. Букатов, А.И. Жегуло. Многопроцессорные системы и параллельное программирование. – Ростов: Ростовский государственный университет, http://rsusu1.rnd.runnet.ru/koi8/index.html

13. Л.Д. Ландау и Е.М. Лившиц. Электродинамика сплошных сред – М.: Наука, 1959.

14. Ю.Н.Карамзин, А.П.Сухоруков, В.А.Трофимов. Математическое моделирование в нелинейной оптике – М.: Издательство Московского университета, 1989.

15. Л.И. Миркин, М.А. Рабинович, Л.П. Ярославский. Метод генерирования коррелированных гауссовских псевдослучайных чисел на ЭВМ // ЖВМ и МФ, 1972. V. № 5. С. 1353-1357.

16. В.М.Волков. Консервативные разностные схемы с улучшенными дисперсионными свойствами для нелинейных уравнений шредингерского типа // Дифференциальные уравнения, 1993, Т.29, №7.

17. J. Kasparian, R. Sauerbrey, S.L. Chin. The critical laser intensity of self-guided light filaments in air // Appl. Phys. B, 2000, №71, pp.877–879.

18. E.T.J.Nibbering, G.Grillon, M.A.Franco at al., J.Opt.SocAm.B, 1997, V.14, p.650

19. M.D.Feit, J.A.Fleck, Appl. Phys. Lett., 1974, V. 24, p. 169.