Глава I. МЕТОДЫ ИЗУЧЕНИЯ СЕМЕЙСТВ

Пусть три точечных тела P₁, P₂ и P₃ движутся в одной плоскости под действием закона тяготения Ньютона. Тела P₁ и P₂ имеют массы m и m₂ соответственно, а масса тела P₃ настолько мала, что ее влиянием на тела P₁ и P₂ можно пренебречь. Будем говорить, что масса тела P₃ равна нулю. Тогда тело P₂ совершает кеплерово движение относительно тела P₁. Если тело P₂ движется по окружности, то задача о движении тела P₃ называется плоской круговой ограниченной задачей трех тел, коротко - ограниченной задачей.

Будем считать, что единицы массы, времени и расстояния выбраны так, что сумма m+m₂, гравитационная постоянная, расстояние P₁ P₂ и угловая скорость P₂ относительно P₁ равны единице. Единственным параметром тогда будет m = m₂ ∈ [0,1/2]. Если ввести вращающуюся вместе с P₂ систему координат, то в этой (синодической) системе координат с центром в P₁ положение x₁, x₂ тела P₃ описывается системой Гамильтона с двумя степенями свободы и одним параметром m (см. [1, гл. III, § 1]):

Ч x   j  =∂ H/∂ yj,        Ч y   j  =-∂ H/∂ xj,    j=1,2,     Ч      = d/dt,

(1.1)

где

H = H0+mR,    H0 =  1 2 (y12+y22)+x2y1-x1y2-r-1, R = r-1+x1-r2-1,     r= Ц   x12+x22   ,     r2 = Ц   (x1-1)2+x22   .

(1.2)

При m ≠ 0 задача не интегрируется в конечном виде. При m = 0 задача интегрируется и можно описать все ее решения, что сделано в [1, гл. III-IV]. Фазовое пространство этой задачи при m = 0 устроено сложно из-за столкновений тела P₃ с телом P₂. При m > 0 эти столкновения вызывают сингулярные возмущения, приводящие к дальнейшему усложнению строения фазового пространства. При этом наибольший интерес представляют семейства периодических решений, ибо они образуют как бы скелет некоторой части фазового пространства. При фиксированном значении параметра m периодические решения системы Гамильтона образуют однопараметрические семейства; при переменном m - двупараметрические.

Орбита - это проекция решения x_j(t),y_j(t), j=1,2 системы (1.1) на плоскость x₁,x₂. Будем называть глобальной кратностью синодического периодического решения число оборотов его орбиты вокруг тела P₁. И хотя кратность может изменяться вдоль семейства при переходе через орбиту столкновения P₃ с P₁, она удобна для классификации семейств. Если пересекаются два семейства периодических решений и периоды на одном семействе в q раз больше периодов на другом семействе, то будем говорить, что первое семейство имеет (локальную) кратность q.

Система (1.1) переходит в себя при подстановке

t,x1,x2,y1,y2 → -t,x1,-x2,-y1,y2,

(1.3)

которая является ее симметрией. При симметрии (1.3) плоскость x₂=y₁=0 является инвариантной и называется [1, гл. III] плоскостью симметрии P. Решения системы (1.1), переходящие в себя при подстановке (1.3), являются симметричными. Симметричное периодическое решение два раза пересекает плоскость симметрии. По этим пересечениям удобно ослеживать взаимные положения таких решений.

Семейство периодических решений системы (1.1) при фиксированном значении параметра m называется натуральным, если оно продолжено в обе стороны до естественных концов, которыми могут быть окончание в неподвижной точке или на другом семействе периодических решений, стягивание орбиты в точку или ее уход в бесконечность, стремление периода к нулю или бесконечности.

Теперь мы начинаем новый цикл работ по изучению и вычислению основных семейств периодических решений для всех значений параметра m ∈ [0,1/2]. До сих пор их изучали и вычисляли либо для фиксированных значений параметра m, либо для малых m. Для m = 1/2 это сделано в работах Стремгрена [2] и Бартлета [3]. Для m = m_M=0.1215585, соответствующего случаю Земля (P₁) - Луна (P₂), - Бруком [4]. Для m = m_J=0.00095388, соответствующего случаю Солнце (P₁) - Юпитер (P₂), - в [5, 6]. Для m = 0 (порождающие семейства) - в книге [1], препринтах [5, 6] и в книгах Хенона [7, 8].

Интерес к такому изучению вызван стремлением описать движение малых тел в Солнечной системе (астероидов, объектов пояса Эджворта-Койпера [20], спутников и частиц колец планет-гигантов и т.д.) и в системах двойных звезд (планеты, пылевые частицы), а также - потребностями навигации в Солнечной системе.

Каждое семейство мы собираемся вычислять для

m = 0,   mJ,    0.1,   0.2,   0.3,   0.4,   0.5

(1.4)

и приводить его расположение в фазовом пространстве в виде кривых на плоскости симметрии P (в трех разных системах координат), а также - периоды его решений, их плоский и вертикальный следы (т.е. индексы устойчивости) - все это в виде графиков. В случае необходимости будем рассматривать и отличные от (1.4) интересные значения m (особенно те, при которых происходят бифуркации). Кроме того - приводить наиболее интересные орбиты семейств, места его пересечений с другими семействами и места бифуркаций самого семейства. Но сначала вкратце напомним известные свойства семейств периодических решений ограниченной задачи трех тел.

 

Общие свойства семейств периодических решений системы Гамильтона с двумя степенями свободы приведены в [9] (подробно) и кратко в [1, гл. II, § 4]. О семействах симметричных периодических решений см. [9, § 4]. Каждое симметричное решение M семейства F имеет период T, след Tr матрицы монодромии системы в вариациях и две точки пересечения с плоскостью симметрии P (через полупериод). Параметром на семействе могут служить значения функции Гамильтона и координаты пересечений с плоскостью симметрии.

В системе (1.1) при m ∈ [0,1/2] семейства симметричных периодических решений являются двупараметрическими, поэтому они могут иметь особенности коразмерности 2, которые изучены в [1, 9]. Но при m = 0 система (1.1) является вырожденной.

Если существующие при некортором m = m₀ решение x(t,m) непрерывно продолжается по m до сколь угодно малых m > 0, то его предел при m→ 0 называется порождающим решением. Очевидно, что порождающее решение составлено из решений задачи при m = 0. Эти решения относятся к двум видам: первый вид - те, на которых тело P₃ не сталкивается с телом P₂; второй вид - те, на которых тело P₃ сталкивается с телом P₂. Решения первого вида - это решения задачи двух тел P₁ и P₃ в синодической (вращающейся) системе координат. Решения второго вида образованы из нескольких кусков решений задачи двух тел P₁ и P₃, причем каждый кусок начинается и кончается столкновением P₃ с P₂, и на всех кусках одинаково значение гамильтониана H (или константы Якоби C=-2H). Все такие куски описаны в гл. VI [1]. Наибольший интерес представляют решения-отрезки, начинающиеся и кончающиеся столкновением P₃ с P₂. Они образуют счетное множество однопараметрических семейств A_i, B_j, C_kl (объединенных в семейства S) и однопараметрических семейств T_N, подробно изученных в гл. III-V [1]. Семейства S симметричных отрезков найдены Хеноном [10] в 1968 г.

В неинтегрируемой системе Гамильтона (при фиксированном m ≠ 0) периодические решения образуют однопараметрические семейства. Пределы этих семейств при m → 0 называются порождающими семействами периодических решений. В [1, Введение] предложена программа изучения семейств периодических решений ограниченной задачи при малых m > 0 через их порождающие семейства. Для этого надо описать все порождающие семейства. В дальнейшем нас будут интересовать только симметричные периодические решения, которые переходят в себя при подстановке (1.3) и орбиты которых на плоскости x₁,x₂ симметричны относительно оси x₁. Каждое симметричное периодическое решение представлено двумя точками на плоскости симметрии P. При фиксированном m каждое семейство таких решений представлено на P двумя кривыми - характеристиками семейства.

Изображать характеристики семейств на плоскости P в координатах x₁,y₂ не удобно, ибо они представляют собой очень тесно расположенные кривые (см. [4]). Поэтому мы будем использовать на этой плоскости три системы координат: одну глобальную: I систему x₁,C=-2H; и две локальных: II систему [(a)\tilde],[(e)\tilde], связанную с телом P₁; и III систему z₁,y₂, связанную с телом P₂.

I система. Отображение плоскости симметрии P = (x₁,y₂) на плоскость x₁,C=-2H двулистно: двум разным значениям y₂ соответствует одно значение C=-2H, причем границей его служит линия, где дискриминант многочлена от y₂

-y22+2x1y2+  2(1-m) |x1| -2mx1 +  2m |x1-1| -C=0,

связывающего на плоскости P константу Якоби C с координатами x₁,y₂, обращается в ноль, т.е. 

x12 +  2(1-m) |x1| -2mx1 +  2m |x1-1| -C=0.

(2.1)

На графиках компоненты этой кривой показаны пунктиром, а прямые x₁=0 и x₁=1, соответствующие телам P₁ и P₂, изображены жирными линиями.

II система. Астрономические координаты

~ a   =   x1 |2-| ~ e   || =   x1 |x1|y22 (1- m)-1 ,    ~ e   = y2  sign x1  |x1 y2| (1- m)-1.

(2.2)

Тогда a=|[(a)\tilde]| и e=|1-|[(e)\tilde]|| - суть большая полуось и эксцентриситет соответствующей сидерической орбиты задачи двух тел P₁ (с массой 1-m) и P₃. Это справедливо для эллиптических орбит (при |[(e)\tilde]| ≤ 2) и гиперболических орбит (при |[(e)\tilde]| ≥ 2). Параболические орбиты здесь выпадают. Отображение x₁,y₂ → [(a)\tilde], [(e)\tilde] имеет разрыв на прямых [(e)\tilde] = ± 2, где проходит граница между эллиптическими и гиперболическими орбитами. На рисунках эти линии показаны пунктиром. Телу P₁, т.е. x₁=0, соответствует прямая [(a)\tilde]=0, телу P₂, т.е. x₁=1, соответствует кривая

~ a   |1-| ~ e   || = 1.

Обе они изображаются жирными.

III система. Координаты

z1=(x1-1)/m,   y2

(2.3)

суть нормированные сидерические координаты в задаче двух тел P₂ (с массой 1) и P₃. Они помогают лучше изучить расположение характеристик семейств вблизи тела P₂ (с массой m). Отображение x₁,y₂ → z₁,y₂ взаимно однозначно при m ≠ 0. На рисунках прямая z₁=0, соответствующая телу P₂, изображается жирной.

Системы координат II и III введены для того, чтобы сравнивать вычисленные семейства для m > 0 с порождающими семействами (т.е. для m = 0), которые соответствуют решениям задач двух тел (P₃, P₁ для системы II и P₃, P₂ для системы III).

При фиксированном m каждое семейство на плоскости P в координатах x₁,C представлено двумя характеристиками. Для одной из них указываются значения нормированного периода T/2p. Значения следов Tr и Tr_v даются как функции от T/2p. Оба следа Tr и Tr_v могут принимать очень большие значения, поэтому вне интервала [-2,2] они изображаются в логарифмической шкале, т.е. [(Tr)\tilde]=sign (Tr) (log₂(|Tr|+1), и аналогично для [(Tr)\tilde]_v.

Плоская круговая ограниченная задача является частью пространственной ограниченной задачи (см. Себехей [11, § 10.2]). Для решения плоской задачи в системе в вариациях пространственные компоненты отделяются в самостоятельную подсистему, по которой определяется пространственный (вертикальный) след Tr_v [12]. Если |Tr_v| ≤ 2, то от плоского периодического решения может ответвляться семейство таких пространственных периодических решений, орбиты которых симметричны относительно плоскости вращения тел P₁ и P₂. Для выделения периодических решений, устойчивых в линейном приближении, надо знать оба следа, ибо эта устойчивость возможна только при

|Tr| ≤ 2     и     |Trv| ≤ 2.

(2.4)

В противном случае периодическое решение неустойчиво.

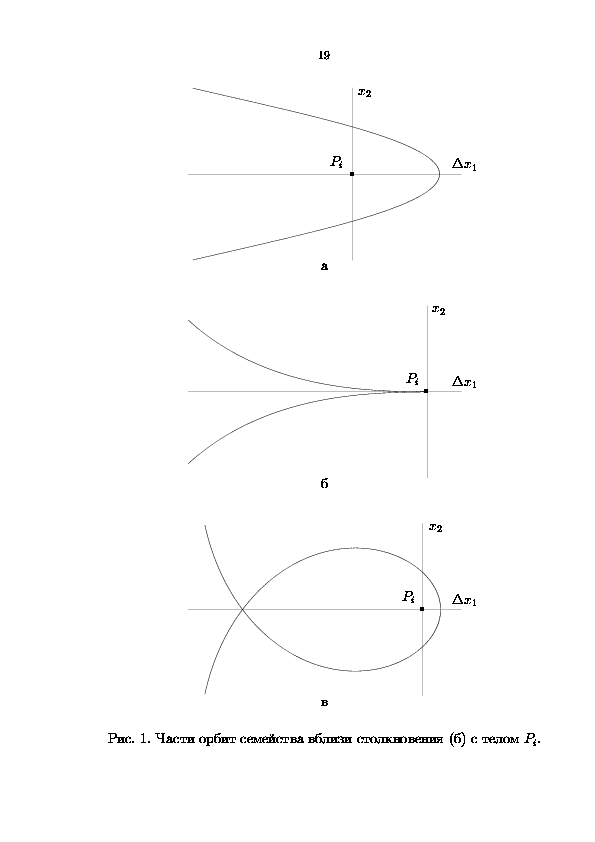
Обычно семейство периодических решений включает в себя несколько орбит столкновения с телами P₁, P₂. Для симметричных орбит последовательность прохождения столкновения с телом P_i при движении по семейству при фиксированном m показана на рис. 1. При этом образуется петля орбиты вокруг тела P_i. На рис. 1 показана одна из двух возможных последовательностей; возможна и обратная последовательность. Кроме того, возможни ситуация, соответствующая зеркальной симметрии картинок рис. 1 относительно вертикальной оси. Отметим, что точка на оси x₁, в которой происходит ортогональное пересечение орбиты с этой осью, остается по ту же сторону от тела P_i до и после столкновения. Это частный случай принципа Брука [4]: на семействе симметричных периодических решений точки ортогонального пересечения оси x₁ не меняют своего расположения относительно тел P₁, P₂.

 

Порождающие семейства симметричных периодических решений состоят из кусков семейств симметричных периодических решений при m = 0, кусков семейств S и кусков пар семейств T_N с бифуркациями между этими кусками. Согласно [1, гл. VII и VIII] при m = 0 все симметричные периодические решения без столкновений P₃ с P₂ являются порождающими. Они образуют два семейства Id и Ir с круговыми орбитами и счетное число семейств E_N ^± с эллиптическими орбитами с фиксированной большой полуосью (одно или два семейства для каждого рационального N=a^-3/2 > 0) [1, рис. 11]. Бифуркации между этими семействами происходят в местах пересечения семейств Id с семействами E_(p+1)/p для p=1, ± 2, ± 3,... Обозначим эти пересечения через Id(N)=Id ∩ E_N. На плоскости P этим пересечениям семейств соответствуют точки с N=(p+1)/p для p=1, ± 2, ± 3,..., т.е. [(a)\tilde]= ± N^-2/3, [(e)\tilde]=1. Они делят семейство Id на куски Id_p с p/(p-1) > N > (p+1)/p для p=1, ± 2, ± 3,...,    а семейства E_(p+1)/p - на две части E_(p+1)/p⁺ (с q = 0) и E_(p+1)/p^- (с q = p). Возмущения и бифуркации семейств Id, Ir и E_N ^± изучены в гл. VII и VIII [1]. В частности, характер бифуркаций кусков Id_p с E_N ^± показан на рис. 90 [1]. Возмущения периода T и следа Tr на некоторых семействах E_N приведены в табл. 2 Приложения [1].

Согласно [1, гл. III и IV] при m = 0 всякое симметричное периодическое решение со столкновением P₃ с P₂ образовано решениями-отрезками из семейств S и четным числом симметрично расположенных отрезков из семейств T_N, причем значение константы Якоби C на всех отрезках одинаково. Повидимому, каждая такая комбинация является порождающей. Но это доказано только для простейших из них, состоящих только из одного или двух отрезков (Перко [13]). Семейства S, T_N и их характеристики на P изучены в гл. III-V [1]. Бифуркации между семействами симметричных периодических решений происходят в местах пересечения семейств Id, Ir, E_N ^± , S. При рациональном N=(p+q)/p, N ≠ 1 пересечения семейства E_N с семействами S происходят на орбитах, у которых

e*=cos(kp/2|p+q|),   k=0,1,...,2|p+q|,   если   a > 1;

e*=dcos(kp/2q),   k=0,1,...,[(x-z0+j(x))/q],   если   a < 1,

где d = ± 1, x=p/q и [y] означает целую часть числа y (см. [1, гл. IV, § 2]). Согласно [1, гл. VI, п. 3.Б] этим значениям e^* соответствуют определенные значения e ′ =(1-e) e ′ и по теореме 2.4 гл. IV - определенная орбита, которую обозначим E_N(k) для a > 1 и E_N(d) для a < 1.

Заметим, что при k=0 и 2|p+q| точка (N^-1,e ′ =(1-e) e ′ ) лежит на границе области w ′ , т.е. e=1-1/a, e ′ =1 для k=0 и e ′ =-1 для k=2|p+q| при a > 1; и e=a^-1-1, e ′ =d для k=0 при a < 1. При этом на плоскости P одна из двух сопряженных точек орбиты из E_N(k) лежит на P₂^**, т.е. x₁=1, а другая является точкой пересечения характеристик семейств второго типа [1, гл. III, п. 3.Д].

Если k ≠ 0, 2|p+q|, то траектория из E_N(k) представлена на P двумя сопряженными точками пересечения первого типа (они лежат внутри областей w_i).

Согласно [1, гл. III, § 3] есть еще две орбиты пересечения:

E₁(-1)={N=1, [(e)\tilde]=-1} (тип III, здесь перескаются семейства Ir, E₁ и S);

E₁(+1)={N=1, [(e)\tilde]=1} (тип IV, здесь перескаются семейства Id, E₁⁺ и S).

Итак, на указанных орбитах Id(1+1/p) и E_N(k) происходят бифуркации между кусками порождающих семейств симметричных периодических решений.

В формировании порождающих семейств большую роль играют так же экстремальные (по константе Якоби C) орбиты семейств S. Их теория развита в гл. IV и V [1], а численные значения опубликовали Хицль и Хенон [14]. На каждом семействе S типа A_i и B_j выбираются начальная экстремальная орбита S(0) и направление возрастания нумерации так, что все экстремальные орбиты обозначаются S(k), где целое k может быть и отрицательным. Для семейств A_i орбита A_i(0) кратна орбите E₁(-1), т.е. [(a)\tilde]= ± 1, [(e)\tilde]=-1. Для семейств B_j орбита B_j(0) - это E₁(1), т.е. [(a)\tilde]=1, [(e)\tilde]=1. На семействах C_ij имеются только две экстремальные точки C_ij(k): C_ij(+1) при [(e)\tilde] > 0 и C_ij(-1) при [(e)\tilde] < 0. Таблицы самих семейств S имеются в [10].

Базовые порождающие семейства Id, Ir, E_N ^± , A_i, B_j, C_ij и T_N описаны в книге [1, гл. III, IV]. Там же описаны точки пересечения их характеристик на плоскости симметрии P. Им соответствуют специальные решения, по которым пересекаются базовые семейства:

Id(N)=Id ∩ EN,        Ir(N)=Ir ∩ EN,        EN(k).

(3.1)

Кроме того, в [1, 5] были выделены описанные выше экстремальные орбиты

Ai(k),    Bj(k),    Cij(k),

(3.2)

на которых возможен возврат (складка) или замыкание соответствующей характеристики порождающего семейства. На специальных решениях происходит бифуркация пересекающихся базовых семейств, т.е. порождающее семейство состоит из кусков базовых семейств, ограниченных специальными решениями. Характер этих бифуркаций обсуждается в [1, 2, 7, 8], но изучен пока не во всех случаях.

На семействе Id (т.е. [(e)\tilde]=1) период T и следы Tr и Tr_v суть

T=2p|a-3/2-1|-1,     Tr=2 cosT=Trv.

(3.3)

На семействе Ir (т.е. [(e)\tilde]=-1) имеем

T=2p|a-3/2+1|-1,     Tr=2 cosT=Trv.

(3.4)

На семействах E_N ^± с рациональным N=a^-3/2=(p+q)/p (т.е. [(a)\tilde]^-3/2=N) имеем

T=2pp,     Tr=2 = Trv.

(3.5)

На порождающих семействах периодических решений второго вида (т.е. со столкновениями тел P₃ и P₂) оба следа Tr и Tr_v= ±∞ . Смена знака Tr происходит только на специальных и экстремальных решениях для семейств, периодические решения которых состоят из одного решения-отрезка семейств S (т.е. A_i, B_j или C_ij) [15]. Для семейств периодических решений, составленных более чем из одного отрезка, кроме этих возможны и другие места смены знака Tr, но о них пока ничего не известно. Но у регулярной системы Гамильтона в месте пересечения двух семейств периодических решений Tr=2 на одном семействе и Tr=2cos(2p/q) - на другом, где натуральное число q есть порядок резонанса и кратность пересечения. Поэтому однокусковые порождающие семейства могут пересекаться только на специальных решениях (3.1) и на экстремальных решениях (3.2), а многокусковые еще и на неизвестных решениях. Места смены знака у Tr_v на решениях второго вида пока не известны.

Хенон [7, 8] построил весьма сложную теорию бифуркаций семейств порождающих решений второго вида. Однако можно узнать характер этих бифуркаций просто вычисляя соответствующее порожденное семейство при малом m > 0. Сами порождающие семейства при m = 0 можно вычислять по более-менее явным формулам см. [1, гл. IV и гл. VI, § 3, п. 3.Б]), но проще использовать общие программы вычисления решений ограниченной задачи, что здесь и делается.

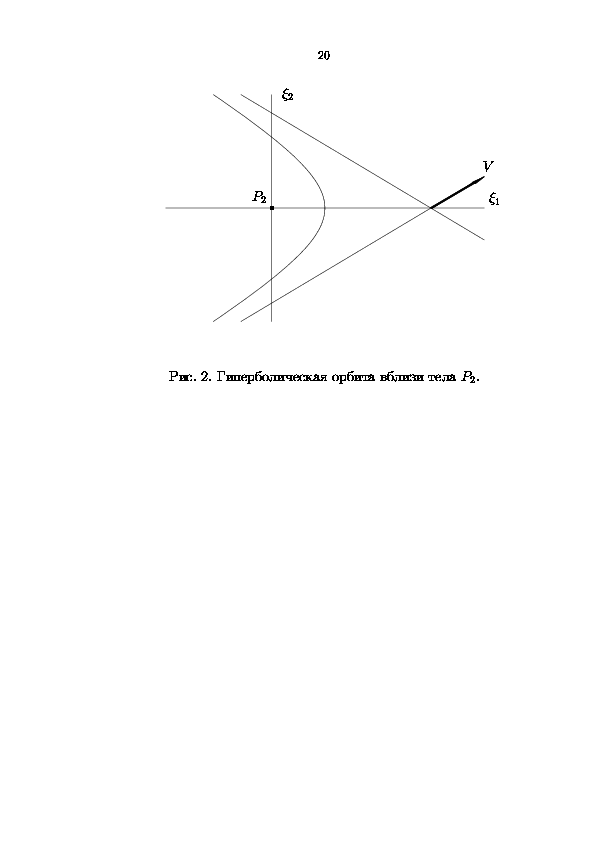
Особого внимания требуют характеристики порождающих семейств второго вида вблизи тела P₂. Характер пролета тела P₃ вблизи тела P₂ описан в [16, 17]. Приближенно он происходит по симметричной гиперболической орбите задачи двух тел P₂ (с массой m) и P₃ (см. рис. 2).

Согласно [18, часть II, § 2.03] движение тела P₃ в локальных координатах x₁=x₁-1, x₂=x₂ описывается формулами

r=  a* (e*2-1) 1+e* cosn ,    x1=r cosn,   x2=r sinn,

где a_*,e_* - большая полуось и эксцентриситет гиперболической орбиты, n - истинная аномалия. При этом трансверсальная к радиус-вектору составляющая скорости есть

vn =   ж Ц  m a* (e*2-1)   (1+e* cosn),

а интеграл инергии есть

V2 = m ж и  2 r +  1 a* ц ш ,

где

V2 = v12+v22= Ч x   2 1  + Ч x   2 2  .

В пересечении с осью x₁ получаем наименьшее расстояние до тела P₂:

|x10|=a*(e*-1)     и     Ч x   2  =vn =   ж Ц  m(e*+1) a* (e*-1)   .

В бесконечно удаленной точке гиперболической орбиты r= ∞ , т.е. 1+e_* cos n_∞=0. Следовательно,

e*=-  1 cosn∞ > 1.

Там же интеграл инергии дает V²=m/a_*, где V² = v₁²+v₂² и (v₁,v₂) - скорость прилета из бесконечности. Следовательно,

a*=m/V2.

Поскольку |cosn_∞|=|v₁|/V, то согласно предыдущим формулам пересечение гиперболической орбиты с осью x₁ происходит в точке

x10 =  m V2 ж и  V |v1| -1 ц ш  sgn  v1

со скоростью

Ч x   2  =   ж Ц  m(1+ V/|v1|) |x10|    sgn  v2 =   ж Ц   2 m |x10| + V2    sgn  v2,

ибо

m(  V |v1| +1) = |x10| V2 +2 m.

Сращивание полученного гиперболического решения с решением-отрезком задачи двух тел P₁ и P₃ произведем самым грубым образом: положим, что скорость прихода из бесконечности (v₁,v₂) для гиперболической орбиты равна скорости столкновения (v₁,v₂) тела P₃ с телом P₂ для решений семейств S. Более аккуратное сращивание составляет предмет многочисленных исследований (см. например, [23]).

Положим

z1 =  1 V ж и  V |v1| -1 ц ш  sgn  v1,    w2 =   ж Ц  2 |z1| +3 -C   ,

(3.6)

ибо V²=3-C, где C - значение константы Якоби. Тогда в пределе при m→ 0 получим, что (x₁-1)/m→ z₁ и y₂ → w₂, поэтому значения (3.6) можно рассматривать как порождающие для нормированной задачи двух тел P₂, P₃ вблизи тела P₂.

Если орбита второго вида состоит из одного решения-отрезка с параметрами a,e, то в (3.6)

|z1| =  1 3-C ж з и   ж Ц  3-C (e2-1)a+2-1/a   -1 ц ч ш .

Решения-отрезки дают скорости входа V=(v₁,v₂) и выхода (-v₁,v₂) решения-отрезка в точку P₂=(1,0). У соответствующих порождающих и порождаемых орбит ортогональное пересечение с осью x₁ происходит слева от точки P₁, если sign v₁ < 0, и справа, если sign v₁ > 0. Если v₂ ≠ 0, то облет происходит так, как описано выше. Если же v₂ = 0, то порождаемые орбиты являются орбитами столкновения. Для них x₁⁰=0 и [(x)\dot]₂ = ∞. Прохождение таких порождаемых орбит через столкновение показано на рис. 1.

 

Предполагается вычислить девять основных семейств, которые в обозначениях Стремгрена, Бартлета и Хенона таковы.

Cемейство a выходит из неподвижной точки Лагранжа L₂.

Cемейство b выходит из точки L₃.

Cемейство c выходит из точки L₁.

Cемейство f начинается как обратные круговые орбиты бесконечно малого радиуса вокруг тела P₂.

Cемейство g начинается прямыми круговыми орбитами бесконечно малого радиуса вокруг тела P₂.

Cемейство h начинается обратными круговыми орбитами бесконечно малого радиуса вокруг тела P₁.

Cемейство i начинается прямыми круговыми орбитами бесконечно малого радиуса вокруг тела P₁.

Cемейство l начинается обратными круговыми орбитами бесконечно большего радиуса с положительным значением C (в сидерических координатах они имеют прямое направление движения).

Cемейство m начинается обратными круговыми орбитами бесконечно большего радиуса с отрицательным значением C (в сидерических координатах они сохраняют обратное направление движения).

Брук [4] и Брюно [5, 6] эти же семейства обозначали по-другому. Ниже приводится таблица этих обозначений.

Стремгрен a b c f g h i l m Брук I J1 G C H1, H2 A1 BD E1 F Брюно L2 L3 L1 E+1/1 2T1 IR+ ID1 ID-1 IR-

Для каждого семейства сначала будет описываться и вычисляться порождающее семейство (т.е. при m = 0), затем будет вычисляться это семейство при остальных значениях (1.4). Для каждого значения m будут даны графики его характеристик на плоскости симметрии P в трех системах координат, описанных в § 2, а также графики нормированного периода T/2p, следа Tr и следа Tr_v. Также будут даны таблицы замечательных орбит и рисунки некоторых из них. Затем для некоторых вычисленных орбит предполагается сравнить некоторые их параметры с тем, что предсказывает для них теория возмущений согласно [1].

Будут также отмечаться места пересечения семейств с другими симметричными и асимметричными плоскими и пространствеными семействами периодических решений.

Заметим, что при подстановке m→ 1-m основные девять семейств испытывают следующую подстановку

a, b, c, f, g, h, i, l, m → c, b, a, h, i, f, g, l, m.

 

Несмотря на значительные усилия, затраченные на численное исследование ограниченной задачи, фактический материал, полученный численно, представляется фрагментарным. Это связано, главным образом, с тем, что до недавнего времени вычислительные мощности были неадекватны задаче. Так, например, в книге Хенона [7], вышедшей в 1997 году, используются численные результаты тридцатилетней давности.

Но вычислительные мощности - не единственная проблема при численном исследовании семейств периодических решений ограниченной задачи. Исключительно сложное поведением решений вблизи орбит столкновения приводит к тому, что традиционные численные методы неэффективны, либо не работают вблизи некоторых особенностей решений. Видимо, это являлось причиной того, что даже девять основных семейств периодических решений, указанные выше, не были вычислены с достаточной полнотой, позволяющей выявить закономерности их строения.

Типичное семейство периодических решений можно условно разбить на участки с различным поведением решений, полученных численно. На некоторых участках не возникает проблем с точностью отслеживания траекторий, а на некоторых - точность катастрофически падает. Наконец, есть участки семейств вблизи столкновений тела P₃ с телами P₁ и P₂, где вычисления невозможны без регуляризации.

Заметим, что точность отслеживания траекторий можно определять, сравнивая константу Якоби C в начале траектории и через полупериод.

Все это приводит к тому, что требуется серия программ, работоспособных на различных участках семейства.

На участках, где не возникает проблем с точностью, мы использовали метод Рунге-Кутта пятого поряда с фиксированным шагом по времени, жертвуя небольшой потерей эффективности в пользу надежности полученных результатов и стабильности вычислительного процесса.

На (небольших) участках вблизи столкновений мы применяли регуляризацию Леви-Чевита [11, § 3.4].

Наконец, на проблематичных участках семейства, где происходит большая потеря точности, если не предпринять дополнительных мер, мы используем масштабирование времени в исходных координатах, которое можно назвать квазирегуляризацией, и метод Рунге-Кутта с фиксированным шагом по времени.

Заметим, что к настоящему времени разработано множество методов численного интегрирования ОДУ с переменным шагом по времени, призванных справляться с указанной потерей точности. Однако все эти методы используют некоторые априорные оценки решений ОДУ при выборе шага интегрирования. Поведение решений ограниченной задачи может быть столь непредсказуемо, что эти априорные оценки окажутся неприменимы. Опыт показывает, что преимущества "продвинутых" методов численного интегрирования ОДУ могут обернуться потерями. Если указанные априорные оценки окажутся слишком оптимистичными, то программа может перескочить на другое семейство периодических решений. Если же оценки окажутся завышенными, то это приведет к неоправданному измельчению шага.

Поэтому вместо того, чтобы модифицировать метод Рунге-Кутта (или какой либо другой), мы модифицировали ограниченную задачу, используя нелинейную замену времени так, что время замедляется вблизи тел P₁ и P₂.

В синодической системе координат с центром в середине отрезка P₁ P₂ положение тела P₃ описывается уравнением в комплексных переменных [11, § 3.4, формула (91)]:

d2 dt2  z(t) + 2i   d dt  z(t) = gradz U,

(5.1)

где z=x₁-1/2+ i x₂, и

gradz U    def =     z + 1/2 - m-  (1 - m) (z + 1/2) |z + 1/2|3 -  m (z - 1/2) |z - 1/2|3 .

В уравнении (5.1) мы делаем двупараметрическую замену времени

t= у х s 0  |z(v)+1/2|p  |z(v)-1/2|q dv,

(5.2)

в результате получаем уравнение

d2 z ds2 = |z+1/2|2p |z-1/2|2q gradz U -(2i  |z+1/2|p  |z-1/2|q -            -p  Re(   dz ds   (z+1/2)   ) |z+1/2|2 -q  Re(   dz ds   (z-1/2)   ) |z-1/2|2 )     dz ds ,

(5.3)

где параметры p ≥ 0, q ≥ 0 выбираются в зависимости от того, в окрестности какого тела P₁ или P₂ требуется замедлить время. Заметим, что, например, при q=2 время движения в окрестности тела P₂ становится неограниченным для орбиты столкновения, однако, как было отмечено, небольшие участки семейств вблизи орбит столкновения просчитываются с помощью регуляризации Леви-Чевита.

Преимущества замены времени (5.2) становятчя очевидными, если вместо численного интегрирования ситемы (5.3) использовать алгоритм без насыщения [19, гл. 9, § 5], когда нечетная периодическая функция - решение уравнения (5.1) или (5.3) - раскладывается в ряд Фурье. Для уравнения (5.1) метод без насыщения непрактичен, так как вблизи орбит столкновения требуется очень большое количество гармоник. Для уравнения (5.3) коэффициенты ряда Фурье убывают значительно быстрее при подходящем выборе p и q. Обычно мы использовали p=1, q=0 для орбит, близких к телу P₁, и p=0, q=1 для орбит, близких к телу P₂.

Индивидуальная траектория симметричного периодического решения уравнения (5.1) вычислялась с помощью метода Ньютона как решение краевой задачи с неопределенной границей, которая в свою очередь вычислялась в момент пересечения траекторией плоскости симметрии P, т.е. траектория вычислялась на полупериоде решения.

Момент пересечения определялся с помощью кубической интерполяции. Поскольку шаг интегрирования достаточно мал, то параметры орбиты, т.е. полупериод T/2 решения и координаты пересечения плоскости симметрии P, отслеживаются с точностью превышающей погрешности численного интегрирования.

После того, как траектория периодического решения фиксирована, вычисляется решение уравнений в вариациях на периоде решения для определения следа Tr матрицы монодромии, и на полупериоде решения для определения следа Tr_v, согласно формуле (18) в [22, стр. 416], т.е. определяется устойчивость решения в линейном приближении.

Параметры орбиты заносятся в базу данных, которая используется для приближенного вычисления очередной орбиты семейства с помощью квадратичной интерполяции. Затем приближенная орбита уточняется с помощью метода Ньютона. Таким образом, семейство периодических решений отслеживается до выполнения критериев, указанных выше.

Метод определения устойчивости в линейном приближении на полупериоде решения, описан в [21, 22].

 

Литература

1. Брюно А.Д. Ограниченная задача трех тел. Плоские периодические орбиты. М.: Наука, 1990. 296 с.
2. Stromgren, E., "Connaissance Actuelle des Orbits dans le Problème des Trois Corps", Publications and Minor Communications of Copenhagen Observatory, Publication 100. Copenhagen University, Astronomical Observatory, Denmark, 1935.
3. Bartlett, J.H., "The Restricted Problem of Three Bodies (1)", Kong. Dan. Vidensk, Selsk., Mat.-Fys. Skr., 1964, vol. 2, no. 7. 48 p.
4. Broucke M.R. Periodic Orbits in the Restricted Three-Body Problem with Earth-Moon Masses. NASA Technical Report 32-1168. Pasadena, 1968, 92 p.
5. Брюно А.Д. Однократные периодические решения ограниченной задачи трех тел в случае Солнце-Юпитер // Препринт N 66 Института прикладной математики. М., 1993. 27 с.
6. Брюно А.Д. Нулькратные и обратные периодические решения ограниченной задачи трех тел // Препринт N 93 Института прикладной математики, М.; 1996. 32 с.
7. Henon M. Generating Families of the Restricted Three-Body Problem. Springer, Berlin etc., LNP NsM 52, 1997. 278 p.
8. Henon M. Generating Families of the Restricted Three-Body Problem. II. Quantitative Study of Bifurcations. Springer, Berlin etc., LNP NsM 65, 2001. 301 p.
9. Брюно А.Д. Исследования по ограниченной задаче трех тел. I. Периодические решения системы Гамильтона // Препринт N 18 Института прикладной математики, М.; 1972. 44 с.
10. Henon M. Sur les orbits interplanetaires qui rencontrent deux fois la terre // Bull. astron., Ser. 3, 1968, t. 3, no. 3, p. 377-402.
11. Себехей В. Теория орбит. Перевод с английского. М: Наука, 1982. 656 с.
12. Hénon M. Vertical stability of periodic orbits in the restricted problem // Astron. & Astrophys., 1973, v. 28, p. 415-426.
13. Perko L.M. Second species solutions with an O(mⁿ), 0 < n < 1, near moon passage // Celest. Mech. 1981, vol. 24, no. 2. p. 155-171.
14. Hitzl D.L., Henon M. Critical generating orbits for second species periodic solutions of the restricted problem // Celest. Mech. 1977, v. 15, no. 4, p. 421-452.
15. Hitzel D.L., Henon M. The stability of second species periodic orbits in the restricted problem (m = 0) // Acta Astronaut. 1977, v. 4, p. 1019-1039.
16. Брюно А.Д. О периодических облетах Луны // Препринт N 91 Института прикладной математики, М.; 1978. 25 с.
17. Bruno A.D. On periodic flybys of the moon // Celest. Mech. 1981, v. 24, no. 3, p. 255-268.
18. Абалакин В.К., Аксенов Е.П., Гребенников Е.А., Рябов Ю.А. Справочное руководство по небесной механике и астродинамике. М.: Наука, 1971. 584 с.
19. Бабенко К.И. Основы численного анализа. Ижевск: РХД, 2002. 848 с.
20. Kotoulas T., Voyatzis G. Comarative study of the 2:3 and 3:4 resonant motion with Neptune: An application of symplectic mappings and low frequency analysis // Celest. Mech. 2004, v. 88, no. 4, p. 343-363.
21. Hénon M. Exploration Numérique du Problème Restreint. II - Masses égales, stabilité des orbites périodique // Ann. Astrophys. 1965, t. 28, N 6, p. 992-1007.
22. Hénon M., Guyot M. Stability of periodic orbits in the restricted problem // Periodic Orbits, Stability and Resonances (G.E.O. Giacaglia, ed.), Dordrecht-Holland: D Reidel P.C., 1970, p. 349-374.
23. Breakwell J.V., Perko L.M. Second order matching in the restricted three-body problem (small m) // Celest. Mech. 1974, v. 9, no. 4, p. 437-450.

Рисунки