Аннотация
В работе высказывается предположение о возможном наличии у некоторых кристаллов асимметричной
проводимости в противоположных направлениях, которая может играть роль «демона Максвелла».
Дается приблизительная количественная оценка эффекта.
Abstract
Author suggests that some crystals may have asymmetric conductivity and work
as “Maxwell daemon”. Approximate evaluation of effect is given.
1. Общие положения.
Один из вариантов «демона
Максвелла» представляет собой диод молекулярных размеров. Если бы удалось
создать или найти среду с односторонней или, хотя бы, асимметричной
проводимостью на уровне отдельных электронов, то их тепловое движение можно
было бы преобразовать в упорядоченное и получить, тем самым, электрический ток.
Наиболее общее
доказательство второго начала термодинамики основано на принципе детального
равновесия, то есть обратимости всех микроскопических процессов по времени, но
если среда с асимметричной проводимостью существует, то в ней принцип
детального равновесия не соблюдается.
Роль асимметричного
проводника может играть монокристалл или специально поляризованная
поликристаллическая среда (подобно пьезокерамике). Кристалл должен обладать
необходимыми свойствами симметрии. Отразим решетку относительно плоскости,
перпендикулярной направлению тока. Если теперь никакими отражениями и
поворотами относительно осей и плоскостей, параллельных направлению тока,
структуру нельзя перевести саму в себя, то такой кристалл по соображениям
симметрии может иметь асимметричную проводимость. Требования к симметрии здесь
те же, что и для пьезоэффекта, а также для наличия квадратичной нелинейности
поляризации, и могут быть сформулированы более коротко: отсутствие у решетки
центра симметрии. [8] Этому условию удовлетворяют 20 кристаллографических групп
из 32.
Даже при соблюдении условий
симметрии асимметричная проводимость невозможна в рамках модели, описывающей
проводимость как движение электрона в потенциальном поле и не учитывающей
обратное воздействие электрона на решетку. Но в некоторых случаях поляризация
среды электроном оказывает сильное влияние на механизм проводимости, и здесь
асимметричная проводимость может оказаться возможной.
Для того, чтобы электрон мог
оказывать существенное воздействие на среду, его движение должно быть
достаточно медленным, характерное время ионов решетки должно быть меньше
времени «пролета» электрона через ячейку. В противном случае среда просто не
успеет поляризоваться.
Известны два механизма
проводимости, отличающихся малой подвижностью электронов. Это - поляронная и
прыжковая проводимости. На самом деле поляроны в большинстве случаев тоже
двигаются прыжками, но необходимо отличать прыжковую проводимость поляронов, локализованных
в узлах кристаллической решетки, от прыжковой проводимости электронов,
локализованных на атомах примеси. Оба
этих механизма могут оказаться пригодными для наших целей. Рассмотрим сначала
поляроны.
2. Поляроны.
Поляроном называется квазичастица,
представляющая собой электрон, окруженный деформированной областью решетки. За
счет поляризации среды вокруг такого электрона возникает потенциальная яма, что
приводит к автолокализации, то есть теперь волновая функция электрона мала
везде кроме области вокруг одного или нескольких узлов кристаллической решетки,
и для того, чтобы выйти из этого состояния, электрону надо преодолеть некоторый
потенциальный барьер. Различают поляроны большого и малого радиуса в
зависимости от размеров области локализации. Поляроны большого радиуса имеют
размеры порядка сотен и тысяч периодов решетки, поляроны малого радиуса –
порядка одного-двух.
Трудно представить себе
какой-то асимметричный эффект в поляронах большого радиуса. Хотя в нелинейной
среде они и могут иметь асимметричную форму, любое их перемещение вызовет
практически симметричное движение атомов среды. Будем поэтому рассматривать
поляроны малого радиуса.
В идеальных условиях, то
есть вблизи абсолютного нуля и в бездефектном кристалле, поляронная проводимость
может быть и зонной, но в большинстве случаев движение поляронов является
прыжковым. Это означает, что в течение некоторого времени электрон совершает
колебания вблизи одного из узлов решетки, потом перескакивает в другой, и там
все повторяется сначала.
Такой механизм как нельзя
лучше соответствует нашим целям. Время перескока имеет порядок периода
собственных колебаний электрона, то есть 10-15 с и много меньше
характерного времени ионов и атомов, составляющих решетку. За время прыжка
среда не успеет переполяризоваться и тем самым обеспечит требуемую
«непотенциальность».
Это, разумеется, касается
только ионной составляющей поляризации. Электронная поляризация будет меняться,
но ее обычно рассматривают как часть потенциального поля. Считается, что характерное
время электронов поляризации много меньше времени прыжка, и поэтому их
состояние можно считать функцией состояния электрона проводимости. Таким
образом, хотя создаваемое ими поле и меняется во времени, оно однозначно
зависит от электрона проводимости, и поэтому его можно считать потенциальным. [1]
Время между прыжками зависит
от температуры, размера полярона и свойств вещества. У полярона малого радиуса
оно может быть от 10-10 с до нескольких секунд, что много больше
характерного времени ионов (10-12 – 10-13 с). Это хорошо,
потому что в противном случае электрон мог бы вернуться в прежнюю локацию
раньше, чем среда перейдет в новое состояние и выполнит свою запирающую
функцию.
Выше было сказано, что все
интересующие нас кристаллы обладают квадратичной нелинейностью поляризации, так
как для нее требуются те же свойства симметрии. Вообще говоря, если эффект
асимметричной проводимости существует, то он связан с нелинейной поляризацией
сложным образом, и необязательно те кристаллы, которые имеют большую квадратичную
нелинейность, будут иметь большую асимметрию проводимости. Но точное
моделирование эффекта потребовало бы сложных квантово-механических расчетов,
поэтому сейчас нам удобнее всего воспользоваться простейшей моделью,
описывающей ту часть асимметрии проводимости, которая обусловлена квадратичной
нелинейностью или, точнее, диагональными квадратичными компонентами тензора
диэлектрической проницаемости.
У многих веществ, таких как
йодат лития LiIO3, ниобат лития LiNbO3, ниобат
калия-лития K3Li2Nb5O15, бета-борат
натрия b-BaB2O4,
прустит Ag3AsS3, пираргирит Ag3SbS3,
селенид кадмия CdSe, киноварь HgS, селен и теллур эти компоненты измерены
экспериментально и достигают значений порядка 10-10 м/В.
Нелинейность поляризации
обычно измеряется оптическими методами, поэтому те значения, которые мы можем
найти в справочниках, представляют собой поляризацию в зависимости от частоты
излучения. Это не очень хорошо для наших целей, поскольку нам нужна только
низкочастотная составляющая поляризации. Её можно оценить приблизительно, взяв
разность между значениями при самых высоких и самых низких, близких к
инфракрасному резонансу частотах, из тех, что у нас имеются. Как правило, эта
разность имеет тот же порядок, что и сами значения, в худшем случае может быть
на порядок меньше.
В одномерной модели поляризацию кристалла с
квадратичной нелинейностью можно описать формулой:
P = e0(c(1)E+c(2)E2+...)
где
E – напряженность электрического
поля, c(1), c(2) – диэлектрические
восприимчивости первого и второго порядков.
В такой среде точечный заряд
будет создавать неодинаковую поляризацию в противоположных направлениях.
Электрон находится в периодическом поле кристаллической решетки,
которое из-за квадратичной нелинейности поляризации асимметрично деформируется.
Потенциальные барьеры с разных сторон электрона приобретают разную форму,
высоту и ширину. Вероятность прыжка через эти барьеры будет различна (рис. 1).

Рис. 1.
В течение времени прыжка все
результирующее поле можно считать постоянным, поскольку время прыжка много меньше
характерного времени ионов кристаллической решетки, смещение которых
обеспечивает поляризацию. После прыжка электрон окажется в потенциальной яме
соседнего узла. Глубина ее поначалу будет меньше, чем глубина той ямы, из
которой он пришел, но высота потенциального барьера достаточна, чтобы задержать
электрон на время, требуемое для исчезновения старой ямы самосогласованного
поля и возникновения новой. Затем все повторяется.
Возникает вопрос, как лучше
учитывать асимметрию барьеров – как отличие высоты или ширины барьера? Мы не
знаем, как будет меняться высота барьеров, возможно и очень незначительно. Но
ширина будет меняться обязательно, из-за смещения ионов и потенциальных ям
вместе с ними, и оценить это смещение легко.
Поляризация среды равна:
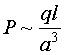
где
a – период решетки, q – заряд единичного иона, l – расстояние, на которое ионы
смещаются под действием поляризующего поля.
Значит:
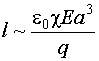
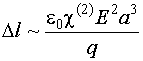 (1) (1)
Напряженность поля электрона на расстоянии порядка размеров ячейки:
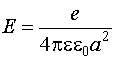 (2) (2)
Частота прыжков зависит от ширины и высоты
потенциального барьера:
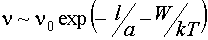 (3) (3)
Изменение ширины потенциального барьера, обусловленное квадратичной
нелинейностью, мало по сравнению с шириной барьера, поэтому формулу (3) можно
разложить в ряд Тейлора. Тогда разность частот прыжков в противоположных
направлениях будет такой:
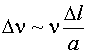
Плотность тока, возникающего из-за
несимметричных прыжков:
J0 ~ aen Dn
J0 ~ en n Dl (4)
где n – концентрация
электронов проводимости.
Из формулы (3) можно вывести и формулу для тока во внешнем поле, только
в этом случае надо раскладывать в ряд Тейлора не по l, а по W, и
разность энергий будет равна изменению потенциальной энергии электрона во
внешнем поле:
DW = aeE
Тогда:
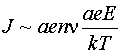
Проводимость:
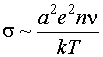
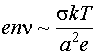
Таким образом, ток, возникший в результате
эффекта “демона Максвелла” будет:
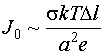 (5) (5)
Казалось бы теперь, зная
экспериментально измеренную проводимость и квадратичный коэффициент
поляризации, нетрудно оценить величину эффекта. Но динамика и статистика
поляронов изучены еще недостаточно, и мы не всегда можем сказать, что проводимость
обеспечивают только поляроны малого радиуса или определить, какая доля
проводимости обеспечивается ими.
Попытки применить формулу
(5) к различным веществам, в которых наблюдались признаки поляронной
проводимости, дают самые разные результаты, в некоторых случаях явно
неправдоподобные.
Возможно, как раз
неправдоподобно большие оценки нелинейных эффектов и следует рассматривать как
доказательство того, что большая часть проводимости в данном веществе
обеспечивается не поляронами малого радиуса, а каким-нибудь другим механизмом –
зонным, прыжковым или поляронами большого радиуса.
Возьмем c(2) = 10-11 м/В, помня о том, что нам нужна
ионная составляющая, а она может быть на порядок меньше поляризации в целом,
для которой типичное значение 10-10 м/В. [4]
Температуру возьмем T=300К, период решетки a=5*10-10 м,
диэлектрическую проницаемость e=10.
Если теперь взять значения
проводимости, полученные в классических опытах с NiO, [1, стр. 190] s=1.6*10-6 Ом-1см-1,
и подставить типичные значения квадратичной нелинейности, получим вполне
правдоподобное значение:
J0 ~ 10-4А/м2
Если же взять кристаллы Fe3O4,
имеющие довольно высокую проводимость, в которых тоже наблюдались поляронные
явления, и считать, что вся их проводимость обеспечивается поляронами малого радиуса,
то мы получим неправдоподобно высокие значения нелинейных эффектов (J0 ~ 107А/м2),
что, скорее всего, свидетельствует о том, что в данном случае механизм
проводимости отличен от поляронов малого радиуса и ближе к прыжковой
проводимости в легированных полупроводниках.
Поляронная проводимость в
упорядоченной структуре химически чистого кристалла удобнее как с точки зрения
математического моделирования, так и с точки зрения перспектив практического
применения. Но из-за проблем с теорией поляронов малого радиуса, возможно,
имеет смысл начать экспериментальный поиск асимметричной проводимости с другого
механизма – прыжковой проводимости в легированных полупроводниках. Её теория
разработана лучше и дает хорошее совпадение с экспериментом.
3. Прыжковая
проводимость.
Прыжковый механизм
проводимости характерен не только для поляронов. Таким же способом может
перемещаться электрон, локализованный на атоме примеси в легированном
полупроводнике. Разумеется, он тоже поляризуют среду и поэтому может
рассматриваться как часть полярона. Важно, что потенциальная яма, создаваемая
атомом примеси, имеет больший радиус, чем яма в узле решетки, и из-за этого
энергия поляризации здесь меньше, и прыжки должны происходить чаще.
Кроме того, если узлы
решетки расположены упорядоченно, то атомы примеси – хаотично. Это приводит к
тому, что в легированном полупроводнике с прыжковой проводимостью электроны
движутся по сложным извилистым траекториям, что сильно затрудняет определение
их подвижности. Для таких расчетов разработан специальный метод сетки
сопротивлений. Но нам сейчас нет необходимости им пользоваться, так как мы
можем выразить величину нашего эффекта через уже известное значение
проводимости.
В остальном наши рассуждения
об асимметрии прыжков остаются такими же. Цепочка атомов примеси – такая же
цепочка потенциальных ям, как и последовательность узлов решетки, разница лишь
в том, что она не всегда ведет в нужном нам направлении, да еще расстояние
между атомами примеси неодинаково. Основной вклад в проводимость вносят атомы
примеси, расположенные на расстоянии боровского радиуса (порядка 10-8 м) друг от друга [6, стр. 111-125 и 184-192],
поэтому среднее расстояние между соседними ямами тоже можно считать известным.
Формула (1) теперь нуждается
в уточнении, поскольку атом примеси искажает решетку вокруг себя и его смещение
под действием внешнего поля может отличаться от смещения атомов решетки, но для
таких грубых оценок, как у нас, это неважно.
Напряженность поля электрона теперь надо вычислять не на расстоянии
порядка размеров ячейки, а на расстоянии средней длины прыжка b:
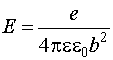 (6) (6)
В формуле для разности частот прыжков тоже
придется заменить размер ячейки на среднюю длину прыжка:
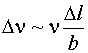
В формуле для плотности тока, введем
коэффициент x, означающий долю участков
траектории, имеющих нужное направление:
J0 ~ xben
Dn
J0 ~ xen n Dl (7)
Тот же коэффициент
фигурирует и в формуле для проводимости:
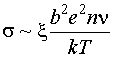
Окончательное же выражение почти не изменится:
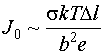 (8) (8)
Dl вычисляется по той же
формуле (1), но значение E в нее надо подставлять
теперь из формулы (6).
Квадратичный коэффициент
поляризации, как и в прошлый раз, возьмем c(2) = 10-11 м/В.
Температуру возьмем T=30К,
поскольку этот механизм проводимости обычно наблюдается при низких
температурах.
Удельное сопротивление
полупроводников с прыжковой проводимостью в зависимости от концентрации
примесей и температуры меняется от 0.001 до 100 Ом*м. [6, стр. 184-192] Возьмем
сопротивление с запасом в один порядок 0.01 Ом*м.
Период решетки: a=5*10-10м,
диэлектрическая проницаемость e=10.
Средняя длина прыжка: b=10-8
м
Подставив все эти значения в формулы (6), (1) и (8),
получим:
J0 ~ 10-4 А/м2
J0 – это плотность тока в
кристалле при нулевой разности потенциалов на противоположных гранях. При
наличии же внешнего поля ток через кристалл будет определяться простой
формулой:
I=U/R+I0
При размерах образца порядка
миллиметра ток будет порядка 10-10 А. Это достаточно мало, чтобы
объяснить, почему эффект до сих пор не был обнаружен, но и достаточно много,
чтобы при помощи современных приборов обнаружить его, если искать специально.
Возможно, эффект иногда
регистрировался в экспериментах случайно, но ему давали другое объяснение.
Удалось найти работу харьковских экспериментаторов 1998 года [7], в которой
исследуются электрические свойства монокристалла La2CuO4+d. Воспроизведем здесь один
график из этой статьи (рис. 2).
Видны полки вольт-амперной
характеристики. Ток остается постоянным при напряжении, стремящемся к нулю. К
сожалению, серия экспериментов доведена только до U ~ 10-3 В. Авторы
объясняют этот эффект сверхпроводимостью. Но не исключено, что настоящая
причина может быть и другой.

Рис. 2.
4.
Перспективы.
До сих пор мы оценивали величину
тока, который может быть обнаружен у наугад взятого кристалла с высокой
квадратичной нелинейностью. Но это не
значит, что таким способом в принципе нельзя извлекать большую энергию. Если
существование эффекта будет доказано в принципе, то мы сможем существенно
повысить это значение, создавая кристаллы и наноструктуры с более сильной
нелинейностью поляризации, работающие при более высоких температурах,
обладающие более высокой плотностью носителей заряда, лишенные тех недостатков,
которыми обладает примесная прыжковая проводимость. Несложно подсчитать, что
возможности повышения эффективности здесь практически неограниченные.
Частота прыжков электронов
не должна быть больше фононной (т. е. частоты колебаний атомов решетки),
поскольку в противном случае среда не успеет поляризоваться за время между
прыжками.
n=1012 с-1
Специально созданные кристаллы могут быть
настолько эффективны, что частота упорядоченных прыжков будет в них иметь тот
же порядок, что и частота неупорядоченных.
Максимальная разность
потенциалов, которую электрон сможет преодолеть за один прыжок, не может быть
больше kT/e.
U~10-2 В
Таким образом, максимальная мощность, которую можно
извлечь из единицы объема кристалла:
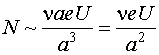
N~109 Вт/м3
Конечно, на практике такая
мощность вряд ли достижима, хотя бы из-за ограничений на подвод тепла извне. Но
данная формула показывает, что микроскопический механизм проводимости
лимитирующим фактором не является.
Автор благодарит А.Ю.Дроздова (Харьков) и А.А.Фомина (Бишкек) за плодотворное
обсуждение, оказавшее большую помощь в работе.
Литература:
1. Аппель Дж, Фирсов Ю.А.,
Поляроны, М., 1975;
2. Ланг И.Г., Фирсов Ю.А.,
Кинетическая теория полупроводников с малой подвижностью. ЖЭТФ, т. 43, с. 1843
(1962);
3. Мясников Э.Н., Мясникова А.Э., Греков А.А., Мастропас З.П.,
Когерентные состояния поляризованности и динамика поляронов малого радиуса,
Электронный журнал «Исследовано в России», http://zhurnal.ape.relarn.ru/articles/2004/067.pdf
4. Гурзадян Г.Г., Дмитриев
В.Г., Никогосян Д.Н., Нелинейнооптические кристаллы. Свойства и применение в
квантовой электронике: Справочник. М., 1991;
5. Ахманов С.А., Хохлов
Р.В., Проблемы нелинейной оптики, М., 1964;
6. Шкловский Б.И., Эфрос
А.Л., Электронные свойства легированных полупроводников, М., 1979;
7. B.I.Belevtsev, N.V.Dalakova, A.S.Panfilov, Non-linear effects in
hopping conduction of single-crystal La2CuO4+d, http://xxx.lanl.gov/abs/cond-mat/9807297
8. Дж. Най, Физические
свойства кристаллов. М., 1960;
|