Содержание

Содержание. 3

Введение. 3

1.. Математическое моделирование социальных процессов. 3

2. Моделирование исторических процессов. 5

3. Постановка задачи. 6

4. Непрерывная модель транспортировок Бекманна. 7

5. Пространственная модель торговли. 12

6. Модель Великого шелкового пути. 15

7. Методика оценки коэффициента товаропроводности территории. 18

8. Оценка коэффициентов транспортного трения на основе дневника путешествий Марко Поло. 26

9. Поправка на фрактальную размерность. 33

10. Результаты моделирования Великого Шелкового Пути. 36

Выводы.. 42

Литература. 44

Введение

В настоящее время остро ощущается необходимость использования научного потенциала, накопленного в естественнонаучных областях, для описания процессов, происходящих в социальных системах. В условиях современного мира на первый план выходят вопросы прогнозирования и принятия решений.

Прогноз будет иметь успех только в том случае, если будут разработаны адекватные математические методы, позволяющие быстро и точно анализировать множество вариантов, не прибегая к экспериментам, которые в социальных системах могут стоить очень дорого, и даже приводить к гибели социальной системы. Несмотря на то, что традиционно существует разделение на естественные и гуманитарные науки, современные междисциплинарные подходы показывают, что в основе различных наук могут лежать единые основания, общие для дисциплин, которые ранее развивались изолировано. В частности, было обнаружено, что одни и те же математические конструкции и уравнения могут описывать различные процессы в физике, химии, биологии, демографии и экономике. Это с одной стороны позволяет использовать уже разработанный концептуальный и математический аппарат в новых областях, а с другой стороны является свидетельством того, что наука во многом едина.

1. Математическое моделирование социальных процессов

Компьютерное моделирование социальных процессов является новым направлением, которое возникло естественным образом как следствие стремительного развития математических методов и вычислительной техники с одной стороны, и значительного усложнения социальных взаимосвязей, роста рисков и угроз – с другой.

Успехи в описании сложных физических процессов создали предпосылку для приложения математического аппарата к другим областям знания, в том числе к тем, которые традиционно считались гуманитарными и находились вне поля интересов естественных наук. Первые попытки применения математики при анализе социальных процессов [1], с одной стороны, показали, что для описания достаточно простых зависимостей действительно можно применять математические методы и даже строить адекватные прогнозы, с другой стороны, выявили ряд фундаментальных проблем, без решения которых невозможно говорить о дальнейших шагах в развитии моделирования социальных процессов. Одна из таких проблем – проблема формализации «человеческого фактора» [2, 3, 4]. Чрезвычайная сложность детерминированного описания поведения человека (как части общества) является естественной преградой на пути разработки формальной теории социальных систем. Более того, достижения в смежных дисциплинах – биологии, системном анализе, синергетике [5, 6, 7, 8] фактически свидетельствуют о принципиальной невозможности детерминированного описания, об ограниченности горизонта прогноза, являющихся не следствием слабости аппарата анализа, но следствием фундаментальных законов функционирования сложных систем.

С другой стороны, четко ограничивая возможности применения детерминированного описания, синергетика и близкие ей области знания, столь же определенно предлагают другие подходы, в которых случайность и неопределенность не являются досадными дестабилизирующими факторами, затрудняющими прогноз и препятствующими развитию, а напротив – являются созидающим и стимулирующим началом, центральным фактором эволюции сложных систем.

Подобное положение дел, при всей кажущейся определенности и осознании концепций и направлений, в которых следует прилагать усилия по созданию формальной социальной теории, свидетельствует о другой проблеме, относящейся скорее не к объекту исследования, а к познающему субъекту. Фактически речь идет о том, что исследователь, изучающий социальные системы, должен владеть методами современной физики, нелинейной динамики и системного анализа. Лишь в этом случае у него есть возможность продвинуться в понимании законов эволюции исследуемых систем. С другой стороны, тот же исследователь должен владеть предметной областью, в данном случае социальными науками, иначе его теоретические построения будут иметь весьма отдаленную связь с действительностью. В то же время, как в общественном сознании, так и в системе образования разделение на естественные и гуманитарные науки фактически привело к их противопоставлению и образовало вакуум специалистов, способных на современном уровне работать в обоих направлениях. Наконец, подобная изоляция привела к формированию качественно различных методов исследования, что создало еще больше препятствий для нахождения общего языка между представителями естественной и гуманитарной области.

Выходом из подобной ситуации может стать только череда реальных успехов в области социального моделирования. С одной стороны, модели должны быть построены, опираясь на современные достижения математики и естественных наук, с учетом нелинейности, флуктуаций, сложности систем, с другой стороны они должны быть доведены до реального применения в прикладной области, получить поддержку специалистов, продемонстрировать свою практическую ценность.

2. Моделирование исторических процессов

Математические исследования социальных систем во многом ведутся с прагматическими целями. Неслучайно самая развитая в плане математизации общественная наука – экономика. Неслучайно самое большое число исследований, посвященное использованию математики, и в частности нелинейной динамике, в экономике, относится к изучению фондовых рынков [9, 10], то есть тем системам, в которых возможны наибольшие выигрыши при относительно небольших затратах. Другой причиной можно назвать большую доступность и полноту временных рядов биржевой статистики, однако, как известно, наибольшая статистика имеется в той области, к которой обращено наибольшее внимание, в том числе и в первую очередь, из прагматических целей.

Современное общество и процессы, проходящие в нем, слишком сложны, чтобы начинать построение фундаментальной теории с их описания. Это почти то же самое, что и начинать построение классической физики с попыток описания гидродинамики или физики плазмы. Не имея теории более простых социальных систем, нельзя строить теорию современного общества.

Кроме того, исследователи неминуемо сталкиваются с тем, что адекватность их моделей и прогнозов можно будет оценить только по прошествии многих лет или даже десятилетий. Подобные теоретические прогнозы невозможно оперативно проверить и скорректировать. Вносить поправки в теорию можно будет только через пару десятков лет, что для науки недопустимо, она развивается гораздо быстрее, краткосрочные прогнозы, хотя и имеют практическую ценность, подчас мало ценны с научной точки зрения, поскольку являются фактически экстраполяцией текущих тенденций, для которых достаточны знания методов экстраполяции и не требуется фундаментальных уравнений.

Времена прогноза зависят также от масштабов социальной системы. Содержательный научный прогноз для небольшой системы может быть проверен на гораздо меньших временах, чем для крупных систем. Однако в малых системах проблемы, связанные с «человеческим фактором»,  стоят особенно остро. Трудно формализуемое поведение отдельного индивидуума вносит тем больший вклад в общую динамику системы, чем она меньше. Для больших систем в некоторых случаях уже можно рассматривать макроскопическое описание, подобно тому, как в термодинамике рассматривается не траектория отдельной молекулы, а интегральные параметры – давление, температура и другие.

Таким образом, при изучении крупных социальных образований иногда можно вообще обойти проблему «человеческого фактора» и моделировать их с позиций интегральных параметров. В некоторых случаях эволюцию государств можно рассматривать без учета человеческого фактора, либо учитывая его некоторым детерминированным уравнением.

Таким образом, если поставить целью создание теории, то наиболее разумным является движение от простого  к сложному. От описания динамики крупных социальных систем к усложнению и детализации. От простых социальных организмов к сложным иерархическим структурам. Очевидно, что наиболее подходящей областью для данных целей является изучение исторических процессов. Именно история предоставляет нам экспериментальные данные по реализации динамики социальных организмов. Исторические масштабы вполне достаточны, чтобы отслеживать динамику крупных систем. Единственный «упрек» к истории, состоит в том, что невозможно повторить эксперимент, что она уникальна. Это, однако, может быть скомпенсировано тем, что некоторые исторические процессы с удивительным постоянством воспроизводились совершенно в различных социальных организмах, в совершенно разные эпохи. Это, с одной стороны, свидетельствует о существовании некоторых объективных законов, которые могут быть выделены, с другой стороны, говорит о возможности отделить эти универсальные тенденции от специфики отдельных организмов и эпох.

Несмотря на перспективы математического моделирования исторических процессов, успешные попытки такого описания немногочисленны [1, 11, 12]. Недостаток некоторых важных исторических данных сильно затрудняет приближение модели к реальным событиям. Отсутствие теории сужает возможность реконструкции и замены отсутствующих данных дополнительными уравнениями. Таким образом, на данном этапе приходится подбирать такой объект моделирования – эпоху, территорию, государство, который, с одной стороны был бы достаточно хорошо описан, а с другой – имел бы достаточно четкую динамику, позволяющую выделить несколько основных факторов, пренебречь остальными и построить формальную модель. Особый упор, безусловно, следует делать на получении фундаментальных зависимостей, то есть строить модели не просто в некотором приближении повторяющие реальную историческую динамику, но также апробирующие созданный математический аппарат, с той целью, чтобы использовать этот отработанный аппарат в других моделях для реконструкции недостающих данных. Примером выявления подобной зависимости являются работы [13, 14] фактически дающие описание, объяснение и формализацию низкочастотных циклических колебаний численности населения аграрных государств.

3. Постановка задачи

Настоящая работа является логическим продолжением работ, посвященных изучению фундаментальных закономерностей динамики народонаселения. В работе [15] было показано, что колебания численности населения, наблюдающиеся в Китае, Египте, Индии, Месопотамии, и других государствах вписываются в единую логическую схему и могут быть описаны формально. В исследованиях [14, 16] предложена математическая модель этих процессов. Суть логической схемы заключается в том, что после превышения некоторой численности дальнейший рост населения приводит к уменьшению ресурса, производимого на душу населения (в связи с ограниченностью ресурсной базы), а уменьшение продукта на душу населения ведет к повышению нестабильности, голоду, эпидемиям, обострению конфликтов, восстаниям и войнам.

В указанных работах, однако, предполагается изолированность исследуемых государств от внешнего мира, отсутствие обмена ресурсом с соседями. С точки зрения исторической реальности, такие предположения в большой степени оправданы. Например, для Китая (династия Хань) импорт и экспорт продукции составлял доли процента от внутреннего товарооборота. Однако в истории известно немалое количество государств, которые гораздо в большей степени зависели от транзитной торговли (например, государства Средней Азии). При описании динамики таких государств модели, предложенные в [14], практически неприменимы в исходном виде и должны быть дополнены уравнениями, описывающими транзит товаров. В данной работе ставится задача построения базовой формальной модели пространственной торговли и апробации ее на реальных исторических данных.

4. Непрерывная модель транспортировок Бекманна

Модели [14, 16], которые являются отправной точной данных исследований, описаны в виде дифференциальных уравнений. Таким образом, логично искать формализацию торговли также в классе дифференциальных уравнений. В качестве переменных логично выбрать цену и объем товара в точке географического пространства, а также учитывать возможности его производства, потребления и транспортировки, зависящие от пространственных координат.

Задачей формализации торговых потоков, расчетом оптимальных маршрутов и распределением цен, производства и потребления занимается отдельная дисциплина – пространственная экономика. Моделью, наиболее близкой по сути к поставленной нами задаче, является модель предложенная М.Бекманном [17]. Изложим кратко суть этой модели.

Рассматривается замкнутая территория, на которой может производиться, потребляться и транспортироваться товар, рассматривается задача нахождения оптимальных транспортных путей, минимизирующих транспортные издержки.

Математически задача формулируется следующим образом: рассматриваемая территория – область R с кусочно-гладкой границей, для каждой точки которой определены следующие величины (сохранены обозначения и формулировки Бекманна):

Граничные условия:

Причем считается, что q(x, y) не обязательно положительна, поскольку отражает разность между реальным производством и потреблением в точке, стоимость транспортировки товара K(x, y, u) не зависит от направления потока в точке.

Задача формулируется Бекманном как поиск такого векторного поля φ = φ(x, y), соотвествующий потоку товара, такого, что суммарная стоимость транспортировки минимальна. Очевидно, что при этом | φ | = u.

Вводя обозначение

и накладывая ограничения

задачу минимизации общих транспортных издержек за единицу времени можно записать в виде

Бекманн показывает, что данная минимизация выполняется при условиях

Для существования решения требуется, чтобы поток товара внутрь области был в точности равен потреблению в этой области

Бекманн доказывает теорему:

Поле транспортировки φ(x,y) эффективно (минимизирует издержки) при заданном производстве q(x,y) и граничных условиях на экспорт g(x,y) тогда и только тогда, когда в дополнение к условиям (4.8 – 4.11) выполняется

Роль этой потенциальной функции в рассматриваемом случае может играть цена за товар в точке. В более поздней и более известной работе [18] Бекманн при описании модели явно выписывает соотношение для оптимальных потоков:

Здесь λ – цена на товар в точке. Фактически соотношение (4.13) является ключевым для всей модели. Экономический смысл его прост: в случае, когда имеют место оптимальные потоки, в каждой точке поток направлен по градиенту цены на товар.

Результат модели Бекманна состоит в том, что при заданных q(x,y), g(x,y) можно рассчитать оптимальные потоки φ(x,y), минимизирующие (в рамках модели) издержки на транспортировку. В частности, он приводит иллюстрацию для случая постоянных издержек

Если имеется некоторое количество точек «производителей» (x_i,y_i), для которых q(x_i,y_i) = q₀ > 0, а для всех остальных точек q(x,y) = q₁ < 0, с учетом (4.12), потоки имеют следующую структуру:

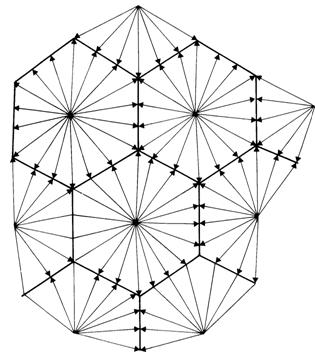
Рис. 1. Структура потоков в модели Бекманна для постоянного k

Таким образом, пространство разбивается на кластеры, каждый из которых «обслуживается» одним производителем.

Описанная модель Бекманна действительно достаточно хорошо вписывается в контекст поставленной нами задачи построения базовой пространственной модели торговли, однако она содержит ряд положений и следствий, которые не вполне удовлетворяют сущности исторических процессов, и должна, таким образом, переработана.

Модель Бекманна создавалась в контексте задач пространственной экономики в предположении рыночного равновесия. С математической точки зрения, рассматривается стационарный случай, для которого логически (из предположения, что в оптимальном случае торговцы не должны получать убытки [18, стр.16]) выводится соотношение (4.14). Историческая же модель должна учитывать эволюцию системы, то есть стационарный случай для нее в корне неприемлем. Спорным местом у Бекманна является рассмотренный им случай,  когда имеется единичный конечный источник и равный ему по модулю, но обратный по значению сток

Кроме того, конфигурация k(x,y) такова, что имеется два пути, абсолютно эквивалентные друг другу по затратам (Рис.2)

Для этих путей имеет место соотношение

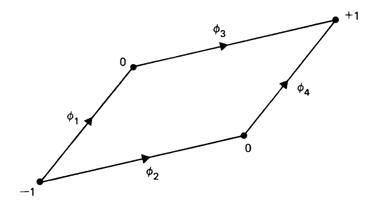
Рис. 2. Два эквивалентных пути

Бекманн утверждает, что в этом случае решением может быть

 Однако из той же модели Бекманна следует, что если сколь угодно мало возмутить значение k(x,y) в какой либо точке одного из путей, например, бесконечно мало увеличить стоимость перевозки в одной точке пути (x₀, y₀):

то путь φ₂-φ₄ сразу перестанет быть оптимальным, и значения потоков должны быть строго

Подобная негрубость модели фактически подтверждает тот факт, что модель Бекманна – оптимизационная модель, строящая некоторые идеальные стационарные потоки, и что она не может быть напрямую применена для моделирования реальных процессов. В реальности, субъекты торговли никогда не располагают полной и достаточно точной информацией о значениях k(x,y) во всей области R. Таким образом, малое возмущение (4.19) не может мгновенно изменить поток на конечную величину 1 – φ*.

Таким образом, модель, претендующая на описание реальных исторических процессов, должна дополнять модель Бекманна, вводя нестационарность (наличие эволюции во времени) и грубость (малое изменение результирующих потоков при малом возмущении издержек на транспортировку).

Мы построим такую модель, исходя из несколько других начальных предположений, и вводя другие, более привычные для математической физики обозначения, а затем покажем, как она стыкуется с моделью Бекманна.

5. Пространственная модель торговли

Также как и в модели Бекманна, рассматривается область R, ограниченная кусочно-гладкой границей Г.

Считаем, что в каждой точке (x, y) области R определены функции

В случае, когда T – отрицательная величина, имеет место дефицит товара, q(x,y) имеет смысл «производство минус потребление» в точке.

Граничные условия:

Поскольку рассматривается нестационарный процесс, то уравнение неразрывности (4.8) в данном случае имеет вид:

где j – поток товара.

Очевидно, что для нестационарного случая уже не требуется соотношение (4.12)

Рассмотрим динамику цены p на продукт. В простейшем случае динамику цены можно описать как

где D – спрос, S – предложение товара, а ζ - чувствительность цены к разности спроса и предложения.

Предполагая, что нет ограничений для реализации товара, можно считать, что

Откуда с учетом (5.4) имеем:

Основным предположением модели является следующее:

то есть поток товара j пропорционален градиенту цены с некоторым коэффициентом пропорциональности k(x,y). Иными словами, товар транспортируется из точек, где цена ниже в точку, где цена выше, причем тем активнее, чем больше разность цен.

Объединяя (5.3), (5.6), (5.7) получаем:

или, внося ζ в коэффициенты  κ = ζ k и Q = ζ q:

Полученное уравнение (5.9) хорошо исследовано – это уравнение теплопроводности. Таким образом, базовое уравнение торговли имеет следующую «физическую» интерпретацию:

Цена играет роль температуры, потребители товара играют роль источников (перед Q в (5.9) стоит минус), а производители – стоков (они понижают цену). Коэффициент k(x,y) играет роль коэффициента теплопроводности, в рамках модели назовем его коэффициентом товаропроводности. Он играет очень важную роль в экономической системе. Именно этот коэффициент фактически предопределяет результирующие товаропотоки при заданном распределении производства и потребления. Более подробно его роль и способ вычисления будет обсуждены ниже.

В силу того, что уравнение (5.8) детально исследовано [19], перейдем к его интерпретации и обсуждению его связи с моделью Бекманна. Как известно, уравнение (5.8) при условии (4.12) имеет единственное стационарное решение, которое достигается при любых начальных условиях при t ® ¥.  Фактически Бекманн рассматривал именно такой случай, и предложенная модель является расширением его модели, переходя в нее при t ® ¥ при условии (4.12). С экономической точки зрения, это означает то, что если достаточно долго параметры системы (q, g, k) не изменяются, то система приходит к рыночному равновесию, при котором потоки оптимальны. Что касается ключевого отличия от модели Бекманна, то оно состоит в различии основных предположений (4.14) и (5.7). У Бекманна поток направлен по градиенту, а в нашей модели он пропорционален градиенту. Подобное незначительное отличие в результате приводит к тому, что снимается парадокс (4.18) – (4.20), поскольку в модели (5.8) малые изменения k(x,y) никогда не приводят к мгновенному изменению потоков на конечную величину.

Коэффициенты k(x,y) в (4.14) и k(x,y) в (5.7) взаимосвязаны. Однако «адаптированы» каждый к своей задаче. У Бекманна k(x,y) – стоимость перевозки единицы продукта. В современных условиях, для которых он создавал свою модель, действительно достаточно легко узнать текущую стоимость транспортировки грузов по той или иной трассе. В случае же исторического моделирования практически невозможно получить информацию о том, сколько стоили те или иные перевозки. С другой стороны, узнать реальные временные затраты и объемы транспортировок можно. По понятным причинам они зависят от многих факторов, однако, предполагая, что выполняется соотношение (5.7), мы фактически даем возможность вычислить модельные значения k(x,y). В частности, коэффициент товаропроводности зависит от габаритов и веса товара, от ландшафта местности, по которой он перевозится, от наличия дорог, от наличия торговцев – перевозчиков товара, от стабильности в регионе, от таможенных пошлин и других причин. Несмотря на множественность факторов, в некоторых случаях можно дать достаточно хорошие оценки для k(x,y), что будет сделано в модели Шелкового Пути. Кроме того, очевидно, что то же многообразие факторов влияет на цену перевозки в модели Бекманна, так что сложность оценки k(x,y) в предлагаемой модели не выше сложности оценки k(x,y) в модели Бекманна.

В результате предлагаемая модель (5.8) в большей степени соответствует реальным историческим процессам, поскольку учитывает эволюцию системы (имеются динамические члены), неопределенность и конечную скорость распространения информации об изменении параметров (мгновенная реакция на изменение в точке убывает как с увеличением расстояния x до этой точки). Кроме того, при заданных q, g, k модель дает пространственное распределение цен во всем пространстве в любой момент времени, а также переходит в модель Бекманна при t ® ¥, освобождая эту модель от «нефизичного» явления сильной зависимости к бесконечно малым изменениям параметра, следующей из (4.18) – (4.20).

Рассмотрим модель Великого Шелкового Пути, построенную на основе предложенной модели.

6. Модель Великого шелкового пути

Великий Шелковый Путь – уникальное экономико-историческое явление. В течение полутора тысяч лет этот путь, то усиливаясь, то иссякая, соединял обширный Евразийский континент в единую систему. Наличие такой связи сыграло важнейшую роль в коэволюции Евразии, прежде всего благодаря информационному и технологическому обмену, хотя, конечно, основной прагматической задачей данного пути был транзит товаров.

Шелковый Путь – удобный объект для апробации предложенной базовой модели, поскольку пространственно-временные масштабы его существования  позволяют рассматривать систему, как непрерывную проводящую среду с устанавливающимися оптимальными потоками при t ® ¥ (временные масштабы таковы, что система успевает достаточно близко подойти к стационарному состоянию).

Прежде всего, определимся с критериями моделирования. Число неопределенностей (практически все нужные данные отсутствуют, либо их достоверность вызывает сомнение) настолько велико, что возникает впечатление, что вообще нельзя говорить о каком-либо адекватном моделировании. Даже если получены уравнения, для решения задачи Коши требуется точно задать начальные данные и только в этом случае можно ожидать корректных результатов. То же и с параметрами, входящими в уравнения.

В исторических данных очень сложно получить практически какие-то более или менее достоверные численные оценки. В исторической науке принято оперировать совсем другими понятиями. Однако эти понятия имеют вполне конкретное наполнение. Историки говорят о росте и об упадке, о стабильности и напряженности, об экспансии и о кризисах. Этим понятиям можно найти вполне конкретные математические эквиваленты в рамках нелинейной динамики.

Современное состояние науки позволяет перейти от описания объекта через его численные характеристики к описанию состояний системы через режимы ее функционирования. Такое понимание дает возможность создавать модели, не претендующие на точность в численном описании, но при этом неплохо описывающие режимы функционирования системы. Именно в этом контексте будет строиться модель Шелкового Пути. В заключение следует заметить, что географические данные (координаты) в отличие от прочих численных характеристик в истории определяются достаточно точно (поскольку археологические данные привязаны к географическому месту раскопок). Для Шелкового Пути, таким образом, можно получить очень точные географические данные по его траекториям в различные эпохи.

Итак, будем считать полученные результаты моделирования приемлемыми, если получающиеся товаропотоки хорошо географически согласуются с историческими данными.

Экономическая формулировка задачи.

Рассмотрим однопродуктовое приближение. Будем считать, что имеется основной потребитель и основной производитель данного продукта, локализованные в пространстве, остальными производителями и потребителями в целях упрощения пренебрегаем. Задача состоит в том, чтобы при заданных объемах производства и потребления, при заданном распределении коэффициента товаропроводности, получить основные траектории Шелкового Пути.

Математическая формулировка задачи.

Задана область R, ограниченная кусочно-гладкой границей Г. Эволюция системы описывается уравнением:

Граничные условия:

В модели граница проводится по океану, в достаточном удалении от берега, чтобы не влиять на прибрежную торговлю, но исключить торговлю между Афроевразией и другими континентами, что соответствует рассматриваемым историческим эпохам.

При этом

В модели точечный источник располагается на территории Китая, а точечный потребитель – в Европе. В зависимости от эпохи точечный потребитель помещается в Риме, затем в Константинополе и, наконец, в Венеции.

При заданном коэффициенте k(x,y) требуется решить задачу Коши, получив пространственную эволюцию потоков. В связи с единственностью решения задачи, начальные данные для T для первой эпохи могут быть заданы произвольно, поскольку через достаточно большое число тактов расчета система приходит к устойчивому состоянию, которое мы будем считать исходным для моделирования динамики Шелкового Пути в дальнейших эпохах.

Метод расчета.

Решается параболическая задача с переменным по пространству k(x,y).  Используется конечно-разностная неявная схема Кранка-Николсона для двумерного случая на однородной сетке. Размер сетки – 300 на 200 точек. Расчет проводится методом переменных направлений с использованием прогонки. Более детальные расчеты были проведены с помощью метода конечных суперэлементов. В этом случае использовались детализированные карты, и размер сетки составил 2080 на 1024 точки.

Задачи исторической модели.

В настоящей модели ставится задача исследовать роль больших империй в процессе формирования и поддержания Шелкового Пути. Кристофер Чейз-Данн и Томас Холл дают в [21] подробное описание и анализ эволюции Шелкового Пути как основного связующего фактора Евразии. В их работе рассматриваются различные факторы, которые предопределяли его динамику и один из важнейших отмеченных факторов, который более явно подчеркивается также в работе Джерри Бентли [22]. Одним из основных предположений о причинах, влияющих на объем перевозок и географическое расположение Пути, является предположение о роли больших империй, которые своим существованием способствовали торговле, повышая объем спроса и предложения, сооружая и поддерживая дороги, обеспечивая стабильность. Мы проверим данное предположение в рамках модели.

Оценка параметров.

Для конкретного расчета потребуются значения производства и потребления и коэффициенты k(x,y).

Сложность точной оценки величины производства и потребления в модели довольно велика. Для исторических событий двухтысячелетней давности практически нет никаких данных, а клиометрические методы восстановления информации по косвенным данным еще недостаточно развиты. В некоторых случаях, например для Древнего Китая, ситуация обстоит лучше благодаря работе чиновников древних империй, которые неустанно все фиксировали и накопили огромную статистику. Но это скорее исключение. Кроме того, даже обладая достаточными сведениями о производстве шелка, мы не можем использовать их в модели, поскольку, во-первых, лишь малая часть шелка шла на экспорт, во-вторых, мы рассматриваем некий обобщенный продукт, в который входит не только шелк, но и другие товары престижа, вывозимые из Китая, и, наконец, поскольку рассматривается некоторый основной потребитель, находящийся в Европе, то должен рассматриваться только тот экспорт из Китая, который в результате прохождения Шелкового Пути оказывается в Европе, а не «оседает» по дороге.

Из такой запутанной ситуации имеется, однако, разумный выход. Поскольку рассматривается процесс, который развивается в течение долгого времени, и система приходит близко к стационарному состоянию, то в силу отсутствия потоков на границе можно заключить, что точечное производство в модели в точности равно потреблению (с обратным знаком). Будем считать значение q₀ равным единице (это всегда можно сделать, масштабируя размерность).

Что касается оценки коэффициента товаропроводности k(x,y), то ее сделать сложнее. В следующей главе будет изложена предлагаемая методика оценки этого коэффициента.

7. Методика оценки коэффициента товаропроводности территории

Коэффициент товаропроводности k, по определению вводимый как отношение потока товара к градиенту цены, безусловно, должен предполагать возможность его оценки. Только в этом случае он может оказаться действительно полезным для моделирования и реконструкции исторических данных.

Ниже будут выведены формулы, раскрывающие физический смысл коэффициента и позволяющие провести его оценку для различных географических точек в различные исторические эпохи.

Будем исходить из следующих предположений:

1.                 В первом приближении будем считать, что в каждую историческую эпоху существует всего несколько типов транспортных средств, использующихся для транспортировки товаров, причем в каждой географической точке используется преимущественно только одно из них.

2.                 Каждое транспортное средство характеризуется следующими величинами:

·        масса M [т],  масса в тоннах ненагруженного транспортного средства;

·        удельная грузоподъемность γ [безразмерная], отношение массы m перевозимого груза к собственной массе M транспортного средства;

·        идеальная скорость перемещения υ [км/день], средняя скорость по идеальной (без каких-либо препятствий и простоев, с покрытием, типичным для качественных дорог соответствующего исторического периода) горизонтальной (отсутствует необходимость подниматься в гору или, наоборот, спускаться) дороге;

·        удельная полезная мощность w [кДж / т ∙ день], средняя полезная мощность транспортного средства - энергия E_д которая может быть потрачена в день транспортным средством собственно на транспортировку груза отнесенная к его массе M(1+γ) (в тоннах) в нагруженном состоянии.

3.                 Каждая географическая точка характеризуется следующими величинами:

·        используемое транспортное средство (соответствующие γ, υ, w), предполагается, что в каждой точке используется только один преобладающий тип транспортного средства;

·        высота над уровнем моря H [км], по сути, более важной характеристикой является показатель разности высот – производная H по направлению движения, что сопряжено с необходимостью совершения работы против действия силы тяжести при перемещении груза.

·        коэффициент «транспортного трения» территории μ [безразмерный], в силу различий типов территорий (равнины, леса, горы, степи, джунгли, пустыни), реальная скорость передвижения может существенно отличаться от идеальной υ, что связано с потерями энергии на преодоление препятствий. Будем считать, что каждому типу территории соответствует коэффициент «транспортного трения», отвечающий за потери энергии транспортного средства (ср. w)

·        степень безопасности r [безразмерная], степень безопасности определяет среднюю долю прибыли, остающуюся у перевозчика товара с учетом риска потерь в связи с различными угрозами – природными (дикие земли) или обусловленными деятельностью человека (войны, пиратство, налоги)

·        удельное предложение труда перевозчиков S_T [т ∙ день / у.е.], число владельцев транспортных средств, готовых предложить свои услуги по перевозке груза при условии соответствующей оплаты в у.е. в день за тонну груза.

Описанные коэффициенты будут использованы при дальнейшем выводе оценочных формул для коэффициента товаропроводности.

Введем вспомогательное понятие силы «транспортного трения» F_тр – значение которой – коэффициент в уравнении

связывающим расстояние, проходимое по идеальной дороге, и энергию, затрачиваемую на это транспортным средством.

В этом случае для введенных нами выше величин для идеальной дороги получаем

откуда

С другой стороны, предполагаем, что «сила транспортного трения» пропорциональна массе нагруженного транспортного средства:

где g – ускорение свободного падения a μ_i – коэффициент «транспортного трения» территории (для наиболее используемого транспортного средства) при движении по идеальной дороге, который исходя из вышесказанного равен

Для неидеальных территорий будем считать, что для каждого транспортного средства коэффициент транспортного трения μ равен:

где μ –коэффициент транспортного трения для данного средства для данной территории, μ_i – коэффициент трения для данного средства по идеальной дороге (зависит  только от типа транспортного средства),  μ_T – относительный коэффициент, который будем считать не зависящим от транспортного средства, но зависящим от типа территории (пустыни, горы, степи и т.п.).

Получим теперь выражение для скорости перемещения по дороге с переменным уровнем высот.

В этом случае кроме работы против силы транспортного трения, необходимо также совершать работу по подъему груза а также самого транспортного средства на соответствующую высоту. В отличие от физической аналогии, утверждающей, что сила трения пропорциональна нормальной реакции опоры, будем считать, сила трения пропорциональна силе тяжести (для горизонтали оба этих варианта эквивалентны, а для наклонной поверхности – в действительности даже при подъеме на очень крутой склон опора все-таки производится на горизонтальные участки) – В любом случае это предположение, которое требует масштабной эмпирической проверки.

Таким образом, будем считать, что затраты энергии (не включающие работу по подъему) при перемещении по наклонному участку пути пропорциональны длине этого участка и весу транспортного средства с коэффициентом пропорциональности, равным «коэффициенту транспортного трения» μ:

где dE_нд – затраты энергии при наклонном движении без учета подъема массы, ds – перемещение по наклонному пути, равное

где dl – соответствующее смещение по горизонтали, - изменение высоты над уровнем моря:

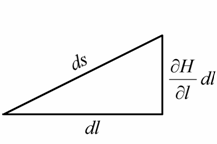
При этом в свою очередь работа по подъему самого транспортного средства вместе с грузом составит

Здесь также наблюдается расхождение с механической аналогией – мы считаем, что спуск вниз также требует затрат энергии, причем таких же как и подъем – такое утверждение не вполне согласуется с реальностью для современного автотранспорта, однако исторически для транспортировок с использованием людей и животных – и спуск, и подъем – процедура сильно энергозатратная. На микроуровне в холмистой местности дороги обычно сильно петляют, чтобы обеспечить небольшой локальный наклон, удобный и для спуска, и для подъема. Очевидно, что такая геометрия дорог сильно увеличивает проходимую дистанцию, по сравнению с дорогой, которая идет прямо с большим уклоном, а следовательно и увеличивает время на общее продвижение. (При этом, очевидно, не практикуются отдельные дороги для подъема и отдельные для спуска – то есть и спуск, и подъем происходит примерно за одинаковое время, что и предопределяет модуль в выражении для dE_пд)

В результате движение по наклонной плоскости отнимает энергию:

Откуда, продифференцировав по t можно вывести общую формулу для скорости передвижения:

С учетом, того, что полезная мощность транспортного средства равна w, получаем:

Поскольку для нас информация о типе используемого транспортного средства и его характеристиках является второстепенной информацией, то было бы разумно представить в каждой точке скорость перемещения как функцию от массы товара, что можно сделать, разделив и умножив правую часть на массу товара:

то есть

Таким образом, скорость переноса единичной массы груза однозначно определяется координатами точки (по предположению, тип транспортного средства, а значит и его параметры w и γ, также однозначно зависят от координаты, равно как и свойства территории μ и H):

Желательно также (при грубой оценке) избавиться от анизотропии – зависимости скорости от направления движения dl, хотя конечно для построения более точный расчетов, можно использовать модель с тензором товаропроводности в уравнении (5.9) вместо коэффициента товаропроводности. 

Очевидно, что

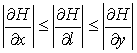, ес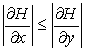ли     или 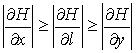   , если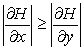

таким образом, можно приблизить  значением 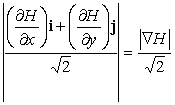. Это грубое приближение, требующее экспериментального подтверждения, однако, в любом случае, в целях грубой оценки, с учетом прочих неточностей в измерении коэффициентов и характеристик, можно принять его в качестве допустимого.

В результате получаем следующую формулу для скорости перемещения единичной массы груза по территории:

Данная характеристика может быть рассчитана для всей карты и считаться постоянной в каждую конкретную эпоху (тип используемого транспорта и рельеф местности меняются достаточно медленно, а их изменение – например открытие новых транспортных средств – обычно знаменует начало новой эпохи, в рамках которой опять же можно рассчитать средние значения v_m, которые в общем случае будут меняться медленно). 

Расчет средних скоростей переноса товара v_m, не является, однако конечным этапом вывода уравнения, поскольку v_m отображает не реальную, а потенциальную скорость переноса. Иными словами, товар будет переноситься в этой точке с такой скоростью, если в этой точке найдутся владельцы транспортных средств, желающие этот товар перевести. Очевидно, однако, что таких переносчиков может не быть – так как они исходят из соображений экономической выгоды и затрат – категорий, скорее экономических, а не физических, таких как свойства территории.

Введем понятие плотности тока j товара, равную переносимой массе товара в точке:

Масса, переносимая в точке равна сумме масс, переносимых всеми транспортными средствами в этой точке. Каждое транспортное средство будем считать максимально загруженным, и вносящим вклад в общий поток равный Mγv, где Mγ – масса груза, v – скорость транспортного средства (обратно пропорциональная массе переносимого груза). Очевидно, что вклад одного транспортного средства в общий поток равен v_m, и, таким образом, суммарный поток равен

где n – плотность транспортных средств в данной точке, переносящих товар, v_m – вектор скорости, равный по модулю v_m.

Что касается направления v_m и j, то, очевидно, оно совпадает с направлением градиента цены на товар (это направление транспортировки обеспечивает максимальную прибыль). Далее мы покажем также, что и абсолютное значение потока также пропорционально градиенту цены, то есть

Рассмотрим прибыль, получаемую одним караваном при транспортировке. Перемещение груза массы m на расстояние dl вдоль градиента цены приводит к его удорожанию на величину , где p – цена за единицу массы груза. Следовательно, караван, двигаясь со скоростью v и перенося массу m в каждый момент времени «зарабатывает» величину

Таким образом, W_c – это заработная плата нагруженного каравана в данной точке.

Из экономической теории известно, что предложение S какого-либо товара в общем случае является монотонно возрастающей функцией от стоимости этого товара. В данном случае товаром является труд перевозчиков и разумно предположить, что количество перевозчиков, готовых перевозить грузы возрастает с ростом зарплаты, получаемой на один караван. Функция предложения труда, вообще говоря, может быть нелинейной (но в любом случае монотонно возрастающей), однако в простейшем случае можно считать ее линейной:

где n – число караванов, готовых перевезти товар, W_c – заработная плата одного каравана, S_T – коэффициент пропорциональности – удельное предложение труда перевозчиков.

Возвращаясь к уравнению потока получаем:

откуда, учитывая сонаправленность направления движения и градиента цены, имеем:

Наконец, необходимо учесть риски. При передвижении по территории, в особенности территории, на которой происходят боевые действия, взимается дань, процветает пиратство и разбой, есть вероятность потери товара, а порой и жизни. Будем считать, что каждая территория характеризуется степенью безопасности r, ответственной за риск потери части прибыли. Этот коэффициент рационально ввести в выражение для реальной прибыли Wr с учетом риска:

Очевидно, аналогично вносятся также коррективы в выражение для количества караванов n, желающих перевозить товар. Поскольку если потери велики (значение r близко к нулю), то и количество желающих будет невелико.

Таким образом, получаем окончательное выражение для плотности потока товара в точке:

что и требовалось вывести. Попутно мы получили явное выражение для оценки коэффициента товаропроводности k:

Легко видеть, что коэффициент товаропроводности является характеристикой среды и зависит от параметров местности, включающих как физические параметры (высоту над уровнем моря H, тип местности μ_T), так и технологические (мощность w, грузоподъемность γ, ограничения мобильности μ_i транспортных средств), как экономические (удельное предложение труда S_T), так и психологические (степень безопасности r).

В процессе вывода уравнения для коэффициента товаропроводности были сделаны достаточно сильные допущения и предположения, несколько идеализирующие реальную ситуацию, однако они представляются целесообразными, поскольку в результате этих допущений удалось получить относительно простое и наглядное выражение для коэффициента товаропроводности, которое допускает как эмпирическую (отношение потока товара к разности цен), так и теоретическую (через предложенную формулу) оценку. Введение самого коэффициента товаропроводности позволяет использовать для оценок исторической динамики хорошо изученный аппарат математической физики и параболических уравнений в частности, что заметно облегчает практическое применение предложенной методики.

Предложенная методика оценки коэффициентов для оценки коэффициентов товаропроводности используется для моделирования динамики Шелкового Пути. В настоящее время ведутся работы по оценке параметров μ_i по историческим материалам. Большую ценность в данном случае представляют дневники путешествий Марко Поло, которые, несмотря на некоторую долю условности и неоднозначности, тем не менее, дают богатую информацию о регионе и о периоде, непосредственно относящемся к одному из моментов расцвета Шелкового Пути.

8. Оценка коэффициентов транспортного трения на основе дневника путешествий Марко Поло

В данном разделе будут оценены коэффициенты транспортного трения, которые в дальнейшем используются в модели Великого Шелкового Пути.

Расчет коэффициентов товаропроводности базируются на значениях скоростей, получаемых из (7.16). В качестве ключевых параметров в это уравнение входят коэффициенты транспортного трения и перепады высот. Остальные параметры γ и w, характеризующие параметры транспортного средства, мы будем считать постоянными (что, вообще говоря, не верно, но допустимо в рассматриваемом приближении). Кроме того, мы пренебрежем градиентом под знаком корня, поскольку реально уклон дороги обычно достаточно маленький для того, чтобы не принимать в расчет ее удлинение в качестве гипотенузы треугольника.  Таким образом, мы имеем дело с уравнением

где C – константа.

 Таким образом, нам потребуются два важнейших источника – карта высот (Рис.3) и карта природных зон (Рис.4).

Рис.3. Карта высот – более высокие точки обозначены более темным цветом.

8

7

6

5

4

3

2

1

    

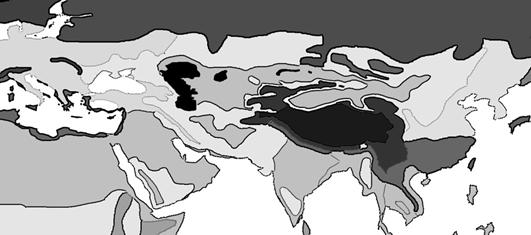
Рис.4. Карта природных зон растительности. (1 – широколиственные леса, 2 - таежные леса,

3 – субтропические леса и кустарники, 4 – степи, 5 – пустыни, 6 – ксерофитные леса и редколесья,

7 –  горные леса и кустарники, 8 - джунгли

Итак, задача заключается в том, чтобы оценить коэффициенты транспортного трения μ для разных зон растительности на основе уравнения (8.1). Данные по градиенту высот в каждой точке можно определить из карты высот, что же касается константы C и скорости передвижения v(x), то для этих величин потребуются дополнительные данные, которые были взяты из обширных дневников венецианского купца и путешественника Марко Поло. Обширный труд «Il millione» включает детальную информацию о его путешествии. Наибольшую ценность для нас представляют записи о географических пунктах его пребывания и о времени, затрачиваемом для перемещения из пункта в пункт. Хотя конечно отнюдь не каждый переход сопровождается указанием на его длительность, а в некоторых случаях само географическое местоположение города не удается определить. Тем не менее, к счастью, информация настолько обширна, что позволяет провести статистический анализ и обоснованный подбор параметров[1].

В таблице 1 отображены записи Марко, которые использовались при оценке коэффициентов[2]:

Таблица 1. Численные данные по путешествиям Марко Поло. X, Y – координаты пунктов в градусах.

Идея оценки коэффициентов состоит в том, чтобы, зная положение начального и конечного пункта, рассчитать время пути, используя алгоритм поиска кратчайшего пути в графе с весами, соответствующими временным затратам на перемещение из ячейки в ячейку, и вычисляемыми по уравнению (8.1). При этом подбираются такие коэффициенты C и μ, при которых наблюдается максимальная близость к временам, затраченным на переход Марко Поло. В качестве критерия близости будем использовать коэффициент детерминации (квадрат коэф. корреляции), употребляемый в корреляционном анализе. В данном случае мы максимизируем линейную корреляцию с нулевой константой между получаемыми временами и временами Марко Поло.

В простейшем случае не будем обращать внимание на различие между природными зонами. Тогда задача является довольно простой – имеется только один параметр μ, варьируя который, мы можем подобрать наилучшее совпадение (рис 5).

Из графика видно, что при малых коэффициентах трения данные сильно расходятся, при μ = 0.025 наблюдается небольшой локальный максимум, а затем увеличение μ несильно сказывается на повышении точности. Таким образом, если не брать в расчет природные зоны, то оптимальным (хотя локально и с небольшой точностью – значение R² достигает лишь 0.37). Физический смысл коэффициента μ = 0.025 состоит в том, что при транспортировке энергетические затраты на перемещение груза на один метр по горизонтали равны энергетическим затратам на перемещение груза на 0.025 метра вверх. То есть альтернатива – провезти груз на 40 метров по горизонтали или поднять на один метр – имеет равные предпочтения.

Однако учет природных зон может заметно улучшить близость данных и модели. На рис.6. приведены вариации коэффициента μ для переходов, полностью лежащих внутри одной из природных зон. На графиках отчетливо видны максимумы, соответствующие наиболее адекватным коэффициентам μ для каждой зоны. Причем также видна разница в этих значениях – для горной зоны μ в десять раз больше, чем для зоны широколиственных лесов. В этом контексте становится ясно, почему для единого коэффициента без разграничения на зоны наблюдалось столь низкое значение детерминации (рис.5). Если для каждой зоны выделить наиболее адекватный коэффициент μ, то точность может заметно повыситься.

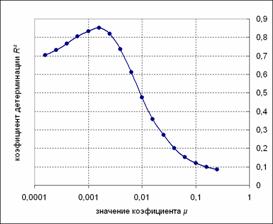
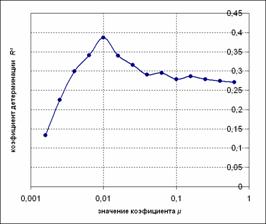
Рис. 6. Детерминация как функция μ для зоны широколиственных лесов и для горной зоны

В рамках исследования был проведен анализ различных комбинаций коэффициентов для различных природный зон, и в результате были получены следующие значения μ для разных зон, дающие максимальную точность из всего множества рассмотренных комбинаций:

На рис 7. Показаны значения длительностей переходов до и после применения разработанной методики оценки коэффициента транспортного трения.

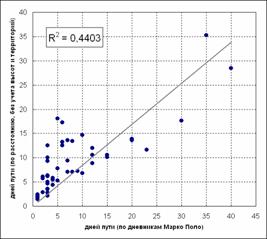
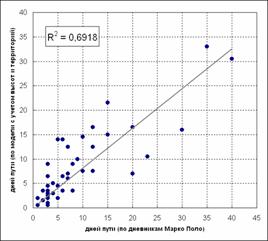
Рис. 7. Повышение точности при учете перепадов высот и территорий

Таким образом, учет природных зон наряду с перепадами высот в уравнении (8.1) позволяет повысить точность оценки коэффициентов.

9. Поправка на фрактальную размерность

Итак, произведена оценка коэффициентов μ для различных территорий. Напомним, что этот коэффициент фактически определяет отношение энергетических затрат по перемещению в вертикальном (работа против силы тяжести) и горизонтальном (работа против силы транспортного трения) направлениях. То есть общие затраты энергии при перемещении по горизонтали на величину dl представляют собой сумму этих двух работ:

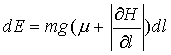
На основе данных Марко Поло по продолжительности переходов и с помощью модели, оценивающей продолжительность этих переходов при различных значениях коэффициентов μ, мы подобрали такие значения μ, при которых наблюдается максимальная близость (с точки зрения метода наименьших квадратов) данных Макро Поло и продолжительности рассчитанных по модели. Для этой оценки мы пользовались географическими данными по высотам над уровнем моря и по пространственному распределению природных зон растительности.

Задача фактически решена, однако требуется обратить внимание на одно обстоятельство, имеющее чрезвычайно важные для дальнейших расчетов последствия. Это обстоятельство состоит в том, что при использовании полученных оценок коэффициентов μ при дальнейшем моделировании необходимо делать поправку на размер сетки. Это связано с фрактальной структурой поверхности Земли.

 Впервые фрактальные свойства географических объектов были обнаружены Л.Ф.Ричардсоном, изучавшим во время второй мировой войны вопрос о длительности береговой линии Великобритании. Как выяснилось, длина береговой линии ключевым образом зависит от размеров «линейки», с помощью которой проводятся измерения. Чем более детальный масштаб используется при измерениях, тем длиннее получается результат.

Результаты Ричардсона были опубликованы Б.Мандельбротом, основателем науки о фракталах, в работе «Какова длина береговой линии Британии? Статистическое самоподобие и фрактальная размерность» [23]. В этой работе Мандельброт использовал понятие дробной размерности, введенное Хаусдорфом и Безиковичем. Суть этого понятия в следующем: Фрактальный объект вложен в n-мерное пространство, разбитое на кубики с длиной ребра ε. Для каждого ε рассчитывается минимальное число N(ε) кубиков, полностью покрывающих исследуемый объект. Тогда фрактальной размерностью Хаусдорфа-Безиковича называется величина

.

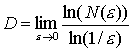Для обычных фигур – точек, отрезков, квадратов, кубов, шаров и т.п. размерность, просчитанная по этой формуле имеет целое значение и в точности совпадает с обычным понятием размерности: 0 – для точки, 1 – для отрезка, 3 – для шара и т.п. Однако для целого класса сложных геометрических объектов размерность Хаусдорфа-Безиковича является дробной величиной. В частности, для побережья Великобритании полученное значение размерности имеет значение D ≈ 1,3.

Таким образом,  можно ожидать, что и поверхность суши также является фрактальной структурой, а значит и перепады высот, рассчитываемые при моделировании, вообще говоря, зависят от шага сетки. Следовательно, и работа, совершаемая при перемещении против силы тяжести, будет зависеть от масштаба. Действительно, при перемещении учитывается модуль разности высот, поэтому усреднение, которого невозможно избежать при увеличении шага сетки, неизбежно замазывает мелкие колебания и уменьшает общую сумму перепадов.

В итоге наша задача состоит в том, чтобы определить зависимость, по которой возрастает сумма перепадов при уменьшении шага сетки.

Задача решалась следующим образом. Использовалась сетка H[i,j] высот Земли в полярных координатах с шагом около 0.1 градуса. Оценки зависимостей возрастания суммы перепадов проводились отдельно для меридианов и для параллелей.

Для меридианов последовательно создавались сетки H_K[i,j] с увеличивающимся шагом по оси y. В качестве значений в узлах новой сетки брались ближайшие значения в исходной сетке:

,

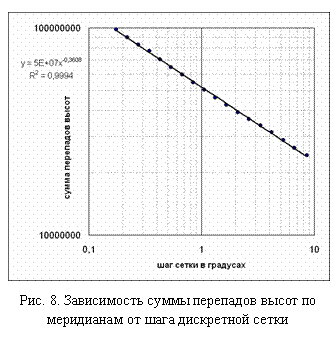
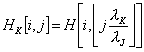где λ_J, λ_K – шаг сетки вдоль меридиана в исходной и, соответственно, в рассчитываемой сетке. Знак «» обозначает округление до ближайшего не превосходящего целого. В случае интерполяции, например линейной, результат существенно не изменяется. Затем по всей сетке вычисляется сумма

и исследуется зависимость суммы перепадов высот S_K от шага сетки λ_K.

В итоге были получены следующие результаты (рис.8). Они свидетельствуют о том, что изменение шага сетки ведет к изменению суммы перепадов, что позволяет вычислить фрактальную размерность перепадов высот, которая для меридианов равна Dм ≈ 1,36.

Аналогичные вычисления для параллелей дают значение Dп ≈ 1,23. Необходимо при этом помнить, что для параллелей имеет место искажение, связанное с тем, что в силу прямоугольности выбранной сетки, для разных параллелей (например, вблизи полюсов и вблизи экватора) одному шагу сетки соответствует различное расстояние в километрах на поверхности Земли.

Вообще говоря, фрактальная размерность перепадов высот в различных точках Земного шара различна. Для повышения точности расчетов целесообразно составить и использовать соответствующие таблицы.

Практический смысл обнаруженных фрактальных зависимостей состоит в том, что при изменении шага сетки необходимо соответствующим образом пересчитывать коэффициенты транспортного трения μ. Поскольку общие затраты энергии, очевидно, не должны зависеть от масштаба сетки

,

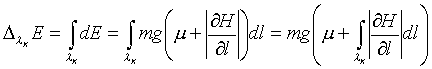а перепад высот между узлами сетки зависит от шага λ_K как

,

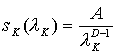где A – константа, а D – фрактальная размерность перепадов высот, то коэффициент транспортного трения μ также должен зависеть от шага сетки, для того,чтобы компенсировать изменение перепада и сохранить затраты энергии неизменными. То есть в силу того что

,

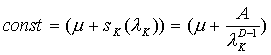должно выполняться ,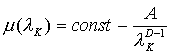

таким образом, целесообразно ввести поправку для μ, зависящую от размера сетки. Если исходить из того, что мы имеем заданное значение коэффициента трения территории μ₀, то разумно привязать его к некоторому характерному масштабу λ₀, например, масштабу порядка десятков метров, характерному для радиуса кривизны дорог, по которым идут транспортные потоки. Тогда можно оценить также и характерный перепад высот s­₀: если имеется сетка высот c шагом λ_K, для которой в каждом узле можно вычислить значения перепадов s_K(x,y), то

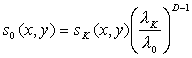
Тогда при моделировании на сетке с шагом λ_{L ,} учитывая, что μ + s₀ = μ_L + s_L, и 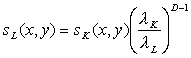, можно учесть фрактальность:

,

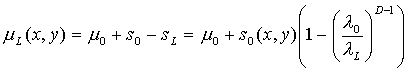где к исходному значению μ₀ добавляется поправка , отвечающая за фрактальную сущность поверхности Земли.

10. Результаты моделирования Великого Шелкового Пути

Результаты оценки транспортного трения использовались для вычисления товаропроводности в модели Шелкового Пути.

В истории Шелкового Пути выделяют три основных периода расцвета, каждый из которых длился несколько столетий и заканчивался спадом и сильным сокращением товаропотоков. Для каждой эпохи приводятся расположения основных империй этой эпохи, траектории Шелкового Пути, соответствующие историческим данным (источник – карты к многотомнику «Всемирная История» [25], [24]), траектории, полученные в модели, и распределения цен.

1. Эпоха древнего Шелкового Пути (II в д.н.э. – III в н.э.)

4

3

2

1

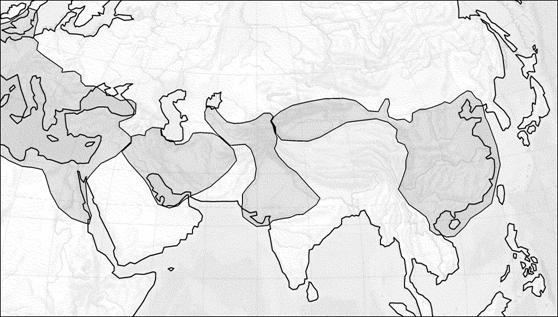
Рис 9. 1 - Римская, 2 - Парфянская, 3 - Кушанская империи, 4 - Китай династии Хань

В эту эпоху почти одновременно произошел рост и расцвет Римской и Ханьской империи. Две следующие друг за другом Ханьских (201 до н. э. – 9 н. э.; 24 – 220 н. э.) династии пришли на смену династии Чин, которая просуществовала всего 15 лет, но сумела объединить Китай после долгих веков раздробленности. Ханьская династия значительно укрепила экономику и выдвинулась в Таримский бассейн, имеющий стратегическое значение для Шелкового Пути, вступив в активное противостояние с кочевой конфедерацией на ее территории и преуспев в этой борьбе. В то же время на другом конце континента Римская Империя укрепила свои позиции и, начав экспансию, подчинила себе практически все Средиземноморье. Одновременный экономический расцвет империй стимулировал потенциальный обмен товарами между ними. Эту связь по Великому Шелковому Пути также обеспечили и укрепили две другие крупные империи – Парфянская и Кушанская. В результате Шелковый Путь практически на всем своем протяжении проходил через территорию, находящуюся под контролем той или иной крупной империи.

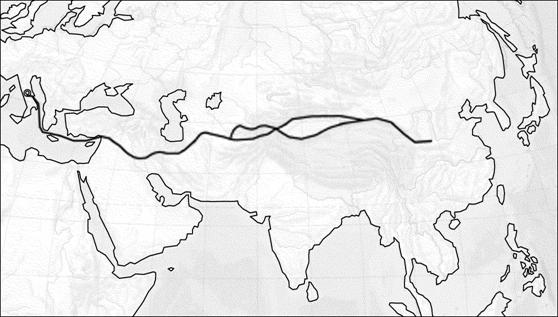
Рис.10. Великий Шелковый путь в начале II века до н.э.

К концу этой эпохи произошло почти одновременное падение Римской империи и Ханьской династии. По мнению некоторых историков, основную роль в этом сыграли внутренние циклические процессы самих империй, некоторые считают, что в определенной степени повлияло похолодание климата, а другие склоняются к мнению, что виновен был сам Шелковый путь, поскольку кроме товаров и технологий вдоль него распространялись возбудители инфекционных заболеваний, против которых население не имело иммунитета. Так или иначе, экономический упадок, значительное снижение численности населения и гибель империй привели к фактическому исчезновению Шелкового пути. Торговля не прекратилась совершенно, но резко ослабла и стала носить локальный характер. Возродилась она лишь через несколько столетий.

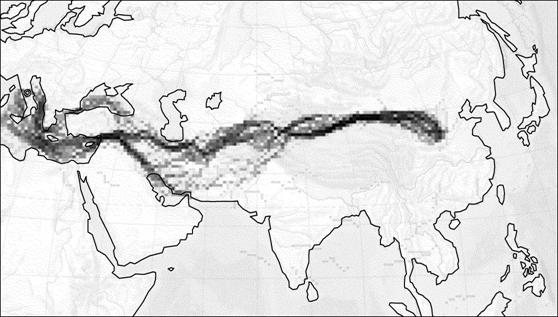
Рис.11. Результаты расчета модели для эпохи древнего шелкового пути

2. Эпоха распространения ислама и возникновения

новых империй (VII – IX вв.)

2

3

1

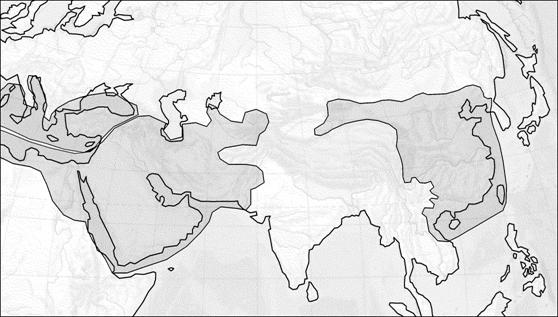
Рис. 12. 1 - Византийская империя, 2 - Исламский мир, 3 - династия Тан в Китае

Для Шелкового пути ключевым событием этой эры стало возникновение и распространение ислама, которое объединило обширные пространства от Китая и Индии до Византии и Испании. Кроме религиозного единства арабы привнесли на завоеванные территории и элементы своего уклада, в частности, будучи преимущественно торговцами (сам Мухаммед был купцом), они установили порядки, при которых торговля не считалась чем-то зазорным, напротив, купцы были привилегированным сословием. Все это резко повысило возможности транзита товаров из возникшей к тому времени империи Тан в Китае. Там после нескольких веков раздробленности вновь образовалась крупная и стабильная империя, которая обеспечивала бурный экономический рост, ознаменованный различными технологическими новшествами. Это, в частности, культивация риса и изобретение пороха. На западе, в регионе Средиземноморья основную роль играла Византийская империя, конкурирующая с исламом.

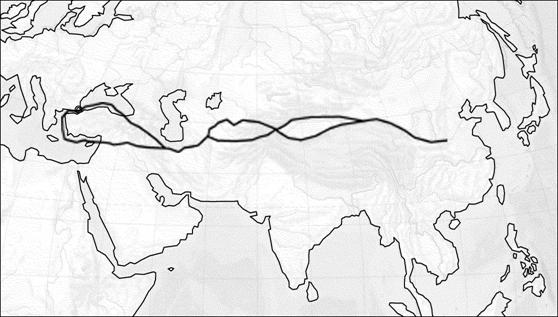
Рис.13. Основные траектории Шелкового пути этой эпохи

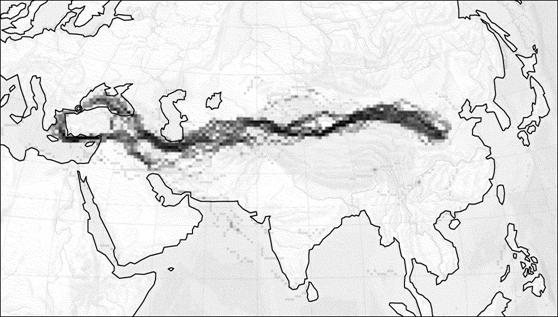
Рис.14. Результаты расчета модели

В IX-X веках одновременно начался закат исламского единства, приведший к дроблению государств и междоусобным войнам, а также активизировались волнения в Китае, в конечном счете спровоцировавшие падение Танской династии и раздробленность Китайской империи. Благоприятные условия для торговли исчезли, а с ними и сама торговля, вновь перешедшая на локальный уровень.

Эпоха монгольских завоеваний. (XII – XIV вв.)

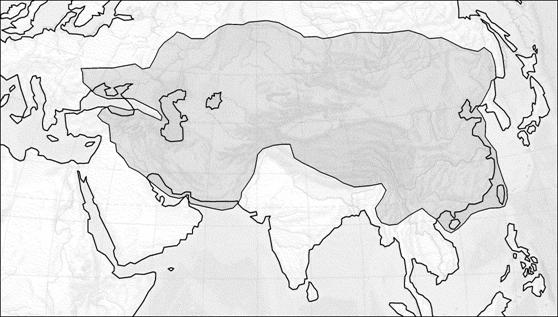
Рис. 15. Монгольская Империя

В XII веке монгольские племена под предводительством Чингисхана (Тимуджина) положили начало созданию Монгольской Империи – крупнейшей за всю историю человечества. Монголы, будучи кочевниками, обладали прекрасными навыками военной коммуникации, логистики и торговли. Огромные размеры империи вынуждали их поддерживать постоянную связь между ее частями, создавать инфраструктуру. Постоянная готовность лошадей, превосходное знание географии и другие факторы во многом способствовали активизации потоков людей, а вместе с ними и товаров по Великому Шелковому пути. Монголы активизировали северный путь, проходящий прямо по степям и огибающий Каспийское море с севера. Этот путь уже был известен и использовался в свое время согданскими торговцами для транспортировки товаров в Византию в обход империи Сасанидов установившей непосильные пошлины, однако только при Монголах он стал столь же оживленным, как и южные пути.

Развитие Европейских государств также благотворно сказалось на объемах торговли. Активная роль Венеции в средиземноморской торговле способствовала ускоренному транзиту восточных товаров престижа в Европу, переживающую бурное развитие городов и рост населения. Именно в эту эпоху стали регулярно происходить непосредственные контакты между Западом и Востоком, одним из которых было знаменитое путешествие Марко Поло.

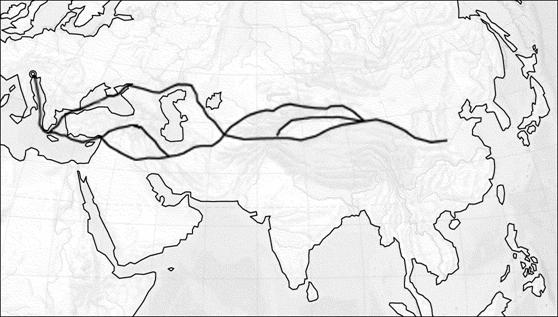
Рис. 16. Основные траектории Шелкового пути этой эпохи

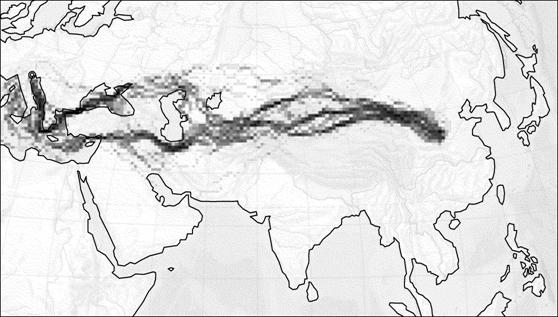
Рис. 17. Результаты расчета модели для Монгольской империи

Территории, завоеванные монголами, оказалось проще захватить, чем удержать. Несмотря на высокую мобильность монгольских войск, империя была чересчур велика. Сильнейший удар по территориям нанесла бубонная чума, уничтожившая как на Востоке, так и на Западе до половины населения. Кроме того, в это время наблюдалось достаточно сильное похолодание, также сократившее урожаи, ослабившее население и опустошившее казну. Монгольская Империя развалилась, товаропоток по Шелковому пути резко сократился. Однако не падение империи привело к тому, что в дальнейшем Шелковый путь уже никогда не возрождался. Причина его окончательного упадка в другом, связана она с морской торговлей.

После падения династии Юань (основанной Хубилаем, потомком Чингисхана) в 1368 году к власти в Китае пришла династия Мин. После господства монголов возобладали националистические настроения, недовольство иностранцами-торговцами привело к резкому сокращению экспорта и даже к запрещению морских экспедиций в 1424 году. В результате акватория Индийского океана оказалась открытой для европейского проникновения. Европейцы не встретили ни сопротивления, ни конкуренции со стороны Китая как морской державы. Стремительное развитие морского транспорта в Европе привело к появлению быстроходных кораблей с невиданным до тех пор водоизмещением. В течение ста лет европейцы фактически полностью утвердили свою гегемонию в акватории Индийского океана. Сухопутный Шелковый путь не выдержал конкуренции с европейскими галеонами и прекратил свое существование.

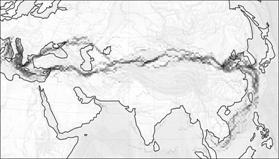
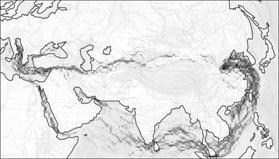
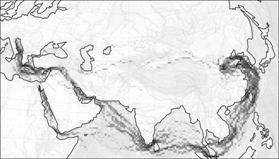
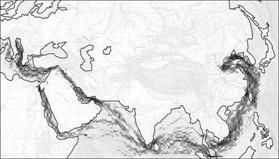
Рис.18. Гибель сухопутного Шелкового пути

В модели этот эффект отражен значительным увеличением коэффициента k(x, y) в акватории Индийского океана и Южно-Китайского моря. На рисунках показаны фазы перехода с сухопутного пути – на морской в результате данного увеличения.

Выводы

Настоящая работа ставила перед собой три задачи. Первая – в том, чтобы предложить, проанализировать и апробировать базовую пространственную модель торговли. Вторая – в том, чтобы предложить методику оценки коэффициентов транспортного трения и товаропроводности, фигурирующих в базовой модели торговли. И, наконец, третья – с помощью этой базовой модели исследовать роль больших империй в эволюции Великого Шелкового пути.

Предложенная пространственная модель торговли, апробированная для случая Шелкового пути, может оказаться чрезвычайно полезной для историков, поскольку дает возможность реконструкции потоков, цен и объемов производства (обратная задача) во всем исследуемом пространстве. Это позволяет восстанавливать отсутствующие данные, если известны значения каких-либо из этих параметров в нескольких географических пунктах. Для этого, однако, требуется более глубокая проработка вопросов, связанных с оценкой коэффициента товаропроводности как функции от географического и социального ландшафта.

Первые шаги в этом направлении были сделаны в рамках настоящей работы. Была предложена методика оценки коэффициента товаропроводности и транспортного трения. Были получены численные значения для коэффициента транспортного трения в предположении, что он считается различным для различных природных зон. Подбор коэффициентов происходил на основе дневников Марко Поло, содержащих около 50 значений длительностей переходов из одного географического пункта в другой.

Точность может быть увеличена путем учета фрактальности поверхности Земли. В работе было показано, что при численных расчетах на сетках с различным шагом по пространству, в коэффициенты транспортного трения должна быть включена поправка, отвечающая за фрактальность поверхности. Была рассчитана фрактальная размерность для Земного шара в целом по меридианам и параллелям. В дальнейших исследованиях в целях повышения точности целесообразно оценить фрактальную размерность различных областей и использовать полученные значения при вычислении поправки.

Результаты оценки коэффициента транспортного трения использовались при оценке коэффициента товаропроводности. При этом, однако, делались допущения, предполагающие постоянство параметров транспортных средств и удельного предложения труда перевозчиков. Такие допущения оправданы для макромодели, однако при моделировании конкретных локальных исторических процессов их необходимо принимать во внимание и разрабатывать соответствующие методы оценки этих параметров. Необходимо также более точно оценивать коэффициент безопасности транспортировки, как было показано, играющих важнейшую роль при формировании товаропотоков.

Таким образом, дальнейшие исследования в описанных направлениях, могут позволить построение достаточно точных моделей – как масштабных, так и локальных – с использованием пространственно-географической компоненты. Можно надеяться, что новые численные исторические данные, восстановленные с помощью подобных моделей, дадут возможность более глубокого математического анализа исторических процессов и, как результат, большего понимания законов развития общества.

Литература

1.     Гусейнова А.С., Устинов В.А., Павловский Ю.Н. Опыт имитационного моделирования исторического процесса. - М.: Наука, 1984.

2.     Малков С.Ю. Математическое моделирование социально-экономических процессов.  Подходы и решения // Стратегическая стабильность, 1998, №1, с.62-67.

3.     Лефевр В.А. Алгебра совести. М.: Когито-Центр, 2003.

4.     Крылов В.Ю. Методологические и теоретические проблемы математической психологии. - М.: Янус-К, 2000.

5.     Эбелинг В., Энгель А., Файстель Р. Физика процессов эволюции. – М.: Эдиториал УРСС, 2000.

6.     Николис Г., Пригожин И. Познание сложного. - М.: Мир, 1990.

7.     Капица С.П., Курдюмов С.П., Малинецкий Г.Г. Синергетика и прогнозы будущего.- М.: Наука, 1997.

8.     Пределы предсказуемости. - М.: ЦентрКом, 1997.

9.     Петерс Э. Хаос и порядок на рынках капитала. Новый аналитический взгляд на циклы, цены и изменчивость рынка. - М.: Мир, 2000.

10. Пу Т. Нелинейная экономическая динамика. - Ижевск: Удмурдский университет, 2000.

11. Turchin P. Historical Dynamics: Why States Rise and Fall - Princeton University Press, Princeton, NJ, 2003

12. Малков С.Ю. Математическое моделирование исторических процессов // Новое в синергетике: Взгляд в третье тысячелетие / Под ред. Г.Г.Малинецкого, С.П.Курдюмова. - М.: Наука, 2002,  с.291-323.

13. Нефедов С.А. Опыт имитационного моделирования демографического цикла [http://hist1.narod.ru/Science/secular trends.htm].

14. Нефедов С.А. Опыт моделирования демографического цикла // Информационный бюллетень Ассоциации "История и компьютер", №29, 2002, с.131-143.

15. Нефедов С.А. О демографических циклах в истории средневекового Египта [http://hist1.narod.ru/Science/Egipt/EgiptSV.htm]; О демографических циклах в истории Ирака и Ирана (VII-XIII вв.) [http://hist1.narod.ru/Science/Babilon/Irak.htm] и др.

16. Малков С.Ю., Коссе Ю.В., Бакулин В.Н., Сергеев А.В. Социально-экономическая и демографическая динамика в аграрных обществах // Математическое моделирование, 2002, т.14, №9, с.103-108

17. Beckmann M.J. A continuous model of transportation // Econometrica, Vol.20 No.4 The University of Chicago, 1952, pp. 643-660

18. Beckmann M.J., Puu T. Spatial Economics: Density, Potential and Flow. North-Holland, Ansterdam, 1985

19. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Государственное издательство технико-теоретической литературы, 1951.

20. Бахвалов И.В., Жидков Н.П., Кобельков Г.М. Численные методы. – М.-С.Пб.: Физматлит, 2000

21. Chase-Dunn C., Hall T.D. Rise and Demise. Comparing World-Systems. - Westview Press, 1997

22. Bentley J.H. Old World Encountrers: Cross-Cultural Contacts and Exchanges in Premodern Times, - Oxford: Oxford University Press, 1993

23. B. B. Mandelbrot, How Long is the Coast of Great Britain, Statistical Self Similarity and Fractional Dimension // Science, 155 (1967) 636-638.

24. http://www.silk-road.com

25. Всемирная История. Т. II-IV, М.: Госполитиздат, 1956-1958
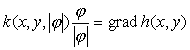
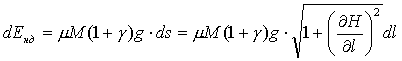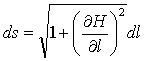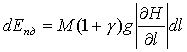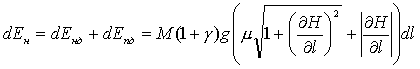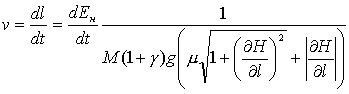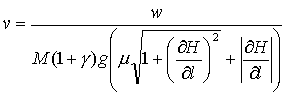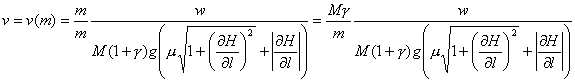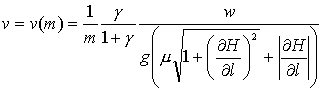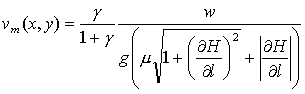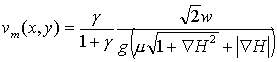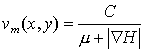