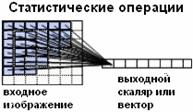
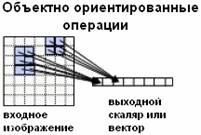
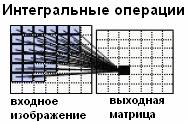
Введение. 4

Детекторы, использующие компоненты градиента яркости. 6

Нахождение компонент градиента яркости. 6

Детекторы контрастных перепадов, использующие компоненты градиента яркости. 7

Детектор Канни. 7

Детекторы углов, использующие компоненты градиента яркости. 8

Детекторы окружностей, использующие компоненты градиента яркости. 8

Преимущества и недостатки детекторов, использующих компоненты градиента яркости. 9

Детекторы, использующие коэффициент совпадения с шаблоном. 9

Детекторы, использующие преобразования пространства. 10

Параметрические модели. 10

Детектор Хюккеля. 11

Детектор Бэкера и др. 12

Преобразование Хука. 12

Детектор прямых линий, использующий преобразование Хука. 12

Детекторы, использующие статистические методы. 14

Детекторы контрастных перепадов, использующие статистические методы. 14

Распараллеливание операций обработки изображений. 15

Группы операций обработки изображений. 15

Аппаратная организация вычислений. 17

Выводы. 19

Благодарности. 19

Список использованной литературы. 20

Введение.

 Простыми элементами изображения считаются: контрастные перепады, угловые точки, прямые линии, пересечения линий, круговые элементы и т.д. Нахождение этих элементов на изображении является важной начальной операцией для дальнейшей обработки изображений таких, как сегментация изображений, отслеживание и распознавание объектов, регистрация видеоинформации и т. п.

Для многих систем технического зрения (СТЗ) выделение контрастных перепадов является одной из первых задач, решаемых при распознавании изображений. Это связанно с интуитивным пониманием того, что в контурных линиях содержится большое количество информации. Долгое время для нахождения контурных линий использовалось два основных метода: первый находит степень совпадения с неким шаблоном (СШ), а второй использует информацию о компонентах градиента (КГ)  на изображении. Оба метода оценивают локальное значение градиента или его проекции на определённое направление и используют фильтрующие маски, но в случае КГ задействованы две маски, определяющих компоненты градиента в двух ортогональных направлениях (см. таб. 1). В случае СШ количество масок определяется необходимой точностью в определении параметров контура и может доходить до 12 и более (см. таб. 2).

Таб. 1. Маски наиболее часто употребляемых дифференцирующих операторов

Маска Робертса	0 1 -1 0	1 0 0 -1
Маска Собеля	-1 0 1 -2 0 2 -1 0 1	1 2 1 0 0 0 -1 -2 -1
Маска Превита (1970 г.)	-1 0 1 -1 0 1 -1 0 1	1 1 1 0 0 0 -1 -1 -1

Таб. 2. Маски наиболее распространённых операторов сравнения с шаблоном.

	0°	45°
Маска Превита (1970 г)	-1 1 1 -1 -2 1 -1 1 1	1 1 1 -1 -2 1 -1 -1 1
Маска Киршча (1971 г)	-3 -3 5 -3 0 5 -3 -3 5	-3 5 5 -3 0 5 -3 -3 -3
Маска Робинсона 3-х уровневая (1977 г)	-1 0 1 -1 0 1 -1 0 1	0 1 1 -1 0 1 -1 -1 1
Маска Робинсона 5-ти уровневая	-1 0 1 -2 0 2 -1 0 1	0 1 2 -1 0 1 -2 -1 0

(примечание: в таблице даны только 2 маски из 8-ми, остальные могут быть получены симметричными операторами. Для 3-х уровневого и 5-ти уровневого операторов четыре из восьми масок могут быть получены инвертированием)

Для более точной оценки направлений контрастных перепадов используются более крупные маски с весовыми коэффициентами, зависящими от расстояния до центра маски.

          Как методы СШ, так и методы КГ, могут быть применены для нахождения других простых элементов изображения.

В данном обзоре детекторы простых элементов на изображении были классифицированы на четыре большие группы (см. рис. 1):

1.    Детекторы, использующие компоненты градиента яркости  (ДКГ) ;

2.    Детекторы, использующие коэффициент совпадения с шаблоном (ДСШ);

3.    Детекторы, использующие преобразования пространства яркости (ДПП);

4.    Детекторы, использующие статистические методы (ДС).

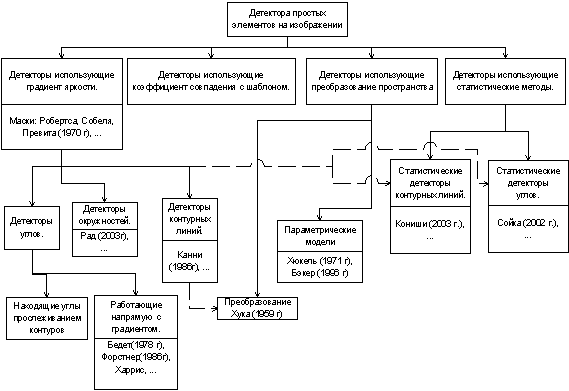
Рис. 1 Классификация детекторов простых элементов изображения.

Детекторы, использующие компоненты градиента яркости.

Нахождение компонент градиента яркости.

Пожалуй, один из самых распространённых типов детекторов. Решение о наличии простых элементов изображения делается на основании значений градиента яркости.

Один из ключевых моментов - это нахождение частных производных (или компонент градиента) на изображении. Этому вопросу посвящен ряд статей [2,3], наиболее простые фильтрующие маски представлены в таблице 1.

Как отметили Торре и Поджио [4], дифференцирование дискретного изображения является некорректным. Сделать это корректно, по их мнению, можно отфильтровав изображение низкочастотным фильтром (например Гауссианом) перед применением дифференцирующих операторов. Один из вариантов - это использование маски, совмещающей в себе фильтрующие и дифференцирующие свойства, например, маска Лапласиан от Гауссиана, датируемая 1980 годом (1) (см. рис. 1),  используемой для оценки длинны вектора градиента.

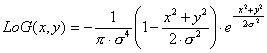     (1)

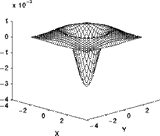
Рис. 2. Импульсная характеристика фильтра Лаплассиана от Гауссиана (Laplacian of Gaussian).

Детекторы контрастных перепадов, использующие компоненты градиента яркости.

Контрастные перепады на изображении находятся в точках локального максимума ||grad(I)||. В случае использования Евклидовой нормы необходимо найти локальные максимумы функции sqrt(I_x²+I_y²). Недостатком Евклидовой нормы являются значительные вычислительные затраты, поэтому иногда прибегают к упрощению в оценке нормы, как |I_x|+|I_y|.

Обычно для определения контрастного перепада используют некоторое пороговое значение, с которым сравнивают длину вектора градиента, это приводит к прерывистости контурных линий или их утолщению. Для борьбы с этим были предложены ряд детекторов, самым лучшим из которых, следует считать детектор Канни.

Детектор Канни.

Канни разработал детектор оптимальной фильтрации контрастных перепадов [5]. Модель контрастного перепада была следующей: перепад типа ступенька (функция Хевисайда), зашумлённый белым шумом с распределением Гаусса. Было предложено три критерия оптимальности:

1.      Высокая вероятность детектирования.

2.      Высокая точность локализации.

3.      Единственность отклика на один контрастный перепад.

Для удовлетворения указанных критериев используется предварительная низкочастотная фильтрация изображения, прослеживание контуров и подавление не максимальных локальных значений компонент градиента.

Детекторы углов, использующие компоненты градиента яркости.

Детекторы углов можно разделить на две группы:

-       Детекторы работающие напрямую с значениями яркости на изображении.

-       Детекторы, которые сначала локализуют контрастные перепады на изображении, а затем оценивают их кривизну, делая вывод о наличии углов.

Дальнейшее обсуждение коснётся только детекторов, работающих напрямую со значениями яркости.

Один из первых алгоритмов предложил Бедет [6]. Он определял положения углов по максимумам определителя Гессиана от функции яркости изображения (1).

Н=I_xxI_yy+I_xy² (1)

Этот метод работает хорошо с углами вида L, но с углами вида X, Y и T хуже. И так, как в методе используются вторые производные от функции яркости, то результат сильно подвержен влиянию шума.

В свою очередь Форстнер [7] предложил детектор углов, использующий только первые производные от функции яркости, и определил углы, как локальные максимумы 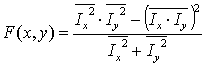(2).

         (2)

Чёрточки над переменными обозначают среднее значение в некоторой области точки (x,y).

 

Метод Харриса определяет углы как локальные минимумы функции 1/F(x,y). В некоторых сравнительных анализах [8] он считается лучшим по точности, но в тоже время проигрывающим по вычислительной нагрузке.

Существенным минусом детекторов углов, использующих компоненты градиента яркости является тот факт, что определение самих компонент градиента основано на дифференциальных масках, по сути моделях горизонтального и вертикального контрастного перепадов. Они плохо работают в местах расположения углов, т. к. маска предполагает, что контрастный перепад может быть продлён по прямой до бесконечности.

Детекторы окружностей, использующие компоненты градиента яркости.

Очевидным методом нахождения окружностей на изображении является прослеживание кривизны контурных линий. 

Али Айдари Рад и др. в [9] предложили алгоритм быстрого поиска окружностей на изображении, используя противоположную направленность пары векторов градиента V₁, V₂ (см. рис. 3), лежащих на противоположных концах окружности, а также тот факт, что их базы P₁, P₂ лежат на прямой параллельной им.

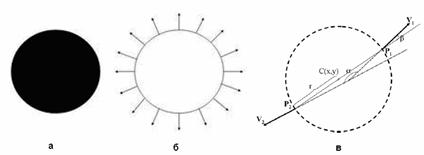
Рис. 3. a -черный круг на белом фоне,  б - вектора градиента (а), в - пара векторов V1 и V2.

 

Как утверждается в [9], метод превзошёл по скорости метод Хука для поиска окружностей на 3 порядка и является более устойчивым к наличию шума типа “соль и перец”.

Преимущества и недостатки детекторов, использующих компоненты градиента яркости.

            Несомненно, такие детекторы хороши тем, что для поиска простых элементов изображения достаточно осуществить фильтрацию всего двумя дифференцирующими масками. Эти операции могут быть выполнены в процессе получения кадра изображения с видео системы с использованием комбинационной логики. Проблемы могут возникнуть лишь при оценке компонент градиента, использующих операции деления, трансцендентные функции и т. д.

Как было отмечено выше, недостатком является наличие существенных погрешностей в определении самих компонент градиента яркости с ростом кривизны линий контрастного перепада.

 

Детекторы, использующие коэффициент совпадения с шаблоном.

 

Как следует из названия, решение о наличии элемента делается на основании значения коэффициента совпадения с шаблоном. Например, в детекторе Робинсона осуществляется фильтрация изображения восемью масками, каждая из которых ориентированна в своём направлении. Если отклик на фильтрацию маской достаточно существенен, то считается, что контрастный перепад найден, и направление этой маски наилучшим образом характеризует направление контрастного перепада. Девис [1] описывает построение шаблонных операторов с разными углами для детектирования контрастных перепадов, вида ступеньки. Веса точек шаблона выбираются в соответствии с площадями, на которые разбиваются точки при прохождении по ним контрастного перепада (см. рис. 4).

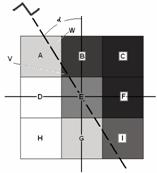
Рис. 4. Шаблон для нахождения прямого контрастного перепада типа ступенька.

Площади, отсекаемые контрастным перепадом от точек

A: ; и B: ;           (3)

 

Вторым важным моментом использования ДСШ является возможность внутриточечной локализации элемента изображения. Например, если известна ориентация контрастного перепада типа ступенька, то можно более точно определить его положение при помощи нахождения коэффициента совпадения с шаблонами, построенными с учётом различного положения контрастного перепада в пределах точки.

Детекторы, использующие преобразования пространства.

Отличительной особенностью данных детекторов является наличие перехода от яркостной картины к другим многомерным пространствам. Элемент определяется в том случае, если значения попали в некий допустимый диапазон в многомерном пространстве.

Параметрические модели.

Подавляющее большинство простых элементов параметрические по своей природе, т. е. их можно представить в виде ограниченного числа параметров. Например, контрастный перепад типа ступенька можно задать с помощью параметров, описывающих уравнение прямой перепада  в некотором небольшом окне и яркости с двух сторон от перепада.  Для данного типа детекторов характерен переход от пространства яркостей к другим пространствам с меньшим количеством измерений. В этом пространстве определяется область допустимых значений для параметрической модели. Попадание в область допустимых значений говорит о наличии простого элемента в данном окне изображения.

Детектор Хюккеля.

Пожалуй, разработчиком первого детектора, использующего параметрические модели можно назвать Хюккеля (1971 г.) [10]. Детектор используется для нахождения контуров на изображении.

Элементы контура ищутся на некотором множестве точек изображения наилучшим образом аппроксимирующим круглое окно (см. рис. 5 а).

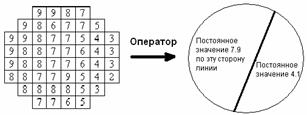
Рис. 5. а – эмпирически полученный элемент контура, б – идеализация элемента

Метод состоит из следующих шагов:

Осуществляется  свёртка изображения с восемью двумерными функциями (разложение функции эмпирического окна по усечённому ортонормированному базису (см. рис. 6)).

 

 

 (i=0,…,7),   (4)

 D – множество точек окна,  - функция яркости в окне, - функции ортонормированного базиса.

В качестве меры близости между эмпирическим элементом контура

и идеальным контуром был выбран квадрат гильбертова расстояния:

,   (5)

c, s, r  – параметры определяющие прямую контрастного перепада. d, b – параметры, определяющие яркости справа и слева от контрастного перепада.

Разложение идеализации элемента контура по ортонормированному базису:       

.   (6)

В результате задача состоит в минимизации функции:

  ,   (7)

т. е. нахождении пятёрки чисел c, s, r, d и b, таких, чтоб  было минимально.

 

 

Рис. 6. Диаграммы нулевых точек первых восьми функций .

Следует отметить, что оператор имеет хорошую устойчивость к наличию шумов, обладая при этом достаточным быстродействием.

Детектор Бэкера и др.

Бэкер и др. (1996 г.)  разработали алгоритм [11] для автоматического конструирования детектора произвольного параметрического элемента. Для увеличения надёжности детектирования при построении параметрической модели учитываются искажения оптической системы и светочувствительной матрицы. Для уменьшения размерности функции окна осуществляется переход к пространству с меньшим количеством измерений при помощи преобразования Карунена-Лоэва.

Преобразование Хука.

Усовершенствованный вид алгоритма также называют преобразованием Радона (Radon transform) [12]. С помощью данного алгоритма можно находить на изображении прямые линии, окружности, эллипсы. Преобразование выполненяется посредством перевода каждого контурного элемента изображения в некоторую кривую в новом пространстве параметров. Коллинеарные элементы порождают семейство кривых, пересекающихся в одной «области пересечения». «Область пересечения» говорит о наличии искомого элемента на изображения, а также характеризует его расположение.

Детектор прямых линий, использующий преобразование Хука.

С точки зрения детектора прямых линий преобразование можно представить как суммирование яркостей точек на контурном изображении вдоль всевозможных направлений. Направления однозначно задаются перпендикулярными им векторами, проведёнными из центра картинной плоскости (см. рис. 8). Вектора задаются в полярной системе координат длинной и углом с вертикалью. На выходе преобразования получается функция, зависящая от двух аргументов угла и расстояния. По значениям  функции можно определить количество точек, лежащих вдоль определённой прямой линии.

Первый этап предполагает выделение контуров (см. рис. 7)

Рис. 7. Выделение контуров на изображении.

Геометрический смысл второго этапа преобразования можно увидеть на рис. 12. Центром изображения ABCD является точка О. Суммирование яркостей точек осуществляется вдоль прямой L. Она задается вектором , который в полярных координатах имеет параметры угол θ (0-180°) и длину .

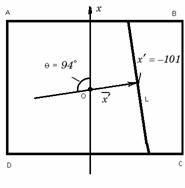
Рис. 8. Геометрический смысл преобразования Радона.

Уравнение прямой L в декартовой системе координат будет иметь следующий вид ():

         (8)

Результатом суммирования по всем прямым линиям является двумерная функция, зависящая от угла θ и расстояния x’ (см.рис. 9).

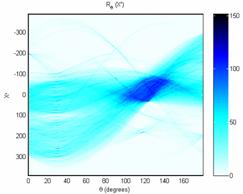
Рис. 9. Результат применения преобразования Радона.

Более тёмные области сигнализируют о большем попадании точек на одни и те же близлежащие линии. Они образуются в местах пресечения траекторий отдельных точек. Полученная функция не несёт информации о расположении отрезков на линии, она лишь говорит, что он есть, поэтому, в дополнение к описанным операциям, потребуется реализация алгоритма локализации отрезка на прямой.

К достоинствам преобразования следует отнести высокую надёжность детектирования прямых линий. Разрывы контурной линии вдоль прямой оказывают незначительное влияние на работу алгоритма.

К недостаткам следует отнести необходимость проведения операции нахождения контуров, поиска областей пересечения траекторий отдельных точек в многомерном пространстве параметров и необходимость дополнительных алгоритмов, для локализации отрезков на найденных прямых линиях.

Детекторы, использующие статистические методы.

Данный тип детекторов обнаруживает элементы изображения, используя статистическую гипотезу. Как было заявлено в [13], не синтезированные изображения имеют высоко структурированные статистические свойства, которые обычно не согласуются с предположениями конкретного детектора. Это приводит к детекторам, основанным на статистической гипотезе. Причём наличие простого элемента  зависит как от статистики фильтров говорящих о наличии элемента, так и от статистики фильтров, говорящих об отсутствии элемента (это позволяет, например, не детектировать элементы текстуры). Кроме того, в случае использования фильтров разного масштаба, в разных цветовых измерениях и т. д.  не всегда бывает понятно, как наиболее оптимально объединить полученные данные. В статистическом детекторе это можно сделать, используя совместное распределение данных различных фильтров. Обычно используется теорема Байеса.

Детекторы контрастных перепадов, использующие статистические методы.

Скот Кониши и др. [14], разработали статистический детектор контурных линий, который использует два типа фильтров (интенсивности градиента Лапласиан от Гауссиана и набор направленных фильтров Габбора разных масштабов и направлений (9) (см. рис. 10)) и объединили информацию зависящую от цвета и масштаба при помощи совместной вероятности.

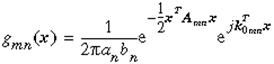                (9)

Рис. 10. а - действительная часть, б  - мнимая часть импульсной характеристики фильтра Габбора.

Единственный требуемый входной параметр – порог T, по которому делается решение о наличии контура log(Pon/Poff)>T (Pon – вероятность присутствия элемента, Poff - вероятность отсутствия элемента). По оценкам авторов детектор показал себя лучше детектора Канни на высоко хаотичных изображениях (линии текстуры были исключены, оставлены только контурные линии).

 

Распараллеливание операций обработки изображений.

Группы операций обработки изображений.

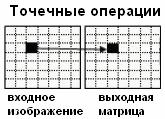
Операции, выполняемые над входным изображением по типу обращения к памяти можно классифицировать на группы в соответствии с таб. 3.

Таб. 3.  Классификация операций обработки изображений по типам обращения к памяти.

Группа операций	Описание	Пример
	Каждой входной точке соответствует выходная точка, расположенная там же.	-      сравнение с порогом. -      преобразование цветов.
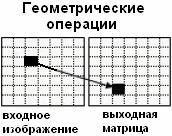
	Каждой входной точке соответствует выходная точка, находящаяся в ином месте.	-    аффинные преобразования.
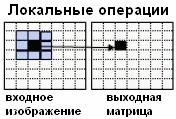
	Некоторой ограниченной области входных точек соответствует своя выходная точка, расположенная там же.	-      двумерные фильтры.
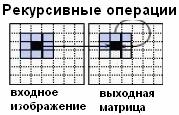
	Входными точками являются не только локальные точки входного изображения, но и некоторые предварительно определённые выходные точки.	-      дистанционное преобразование [15].
	Исходные яркости точек аккумулируются для получения скалярного или векторного выходного значения.	-      вычисление гистограмм. -      преобразование Хука.
	Входные точки определяются по содержанию изображения.	-    операция разрастания регионов. -    разметка связанных компонент.
	Все входные точки должны быть задействованы для вычисления значения результирующей точки.	-    преобразование Фурье.

Практически у всех операторов, нахождения простых элементов изображения операцией первой, очереди является операция фильтрации. Эта операция требует наибольшее количество однотипных вычислений с наперёд известным, близким расположением данных. Операциями второй очереди, в большинстве случаев, идут точечные операции (операции сравнения с порогом). И заключительным этапом работы детекторов, в большинстве случаев, могут являться рекурсивные операции или объектно-ориентированные операции. Эти операции имеют меньший объём данных, нежели операции первой очереди, но трудность их выполнения заключается в произвольности доступа к памяти. В следующем разделе мы попытаемся обосновать выбор оптимальной аппаратной организации вычислений.

Аппаратная организация вычислений.

При обработке изображений имеется большой объём однотипных данных. Обрабатывать эти данные процессором общего назначения в реальном времени зачастую невозможно,  так как большую часть времени процессор тратит на организацию собственной работы (выборку команд, данных) нежели на саму обработку. Такие процессоры принято относить к SISD (Single Instruction Single Data/Одна Инструкция Одни Данные) архитектуре.

Более приспособленными  к обработке больших  частей однотипных данных являются процессоры с SIMD (Single Instruction Multiple Data/Одна Инструкция Множество Данных) архитектурой (см. рис. 11).

На рынке электронных компонентов имеется ряд сигнальных процессоров, оптимизированных для обработки изображений. Можно отметить семейство процессоров BlackFin фирмы Analog Devices, а так же TMS320C64x фирмы Texas Instruments. Все они имеют SIMD архитектуру и как минимум два вида памяти, одну – работающую на частоте ядра и другие – работающие на меньших частотах.

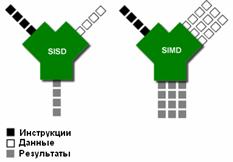
Рис. 11. Схема работы процессоров SISD и SIMD архитектуры.

Слабым звеном в аппаратной организации обработки изображений является именно доступ к памяти. Необходимо загрузить вычислительные модули данными. Быстрая память очень дорога, да и для организации вычислений с множеством входных параметров она должна иметь несколько независимых каналов для выборки значений из её разных концов (случай с интегральными операциями).

Пожалуй, лучшую производительность в обработке изображений показывает IMAP (Integrated Memory Array Processor/Процессор с Интегрированным Массивом Памяти) процессор [16]. Данный процессор состоит из матрицы, полностью параллельных процессорных SIMD модулей, имеющих некоторый объём локальной памяти и объединённых между собой локальными взаимосвязями. Такая архитектура обеспечивает наилучшую возможность для  распараллеливания операций и непоследовательных (рваных) доступов к памяти. И в отличие от реализаций на ПЛИС (Программируемая Логическая Интегральная Схема) такой процессор обеспечивает большую гибкость в смене алгоритмов в процессе работы.

С другой стороны при известном, ограниченном наборе алгоритмов, использующих локальные операции по экономическим показателям, целесообразно применять ПЛИС. В таком случае вычисления можно проводить построчно, используя набор параллельных вычислительных модулей (см. рис. 12).

 

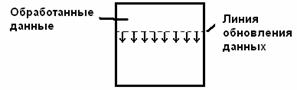
Рис. 12. Распараллеливание локальных операции вдоль строки изображения.

Такая модель вычислений оптимальна, например, в случае получения данных построчно с видеодатчика (см. рис. 13).

 

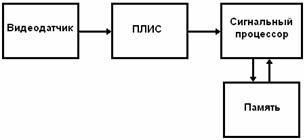
Рис. 13. Блок схема СТЗ реального времени.

При такой аппаратной реализации для задач детектирования простых элементов изображения оптимально выполнять операции фильтрации (см. Таб. 3) на ПЛИС, точечные операции также выгодно организовать на ПЛИС.  В то время как рекурсивные или объектно-ориентированные операции гораздо производительней и экономичнее организовывать программно на сигнальном процессоре.

Необходимо отметить, что такая организация работы позволяет получать каждый новый кадр изображения в сопровождении с данными от локальных и точечных операций. Также на долю вычислений ПЛИС имеет смысл возложить статистические операции, такие например, как вычисление гистограмм.

Подобная организация системы технического зрения была использована автором при реализации проекта видеосканера штрихового кода [17].

 

Выводы.

История развития детекторов простых элементов изображения показывает, что они идут по пути усложнения, увеличения количества входных параметров. В тоже время виден явный уход всё дальше и дальше от яркостной картины в область параметров, характеризующих некую окрестность каждой точки или даже всего изображения в целом, и это не случайно. Исследования [13] показали, что не синтезированные изображения имеют высоко структурированные статистические свойства, которые обычно не согласуются с предположениями конкретного детектора. В сам детектор вкладывается всё более и более интеллектуальный смысл, например, он должен находить простые элементы контура, но не видеть их на изображении текстуры.  Увеличение сложности алгоритмов, а также требование к работе большинства устройств в реальном масштабе времени, приводит к усложнению и ускорению аппаратуры занятой обработкой изображений. Большинство таких устройств содержит наряду с универсальными вычислительными модулями специализированные модули для выполнения наиболее часто используемых операций.

Наиболее оптимально выполнение операций фильтрации на комбинационной логике, что связанно с использованием фильтром данных из некоторой предопределённой, небольшой области изображения.          Количество фильтров, применяемых в одной системе для обработки изображения, растёт, что приводит к увеличению количества обращений к памяти, занимающих значительное время. Отсюда возникает требование одновременной подачи данных на вход нескольких фильтров. Что можно сделать, используя несколько физически реализованных фильтров. Наиболее дешёвый способ - использование комбинационной логики.

Появление на электронном рынке ПЛИС привело к возможности создания дешёвых модулей комбинационной и конвейерной обработки изображений наиболее оптимально подходящих для каждой конкретной задачи.

Благодарности.

 

Автор выражает благодарность профессору А. К. Платонову за ценные советы и за помощь при подготовке этой публикации.

Список использованной литературы.

1.                  E. Davis. Machine Vision : Theory, Algorithms, Practicalities. (2nd Edition), Academic Press (1996).

2.                  I. Weiss. High-order differential filters that work. IEEE Transaction on Pattern Analysis an Machine Intelligence, 16(7):734-739, July 1994.

3.                  P. Meer and I. Weiss. Smoothed differentiation filters for images. Journal of Visual Communication and Image Representation, 3(1):58-72, March 1992.

4.                  V. Torre and T. A. Poggio. On edge detection. IEEE Transaction on Pattern Analysis and Machine Intelligence, 8(2):147-163, March 1986.

5.                  J. Canny. A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 8(6):679{698, November 1986.

6.                  P. Beaudet. “Rationally Invariant Image Operations,” in International Joint Conference on Pattern Recognition, pp. 579-583, Kyoto, Japan, 1978.

7.                  W. Forstner. A feature based correspondence algorithm for image matching. Intl. Arch. Photogramm. Reemote Sensing, 26:150-166, 1986.

8.                  M. Trajkovich and M. Handley. Fast corner detection. Image and Vision Computing, 16:75-87, 1998.

9.                  Ali Ajdari Rad, Karim Faez and Navid Qaragozlou. Fast Circle Detection Using Gradient Pair Vectors. Proc. VIIth Digital Image Computing, pp. 879-887, Sydney, Australia, 2003.

10.             Hueckel M. H., «An operator which Locates Edges in Digitized Pictures», JACM, 18, №1, 113-125 (1971).

11.             S. K. Nayar, S. Baker, and H. Murase, “Parametric feature detection,” In Proceeding of IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, June 1996.

12.             Illingworth, J., and Kittler, J., ``A Survey of the Hough Transform," CVGIP, vol. 44, pp. 87-116, 1988.

13.             D.J. Field, “Relations between the Statistics and Natural Images and the Responses Properties of Cortical Cells” J. Optical Soc. Am., vol. A, no. 4, pp. 2379-2394, 1987.

14.             S. Konishi, A.L. Yuille, and J.M. Coughlan, “A Statistical Approach to MultiScale Edge Detection,” Proc. Workshop Generative-Model-Based Vision: GMBV ’02, 2002.

15.             G. Borgefors: ”Distance Transformations in Digital mages”, Computer Vision, Graphics, and Image Processing, Vol.34, pp.344–371, 1986.

16.             S.Kyo, et al.: ”A 51.2GOPS Scalable Video Recognition Processor for Intelligent Cruise Control based on a Linear Array of 128 4-Way VLIW Processing Elements”, ISSCC Digest of Technical Papers, 2.6, pp.48–49, 2003

17.              Краснобаев А. А., Алгоритмы распознавания штриховых кодов. Препринт ИПМ РАН, 2004 г., 28 с. с ил.