Аннотация
Предлагается для расчета подвижных двумерных сеток при решении нестационарных задач
использовать универсальные вариационные функционалы. Для их основной (опорной) части
коэффициенты определяются метрическими параметрами сетки предыдущего шага по времени.
Они корректируются другими вариационными функционалами с весовыми коэффициентами,
пропорциональными величине шага по временной координате. Подробно рассмотрены возможности
конструирования таких функционалов. Обсуждаются вопросы реализации соответствующих алгоритмов.
Abstract
Universal variation functionals are supposed to be used for calculation of moving 2D grids
in nonstationary problems. For their basic part the coefficients are defined by grid metric
parameters calculated on the previous time step. They are corrected by others variation
functionals with weighted coefficients proportionally to time step along the time coordinate.
The possibilities to construct such functionals are considered in detail. The implementation
of corresponding algorithms are discussed.
Посвящается
памяти
Глеба Борисовича Алалыкина
В
апреле 2004 г.
на тихой московской улице случилось трагическое дорожное происшествие, и 5 мая 2004 г. не стало нашего
коллеги Глеба Борисовича Алалыкина.
После
окончания Томского государственного университета в 1953г. он был по
распределению направлен на работу в Москву, в только что организованное
Отделение прикладной математики Математического института Академии наук,
которое впоследствии стало Институтом прикладной математики имени М.В.Келдыша
Российской Академии наук. Всю жизнь он проработал в одном отделе, которым
сначала руководил известный ученый К.А.Семендяев, затем С.К.Годунов – ныне
академик РАН, а сейчас руководит член-корреспондент РАН А.В.Забродин. В этом же
отделе еще до окончания в 1960 году механико-математического факультета МГУ
начал работу и автор этой публикации.
Несколько
последних лет автору довелось работать непосредственно с Г.Б.Алалыкиным. Мы
занимались разработкой алгоритмов и вопросами применения расчетных сеток для
решения прикладных газодинамических задач. Плодотворная научная работа приятно
дополнялась общением с доброжелательным и скромным товарищем и коллегой.
Публикуя результаты научных исследований, автор всегда считал своим долгом
выразить благодарность Г.Б.Алалыкину за реализацию разрабатываемых алгоритмов
на ЭВМ и участие в проведении численных экспериментов по их апробации.
Внезапный
и трагический уход Г.Б.Алалыкина серьезно нарушил ритм и содержание этой работы
и наложил отпечаток на предлагаемую публикацию.
Впервые
автор представляет результаты, которые еще не прошли всесторонней
численно-экспериментальной проверки. Уверенность автора основана на том, что
речь идет об обосновании и развитии уже апробированных (при участии
Г.Б.Алалыкина) алгоритмов, а также многолетнем вычислительном опыте. Отчасти
это делается и сознательно, с тем, чтобы привлечь внимание к такой проверке.
Предлагаемая
работа – дань светлой памяти прекрасного товарища и коллеги.
Содержание
стр.
Введение ………………………………………………………………… 4
§ 1. Реализация опорного функционала без якобиана
……………….. 5
§ 2. Реализация опорного функционала с
якобианом………………… 10
§ 3. Об интерполяции и параметрическом портрете
сетки …………. 15
§ 4. Корректирующие функционалы для функционала без
якобиана. 18
§ 5. Корректирующие функционалы для функционала с
якобианом.. 23
§ 6. Некоторые соображения общего характера………………………
29
Заключение
………………………………………………………….. 34
Список литературы ………………………………………………….. 35
Введение
Настоящая
работа является непосредственным
продолжением и развитием [1], в которой были рассмотрены вопросы
построения двумерных сеток в ходе расчета нестационарных задач с подвижными
границами областей. В качестве одного из путей решения этой проблемы эффективно
применяются вариационные функционалы универсального характера. Расчет подвижных
сеток имеет свою специфику и предъявляет дополнительные требования к алгоритмам
их построения.
Настоящая
публикация по сравнению с [1] более четко акцентирует внимание на некоторых аспектах
проблемы и представляет их дальнейшее развитие. Мы старались избегать излишних
повторов и поэтому непосредственно ссылаемся на текст работы [1], хотя для
связности изложения полностью исключить повторение невозможно. Особое внимание
уделено вопросу полноты сводки расчетных формул. Это обусловлено тем
немаловажным обстоятельством, что иногда «безобидное», казалось бы, изменение
формул приводит к утрате важных свойств.
Сочтено
целесообразным сначала (в §1 и §2) произвести изложение для «чистых» опорных
функционалов (термины будут разъяснены чуть ниже), а затем – в §4 и §5 –
изложить технологию использования корректирующих их функционалов, которым в
работе [1] было уделено минимальное внимание. Далее в §6 представлены некоторые
соображения общего характера, касающиеся практической реализации предлагаемых
алгоритмов.
§ 1. Реализация
опорного функционала без якобиана.
Как и в [1], для упрощения описания математического
содержания алгоритмов построения сеток избран простейший вариант регулярной
сетки, упорядоченной по двум индексам (n,m), применительно к
изолированной области W. Она рассматривается как
четырехугольник с криволинейными границами. Задача построения сетки
рассматривается как дискретная реализация невырожденного отображения единичного
квадрата Q: (0£x£1, 0£h£1)
на область W в плоскости переменных (х,у).
Для этой
цели привлекается один из двух функционалов:
(1.1) 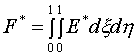 или или 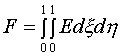 , ,
которые будем в интересах последующего изложения называть
опорными. Подинтегральные функции, называемые плотностью энергии отображения,
задаются формулами:
(1.2) 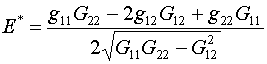 . .
(1.3) 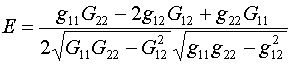
Они различаются только отсутствием или наличием в
знаменателе якобиана отображения. Условимся для краткости и наглядности
называть F*
функционалом без якобиана, а F – функционалом с якобианом.
Справедливость требует
отметить, что использование этих функционалов инициировалось работами [2] и
[3], хотя в них и рассматривался только функционал F.
Благодаря
якобиану достигается его важное практическое преимущество: такой
функционал (при соблюдении некоторых условий) гарантирует
невырожденность отображения, а следовательно, и расчетной сетки. Но за это, как
мы увидим в дальнейшем, приходится дорого платить.
Входящие
в (1.2)–(1.3) величины представляют метрические параметры отображения:
(1.4) 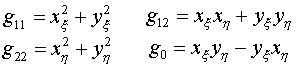
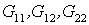 - элементы аналогичной
симметричной и положительно определенной матрицы G. - элементы аналогичной
симметричной и положительно определенной матрицы G.
Невырожденность отображения
и положительная определенность матриц
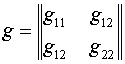 , , 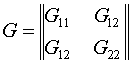
взаимосвязаны ввиду очевидного тождества:
(1.5) 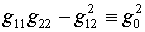 . .
Функционалы
минимизируются на классе функций 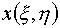 , , 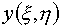 , являющихся гладким продолжением внутрь квадрата Q
заданных на его границе функций , являющихся гладким продолжением внутрь квадрата Q
заданных на его границе функций 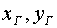 . Эти последние осуществляют гладкое взаимнооднозначное
отображение границы квадрата Q на границу области W, в которой должна быть
построена сетка. . Эти последние осуществляют гладкое взаимнооднозначное
отображение границы квадрата Q на границу области W, в которой должна быть
построена сетка.
Удобно
ввести матрицу 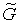 с нормированными
элементами: с нормированными
элементами:
(1.6) 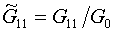 , , 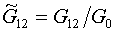 , , 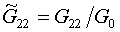
Нормирующий коэффициент G0
определим формулой:
(1.7) 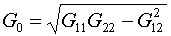 . .
Дискретные аналоги функционалов записываются в виде
суммы «вкладов» отдельных ячеек сетки. Для получения разностных уравнений в
отдельном узле сетки с номером (n,m) достаточно рассмотреть «шаблон»,
в котором участвуют 4 ячейки, примыкающие к этому узлу. Для упрощения описания
расчетных формул узлам шаблона присваиваются более простые номера в
соответствии со схемой:
(1.8)
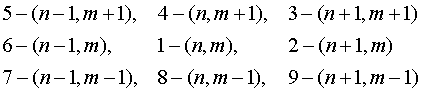
Дополнительно присвоим узлу 2-(n+1,m) еще и номер 10.
Соответствующие рисунки представлены на стр.13 работы [1].
Четырем
ячейкам шаблона присваиваются номера 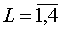 . В свою очередь, каждую из ячеек с номером L,
вершины которой имеют номера (1,2L,2L+1,2L+2) , разделим на две пары
треугольников, проведя ее диагонали (1,2L+1) и, независимо, (2L,2L+2). Образующимся
треугольникам присвоим номера (k,L), . В свою очередь, каждую из ячеек с номером L,
вершины которой имеют номера (1,2L,2L+1,2L+2) , разделим на две пары
треугольников, проведя ее диагонали (1,2L+1) и, независимо, (2L,2L+2). Образующимся
треугольникам присвоим номера (k,L), 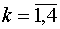 . .
Треугольник
с номером k имеет в качестве «средней» из трех вершин некоторый
узел (x,y)0, а в качестве двух других
вершин – узлы (x,y)- и (x,y)+ , свои для каждого из
номеров (k,L). Символами «-» и «+»
отмечены соответственно «предшествующая» и «последующая» вершина, так, чтобы
обход вершин -,0,+ осуществлялся против часовой стрелки (нам представляется,
что измененные, по сравнению с [1], обозначения более удачны с точки зрения
описания алгоритма и его последующего программирования на ЭВМ).
Для
вычисления метрических параметров в треугольнике с номером k
применяются простейшие разностные формулы:
(1.9) 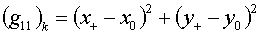 , ,
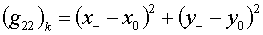
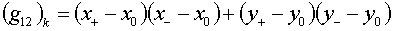
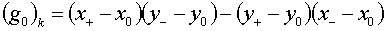
Величины 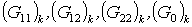 будут определены
аналогичным образом. После этого определяется энергия для треугольника: будут определены
аналогичным образом. После этого определяется энергия для треугольника:
(1.10)
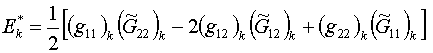
и энергии для ячейки:
(1.11) 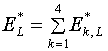 , (сомножитель 1/4
опущен без ущерба для дела) , (сомножитель 1/4
опущен без ущерба для дела)
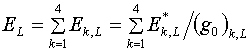
Здесь и далее индекс (k,L)
означает, что соответствующая величина определяется в треугольнике с номером k и
ячейке с номером L.
Для
вариационного функционала F* без якобиана условия
минимизации его дискретной формы в узле
(x1,y1) записываются в виде:
(1.12)
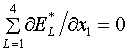 , , 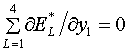
Остановимся на этом более подробно, чем
в [1], поскольку соответствующие формулы будут использованы далее в §2.
Рассмотрим
ячейку с номером L=1, имеющую самые простые номера узлов шаблона (1.8):
1, 2, 3, 4.
Для
треугольника с номером k=1 будем иметь:
(1.13) (x,y)-=(x,y)4
, (x,y)0=(x,y)1
, (x,y)+=(x,y)2
и, в соответствии с (1.9):
(1.14) 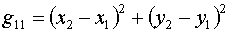 , , 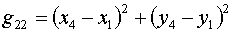
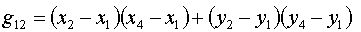
Поэтому для этого треугольника (k=1) получаем:
(1.15) 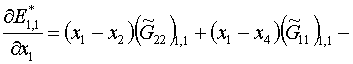

Для треугольника с номером k=2 имеем:
(1.16) (x,y)-=(x,y)1
, (x,y)0=(x,y)2
, (x,y)+=(x,y)3
и, в соответствии с (1.9):
(1.17) 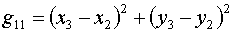
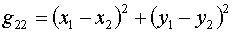
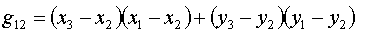
Следовательно, для треугольника k=2 получаем:
(1.18) 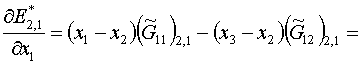
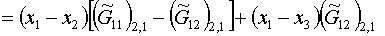
Обратим внимание, что при выводе этой формулы
использовано представление
(1.19)
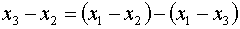 . .
Если это не сделать, то в дальнейшем не удалось бы
добиться важного утверждения, что сумма коэффициентов с0 в
формулах (1.25) положительна.
Далее,
для треугольника с номером k=3 имеем:
(x,y)-=(x,y)2
, (x,y)0=(x,y)3
, (x,y)+=(x,y)4
Очевидно, что его можно не рассматривать, поскольку
в нем узел (x,y)1 не участвует.
Наконец, для треугольника с номером k=4:
(1.20) (x,y)-=(x,y)3 , (x,y)0=(x,y)4
, (x,y)+=(x,y)1
и можно сразу, по аналогии с k=2, получить:
(1.21) 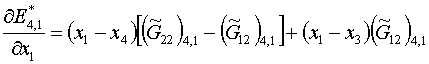
При
получении результатов для других номеров ячеек L примем во внимание, что
формулы инвариантны относительно поворота системы координат 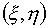 , поэтому расчетные формулы для треугольников сохраняются,
независимо от возможной перемены ролей , поэтому расчетные формулы для треугольников сохраняются,
независимо от возможной перемены ролей 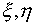 , после отбора координат их вершин. , после отбора координат их вершин.
Суммируя,
в соответствии с (1.11) и (1.12), результаты (1.15), (1.18), (1.21) и
аналогичные для других номеров L, получим уравнение:
(1.22) 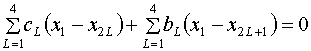 , ,
где коэффициенты 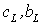 вычисляются по
формулам: вычисляются по
формулам:
(1.23)
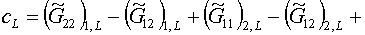
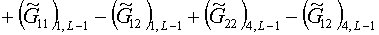
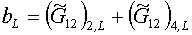
Легко видеть, что второе из условий (1.12) дает
аналогичное уравнение с теми же коэффициентами:
(1.24) 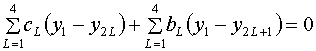 . .
В работе [1] на стр.17 было
объяснено, что для решения возникающей линейной системы разностных уравнений
естественно воспользоваться простейшим итерационным процессом:
(1.25) 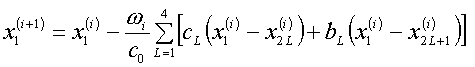 , ,
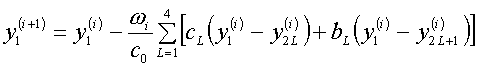 , ,
где
(1.26) 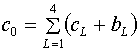 . .
Из выписанных выше формул (1.15), (1.18), (1.21) следует,
что для ячейки с номером L=1
получаем:

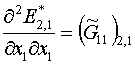 , , 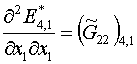
Заменив второй индекс 1 на L,
получим аналогичные формулы для всех номеров L. Поэтому, как отмечено в
[1] на стр.19, сумма коэффициентов с0 в формулах
(1.25)-(1.26) положительна, поскольку каждый из 12 треугольников дает
положительный вклад в нее. Об этом пришлось специально позаботиться при
получении (1.18) с помощью (1.19). К сожалению, как показывают формулы (1.23),
этого нельзя сказать о каждом из коэффициентов cL,bL в отдельности. Возможно для практики расчетов представляло бы интерес
выяснение вопроса о том, какие сетки условию положительности всех
коэффициентов cL,bL удовлетворяют. Это весьма полезное свойство,
известное как принцип максимума.
Далее, обратясь к §2 работы
[1], пришло время напомнить, что в случае, если при расчете нестационарной
задачи используются «чистые» опорные функционалы (1.1)-(1.3), то их
коэффициенты 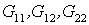 вычисляются как
метрические параметры сетки, полученной на предыдущем шаге по времени. Они
остаются постоянными на всех итерациях процесса (1.25). Только итерационный
параметр вычисляются как
метрические параметры сетки, полученной на предыдущем шаге по времени. Они
остаются постоянными на всех итерациях процесса (1.25). Только итерационный
параметр 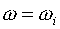 может меняться от
итерации к итерации. Стратегия его изменения описана в [1] на стр.19-20, и мы
ее не будем повторять. может меняться от
итерации к итерации. Стратегия его изменения описана в [1] на стр.19-20, и мы
ее не будем повторять.
§ 2. Реализация
опорного функционала с якобианом.
Теперь
обратимся к рассмотрению опорного вариационного функционала (1.1), (1.3) с
якобианом в знаменателе плотности энергии Е. После его дискретизации,
уже описанной в §1, аналогичные (1.12) уравнения:
(2.1) 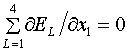 , , 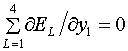
становятся
нелинейными. Как описано в [1] на стр.17-18 со ссылкой на работу [2],
для решения таких нелинейных уравнений может использоваться итерационный
процесс, который представляет вариант метода Ньютона-Рафсона. Он отличается от
стандартного тем, что в расчете участвует только блочная диагональ матрицы
вторых производных.
В расчетных
формулах итерационного процесса используются первые и вторые производные
разностного функционала F для центральной точки (x,y)1 того же шаблона, что и
в §1. Они вычисляются по сетке,
полученной на предыдущей итерации, и, кроме того, используют значения
коэффициентов 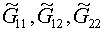 , вычисленные с помощью сетки предыдущего шага по времени. , вычисленные с помощью сетки предыдущего шага по времени.
Все это, как очевидно, приводит к
достаточно громоздкой процедуре и значительным затратам вычислительных
операций. Несмотря на обнадеживающие слова о модифицированных вариантах метода
Ньютона-Рафсона, практическая скорость сходимости итерационных процессов крайне
медленная.
Положение
спасают следующие обстоятельства. Во-первых, в случае использования «чистого»
опорного функционала на каждом очередном шаге по времени система разностных
уравнений конструируется так, что сетка предыдущего шага ей удовлетворяет
точно, с нулевой невязкой. Поэтому предстоит погасить итерационным
процессом невязки, порождаемые тем, что сетка должна быть привязана к слегка
изменившим свое положение новым границам. Для времени t, равному временному
интервалу для очередного шага нестационарного процесса, эти невязки можно
считать величинами О(t). Этим предлагаемые алгоритмы
принципиально отличаются от других, тянущих за собой «шлейф недоитерированности»
уравнений, которые практически до сходимости довести не удается.
Во-вторых,
задача итерационного процесса состоит только в том, чтобы обеспечить
невырождение и гладкость сетки. И не так уж важно, будут полностью погашены
упомянутые невязки или нет. Следующий шаг начнется «с белого листа» -
конструирования новой системы разностных уравнений. Это и создает надежду, что
необходимое число итераций (пусть и
очень медленно сходящихся), как правило, не придется назначать большим.
Отметим
однако, что расчеты газодинамических задач (например, в трехтемпературной
модели) ведутся при очень малых значениях шага t и требуют огромного
количества временных шагов. Поэтому вопрос об «удешевлении» расчета сеток имеет
весьма существенное практическое значение.
В
связи с высказанными соображениями у автора возникло предложение. А что если
«заморозить» коэффициенты возникающей на очередном шаге системы разностных
уравнений, не пересчитывая их на каждой итерации, и воспользоваться более
простым итерационным процессом, аналогичным описанному в §1?
Это
предложение потерпело неудачу еще, так сказать, на этапе проектирования.
Несмотря на это, мы считаем полезным и целесообразным его рассмотреть. Тем
более, что при этом подавляющая часть усилий будет затрачена на получение
формул для производных дискретной формы вариационного функционала F,
которые необходимы для практической реализации «настоящего» итерационного
процесса.
Итак,
займемся получением уравнений (2.1).
Согласно формулам
(1.2)-(1.3),
(2.2) 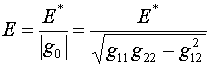
При вычислении производной 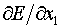 мы сознательно
воспользуемся более громоздким вторым выражением, чтобы получить «независимые»
(условно) уравнения для х и у, а не систему двух уравнений. Тогда
получаем: мы сознательно
воспользуемся более громоздким вторым выражением, чтобы получить «независимые»
(условно) уравнения для х и у, а не систему двух уравнений. Тогда
получаем:
(2.3) 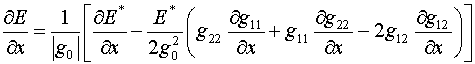
Аналогичная формула получается и для 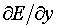 . .
Далее,
как и в §1, рассмотрим ячейку с номером L=1 и в ней по очереди
треугольники k=1,2,4. Отложив пока k=1, начнем с k=2. Для него используются
координаты вершин (1.16) и производятся вычисления по формулам (1.17)-(1.18). В
результате получим:
(2.4)
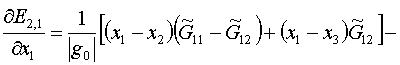
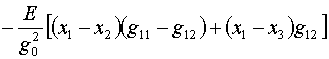
Мы опустили у величин в правой части номер (2.1)
рассматриваемого треугольника, полагая достаточным его обозначение слева. Для
треугольника с k=4 формула выписывается автоматически по аналогии:
(2.5)
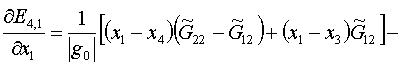

Отложенная формула для k=1 такова:
(2.6) 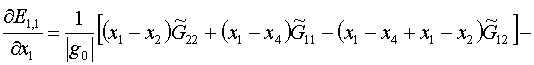
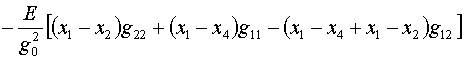
Очевидно, что в силу (2.3) формулы для производных
по у1 получаются путем замены х на у.
Результирующие
уравнения (2.1) получаются суммированием полученных выражений по всем 12 треугольникам
для четырех ячеек шаблона. Не выписывая их, обратимся к вышесказанному
предложению о «замораживании» коэффициентов с целью превратить уравнения в
линейные. Естественнее всего представляется «замораживание» 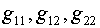 посредством вычисления
их на сетке предыдущего шага по времени. Тогда посредством вычисления
их на сетке предыдущего шага по времени. Тогда
(2.7)
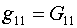 , , 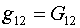 , , 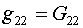
И вот здесь обнаруживается, что в формулах
(2.4)-(2.6) коэффициенты при всех слагаемых 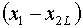 в случае (2.7) равны
нулю, т.е. никаких линейных уравнений не получается. В общем-то, это не
удивительно, поскольку в случае (2.7) получаем Еº1 и речь, следовательно, идет
о «скрытом» дифференцировании этой единицы. в случае (2.7) равны
нулю, т.е. никаких линейных уравнений не получается. В общем-то, это не
удивительно, поскольку в случае (2.7) получаем Еº1 и речь, следовательно, идет
о «скрытом» дифференцировании этой единицы.
Есть
еще одна возможность: вычислить 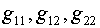 по сетке, задаваемой в
качестве начального приближения (как и будет делаться на первой итерации
«настоящего» итерационного процесса) и затем «заморозить» (а вот этого делаться
не будет). Но эта сетка вызывает
серьезные сомнения с точки зрения гладкости. «Замораживая» коэффициенты,
мы процесс сглаживания отключаем. Короче говоря, от выдвинутого предложения
приходится отказываться. по сетке, задаваемой в
качестве начального приближения (как и будет делаться на первой итерации
«настоящего» итерационного процесса) и затем «заморозить» (а вот этого делаться
не будет). Но эта сетка вызывает
серьезные сомнения с точки зрения гладкости. «Замораживая» коэффициенты,
мы процесс сглаживания отключаем. Короче говоря, от выдвинутого предложения
приходится отказываться.
Полезным
его результатом является получение формул (2.4)-(2.6) для первых производных
функционала. Для практической реализации «настоящего» итерационного процесса,
описанного (без формул) в начале этого параграфа, необходимы еще формулы для
вторых производных
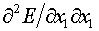 , , 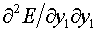 , , 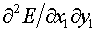 . .
Поскольку
последняя (смешанная) производная, как правило, не равна нулю, в результате
возникнет система двух уравнений для х1, у1 . В
такой ситуации вместо (2.3) имеет смысл воспользоваться менее громоздкой
формулой:
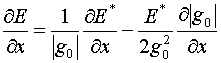
Напомним, что как указано в [1] на стр.15,
конструкция интегральной суммы для дискретной формы вариационного функционала F
предполагает, что
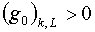 для всех k,L. для всех k,L.
Поэтому на знак модуля можно не обращать внимания. С
учетом последней из формул (1.9) и назначений величин (1.13), (1.16) и (1.20)
будем иметь:
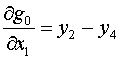 , ,  для k=1 для k=1
(2.8) 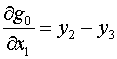 , , 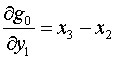 для k=2 для k=2
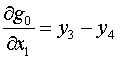 , , 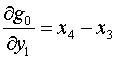 для k=4 для k=4
Это позволяет заменить формулы (2.4)-(2.6) на
следующие (индексы треугольников в правых частях, как и ранее, опущены):
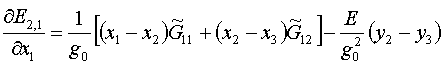
(2.9) 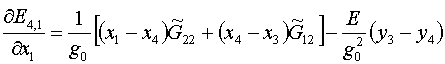
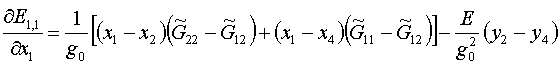
При выписывании по аналогии формул производных по у1
следует учитывать, что из-за (2.8) они не совсем сводятся к замене х
на у и наоборот:
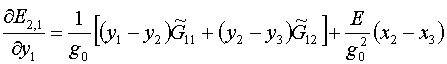
(2.10) 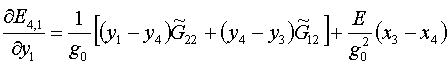
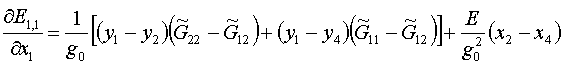
Дифференцированием формул (2.9) по х1
проще, чем из (2.4)-(2.6), получаются
формулы 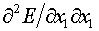 для отдельных
треугольников. При этом потребуются производные для отдельных
треугольников. При этом потребуются производные 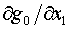 и и 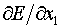 , которые уже имеются в нашем распоряжении – (2.8) и (2.9).
Поэтому чтобы не загромождать изложение, ограничимся результатом
дифференцирования только первой из формул (2.9): , которые уже имеются в нашем распоряжении – (2.8) и (2.9).
Поэтому чтобы не загромождать изложение, ограничимся результатом
дифференцирования только первой из формул (2.9):
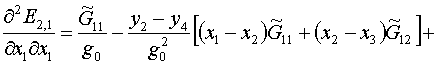
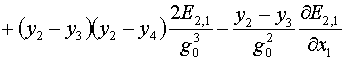
Аналогично
дифференцированием по у1 формул (2.10) получаются вторые
производные 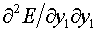 для треугольников.
Формулы смешанных производных для треугольников.
Формулы смешанных производных 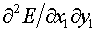 получаются либо
дифференцированием (2.9) по у1, либо (2.10) по х1. получаются либо
дифференцированием (2.9) по у1, либо (2.10) по х1.
Суммированием
соответствующих значений для всех 12 треугольников четырех ячеек шаблона получаются величины
(2.11) 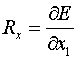 , , 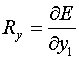 , , 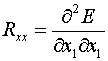 , , 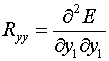 , , 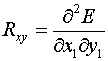 . .
После этого может быть вычислено новое приближение 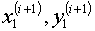 по формулам,
выписанным на стр.18 работы [1]. В интересах последующего изложения в §5 эти
формулы целесообразно привести: по формулам,
выписанным на стр.18 работы [1]. В интересах последующего изложения в §5 эти
формулы целесообразно привести:
(2.12) 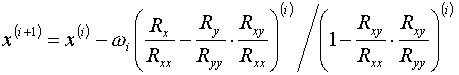
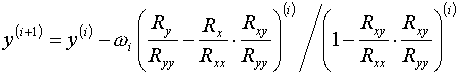
Другие подробности, касающиеся практической
реализации итерационного процесса, повторять не будем.
Уместно
еще раз вернуться к предложению автора о «замораживании» коэффициентов. Если
его реализовать сейчас, для уравнений, полученных после вычисления вторых
производных функционала, то, в отличие от описанной выше попытки, полагая
(2.7), должны быть получены вполне «разумные» коэффициенты. Получатся
разностные уравнения, которые аппроксимируют вариационные уравнения
Эйлера-Лагранжа для функционала с якобианом, следствия из которых приведены на
стр.8 работы [1], со ссылкой на [3].
Теперь речь может идти только об экономии времени ЭВМ (если хранить
«замороженные» коэффициенты), но не об экономии интеллектуальных ресурсов на
вывод и программирование формул для вторых производных. А будет ли эффективно
работать «замораживание» коэффициентов, неизвестно.
Напомним,
что пока речь шла о «чистых» опорных функционалах (1.1)-(1.3). Необходимость их
корректировки будет обсуждаться в §4 и §5.
§ 3. Об
интерполяции и параметрическом портрете сетки.
При
организации расчета сеток есть несколько моментов, когда возникает
необходимость применения интерполяционных формул.
Во-первых,
это расчет исходной сетки в начале расчета, если заданы только узлы на контурах
границ исходных областей.
Во-вторых,
как описано в §2 работы [1], расчет сетки на каждом очередном временном шаге
начинается с движения границ расчетных областей.
В
результате получаются величины сдвига граничных узлов за интервал времени 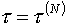 . После этого целесообразно по интерполяционным формулам
рассчитать значения сдвигов для внутренних узлов сетки, и после их учета
(прибавления к координатам узлов сетки на предыдущем шаге) получается начальное
приближение для будущей сетки на текущий момент времени. Граничные узлы при
этом занимают положение, которое при дальнейшем расчете сетки текущего шага,
как правило, изменяться не будет (хотя не исключается возможность включить в
итерационный процесс и пересчет положения граничных узлов, которую мы
рассматривать не будем). . После этого целесообразно по интерполяционным формулам
рассчитать значения сдвигов для внутренних узлов сетки, и после их учета
(прибавления к координатам узлов сетки на предыдущем шаге) получается начальное
приближение для будущей сетки на текущий момент времени. Граничные узлы при
этом занимают положение, которое при дальнейшем расчете сетки текущего шага,
как правило, изменяться не будет (хотя не исключается возможность включить в
итерационный процесс и пересчет положения граничных узлов, которую мы
рассматривать не будем).
Следует
также отметить вообще начальную стадию расчета нестационарного процесса. Если
форма границ счетных областей относительно проста, то зачастую приемлемые
сетки получаются по интерполяционным формулам. Почему бы этим не
воспользоваться вместо сложных алгоритмов, к которым придется прибегнуть на
более поздней стадии.
Интерполяционные
формулы собственно тоже можно рассматривать как дискретную реализацию
отображения параметрического квадрата Q на расчетную область W. При этом сразу же
возникает вопрос, какие значения 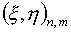 ставить в соответствие
узлу сетки с номером (n,m).
Как показывает практика расчетов, простейший вариант ставить в соответствие
узлу сетки с номером (n,m).
Как показывает практика расчетов, простейший вариант
(3.1)
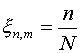 , , 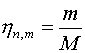 , ,
где N, M –
число интервалов сетки по двум координатным направлениям, редко оказывается
приемлемым. Прежде всего это происходит потому, что исполнитель при расстановке
узлов на контуре области, как правило, старается учитывать индивидуальные особенности
рассчитываемого решения основной задачи (например, для расчета пограничных
слоев сетка должна сильно сгущаться к соответствующей границе, сгущение сетки
целесообразно в областях больших градиентов искомых функций и т.п.).
Одним
из эффективных практических способов реализации такой адаптации
оказалось использование законов расстановки узлов сетки вдоль границы,
описанных, например, в §23 монографии [4]. Для этого на каждой из четырех
границ параметрического единичного квадрата рассчитывается (или задается)
монотонно возрастающая последовательность чисел:
(3.2)
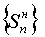 , , 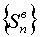 , , 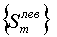 , , 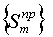 , ,
изменяющаяся от 0 до 1.
Соединим
отрезками прямых точки с одинаковыми номерами на двух противоположных границах.
Точки их пересечения и рассматриваются как параметрические координаты 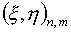 , приписываемые узлу сетки. Полученная картина
рассматривается как параметрический портрет сетки и может быть положена
в основу преобразования координат. Очевидно, что невырожденность его
гарантирована, т.е. якобиан отличается от нуля на всем параметрическом квадрате
Q. , приписываемые узлу сетки. Полученная картина
рассматривается как параметрический портрет сетки и может быть положена
в основу преобразования координат. Очевидно, что невырожденность его
гарантирована, т.е. якобиан отличается от нуля на всем параметрическом квадрате
Q.
В
качестве примера сошлемся на замену переменных, описанную на стр.229-230
монографии [4], которая применялась ранее для расчета сеток в работе [5].
Аналогичный параметрический портрет сетки использовался и в одной из первых
наших публикаций по проблеме построения сеток [6]. Следует признать, что он
приводил к весьма громоздким формам уравнений и алгоритмам.
Позднее,
в процессе использования различных вариантов трансфинитной интерполяции,
было обнаружено, что при произвольных упомянутых выше законах расстановки на
всех четырех границах невырожденная сетка на параметрическом квадрате
получается, если задать в качестве значений управляющих параметров полусуммы
законов расстановки на противоположных границах:
(3.3)
 , , 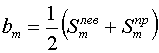
Подчеркнем, что при других способах их
назначения невырожденность параметрического портрета сетки не гарантируется.
Этот факт отмечен в [1] на стр.26-27, а доказан в работе [7]. Он позволяет
ограничиться для преобразования параметрических координат двумя одномерными
функциями  a(x) , b(h), что приводит к куда менее
существенному усложнению уравнений, чем в упомянутом выше случае. Мы
воспользуемся этим в §4 и §5. a(x) , b(h), что приводит к куда менее
существенному усложнению уравнений, чем в упомянутом выше случае. Мы
воспользуемся этим в §4 и §5.
Для
полноты сводки формул выпишем интерполяционную формулу для функции f(x,h) на единичном квадрате Q:
(0£x£1, 0£h£1) по ее значениям на контуре
квадрата для случая (3.3):
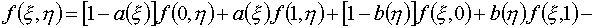
(3.4)
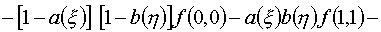
 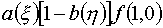
Она
используется в дискретном варианте для обеих координат х и у
со значениями параметров (3.2)-(3.3).
На
усложнение уравнений для расчета сеток приходится идти по следующим причинам.
Как отмечалось, например, авторами работы [8], несмотря на эллиптический
характер этих уравнений, влияние распределения узлов вдоль границ может не
распространяться глубоко внутрь области. Характер сетки внутри области
определяется свойствами производящей сетку системы уравнений в значительно
большей степени, чем выбранные граничные расстановки узлов. В работе [9] это
иллюстрировалось на примере исследования вопроса о воспроизведении произвольной
неравномерной прямоугольной и полярной сетки различными уравнениями.
Содержательность этого
примера объясняется, например, следующим. При расчете так называемых «слоистых»
конструкций весьма важно, чтобы неравномерная полярная сетка по возможности
сохранялась в случае, если в процессе сжатия и разлета такой конструкции не
происходит значительных отклонений от сферической формы (при существенном
изменении размеров в ходе процесса). На стр.224 монографии [4] отмечается, что
при разработке методики расчета газодинамических течений ставилась цель, чтобы
она позволяла рассчитывать двумерные течения, мало отличающиеся от одномерных
(плоских, цилиндрически симметричных или сферически симметричных), с небольшим
числом счетных точек по той пространственной переменной, от изменения которой
течение слабо зависит. Естественно, важно, чтобы и алгоритмы построения сетки
не мешали достижению этой цели.
Таким образом, желательно,
чтобы решения вида:
(3.5)
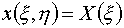 , , 
(3.6)
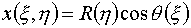 , , 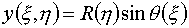
воспроизводились уравнениями, генерирующими сетки,
при произвольных функциях X(x), Y(h), q(x), R(h). Описанная выше
интерполяция, конечно же, такое тестирование выдерживает.
§ 4.
Корректирующие функционалы для функционала без якобиана.
Опорные вариационные функционалы (1.1)-(1.3) обладают
замечательным свойством: если задать
(4.1) 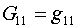 , , 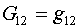 , , 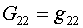 , ,
то они воспроизводят заданное невырожденное
отображение параметрического квадрата Q на заданную область W. Поэтому реализующие их
дискретные аналоги можно считать универсальными генераторами сеток.
При
расчете нестационарных задач с подвижными границами можно использовать сетку,
полученную на предыдущем шаге по времени, и условия (4.1) для расчета сетки на
новом шаге по времени. Казалось бы, это полностью решает проблему
конструирования сетки для нестационарной задачи. К сожалению, на практике дело
обстоит не так просто. При таком алгоритме рассматриваемые опорные функционалы
обнаруживают «равнодушие» к судьбе конструируемой сетки, поскольку для любой
сетки значение функционала близко к абсолютному
минимуму, отличаясь от него лишь на величину порядка
t из-за новых, слегка
изменивших положение, границ расчетной области. При отсутствии обратной связи
ухудшение качества сетки постепенно может приводить к необратимым
последствиям, вплоть до «аварийных».
Эмоциональное
слово «равнодушие», конечно, не очень уместно в математической работе. Автора
беспокоило, не означает ли это некорректность математической постановки
задачи.
Понятие
математической корректности включает три аспекта: существование, единственность
решения и его непрерывную зависимость от входной информации. Непрерывность
подразумевает, в классической e-d терминологии, что при
достаточно малом возмущении входных данных будет мало изменяться и искомое
решение.
Размышления
по поводу рассматриваемых алгоритмов приводят к следующему. На каждом отдельном
шаге нестационарного расчета можно предполагать, что в дифференциальной
постановке все в порядке со всеми тремя аспектами математической корректности.
При ее разностной реализации (с конкретным ограниченным числом интервалов разностной
сетки, не чрезмерным искривлением границ областей и т.п.) тоже должно быть все
в порядке, если исключить «патологические» вырожденные ситуации. (Автор
разделяет мнение коллеги Р.П.Федоренко, который как-то всерьез сказал, что «для
любого метода можно придумать специальный тест, который его погубит».
Добавим еще, что производственные расчеты – «поле чудес» для головоломок, про
которые можно сказать – нарочно не придумаешь).
Сложнее
обстоит дело с развитием процесса по времени t. Зависимость упомянутых
выше параметров e, d , характеризующих, скажем
так, надежность метода, от времени t может оказаться
неприемлемой для практики.
Чтобы
этого избежать (по крайней мере, для реального, по возможности большего
временного интервала), процесс построения сетки необходимо направлять. В
качестве такого рулевого механизма предлагается использовать
вариационные функционалы, корректирующие описанные выше, которым
доверяем основную, опорную роль.
Наиболее
просто это реализуется в аддитивной форме, когда корректирующие
функционалы подключаются в виде дополнительных слагаемых со своими весовыми
коэффициентами. Чтобы не нарушить требование о «разумных» значениях скоростей
движения узлов расчетной сетки, эти весовые коэффициенты 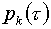 должны быть порядка должны быть порядка 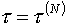 , где , где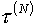 - текущий шаг по временной координате. Особенно важно это в
«переходные» моменты, когда происходит смена функционалов или изменение их
управляющих параметров (по причинам, в обсуждение которых вдаваться не будем). - текущий шаг по временной координате. Особенно важно это в
«переходные» моменты, когда происходит смена функционалов или изменение их
управляющих параметров (по причинам, в обсуждение которых вдаваться не будем).
После
этого, несколько пространного, вступления, обратимся к изложению конструкции
корректирующих функционалов. При этом очевидна необходимость согласования
их размерности с опорными функционалами. Поэтому в этом параграфе будем
рассматривать корректирующие функционалы для опорного функционала F* без якобиана, отложив F до
следующего §5.
Особый
интерес для практики расчетов представляют сетки, порождаемые ортогональными
отображениями. Они должны удовлетворять условию:
(4.2)
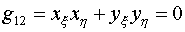
Заметим,
что «навязывание» этого условия, с учетом вариационных уравнений
Эйлера-Лагранжа, фактически означало бы, что две искомые функции 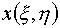 , , 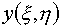 должны удовлетворять трем
уравнениям с соответствующими граничными условиями. Вопрос о существовании
такого решения далеко не ясен. Поэтому обычно говорят о конструировании «квазиортогональных»
сеток, в некотором смысле близких (или старающихся приблизиться)
к ортогональным. должны удовлетворять трем
уравнениям с соответствующими граничными условиями. Вопрос о существовании
такого решения далеко не ясен. Поэтому обычно говорят о конструировании «квазиортогональных»
сеток, в некотором смысле близких (или старающихся приблизиться)
к ортогональным.
Как
видно из (1.2), условие g12=0 превращает универсальный
опорный функционал F* в функционал 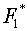 с энергией с энергией
(4.3) 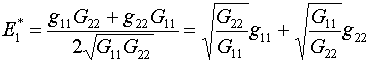
Очевидно,
что любая ортогональная сетка (конечно, удовлетворяющая нужным граничным
условиям) обеспечивает минимизацию функционала 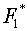 , т.е. удовлетворяет соответствующим ему уравнениям
Эйлера-Лагранжа. Но – увы! – не наоборот: минимизация , т.е. удовлетворяет соответствующим ему уравнениям
Эйлера-Лагранжа. Но – увы! – не наоборот: минимизация 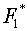 не обязательно дает
ортогональную сетку. Исключение составляют случаи, когда в результате
минимизации не обязательно дает
ортогональную сетку. Исключение составляют случаи, когда в результате
минимизации 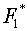 достигается его абсолютный
минимум. достигается его абсолютный
минимум.
Содержательным
примером является ситуация, которая рассматривалась в статье [6]. В ней для
расчета сеток были привлечены идеи конформных отображений.
Из
курсов теории функций комплексного переменного хорошо известна теорема Римана о
том, что существует конформное отображение произвольной плоской односвязной
области, ограниченной кусочно-гладкой кривой, на другую аналогичную область.
Оно определяется однозначно, если указать соответствие для трех
произвольных граничных точек (с соблюдением порядка их следования при обходе
границ областей).
Назначим
на границе односвязной области четыре «угловых» точки, т.е. реализуем ее
как криволинейный четырехугольник. Тогда существует (и определенно однозначно)
конформное отображение на нее прямоугольника с определенным отношением
сторон, при котором четырем «углам» области будут соответствовать четыре угла
прямоугольника. Отношение его сторон является конформным инвариантом
криволинейного четырехугольника, заранее неизвестно и подлежит определению в
ходе расчета. Кроме того, при этом должно быть установлено взаимно
однозначное соответствие между заданными
точками на контуре области и строго определенными точками на контуре
прямоугольника.
Введем
дополнительное растяжение координат, чтобы превратить конформный прямоугольник
в канонический единичный квадрат Q. Суперпозиция двух этих
отображений и будет одним из возможных решений задачи о построении сетки в
дифференциальной постановке.
В
качестве линий сетки были выбраны образы прямолинейных отрезков на
прямоугольнике, соединяющих точки на его противоположных сторонах,
соответствующие заданным узлам на контуре области. Точки пересечения этих двух
возникающих семейств линий и представляют искомые узлы сетки (точнее, один из
возможных ее примеров).
То
обстоятельство, что вместо допустимого по теореме Римана соответствия трех
точек «навязывается» соответствие всех узловых точек на контуре,
приводит к следующему. Множество допустимых функций при минимизации функционала
оказывается настолько узким, что не содержит конформного отображения (как
правило, за исключением редких ситуаций). Между тем именно оно обеспечило бы абсолютную
минимизацию функционала. Обычно же достигаемый минимум абсолютным не является.
Мы
столь подробно остановились на этом примере, поскольку он иллюстрирует
любопытную ситуацию: вопрос о существовании невырожденных сеток и
алгоритмов для их построения никогда сомнению не подвергался.
Функционал
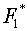 , определенный (4.3), представляет один из возможных примеров
корректирующих функционалов для опорного функционала F* без якобиана. , определенный (4.3), представляет один из возможных примеров
корректирующих функционалов для опорного функционала F* без якобиана.
Наряду
с ним можно рассматривать и функционал 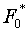 с энергией с энергией
(4.4)
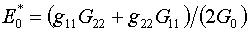 , ,
который предлагался на стр.11 работы [1].
Заметим, что
(4.5) 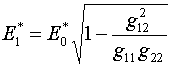 , ,
и на любой ортогональной сетке (4.3) и (4.4)
просто совпадают. Представляется логичным заключить, что 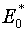 более «энергично»
реагирует на уклонение от ортогональности и стимулирует «квазиортогональность».
В силу самого смысла корректирующего функционала, по-видимому, это следует
рассматривать как аргумент в его пользу. более «энергично»
реагирует на уклонение от ортогональности и стимулирует «квазиортогональность».
В силу самого смысла корректирующего функционала, по-видимому, это следует
рассматривать как аргумент в его пользу.
Напомним,
что, как описано в [1], подключение 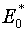 с управляющим
параметром с управляющим
параметром 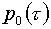 достигается предельно
просто: заменой формул (1.6)-(1.7) на следующие: достигается предельно
просто: заменой формул (1.6)-(1.7) на следующие:
(4.6)  , , 
с сохранением 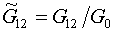 , , 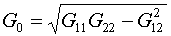 . .
Очевидное, ввиду (4.5), аналогичное изменение при
подключении 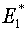 приводить не будем. приводить не будем.
В
качестве еще одного возможного примера корректирующего функционала рассмотрим
(4.7)
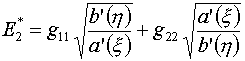
Здесь a(x),b(h) – те управляющие функции,
которые описаны в §3,
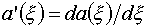 , , 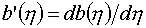 . .
В частном случае
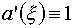 , , 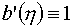 реализуются
гармонические сетки. Поэтому условно можно говорить об обобщенных гармонических
сетках. Дополнительное подключение и такого функционала с коэффициентом реализуются
гармонические сетки. Поэтому условно можно говорить об обобщенных гармонических
сетках. Дополнительное подключение и такого функционала с коэффициентом 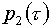 сводится к замене
формул (4.6) на следующие: сводится к замене
формул (4.6) на следующие:
(4.8)  , ,
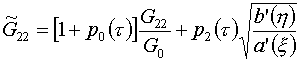
В дискретной постановке последние сомножители
реализуются в разностной форме. Для четырех ячеек шаблона, описанного в §1, это
сводится к дополнительным слагаемым в формулах 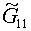 и и 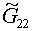 с коэффициентом с коэффициентом 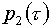 : :
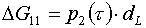 , , 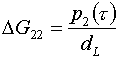
(4.9) 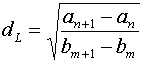 для L=1, для L=1, 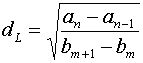 для
L=2, для
L=2,
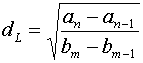 для L=3 , для L=3 , 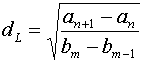 для L=4. для L=4.
Условно
можно говорить, что 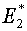 работает в пользу
соблюдения сеткой избранных исполнителем законов расстановки узлов на границах.
Стоит ли на них «настаивать» - это уже другой, независимый вопрос (см.
ниже, п. 6 в §6). работает в пользу
соблюдения сеткой избранных исполнителем законов расстановки узлов на границах.
Стоит ли на них «настаивать» - это уже другой, независимый вопрос (см.
ниже, п. 6 в §6).
Отметим,
что соответствующие разностные уравнения для функционала с плотностью энергии
(4.7) среди своих решений содержат произвольные неравномерные прямоугольные
сетки (3.5), а при некоторых условиях и неравномерные полярные сетки (3.6). Как
уже упоминалось в §3, этот вопрос исследовался в работе [9].
Этими
примерами мы ограничим описание корректирующих функционалов для вариационного
опорного функционала без якобиана. Очевидно, что они позволяют сохранить его
достоинства при очень незначительных изменениях расчетных формул.
Еще один интересный пример корректирующего
функционала мог бы представлять функционал с плотностью энергии отображения
(4.10) 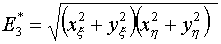
Он имеет нужную размерность 2 по переменным х
и у, но является не квадратичным, а нелинейным. Поэтому его реализацию
целесообразно осуществлять только с «замораживанием» коэффициентов. Это
«замораживание» делается вполне успешно (в отличие от описанного в §2 для
опорного функционала с якобианом). Однако оно будет иметь результатом как раз
функционал (4.3), а поэтому не привнесет ничего нового. Отметим, что функционал
с плотностью энергии (4.10) рассматривался в [4] на стр.234-235 со ссылкой на
более раннюю работу автора.
§ 5. Корректирующие функционалы для функционала с якобианом.
Прежде
всего отметим, что они должны быть безразмерными по переменным х,у. С
учетом якобиана в знаменателе (1.3) на роль корректирующего годится функционал
с плотностью энергии
(5.1) 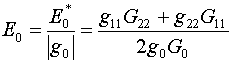
аналогичный (4.4) и рассматривавшийся в [1] на
стр.18, а также функционал, аналогичный (4.7) с плотностью
(5.2) 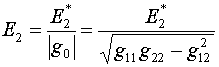
Легко
убедиться, что их подключение в качестве корректирующих опорный функционал с
якобианом осуществляется точно таким же образом, как описано в §4, т.е.
посредством замены формул для 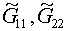 соответственно на
(4.6) и (4.8) или (4.9) в разностной реализации. соответственно на
(4.6) и (4.8) или (4.9) в разностной реализации.
Если безразмерности функционала (4.10) достигать
также с помощью якобиана, то это приводит к плотности энергии
(5.3)
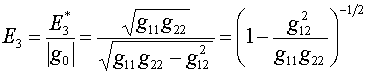
Возможно,
такой функционал тоже заслуживает внимания в качестве корректирующего, но он
требует разработки новых расчетных формул. Как мы видели в §2, это достаточно
трудоемкая процедура, и мы ей заниматься не будем, ограничившись упоминанием о
такой возможности.
Гораздо
больший интерес мы собираемся проявить к возможности использовать в качестве
корректирующего модификацию вариационного функционала, который рассматривался в
работах академика РАН А.Ф.Сидорова и его учеников. Первой публикацией его
двумерного варианта, по-видимому, следует считать [10]; позже см. [12],[14]. Хотя
для него существует и некоторый дифференциальный аналог, целесообразно сразу
рассматривать его дискретную форму:
(5.4) 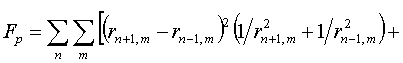
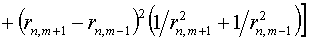
Здесь
(5.5) 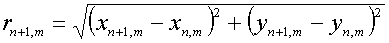
представляет расстояние между центральным узлом шаблона и
соседним узлом  . .
Аналогично определяются и остальные величины.
В отличие от предыдущего,
суммирование производится по узлам сетки, а не по ячейкам.
Минимизация
функционала ориентирована на получение сеток, близких к равномерным. Поэтому он
был назван критерием равномерности.
Автору
представляется целесообразным вместо (5.4) в качестве критерия равномерности
использовать другую формулу:
(5.6)
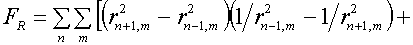
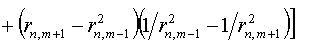
Заметим, что для любых r1, r2 (r1>0, r2>0) будем иметь:
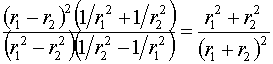
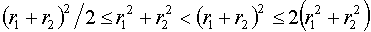
Применяя эти оценки к каждому из слагаемых сумм
(5.4) и (5.6), обнаруживаем, что критерии (5.4) и (5.6) энергетически эквивалентны:
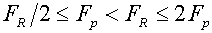
Следовательно, они равноценны с точки зрения
вариационного подхода.
Но
не содержащая радикалов форма (5.6) предпочтительнее для вычисления первых и
вторых производных функционала, которые
потребуются для итерационного процесса. Дополнительно заметим, что
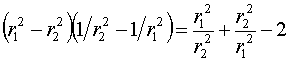
Постоянная величина –2 не будет играть никакой роли
при выводе разностных уравнений, и ее можно опустить.
Наконец,
для обеспечения более широких возможностей функционала (5.6) рассмотрим такую
его модификацию:
(5.7) 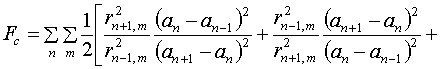
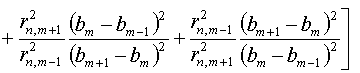
Здесь  - те же значения
управляющих функций a(x), b(h), которые были описаны в §3 и
уже использовались в §4. Множитель 1/2
удобно ввести для получения будущих разностных уравнений, точно так же,
как и в формулах (1.2)-(1.3). Этот обобщенный функционал должен успешно
работать для произвольных, а не только равномерных, расстановок граничных
узлов сетки на
контуре области. - те же значения
управляющих функций a(x), b(h), которые были описаны в §3 и
уже использовались в §4. Множитель 1/2
удобно ввести для получения будущих разностных уравнений, точно так же,
как и в формулах (1.2)-(1.3). Этот обобщенный функционал должен успешно
работать для произвольных, а не только равномерных, расстановок граничных
узлов сетки на
контуре области.
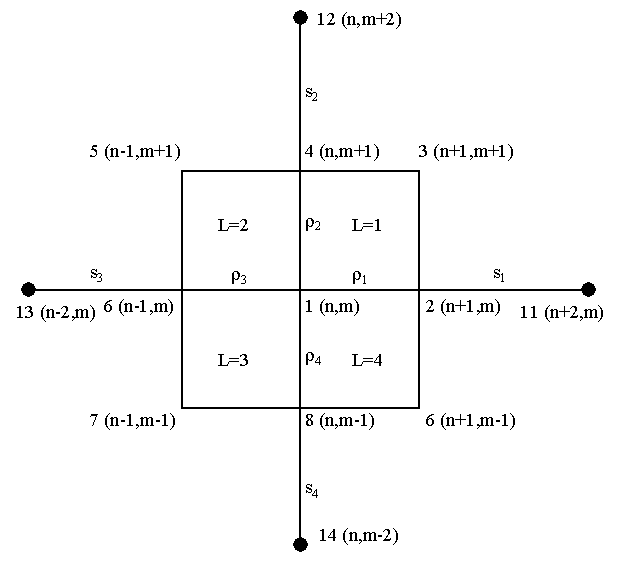
Рис. Расширенный шаблон для
функционала Fc.
Функционал является
безразмерным и к опорному функционалу F подключается с
коэффициентом 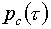 . .
Обратим
также внимание, что, в отличие от описанного в §1, для получения разностных
уравнений в узле с номером (n,m)
прежний девятиточечный шаблон (1.8) должен дополняться еще четырьмя узлами (см.
рис. на стр. 26), для которых мы сразу вводим простые номера:
(5.8) 11-(n+2,m), 12-(n,m+2), 13-(n-2,m), 14-(n,m-2).
Приступим
к получению необходимых расчетных формул для величин
(5.9)
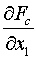 , , 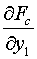 , , 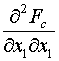 , , 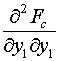 , ,  . .
Прежде
чем выписывать достаточно громоздкую формулу, учитывающую все слагаемые
функционала, содержащие координаты (х,у)1, введем упрощающие
обозначения (см. рис. ):
(5.10)
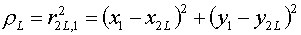
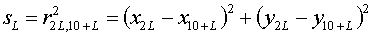
Кроме того, чтобы сделать наглядной запись и
разделение всех членов предстоящих формул по четырем направлениям, введем
обозначения:
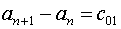 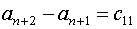
(5.11)
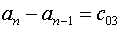 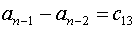
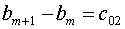 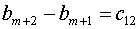
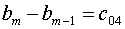 
С использованием обозначений (5.10)-(5.11) часть
функционала (5.7), зависящая от координат (х,у)1 , может быть
записана в виде:
(5.12) 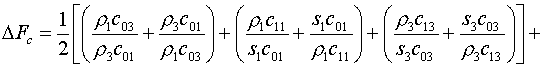
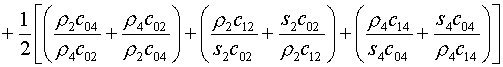
Как видно из (5.10) и (5.11), в этой формуле от
координат (х,у)1 зависят только величины 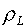 . Поэтому, дифференцируя (5.12) по х1,
получим: . Поэтому, дифференцируя (5.12) по х1,
получим:
(5.13)
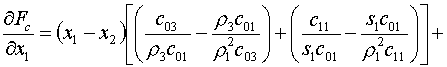
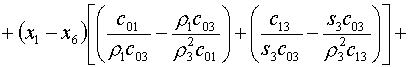
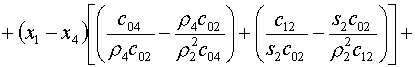
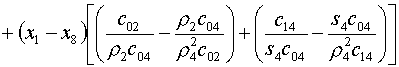
Введем обозначения для коэффициентов этой формулы:
(5.14) 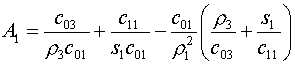
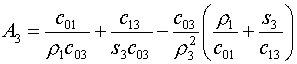
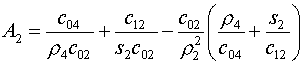
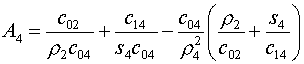
Тогда (5.13) перепишется в виде:
(5.15) 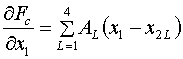 , ,
и аналогичная формула выписывается для производной
по у1:
(5.16) 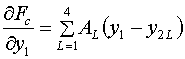 . .
Для вторых производных получим следующие формулы:
(5.17)

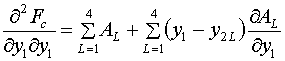
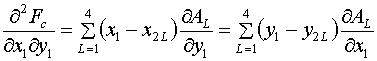
Осталось получить производные AL по х1 и у1.
(5.18) 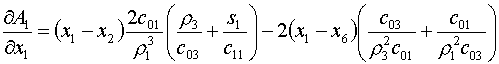
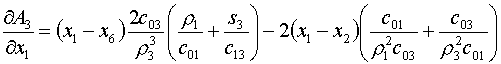
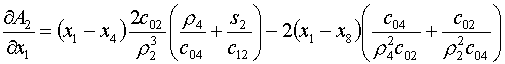
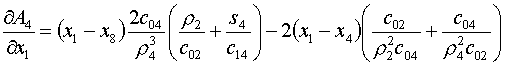
Формулы для 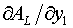 получаются заменой в
них х на у, т.е. с теми же коэффициентами при (у1-у2L). получаются заменой в
них х на у, т.е. с теми же коэффициентами при (у1-у2L).
Работа
по получению формул для производных (5.9) завершена. В силу аддитивного
подключения функционала Fc необходимо присуммировать полученные значения
с коэффициентом 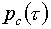 к описанным в конце §2
значениям, может быть уже корректированным и другими функционалами. к описанным в конце §2
значениям, может быть уже корректированным и другими функционалами.
Теперь
следует обратить внимание на то обстоятельство, что функционал Fc использует 13-точечный шаблон: девятиточечный расширяется «на все
четыре стороны». Это потребует специальных мер при получении уравнений в
приграничных узлах (расположенных на первой линии вдоль всех границ). Эти меры
состоят в исключении несуществующих слагаемых в формуле функционала
(5.7) и, соответственно, в формулах для производных (5.9).
На
этом мы закончим изложение примеров корректирующих функционалов для опорного
функционала с якобианом. Заметим, что в аддитивном варианте формально возможно
подключение в качестве корректирующего произвольного безразмерного
функционала в дискретной форме, позволяющей вычислить первые и вторые
производные по координатам узла разностной сетки. Описанный пример с
функционалом (5.7) хорошо это иллюстрирует.
§ 6. Некоторые соображения общего характера.
Автор
считает необходимым высказать некоторые соображения, касающиеся возможного
использования вариационных функционалов, которые описаны в настоящей работе,
для конструирования двумерных сеток при расчете нестационарных задач.
1. Предложенных корректирующих функционалов
несколько. Хотя представлено, конечно, далеко не все, что накоплено многими
авторами за многие годы и, возможно, полезно для дела. В качестве примера
упомянем «квазиизометрические» отображения (см., напр., [11] и главу 2 в
[12]). Они представляют интересный класс, для которого доказываются теоремы о
существовании и единственности решения, а получающиеся сетки могут быть специально
интересны для практики.
Второй пример – вариационные
функционалы, ориентированные на получение адаптивных сеток. Они имеют
целью, например, адаптацию сетки к заданной функции или некоторой
функции, получаемой в процессе решения нестационарной задачи. Одна из
возможных конструкций такого функционала предложена в работе [2]. После
принятия решения о выборе управляющей функции и вычисления ее значений в узлах
расчетной сетки практическая реализация сводится лишь к усложнению расчетных
формул при вычислении первых и вторых производных разностного функционала для
реализации итерационных процессов.
2. Идея использования при
расчете сеток комбинации из нескольких вариационных функционалов со своими
весовыми коэффициентами, конечно, не нова. В качестве примера упомянем работу
[10], а также работу [13], после публикации которой такое направление получило
широкое распространение. Автор не ставит целью давать сколько-нибудь подробную
библиографию, а поэтому этими двумя ссылками и ограничимся. Отношение автора к
этому варианту действий всегда было настороженным (см, напр., [9],
стр.22) по следующим причинам. Во-первых, вопрос о назначении весовых
коэффициентов, как правило, оставался открытым. Между тем, если в задаче о
построении сетки в отдельно взятой области возможно какое-то
экспериментирование, то при решении нестационарной задачи, особенно с
непредвиденно деформирующимися границами, такая возможность практически
исключена.
Между тем, как прямо
отмечается, например, в [14] на стр.19, «варьирование весов в широких пределах
может привести к неустойчивости численной процедуры решения уравнений».
Во-вторых, разные цели,
которые ставятся при подключении отдельных функционалов (говоря условно, в
терминах, которые употреблялись, - гладкость, ортогональность, равномерность,
адаптация к функции и т.п.), могут
вступить в конфликт друг с другом. Авторы таких предложений явно рассчитывают
на сценарий Агафьи Тихоновны – невесты из «Женитьбы» Н.В.Гоголя: «Если бы губы
Никанора Ивановича да приставить к носу Ивана Кузьмича, да взять сколь-нибудь
развязанности…, да, пожалуй, прибавить к этому еще дородности…». Между тем,
скорее уж события будут развиваться, как в басне И.А.Крылова «Лебедь, рак и
щука» или по русской поговорке: «За двумя зайцами погонишься – ни одного не
поймаешь».
3. Не противоречит ли себе
автор, предлагая целый набор корректирующих функционалов да еще добавляя, что
он неполный? Нет, не противоречит.
Во-первых, предлагается лишь
некоторый набор «продуктов», из которых потребитель мог бы приготовить «блюдо»
по своему вкусу. Никакая хозяйка не положит нужную почти всегда «соль»,
если готовится нечто «сладкое».
Во-вторых, предприняты
определенные, достаточно серьезные усилия, направленные на то, чтобы
функционалы не противоречили друг другу. Например, хотя бы с точки
зрения воспроизведения произвольной неравномерной прямоугольной или полярной
сетки. Именно поэтому мы пошли на введение в уже достаточно громоздкий
функционал (5.6) еще и управляющих параметров, усложнив его до (5.7).
В-третьих, в процессе
апробации и практической эксплуатации, по-видимому, произойдет «искусственный
отбор»: какие-то из корректирующих функционалов «оправдают надежды», а какие-то
нет. Возможно, список сократится настолько, что назначение корректирующих
функционалов станет почти детерминированным.
Наконец, и это наиболее
важная мысль, предполагается доминирующая роль опорных функционалов, а
корректирующие функционалы – только «приправы», добавляемые, возможно, в
«гомеопатических» (но достаточных) дозах.
4. Опорные функционалы выбраны
потому, что они универсальны: могут точно воспроизводить произвольную
невырожденную сетку. Это очень важно с точки зрения обеспечения «разумных» скоростей
движения узлов сетки. И об этом нужно очень старательно заботиться,
обеспечивая малые величины невязок разностных уравнений для сетки. Не
надеясь, например, на малость погрешности аппроксимации при формальной
прямой замене производных разностями в дифференциальных уравнениях
Эйлера-Лагранжа (или более простых следствиях из этих уравнений, что
сэкономило бы вычислительную работу). При нестационарных расчетах с очень
малыми шагами по времени (например, в газодинамических задачах для
трехтемпературной модели, да и вообще при почти любых расчетах по явным
схемам из-за требований устойчивости) гарантировать допустимые скорости
узлов сетки достаточно трудно.
5. Роль корректирующих
функционалов состоит в том, чтобы служить лоцманами в необозримом море
возможных сеток. Слова о «гомеопатических дозах» не должны создавать иллюзию,
что под сенью опорного функционала пройдет любой корректирующий функционал.
Наоборот, для корректирующего функционала особенно важна математическая
корректность – именно он определит, в каком направлении пойдет изменение
качества сетки на огромном числе временных шагов нестационарного процесса.
Поэтому так важны теоремы о
существовании и единственности решения, которые были упомянуты выше в связи с
«квазиизометрическими» сетками. Или хотя бы уверенность в том, что
реализуется именно такая ситуация. В связи с этим приходится с грустью обратить
внимание на высказывание по поводу функционала (5.4) или его комбинаций с
другими функционалами в [14] на стр.17: «К сожалению, теоремы о существовании
решения, единственности его и корректности поставленных задач, в отличие от
одномерных задач, в настоящее время неизвестны. Лишь формальные соображения и
большой опыт расчетов сеток подтверждают гипотезу о существовании таких
теорем».
6. Наш интерес к выбору в
качестве корректирующего функционала Fc вызван следующим. Как уже отмечено, при
решении нестационарных задач с использованием явных разностных схем
(например, газодинамических задач по известному и пользующемуся популярностью
методу Годунова) одной из серьезных практических трудностей является малое
значение шага t по временной координате.
Поэтому, по крайней мере для той расчетной области, которая «диктует» значение t для всей задачи, можно
попытаться, пожертвовав другими интересами, постараться его увеличить.
Значение t определяется специальным
критерием, зависящим и от локальных значений поля газодинамических величин, и
от геометрических размеров «худшей» из ячеек. Учитывая последнее, для
упомянутой области может представлять интерес равномерная сетка,
независимо от того, по каким законам расставлены узлы на ее границах. К такой
сетке можно приблизиться, используя в качестве корректи-рующего
функционала Fc . Для этого управляющие параметры 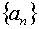 , , 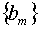 следует назначать не
по формулам (3.3), а по простейшим (3.1). следует назначать не
по формулам (3.3), а по простейшим (3.1).
Есть и вторая возможность –
управляющие параметры 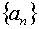 , ,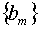 убираются как ненужная «обуза». Вместо обобщенного
функционала (5.7) реализуется более простой критерий равномерности (5.6). Это
заметно упростит и расчетные формулы, описанные в §5. Однако подчеркнем, что
тогда не приходится рассчитывать на воспроизведение сеток вида (3.5)-(3.6). убираются как ненужная «обуза». Вместо обобщенного
функционала (5.7) реализуется более простой критерий равномерности (5.6). Это
заметно упростит и расчетные формулы, описанные в §5. Однако подчеркнем, что
тогда не приходится рассчитывать на воспроизведение сеток вида (3.5)-(3.6).
Заметим, что
«индивидуальный» подход может быть реализован, если предусмотреть задание
весовых коэффициентов 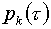 отдельно для каждой
области, как обычно и делается. отдельно для каждой
области, как обычно и делается.
Все сказанное может быть
отнесено и к функционалам с плотностями (4.7) и (5.2), условно названным
обобщенными гармоническими.
7. При расчете нестационарной
задачи, как правило, у исполнителя практически нет возможности вмешиваться в
расчет. За него это делает ЭВМ, причем, к сожалению, зачастую слишком поздно.
Приходится возвращаться назад (хорошо, если не к исходному моменту) и менять
принятые решения. Это почти всегда было болезненно для сетки. В предлагаемой
технологии заложены определенные возможности, позволяющие «смягчать» переходы к
другим функционалам или другим управляющим параметрам. Насколько они эффективны
и в какой степени могут быть автоматизированы, автор обсуждать пока не готов.
8. Собственно, из всех управляющих параметров
главными неопределенными остались р(t), с которыми подключаются те
или иные корректирующие функционалы. Для них на стр.12 работы [1] рекомендована
формула:
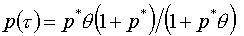 , ,
где 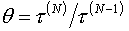 - отношение текущего и
предыдущего шага по времени. p* - тот безразмерный коэффициент, который
исполнитель наметил для подключения конкретного корректирующего
функционала (или его отключения, если задается p*=0). - отношение текущего и
предыдущего шага по времени. p* - тот безразмерный коэффициент, который
исполнитель наметил для подключения конкретного корректирующего
функционала (или его отключения, если задается p*=0).
Смысл
этой формулы, по сравнению с простейшей 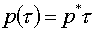 , состоит в следующем. Как легко видеть, , состоит в следующем. Как легко видеть,
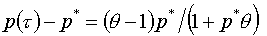 . .
Если задача считается
«спокойно», то 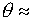 1 и реализуется 1 и реализуется 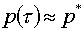 , как и намечалось. , как и намечалось.
Если 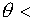 1 - «сигнал неблагополучия», то р(t) уменьшается по сравнению с р*
(естественно, в любом случае оставаясь положительной величиной). 1 - «сигнал неблагополучия», то р(t) уменьшается по сравнению с р*
(естественно, в любом случае оставаясь положительной величиной).
Если 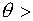 1, то можно попробовать р(t) увеличить, но «не слишком
увлекаясь»: при 1, то можно попробовать р(t) увеличить, но «не слишком
увлекаясь»: при 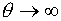 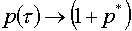 . .
Если 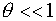 - «чрезвычайное
происшествие»: - «чрезвычайное
происшествие»: 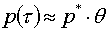 , т.е. практически отключаются корректирующие функционалы и
работают только опорные, избавляя сетку от управляющих, которые подозреваются в
«некомпетентности». , т.е. практически отключаются корректирующие функционалы и
работают только опорные, избавляя сетку от управляющих, которые подозреваются в
«некомпетентности».
Если действительно «виноваты»
они (например, значение р* задано неудачно), то ситуация постепенно
должна автоматически исправиться (ведь происходит неполное отключение и
имеется возможность увеличения р(t), как описано выше), если,
конечно, «беда» не зашла слишком глубоко. Ну а уж если нет, то принимать меры
(или расхлебывать последствия) придется исполнителю.
9. Одной из возможных причин неприятностей, о
которых шла речь, могут быть недопустимые (систематически завышаемые или
занижаемые) величины скоростей узлов сетки. Как отмечалось в [1] на стр.26,
казалось бы естественным требовать, чтобы скорости «внутренних» узлов были
заключены в пределах, в которых изменяются скорости «граничных». Однако такое требование практически едва ли
выполнимо. Поэтому реально можно говорить только о том, что алгоритм построения
сеток должен непрерывно обеспечивать адекватное изменение положения
узлов внутри подвижных границ. Выше (в п.4) мы условно назвали это «разумными»
скоростями движения узлов сетки.
В §2 работы [1] были
приведены рассуждения, которые дают основания надеяться на такие скорости при
достаточно малых значениях управляющих параметров 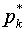 . В то же время
параметры . В то же время
параметры 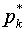 не могут быть слишком
малыми, иначе они не выполнят свою корректирующую роль. не могут быть слишком
малыми, иначе они не выполнят свою корректирующую роль.
Заметим, что в случае, если в
ходе итерационного процесса узел движется «прямолинейным курсом», его
сдвиг, а, следовательно, и величина скорости накапливается. Хотя, как
правило, курс узла носит «зигзагообразный» или «спиралевидный» характер.
Заслуживает внимания, что не исключен и такой вариант: при достаточно малых
значениях шага по времени t итерационный процесс можно
ограничить одной итерацией, поскольку уже ее результат обеспечит
адекватное изменение положения узлов при сохранении гладкости сетки. Пока можно всерьез говорить только о
необходимости численного эксперимента и накопления опыта.
Заключение
Прежде всего, как дополнение к
высказанным соображениям, автор считает нужным обратить внимание на заключение
в работе [1]. В нем изложены положения, от которых автор отказываться не
собирается, но повторять их еще раз нет необходимости.
В
порядке исключения повторим (см. [1], стр.30), что «автор далек от того, чтобы
претендовать на создание полностью автоматизированных алгоритмов построения
сеток, позволяющих считать нестационарные задачи без вмешательства
исполнителя». Как бы заманчиво это ни звучало с точки зрения запросов практики.
Такая
позиция объясняется изначальной оценкой возможностей регулярных
подвижных сеток, которые автор в меру сил и способностей старался увеличить.
Приведем в качестве аналогии следующий пример. Когда происходит автомобильная
авария, в некоторых ситуациях следует приговор: автомобиль восстановлению не
подлежит. Такое же может происходить и с регулярными сетками. Иногда просто
диву даешься, как это задача считается при той сетке, которую видит
исполнитель. Более того, иногда почти невозможно представить, что приемлемая
сетка вообще существует.
Собственно,
это и было главным аргументом в пользу развития технологий нерегулярных
сеток, которые, конечно же, потенциально обладают гораздо большими
возможностями. Но и работать с ними и обосновывать приемлемую точность (или
хотя бы достоверность) результатов труднее, чем для регулярных сеток (хотя и
для них это нелегко). Но ведь решать задачи нужно. Вот и приходится спасать
ситуацию всеми доступными способами и средствами. (Даже не обязательно допустимыми.
Такое утверждение пусть останется на совести автора как явный камень в огород
борцов на «безавостность» программ).
Автор
выражает благодарность М.С.Гавреевой за помощь в оформлении работы.
Список литературы
1.
Прокопов Г.П. Вариационные методы расчета двумерных
сеток при решении нестационарных задач.// М., Препринт ИПМ им.М.В.Келдыша РАН,
2003, №4, 32 стр.
2. Иваненко С.А. Управление
формой ячеек в процессе построения сеток.// ЖВМ и МФ, 2000, т.40, № 11,
1662-1684.
3. Иваненко С.А. О
существовании уравнений для описания классов невырожденных криволинейных
координат в произвольной области //ЖВМ и МФ, 2002, т.42, №1, 47-52.
4. Численное решение
многомерных задач газовой динамики. Под общей редакцией С.К.Годунова.//М.,
«Наука», 1976, 400 стр.
5.
Годунов С.К., Прокопов Г.П. Об использовании подвижных
сеток в газодинамических расчетах.// ЖВМ и МФ, 1972, т.12, №2, 429-440.
6. Годунов С.К., Прокопов Г.П.
О расчетах конформных отображений и построения разностных сеток.// ЖВМ и МФ,
1967, т.7, №5, 1031-1059.
7. Антонова Р.Н., Прокопов Г.П.
Сравнение нескольких вариантов построения двумерных разностных сеток
посредством интерполяционных формул.// ВАНТ, Сер.: Мат. моделир. физ.
процессов, 1994, вып.1, 78-84.
8.
Томас П.Д., Миддлкофф Дж.Ф. Прямое управление
распределением узловых точек в сетках, порождаемых решениями эллиптических
уравнений.// Ракет. техн. и косм., 1980, №7, 55-61.
9.
Прокопов Г.П. Некоторые общие вопросы конструирования
алгоритмов построения разностных сеток.//ВАНТ, Сер.: Матем. моделир. физ.
процессов, 1988, вып.1, 3-13.
10.
Сидоров А.Ф., Шабашова Т.И. Об одном методе расчета оптимальных
разностных сеток для многомерных областей.// Численные методы механики сплошной
среды. Новосибирск, ИТПМ СО АН СССР, 1981, т.12, №5, 106-124.
11.
Godunov S.K., Zhukov V.T.,
Feodoritova O.B. An algorithm for construction of quasi-isometric grids in
curvilinear quadrangular regions.// Proc. 16-th Internal. Conf. on Numer. Meth.
Fluid Dynamics. Arcachon, France, July 6-10, 1998, p.48-54.
12.
Advances
in Grid Generation. Edited by Olga V.Ushakova, Nova Science Publishers, 2005.
13.
Brackbill J.U., Saltzman
J.S. Adaptive zoning for singular problems in two dimensions.// J. Comp. Phys.
1982, 46, 342-368.
14.
Сидоров А.Ф., Ушакова О.В., Хайруллина О.Б. Вариационные методы
построения оптимальных сеток.// Препринт Инст. матем. и мех. УрО РАН,
Екатеринбург, 1997, 50 стр.
|