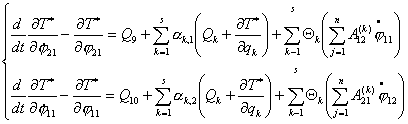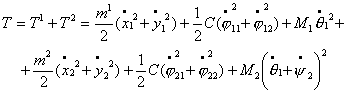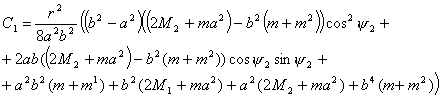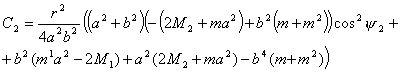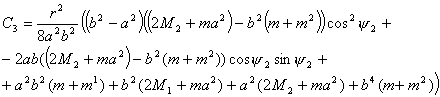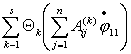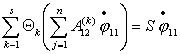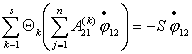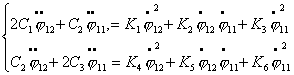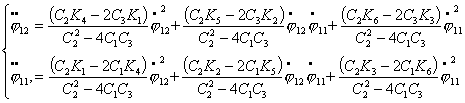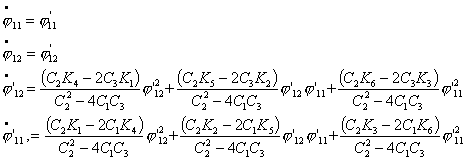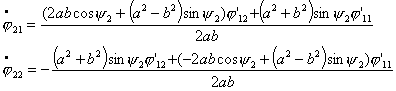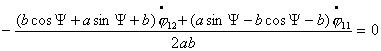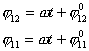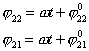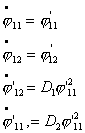Аннотация
Дано описание каждого элемента цепочки подвижных роботов и модели в целом. Построены уравнения
Воронца, которые используются для вывода уравнений цепочки мобильных роботов для произвольного
числа элементов цепочки. Рассмотрены некоторые частные решения полученных уравнений.
Abstract
The description of model of a chain of mobile robots is given. Voronec equations, which are
used for a conclusion of the equations of the chain of mobile robots for any number of
elements of the chain, are constructed. Some particular solutions of the received equations
are considered.
Содержание
Введение…………………………………………………………………………………3
1.Описание механической системы и
постановка задачи…………………………....3
2.Уравнения движения для двух тележек……………………………………………..8
3.Частные решения для двух тележек.
Свободные (баллистические) движения…15
4.Уравнения движения для n тележек………………………………………………..20
5.Частные решения для n тележек. Свободные (баллистические) движения ….…26
Заключение…………………………………………………………………………….30
Список
литературы……………………………………………………………………31
Введение
Цепочка мобильных
объектов «робопоезд» – это сложная неголономная система. Задача об управлении
движением такой системы имеет важное теоретическое и прикладное значение.
Исследования в этой области стимулируются многочисленными прикладными задачами,
возникающими в процессе жизнедеятельности человека. К ним можно отнести,
например, задачу автоматизированной транспортировки грузов (аэропорты, вокзалы,
гипермаркеты, склады) или работу в опасной
среде или в среде с заранее неизвестными свойствами (доставка в опасную зону
многомодульного состава для выполнения различных операций, связанных с риском
для жизни человека).
В настоящее время активно развивается
целый класс задач, в которых рассматриваются различные многозвенные,
змееподобные системы [1-3]. К ним же относится рассматриваемая в данной работе
модель.
Успешное функционирование любой робототехнической системы невозможно
без построения математической модели и изучения её свойств. Данная работа
посвящена описанию математической модели цепочки мобильных систем «робот-тягач
с прицепом» и выводу уравнений движения такой системы. Построены частные
решения полученных уравнений.
1. Описание
механической системы и постановка задачи.
Рассматривается система, состоящая из объектов,
которые мы будем называть «тележками». Каждая тележка представляет собой
невесомую ось L длины 2b и перпендикулярную ей невесомую ось длины 2a, на
которую насажены два одинаковых колеса. Каждое колесо является плоским однородным
диском массы m, радиуса r, перпендикулярным оси тележки. Кузов тележки имеет
массу 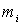 и может перемещаться
только параллельно плоскости движения. Вообще говоря, массы кузова у разных
тележек могут быть различными. Будем считать, что центр масс тележки совпадает
с центром оси колес. Тележки соединены друг с другом при помощи шарнира.
Активной назовем тележку, вращением колес которой можно управлять при помощи
электродвигателей. Пассивной назовем тележку без управления. Тележки движутся
по абсолютно шероховатой горизонтальной плоскости в однородном поле силы тяжести. и может перемещаться
только параллельно плоскости движения. Вообще говоря, массы кузова у разных
тележек могут быть различными. Будем считать, что центр масс тележки совпадает
с центром оси колес. Тележки соединены друг с другом при помощи шарнира.
Активной назовем тележку, вращением колес которой можно управлять при помощи
электродвигателей. Пассивной назовем тележку без управления. Тележки движутся
по абсолютно шероховатой горизонтальной плоскости в однородном поле силы тяжести.
Пусть OXYZ -
неподвижная система координат, плоскость OXY совпадает с горизонтальной плоскостью; C1 … Сn - соответственно центры осей тележек; C1xyz … Cnxyz - системы координат, жестко связанные с тележками
(осями тележек), 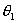 , , 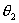 ,..., ,...,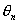 - углы поворота осей L соответствующих тележек вокруг вертикали, в
дальнейшем кроме углов - углы поворота осей L соответствующих тележек вокруг вертикали, в
дальнейшем кроме углов 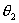 ,..., ,...,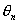 будем рассматривать углы поворота оси L i-й
тележки ( будем рассматривать углы поворота оси L i-й
тележки (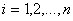 ) относительно оси L
предыдущей тележки ) относительно оси L
предыдущей тележки 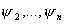 , где , где 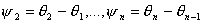 , x1, y1 ,…,xn, yn - координаты точек C1,…,Сn
соответственно, , x1, y1 ,…,xn, yn - координаты точек C1,…,Сn
соответственно, 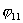 , , 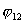 , … , , … , 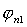 , , 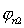 - углы поворота колес
соответствующих тележек относительно их осей, отсчитываемые от проекции
положительного направления оси Cz на плоскость
колеса против часовой стрелки (если смотреть в сторону вектора - углы поворота колес
соответствующих тележек относительно их осей, отсчитываемые от проекции
положительного направления оси Cz на плоскость
колеса против часовой стрелки (если смотреть в сторону вектора 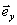 ). ).
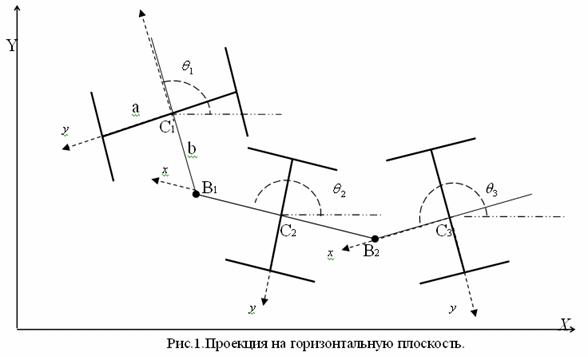
На рис.1 изображена проекция описанной системы на
горизонтальную плоскость.
На i-ю тележку в точках 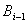 , , 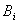 действуют неизвестные
силы реакции соответственно - действуют неизвестные
силы реакции соответственно -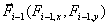 и и 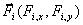 . Условие качения без проскальзывания обуславливает наличие
неинтегрируемых связей. . Условие качения без проскальзывания обуславливает наличие
неинтегрируемых связей.
Обобщенные координаты q = (x1, y1,…, xn, yn; 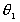 , ,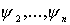 ; ; 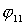 , , 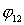 ,…, ,…, 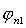 , , 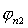 ) определяют положение
механической системы в каждый момент времени. ) определяют положение
механической системы в каждый момент времени.
Рассмотрим связи, наложенные на одну тележку, как на
элемент цепочки тележек. Так как плоскость абсолютно шероховатая, то скорость
точек 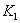 , , 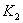 контакта соответствующих колес с плоскостью
должна быть равна нулю. Используя теорему Эйлера для расчета скорости точки
контакта, получаем уравнения дифференциальных связей: контакта соответствующих колес с плоскостью
должна быть равна нулю. Используя теорему Эйлера для расчета скорости точки
контакта, получаем уравнения дифференциальных связей:

или
 (1.1)
(1.1)
Из полученных уравнений видно, что эти связи, наложенные
на систему, неголономны [5].
Кроме того, на тележку в цепи наложены
связи, определяемые сцепкой с соседними тележками. А именно, условие что любые две соседние тележки имеют одну общую
точку - точку сцепки. Это условие из простых геометрических соображений для
двух тележек i и i+1 имеет вид:
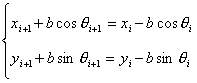 , ,
или в
дифференциальной форме:
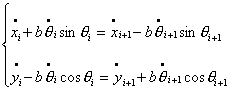 (1.2)
(1.2)
Для описания движения системы в общем случае будем
использовать уравнения движения неголономных систем в виде уравнений Воронца. В
случае одной тележки, как показывается ниже, можно применить уравнения
Чаплыгина.
Рассмотрим движение одной свободной тележки. Найдем её
кинетическую энергию T. Очевидно, T=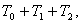 где где 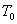 - кинетическая энергия
кузова, - кинетическая энергия
кузова, 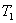 , , 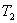 - кинетические энергии правого и левого колес соответственно.
Пусть A1, A2 – центр
масс левого и правого колес (если смотреть в сторону вектора - кинетические энергии правого и левого колес соответственно.
Пусть A1, A2 – центр
масс левого и правого колес (если смотреть в сторону вектора 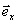 ). Кинетическая энергия кузова тележки определяется выражением: ). Кинетическая энергия кузова тележки определяется выражением:
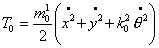 , ,
где 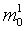 - масса кузова, - масса кузова, 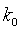 - радиус инерции кузова
относительно вертикали, проходящей через точку - радиус инерции кузова
относительно вертикали, проходящей через точку 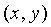 . .
Составим выражение для кинетической энергии колес.
Известно, что 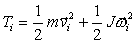 , где , где 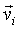 - абсолютная скорость точки - абсолютная скорость точки 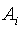 , ,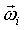 - абсолютная угловая скорость i-го колеса, J - тензор инерции колеса, построенный для его центра.
Тогда для первого колеса получим - абсолютная угловая скорость i-го колеса, J - тензор инерции колеса, построенный для его центра.
Тогда для первого колеса получим

где 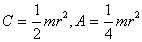 - моменты инерции относительно оси колеса и
вертикали соответственно. - моменты инерции относительно оси колеса и
вертикали соответственно.
Аналогично для второго колеса:
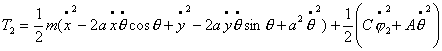
Следовательно,
кинетическая энергия одной тележки равна:
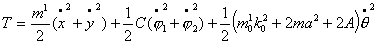 (1.3)
(1.3)
где 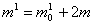 . Обозначим . Обозначим 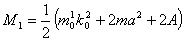
Тогда, учитывая
соотношения (1.2), получаем
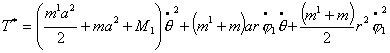 (1.4) (1.4)
Для того чтобы написать уравнения движения, перепишем
уравнения связей (1.2) в следующем виде:
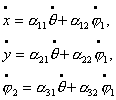 , где , где 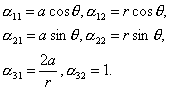
Так как коэффициенты уравнений связей и кинетическая
энергия тележки не зависят от координат x, y,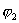 , то рассматриваемая система является системой Чаплыгина и
можно написать соответствующие уравнения, которые для данной системы имеют вид: , то рассматриваемая система является системой Чаплыгина и
можно написать соответствующие уравнения, которые для данной системы имеют вид:
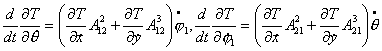 , ,
где
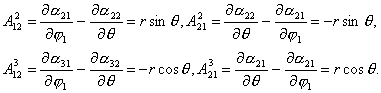
Поскольку
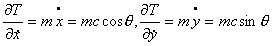 , ,
где 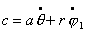 , ,
то имеем
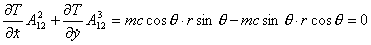 , ,
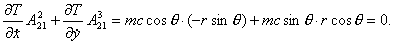
Окончательно получаем, что
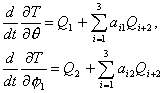 (1.5) (1.5)
Поскольку в
данном случае рассматривается свободная тележка и все обобщенные силы равны
нулю, то, используя (1.2), получаем следующие динамические уравнения движения
свободной тележки:
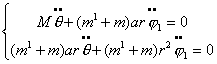 (1.6) (1.6)
где 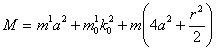 , ,
или
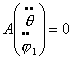 , где , где 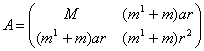 . .
Уравнения (1.1)
и (1.6) образуют замкнутую систему уравнений. При этом уравнения (1.6)
отделяются от уравнений связей (1.1). Так
как 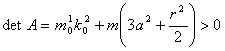 , то система (1.6) имеет лишь тривиальное решение: , то система (1.6) имеет лишь тривиальное решение:
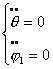 , т.е. , т.е. 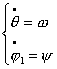 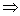 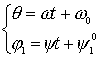
Тогда
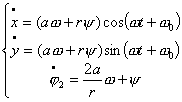
Очевидно, выделяются два
различных случая: 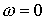 и и 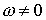 . .
1. Если 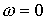 , то , то 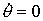 и и 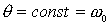 , ,
 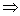 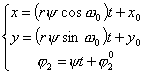
где 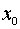 , , 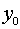 - начальные значения - начальные значения 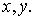
В этом случае
центр масс тележки движется по прямой, угол между осью катушки и осью OX остается постоянным.
2. Если 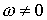 , то , то 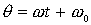 и, следовательно, имеем и, следовательно, имеем
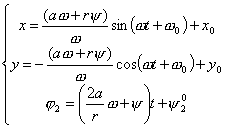
Если 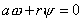 , то , то 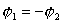 , т.е. колеса тележки вращаются в противоположных
направлениях, , т.е. колеса тележки вращаются в противоположных
направлениях,  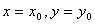 - центр масс тележки
остается неподвижным, тележка вращается вокруг него. - центр масс тележки
остается неподвижным, тележка вращается вокруг него.
Если 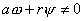 , то центр масс тележки движется по некоторой окружности. , то центр масс тележки движется по некоторой окружности.
2. Уравнения движения двух тележек.
Рассмотрим
систему из двух тележек. Тогда уравнения связей можно записать в следующем
виде:
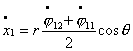
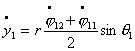
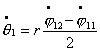
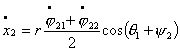
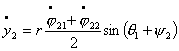
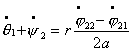
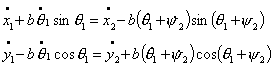
Где первые шесть уравнений – условия
«непроскальзывания» колес, а последние два – условие сцепки. Преобразуя
полученную систему, получим:
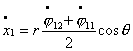
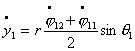
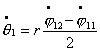
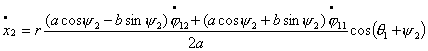 (2.1)
(2.1)
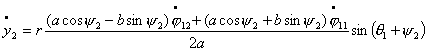
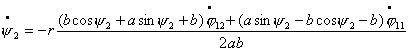
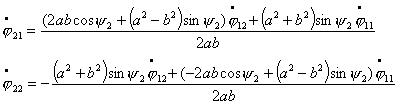
Тогда
коэффициенты связей будут иметь вид:
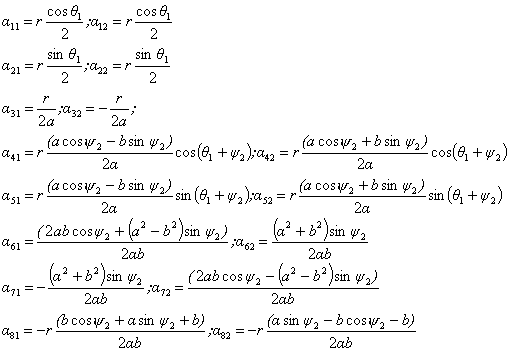 (2.2) (2.2)
Из полученных уравнений видно, что в рассматриваемой
системе две координаты являются независимыми,
в данном случае положим, что это 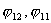 . Так как коэффициенты . Так как коэффициенты 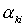 ( (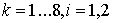 ) в уравнениях связей зависят от обобщенной координаты ) в уравнениях связей зависят от обобщенной координаты 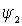 , то система не является системой Чаплыгина, как в случае
одной тележки. Тогда будем использовать уравнения Воронца для неголономных
систем [4-6] со связями вида: , то система не является системой Чаплыгина, как в случае
одной тележки. Тогда будем использовать уравнения Воронца для неголономных
систем [4-6] со связями вида:
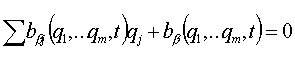 . .
Уравнения Воронца имеют вид:
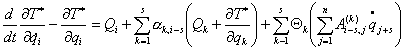 (2.3)
(2.3)
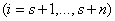 ,
,
где
n – число степеней свободы,
s - кол-во наложенных связей,
 - функция, получающаяся в результате исключения при помощи
равенств (2.1), величин - функция, получающаяся в результате исключения при помощи
равенств (2.1), величин 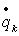 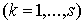 из выражения для
кинетической энергии из выражения для
кинетической энергии 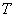 : :
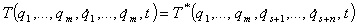 , ,
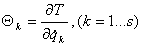 - импульсы системы, - импульсы системы,
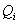 - обобщенная сила, соответствующая обобщенной координате - обобщенная сила, соответствующая обобщенной координате 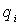 , ,
 . .
Полученные уравнения должны рассматриваться совместно
с уравнениями связей (2.1). Полученная система содержит n+s уравнений, что
совпадает с числом обобщенных координат.
В случае двух тележек уравнения Воронца примут вид:
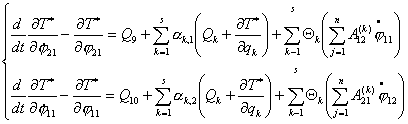 (2.4) (2.4)
Для составления
уравнений движения системы необходимо выписать все вышеприведенные величины.
Сначала выпишем выражение для кинетической энергии системы из двух тележек.
Кинетическая энергия двух тележек есть сумма кинетических энергий первой и второй
тележек. Учитывая выражение для кинетической энергии одной тележки (1.3), для
двух тележек получаем:
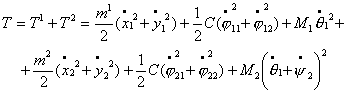 (2.5)
(2.5)
где
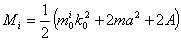 , , 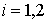 . .
После исключения зависимых скоростей с помощью
уравнений связей (2.1), будем иметь:
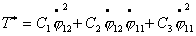 (2.6) (2.6)
где
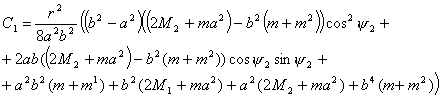
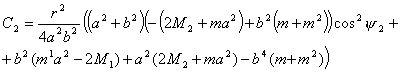
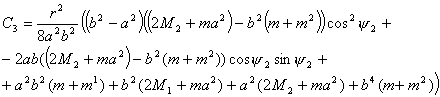
Используя (2.5), можно записать
выражения для импульсов 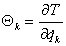 : :


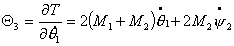
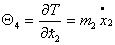
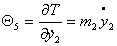
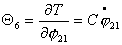
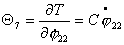
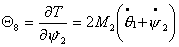
Или, учитывая (2.1), имеем
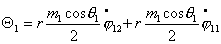
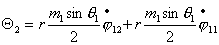
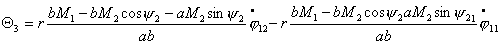 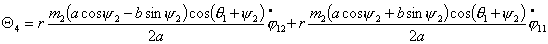 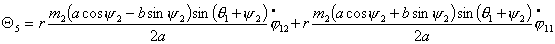 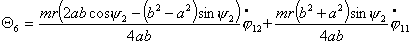 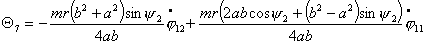 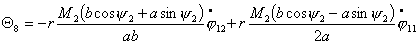
(2.7)
Запишем выражения
для величин  . Так как . Так как 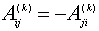 , то достаточно записать выражения для: , то достаточно записать выражения для: 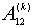 : :
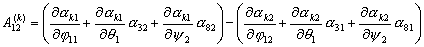
Так как все коэффициенты 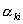 не зависят от не зависят от 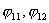 , т.е. , т.е. 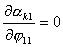 и и 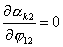 , то для величины , то для величины 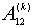 окончательно имеем: окончательно имеем:
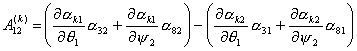
И, следовательно,
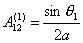
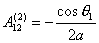
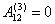
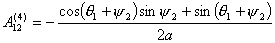 (2.8)
(2.8)
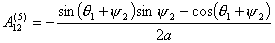
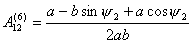
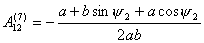
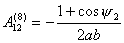 . .
Обозначим: 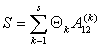 , тогда выражения , тогда выражения 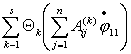 примут соответственно вид: примут соответственно вид:
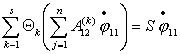 ,
и ,
и 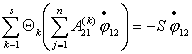 . .
Используя (2.7) и (2.8), получим
выражение для S:
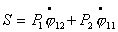 (2.9)
(2.9)
где 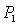 и и 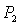 соответственно равны: соответственно равны:
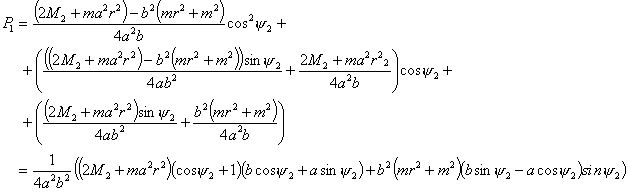
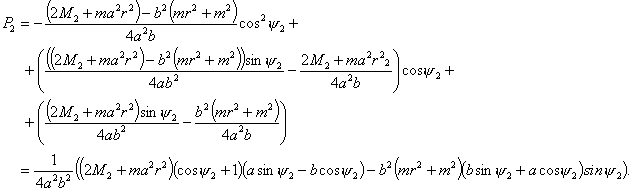
Теперь найдем
выражения для 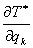 .
Так как .
Так как 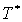 зависит только от координаты зависит только от координаты 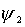 , то все , то все 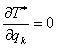 ,
кроме ,
кроме 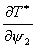 .
Найдем это выражение: .
Найдем это выражение:
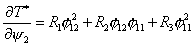 (2.10) (2.10)
где коэффициенты 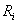 соответственно равны: соответственно равны:
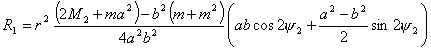
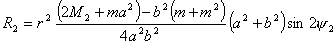
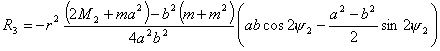
Используя (2.6), найдем выражения для 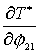 и и 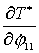 : :
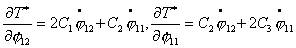 . (2.11) . (2.11)
Для нахождения обобщенных сил рассмотрим
силы, действующие в системе. В случае двух тележек в системе действуют
неизвестные силы реакции 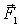 и и 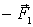 приложенные в точке приложенные в точке 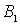 , равные по модулю и противоположные по направлению. Пусть , равные по модулю и противоположные по направлению. Пусть 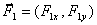 , Действительное перемещение точки , Действительное перемещение точки 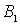 , к которой приложена сила, имеет вид: , к которой приложена сила, имеет вид:
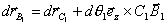 , где , где 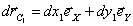 . .
Тогда
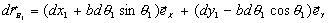
С другой стороны действительное
перемещение точки 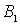 , к которой приложена сила , к которой приложена сила 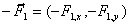 , имеет вид: , имеет вид:
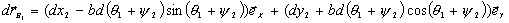 . .
и элементарная работа
действующей силы имеет вид
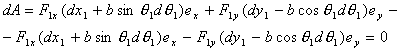
и, следовательно, все обобщенные
силы равны нулю: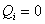 . .
Используя все
предыдущие преобразования и выводы, можно записать динамические уравнения
движения (2.4) в следующем виде:
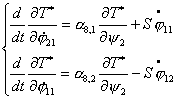
или
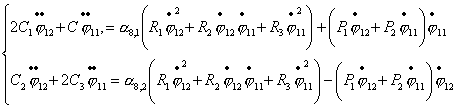 (2.12) (2.12)
Преобразуя
(2.12), получим:
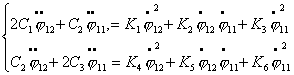 (2.13)
(2.13)
где
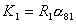
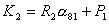
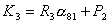
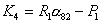
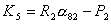
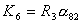 . .
Приведем систему к форме Коши. Для этого из (2.13)
явно выразим 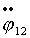 и и 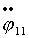 , преобразуя (2.4) к виду: , преобразуя (2.4) к виду:
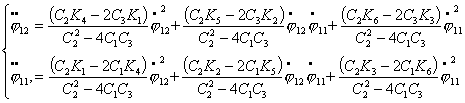
Теперь, произведя замену вида 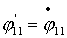 , , 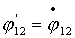 получим систему уравнений в форме Коши: получим систему уравнений в форме Коши:
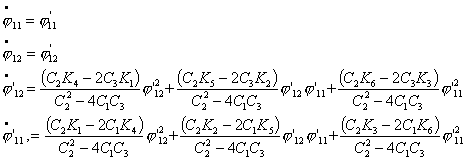
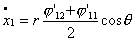
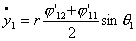 (2.14)
(2.14)
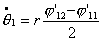
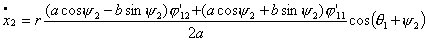
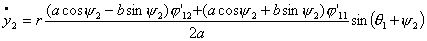
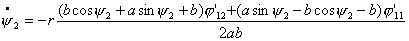
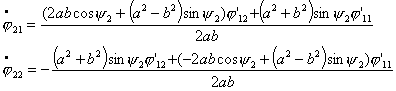
3.
Частные решения уравнений движения для двух тележек. Свободные (баллистические)
движения.
Рассмотрим частные решения системы (2.14). Пусть угол
между тележками 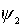 остается постоянным,
т.е. остается постоянным,
т.е. 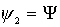 , тогда , тогда 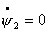 . Следовательно, выполняется следующее условие: . Следовательно, выполняется следующее условие:
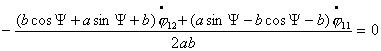
Или,
справедливо следующее соотношение:
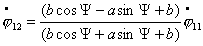 (3.1)
(3.1)
на
угловые скорости вращения правого и левого колеса ведущей тележки. Тогда,
возможны 2 случая:
1. 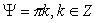 , тогда , тогда 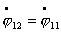 и система движется по
прямой. Найдем решение системы, если и система движется по
прямой. Найдем решение системы, если 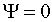 , и , и 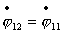 . Тогда решение системы
(2.14) примет вид: . Тогда решение системы
(2.14) примет вид:
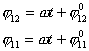
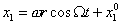
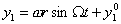
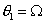 (3.2) (3.2)

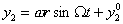
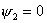
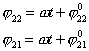
2.
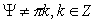 , тогда соотношение , тогда соотношение 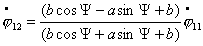 постоянно и система
движется по окружности фиксированного радиуса. Покажем это. Запишем систему
(2.14), учитывая эти условия, имеем: постоянно и система
движется по окружности фиксированного радиуса. Покажем это. Запишем систему
(2.14), учитывая эти условия, имеем:
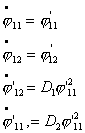
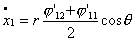
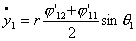 (3.3)
(3.3)
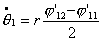
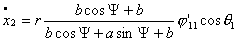
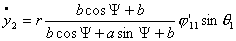
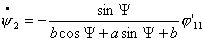
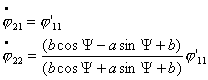
где

Подставив в коэффициенты 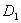 и и 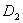 выражения для выражения для 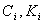 ,
получим, что ,
получим, что 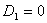 и и 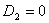 .
Тогда .
Тогда 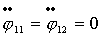 и, следовательно, и, следовательно, 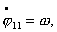 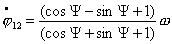 .
Тогда решение системы (3.3) выглядит следующим образом: .
Тогда решение системы (3.3) выглядит следующим образом:
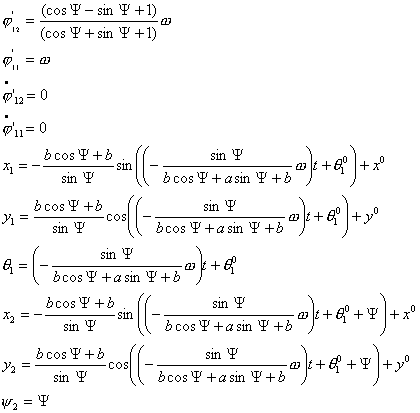
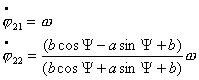
где 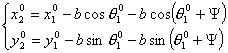 - начальные координаты
центра второй тележки. - начальные координаты
центра второй тележки.
Из полученных уравнений видно, что траекторией данного
движения является окружность заданного
радиуса 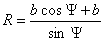 с центром в точке с центром в точке 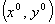 . Найдем координаты
центра установившейся окружности. . Найдем координаты
центра установившейся окружности.
Пусть в начальный момент координаты первой тележки - 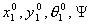 , тогда справедливо , тогда справедливо
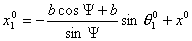
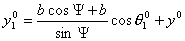
откуда
выражаем 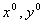
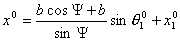
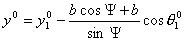
Следовательно, координаты центра окружности зависят от
начальных координат центра первой тележки, начального угла поворота оси первой
тележки относительно оси ОХ и угла между тележками. Из формулы для радиуса
видно, что он зависит только от угла между тележками.
Итак, получены два частных решения для системы из двух
тележек: движение по прямой и окружности. Из выведенных формул видно, что
движение по прямой осуществляется при любых начальных условиях и параметрах
системы, если угол между тележками 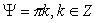 (следует заметить, что
для общности решение допускается и при (следует заметить, что
для общности решение допускается и при 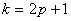 - нечетном) и угловые
скорости вращения правого и левого колес совпадают. - нечетном) и угловые
скорости вращения правого и левого колес совпадают.
Движение по окружности же возможно только при
определенных соотношениях угловых скоростей вращения первого и второго колес
ведущей тележки: 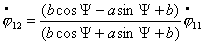 . При этом радиус описываемой окружности зависит только от угла
между тележками, а положение ее центра от начальных координат центра первой
тележки, начального угла поворота оси первой тележки относительно оси ОХ и угла
между тележками. . При этом радиус описываемой окружности зависит только от угла
между тележками, а положение ее центра от начальных координат центра первой
тележки, начального угла поворота оси первой тележки относительно оси ОХ и угла
между тележками.
Следует заметить, что
приведенные выше частные решения не являются единственно возможными. На
рис. 2 приведены траектории баллистических движений для различных начальных
условий (начальные скорости вращения колес одинаковы и равны единице, меняется лишь начальный угол между
тележками). На первом подграфике приведены семейства траекторий для 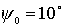 , , 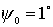 , , 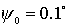 , , 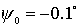 , , 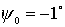 , , 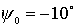 (слева на право). На
втором подграфике для (слева на право). На
втором подграфике для 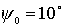 , , 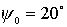 , , 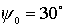 , , 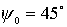 , , 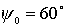 , , 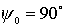 . .
 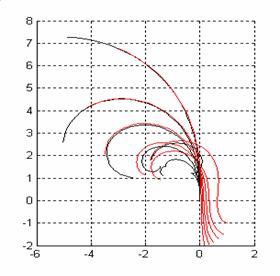
Рис2. Примеры траекторий баллистических движений
Из первого графика видно, что при небольших начальных
отклонениях система совершает движение по дугам кривых с достаточно большим
радиусом кривизны. С ростом угла отклонения одной тележки от другой, радиус
кривизны дуги, по которой система совершает движение, уменьшается, при этом
тележки могут «складываться».
На рис. 3 приведены траектории баллистических движений
в случае, если начальный угол между тележками остается постоянным (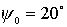 ), а меняются начальные скорости вращения колес. Начальные
скорости вращения колес приведены в Таблице 1. ), а меняются начальные скорости вращения колес. Начальные
скорости вращения колес приведены в Таблице 1.
|
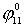
|
1
|
1
|
1
|
1
|
1.1
|
1.2
|
1.3
|
1.4
|
1.5
|
1.8
|
2
|
|
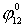
|
1.3
|
1.2
|
1.1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
Таблица 1.
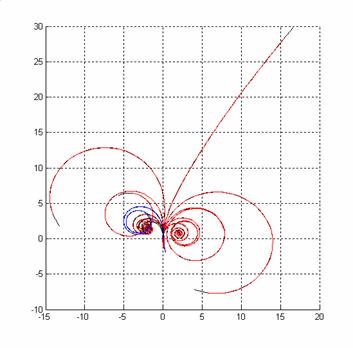
Рис.3 Примеры траекторий баллистических движений
Следует заметить, что при равных начальных скоростях
вращения колес ведущей тележки система начнет двигаться относительно начального направления оси
ведущей тележки в полуплоскости, отличной от той, в которой лежал центр второй
тележки в начальный момент.
4.
Уравнения движения для системы из n тележек.
В
данном параграфе будем рассматривать «робопоезд», состоящий из n. Уравнения связей можно записать в следующем виде:
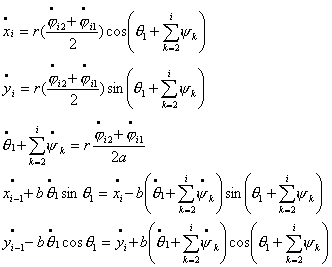 (4.1)
(4.1)
где 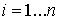
 Первые три уравнения – условия «непроскальзывания» колес для
каждой тележки, а последние – условия сцепки ( Первые три уравнения – условия «непроскальзывания» колес для
каждой тележки, а последние – условия сцепки (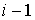 )-й и )-й и 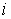 –й тележки. Преобразуя полученную систему, получим: –й тележки. Преобразуя полученную систему, получим:
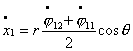
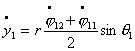
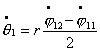
для 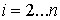
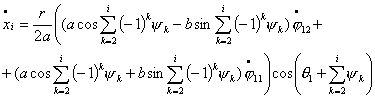
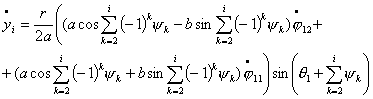 (4.2)
(4.2)
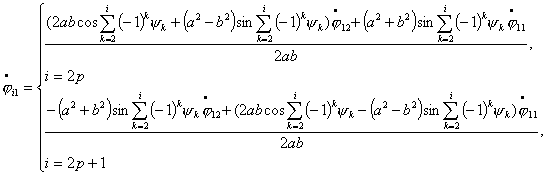
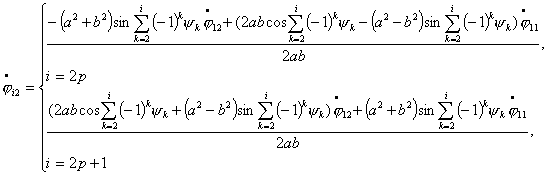
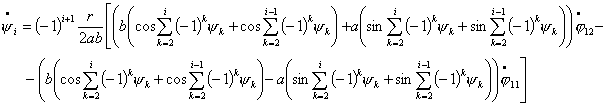
Из полученных уравнений видно, что в рассматриваемой
системе две координаты являются независимыми,
в данном случае положим, что это 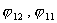 . Таким образом, можно сделать вывод, что число степеней
свободы не зависит от количества тележек в системе и всегда равно двум. Так как
коэффициенты . Таким образом, можно сделать вывод, что число степеней
свободы не зависит от количества тележек в системе и всегда равно двум. Так как
коэффициенты 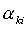 ( (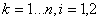 ) в уравнениях связей зависят от обобщенных координат ) в уравнениях связей зависят от обобщенных координат 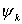 , то система не является системой. Тогда, как и в случае двух
тележек будем писать уравнения Воронца для неголономных систем. , то система не является системой. Тогда, как и в случае двух
тележек будем писать уравнения Воронца для неголономных систем.
В случае n тележек уравнения Воронца примут вид:
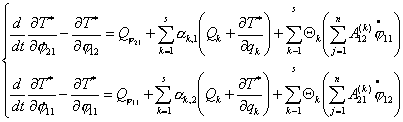 (4.3) (4.3)
Кинетическая
энергия n тележек есть сумма кинетических энергий каждой из
тележек. Учитывая выражение для кинетической энергии одной тележки (1.3), для n тележек
получаем:
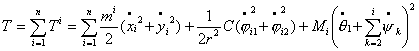 (4.4) (4.4)
где
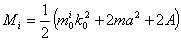 , , 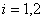 . .
После исключения зависимых скоростей с помощью
уравнений связей (4.2), будем иметь:
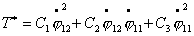 (4.5) (4.5)
Где
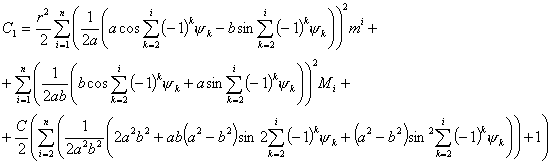
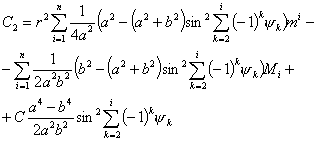
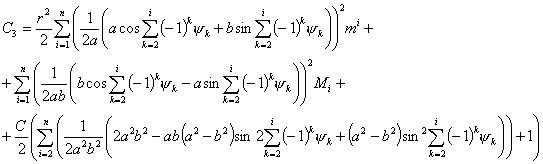
Используя выражение
для кинетической энергии (4.4), можно записать выражения для импульсов 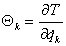 : :


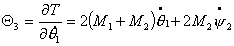
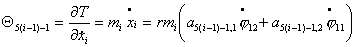
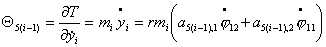
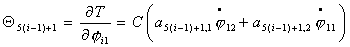
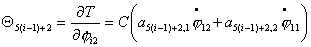
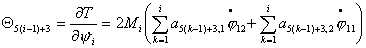
Запишем выражения
для величин 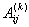 . Так как . Так как 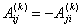 , то достаточно записать выражения для , то достаточно записать выражения для 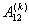 : :
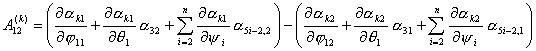
Так как все коэффициенты 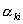 не зависят от не зависят от 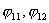 , т.е. , т.е. 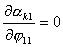 и и 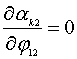 , то для величины , то для величины 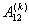 окончательно имеем: окончательно имеем:
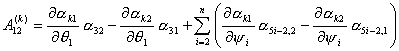 (4.6) (4.6)
Обозначим : 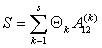 ,
тогда общий вид ,
тогда общий вид 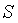 таков: таков:
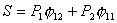 (4.7)
(4.7)
где 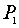 и и 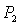 соответственно равны: соответственно равны:
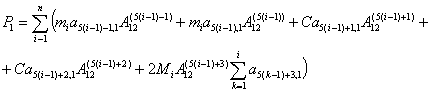
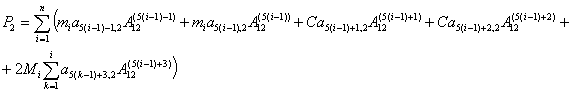
где 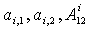 - известные функции - известные функции 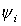 . .
Теперь найдем выражения для 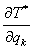 .
Так как .
Так как 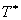 зависит только от координат зависит только от координат 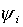 , то все , то все 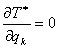 , кроме , кроме 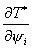 . Найдем это выражение: . Найдем это выражение:
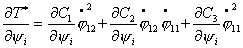 (4.8) (4.8)
или
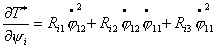
где коэффициенты соответственно
равны:
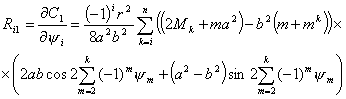
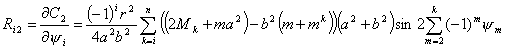
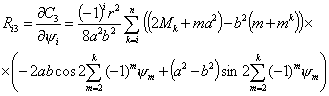
Используя (4.5), найдем выражения для 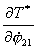 и и  : :
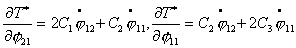 . (4.9) . (4.9)
Все обобщенные силы, как и в случае двух тележек равны нулю.
Используя все
предыдущие преобразования и выводы, можно записать динамические уравнения
движения (4.3) в следующем виде:
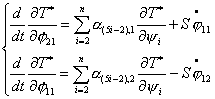
или
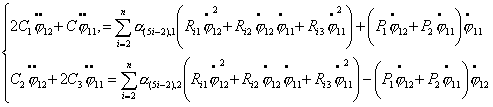 (4.10) (4.10)
Преобразуя
(4.10), получим:
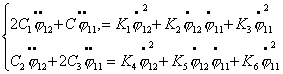 (4.11) (4.11)
где
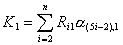
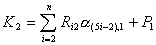
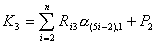
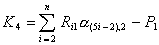
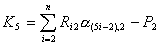
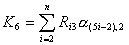 . .
Приведем систему к форме Коши. Для этого из (4.11)
явно выразим 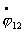 и и 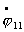 : :
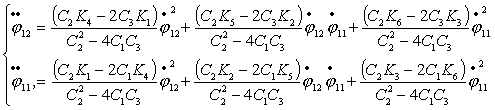
Теперь,
произведя замену вида 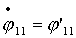 , , 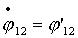 получим систему уравнений в форме Коши: получим систему уравнений в форме Коши:
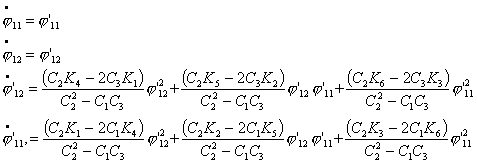
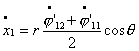
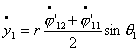
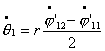
…
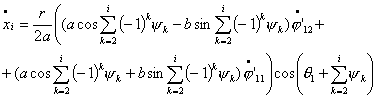
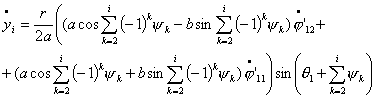 (4.12) (4.12)
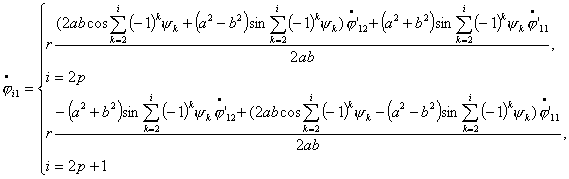 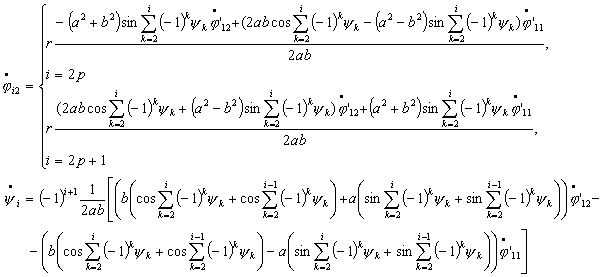
5. Частные
решения уравнений движения для n тележек.
Рассмотрим частные решения системы (4.12). Пусть угол
между тележками 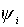 остается постоянным,
т.е. остается постоянным,
т.е. 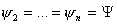 , тогда , тогда 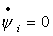 . Следовательно, выполняются следующие условия: . Следовательно, выполняются следующие условия:
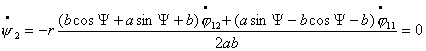
…..
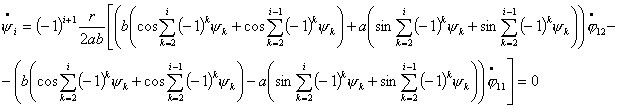
или,
используя условие 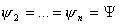 , получим : , получим :
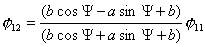
-
соотношение на угловые скорости вращения правого и левого колеса первой
тележки.
Тогда, возможны 2 случая:
1. Пусть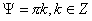 , тогда , тогда 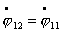 и частное решение
системы будет таким: и частное решение
системы будет таким:
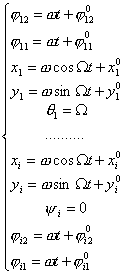
Из уравнений видно, что система движется по прямой,
сохраняя постоянный угол относительно оси ОХ.
2. Пусть 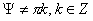 , тогда, как было показано выше соотношение , тогда, как было показано выше соотношение 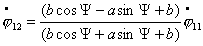 постоянно. Запишем
систему (4.12), учитывая эти условия: постоянно. Запишем
систему (4.12), учитывая эти условия:
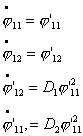
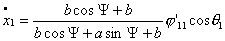
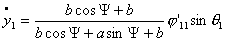
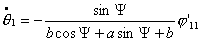
…
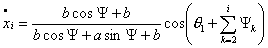
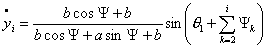 (5.1)
(5.1)
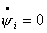
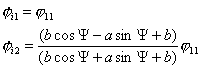
…
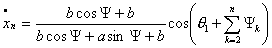

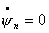
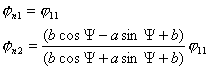
где
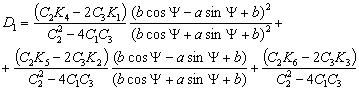
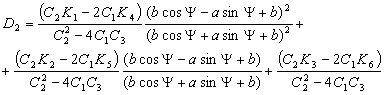
Подставив в эти коэффициенты выражения для 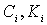 получим что, получим что, 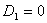 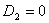 . Тогда . Тогда 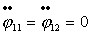 и, следовательно, и, следовательно,
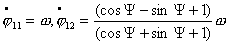 , ,
Тогда решение системы (4.12) выглядит
следующим образом:
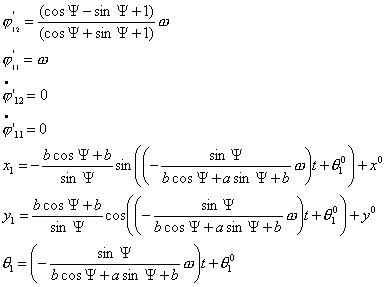
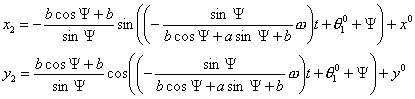
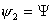
…
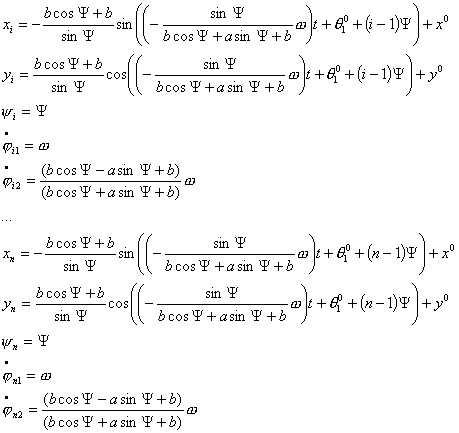
где 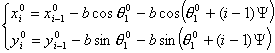 - начальные координаты
центра - начальные координаты
центра 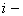 й тележки. й тележки.
Из полученных уравнений видно, что траекторией данного
движения является окружность заданного
радиуса 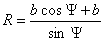 с центром в точке с центром в точке 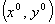 . Найдем координаты
центра установившейся окружности. Пусть в начальный момент координаты первой
тележки - . Найдем координаты
центра установившейся окружности. Пусть в начальный момент координаты первой
тележки - 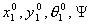 , тогда справедливо , тогда справедливо
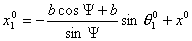
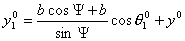
откуда
выражаем 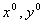
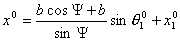
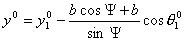
Следовательно,
координаты центра окружности зависят от начальных координат центра первой
тележки, начального угла поворота оси первой тележки относительно оси ОХ и угла
между тележками. Из формулы для радиуса видно, что он зависит только от угла
между тележками.
Итак, получены два частных решения для системы из n тележек: движение по прямой и окружности. Из
выведенных формул видно, что движение по прямой осуществляется при любых
начальных условиях и параметрах системы, если угол между тележками 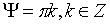 и угловые скорости
вращения правого и левого колес совпадают. Движение по окружности же возможно
только при определенных угловых скоростей вращения первого и второго колес
первой тележки ( и угловые скорости
вращения правого и левого колес совпадают. Движение по окружности же возможно
только при определенных угловых скоростей вращения первого и второго колес
первой тележки (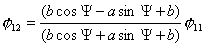 ). При этом радиус описываемой окружности зависит только от
угла между тележками, а положение ее центра от начальных координат центра
первой тележки, начального угла поворота оси первой тележки относительно оси ОХ
и угла между тележками. ). При этом радиус описываемой окружности зависит только от
угла между тележками, а положение ее центра от начальных координат центра
первой тележки, начального угла поворота оси первой тележки относительно оси ОХ
и угла между тележками.
Заключение.
В работе построены уравнения движения системы «робопоезд», состоящей из
n тележек для свободного движения. В частности,
приведен вывод уравнений для n=2. Показано,
что изменение числа объектов в системе не влечет изменения числа степеней
свободы, которое всегда равно двум. Получены базовые решения уравнений.
Показано, что такие частные решения как
«прямая» и «окружность» существуют для любого n.
После вывода уравнений движения цепочки мобильных
роботов можно рассматривать задачи управления такой системой: исследовать
условия, обеспечивающие реализацию программных движений и предлагать алгоритмы
управления при движении в заданную точку плоскости.
Список литературы
1.
Y. Nakamura, H.Ezaki, Y.Tan,
W.Chung. «Design of Steering Mechanism and Control of Nonholonomic Trailer
Systems» in Proc. 2000 IEEE International Conference on Robotics & Automation,
pp. 247-254, 2000.
2.
M.Vendittelli, G.Oriolo. “Stabilization of the general two-trailer
system” in Proc. 2000 IEEE International Conference on
Robotics & Automation, pp. 1817-1823, 2000.
3.
K.-U. Scholl, V. Kepplin, K. Berns, R. Dillmann “Controlling a Multijoint Robot for Autonomous
Sewer Inspection”
in Proc. 2000 IEEE International Conference on
Robotics & Automation, pp. 1701-1706, 2000.
4.
Неймарк Ю.И.,
Фуфаев Н.А. Динамика неголономных систем. − М.: Наука, 1967.−520 с.
5. Голубев Ю.Ф.
Основы теоретической механики: Учебник.
М.: Изд-во Моск. Ун-та., 2000.-719c.
6. Маркеев А.П.
Теоретическая механика: Учебное пособие.
М.: Наука, 1990.-416c.
|

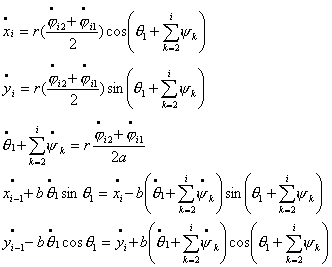 (4.1)
(4.1)![]()
![]() Первые три уравнения – условия «непроскальзывания» колес для
каждой тележки, а последние – условия сцепки (
Первые три уравнения – условия «непроскальзывания» колес для
каждой тележки, а последние – условия сцепки (![]() )-й и
)-й и ![]() –й тележки. Преобразуя полученную систему, получим:
–й тележки. Преобразуя полученную систему, получим: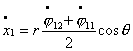
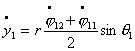
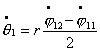
![]()
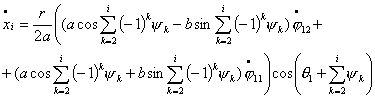
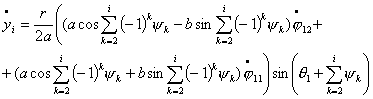 (4.2)
(4.2)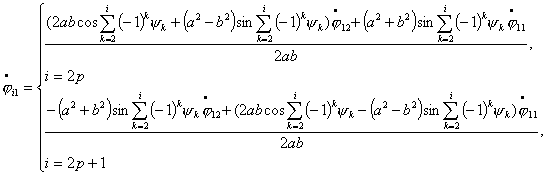
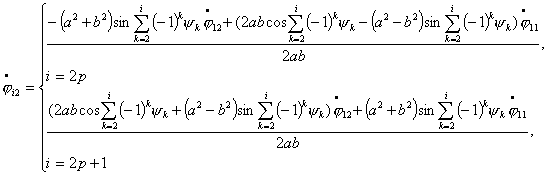
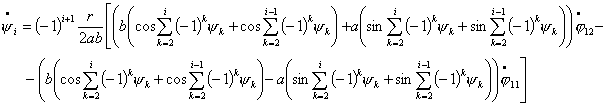
![]() . Таким образом, можно сделать вывод, что число степеней
свободы не зависит от количества тележек в системе и всегда равно двум. Так как
коэффициенты
. Таким образом, можно сделать вывод, что число степеней
свободы не зависит от количества тележек в системе и всегда равно двум. Так как
коэффициенты ![]() (
(![]() ) в уравнениях связей зависят от обобщенных координат
) в уравнениях связей зависят от обобщенных координат ![]() , то система не является системой. Тогда, как и в случае двух
тележек будем писать уравнения Воронца для неголономных систем.
, то система не является системой. Тогда, как и в случае двух
тележек будем писать уравнения Воронца для неголономных систем.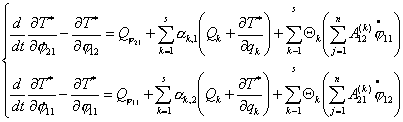 (4.3)
(4.3)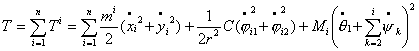 (4.4)
(4.4)![]() ,
, ![]() .
.![]() (4.5)
(4.5)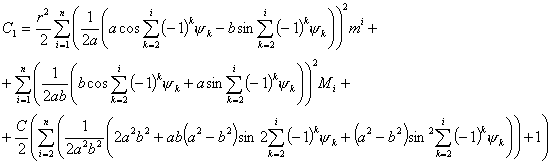
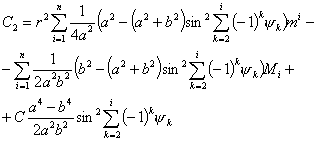
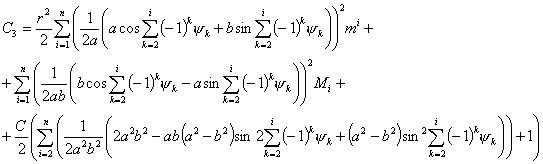
![]() :
:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Так как
. Так как ![]() , то достаточно записать выражения для
, то достаточно записать выражения для ![]() :
: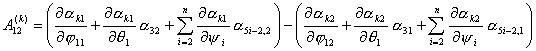
![]() не зависят от
не зависят от ![]() , т.е.
, т.е. ![]() и
и 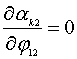 , то для величины
, то для величины ![]() окончательно имеем:
окончательно имеем: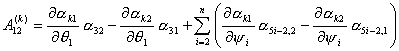 (4.6)
(4.6)![]() ,
тогда общий вид
,
тогда общий вид ![]() таков:
таков:![]() (4.7)
(4.7)![]() и
и ![]() соответственно равны:
соответственно равны: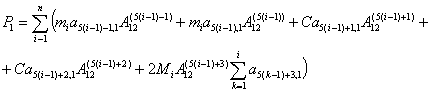
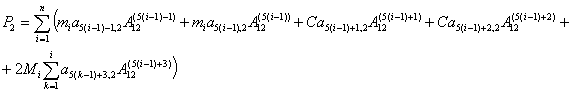
![]() - известные функции
- известные функции ![]() .
.![]() .
Так как
.
Так как ![]() зависит только от координат
зависит только от координат ![]() , то все
, то все ![]() , кроме
, кроме ![]() . Найдем это выражение:
. Найдем это выражение:![]() (4.8)
(4.8)![]()
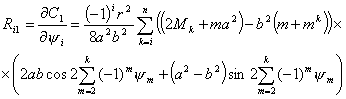
![]()
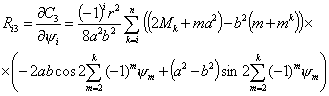
![]() и
и ![]() :
:![]() . (4.9)
. (4.9)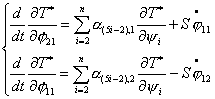
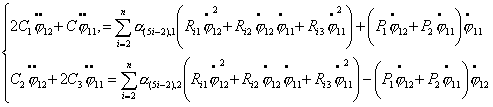 (4.10)
(4.10)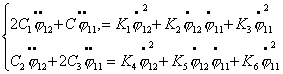 (4.11)
(4.11)![]()
![]()
![]()
![]()
![]()
![]() .
.![]() и
и ![]() :
: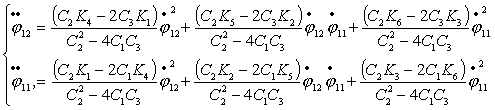
![]() ,
, ![]() получим систему уравнений в форме Коши:
получим систему уравнений в форме Коши: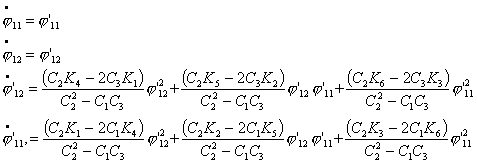
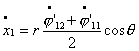
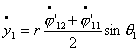
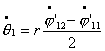
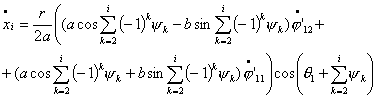
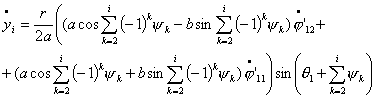 (4.12)
(4.12)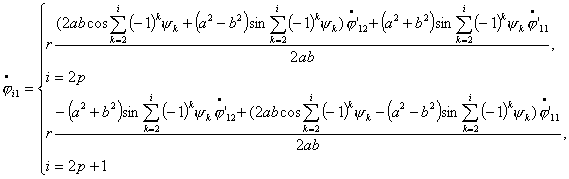
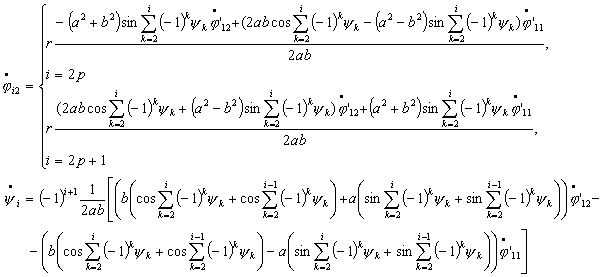
![]() остается постоянным,
т.е.
остается постоянным,
т.е. ![]() , тогда
, тогда ![]() . Следовательно, выполняются следующие условия:
. Следовательно, выполняются следующие условия: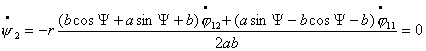
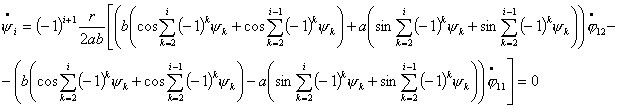
![]() , получим :
, получим :![]()
![]() , тогда
, тогда ![]() и частное решение
системы будет таким:
и частное решение
системы будет таким: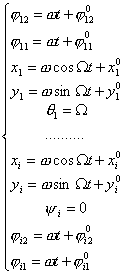
![]() , тогда, как было показано выше соотношение
, тогда, как было показано выше соотношение ![]() постоянно. Запишем
систему (4.12), учитывая эти условия:
постоянно. Запишем
систему (4.12), учитывая эти условия: 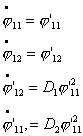
![]()
![]()
![]()
![]()
![]() (5.1)
(5.1)![]()
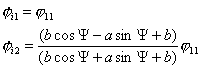
![]()
![]()
![]()
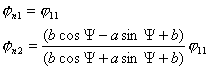
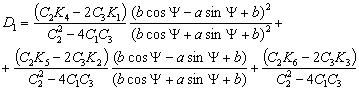
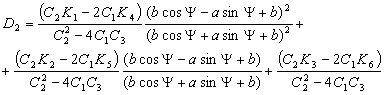
![]() получим что,
получим что, ![]()
![]() . Тогда
. Тогда ![]() и, следовательно,
и, следовательно,![]() ,
,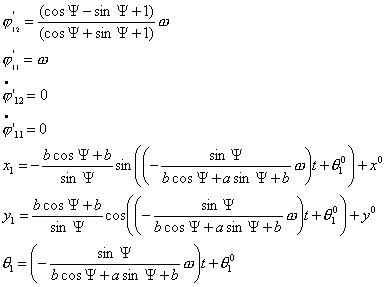
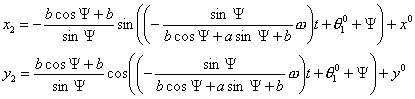
![]()
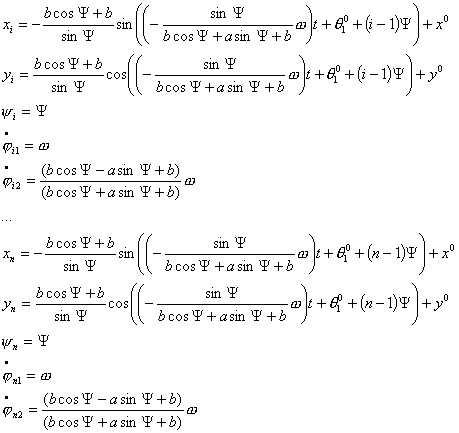
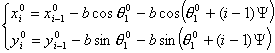 - начальные координаты
центра
- начальные координаты
центра ![]() й тележки.
й тележки.![]() с центром в точке
с центром в точке ![]() . Найдем координаты
центра установившейся окружности. Пусть в начальный момент координаты первой
тележки -
. Найдем координаты
центра установившейся окружности. Пусть в начальный момент координаты первой
тележки - ![]() , тогда справедливо
, тогда справедливо![]()
![]()
![]()
![]()
![]()
![]() и угловые скорости
вращения правого и левого колес совпадают. Движение по окружности же возможно
только при определенных угловых скоростей вращения первого и второго колес
первой тележки (
и угловые скорости
вращения правого и левого колес совпадают. Движение по окружности же возможно
только при определенных угловых скоростей вращения первого и второго колес
первой тележки (![]() ). При этом радиус описываемой окружности зависит только от
угла между тележками, а положение ее центра от начальных координат центра
первой тележки, начального угла поворота оси первой тележки относительно оси ОХ
и угла между тележками.
). При этом радиус описываемой окружности зависит только от
угла между тележками, а положение ее центра от начальных координат центра
первой тележки, начального угла поворота оси первой тележки относительно оси ОХ
и угла между тележками.


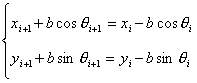
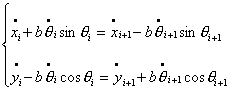

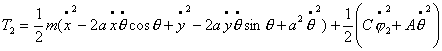
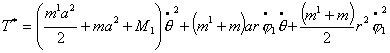
 ,
,
 ,
,
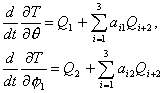
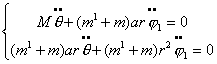
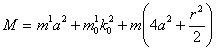 ,
,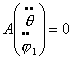 ,
,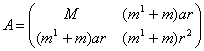 .
.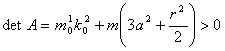 , то система (1.6) имеет лишь тривиальное решение:
, то система (1.6) имеет лишь тривиальное решение: 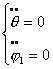
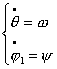
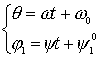
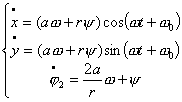

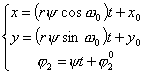
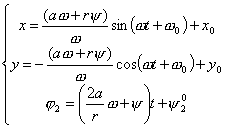
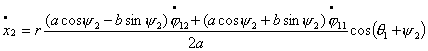
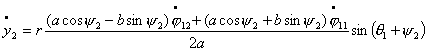
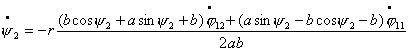
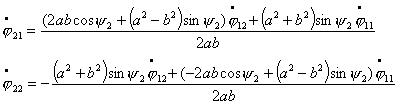
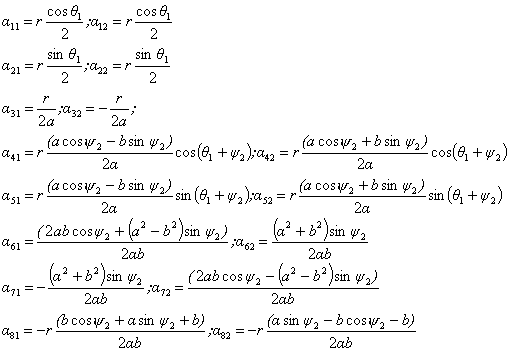
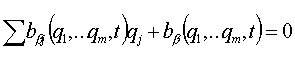 .
.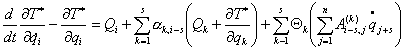
 .
.