Аннотация
Рассматриваются вопросы применения отладчика программ на языке Норма для решения нестационарных
задач газовой динамики.
Приведены результаты решения задачи о распространении возмущений в замкнутом объеме.
Abstract
The application of the debugger for NORMA-programs for the solution of the nonstationary
gas dynamics problems is considered.
The results of gas distortion propagation inside closed chamber are indicated.
Содержание
Введение. 3
Новые возможности отладчика
отладчика программ на языке НОРМА.. 3
Математическая модель и метод численного решения. 5
Результаты расчетов. 8
Литература. 11
В данной работе приводятся
результаты решения пространственной нестационарной задачи газовой динамики,
программная реализация которых на многопроцессорных ЭВМ выполнена с помощью
языка Норма [1]. Создание программного обеспечения и его отладка осуществлялись
с помощью отладчика для этого языка [2,3].
В новой версии отладчика
реализованы возможности отладки внешних модулей, написанных на языке Фортран.
Напомним, что в программе на языке НОРМА могут быть использованы внешние
модули, написанные непосредственно программистом на языках Фортран или Си с
использованием функций библиотеки передачи сообщений MPI. Внешние модули на языках Фортран или Си не обрабатываются транслятором с
языка Норма, поэтому они не содержат никакой информации для отладчика. В общем
случае отладка таких модулей в системе Норма требует решения тех же проблем,
что и отладка программ на параллельном Фортране или Си.
На первом этапе, в первой версии
отладчика для программ на языке НОРМА, было принято решение не отлаживать
внешние модули вообще, рассматривая их как “черные ящики”. Информация о том,
что происходит внутри этих модулей, для отладчика недоступна, поэтому для
пользователя выполнение внешнего модуля в первой версии отладчика
рассматривалось как выполнение одного оператора программы, в котором есть вызов
этого внешнего модуля. Здесь можно провести аналогию, например, с отладкой
программы на Си, в которой используется функция на ассемблере.
Как
показывает практика, в отличие от использования ассемблера в программах на Си,
внешние модули на языках Си или Фортран достаточно часто используются при
программировании на языке НОРМА. Поэтому в новой версии отладчика возможность
отладки внешних модулей на языке Фортран реализована. В этом случае появляется
целый ряд новых проблем для отладчика, например, возможные блокировки в
операторах приёма-передачи данных, различные ветви выполнения у различных
процессов, различные значения переменных в различных процессах, визуализация
нескольких потоков выполнения программы и т.п.
При реализации отладки внешних
модулей на языке Фортран была применена и несколько расширена схема отладчика
[3], реализованная для отладки “чистых” НОРМА-программ, основанная на использовании
монитора отладки, библиотеки связи с монитором, интерфейса пользователя и
препроцессора. В выполняемый программный код, написанный на Фортране,
препроцессором вставляются операторы обращения к функциям библиотеки связи с
монитором; монитор, взаимодействуя с параллельными процессами через функции
библиотеки связи с монитором, собирает информацию по процессам, а также
посылает/принимает команды от интерфейса пользователя. Поскольку во внешних
модулях отладочная информация изначально отсутствует, препроцессор также
анализирует внешний модуль и вставляет в него отладочную информацию.
Препроцессор был реализован
полностью, с одним ограничением: он не поддерживает переменные, не
декларированные в модуле на Фортране. Поэтому значения таких переменных в отладчике
будут недоступны.
Были написаны также необходимые
функции библиотеки связи с монитором, вызываемые из внешних модулей.
В мониторе реализованы новые
схемы управления процессами, их синхронизации, контроля достижения точки
останова и т.д. Эти схемы отличаются от тех, которые применялись в случае
“чистой” программы на языке НОРМА. Основное отличие состоит в том, что
отлаживаемые параллельные процессы могут отличаться в путях выполнения
операторов программы, а также некоторые из них могут остановиться в точках
приёма-передачи сообщений и, соответственно, перестать отправлять информацию
монитору. Кроме этого, возможности отладчика по показу значений переменных
также были расширены: значения переменных во внешнем модуле показываются
отдельно для каждого процесса.
В интерфейсе пользователя
появилось новое окно - окно процессов, где показывается состояние каждого
процесса - в какой точке отлаживаемой программы он находится (теперь он может
находиться во внешнем модуле) и его статус: готов к продолжению вычислений или
недоступен (ожидает какого-то события или “завис”). В окне переменных значения
переменных внешнего модуля показываются отдельно для каждого процесса.
Вид окна интерфейса пользователя
приведен ниже.

Рассматривается течение невязкого
сжимаемого идеального нетеплопроводного газа. Описание такого течения
проводится в переменных Эйлера. Трехмерные нестационарные уравнения берутся в
виде следующей системы.
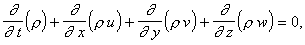
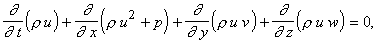
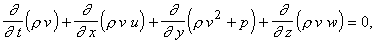

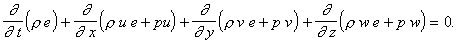
Здесь t – время, x, y, z –
декартовы пространственные координаты, u,
v, w – компоненты вектора скорости по x,
y, z соответственно, r – плотность, p – давление, e – удельная полная энергия. Система замыкается уравнением
состояния газа в виде
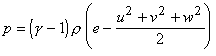 , где g – показатель адиабаты газа. , где g – показатель адиабаты газа.
Численное решение проводится
методом С.К.Годунова [4]. Рассмотрим реализацию метода в трехмерном случае.
Поле течения разбивается на ячейки, представляющие собой прямоугольные
параллелепипеды со сторонами  , , 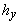 , ,  . Каждой ячейке сопоставляются три полуцелых индекса,
например (i-1/2, j-1/2, k-1/2)
обозначает ячейку с гранями . Каждой ячейке сопоставляются три полуцелых индекса,
например (i-1/2, j-1/2, k-1/2)
обозначает ячейку с гранями 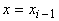 , , 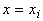 , , 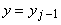 , , 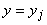 , ,  , , 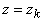 . Значения параметров внутри ячеек считаются постоянными и
обозначаются ( p, r, u, v, w, . Значения параметров внутри ячеек считаются постоянными и
обозначаются ( p, r, u, v, w,  . Расчёт ведётся последовательными шагами по времени, каждый
шаг состоит в определении тех же постоянных величин в каждой ячейке в момент
времени . Расчёт ведётся последовательными шагами по времени, каждый
шаг состоит в определении тех же постоянных величин в каждой ячейке в момент
времени  . Полагаем, что на границах ячеек параметры (и, естественно,
их комбинации) постоянны в течение всего шага по времени . Полагаем, что на границах ячеек параметры (и, естественно,
их комбинации) постоянны в течение всего шага по времени 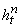 . Обозначим их и образуемые из них выражения соответствующими
заглавными буквами P, R, U, V, W, E.
Так, например, . Обозначим их и образуемые из них выражения соответствующими
заглавными буквами P, R, U, V, W, E.
Так, например, 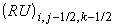 означает постоянную
величину (r u) на границе между ячейками (i-1/2, j-1/2, k-1/2) и (i+1/2, j-1/2, k-1/2). Тогда разностная
схема записывается следующим образом: означает постоянную
величину (r u) на границе между ячейками (i-1/2, j-1/2, k-1/2) и (i+1/2, j-1/2, k-1/2). Тогда разностная
схема записывается следующим образом:
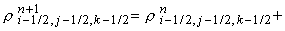
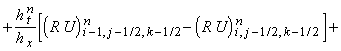
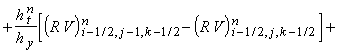
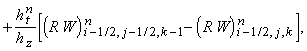
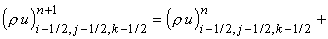
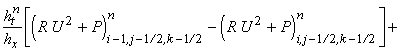
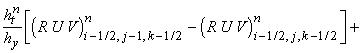
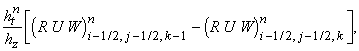
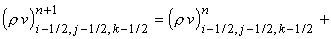
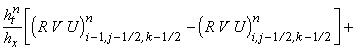
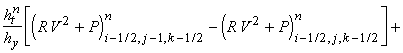



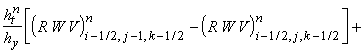
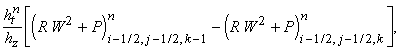
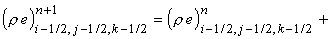
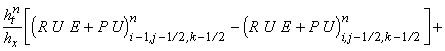

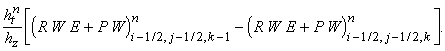
Приведённая схема аппроксимирует
исходные уравнения с первым порядком точности по времени и пространству.
Определение величин P, R, U, V, W, E
осуществляется посредством решения задачи о распаде произвольного разрыва параметров
на границах ячеек. Расчёт в ячейках, прилегающих к неподвижным непроницаемым
стенкам (или к плоскостям симметрии), заключается в расчёте распада разрыва с
фиктивной ячейкой, в которой давление, плотность и продольная скорость такие
же, а скорость по нормали к внешней границе имеет противоположный знак. Шаг по
времени выбирается из условия 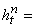 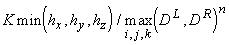 , ,  , ,  – скорости
соответственно крайних левой и правой волн, образующихся при распаде разрыва (в
описываемых ниже расчетах коэффициент запаса К полагался равным 0.3). – скорости
соответственно крайних левой и правой волн, образующихся при распаде разрыва (в
описываемых ниже расчетах коэффициент запаса К полагался равным 0.3).
В соответствии с вышеизложенным
для описания задачи на языке НОРМА использовались следующие разностные сетки:
основная сетка, т.е. сетка, на которой в точках (i-1/2, j-1/2, k-1/2) ищется решение, а также вспомогательные сетки
(у каждой размерность по координате, соответствующей направлению вычисляемых
потоков, на единицу больше, чем у основной сетки), в точках которых вычисляются
соответствующие потоки массы, импульса и энергии по трем направлениям. На
границах этих сеток потоки вычисляются особым образом, то есть реализуются либо
условия продолжения течения с нулевым градиентом, либо условия непротекания.
Приведем результаты проведенных
расчетов. Решалась задача о разлете газа (с показателем адиабаты g = 1.4 ) в следующей постановке. Решение ищется в
кубической области, ограниченной непроницаемыми плоскостями x=0, y=0,
z=0, x=100, y=100, z=100. В
начальный момент времени область заполнена невозмущенным газом с параметрами
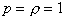 , ,
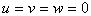 , а в одной ячейке давление и плотность повышены ( , а в одной ячейке давление и плотность повышены ( 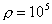 ),
а газ также неподвижен: ),
а газ также неподвижен: 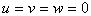 .
.
В
различных расчетных вариантах варьировалось положение ячейки с повышенными
параметрами. Поскольку задавались равные пространственные шаги  = =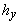 = = =1, то такую ячейку будем задавать ее индексами (целыми, т.е
-1/2 для простоты опускается) по
соответствующим координатам. =1, то такую ячейку будем задавать ее индексами (целыми, т.е
-1/2 для простоты опускается) по
соответствующим координатам.
|
Номер варианта
|
Индекс по Х
|
Индекс по Y
|
Индекс по Z
|
|
1
|
10
|
1
|
1
|
|
2
|
20
|
1
|
1
|
|
3
|
30
|
1
|
1
|
|
4
|
40
|
1
|
1
|
|
5
|
40
|
10
|
1
|
|
6
|
40
|
20
|
1
|
|
7
|
40
|
30
|
1
|
|
8
|
40
|
40
|
1
|
|
9
|
40
|
40
|
10
|
|
10
|
40
|
40
|
20
|
|
11
|
40
|
40
|
30
|
|
12
|
40
|
40
|
40
|
|
13
|
30
|
30
|
30
|
|
14
|
20
|
20
|
20
|
|
15
|
10
|
10
|
10
|
В процессе расчета на каждом шаге
по времени осуществлялась запись значения давления в ячейки – аналоги датчиков
давления в физическом эксперименте, установленных в каждой из восьми вершин
замкнутого кубического объема.
|
Номер
датчика
|
Индекс по Х
|
Индекс по Y
|
Индекс по Z
|
|
I
|
1
|
1
|
1
|
|
II
|
1
|
100
|
1
|
|
III
|
100
|
1
|
1
|
|
IV
|
100
|
100
|
1
|
|
V
|
1
|
1
|
100
|
|
VI
|
1
|
100
|
100
|
|
VII
|
100
|
1
|
100
|
|
VIII
|
100
|
100
|
100
|
Очевидно, что в результате
расширения газа будет реализовываться следующее течение: образуется волна
взрывного типа, которая через какое-то время достигает границ области (разных
границ-плоскостей в разные моменты времени) и отражается от них. При этом
картина течения усложняется интерференцией отраженных волн и результирующие
волны приводят к следующему повышению давления в угловых точках. За рассмотренный
промежуток (1000 шагов по времени) происходит несколько таких отражений.
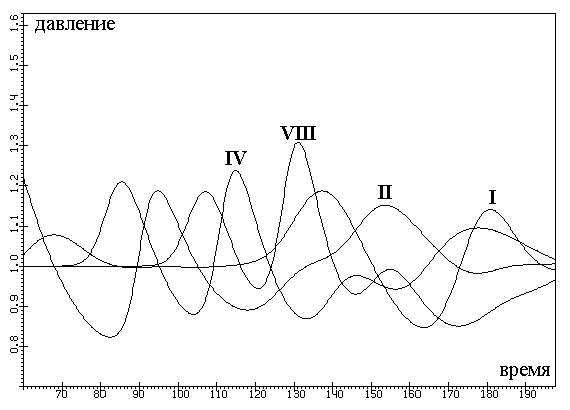
Характерная картина поведения по времени давления в датчиках приведена на рис.
1 (вариант № 14).
Рис.1. Изменение по времени давления в датчиках (вариант
№ 14).
Такое сложное взаимодействие волн
может приводить к тому, что в результате следующего цикла отражений локальный
(по времени) максимум давления, регистрируемый датчиком, может превышать
предыдущее локальное максимальное значение: рис.2 (вариант № 3, датчик № VII).
Рис.2. Изменение по времени
давления в датчике № VII (вариант № 3).
Приведем полученные в расчетах
максимальные значения давления, зафиксированных датчиками, не учитывая при этом
первый локальный максимум.
|
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
VIII
|
|
1
|
1.25
|
1.3
|
1.44
|
1.36
|
1.3
|
1.26
|
1.35
|
1.05
|
|
2
|
1.17
|
1.23
|
1.34
|
1.29
|
1.23
|
1.22
|
1.28
|
1.04
|
|
3
|
1.14
|
1.16
|
1.34
|
1.23
|
1.12
|
1.28
|
1.22
|
1.04
|
|
4
|
1.14
|
1.14
|
1.29
|
1.22
|
1.13
|
1.33
|
1.23
|
1.21
|
|
5
|
1.07
|
1.13
|
1.17
|
1.17
|
1.14
|
1.24
|
1.22
|
1.16
|
|
6
|
1.07
|
1.16
|
1.13
|
1.16
|
1.15
|
1.13
|
1.23
|
1.1
|
|
7
|
1.11
|
1.15
|
1.1
|
1.21
|
1.23
|
1.15
|
1.23
|
1.36
|
|
8
|
1.14
|
1.12
|
1.12
|
1.21
|
1.32
|
1.23
|
1.23
|
1.5
|
|
9
|
1.16
|
1.12
|
1.12
|
1.23
|
1.28
|
1.17
|
1.17
|
1.34
|
|
10
|
1.22
|
1.12
|
1.12
|
1.23
|
1.18
|
1.15
|
1.15
|
1.14
|
|
11
|
1.29
|
1.12
|
1.12
|
1.23
|
1.14
|
1.19
|
1.19
|
1.28
|
|
12
|
1.26
|
1.16
|
1.16
|
1.24
|
1.16
|
1.24
|
1.24
|
1.31
|
|
13
|
1.33
|
1.16
|
1.16
|
1.32
|
1.16
|
1.32
|
1.32
|
1.49
|
|
14
|
1.18
|
1.18
|
1.18
|
1.23
|
1.18
|
1.23
|
1.23
|
1.31
|
|
15
|
1.2
|
1.21
|
1.21
|
1.21
|
1.21
|
1.21
|
1.21
|
1.06
|
Полученные
результаты позволяют сделать вывод о том, что многократное переотражение волн в
замкнутом объеме может приводить к их локальному усилению в зависимости от
местоположения точки с повышенными параметрами.
1. А.Н.Андрианов, А.Б.Бугеря, К.Н.Ефимкин, И.Б.Задыхайло.
НОРМА. Описание языка. Рабочий стандарт. Препринт ИПМ им.М.В.Келдыша РАН, N120, 1995, 52с.
2. А.Н.Андрианов, С.Б.Базаров, А.Б.Бугеря, П.И.Колударов, И.М.Набоко. Применение отладчика параллельных
программ при решении задачи о фокусировке ударных и взрывных волн на
многопроцессорных ЭВМ. Препринт ИПМ
им.М.В.Келдыша РАН, N50, 2004, 15 с.
3. Бугеря А.Б. Диалоговый отладчик параллельных программ.
Информационные и математические технологии в науке, технике и образовании.
сборнике Труды X Байкальской Всероссийской
конференции. Часть 1. Иркутск,
2005, с.215-219.
4.
Годунов С.К., Забродин А.В., Иванов М.Я. и др. Численное решение многомерных
задач газовой динамики. М., Наука, 1976.
|


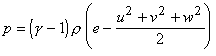 , где
, где 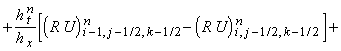
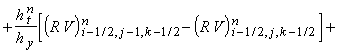
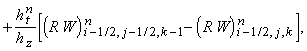
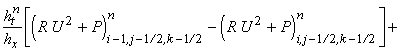
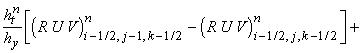
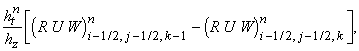
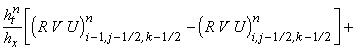
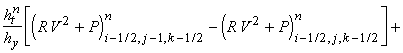


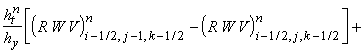
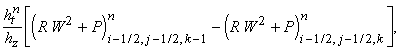
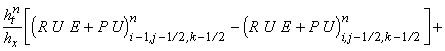

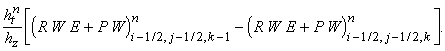
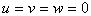 , а в одной ячейке давление и плотность повышены (
, а в одной ячейке давление и плотность повышены (