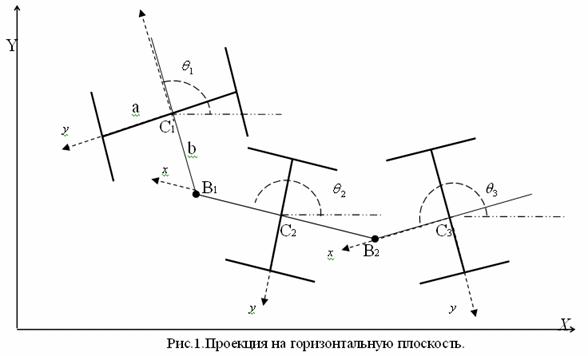
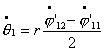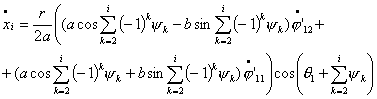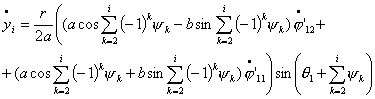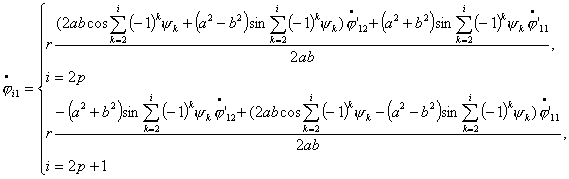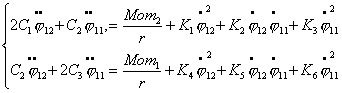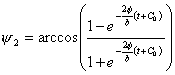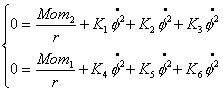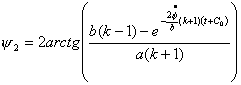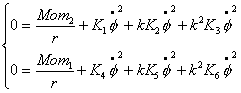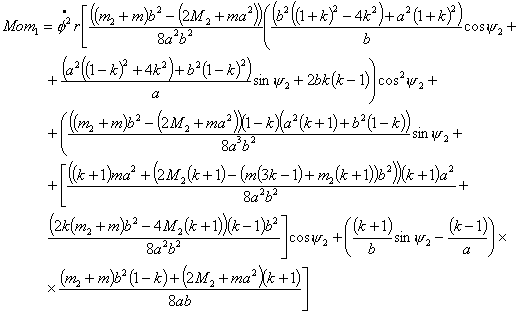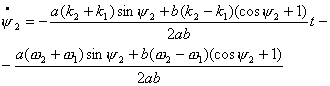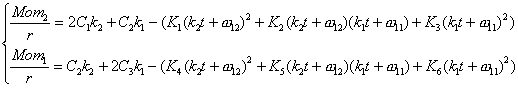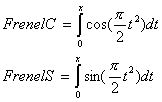Исследование динамики движения цепочки "Робопоезд". Управляемое движение

( Research of dynamics of movement of a chain of "Robotrain". Controlled movement
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Павловский В.Е., Петровская Н.В., Евграфов В.В.
(V.E.Pavlovskiy, N.V.Petrovskaya, V.V.Evgrafov)

ИПМ им. М.В.Келдыша РАН

Москва, 2005
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проекты №№ 01-01-00079, 02-01-00750, 04-01-00065), а так же гранта по программе «Государственная поддержка ведущих научных школ» НШ-1835.2003.1

Аннотация

Построены основные программные движения системы (прямая, окружность, спираль). Решена задача определения моментов, которые необходимо приложить к колесам ведущей тележки для совершения заданного программного движения. Дана оценка точности отклонения траектории движения хвостовой части системы от траектории движения ведущей тележки.

Abstract

The basic program movements of system (a straight line, a circle, a spiral) are constructed. The problem of definition of the torques, which are necessary for applying to wheels of the leading carriage for fulfillment of the set program movement is solved. The accuracy estimation of deviation of a trajectory of a tail part of system from a trajectory of movement of the carrying on leading is given.

 

Содержание

 

Введение…………………………………………………………………………….….………3

1. Краткое описание механической системы ………………………………...…….………..3

2. Уравнения управляемого движения……………………………………….…….…………5

3. Движение по прямой для двух тележек (прямой ход)………………………..………......7

4. Движение по окружности для двух тележек (прямой ход)……………………………....8

5. Переходный процесс. (прямой ход.)…………………………………………………….....9

6. Движение по прямой и окружности для двух тележек в случае обратного хода……...18

7. Переходный процесс. (обратный ход.) Точность……………………………………......23

8. Комбинированное движение……………………………………………………..……….26

Заключение………………………………………………………………………….………..30

Список литературы…………………………………………………………….…………….31

 

Введение

 

Данная работа является продолжением работы [1], в которой дано полное описание системы, рассмотрено свободное движение цепочки подвижных колесных тележек, построены уравнения движения и их частные решения. Здесь будем рассматривать управляемое движение данной системы, строить программные движения вида прямая, окружность, спираль.

 

1.     Краткое описание механической системы.  

 

Рассматривается система, состоящая из объектов, которые мы будем называть «тележками». Каждая тележка представляет собой невесомую ось L длины 2b  и перпендикулярную ей невесомую ось длины 2a, на которую насажены два одинаковых колеса. Каждое колесо является плоским однородным диском массы m, радиуса r, перпендикулярным оси тележки. Кузов тележки имеет массу  и может перемещаться только параллельно плоскости движения. Вообще говоря, массы кузова у разных тележек могут быть различными. Будем считать, что центр масс тележки совпадает с центром оси колес. Тележки соединены друг с другом при помощи шарнира. Активной назовем тележку, вращением колес которой можно управлять при помощи электродвигателей. Пассивной назовем тележку без управления. Тележки движутся по абсолютно шероховатой горизонтальной плоскости в однородном поле силы тяжести.

На рис.1 изображена проекция системы на горизонтальную плоскость.

 

Пусть OXYZ - неподвижная система координат, плоскость OXY совпадает с горизонтальной плоскостью; C1 … Сn - соответственно центры осей тележек; C1xyz … Cnxyz - системы координат, жестко связанные с тележками (осями тележек), , ,..., - углы поворота осей L соответствующих тележек вокруг вертикали, в дальнейшем кроме углов ,..., будем рассматривать углы поворота оси L i-й тележки () относительно оси  L предыдущей тележки , где , x1, y1 ,…,xn, yn - координаты точек C1,…,Сn  соответственно, , , … , , - углы поворота колес соответствующих тележек относительно их осей, отсчитываемые от проекции положительного направления оси Cz на плоскость колеса против часовой стрелки (если смотреть в сторону вектора ).

На i-ю тележку в точках ,  действуют неизвестные силы  реакции соответственно - и . Условие качения без проскальзывания обуславливает наличие неинтегрируемых связей.

Обобщенные координаты q = (x1, y1,…, xn, yn; ,; , ,…, , ) определяют положение механической системы в каждый момент времени.

Движение системы из n тележек в случае свободного движения описывается системой уравнений:

…

                                       (1.1)

 

 

Где -  известные функции ,…,.

 

2. Уравнения управляемого движения.

 

Рассмотрим случай управляемого движения системы: будем считать, что колеса первой тележки приводятся в движение двигателями, причем двигатель задается развиваемым им моментом. Рассмотрим вначале случай двух тележек. Учитывая, что работа всех внутренних сил равна нулю, элементарную работу  приложенных к системе сил и моментов вычислим- следующим образом:                                                                                                                                                     

,

где - моменты, развиваемые двигателями первого и второго колес соответственно,  - абсолютная угловая скорость i-го колеса, i=1,2. Поскольку , i=1,2, то получаем, что

.

Следовательно, обобщенные силы  имеют вид: , . Тогда, используя уравнения, полученные в [1], запишем уравнения управляемого движения [3-5] для двух тележек:

или

                                               (2.1)

 Преобразуем полученную систему к виду:

 

                                                       (2.2)

Рассмотрим движение системы в случае n тележек. Тогда получаем то же самое, что и для двух тележек: обобщенные силы  равны соответственно ,   и уравнения движения принимают вид:

 

или

 

Где -  известные функции ,…,.

 

3. Движение по прямой для двух тележек (прямой ход).

 

Условием движения ведущей тележки по прямой, в направлении её ориентации, является условие равенства угловых скоростей ведущей тележки:

 

Тогда из кинематических уравнений следует:

 

Из данного дифференциального уравнения уголнаходится в явном виде:

 

                                           (3.1)

Тогда, для движения вперед, т.е. при   имеем  при . Это означает, что угол между тележками  стремится к 0, и траектория «хвостовой» части системы асимптотически стремится к прямой. Если , то  при  и тележки «складываются».

Теперь для реализации такого движения найдем закон изменения моментов, прикладываемых на передние колеса. Так как , то , то из динамических уравнений (2.1) для управляемого движения получаем следующие соотношения:

 

                                                                        (3.2)

 

откуда имеем

(3.3)

- законы изменения моментов для совершения программного движения по прямой.

Подставив в выражения для моментов (3.3), закон изменения угла  (3.1) получим законы изменения моментов для выполнения программного движения по прямой как функции времени. 

 

4.  Движение по окружности для двух тележек (прямой ход).

 

Условием движения ведущей тележки по окружности в направлении ее ориентации, является следующее соотношение на угловые скорости вращения колес ведущей тележки:

 

 

 

Учитывая расположение мгновенного центра вращения корпуса ведущей тележки легко показать, что радиус результирующей окружности равен . Тогда из кинематических уравнений следует:

 

 

Следовательно, угол  находится в явном виде:

 

                                   (4.1)

 

Тогда, для движения вперед, т.е. при   имеем  при . Это условие соответствует движению системы по окружности радиуса . Если , то  при  и тележки «складываются».

Динамические уравнения (2.1) в данном случае примут вид:

 

 

 

откуда имеем

 

          (4.2)

 

Подставив в выражения для моментов (4.2), закон изменения угла  (4.1) получим законы изменения моментов для выполнения программного движения по окружности как функции времени. 

Таким образом, если в начальный момент времени выполнено условие: , то, при приложении вышеуказанных моментов Mom1 и Mom2, система будет двигаться по окружности радиуса , при этом задняя тележка асимптотически выйдет на ту же окружность.

 

5. Переходный процесс (прямой ход.)

 

В двух предыдущих параграфах были определены моменты, которые необходимы для поддержания заданного стационарного движения (угловые скорости колес ведущей тележки остаются постоянными). Теперь определим моменты, которые необходимы для перехода из одного стационарного состояния в другое. Рассмотрим линейный закон изменения скоростей вращения колес ведущей тележки. 

                                  (5.1)

где - начальные угловые скорости вращения колес ведущей тележки.

Тогда из кинематических уравнений следует:

                (5.2)

Из данного дифференциального уравнения получаем интегральное соотношение на угол . На подграфике 1 рис.2 приведено семейство решений этого уравнения для следующих начальных условий: . В этом семействе меняется соотношение . Из графика видно, что угол между тележками стремится к постоянному значению, назовем его углом стабилизации. Значение угла стабилизации  при этом определяется  соотношением  . На подграфике 2 рис.2 изображено семейство решений, соответствующее начальным условиям: ;   меняется начальный угол между тележками . Из графика видно, что значение угла между тележками стабилизируется возле одного значения вне зависимости от начального угла. Это значение определяется соотношением


Рис.2. Численные решения уравнения (5.2).

 

Теперь, для реализации такого движения, найдем закон изменения моментов, прикладываемых на передние колеса из динамических уравнений (2.1).

Так как  то , и динамические уравнения (2.1) примут вид:

             (5.3)

На рис. 3 приведено семейство численных решений уравнений (5.3) при условии, что законы изменения скоростей вращения колес ведущей тележки заданы следующим образом ;  геометрические параметры удовлетворяют условиям: ; меняется начальный угол между тележками . На подграфике 1 рис.3 изображены законы изменения моментов прикладываемых на колеса ведущей тележки, а на подграфике 2 – закон изменения их угловых скоростей.  Из графика изменения скоростей видно, что при задании моментов вышеуказанным способом, угловые скорости вращения ведущих колес будут меняться по заданному закону  вне зависимости от начального угла между тележками.

 

Рис.3. Численные решения уравнений (5.3)

 

На рис.4 изображены графики практически с теми же начальными условиями, что и на рис.3, но изменено только соотношение масс   (суммарная масса системы остается постоянной). Сравнивая рис.3 и рис.4, можно сделать вывод, что распределение масс влияет на начальную амплитуду моментов и конечное значение угла стабилизации.

 

Рис.4. Численные решения уравнений (5.3)

 

На рис.5 видно, что на результирующие моменты также влияет соотношение геометрических характеристик тележки, таких как длина продольной и поперечной осей  a и b (.)

 

Рис.5 Численные решения уравнений (5.3)

 

Исследуем, какова траектория движения ведущей тележки при линейном законе изменения скоростей вращения её колес. Для этого подставим закон изменения угловых скоростей  ведущей тележки в кинематические уравнения связей [1], получим:

 

 

 

                                                                                        (5.4)

 

 

 

                                     

 

 

 

 

 

Как видно из уравнений, траектории движения первой и второй тележки строго друг друга не повторяют, но с течением времени траектория второй тележки асимптотически стремится к траектории ведущей тележки. Рассмотрим подробнее каждую из получающихся траекторий.

Проинтегрируем первые три уравнения  из (5.4), получим

 

 

 

 

 

где           

    

    

 

Здесь введены функции FrenelS, FrenelC, являющиеся интегралами Френеля:

Из полученных уравнений следует, что траектория ведущей тележки при линейном законе изменения скоростей вращения ее колес, представляет собой отрезок спирали Корню [2], при этом движение «хвостовой» части системы будет асимптотически к этой спирали стремиться. Покажем это, численно исследуя разность  между получаемыми траекториями.

На рис. 6 приведены графики четырех различных семейств основных характеристик движения для следующих начальных условий: ;   меняется начальный угол между тележками .

На первом подграфике изображено семейство моментов прикладываемых к колесам ведущей тележки, на втором – семейство угловых скоростей колес ведущей тележки, на третьем – семейство углов между тележками, на четвертом – семейство траекторий движения ведущей и ведомой тележек.  Из графиков видно, что траектория движения второй тележки  максимально отличается от траектории ведущей тележки в начальный момент времени. Исследуем численно эти отклонения.

 

Рис. 6 Характеристики движения при «переходном процессе»

 

Таблица 1.

Таблица1. Отклонение траектории движения второй тележки  от траектории движения ведущей тележки, в зависимости от начального угла между тележками и от времени движения

время, t

1.12

1.3

1.47

2.07

2.9

psi=90

0.35

0.23

0.15

0.03

0.001

psi=80

0.3

0.2

0.13

0.027

0.001

psi=70

0.25

0.17

0.11

0.025

0.001

psi=60

0.22

0.15

0.1

0.023

0.001

psi=50

0.19

0.13

0.09

0.021

0.001

psi=40

0.16

0.11

0.08

0.019

0.001

psi=30

0.14

0.1

0.07

0.018

0.001

psi=20

0.11

0.085

0.06

0.017

0.001

psi=10

0.08

0.07

0.05

0.016

0.001

psi=0

0.06

0.055

0.04

0.015

0.001

 

В Таблице 1 приведены данные, полученные при помощи вычислений в пакете Matlab. Первый столбец соответствует моменту времени t=1.12c. В этот момент координата x второй тележки равна нулю (как координата ведущей тележки в начальный момент времени), а координата y отличается от начальной  координаты y ведущей тележки на величину указанную в первом столбце для каждого начального угла между тележками. Далее приведены отклонения между траекториями в точках с абсциссой x=0,5 момент времени ), далее в точках с абсциссой x=1 (момент времени ), далее с абсциссой x=3 (момент времени ) и с ординатой y=4 (момент времени ).

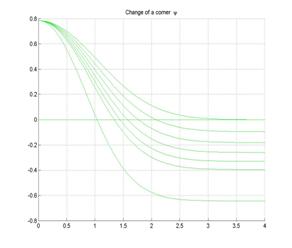
На рис.7 изображено поведение отклонений между траекториями в зависимости от начального угла между тележками. Из графика видно, что отклонения достаточно быстро стремятся к минимуму, они максимальны в начальный момент времени. Величина отклонения  зависит от начального угла между тележками. Отклонение становится минимальным при относительной стабилизации угла между тележками (здесь под относительной стабилизацией мы понимаем, что отклонение между траекториями не выходит из некоторого фиксированного допуска). При этом время относительной стабилизации практически не зависит от начального угла между тележками. Время относительной стабилизации зависит от начальной угловой скорости вращения колес передней тележки и скорости разгона (коэффициентов k1, k2).

 

 

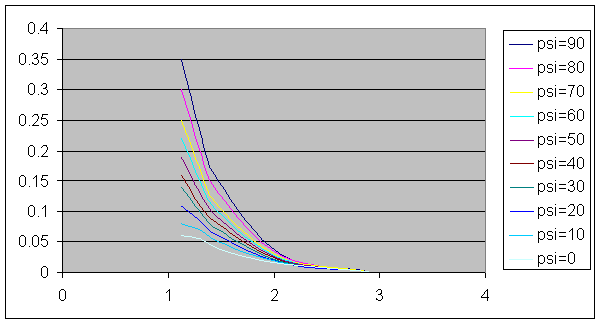
Рис.7. Отклонения от траектории ведущей  тележки

 

На рис.8 приведено семейство траекторий, соответствующее следующим начальным условиям: ;  ,  меняется соотношение  Из графика видно, что наименьшее отклонение будет в случае наименьшего соотношения .

 

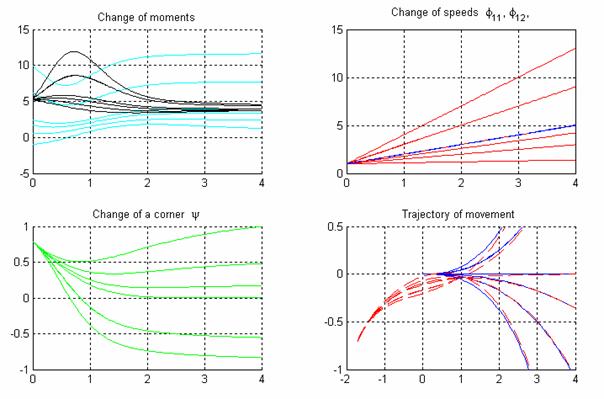
Рис.8. Зависимость величины отклонения между траекториями от соотношения

 

Зависимость отклонения при  показана на рис.9. В этом примере рассмотрены траектории движения при 

 

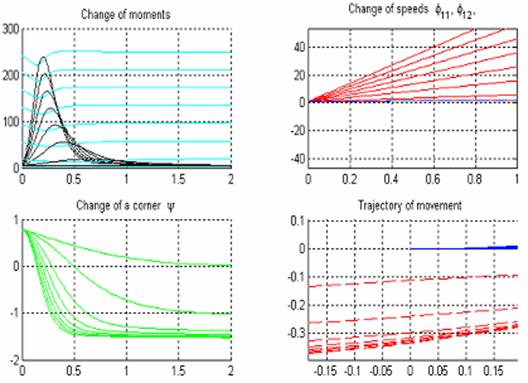
Рис.9. Зависимость величины отклонения между траекториями от соотношения

На последнем графике видно, что максимальное отклонение будет в точке с абсциссой x=0, при этом следует заметить, что при неограниченном возрастании соотношения  отклонение будет ограничено (его предельная величина).

Зависимость отклонения при  показана на рис.10. В этом примере рассмотрены траектории движения при следующих соотношениях 

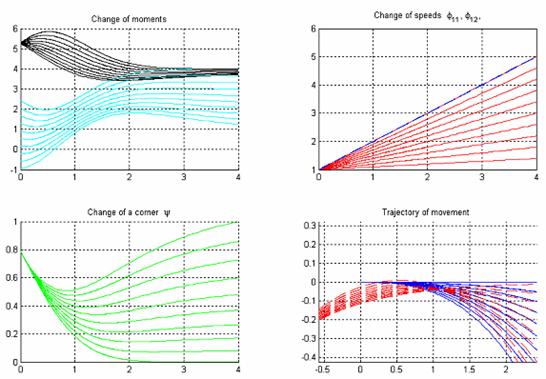
Рис.10. Зависимость величины отклонения между траекториями от соотношения

 

Таким образом, по численным результатам можно сделать вывод, что траектория движения хвостовой части системы действительно асимптотически стремится к траектории движения ведущей тележки. Отклонение максимально в начальный  момент.

 

6. Движение по прямой и окружности для двух тележек в случае обратного хода.

 

В этом параграфе  найдем моменты, необходимые для осуществления программных движений задней тележкой в направлении, обратном её  ориентации. Условием движения по прямой задней тележки является условие равенства угловых скоростей колес задней тележки:

 

 

Тогда из кинематических уравнений

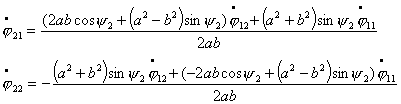
следует соотношение на ,:

                                    (6.1)

С другой стороны    т.е.

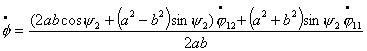                  (6.2)                                

Используя соотношения (6.1) и (6.2) получим:

 

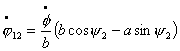
Подставим полученные выражения для , в уравнения для , тогда

 

.

 

Следует заметить, что в данном случае закон изменения угла между тележками такой же, как и в случае прямого хода, только с противоположным знаком. Аналогично предыдущему,    находится в явном виде:

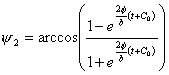                                                 (6.3)

Тогда, для движения вперед задней тележки, т.е. при   имеем  при . Это также означает, что угол между тележками  стремится к 0. Если , то  при  и тележки «складываются».

Теперь для реализации такого движения по прямой задней тележки найдем закон изменения моментов, прикладываемых на передние колеса из динамических уравнений (2.1).

Так как                    

 

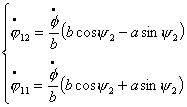
то    справедливо:

                                

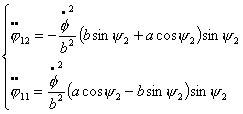
и динамические уравнения (2.1) примут вид:

 

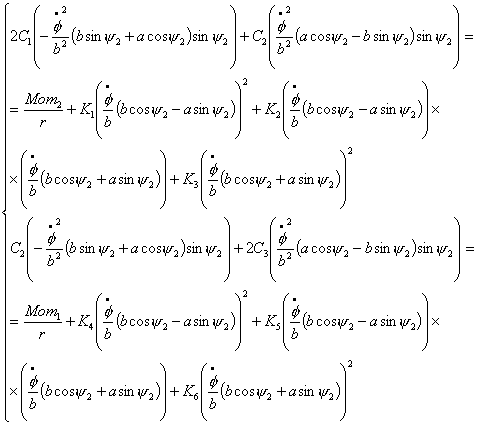
откуда имеем:

 

 

Подставляя в полученные выражения закон изменения угла  (6.3), получим законы изменения моментов, как функции времени.

Условием движения задней тележки по окружности, является следующее соотношение на  ее угловые скорости:

 

 

 

Радиус результирующей окружности равен .

Тогда из кинематических уравнений

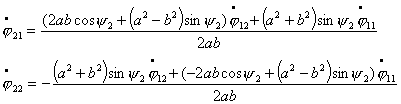
следует соотношение на ,:

 

                       (6.4)

С другой стороны    т.е.

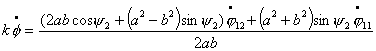                 (6.5)                                 

Используя соотношения (6.1) и (6.2), получим:

 

 

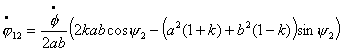
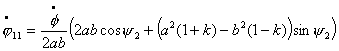
Подставим полученные выражения для , в уравнения для , тогда из кинематических уравнений следует:

Аналогично предыдущему угол  находится в явном виде:

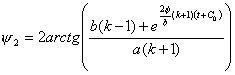                            (6.6)

Тогда, для движения задней тележки назад, т.е. при   имеем  при . Это соответствует движению системы по окружности радиуса . Если , то  при  и тележки «складываются».

Законы изменения моментов, прикладываемых на колеса ведущей тележки определяются из динамических уравнений (2.1).

Так как

 

 

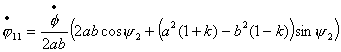
то справедливы следующие выражения:

 

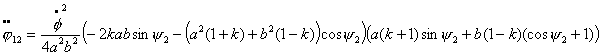
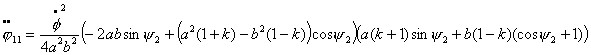
Используя, динамические уравнения (2.1), получим выражения для моментов:

 

 

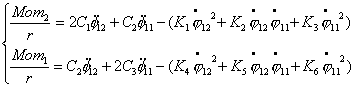
откуда, имеем:

 

 

 

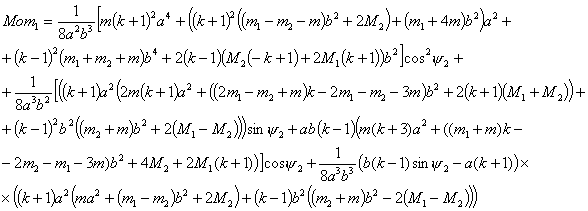
Таким образом, если в начальный момент времени выполнено условие: , то, прикладывая вышеуказанные моменты Mom1 и Mom2 на колеса ведущей тележки, получим, что задняя тележка будет двигаться по окружности заданного радиуса  в направлении противоположном ее начальной ориентации.

 

7.  Переходный процесс (обратный ход). Точность.

 

Определим моменты, которые необходимо прикладывать к колесам ведущей тележки для перехода из одного стационарного состояния в другое, если программное  движение осуществляется задней тележкой. Это означает, что в процессе такого движения угловая скорость вращения колес последней тележки должна меняться по линейному закону: 

 

                                   (7.1)

 

где - начальные угловые скорости задней тележки.

Тогда из кинематических уравнений имеем:

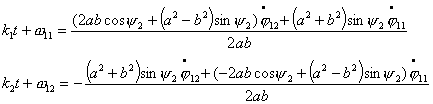
Выражаем , следующим образом:

 

        

    (7.2)

        

Подставим полученные выражения для , в уравнения для , тогда из кинематических уравнений следует:

 

(7.3)

Следует заметить, что в данном случае закон изменения угла между тележками такой же, как и в случае прямого хода, только с противоположным знаком, (аналогично случаю стационарного движения). Из данного дифференциального уравнения (7.3) получаем интегральное уравнение на угол .

Решения этого уравнения будут такими же, как и в случае прямого хода. Угол между тележками в обоих случаях меняется по одному и тому же закону. Движение в этом смысле обратимо.

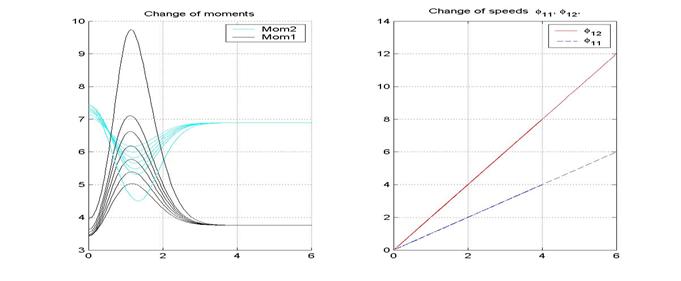
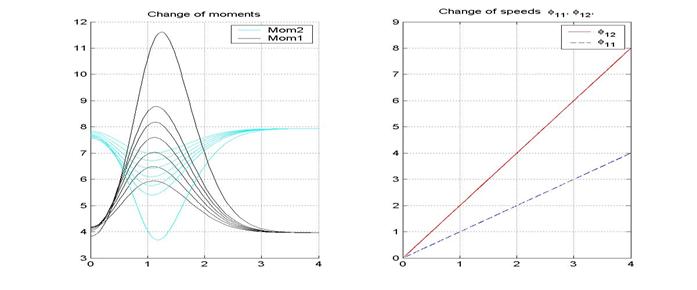
На рис. 11 изображены графики моментов прикладываемых на колеса ведущей тележки и их угловых скоростей соответственно.  Начальные условия для этого семейства кривых таковы: ;   меняется начальный угол между тележками . Из графика изменения скоростей видно, что скорости вращения колес передней тележки в начальный период меняются не по линейному закону, но с течением времени к нему стремятся вне зависимости от начального угла между тележками.

 

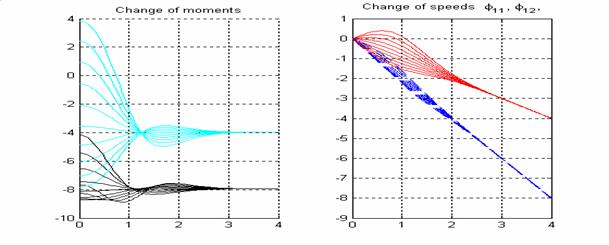
Рис.11. Основные характеристики ведущей тележки при «обратном ходе»

 

Из рис.12 видно, что на результирующие моменты также влияет соотношение геометрических характеристик тележки: длины продольной оси b к длине поперечной оси  a. ()

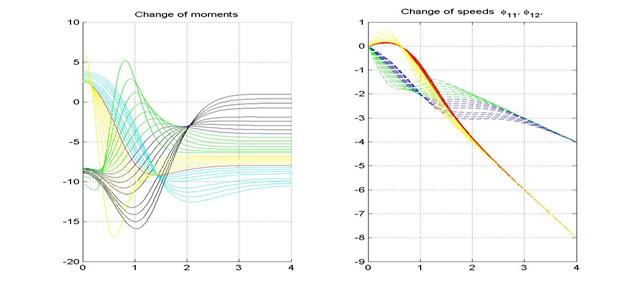
Рис.12. Влияние геометрических параметров тележки на основные характеристики.

 

Анализируя графики рис.12, можно сделать вывод, что стабилизация системы происходит тем быстрее, чем меньше соотношение b/a.

Очевидно, что траектория движения  задней тележки назад будет аналогична движению при «переходном процессе» [2] ведущей тележки вперед, т.е. движению по спирали.

Теперь, рассмотрим, насколько будет отличаться траектория передней тележки от траектории задней при таком движении.

На рис.13 приведены графики четырех различных семейств основных характеристик движения при условии, что законы изменения скоростей вращения колес задней тележки заданы следующим образом  для следующих начальных условий: ;  ; меняется начальный угол между тележками . Как и в случае прямого хода, первое семейство – семейство  моментов прикладываемых к колесам ведущей тележки, второе – семейство угловых скоростей колес ведущей тележки, третье – семейство углов между тележками, четвертое – семейство траекторий движения ведущей и ведомой тележек.

 

Рис.13. Основные характеристики движения. Обратный ход.

 

 На рис.14 сравниваются  изменения основных характеристик движения в случае прямого и обратного хода. Из подграфика 4 видно, что траектория движения второй тележки  аналогична траектории движения  ведущей тележки в случае прямого хода и, напротив, траектория движения ведущей тележки в случае обратного хода аналогична траектории задней тележки в случае прямого хода. Следовательно, все выводы, сделанные относительно возможных отклонений между траекториями движения ведущей и задней тележки в случае прямого хода справедливы и в случае обратного хода.

 

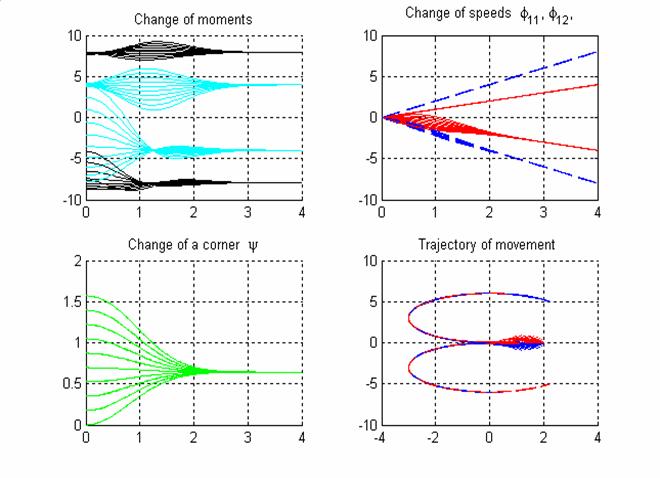
Рис.14. Основные характеристики движения. Прямой и обратный ход.

 

 

8. Комбинированное движение.

 

В предыдущих параграфах рассматривались возможные траектории движения системы при различных законах изменениях угловых скоростей вращения колес ведущей тележки. Для рассматриваемых законов получилось, что возможно три принципиально разных траектории – это прямая, окружность и спираль. Для движения системы будем далее пользоваться тремя этими режимами. Следует отметить, что абсолютно точно по этим траекториям движется лишь одна из тележек (а именно та, для которой эти траектории задаются), движение второй к этим траекториям асимптотически стремится.

Рассмотрим следующий пример 1.

Пусть движение состоит из семи этапов (название этапов подразумевает описание движения тележки, траектория движения которой соответственно задается):

1.     «равномерный» разгон;

2.     равномерное движение с одинаковыми начальными скоростями;

3.     «неравномерный» разгон с одинаковыми начальными скоростями;

4.     «неравномерный» разгон с разными начальными скоростями;

5.     равномерное движение с разными начальными скоростями;

6.     «равномерное торможение» с разными начальными скоростями;

7.     «неравномерное торможение» с разными начальными скоростями.

На подграфике 2 рис.15 показано как меняется угловая скорость вращения колес ведущей тележки на каждом этапе. Остановимся подробнее на каждом из этих этапов. Каждый этап характеризуется несколькими параметрами: начальное и конечное время интервала Т1 и Т2; и режим, который задается коэффициентами k1 и k2.

1. «Равномерный» разгон. T1=0, T2=1, , k1=1, k2=1 , ведущая тележка движется по прямой, скорость движения линейно растет, угол между тележками сокращается. В конечный момент этапа t=T2: . Значения всех характеристик движения системы в этот момент становятся начальными условиями для следующего этапа.

 

2. Равномерное движение с одинаковыми начальными скоростями. T1=1, T2=3, , k1=0, k2=0 . Так как в конечный момент предыдущего этапа угловые скорости вращения колес ведущей тележки равнялись друг другу и единице, то при равномерном движении эти скорости будут сохраняться, при этом угол между тележками сократится. Ведущая тележка движется по прямой.

 

3. «Неравномерный» разгон с одинаковыми начальными скоростями. T1=3, T2=5, , k1=1, k2=2 . Движение с таким законом изменения угловых скоростей является переходным процессом, и, следовательно, ведущая тележка движется по дуге спирали, угол между тележками при этом растет. В конечный момент времени угловые скорости вращения колес передней тележки имеют различные значения.

 

4. «Неравномерный» разгон с разными начальными скоростями. T1=5, T2=6, , k1=1, k2=0 . Это тоже переходный процесс, при котором скорость одного из колес остается постоянной, а скорость другого равномерно растет. Ведущая тележка движется по спирали. Угол между тележками  сокращается. В конечный момент времени угловые скорости вращения колес различные.

 

5. Равномерное движение с разными начальными скоростями. T1=6, T2=7, , k1=0, k2=0 . Так как начальные скорости различны и нет разгона (т.е. изменения скорости), то движение будет проходить по дуге окружности. Угол между тележками стремится к фиксированному значению (характерному для данной окружности).

 

6. «Равномерное торможение» с разными начальными скоростями. T1=7, T2=8, , k1=-1, k2=-1 . Это переходный процесс. Движение ведущей тележки осуществляется по дуге спирали. Угловые скорости вращения колес равномерно падают, но не до нуля и в конечный момент различны.

 

7. «Неравномерное торможение» с разными начальными скоростями. T1=8, T2=10, , k1=-1,5, k2=-2  . Это опять переходный процесс, но уже с неравномерным изменением скоростей различных колес ведущей тележки. Ведущая тележка движется по дуге спирали и в конечный момент останавливается.

На рис.15 приведены 4 различных семейства основных характеристик движения для описанного комбинированного движения, удовлетворяющие одинаковым начальным условиям, за исключением начального угла между тележками .

 

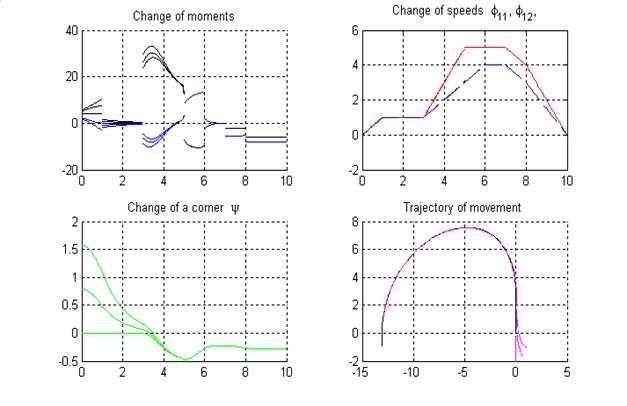
Рис.15. Основные характеристики комбинированного движения.

 

На подрафике 1 рис.15 представлены моменты, которые необходимо прикладывать в каждый момент времени к колесам ведущей тележки для осуществления вышеописанного движения. На подграфике 3 изображено изменения угла между тележками в течение всего интервала времени. На подграфике 4 изображена траектория заданного выше комбинированного движения. Из подграфика 4 можно сделать вывод, что начальный угол между тележками не влияет на траекторию движения системы, он влияет лишь на величину моментов, которые необходимо приложить  к колесам ведущей тележки.

Теперь рассмотрим комбинированное движение для задней тележки (т.е. будет задаваться траектория движения именно задней тележки, при управление моментами, прикладываемыми к колесам ведущей тележки). Пусть движение состоит из тех же этапов, что и в примере 1. Для каждого этапа основные характеристики движения меняются по несколько другим законам. Изменения основных характеристик движения системы приведены на рис.16.

В отличие от прямого хода  значение начального угла между тележками влияет не только на моменты, прикладываемые к колесам ведущей тележки, но и на их угловые скорости. Тем не менее, из подграфика 2 следует, что закон изменения угловых скоростей ведущей тележки для обратного хода достаточно близок к закону изменения угловых скоростей для прямого хода.

 

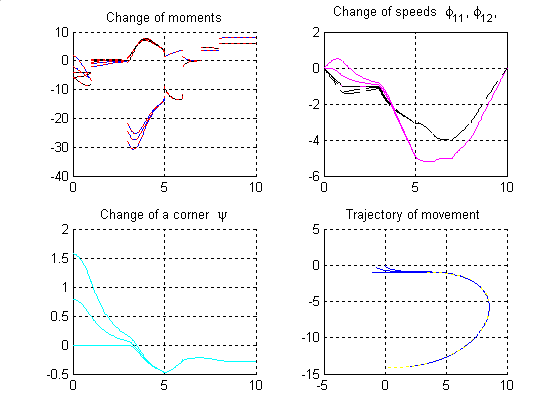
Рис.16.  Основные характеристики комбинированного движения. Обратный ход.

 

На следующем рис.17 сравниваются 2 полученных движения: прямой и обратный ход с одинаковыми начальными условиями и одинаковыми этапами комбинированного движения.

 

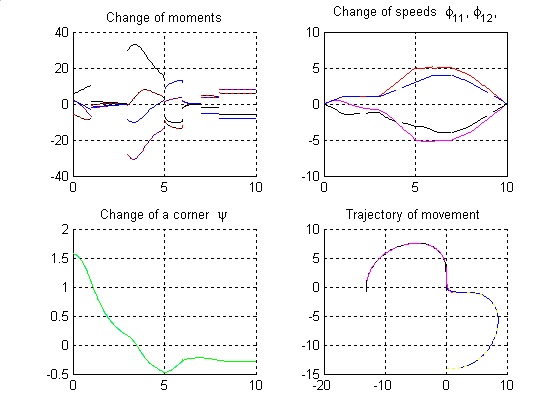
Рис.17. Комбинированное движение. Прямой и обратный ход.

 

Из полученных графиков можно сделать вывод, что движение при прямом и обратном ходе происходит по траекториям, симметричным относительно некоторой оси (биссектрисы начального угла между тележками), при одинаковых начальных условиях и этапах комбинированного движения. Заметим, что вместо точного совпадения траекторий возникает симметрия. Это связано с тем, что коэффициенты k1 и k2, в случае обратного хода имеют противоположные по знаку значения. Также, надо учесть, что начальные координаты тележки, траекторию движения которой мы задаем, в первом и втором примерах разные.

 

ЗАКЛЮЧЕНИЕ

 

В работе построен алфавит базовых управляемых движений и исследованы их характеристики. Выведены законы изменения моментов, которые необходимо приложить к колесам ведущей тележки для движения с заданными законами изменения скоростей колес ведущей тележки, а, следовательно, совершения ведущей тележкой программных движений (по прямой, окружности и спирали Корню). Построены алгоритмы управления «робопоездом» при движении «вперед» и «назад». Аналитически показана обратимость таких движений

Проведен численный анализ движения хвостовой части системы относительно движения ведущей тележки. Найдены точности отклонений между траекториями ведущей тележки и хвостовой части.

Используя реализацию вышеописанных программных движений, можно строить с их помощью различные алгоритмы планирования движения цепочки «робопоезд», выбирать оптимальные способы прохождения такой системой трасс различной сложности.

 

 

Список литературы

 

  1. В.Е.Павловский, Н.В.Петровская. Исследование динамики движения цепочки «робопоезд». Уравнения движения, частные решения. Препринт ИПМ им.М.В.Келдыша РАН, 2005г.

 

  1. В.Е.Павловский, В.В.Евграфов, В.В.Павловский. Планирование и реализация гладких движений мобильного робота с дифференциальным приводом.// Тр. 9 Междунар. Конф. "Stability, Control, and Rigid Bodies Dynamics",
    ICSCD-2005,     с.54-55.

 

3.     Неймарк Ю.И., Фуфаев Н.А. Динамика неголономных систем. − М.: Наука, 1967.−520 с.

 

  1. Голубев Ю.Ф.  Основы теоретической механики: Учебник.  М.: Изд-во Моск. Ун-та., 2000.-719c.

 

  1. Маркеев А.П.  Теоретическая механика: Учебное пособие.  М.: Наука, 1990.-416c.