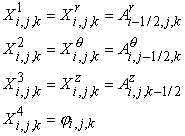Abstract
A numerical method of calculating harmonic three-dimensional electromagnetic field in
the metallic pipe with local defects is described. The problem is subdivided onto two
stages: calculation of the two-dimensional field in infinite domain for a clean pipe,
and calculation of a local three-dimensional field “generated” by a defect. A second-order
difference scheme for the four-component equations system of potentials is written out.
Several iteration methods of finding the solution of the governing linear equations are
investigated. A strategy of the multigrid approach for the considered class of problems
is proposed.
Àííîòàöèÿ
Îïèñûâàåòñÿ ÷èñëåííûé ìåòîä ðàñ÷åòà ãàðìîíè÷åñêîãî òðåõìåðíîãî ýëåêòðîìàãíèòíîãî ïîëÿ â
ìåòàëëè÷åñêîé òðóáå ñ ëîêàëüíûì äåôåêòîì. Çàäà÷à ðàçäåëåíà íà äâà ýòàïà: ðàñ÷åò äâóìåðíîãî
ïîëÿ â áåñêîíå÷íîé îáëàñòè äëÿ òðóáû áåç äåôåêòà, è ðàñ÷åò ëîêàëüíîãî òðåõìåðíîãî ïîëÿ,
«íàâåäåííîãî» äåôåêòîì. Âûïèñàíà ðàçíîñòíàÿ ñõåìà âòîðîãî ïîðÿäêà òî÷íîñòè äëÿ
÷åòûðåõêîìïîíåíòíîé ñèñòåìû óðàâíåíèé â ïîòåíöèàëàõ. Èññëåäîâàíû íåêîòîðûå èòåðàöèîííûå
ìåòîäû íàõîæäåíèÿ ðåøåíèÿ ïîëó÷àåìîé ñèñòåìû ëèíåéíûõ óðàâíåíèé. Âûðàáîòàíà ñòðàòåãèÿ
ïðèìåíåíèÿ ìíîãîñåòî÷íîãî ìåòîäà äëÿ ðàññìàòðèâàåìîãî êëàññà çàäà÷.
1
Introduction:
class of problems under solution and structure of the algorithm
We consider a cylindrical pipe
that can have a defect like a pit or hole. The cylindrical system of
coordinates with the same axes as the pipe is used. It is supposed that defects
are formed by set of hexahedral cells.
In order to avoid solution of
a full external problem we subdivide it onto two stages. First the unperturbed
two-dimensional field is calculated for the clean pipe (without defects) with a
given geometry and excitation conditions. Than a three-dimensional subdomain
(box) with the given defect is considered, and the three-dimensional problem
for Maxwell equations with Dirichlet boundary conditions of the electrical
field on the external boundaries is solved, see Figure 1 and Figure
2.
The two-dimensional
unperturbed problem is solved by the algorithm described in [1]; so we have the solution for the azimuth
component 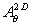 of the vector potential
of an axis-symmetric background solution. For the three-dimensional problem the
electrical field of the vector potential
of an axis-symmetric background solution. For the three-dimensional problem the
electrical field 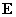 is represented in the
box by sum of vector and scalar potentials is represented in the
box by sum of vector and scalar potentials
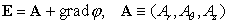
with the boundary
values
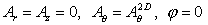 . .
It is supposed that the box is
big enough to believe that the Dirichlet conditions from unperturbed problem
can provide a required accuracy of modeling.
The three-dimensional problem
in the box is solved by an iteration method (GMRES or MultiGrid algorithms, see
Section 4) starting from the two-dimensional solution as an
initial guess. Evidently this mixed (2D-3D) approach permits to drastically
save computational efforts.
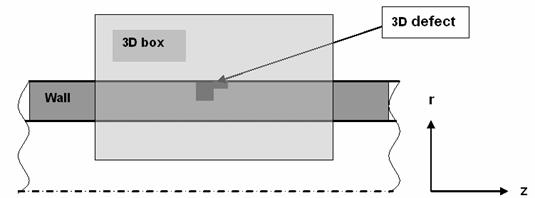
Figure 1: Computational domain with the pipe wall,
cross-section at θ=const
Figure 2: Computational domain, cross-section at z=const
This work was supported by the RFBR grant No. 04-01-00567
and grant RM0-1298, CRDF.
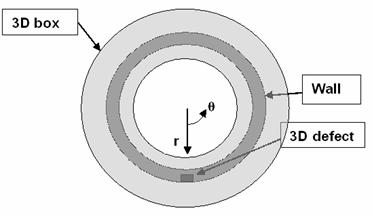
The Maxwell equations
written for the harmonic-in-time electromagnetic field (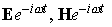 ) in media with a non-constant magnetic permeability ) in media with a non-constant magnetic permeability 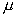 , conductivity , conductivity  , and electrical permittivity , and electrical permittivity
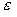 read read
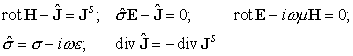
where 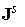 is a given source
current density. is a given source
current density.
Numerical solution of
these equations in three dimensions for media containing
dielectric-ferromagnetic boundaries remains a challenge problem still. The known
difficulties are discussed, e.g., in Introduction section of the paper [2], and we just remind two those important in our
case:
·
handling regions of vanishing
conductivity. The operator of the system has a non-zero kernel in these
regions;
·
handling regions of strongly
jumping conductivity and magnetic permeability at boundaries metal-air.
A more or less
compromise approach to resolve the above mentioned issues consists of using a
second order difference scheme on a staggered regular non-uniform grid to
approximate the following corrected system of equations
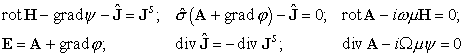
with auxiliary functions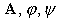 , and a constant , and a constant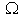 , see details in the cited paper. , see details in the cited paper.
This system is not the
final one. It is possible to reduce the system to the second-order equations
with 4 unknown scalar functions: three components of the vector potential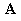 and the scalar potential and the scalar potential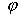 : :
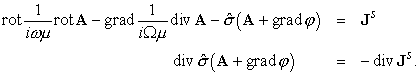
3
Difference
scheme
our system of equations reads in the scalar form:


The
three-dimensional solution is obtained in the computational domain (box)
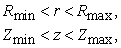
for
the whole azimuth angle 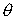 . The box is covered by a structured grid having the
hexahedral cells: . The box is covered by a structured grid having the
hexahedral cells:
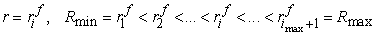 , ,
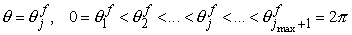 , ,
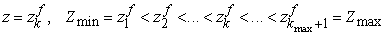 , ,
the
number of cells is 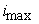 , , 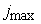 , and , and 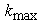 in in 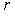 , , 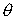 , and , and 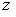 directions,
respectively. directions,
respectively.
We
represent the computational domain by finite volumes with the central point
corresponding to the index 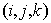 . Grid functions are defined on the following points referred
to different faces and the center of the cell, respectively: . Grid functions are defined on the following points referred
to different faces and the center of the cell, respectively:
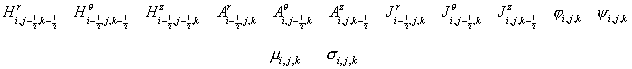
The
cell centers with prescribed conductivity 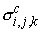 and magnetic
permeability and magnetic
permeability 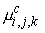 are calculated by are calculated by
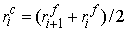 , ,
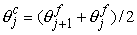 , ,
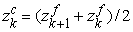 . .
The
corresponding difference equations on a non-uniform grid with spacing 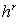 , , 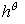 and and 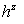 read as follows: read as follows:
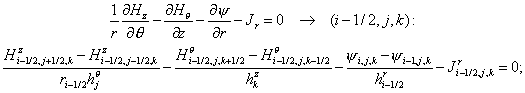 (2.1) (2.1)
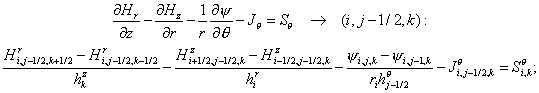 (2.2) (2.2)
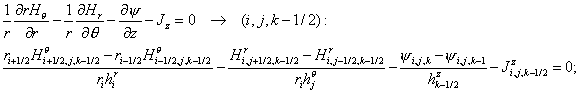 (2.3) (2.3)
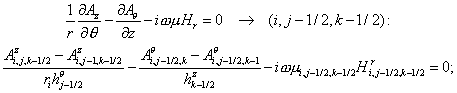 (2.4) (2.4)
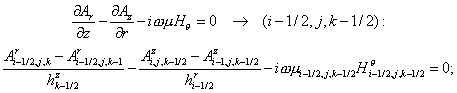 (2.5) (2.5)
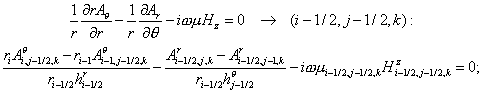 (2.6) (2.6)
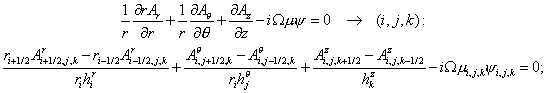 (2.7) (2.7)
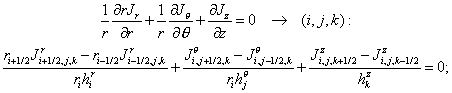 (2.8) (2.8)
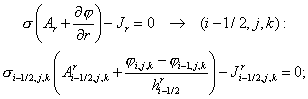 (2.9) (2.9)
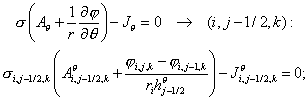 (2.10) (2.10)
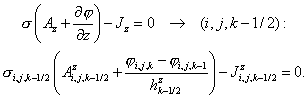 (2.11) (2.11)

(we give also the grid index for the right hand side of each equation).
Let us remove the half-integer indices by introducing notation
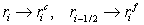 , ,
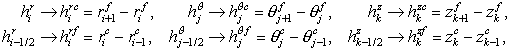 , ,
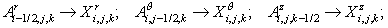
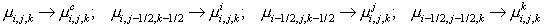 , ,
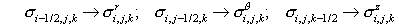
where
superscripts “c” and “f” refer to the points located at the center and on a
face of the cell, respectively; value of
μ at the cell edges is
evaluated by the arithmetic averaging, and
σ at the cell faces is
evaluated by the harmonic averaging.
The
vector 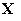 of unknown difference
functions consists of the four potential components: of unknown difference
functions consists of the four potential components:
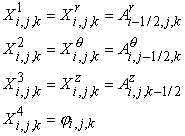 (3)
(3)
After
some algebra, we exclude the functions 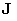 , , 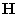 , and , and 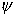 from (2.1) to (2.11),
and obtain the system of four difference equations: from (2.1) to (2.11),
and obtain the system of four difference equations:



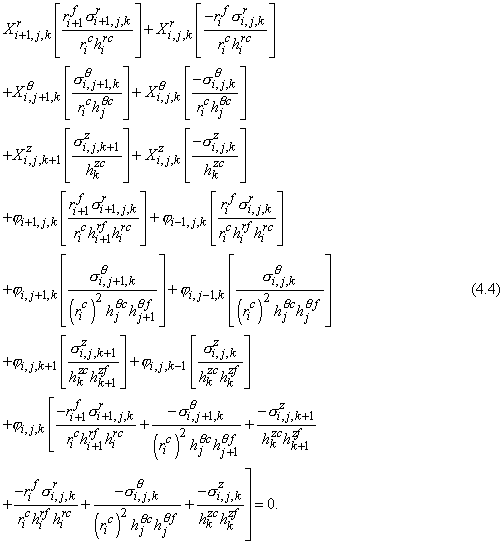
We write the system of the algebraic equations for
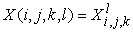
as
follows:
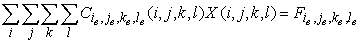
or
in the matrix form
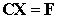
where 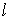 is a number of the
unknown function (corresponds to the superscript of is a number of the
unknown function (corresponds to the superscript of 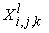 ), ), 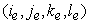 is the equation vector
number (number of the matrix row). is the equation vector
number (number of the matrix row).
Let us describe the rules of forming the matrix entries. The calculation
domain consists of 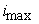 , , 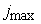 , , 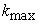 cells along the
coordinates cells along the
coordinates 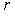 , , 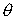 , and , and 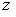 , respectively. The rows of the matrix , respectively. The rows of the matrix 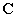 and the
right-hand-side vector and the
right-hand-side vector 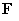 are calculated
depending on the equation number are calculated
depending on the equation number 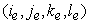 , i.e. according to equations (4.1) to (4.4) if the index
corresponds to an internal point, and according to the Dirichlet condition
otherwise (other coefficients for ghost unknowns must be zero). , i.e. according to equations (4.1) to (4.4) if the index
corresponds to an internal point, and according to the Dirichlet condition
otherwise (other coefficients for ghost unknowns must be zero).
The system of
algebraic equations obtained after the discretization is really huge: more than 250000 unknown complex values for a
mesh of 40´40´40 cells (the typical mesh for a single simple defect). The system has a
large conditional number because of a non-uniform grid and discontinuous
coefficients on the metal-air boundaries. That is why finding of solution to
this system is a difficult problem. Only iterative methods can be used. Here we
consider use of GMRES with ILU preconditioning and Multigrid methods.
4.1
GMRES-ILU
solver
The iteration Krylov
subspaces method (GMRES algorithm) with an Incomplete Lower-Upper
preconditioner is used by calling the correspondent procedures from the IMSL mathematical library. The solution
procedure consists of two stages: calculation of the ILU factorization
precondition matrix, and GMRES iterations with this preconditioner. The first
stage requires large enough computational time comparing the iterations time:
for instance 484sec versus 40sec. However, for the problem with multiple RHSs
in (4.2), say N, one must calculate the preconditioner only once, and then it
is used for iteration solution with each RHS. Hence the total computational
time in this example equals 484 + N*40.
The main drawback of
the GMRES-ILU approach consists of a large additional memory required by the
ILU precondition matrix: in our computations the latter is usually at least 10
times greater than memory occupied by the matrix of the original system. This
ILU matrix must be kept in computer memory. That is why there exists a
limitation to the grid volume about 60´40´40 cells for the Windows PC (2 GB application memory).
An optimal choice of
the parameter Ω that drastically influence the number of iterations is
Ω=0.5ω.
According to the
original idea of the author of the multigrid method, see [3] to [6] the multigrid approach is based on the following
observation. It is known that while exploring simple iteration methods the
high-frequency components of the residual vanish much faster than the
low-frequency ones. Therefore after several iterations on the initial fine
grid, one can try to reduce the low-frequency part of the residual by using
coarser grid. The coarser grid requires much smaller time for a single
iteration and suppresses more efficiently the low-frequency harmonics.
Let us make general
remarks concerning the efficiency of the multigrid method. Evidently it depends
on all elements of the construction:
·
grid coarsening algorithm,
“coarse” operators (matrices) 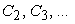
·
smoother strategy (operators 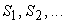 and numbers of
subiterations and numbers of
subiterations 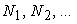 ) )
·
restriction operators 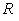
·
prolongation operators 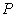
Additional
difficulties for our case are caused by the following circumstances:
·
the staggered grids are used
for difference equations; therefore the corner points of solutions at the
metal-air frontiers do not match each other on the grids 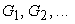
·
high contrasts in 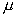 influence strongly the
choice of the smoother strategy. influence strongly the
choice of the smoother strategy.
However, theoretically
the multigrid approach can provide a very efficient solution procedure for both
memory and computational costs.
We consider the above
listed elements in the subsections below.
Note that our current
multigrid version permits to handle grids with 72´80´80 cells.
It is known that if we
define the difference operator on a coarse grid by

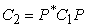 (5)
(5)
then it ensures the
closeness of solutions on coarse and fine grids in the "weak", or
"galerkin", sense. This choice of 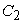 is called Galerkin
coarse grid approximation. The formula has theoretical advantages but its realization can be too computationally
expensive in practice. is called Galerkin
coarse grid approximation. The formula has theoretical advantages but its realization can be too computationally
expensive in practice.
Another construction
of the difference operator on a coarse grid is encountered in literature: the
operator 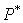 is replaced by is replaced by 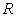 . It simplifies the realization significantly, yet its
computational complexity is still very high. . It simplifies the realization significantly, yet its
computational complexity is still very high.
An alternative method
to obtain the coarse grid matrix 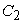 consists of a direct
discretization of governing differential equations on the grid consists of a direct
discretization of governing differential equations on the grid 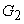 . This method is called discretization coarse grid
approximation. The approach is quite simple and computationally cheap since the
matrix coefficients are calculated by the same algorithm as for the fine grid.
That is why we chose it currently. . This method is called discretization coarse grid
approximation. The approach is quite simple and computationally cheap since the
matrix coefficients are calculated by the same algorithm as for the fine grid.
That is why we chose it currently.
Another source of
different variants influencing the convergence rate originates from the
possible structure of the matrixes 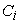 themselves. First of
all, a rule of the unknown values themselves. First of
all, a rule of the unknown values 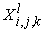 ordering in the
one-dimensional vector ordering in the
one-dimensional vector 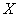 is critical. We have
examined 14 different variants. Four of them are described by using
construction of the implicit FORTRAN cycle: is critical. We have
examined 14 different variants. Four of them are described by using
construction of the implicit FORTRAN cycle:
A.
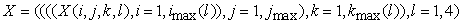 , ,
B.
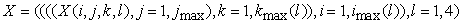 , ,
C.
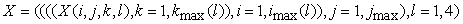 , ,
D.
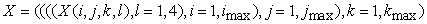 , ,
The number of unknown
values for the indexes 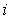 and and 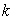 that correspond to that correspond to 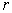 and and 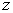 coordinates,
respectively, is various for different function numbers coordinates,
respectively, is various for different function numbers 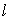 since some of them are
referred to the centers of the grid cells and the others – to the faces. In
case D, the variation limits of the function indexes are artificially set to be
the same for all since some of them are
referred to the centers of the grid cells and the others – to the faces. In
case D, the variation limits of the function indexes are artificially set to be
the same for all 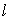 by adding fictitious
unknowns with correspondent identity equations. Otherwise the extra unknowns
should be put to the end of the vector by adding fictitious
unknowns with correspondent identity equations. Otherwise the extra unknowns
should be put to the end of the vector 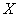 . This case has also been tested but it has no advantages
over the case D. . This case has also been tested but it has no advantages
over the case D.
A variant of modifying
matrix 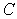 by eliminating the
unknowns at the boundary points from the vector by eliminating the
unknowns at the boundary points from the vector 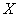 has been examined
separately. Such elimination is possible because the values has been examined
separately. Such elimination is possible because the values 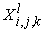 are explicitly defined
at the boundary points (Dirichlet conditions). So the corresponding entries are
put to the right-hand-side. One of the advantages of such modification is a
noticeable reduction of the number of unknowns, especially for the coarse
grids. For instance, in case of are explicitly defined
at the boundary points (Dirichlet conditions). So the corresponding entries are
put to the right-hand-side. One of the advantages of such modification is a
noticeable reduction of the number of unknowns, especially for the coarse
grids. For instance, in case of 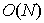 grid cells in each
direction, the number of difference equations is grid cells in each
direction, the number of difference equations is 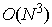 , the number of the boundary entries is about , the number of the boundary entries is about 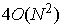 (the condition of
periodicity was taken into account earlier). (the condition of
periodicity was taken into account earlier).
The following
renormalization of matrix 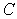 rows gives an
additional advantage while eliminating the boundary points: we multiply (4.1)
by rows gives an
additional advantage while eliminating the boundary points: we multiply (4.1)
by 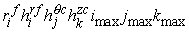 , (4.2) by , (4.2) by 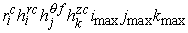 , (4.3) by , (4.3) by 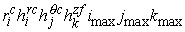 , and (4.4) by , and (4.4) by 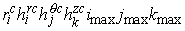 . Thus the solution of the system remains the same but the
matrix . Thus the solution of the system remains the same but the
matrix 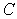 becomes symmetrical
(the factor becomes symmetrical
(the factor 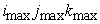 provides independency
of the matrix norms on the coarse/fine grid). The matrix symmetry property
permits to double reduce the memory for matrix elements keeping. provides independency
of the matrix norms on the coarse/fine grid). The matrix symmetry property
permits to double reduce the memory for matrix elements keeping.
The smoothing methods
in multigrid algorithms are usually chosen from the class of basic iterative
methods. We are exploring the so-called two-layers iteration methods having the
form
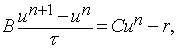 (6)
(6)
or
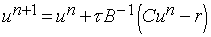
where 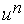 is the n-th iteration
to the solution of the equation is the n-th iteration
to the solution of the equation 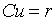 , , 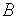 is a preconditioner, is a preconditioner, 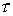 is the parameter of
iterations, which is chosen from the condition of a fastest convergence. is the parameter of
iterations, which is chosen from the condition of a fastest convergence.
Choice of the
preconditioner is very critical. The
next two preconditioners have been constructed after analysis of the matrix 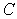 structure. Figure
shows a
general fragment of structure. Figure
shows a
general fragment of 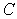 for the ordering
variant A, see subsection 4.2.1, on a coarse grid for the ordering
variant A, see subsection 4.2.1, on a coarse grid 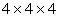 cells. The squares
denote non-zero entries; the black squares belong to the main diagonal. One can
observe that the density of the non-zero elements is sufficiently high at the
three diagonals: main, and two neighboring. The remaining entries belong to
diagonals that are separated by a distance from the main one, which grows while
increasing the grid volume. That is why we take a simple preconditioner matrix
having these three diagonals (with the minus sign). The matrix structure for
the variants B and C is very similar. The matrix structure for the variant D is
shown in Figure 4 (for the same grid volume). Now the non-zero entries occupy
densely already nine diagonals: main, four above, and four below. Therefore a
ninth-diagonal preconditioner matrix cells. The squares
denote non-zero entries; the black squares belong to the main diagonal. One can
observe that the density of the non-zero elements is sufficiently high at the
three diagonals: main, and two neighboring. The remaining entries belong to
diagonals that are separated by a distance from the main one, which grows while
increasing the grid volume. That is why we take a simple preconditioner matrix
having these three diagonals (with the minus sign). The matrix structure for
the variants B and C is very similar. The matrix structure for the variant D is
shown in Figure 4 (for the same grid volume). Now the non-zero entries occupy
densely already nine diagonals: main, four above, and four below. Therefore a
ninth-diagonal preconditioner matrix  has been examined in
this case. has been examined in
this case.
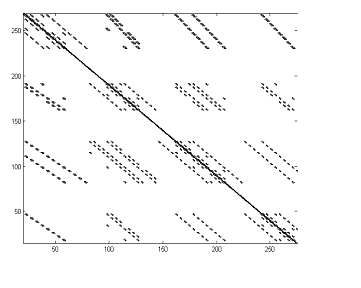
Figure 3: Non-zero entries of the matrix  (ordering variant A) (ordering variant A)
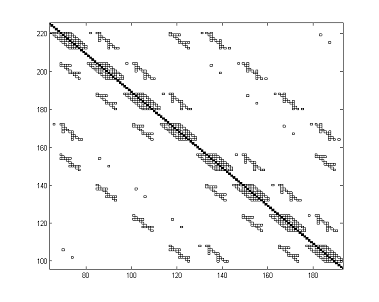
Figure 4: Non-zero entries of the matrix  (ordering variant D) (ordering variant D)
Below we describe some
of the most important results (from our viewpoint) balking many others beyond
the description.
The fastest
convergence provides the three-diagonal preconditioner for the ordering A. The
variant works about 10 times faster than the variant with the diagonal
preconditioner (Jacobi method). The variant with the ninth-diagonal
preconditioner has approximately the same number of multigrid cycles needed to
diminish the residual 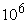 times as the
three-diagonal variant. However, it requires more computational time per single
iteration. times as the
three-diagonal variant. However, it requires more computational time per single
iteration.
Important question is
choice of values 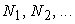 . We made experiments mainly for the two-grid algorithm with
the three-diagonal preconditioners. A typical result for the clean pipe with
the grid volume . We made experiments mainly for the two-grid algorithm with
the three-diagonal preconditioners. A typical result for the clean pipe with
the grid volume 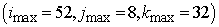 is collected in Table 1. Table cells contain total number of
iterations for the fine and coarse grids (separated by the “plus” sign) that is
needed to reduce the residual for is collected in Table 1. Table cells contain total number of
iterations for the fine and coarse grids (separated by the “plus” sign) that is
needed to reduce the residual for 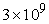 times; the total
computational time is given as well. times; the total
computational time is given as well.
|
|
N1=8
|
N1=16
|
N1=32
|
|
N2=8
|
144+136
9.83 sec
|
202+96
11.19 sec
|
297+72
14.48 sec
|
|
N2=16
|
104+192
7.50 sec
|
128+112
7.36 sec
|
203+96
10.27 sec
|
|
N2=32
|
80+288
6.45 sec
|
90+160
5.64 sec
|
139+128
7.28 sec
|
|
N2=64
|
72+512
7.05 sec
|
75+256
5.22 sec
|
107+192
6.14 sec
|
|
N2=128
|
72+1024
9.39 sec
|
74+512
6.41 sec
|
107+384
6.97 sec
|
Table 1
Solution of the same
problem on a single grid requires 530 iterations and 23.4 seconds. Thus the
two-grid method saves the computational time for about 4.5 times at 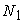 =16 and =16 and  =64. Note that the gain remains still enough if the
parameters are significantly changed. =64. Note that the gain remains still enough if the
parameters are significantly changed.
Similar results for
the pipe with a groove defect (revolution symmetry) are collected in Table 2. The grid volume is 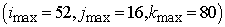 , residual drops , residual drops 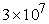 times. The single-grid
problem requires 1822 iterations and 647 seconds. Thus the gain is about 16
times in computational time if times. The single-grid
problem requires 1822 iterations and 647 seconds. Thus the gain is about 16
times in computational time if 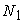 =16 and =16 and  =128. =128.
|
|
N1=8
|
N1=16
|
|
N2=16
|
216+416
121 sec
|
364+352
141 sec
|
|
N2=32
|
128+480
77 sec
|
217+416
90 sec
|
|
N2=64
|
72+512
48 sec
|
122+448
56 sec
|
|
N2=128
|
48+460
40 sec
|
74+512
40 sec
|
|
N2=256
|
39+1024
45 sec
|
57+768
40 sec
|
|
N2=512
|
35+2048
71 sec
|
53+1536
59 sec
|
Table 2
Optimization of
parameters N1, N2, N3 for a three-grid method requires much more variants. We
report the final result here for the same problem but another groove defect:
575, 52, and 23 seconds of computational time for single-grid, two-grid, and
three-grid methods, respectively.
At the moment we use
coarse grids constructed by joining two cells along each direction. Speaking
more precisely, eight grid cells of a fine grid with the same vertex are
combined pair-wise in each direction into a single cell of the coarse grid.
All four unknown grid
functions are referred to different points of the cell: the first three are
referred to the centers of corresponding faces and the fourth one is referred
to the cell center. Therefore individual interpolation formulas for each
function are needed.
Consider the
coarsening for one of the first three functions. The reduction is made
consequently for each direction. As initial direction we take that
corresponding to the considered function (function is referred to the center of
faces orthogonal to the direction). The face coordinate of the coarse grid in
this direction coincides with one of the face coordinate on the fine grid.
Therefore the simplest way is to assign the function value on a fine grid to
the function value on a coarse grid. However it is reasonable sometimes to
filter the undesirable high-frequency component having the form of 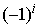 where where 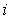 is the point number
along the considered direction. It is convenient to write the reduction as
follows: is the point number
along the considered direction. It is convenient to write the reduction as
follows:
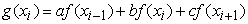
where 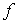 is the fine grid
function, is the fine grid
function, 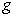 is the coarse grid
function, is the coarse grid
function, 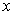 is the coordinate
along the considered direction. In order to exactly reconstruct linear
functions, the coefficients is the coordinate
along the considered direction. In order to exactly reconstruct linear
functions, the coefficients 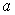 and and 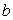 should be calculated
by the following formulas: should be calculated
by the following formulas:
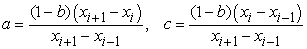
The high-frequency component is filtered entirely at the
value 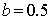 . The point-to-point transfer is done if . The point-to-point transfer is done if 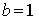 , i.e. , i.e. 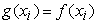 . .
Along other directions
the functions are referred to coordinates corresponding to the cell centers.
The coarse cell center is located between the fine cell centers. Therefore
either two-points linear interpolation or four-points cubic interpolation is
explored.
The same consequent
interpolation procedure is used for the fourth function.
Notice that the
residuals are evaluated by different operators at the boundary and internal
points. Therefore, the discrete function usually has a jump nearby the boundary
(because of the Dirichlet conditions, the residual just vanishes at the
boundary). Evidently, one cannot use the interpolation at the border points: an
extrapolation from inner points is explored instead. It can generate unwanted
perturbations.
4.2.4
Prolongation operators
Construction of the
prolongation operators consists of subsequent linear or cubic interpolation for
each direction.
An issue arises on the
air-metal frontier because of discontinuity of the first derivatives in
solution. Since we use a staggered grid, the points of discontinuity don’t
coincide on fine and coarse grids. Therefore the prolongation operator
generates undesirable perturbations of the residual in points nearby the
frontier. One needs additional computational work on the fine grid to suppress
these perturbations. Let us look at
Figure 5 in order
to illustrate the problem.
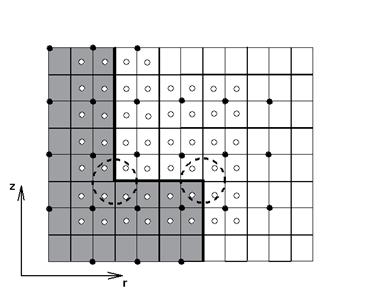
Figure 5: Coarse and fine grids
We show a
two-dimensional cross-section 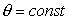 of the computational
domain fragment. The gray color denotes
the subdomain occupied by the metal. Coarse and fine grid cells are drawn by
thick and thin lines, respectively (each coarse cell joints four fine cells
(eight in three dimensions)). The location of the azimuth component of the computational
domain fragment. The gray color denotes
the subdomain occupied by the metal. Coarse and fine grid cells are drawn by
thick and thin lines, respectively (each coarse cell joints four fine cells
(eight in three dimensions)). The location of the azimuth component 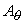 considered on the
coarse and fine grids is shown by the black and white circles, respectively. We
see that these points do not coincide in the staggered coarse and fine grids
(moreover black and white circles are also shifted in the considered on the
coarse and fine grids is shown by the black and white circles, respectively. We
see that these points do not coincide in the staggered coarse and fine grids
(moreover black and white circles are also shifted in the 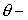 direction normal to the sheet). Function direction normal to the sheet). Function 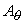 is not smooth near the
metal-air boundary: it has the discontinuous derivative with respect to the
normal direction. A typical one-dimensional graph along the is not smooth near the
metal-air boundary: it has the discontinuous derivative with respect to the
normal direction. A typical one-dimensional graph along the 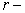 direction is shown in Figure
6. direction is shown in Figure
6.
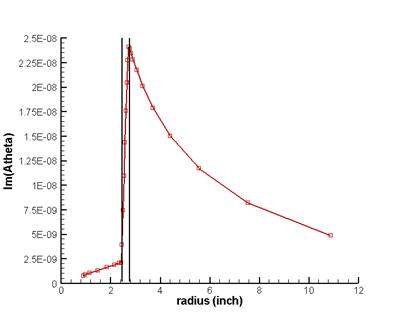
Figure 6: Imaginary part of 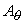 along radius at fixed along radius at fixed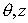 . .
Vertical lines denote the metal-air boundaries
Two typical
two-dimensional graphs near the defect on the 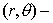 plane and plane and 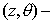 plane are drawn in Figure
7 and Figure 8, respectively. plane are drawn in Figure
7 and Figure 8, respectively.
Therefore the
prolongation operators, i.e. the evaluation of the correction function in the
white circles from the values in the black circles (which is based on an
interpolation procedure), can give and, in fact, does give “wrong” magnitudes
near the boundary, especially in the corner regions shown by the dashed circles
in Figure 5.
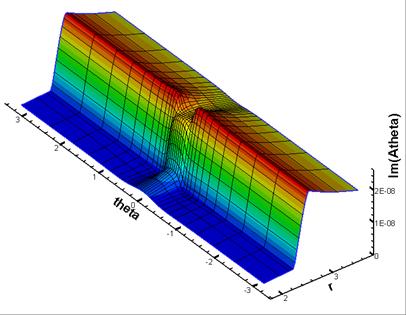
Figure 7: Imaginary part of 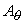 on the plane on the plane 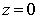 corresponding to corresponding to
the defect center
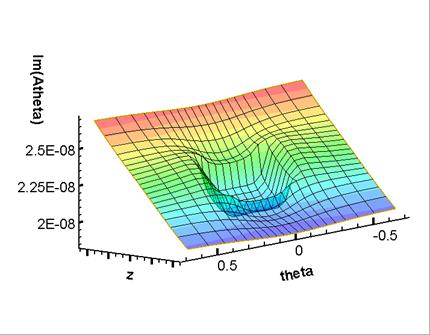
Figure 8: Imaginary part of 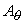 on the plane on the plane 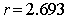 corresponding to corresponding to
the defect bottom face
The correction
function prolonged from the coarse grid to the fine one has a wider domain of
the singular behavior near the boundary (in terms of the number of cells). During the multigrid cycle this implies the
sharp growth of the local residual on the fine grid while adding the
correction.
In order to overcome
the issue we decided to make additional smoother iterations in the “singular”
subdomains just after the prolongation operator. The correction function is
changed locally in these subdomains (having several points width), and it
becomes sharper near the air/metal boundary. Evidently this procedure is
sufficiently computationally cheap, and it can be treated as a special kind of
the interpolation correspondent to the solution structure. The procedure can be
called the local smoother.
As to the way of
interpolation, the preliminary observation is as follows: two-grid experiments
show that the cubic interpolation has practically no advantage over the linear
one. Moreover, it leads sometimes to instability of iterations.
In this example we
consider the outer conical defect in the iron pipe with the wall thickness 8mm.
The defect has 4mm depth, 16mm top diameter (on the wall surface) and 3mm
bottom diameter. This defect is located
inside the uniform grid box of 8 r-cells, 16 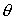 -cells, and 16 z-cells. Each cell is considered as the
“metal” one if it lies strongly outside the cone. The “defect” box is a part of the whole
non-uniform (r, -cells, and 16 z-cells. Each cell is considered as the
“metal” one if it lies strongly outside the cone. The “defect” box is a part of the whole
non-uniform (r,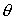 ,z) grid having the volume of 56´80´80 cells. In Figure 9 the component ,z) grid having the volume of 56´80´80 cells. In Figure 9 the component 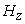 of electromagnetic
field inside the pipe (surface of electromagnetic
field inside the pipe (surface 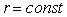 , 5mm from the wall) near the defect is shown. , 5mm from the wall) near the defect is shown.
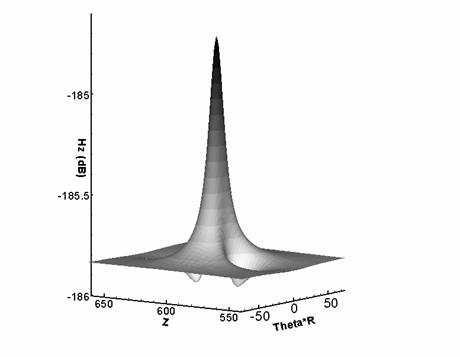
Figure 9: Conical defect: component 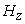 of EM field inside the
pipe is mapped of EM field inside the
pipe is mapped
In this example we use
four grid levels. The graph of the residual history is shown in Figure 10. We stop the iterations after
15 MG cycles. Each MG cycle requires about 50 multiplications of the “main”
matrix on the finest grid. One can
observe that the convergence rate is sharply drops after 11-th cycle. This is a
typical behavior and we can not still overcome this effect. Note that already 10 MG cycles are enough in this example to obtain the
solution with required accuracy.
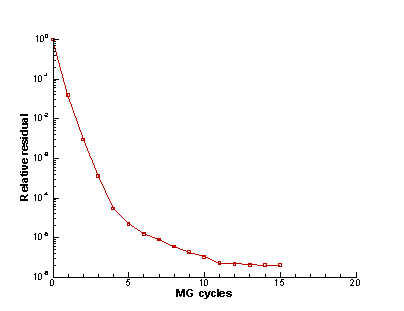
Figure 10: Convergence history for 4 grid levels, the finest grid is 56´80´80
Bibliography
[1] N. Zaitsev and Ivan
Sofronov. “Method of calculating low-frequency electromagnetic problems in
cylindrical geometry” Preprint of Keldysh Institute of Applied Mathematics, No.
61, 2004.
[2] Haber and U.M. Ascher,
Fast finite volume simulation of 3D electromagnetic problems with highly
discontinuous coefficients. SIAM J. Sci. Comput. Vol. 22, No. 6, pp. 1943—1961, (2001)
[3] R.P. Fedorenko,
“Introduction to the computational physics”, Moscow, MIPT, 1994, 526 pp.
[4] R.P. Fedorenko
“Relaxation method for solving difference elliptic equations”, Jour.
Comp.Math&Math.Phys., 1961, V.1, No.5
[5] R.P. Fedorenko,
“About the convergence rate of an iteration method”, Jour. Comp.Math&Math.Phys., 1964, V.4,
No.3
[6] R.P. Fedorenko,
“The iterative solution of the difference elliptic equations”, Adv.
Math.Sci.,1973, V. 28, No.2
|
![]() =16 and
=16 and ![]() =64. Note that the gain remains still enough if the
parameters are significantly changed.
=64. Note that the gain remains still enough if the
parameters are significantly changed.![]() , residual drops
, residual drops ![]() times. The single-grid
problem requires 1822 iterations and 647 seconds. Thus the gain is about 16
times in computational time if
times. The single-grid
problem requires 1822 iterations and 647 seconds. Thus the gain is about 16
times in computational time if ![]() =16 and
=16 and ![]() =128.
=128.![]() where
where ![]() is the point number
along the considered direction. It is convenient to write the reduction as
follows:
is the point number
along the considered direction. It is convenient to write the reduction as
follows:![]()
![]() is the fine grid
function,
is the fine grid
function, ![]() is the coarse grid
function,
is the coarse grid
function, ![]() is the coordinate
along the considered direction. In order to exactly reconstruct linear
functions, the coefficients
is the coordinate
along the considered direction. In order to exactly reconstruct linear
functions, the coefficients ![]() and
and ![]() should be calculated
by the following formulas:
should be calculated
by the following formulas: ![]()
![]() . The point-to-point transfer is done if
. The point-to-point transfer is done if ![]() , i.e.
, i.e. ![]() .
.
![]() of the computational
domain fragment. The gray color denotes
the subdomain occupied by the metal. Coarse and fine grid cells are drawn by
thick and thin lines, respectively (each coarse cell joints four fine cells
(eight in three dimensions)). The location of the azimuth component
of the computational
domain fragment. The gray color denotes
the subdomain occupied by the metal. Coarse and fine grid cells are drawn by
thick and thin lines, respectively (each coarse cell joints four fine cells
(eight in three dimensions)). The location of the azimuth component ![]() considered on the
coarse and fine grids is shown by the black and white circles, respectively. We
see that these points do not coincide in the staggered coarse and fine grids
(moreover black and white circles are also shifted in the
considered on the
coarse and fine grids is shown by the black and white circles, respectively. We
see that these points do not coincide in the staggered coarse and fine grids
(moreover black and white circles are also shifted in the ![]() direction normal to the sheet). Function
direction normal to the sheet). Function ![]() is not smooth near the
metal-air boundary: it has the discontinuous derivative with respect to the
normal direction. A typical one-dimensional graph along the
is not smooth near the
metal-air boundary: it has the discontinuous derivative with respect to the
normal direction. A typical one-dimensional graph along the ![]() direction is shown in Figure
6.
direction is shown in Figure
6. 
![]() along radius at fixed
along radius at fixed![]() .
. ![]() plane and
plane and ![]() plane are drawn in Figure
7 and Figure 8, respectively.
plane are drawn in Figure
7 and Figure 8, respectively. 
![]() on the plane
on the plane ![]() corresponding to
corresponding to
![]() on the plane
on the plane ![]() corresponding to
corresponding to![]() -cells, and 16 z-cells. Each cell is considered as the
“metal” one if it lies strongly outside the cone. The “defect” box is a part of the whole
non-uniform (r,
-cells, and 16 z-cells. Each cell is considered as the
“metal” one if it lies strongly outside the cone. The “defect” box is a part of the whole
non-uniform (r,![]() ,z) grid having the volume of 56´80´80 cells. In Figure 9 the component
,z) grid having the volume of 56´80´80 cells. In Figure 9 the component ![]() of electromagnetic
field inside the pipe (surface
of electromagnetic
field inside the pipe (surface ![]() , 5mm from the wall) near the defect is shown.
, 5mm from the wall) near the defect is shown.
![]() of EM field inside the
pipe is mapped
of EM field inside the
pipe is mapped 

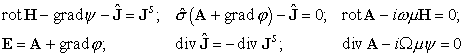
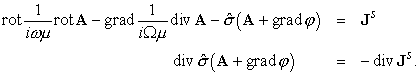

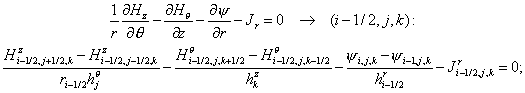
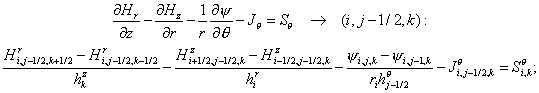 (2.2)
(2.2)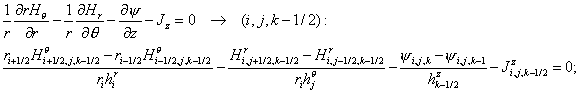 (2.3)
(2.3)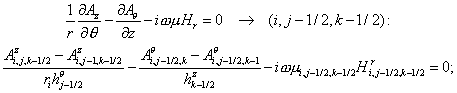
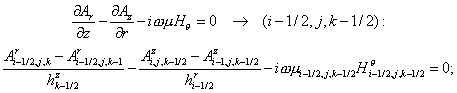
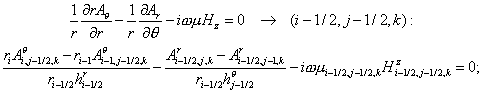
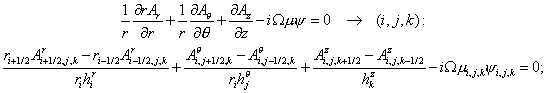 (2.7)
(2.7)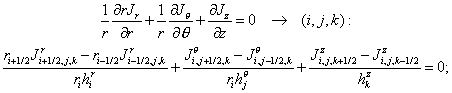
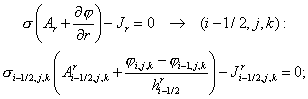
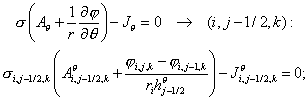
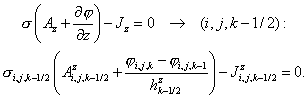
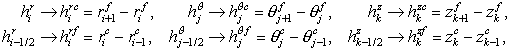 ,
,