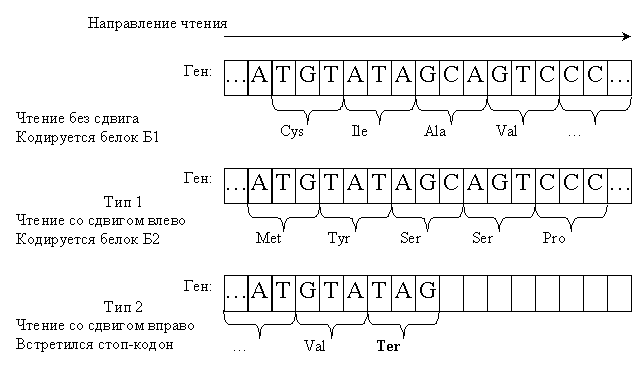1. Введение

Важнейшей составляющей живых организмов служат биополимеры – нуклеиновые кислоты (ДНК и РНК) и белки. Оба этих типа молекул являются линейными гетерополимерами, т.е. представляют собой цепочки, составленные из различных мономерных звеньев. В состав белков входят 20 видов мономеров – аминокислот, а нуклеиновые кислоты образуются 4 видами мономеров – нуклеотидов.

Природа возложила на разные типы биополимеров решение различных задач. Белки – это функциональная основа жизни, тогда как нуклеиновые кислоты – ее информационная основа. И если белки участвуют в построении клеток и обеспечивают протекание биохимических реакций, то нуклеиновые кислоты управляют свойствами самих белков, задавая последовательность, в которой выстраиваются образующие их аминокислоты.

Аминокислотная последовательность белка определяется нуклеотидной последовательностью кодирующего его гена в соответствие с правилами, называемыми генетическим кодом. Процедура синтеза белка по задающему его гену называется экспрессией гена.

Поскольку количество существующих различных аминокислот превосходит количество различных нуклеотидов, одну аминокислоту задает нуклеотидный триплет, или кодон, – три последовательно идущих нуклеотида.

Порядок нуклеотидов в триплете значим, поэтому всего существует 4³ = 64 различных кодонов. Из них 61 является смысловым, т.е. кодирующим аминокислоты, а 3 – терминирующими, или стоп-кодонами, дающими сигнал к прекращению синтеза белка. Каждому смысловому кодону соответствует одна определенная аминокислота, вследствие чего код вырожден и некоторые аминокислоты кодируются двумя, тремя, четырьмя и даже шестью различными нуклеотидными триплетами. Различные кодоны, задающие одну и ту же аминокислоту, называются синонимичными.

Кодоны, различающиеся между собой лишь одним нуклеотидом в одном и том же положении (т.е. на первом, втором или третьем месте в триплете), будем называть соседними. Соседние кодоны могут быть получены друг из друга в результате точечных мутаций – замены одного нуклеотида другим из-за ошибок в процессе воспроизводства или прочтения генома. Точечные мутации (смысловых) кодонов подразделяются на миссенс-мутации и нонсенс-мутации в зависимости от того превращается ли кодон в результате в другой смысловой кодон или становится терминирующим.

С формальной точки зрения генетический код есть отображение имеющего определенную структуру алфавита из 64 триплетов на множество, состоящее из 20 символов (аминокислот) и 1 знака препинания. Реализовавшийся в природе генетический код является одним из огромного числа возможных, однако он универсален, т.е. един для всех организмов за несколькими незначительными исключениями – девиантными кодами[1].

Различие нуклеотидов между собой составляют входящие в их состав азотистые основания: аденин (A), гуанин (G), цитозин (C) или тимин (T), по которым обозначаются и собственно нуклеотиды[2]. Молекула ДНК обычно состоит из двух полинуклеотидных цепей. Между основаниями различных цепей образуются водородные связи, обеспечивающие стабильность молекулы. Аденин всегда связывается с тимином, гуанин – с цитозином, т.е. основания образуют две комплементарные пары. Тем самым обеспечивается возможность получения реплик – точных комплементарных копий нуклеотидной цепи, необходимых как для синтеза белка, так и размножения.

Аминокислоты обычно обозначаются трехбуквенными сокращениями. Ради единообразия терминирующие кодоны будем обозначать символом "Ter". В табл. 1 представлен универсальный генетический код, определяющий соответствие аминокислот нуклеотидным триплетам.

Таблица 1. Универсальный генетический код

Основные свойства генетического кода были установлены на рубеже 1950‑60-х годов Ф. Криком и его сотрудниками. Первый и самый значимый шаг в расшифровке генетического кода предприняли в 1961 г. М. Ниренберг и Дж. Маттеи. Окончательно код был расшифрован к 1967 г. [3].

1.1. Закономерности в генетическом коде

Вне всякого сомнения, генетический код не произволен, как произвольно, скажем, отображение порядкового номера буквы в латинском алфавите в ее символьный вид. Соседним кодонам, как правило, соответствуют схожие в химическом отношении аминокислоты, что становится особенно заметно, если огрубить генетический код.

Из табл. 1 видно, что то, какую аминокислоту кодирует некоторый смысловой кодон, во многих случаях определяется его первыми двумя нуклеотидами. Следовательно, генетический код сильно вырожден по третьему нуклеотиду, поэтому при рассмотрении огрубленного кода мы ограничимся первыми двумя нуклеотидами, перейдя тем самым от 64 триплетов к 16 дублетам.

Множество кодируемых значений сузим с 21 до 4, объединив аминокислоты в группы по химическим свойствам, которые определяются структурой боковой (т.е. не вовлеченной в образование остова полимера) цепью аминокислотной молекулы. Нас будет интересовать лишь то, полярна боковая цепь или нет. Такая классификация является общепринятой и обусловлена тем, что молекулам из каждой группы энергетически выгоден контакт с себе подобными.

Выделение чистых классов всегда порождает и промежуточные, представители которых либо вообще не обладают свойствами, по которым была произведена классификация, либо обладают сразу несколькими из них. В соответствии с химическими свойствами боковых цепей аминокислоты объединяются в 4 класса:

I – неполярная боковая цепь: Ala, Ile, Leu, Pro, Val, Phe, Met;

II – полярная боковая цепь: Asn, Gln, Asp, Glu, Arg, His, Lys, Ser, Thr;

III – нейтральная боковая цепь (просто атом водорода): Gly;

IV – боковая цепь со слабо выраженной полярностью: Trp, Tyr, Cys

В последний класс включим также и стоп-кодон Ter.

В табл. 2 приведен вид огрубленного генетического кода как отображения множества дублетов на множество групп аминокислот. Легко видеть, что чистые классы I и II образуют компактные связные области (кластеры). Промежуточные классы III и IV оказываются по соседству друг с другом (табл. 2 представляет собой тор) и на стыке чистых классов.

Мы не будем здесь анализировать то, почему стоп-кодоны приписаны именно к классу IV, почему именно в таком порядке расположены нуклеотиды по осям табл. 2, уместно ли выделение промежуточных классов или следовало, как иногда делают, включить их представителей в один из чистых классов, и другие вопросы подобного рода. Обсуждение деталей построения огрубленного кода, равно как и объяснение обнаруженной закономерности выходит за рамки настоящей работы. Достаточно того факта, что какую-то закономерность удалось обнаружить, а, следовательно, имеет смысл искать и другие, которые окажутся достаточно простыми, чтобы их удалось объяснить на современном уровне понимания проблемы.

Отметим, что подход к поиску закономерностей в коде, в чем-то схожий с описанным, но уже не качественный, а количественный использовали С. Фриленд и Л. Херст в работах [1,4]. Они сопоставили аминокислотам числовую характеристику, выбрав в качестве таковой их гидрофобность, т.е. энергетическую цену, которую приходится платить за помещение молекулы в водную среду[3]. В качестве меры случайности генетического кода было взято среднеквадратичное различие в гидрофобности аминокислот, соответствующих соседним кодонам. Чем эта величина меньше, чем менее случайным следует считать генетической код.

С. Фриленд и Л. Херст ограничились рассмотрением генетических кодов, которые совпадают с существующим с точностью до переобозначения аминокислот (при неизменных положениях стоп-кодонов и структуре вырождения кода). Оказалось, что если перебирать разные варианты таких переставленных кодов, то только один вариант на десять тысяч дает значение рассматриваемой меры меньшее, чем у существующего кода. Если, кроме того, учесть характер ошибок, реально происходящих при прочтении генома[4], то это число снизится до одного варианта на миллион.

Таким образом, генетический код можно считать в каком-то смысле непрерывным или почти непрерывным как отображение, если в качестве изменения аргумента использовать переход к соседним кодонам. Однако мутации замены, обуславливающие такой переход, не единственный механизм изменения генетической информации.

1.2. Чтение генов со сдвигами

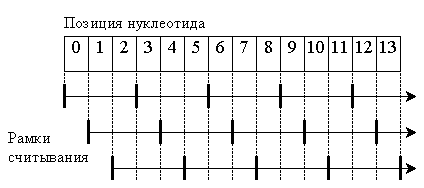
Признаки конца одного нуклеотидного триплета и начала следующего в геноме отсутствуют. Чтение нуклеотидной цепи происходит последовательно, триплет за триплетом. Вследствие этого существует три принципиально разных способа прочесть одну и ту же нуклеотидную последовательность, которые определяются рамкой считывания – положением первого нуклеотида при чтении (см. рис. 1).

Обычно функциональный белок синтезируется только при одной рамке считывания. Но некоторые вирусы используют две или даже три рамки, получая при этом, соответственно, два или три совершенно различных белка с одного и того же гена.

Рассмотрим ген, изображенный на рис. 2. При чтении без сдвига он кодирует один белок Б1 (рис. 2, вверху), однако если сместить рамку на один нуклеотид влево, то получится совершенно иной белок Б2 (рис. 2, по центру). Тем самым, один информационный носитель может использоваться более одного раза.

Однако чтение со сдвигом не всегда возможно. Для того же гена чтение со смещением рамки на один нуклеотид вправо заблокировано появлением терминирующего кодона (рис. 2, внизу). При этом вся информация, которая находится правее него, становится недоступна.

Условимся считать, что способ чтения гена со сдвигом по основной цепи на один нуклеотид влево – это сдвиг 1, а способ чтения гена со сдвигом по основной цепи на один нуклеотид вправо – это сдвиг 2. Отметим, что сдвиги 1 и 2 не предполагают чтения комплементарной цепи молекулы ДНК.

Невозможность прочитать ген тем или иным отличным от основного способом понимается здесь исключительно как возникновение терминирующего кодона. Если же при чтении со сдвигом все кодоны оказались смысловыми (безотносительно функциональности полученной аминокислотной последовательности) – то, это значит, такое прочтение возможно. В случае, показанном на рис. 2 мы получили терминирующий кодон при чтении со сдвигом пары кодонов ATA+GCA, которые соответствовали паре аминокислот Ile+Ala.

Пары идущих подряд смысловых кодонов, при чтении которых со сдвигом получается терминирующий кодон, называются запретными. Пара идущих подряд аминокислот будет запретной лишь в том случае, если для нее все возможные пары задающих ее кодонов запретны. Например, пара кодонов ATA+GCA запретна, но задаваемая ею пара аминокислот Ile+Ala – нет, т.к. ее же можно закодировать и сочетанием ATT+GCA, не приводящим к появлению терминирующего кодона при чтении с иной рамкой. А вот пара аминокислот Met+Lys является запретной, т.к. любая пара соотвествующих ей кодонов (ATG+AAA или ATG+AAG) при чтении со сдвигом 2 порождает стоп-кодон.

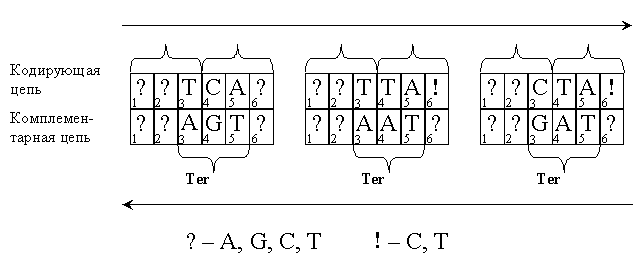
При сдвигах 1 и 2 читается кодирующая цепь. Следуя работе [5] и для полноты картины рассмотрим также еще 3 типа сдвигов, при которых читается комплементарная цепь. В случае сдвига 4 она читается при том же положении рамки, а в случае сдвигов 3 и 5 – при смещении рамки, соответственно, на один нуклеотид влево и вправо (относительно кодирующей цепи). Рис. 3 демонстрирует примеры чтения с этими типами сдвигов.

Следует отметить, что с точки зрения синтеза белка в реальных клетках, рассмотрение случаев сдвигов 1 и 2 имеет значительно больший приоритет, чем случаев 3, 4 и 5, т.к. данная процедура не предполагает чтения комплементарной цепи. Подразделение цепей на кодирующую и комплементарную ей не является условностью. Оно вполне однозначно и определяется наличием на кодирующей цепи перед геном специальной нуклеотидной последовательности – промотора, с которым связывается фермент, читающий ген [6]. Комплементарная цепь промоторов не содержит и потому не читается. Однако такой способ предотвращения экспрессии второй цепи является, скорее всего, эволюционным приобретением значительно более поздним, чем возникновение генетического кода. Поэтому при анализе его свойств рассмотрение сдвигов 3, 4 и 5 не лишено смысла.

Итак, всего рассматривается 5 типов чтения гена со сдвигом. Два из них происходят без участия комплементарной цепи молекулы ДНК, а оставшиеся 3 – с ее участием. Поскольку кодон имеет длину 3 нуклеотида, этими случаями исчерпываются все возможности последовательного прочтения гена со сдвигами.

2. Обзор результатов Н.Н. Козлова

В ИПМ им. М.В. Келдыша РАН Н.Н. Козловым был проведен цикл работ по математическому анализу взаимосвязи структуры генетического кода и необычных способов записи генетической информации – так называемых перекрывающихся генов. По результатам был опубликован ряд работ [5,7].

В этих работах исследованы гены организмов, которые используют чтение со сдвигом, т.е. используют перекрывающиеся гены: фаги ФХ174 и G4, вирусы GSHV, RSV, TMV‑L, HIV‑2. В данном случае возможность перекрытия генов оценивается положительно: за счет перекрытия генов перечисленные организмы имеют возможность более компактной записи своего генома.

Предметом исследований [5,7] является перекрываемость генома. «Под перекрываемостью понимаются такие случаи, когда в гене, прочитанном с соответствующим сдвигом, не может возникнуть ни один из кодонов Ter. Назовем перекрываемость полной, если она имеет место для последовательности любой протяженности с произвольным сочетанием аминокислот». [5]

В результате исследований была сформулирована теорема для генетического кода [5]. Понятие перекрываемости следует понимать в том смысле, что для аминокислотной последовательности, которую кодирует ген, можно подобрать такую нуклеотидную запись, что при ее чтении со сдвигами не будет возникать запретных пар кодонов. Иными словами, перекрываемость генома – это отсутствие в нем запретных пар аминокислот.

Для сдвига 2 существует 5 запретных пар аминокислот: Met–Met, Met–Asn, Met–Lys, Met–Ile, Met–Thr, для сдвига 3 – 6 пар: Phe–Tyr, Tyr–Tyr, His–Tyr, Asn–Tyr, Asp–Tyr, Cys–Tyr, и для сдвига 5 – 5 пар: Phe–Met, Phe–Asn, Phe–Lys, Phe–Ile, Phe–Thr. Для сдвигов 1 и 4 запретных пар аминокислот нет. В том случае если ген не кодирует указанных пар, то возможна его полная перекрываемость [5].

Отметим, что в теореме о генетическом коде [5] речь идет о запретных парах аминокислот, т.е. тех парах аминокислот, для которых любое сочетание синонимичных кодонов будет запретным.

Также в работах [5,7] было обнаружено, что одиночные перестановки смысловых кодонов в терминаторные в структуре существующего генетического кода приводят к возникновению запретов на перекрываемость, которые для канонического кода не существуют. Такие перестановки рассматривались в соответствии с имеющимися данными о девиантных кодах. Отсюда был сделан вывод о том, что одним из решающих факторов в "выборе" структуры существующего генетического кода явилась его способность к почти полной перекрываемости для каждого из возможных случаев сдвига. Такой вывод был сделан потому, что для рассмотренных девиантных кодов количество запретных пар аминокислот было больше, чем для канонического кода.

Как уже было сказано, кодирование белков с двумя или даже тремя рамками считывания действительно имеет место. Однако оно есть результат дегенерации, и наблюдается только у некоторых вирусов, для которых принципиальной является компактность упаковки генетического материала. Расплатой за это оказывается уменьшение эволюционных возможностей. Мутация, улучшающая белок, закодированный с одним положением рамки считывания, почти наверняка сделает полностью нефункциональными белки, которые кодируются при чтении со сдвигами. Поэтому неудивительно, что клеточными организмами компактная запись генетической информации оказалась невостребованной.

Таким образом, использование кодирования с перекрытием является весьма специальным случаем. Из его рассмотрения вряд ли можно сделать выводы о свойствах генетического кода в общем. Особенно, если учесть, что с биологической точки зрения целесообразным является как раз всяческое ограничение экспрессии генов, прочитанных со сдвигом, дабы не растрачивать ресурсы клетки на синтез белков, имеющих, скорее всего, бессмысленную аминокислотную последовательность.

Что же касается сдвигов 3, 4 и 5, то, насколько нам известно, ситуация, когда бы один и тот же участок и кодирующей, и комплементарной цепи молекулы ДНК кодировал белок, не реализуется ни у одного существующего организма. Возможностью прочитать комплементарную цепь природа не воспользовалась, оставив ей только роль взаимно-обратного дополнения кодирующей цепи. Поэтому разумно придать первостепенное значение рассмотрению случаев сдвига 1 и 2, а остальные типы сдвигов считать дополнением до общей картины.

3. Разметка кода

Нет никаких оснований полагать, что при зарождении жизни генетический код сразу возник таким, каков он есть сейчас и, в частности, что он изначально задавал такое большое количество аминокислот. По-видимому, на ранней стадии эволюции распознавание кодонов осуществлялось непосредственно аминокислотами на основе их химического сродства к нуклеотидным триплетам. Вряд ли такой способностью в должной мере обладают все 20 кодируемых ныне аминокислот. Однако в дальнейшем с появлением опосредованного механизма синтеза белка сродство аминокислот и триплетов утратило значение.

Возникла возможность изменения и расширения генетического кода за счет мутации генов, кодирующих собственно аппарат белкового синтеза. При этом смысловые кодоны могли менять свои значения, приводя к включению в синтезируемую белковую цепь других или даже совсем новых аминокислот. Этот механизм, видимо, и позволил природе расширить алфавит аминокислот до весьма значительного объема в 20 символов, достаточного, чтобы получить белок с практически любыми химическими свойствами.

Есть, однако, существенная разница между мутациями, сохраняющими разметку генетического кода, т.е. его разделение на смысловые и терминирующие кодоны, и мутациями, не сохраняющими ее. Мутации второго рода значительно менее вероятны. Ведь чтобы смысловой кодон стал терминирующим надо не только лишить его возможности кодировать аминокислоту, но и сообщить ему способность прерывать синтез белка. И наоборот, чтобы придать смысл стоп-кодону, надо не только сопоставить ему аминокислоту, но и блокировать его терминирующую функцию. То есть, для изменения разметки кода необходимо сочетание нескольких мутаций.

В свете сказанного можно предположить, что разметка генетического кода, является более древним и менее случайным образованием, чем соответствие кодонов определенным аминокислотам. Поэтому на данном этапе исследований представляется разумным упростить задачу о природе генетического кода до задачи о природе его разметки: почему в универсальном генетическом коде терминирующими являются именно кодоны TAA, TAG и TGA?

В данной работе мы ограничиваемся рассмотрением разметок генетического кода, имеющих 3 стоп-кодона. Всего существует

таких разметок. Разметку существующего кода будем для краткости называть канонической.

3.1. Информационные критерии оптимизации

В теории кодирования, для любого кода решающее значение имеет устойчивость к ошибкам при передаче данных. В случае генетического кода можно выделить два основных источника ошибок – чтение со сдвигом и точечные мутации. Задачи обеспечения устойчивости по отношению к ошибкам этих классов принципиально различны.

I. Блокировка чтения со сдвигом. Смещение рамки считывания или чтение комплементарной цепи вместо кодирующей – это нелокальные ошибки, полностью искажающие содержание генетической информации. Обеспечить ее восстановление в этом случае невозможно, и единственный выход – как можно скорее пресечь экспрессию несуществующего гена. Чем быстрее в нем встретится терминирующий кодон, тем меньше ресурсов клетка растратит впустую. Таким образом, оптимальной, с точки зрения устойчивости к ошибкам этого класса, является та разметка кода, которая обеспечивает максимальную вероятность появления запретной пары кодонов при чтении со сдвигом.

Здесь следует, вообще говоря, различать задачи, с одной стороны, блокировки чтения кодирующей цепи со сдвигами 1 и 2, и, с другой стороны, чтения комплементарной цепи со сдвигами 3, 4 и 5.

Чтение комплементарной цепи вообще не имеет места, т.к. она не содержит промоторов. То есть, реальная необходимость имеется только в блокировке чтения кодирующей цепи со сдвигом 1 и 2, что может быть обусловлено как сбоем позиционирования при прочтении гена, так и мутацией выпадения/вставки нуклеотида[5]. Поскольку механизм синтеза белка не дает возможности отличить полученную таким образом бессмысленную информацию от осмысленной, то защиту от выполнения бесполезной работы клетке может обеспечить только оптимальная структура разметки генетического кода.

Таким образом, задача I обеспечения максимальной устойчивости к ошибкам сдвига распадается на две подзадачи: основную задачу I‑a, связанную с блокировкой сдвигов 1–2, и вспомогательную задачу I‑b, связанной с блокировкой сдвигов 3–4–5. Задача I‑b не является бессодержательной, т.к. нельзя исключать возможности того, что в пору формирования генетического кода чтение комплементарной цепи еще было возможно.

II. Устойчивость к точечным мутациям. Случайная замена одного нуклеотида на другой (при том, что чтение гена осуществляется без сдвигов) является локальной ошибкой, последствия которой возможно уменьшить. Здесь оптимальна разметка, минимизирующая вероятность нонсенс-мутаций, ведущих к появлению одного из стоп-кодонов внутри кодирующего белок гена. Миссенс-мутации, заменяющие один смысловой кодон другим, не очень опасны. Исходный и производный триплеты могут кодировать одну и ту же аминокислоту (синонимичные кодоны) или родственные в химическом отношении аминокислоты (как правило, соседним кодонам соответствуют похожие по свойствам аминокислоты). А вот нонсенс-мутации почти наверняка делают невозможным получение нормального белка. Смысловые кодоны, соседствующие с терминирующими и вследствие этого подверженные нонсенс-мутациям, будем называть уязвимыми.

Задача II обеспечения максимальной устойчивости к точечным мутациям вновь распадается на подзадачи, относительная важность которых уже не столь очевидна как в случае задачи I блокировки чтения со сдвигом.

Подзадача II‑a формулируется как минимизация суммарного (по всему коду) числа возможных нонсенс-мутаций, а подзадача II‑b – как минимизация числа смысловых кодонов, которые могут быть точечной мутацией превращены в терминирующий. Первая постановка (II‑a) означает уменьшение общей уязвимости смысловой части генетического кода к мутациям, а вторая (II‑b) – уменьшение числа уязвимых кодонов.

Наличие двух в чем-то противоположных друг другу критериев оптимизации отчасти оправдывает анализ только тех разметок, которые содержат три терминирующих кодона. Понятно, что слишком маленькое количество стоп-кодонов уменьшает устойчивость по отношению к ошибкам чтения со сдвигом, а слишком большое – по отношению к нонсенс-мутациям. Однако чтобы найти оптимальную пропорцию между смысловыми и терминирующими кодонами, необходимо знать вероятности ошибок каждого класса, а также относительную цену, которую платит организм за каждую из них. Не обладая такой информацией, мы исходим из того, что природа правильно решила эту оптимизационную задачу, и наличие именно трех стоп-кодонов является наилучшим вариантом.

3.2. Эволюционный критерий оптимизации

Помимо критериев оптимизации информационной природы можно сформулировать еще один, связанный с предполагаемыми особенностями процесса зарождения жизни. Сразу оговоримся, что, хотя этот критерий не столь бесспорен и достоверен, как два предыдущих, мы сочли возможным рассматривать их наравне.

На заре эволюции – до появления фотосинтезирующих организмов – единственным источником простых органических молекул были абиогенные процессы. С точки зрения их протекания азотистые основания не равноценны. Абиогенный синтез аденина, в состав которого не входит кислород, намного проще, чем синтез всех прочих – кислородсодержащих – оснований. Аденин образуется в результате протекающей в восстановительной среде поликонденсации пяти молекул синильной кислоты, тогда как для получения остальных азотистых оснований необходима также окислительная фаза. [8]

Более простой путь образования аденина означает его большую концентрацию в "первичном бульоне" и, следовательно, преимущественное участие в различных процессах[6].

Нуклеиновые кислоты, хранящие генетическую информацию, имеют вид пары комплементарных цепей, где каждому нуклеотиду A соответствует нуклеотид T, а каждому нуклеотиду G – нуклеотид C. Три стоп-кодона – это 9 пар комплементарных нуклеотидов. Аденин входит только в состав пар вида AT, которых, соответственно, должно быть, как можно больше (причем разницы между A и T в данном случае нет, т.к. на каждый тимин кодирующей цепи придется аденин комплементарной и наоборот). Количество нуклеотидов из набора {A; T}, входящих в состав терминирующих кодонов, назовем AT‑индексом разметки.

Эволюционно более вероятны варианты разметки, максимально использующие аденин в своей древнейшей части – терминирующих кодонах. Тем самым возникает еще одна оптимизационная задача.

III. Максимизация AT-индекса разметки, но только при условии оптимальности решения задач I‑a и II‑b. Формулировка данной задачи с грифом "по возможности" означает первичность информационных критериев оптимальности кода по отношению к химическим. Способность воспользоваться избытком аденина на перспективах эволюции могла сказаться только при прочих равных обстоятельствах. Организмы, имевшие разметку кода с богатыми аденином стоп-кодонами, но не обеспечивающую должной устойчивости к ошибкам, должны были неизбежно исчезнуть по мере накопления в природе достаточного количества органической материи. А вот среди разметок, устойчивых к ошибкам, наибольшие шансы возникновения имели именно те, которые обладали наибольшим AT-индексом.

Отметим, что стоп-кодоны в существующем коде содержат два или три нуклеотида из набора {A; T}. Всего подобных триплетов, как не трудно понять, ровно половине от их полного количества. Т.е. даже если появление в триплете более чем одной буквы из набора {G; C} невероятно, код все равно позволяет задавать большое количество аминокислот.

3.3. Решение оптимизационной задачи I

Генетический код отображает алфавит триплетов на множество аминокислот, дополненное символом "Ter". Огрубив генетический код до его разметки, мы сузили множество значений отображения всего до двух: смысловой кодон или терминирующий. Соответственно, мы утратили возможность говорить о гене в терминах аминокислот, как это делается в работах [5,7]. Далее нас будут интересовать не запретные пары аминокислот, а только запретные пары кодонов. Причем каждый раз говоря, что пара запретна, мы всегда будем иметь в виду тот тип сдвига, относительно которого она запретна.

В этих терминах задача I формулируется так: каково максимально возможное количество запретных пар кодонов для каждого типа сдвига при различных вариантах разметки генетического кода, содержащих 3 терминирующих кодона.

Случай сдвига 4 тривиален. В этом случае можно ограничиться рассмотрением одиночных кодонов. Нет необходимости анализировать пары, т.к. комплементарная цепь читается без сдвига относительно кодирующей. Здесь возможны всего 2 варианта: либо какие-то два стоп-кодона комплементарны друг другу (например, ATC и GAT), либо нет, как это имеет место для существующего кода. Соответственно, существует либо 1, либо 3 запретных смысловых кодона.

Сдвиги по остальным четырем – нетривиальным – типам имеют много общего. Всего существует 61´61 = 3 721 пара смысловых кодонов – таких последовательностей из шести букв, принадлежащих набору {A; G; C; T}, ни одна из трехбуквенных половин которых, стоящая в положениях 1–2–3 и 4–5–6 кодирующей цепи (см. рис. 4), стоп-кодоном не является. Пара смысловых кодонов запретна, если она содержит в себе или в своем комплементарном дополнении три подряд идущих буквы, образующих стоп-кодон, в положениях 2–3–4 или 3–4–5.

Максимально возможное число запретных пар для каждого типа сдвига есть 192=3´4³ (3 варианта стоп-кодона ´ 4³ вариантов остальных нуклеотидов (3 позиции по 4 возможных нуклеотида в каждой из них)). Однако не для любых разметок генома максимум количества запретных пар достижим при том или ином типе сдвига.

Очевидно, что 192 запретных пары для сдвигов 1 и 2 может быть только одновременно. Необходимым и достаточным условием оптимальности разметки в смысле задачи I‑a является отсутствие таких стоп-кодонов, что конец одного из них является продолжением другого (например, TAG и GCT или TAG и AGC) или его самого (например, CCC или GTG). Если какой-то терминирующий кодон начинается с одного или двух концевых нуклеотидов другого, то найдутся такие пары кодонов, содержащие в себе стоп-кодон, которые, не будучи смысловыми, не являются, тем самым, и запретными. При этом количество запретных пар для обоих типов сдвигов кодирующей цепи будет меньше максимально возможного.

На основе полного перебора вариантов разметки удалось установить, что если запретных пар для одного из сдвигов 1 или 2 оказывается 176 или более, то и для другого сдвига будет столько же. Более того, количества запретных пар кодонов, возникающие при прочтении кодирующей цепи с одним и другим смещением рамки вообще не могут отличаться более чем на 3. Распределение разметок кода по абсолютной величине различия в количестве запретных пар для этих сдвигов представлено в табл. 3. Из нее видно, что различие количества запретных пар, возникающих, при неправильном чтении кодирующей цепи крайне невилико и составляет в среднем 0,26.

Совершенно иная ситуация имеет место в случае сдвигов 3 и 5. Доля разметок, для которых количество запретных пар, возникающих при одном и другом типе сдвига одинаково, не превышает 13%. Причем разница их количества может достигать 146 (например, для набора стоп-кодонов AAT, GAT и CAT при сдвиге 3 возникает 192 запретных пары, а при сдвиге 5 – только 46), а среднее значение модуля разницы составляет почти 18,5.

Легко убедиться, что каноническая разметка оптимальна, т.е. дает 192 запретных пары кодонов, в отношении сдвигов 1 и 2 (чтение кодирующей цепи со смещением рамки), а также сдвига 5 (чтение комплементарной цепи со смещением рамки вправо). Однако при сдвиге 3 (чтение комплементарной цепи со смещением рамки влево) существующий код дает меньшее количество запретных пар.

Как можно видеть из рис. 4 (выше), в случае этого типа сдвига два варианта возникновения стоп-кодона ограничивают число допустимых букв в одном из положений кодирующей цепи до двух, поскольку в ней стоп-кодон недопустим. Соответственно, количество запретных пар сокращается до 4³+2´4²´2 = 128.

Как показывает перебор вариантов, не существует разметок кода, обеспечивающих оптимум задаче I в случае всех пяти типов сдвигов сразу. Однако существуют 32 разметки, дающие для каждого нетривиального типа сдвига 192 запретных пары кодонов, но при этом для сдвига 4 запретным оказывается лишь 1 кодон[7].

С другой стороны, существуют разметки кода, обеспечивающие максимальное количество запретных кодонов для сдвига 4 и запретных пар – для сдвигов 1, 2, и 5, так же как и каноническая разметка, но дающие для сдвига 3 заметно большее, чем она, количество запретных пар – 176 штук[8].

Как следует из сказанного выше, если потребовать одновременно достижения максимума числа запретов при сдвигах 3, 4 и 5, то и для сдвига 1, и для сдвига 2 удается получить не более 176 запретных пар. Таким образом, если максимизировать число запретов для четырех сдвигов из пяти, то пожертвовать придется одним из сдвигов 3, 4 или 5, связанных с прочтением комплементарной цепи.

Как мы видим, природа выбрала разметку кода, оптимальную в смысле критериев задачи I‑a, но не стала до конца оптимизировать ее в смысле критериев задачи I‑b. Отсюда можно сделать один из двух выводов. Либо блокировка прочтения комплементарной цепи вместо кодирующей не столь существенна по сравнению с какими-то другими, еще не изученными, особенностями разметки кода, либо же блокировка такого прочтения вообще не значима, поскольку, как уже говорилось, эту задачу можно решать и на уровне механизма экспрессии генов.

А вот блокировка прочтения кодирующей цепи со сдвигом важна. Каноническая разметка оптимальна в смысле задачи I‑a, т.е. порождает максимальное количество запретных пар как в случае сдвига 1, так и в случае сдвига 2. Всего существует 2 432 таких разметок (5,8% от общего числа). Гистограмма распределения разметок по количеству запретных пар кодонов для сдвига 1 представлено на рис. 5. Распределение для сдвига 2 выглядит точно так же.

Что касается чтения комплементарной цепи, то существует 820 (2,0%) разметок, максимизирующих количество запретных пар, возникающих при сдвигах 3 и 5. Причем 780 (1,9%) из них также максимизируют количество запретов и при сдвиге 4, т.е. являются оптимальными в смысле задачи I‑b. Однако каноническая разметка здесь очень далека от оптимума. Почти 75% разметок превосходят ее по способности блокировать чтение комплементарной цепи. А если ограничиться только сдвигами 3 и 5, то свыше 80% возможных разметок порождают не меньшее, чем каноническая, количество запретных пар кодонов. Гистограмма распределения этой величины приведена на рис. 6.

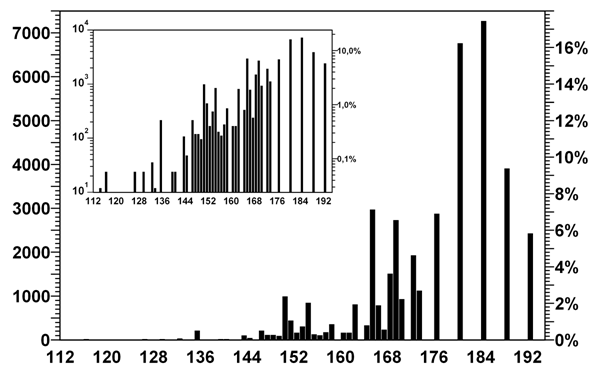
Рис. 5. Распределение разметок по числу запретных пар кодонов в кодирующей цепи

Гистограмма показывает количество и долю разметок, для которых при сдвиге 1 или 2 возникает данное количество запретных пар. Поскольку для этих типов сдвигов разметки дают почти одинаковое количество запретных пар, распределение суммарного показателя будет практически таким же с точностью до удвоения подписей к оси абсцисс.

На врезке – те же данные с логарифмическим представлением по оси ординат.

Если рассматривать задачу I в целом, то существующую разметку также нельзя счесть оптимальной. Существует всего 13 648 (32,8%) и 15 504 (37,2%) разметок кода, порождающих большее и, соответственно, не меньшее суммарное количество запретных пар для сдвигов 1, 2, 3 и 5, чем каноническая разметка. При требовании максимальности числа запретов в случае сдвига 4 эти величины уменьшаются до 13 024 (31,3%) и 14 656 (35,2%), соответственно.

Таким образом, существующая разметка, оптимальная в смысле задачи I‑a и почти пессимальная в смысле задачи I‑b, замыкает первую треть списка решений задачи I. Это позволяет судить как о ценности блокировки неверного прочтения гена вообще, так и о значимости различных типов ошибок в частности.

3.4. Решение оптимизационной задачи II

Генетические коды, которые можно получить друг из друга перестановкой положений в триплете или независимым переобозначением нуклеотидов в каждом из трех положений триплета, являются эквивалентными с точки зрения устойчивости кода по отношению к нонсенс-мутациям, превращающим смысловой кодон в терминирующий.

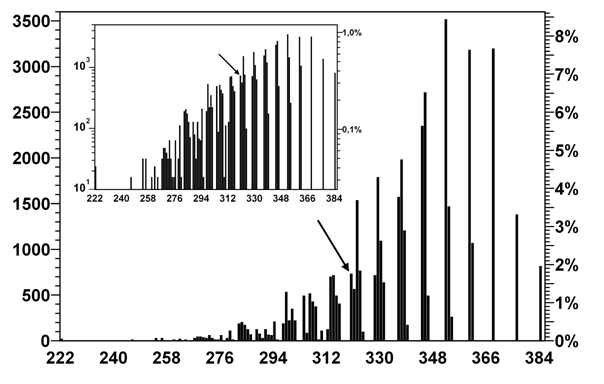
Рис. 6. Распределение разметок по суммарному числу запретных пар кодонов в комплементарной цепи (без учета сдвига 4)

Гистограмма показывает количество и долю разметок, для которых при свингах 3 и 5 суммарно возникает данное количество запретных пар.

Стрелочкой помечено положение канонической разметки.

Не составляет труда перебрать все возможные варианты разметки кода, различающейся по устойчивости к точечным мутациям. При этом мы будем следить как за числом кодонов, подверженных нонсенс-мутациям (задача II‑b), так и за полным числом таких мутаций (задача II‑a). Полное число возможных мутаций определяется как сумма числа подверженных мутации кодонов, взятых столько раз, какова кратность нонсенс-мутаций для них (т.е. смысловые кодоны, соседствующий с одним стоп-кодоном считаются, один раз, с двумя – два и с тремя – три раза).

Существует всего 10 вариантов разметки, различных в указанном выше смысле, которые можно собрать в 4 группы, определяемые взаимным соседством стоп-кодонов (см. табл. 4 ниже).

Таблица 4. Варианты разметки кода с точки зрения устойчивости к мутациям

a) Каждый стоп-кодон является соседним по отношению к двум другим. В этом случае 1 смысловой соседствует сразу со всеми тремя стоп-кодонами, и еще по 6 смысловых кодонов соседствует с каждым из них (2 положения в триплете, по которым совпадают стоп-кодоны, ´ 3 основания, отличных от основания, стоящего в них в этих положениях). Итого получается 1+6+6+6 = 19 уязвимых кодонов и 1´3+6+6+6 = 21 возможная мутация. Последнее значение является минимально возможным.

Всего может быть ровно 27 мутаций, превращающих некие кодоны в терминирующие (3 стоп-кодона ´ 3 положения в триплете ´ 3 основания, на которые заменяется основание в мутирующем кодоне). Каждая точечная мутация, превращающая один стоп-кодон в другой, уменьшает число мутаций, отстающих на то, чтобы превращать в них смысловые кодоны. Количество мутаций, переводящих стоп-кодоны друг в друга, не может быть более 6, а именно столько их в данном случае.

b) Один стоп-кодон соседствует с двумя другими, но те, в свою очередь, друг другу соседями уже не являются. Именно такова каноническая разметка генетического кода (стоп-кодоны: TAA, TAG и TGA – первый соседствует с остальными). Мутаций, переводящих стоп-кодоны друг в друга, здесь уже только 4, соответственно, на смысловую часть кода остаются 23 нонсенс-мутации.

В этом случае найдется 5 смысловых кодонов, соседствующих сразу с двумя стоп-кодонами (TAC, TAT, TCA, TTA, TGG) и еще 23‑5´2 = 13, которые являются соседями только одного стоп-кодона (AAA, AAG, AGA, GAA, GAG, GGA, CAA, CAG, CGA, TCG, TTA, TCG, TTA). Итого: 5+13 = 18 уязвимый кодон, что, как показывает анализ всех вариантов, является минимально возможным значением.

c) Два стоп-кодона являются соседями, а третий не соседствует ни с одним из них. Мутаций, переводящих стоп-кодоны друг в друга, остается всего 2, что дает 25 нонсенс-мутаций. В эту группу попадает 3 варианта разметки кода с числом уязвимых кодонов от 20 до 23.

d) Соседней среди стоп-кодонов нет. Все 27 нонсенс-мутаций приходятся на смысловую часть кода. В этой группе уже 5 вариантов его разметки с числом уязвимых кодонов от 21 до 27.

Все варианты с указанием количества их возможных реализаций, найденного путем перебора вариантов, сведены в табл. 4.

Группы c и d мы не рассматривали подробно, т.к. они не относятся к Парето-оптимуму[9] задачи II, образуемому группами a и b, которые решают оптимизационные задачи II‑a и II‑b, соответственно. Отметим также, что для вариантов 9 и 10 в задаче I‑a теоретический оптимум оказывается недостижим.

Природа предпочла вариант 2, варианту 1. Не исключено, что этот выбор случаен и обусловлен девятикратным превышением количества способов разметки кода для варианта 2 по сравнению с вариантом 1 (см. табл. 4). Однако возможна и обратная ситуация – такой выбор был закономерен. Если это так, то можно высказать определенные предположения об особенностях протекания биохимических процессов в ту далекую пору, когда их современные аналоги еще не сложились.

Предпочтительность варианта разметки кода, минимизирующего количество кодонов, уязвимых по отношению к точечным мутациям, видимо, означает, что использовался не весь код, а только его часть, неуязвимая к нонсенс-мутациям. Это вполне естественно в условиях высокой вероятности ошибок при получении реплик нуклеиновых кислот. При этом устойчивость кода в целом не имеет значения, поскольку весь он начнет использоваться на более позднем этапе развития живой материи.

В дополнение к задаче оптимизации устойчивости разметки генетического кода к точечным мутациям рассмотрим и задачу по оптимизации его устойчивости к двухточечным мутациям, оставляющим незатронутым лишь один нуклеотид в триплете (точечную мутацию мы здесь считаем частным случаем двухточечной).

Сложно сказать, насколько такая постановка содержательна с биологической точки зрения. С одной стороны, двухточечная мутация является исключительным событием, а с другой – она позволяет превратить любой триплет в 64‑3´3´3‑1 = 36 триплетов, т.е. практически во всё, что угодно. Тем не менее, представляется интересным взглянуть на разметку кода и под таким углом.

Как показывает анализ, здесь для разметки имеются те же самые 10 вариантов, что и в случае точечных мутаций (описание вариантов и их групп дано в табл. 4 выше). Однако в характеристиках решения для этих вариантов есть существенные отличия. Более нет необходимости рассматривать Парето-оптимум, т.к. выделился единственный оптимальный вариант (см. табл. 5).

Вариант 2, соответствующий существующему коду, по-прежнему обеспечивает минимальное количество уязвимых кодонов, однако и по количеству нонсенс-мутаций он теперь не хуже прочих вариантов. Абсолютный минимум количества нонсенс-мутаций для варианта 1, имевшее место в случае точечных мутаций, теперь размыт и реализуется в пяти вариантах из десяти.

Тем самым, мы получаем дополнительные свидетельства того, что сделанный природой выбор между вариантами 1 и 2 не был случаен. Он связана с большей важностью наличия отдельных неуязвимых кодонов по сравнению с общей устойчивостью кода. Каноническая разметка генетического кода избавляет 45 смысловых кодонов от риска быть превращенным в терминирующий в результате точечной мутации, а 12 – даже в результате двухточечной.

3.5. Уточнение задачи III

Три стоп-кодона могут содержать от 0 до 9 нуклеотидов с основанием аденин или тимин. Количество возможных реализаций разметки с заданным числом этих нуклеотидов приведено в табл. 6 (поскольку нас интересуют только случаи, когда их число превышает половину, мы ограничились частью таблицы).

Существующий код имеет 4 A и 3 T – итого 7 нуклеотидов, или почти 78% максимально возможного значения AT-индекса. А можно ли больше? Ответ на этот вопрос оказался отрицательным: если 8 или 9 нуклеотидов в терминирующих кодонах принадлежат набору {A; T}, то оптимальный результат в задаче I‑a (равно как и в задаче I‑b) не достигается. В случае AT-индекса, равного 9, может быть не более 158 запретных пар кодонов для сдвигов 1 и 2, а в случае 8 – не более 184. И лишь при AT-индексе, равном 7, становится достижим оптимум в 192 запретных пары.

Таким образом, задачу III можно переформулировать в безусловной форме: терминирующие кодоны должны содержать 7 или более нуклеотидов из набора {A; T}. Тогда ее решение не препятствует достижению оптимума в задачах I‑a и II‑b.

3.6. Многокритериальная оптимизация

Каноническая разметка кода является решением и задачи I‑a, и задачи II‑b, для которых имеется всего, соответственно, 1 728 и 2 432 оптимальных разметки. Если же поставить задачу оптимизации по обоим критериям, то количество возможных решений уменьшится до 528, что составляет менее 1,3% всех возможных разметок. Однако оказывается, что, это далеко не предел, если к критериям оптимизации информационной природы добавить эволюционно-химический.

В табл. 7 собраны данные о числе возможных решений каждой из трех сформулированных оптимизационных задач, а также их комбинаций.

Как мы видим, добавление критерия III существенно уменьшает количество возможных реализаций разметки генетического кода. При решении всех трех оптимизационных задач мы получаем всего 40 вариантов (из 41 664 возможных), к числу которых принадлежит и каноническая разметка.

Заметим, что многокритериальная оптимизация I‑a + III дает всего вдвое большее количество вариантов разметки (80), чем трехкритериальная (40). Следует ли отсюда, что решение задачи II‑b, связанной с уменьшением уязвимости генов по отношению к точечным мутациям, не очень важно? И да, и нет.

С одной стороны, выигрыш от решения оптимизационной задачи II‑b, если уже решены две других, не очень велик. Набор их решений состоит из 40 вариантов разметки с 18 уязвимыми триплетами, 12 – с 19, 20 – с 20 и 8 – с 21. Таким образом, среднее число смысловых кодонов, которые точечная мутация может превратить в терминирующие, для множества решений задачи I‑a + III составляет 18,95. Соответственно, неуязвимых к точечным мутациям кодонов остается в среднем 42,05, что всего на 2,2% хуже оптимума. Даже если выбрать наихудший с точки зрения задачи II вариант 10 (21 уязвимый кодон), то количество неуязвимых кодонов (40 штук) будет лишь на 7,0% хуже оптимального значения.

Однако, с другой стороны, критерий III в известной степени спекулятивен. Его мягкость порождает неопределенность. Не имея возможности удовлетворить критерию I‑a при AT-индексе, равном 9 или 8, мы согласились на 7. Почему тогда нельзя согласиться на 6 или 5? Все равное в этом случае более половины нуклеотидов, составляющих стоп-кодоны, будут принадлежать набору {A; T}.

Строгая постановка задачи III должна была бы учитывать вероятность наличия определенного количества нуклеотидов заданного типа в составе стоп-кодонов, исходя из соотношения реальных концентраций соответствующих азотистых оснований в "первичном бульоне". Однако ни сами концентрации, ни то, как они изменялись со временем, определить не представляется возможным.

Чем меньшей насыщенности аденином стоп-кодонов мы потребуем, тем больше будет роль оптимизации по критериям задачи II‑b. В табл. 8 представлены данные о количестве разметок когда, оптимальных в смысле задачи I‑a и имеющих заданный AT-индекс. По мере ее уменьшения отношение между полным числом решений и количеством решений, оптимальных в смысле задачи II‑b, возрастает. А тем самым увеличивается и ее значимость как критерия оптимизации по мере развития жизни и сближения концентраций различных азотистых оснований в природе.

4. Выводы

Существующий генетический код обладает рядом закономерностей. Одна из них – экстремальность канонической разметки с точки зрения рассмотренных оптимизационных задач I‑a, II‑b и III. Только 40 вариантов разметки кода из 41 664 возможных удовлетворяют критериям сразу трех этих задач.

В задаче блокировки чтения со сдвигом (I) природа выбрала тот вариант разметки кода, который наилучшим образом блокирует прочтение кодирующей цепи со смещением рамки (сдвиги 1 и 2), но отказалась от оптимизации разметки по ее способности блокировать прочтение комплементарной цепи вместо кодирующей (сдвиги 3, 4 и 5). Для канонической разметки при чтении кодирующей цепи с неправильным положением рамки запретными являются 192 пары смысловых кодонов. Этот результат – максимально возможный.

В задаче обеспечения устойчивости к точечным мутациям (II) природа предпочла минимизацию количества уязвимых кодонов минимизации числа нонсенс-мутаций для всего кода. Для канонической разметки всего 18 смысловых кодонов могут быть точечной мутацией превращены в один из терминирующих. Это результат – минимально возможный.

Всего существует 528 вариантов разметки, удовлетворяющих критериям этих двух задач, т.е. обеспечивающих наилучшую устойчивость генетической информации к ошибкам.

Задача максимизации AT-индекса разметки (III) отягощена необходимостью обеспечить информационную устойчивость. AT-индекс для канонической разметки равен 7. Это наибольшее его значение, не препятствующее решению задачи блокировки чтения со сдвигом.

Литература

1.   Фриленд С., Херст Л. Закодированная эволюция// В мире науки. 2004, №7. http://www.sciam.ru/2004/7/biotechnology.shtml

2.   Инге-Вечтомов С.Г. Трансляция как способ существования живых систем, или в чем смысл «бессмысленных» кодонов// Соросовский образовательный журнал. 1996. №12, с.2‑10. http://journal.issep.rssi.ru/articles/pdf/9612_002.pdf

3.   Франк-Каменецкий М.Д. Век ДНК. – М.: КДУ, 2004. – 240с.

4.   Freeland S.J., Hurst L.D. The genetic code is one in a million// J. Mol. Evol. 1998. N47, p.238‑248. http://www.evolvingcode.net/PDF/1inamillion.pdf

5.   Козлов Н.Н. Теорема для генетического кода// ДАН. 2002. Т.382, №5, с.593-597.

6.   Рис. Э., Стернберг М. От клеток к атомам: Иллюстрированное введение в молекулярную биологию/ Пер. с англ. – М.: Мир, 1988. – 144 с.

7.   Козлов Н.Н. Молчащие мутации в области перекрывания генов// ДАН. 1996. Т.350, №5, с.699‑703. Перекрывающиеся гены и генетический код// ДАН. 1997. Т.355, №6, с.830‑833. Терминаторные кодоны в генетических перекрытиях// ДАН. 1998. Т.360, с.550‑553. О востребованности каждого из 64 кодонов в генетических перекрытиях// ДАН. 1999. Т.367, №4, с.544‑547. К вопросу о произвольности "выбора" генетического кода// ДАН. 1999. Т.369, №4, с.553‑556. Анализ полного множества перекрывающихся генов// ДАН. 2000. Т.373, №1, с.108‑111. Применение теоремы для генетического кода// ДАН. 2004. Т.396, №6, с.740‑745.

8.   Галимов Э.М. Феномен жизни: Между равновесием и нелинейностью. Происхождение и принципы эволюции. – М.: Эдиториал УРСС, 2001. – 256 с.