Математическая модель роста населения Земли, экономики, технологии и образования
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
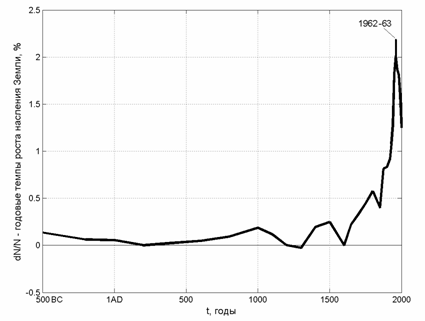
Рис.1. Темпы роста населения Земли |
Действительно, если рассмотреть график темпов роста населения, то в глаза бросается стремительное падение темпов роста, произошедшее за последние несколько десятков лет – микроскопическое по историческим масштабам время. Общий вид графика, его колебательный характер, может подтолкнуть к мысли, что, вполне возможно, нынешнее падение темпов роста – это проявление одного из циклов, которых за историю было немало и что это временное явление, которое в скором будущем сменится столь же стремительным ростом. Однако это логичное заключение имеет серьезный изъян. В действительности, нынешнее падение темпов роста коренным образом отличается от спадов и колебаний прошлого. Это не очередное колебание, это – переход на новый, не типичный для всей прежней истории, режим развития. Если все предыдущие спады были вызваны прежде всего увеличением смертности вследствие различных катаклизмов – войн, голода, эпидемий, и по мере завершения этих бедствий человечество быстро восстанавливалось и выходило на прежнюю траекторию, то нынешнее падение вызвано качественно отличными причинами – резким снижением рождаемости. Это снижение связано не с приближением к потолку несущей способности среды, а с причинами, заключенными в самом человеке. С.П. Капица подчеркивает информационный аспект развития общества, доминанту психологии и поведенческих функций над ресурсными и прочими материальными факторами.
Убедительность данного подхода, опирающегося на строгую математическую теорию, на логичные выводы из уравнения (7), показывающего феноменальное совпадение с эмпирическими данными, тем не менее, встречает достаточное сопротивление в среде исследователей, традиционно придерживающихся примата материального перед идеальным. Многовековая экономическая традиция, связывающая любые изменения в социуме прежде всего с ресурсно-производственными изменениями, естественным образом видит рост населения не самопричинным явлением, а всего лишь следствием развития экономических отношений и роста производительности труда. Основное положение было сформулировано еще в XVIII веке Томасом Мальтусом [31]. Его можно сформулировать следующим образом:
|
«На протяжении большей части существования человечества
рост его численности на каждый данный момент времени был ограничен потолком
несущей способности земли, обусловленным наблюдаемым в данный момент времени
уровнем развития жизнеобеспечивающих технологий». |
(12) |
В той или иной форме данное положение использовалось многими более поздними исследователями [15], [19], [20], [23], [26], [27], [35]. Таким образом, многочисленные работы на стыке экономики и демографии отдают главную роль именно экономико-технологическому фактору, предполагая демографическую составляющую подчиненной, что коренным образом противоречит идее демографического императива и выдвигает императив экономический.
Примечательно, что, как и теория С.П. Капицы, данное направление опирается и на эмпирические данные, и на математические модели, также дающие замечательное совпадение с демографическими данными, но по-своему их трактующие.
Наиболее математизированной и разработанной работой в этой области представляется работа Майкла Кремера [27] «Population Growth and Technological Change: One Million B.C. to 1990». (Рост населения и технологические изменения: от одного миллиона лет до нашей эры до 1990 года). В этой работе представлены сразу несколько моделей, с разных сторон описывающих процесс взаимного роста численности населения и уровня технологии.
Простейшая модель, предлагаемая Кремером, предполагает, что производство продукта зависит от двух факторов: уровня технологии и численности населения. У М. Кремера для величин используются обозначения Y – производимый продукт, p – численность населения, A – уровень технологии и т.п., мы же при описании запишем его модель в обозначениях, используемых в предложенной нами модели и более близких к обозначениям С.П. Капицы, не искажая при этом сути уравнений М. Кремера.
Кремер считает, что совокупный производимый человечеством продукт равен
![]() ,
,
где G – общий продукт, T – уровень технологии, V – используемые земельные ресурсы, 0 < α < 1 – параметр. Фактически, отдавая дань экономической теории, М. Кремер использует функцию типа Кобба–Дугласа, применение которой в данном случае, на наш взгляд, не вполне оправданно. В его теории переменная V в результате нормализации приравнивается к единице (что также спорно, поскольку используемые для производства территории серьезно расширялись со временем). В любом случае, уравнение для производимого продукта в результате имеет вид:
![]() , (13)
, (13)
где r, α – некоторые константы.
М. Кремер использует положение Мальтуса (12),
переформулировав его следующим образом: «В упрощенной модели будем считать, что
численность населения мгновенно приближается к равновесному уровню ![]() ». Величина
». Величина ![]() в его модели
соответствует уровню населения, при котором оно производит на душу населения
равновесный продукт
в его модели
соответствует уровню населения, при котором оно производит на душу населения
равновесный продукт ![]() , такой, что население увеличивается, если подушевой продукт
выше
, такой, что население увеличивается, если подушевой продукт
выше ![]() , и уменьшается, если подушевой продукт меньше
, и уменьшается, если подушевой продукт меньше ![]() .
.
Равновесный уровень населения ![]() , таким образом, равен
, таким образом, равен
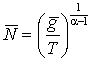 . (14)
. (14)
Таким образом, уравнение для численности населения фактически не является динамическим. В модели М. Кремера динамика заложена в уравнение для технологического роста, который, как отмечалось в широкой среде исследователей-экономистов, рассматривается как первичный фактор развития человечества, в частности, вызывающий рост населения. М. Кремер уделяет большое внимание этому фактору, анализируя различные гуманитарные концепции и математические модели роста технологии.
Наряду с другими исследователями [13], [14], [22] он
исходит из Босерупианского [18] предположения о том, что рост населения
подталкивает людей к разработке новых технологий, и, в конечном счете, рост
технологии пропорционален населению. Данный тезис ранее выдвигался
С. Кузнецом [28] и Саймоном [37] в формулировке «Большее население
означает большее количество потенциальных изобретателей». Кремер уточняет его: [27, c.685]
|
«Простая модель предполагает, что при прочих равных,
вероятность изобретения чего-либо одним человеком не зависит от численности населения.
То есть среди большего населения будет пропорционально больше людей,
достаточно удачливых и сообразительных, чтобы предложить новые идеи». |
(15) |
Математически данное положение М. Кремер выражает как
![]() , (16)
, (16)
где b – средняя продуктивность работы одного изобретателя.
Как ни странно, но материалистическое предположение о ведущей роли экономики и развития производственных сил в развитии человеческого общества, в конечном счете, сводится к уравнению, которое явно апеллирует к сознательной деятельности человека, его способности к поиску технических решений. Понятно, что попытка формализовать и вывести законы процесса открытий новых законов неизбежно вызывает град критики. Весьма сомнительным, в частности, кажется введение постоянной средней продуктивности работы изобретателя. Одни изобретения являются судьбоносными, другие – вспомогательными, а подавляющая часть мелких усовершенствований вообще не привносит сколь-либо существенных изменений в общий технологический уровень. И хотя мы имеем достаточно примеров эффективного осреднения, например осреднения, позволяющие говорить о температуре или давлении идеального газа, в этих случаях мы сталкиваемся с вполне определенными законами распределения, для которых осреднение имеет смысл. В любом случае введение любого осреднения требует четкого математического обоснования и явной эмпирической верификации. Таким образом, несмотря на материальные основы экономики, ключевой фактор инноваций опять же, по выражению Ф. Фукуямы, «лежит в области духа».
Тем не менее то, что изобретения происходят в сознании людей и являются следствием творчества, не означает, что можно легко закрыть вопрос о каком-либо изучении данной темы, провозгласив, что человеческое сознание слишком сложно для описания и никому никогда не удастся в него проникнуть, а тем более описать формально. Тот факт, что новые технологии появляются в результате акта творчества, отнюдь не значит, что технический прогресс имеет субъективную природу. У него есть вполне объективные, не зависящие от человеческого сознания причины.
Рост технологического уровня вовсе не ограничивается актом изобретения. Для того чтобы оно утвердилось и внесло вклад в общий технологический уровень, необходимо также, чтобы оно победило в конкурентной борьбе с возникшими ранее технологиями, допускало внедрение и тиражирование – то есть было адекватно существующим технологиям, а также оно должно пространственно распространиться. Таким образом, если изобретение дает слишком малые преимущества по сравнению с текущим уровнем, то оно, скорее всего, не утвердится в конкурентной борьбе, которая обладает большой инерцией, а если же оно слишком революционно, то у него также малые шансы на утверждение, поскольку общий уровень технологии слишком низок для его обслуживания. Так было с изобретениями Леонардо да Винчи, так получилось с пилотируемой космонавтикой, которая не оправдала ожиданий бума космических путешествий в конце XX века, то же можно сказать и о многих изобретениях древности, не дошедших до нас, поскольку они не были поддержаны существующим на тот момент уровнем технологии. В итоге успех имеют те инновации, которые продвигают технологический уровень на величину, одновременно не слишком малую и не слишком большую по сравнению с текущим уровнем.
Таким образом, озарение изобретателя – это только флуктуация, во многом случайная мутация, которая затем проходит более суровый и объективный отбор, жестко связанный с текущим уровнем технологии. При этом интенсивность флуктуаций – число изобретений и (что не менее важно) попыток их внедрения, также является важным фактором наряду с технологическим уровнем.
Эти объективные, не зависящие от сознания человека механизмы, фактически и определяют общий смысл соотношения (16).
В любом случае сам М. Кремер понимает уязвимость столь простого описания развития технологии. Действительно, хотя очевидна зависимость роста от текущего уровня и от интенсивности изобретений, эта зависимость вовсе не обязана быть линейной (если обратное не доказано эмпирически). Поэтому Кремер апеллирует к уравнению роста технологии С. Джонса [25]:
![]() ,
,
где ![]() – показатель, не
равный единице и связывающий текущий уровень технологии со скоростью ее
прироста. С математической точки зрения, в случае если
– показатель, не
равный единице и связывающий текущий уровень технологии со скоростью ее
прироста. С математической точки зрения, в случае если ![]() > 1, с ростом технологии
наблюдается ускорение относительных темпов роста, то есть, по сути, увеличение
относительной производительности одного изобретателя, если же
> 1, с ростом технологии
наблюдается ускорение относительных темпов роста, то есть, по сути, увеличение
относительной производительности одного изобретателя, если же ![]() < 1, то наоборот, относительная
производительность изобретателя падает по мере того как технология развивается.
< 1, то наоборот, относительная
производительность изобретателя падает по мере того как технология развивается.
Сам С. Джонс считает, что ![]() < 1, поскольку это,
по его мнению, объясняет замедление технологического роста в послевоенный
период. Однако Кремер отмечает [27, c.689], что вполне возможно, что все-таки
< 1, поскольку это,
по его мнению, объясняет замедление технологического роста в послевоенный
период. Однако Кремер отмечает [27, c.689], что вполне возможно, что все-таки ![]() = 1, то есть модель
(16) верна, ссылаясь на долгосрочные экономические тренды роста технологии
[36].
= 1, то есть модель
(16) верна, ссылаясь на долгосрочные экономические тренды роста технологии
[36].
Наконец, дабы охватить все возможные зависимости, Джонс предлагает также ввести степенную зависимость для численности населения, получая наиболее общее уравнение:
![]() . (17)
. (17)
Таким образом, в общем случае относительная производительность одного изобретателя зависит и от текущего уровня технологии, и от количества других изобретателей.
Опираясь на данное уравнение, М. Кремер
модифицирует свою модель и дает оценки для параметров ![]() ,
, ![]() .
.
В результате общая модель, учитывающая рост населения
и технологии, удовлетворительно описывает гиперболический рост населения, но,
даже несмотря на искусственное снижение темпов роста, связанное с тем, что ![]() < 1, она не
описывает демографического перехода, то есть резкого снижения темпов роста
населения Земли за последние четверть века.
< 1, она не
описывает демографического перехода, то есть резкого снижения темпов роста
населения Земли за последние четверть века.
Понимая недостатки своей модели, М. Кремер пытается модифицировать ее с тем, чтобы она учла и это явление. Для того чтобы ввести в модель ограничения на рост населения, не выходя за рамки двух переменных, М. Кремер вынужден ввести достаточно сложную функцию, описывающую рождаемость как функцию от дохода.
Здесь A – разница между рождаемостью
и смертностью как функция от g – доход на душу
населения, который в модели рассчитывается как g = G / N, то есть общий продукт G, полученный по формуле (13) и поделенный между N членами популяции.
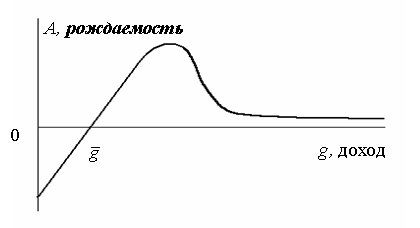
Рис.2. Зависимость рождаемости от доходов в модели Кремера
Из графика видно, что если продукт, приходящийся на
одного человека, меньше, чем критическое значение ![]() , то наблюдается депопуляция, если он больше, но ненамного,
то идет рост населения, если же общество становится достаточно богатым, то рост
населения резко сокращается, поскольку богатые семьи не склонны иметь много
детей.
, то наблюдается депопуляция, если он больше, но ненамного,
то идет рост населения, если же общество становится достаточно богатым, то рост
населения резко сокращается, поскольку богатые семьи не склонны иметь много
детей.
Благодаря введению такой нелинейной функции у М. Кремера возникает возможность описания демографического перехода. Однако полученная в результате модель обладает рядом недостатков:
1. Введение
функции A(g) ведет к дополнительному усложнению модели, поскольку для ее
описания нужно вводить в модель несколько новых параметров, которые, наряду с ![]() ,
, ![]() и другими
коэффициентами следует эмпирически оценивать, то есть модель из двух уравнений
оказывается перегружена коэффициентами, что не всегда оправдано, так как не все
посылки легко верифицируемы.
и другими
коэффициентами следует эмпирически оценивать, то есть модель из двух уравнений
оказывается перегружена коэффициентами, что не всегда оправдано, так как не все
посылки легко верифицируемы.
2. Модель демографического перехода, включающая функцию A(g), хотя и опирается на правдоподобные допущения о том, что большие заработки соответствуют меньшей рождаемости, а низкие заработки – высокой рождаемости, не может быть принята. Против этой модели явно говорит нынешняя ситуация в России – резкое снижение уровня доходов вовсе не вызвало всплеска рождаемости, как это предсказывает функция A(g).
Таким образом, необходимо искать иные, хотя, вероятно, и близкие причины демографического перехода. Возможно, для адекватного описания процесса придется увеличить число динамических переменных и рассмотреть динамику еще одного показателя наряду с численностью населения и уровнем технологии. Добавление еще одной переменной не обязательно должно вызвать нежелательное усложнение модели, поскольку оно может привести к сокращению числа параметров и упрощению зависимостей.
Любопытно также отметить, что опять же, несмотря на материальный экономический императив работы М. Кремера, причины демографического перехода он видит в человеческом факторе – сознательном ограничении рождаемости при высоком уровне доходов.
В итоге работа М. Кремера дала очень серьезное и правдоподобное описание гиперболического роста населения Земли, опиралась она прежде всего на экономические механизмы и дала при этом не худшие результаты, чем теория С.П. Капицы. Однако в той части, где она касалась демографического перехода, ее объяснение все еще нельзя считать достаточным, даже несмотря на сильное усложнение модели и введение нескольких дополнительных параметров.
Модель
роста жизнесберегающих технологий А.В. Подлазова
Таким образом, если причины гиперболического роста к настоящему времени оказались достаточно хорошо объяснены, то механизм глобального демографического перехода пока остается загадкой. Попытка объяснить это явление, найти объективные причины пределов роста была предпринята в работах А.В. Подлазова [8], [9], [34].
В них фактически проведен синтез обеих описанных теорий. С одной стороны, он, подобно М. Кремеру, видит причины гиперболического роста в совместном процессе роста человечества и технологии. С другой стороны, причину демографического перехода, как и С.П. Капица, он ищет в самом естестве человека, его биологических параметрах и продолжительности жизни.
В безразмерных величинах модель гиперболического роста можно записать в виде
![]() , (18)
, (18)
![]() , (19)
, (19)
где N – численность населения, а P – уровень технологии. Хотя для уровня технологии мы использовали переменную T, для модели А.В. Подлазова технология будет обозначаться как P, поскольку М. Кремер и А.В. Подлазов понимают смысл технологии по-разному.
Уравнение (19) является аналогом уравнения (15). А уравнение (17) – очевидным дополнением к (18) для того, чтобы выполнялась эмпирическая зависимость (5). Она отражает тот факт, что емкость ниши пропорциональна уровню технологии (М. Кремер говорит о ресурсной нише, А.В. Подлазов – о технологической), и, следовательно, численность населения N будет следовать за емкостью ниши P:
![]() , (20)
, (20)
где c – константа.
В отличие от М. Кремера, для которого технологии – это средство производства продукта (13), А.В. Подлазов видит роль технологий иначе. Он вводит понятие жизнесберегающие технологии. Роль технологий он видит в предотвращении смерти и продлении жизни безотносительно того, каким образом это достигается – за счет производства пищи или за счет религиозных норм морали.
Таким образом, само понятие жизнесберегающих технологий является оптимальным для демографических исследований, поскольку оно явным образом связано с параметром смертности D в формуле (1), которую можно расписать в виде:
![]() , (21)
, (21)
где kb и kd
– коэффициенты рождаемости и смертности, из которых А.В. Подлазов полагает
kb постоянным и равным ![]() – коэффициенту рождаемости
на начало фазы роста, а коэффициент смертности kd
– переменным, существенно зависящим от уровня жизнесберегающих технологий,
собственно и определяемых как
– коэффициенту рождаемости
на начало фазы роста, а коэффициент смертности kd
– переменным, существенно зависящим от уровня жизнесберегающих технологий,
собственно и определяемых как
![]() , (22)
, (22)
причем в силу отсутствия роста на стадии, предшествующей
стадии роста, А.В. Подлазов считает, что ![]() .
.
Таким образом, уравнение (21) дает следующую формулу:
![]() , (23)
, (23)
а с учетом (19) имеем
![]() , (24)
, (24)
где ![]() ,
, ![]() и
и ![]() – постоянные,
очевидно, что с учетом равенства
– постоянные,
очевидно, что с учетом равенства ![]() уравнение (24) эквивалентно
уравнению (7).
уравнение (24) эквивалентно
уравнению (7).
Любопытно провести аналогии между соотношениями (24) и (3). Они отличаются лишь знаком квадратичного члена, однако это различие в одном случае приводит к стагнации населения, а в другом – ведет к взрывообразному росту. Тем не менее уравнения вида (24) не являются специфичными только для описания численности населения, такие уравнения используются и в биологии, когда между членами популяции существует взаимопомощь.
Что же касается ограничения гиперболического роста, то А.В. Подлазов видит причину демографического перехода в том, что невозможно до бесконечности понижать коэффициент смертности. Таким образом, уровень P ограничивается биологическим пределом человеческого организма, что дает ограничение P∞ ≈ 0,05 год‑1. При этом стадию демографического перехода А.В. Подлазов предлагает описывать уравнением
![]() (25)
(25)
Таким образом, демографический переход, по мнению А.В. Подлазова, неизбежен и связан не с какими-то ни было ресурсными ограничениями, а исключительно с внутренними особенностями человеческого организма.
Итак, А.В. Подлазову, вслед за М. Кремером, удалось объяснить механизм гиперболического роста с позиций развития технологий. При этом он ввел понятие жизнесберегающих технологий, тесно связанных с демографической смертностью. Что касается демографического перехода, то, по мнению А.В. Подлазова, он связан с бессмысленностью увеличения уровня жизнесберегающих технологий, так как внутренний ресурс человеческого организма не востребует такого увеличения.
Работа А.В. Подлазова, безусловно, является шагом вперед в области теоретической демографии. Введенное понятие жизнесберегающих технологий позволяет проводить ввести единую шкалу измерения для различных и плохо сопоставимых технологических нововведений. Например, с помощью этой меры можно сравнить роль экономики, религии, политики, образования в едином масштабе. Однако, несмотря на подобные перспективы, практическое использование этой меры на данный момент затруднено, поскольку выделение влияния различных факторов на смертность само по себе является сложной, пока не решенной задачей. При этом в свете описания глобального демографического процесса важность адекватного измерения уровня технологии очевидна.
Другим важным недостатком модели А.В. Подлазова является противоречащее действительности суждение о том, что демографический переход связан с невозможностью уменьшения смертности. Демографические данные четко указывают на то, что переход связан с резким уменьшением рождаемости. Действительно, в (23) А.В. Подлазов постулирует постоянный уровень рождаемости, что для стадии демографического перехода неприемлемо. Выходом из такой контрафактической ситуации могло бы стать признание А.В. Подлазовым смысла жизнесберегающих технологий не как технологий, ограничивающих смертность, а как технологий, увеличивающих разницу между рождаемостью и смертностью, однако и такое объяснение не согласуется с его предположениями, поскольку в этом случае на стадии стабилизации населения эта разница должна стать равной нулю, что мало согласуется с понятием уровня технологии. Наконец, не проработанным у А.В. Подлазова остается переход от формулы (19) к формуле (25), то есть переход с режима роста на режим демографического перехода.
Итак, можно подытожить нынешнее состояние науки в области теоретической демографии следующим образом.
– Причина гиперболического роста близка к объяснению с позиций роста технологического уровня.
– Причины демографического перехода, связанного, судя по данным, с резким снижением рождаемости, не получили нефеноменологического объяснения, хотя и описаны математическими моделями, апеллирующими к внутренней природе человека и характерным временам его биологической жизни.
Таким образом, необходимо решить следующие задачи:
– Определить, какую величину следует рассматривать в качестве уровня технологии и каким образом ее можно измерять.
– Операционализировать зависимость (20), показав ее связь с общепринятыми научными положениями в области демографии и популяционной динамики.
– Объяснить явление демографического перехода и описать его механизм, если потребуется, с привлечением дополнительных показателей развития человечества.
Производительность
труда как показатель уровня технологии
Обсуждаемые выше модели с математической точки зрения хорошо описывают гиперболическую зависимость (5), однако нередко они оперируют общими теоретическими соображениями, не подкрепленными численными данными, вводят плохо измеримые показатели. Поэтому чрезвычайно важно свести теоретические построения с наблюдаемыми эмпирическими данными. Понятно, что в нынешних условиях, когда имеющиеся данные малочисленны и не всегда заслуживают доверия, построение опирающейся на них модели необходимо проводить чрезвычайно осторожно, однако иного пути нет.
Работы М. Кремера и А.В. Подлазова предполагали, что численность населения и уровень технологии существенно связаны друг с другом. Однако в явном виде связь между этими показателями была представлена только на теоретическом уровне. Предложенные зависимости (16) и (19) исходят из общих соображений, не в полной мере опирающихся на эмпирическую базу, кроме того, уравнения (16) и (19) по-разному трактуют понятие «уровень технологии».
Таким образом, первой задачей является определиться с пониманием «уровня технологии», которое в дальнейшем мы будем использовать в модели. По нашему мнению, наиболее естественным измеримым интегральным показателем, соответствующим понятию «уровень технологии», является производительность труда.
При всех тонкостях измерения данного показателя, в рамках макромодели мы будем измерять его простым образом:
![]() , (26)
, (26)
где T – производительность труда, в рамках нашей модели понимаемая как уровень технологии, G – мировой ВВП, N – численность населения.
Очевидно, что производительность труда не является одинаковой для разных регионов мира, но макроуровень, на котором проводится моделирование, допускает введения таких обобщенных показателей, подобно тому, как модели С.П. Капицы, М. Кремера и А.В. Подлазова не учитывают неравномерности распределения населения и берут общую численность населения в виде интегрального показателя.
Выбор производительности труда в качестве «уровня технологии» является вполне естественным. Причем мы рассматриваем производительность труда не локально – как эффективность производства тех или иных конкретных благ, а интегрально, как эффективность производства всех благ в данную эпоху. Таким образом, во введенное нами понятие уровня технологии неявно входят не только собственно производственные технологии, но и политические, социальные, религиозные, образовательные и прочие технологии, в конечном счете приводящие к увеличению ВВП. Следует заметить, что наше понятие T в (26) близко по смыслу к понятию уровня технологии М. Кремера, хотя он отдельно не делает акцент на том смысле, которое он вкладывает в используемый им в (13) показатель T.
Эмпирическое
подтверждение связи численности населения и уровня технологии
Следующим шагом является обоснование использования введенного нами показателя T при моделировании глобального демографического процесса и построения модели, опирающейся на общепринятые в демографической науке уравнения.
Как отмечалось, одним из наиболее общих положений в популяционной динамике является использование логистического уравнения Ферхюльста (2). Оно описывает динамику популяции в условиях ресурсного ограничения и замечательно работает для многих биологических видов – от микроогранизмов до крупных животных. Что касается его применимости к описанию демографического процесса, то эмпирические данные по квадратичному росту населения (4) и постоянный рост потолка несущей плотности Земли, казалось бы, делают уравнение (2) неприменимым для описания роста численности населения.
Тем не менее есть предпосылки к использованию этого уравнения, поскольку в его пользу явно говорит мальтузианский тезис (15), а также то, что потолок несущей способности Земли вполне можно описывать переменой, зависящей от объема производимого продукта и, следовательно, от уровня технологии (26).
Если обобщить эти выводы, то их можно записать в виде:
![]() , (27)
, (27)
где r, w – коэффициенты.
Уравнение имеет вид (2) и строится из тех соображений, что потолок несущей способности Земли ограничен уровнем существующей технологии. При возникновении относительной перенаселенности население возвращается к сбалансированной численности – как правило, за счет войн и эпидемий, при недонаселенности возникает быстрый рост в условиях пониженной конкуренции и население стабилизируется на уровне потолка, пока какое-нибудь, возможно малое, воздействие не отклонит его, вызывая очередное колебание.
Скорость выхода на уровень потолка несущей способности как сверху – военные конфликты и эпидемии – так и снизу – восстановление после этих бедствий, зависит от способности людей оперативно уничтожать и восстанавливать друг друга и инфраструктуру. В этом предположении коэффициент r, отвечающий за скорость выхода на потолок несущей способности, также должен зависеть от уровня технологии. В простейшем случае линейной зависимости можно представить следующую модель роста населения:
![]() , (28)
, (28)
где v и w – постоянные коэффициенты. В подобной формулировке отношение T к w приобретает вполне четкий смысл – это количество людей, которое может прокормить Земля при заданном уровне технологии T.
Модель (28), будучи также объединена с уравнением (16), асимптотически дает гиперболический рост. При задании начальных условий, для которых население сильно отличается от заданного уровнем технологии потолка несущей способности, население очень быстро выходит на него и затем следует за этим потолком, который в свою очередь растет ускоренными темпами.
Таким образом, модели популяционной динамики не теряют своей актуальности и в описании демографических процессов, особенно процессов, идущих на сравнительно малых временных масштабах. Действительно, моделирование демографических циклов и колебаний вокруг тренда под воздействием дестабилизирующих факторов может быть хорошо описано с позиций уравнения (27) и его модификаций. Однако при описании макродинамики такого рода быстрые процессы выхода на траекторию, вдоль которой система движется относительно медленно, вообще часто не выделяются в отдельные уравнения. Согласно теореме Тихонова [12], в системе уравнений дифференциальное уравнение для переменной, имеющей значительно меньшее характерное время изменения по сравнению с другими переменными, может быть заменено алгебраическим (при условии, что характер решения не меняется при устремлении малого параметра при производной к нулю). В работах М. Кремера и А.В. Подлазова фактически использовалось это положение теоремы Тихонова, а также неявно задавалось ограничение (27) численности населения уровнем технологии: М. Кремер (14), А.В. Подлазов (20).
Что же касается более медленных изменений, то для их описания следует использовать модели, учитывающие другой порядок характерных скоростей.
Так с учетом того, что население быстро выходит на квазистационарную траекторию, ресурсные ограничения выступают в качестве членов другого порядка малости:
![]() , (29)
, (29)
то есть как ограничения, связанные с необходимостью излишка, обеспечивающего устойчивый рост тренда, вокруг которого совершаются колебания. Уравнение (29) перепишем в виде
![]() , (30)
, (30)
где a и m – коэффициенты. Данное уравнение также имеет вполне популяционную трактовку: прирост наблюдается в случае, когда производится продукта больше, чем необходимо для выживания. Коэффициент m играет роль «прожиточного минимума» – доли произведенного ресурса, строго направляемого на поддержание достигнутой численности населения. Прирост возможен только если наблюдается разница между продуктом, произведенным и потраченным на одного человека. Согласно модели T – производительность труда, а m – минимально необходимый продукт на одного человека, таким образом, разность (T – m) – это ресурс на душу населения, который может быть потрачен на дополнительные цели – размножение, науку, искусство, развлечения и пр.
Таким образом, целесообразно ввести переменную
![]() , (31)
, (31)
имеющую смысл излишков на душу населения, которые могут быть использованы на дополнительные цели помимо поддержания достигнутой численности населения.
С учетом данной поправки можно записать следующую модель:
![]() , (32)
, (32)
![]() , (33)
, (33)
где a и b – константы. Уравнение (32) является записью уравнения (30) с учетом (31), а уравнение (33) является уравнением роста технологии, поскольку, очевидно, с учетом предположения о постоянстве m в (31), имеет место равенство
![]() . (34)
. (34)
Уравнения (33), (19) и (16), с математической точки зрения, абсолютно идентичны, и, как нетрудно убедиться, в сочетании с (32) или, что то же, (18) дадут гиперболический рост переменной N, однако существенным различием является понимание переменных, отражающих технологический смысл. Напомним, что T в уравнении (16) – это, по сути, коэффициент при производственной функции Кобба–Дугласа, не вполне четко декларированный М. Кремером, P в уравнении (19) – это уровень жизнесберегающих технологий, используемых А.В. Подлазовым, которые также не имеют четкого операционализированного определения и способов измерения, в то время как S в (33) – это излишек на одного человека, производимый при данном уровне технологии, определяемом как квазистационарная производительность труда и измеряемом как отношение мирового ВВП к населению Земли.
Понятно, что введение дополнительных переменных и показателей может быть оправданным только тогда, когда это введение дает какое-то новое качество. На наш взгляд, введение новых понятий и модификация уравнений должны служить цели более адекватного описания действительности и эмпирических данных.
Для подтверждения уравнений (32) и (33) целесообразно использовать данные по динамике мирового ВВП.
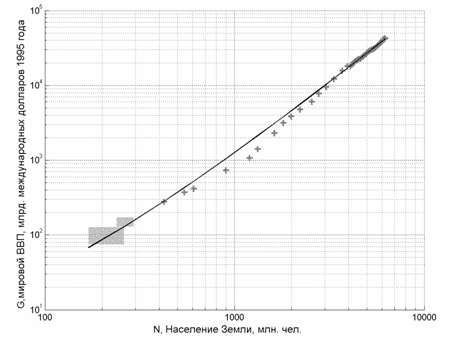
Рис.3. Мировой ВВП и численность населения Земли
Прямоугольниками обозначены точки, соответствующие 1 и 1000 н.э., для которых имеется разброс оценок.
За последние 2000 лет (существуют оценки и для более ранних периодов, которые не противоречат формуле, но мы их не рассматриваем, поскольку их достоверность должна быть еще должным образом обоснована) мировой ВВП (источники: [6], [29], [30], [40]) хорошо описывается формулой
![]() , (35)
, (35)
где ![]() , γ
– константы. (на Рис 3. γ
=
, γ
– константы. (на Рис 3. γ
= ![]() ;
; ![]() = 221,15; ВВП
измерялся в международных долларах 1995 года) Этот факт дает основание
рассматривать систему (32) – (33) с позиций эмпирических данных. Можно сделать
предположение относительно значения m в (31). Поскольку в
силу сделанных выше предположений рост населения и технологии в (31) и (32)
наблюдается только в том случае, если S > 0, то изначальный крайне маленький прирост
у предков человека мы можем считать нулевым, то есть S0 =
0, что значит, что производительность труда у предков человека была в
точности равна их минимальным потребностям:
= 221,15; ВВП
измерялся в международных долларах 1995 года) Этот факт дает основание
рассматривать систему (32) – (33) с позиций эмпирических данных. Можно сделать
предположение относительно значения m в (31). Поскольку в
силу сделанных выше предположений рост населения и технологии в (31) и (32)
наблюдается только в том случае, если S > 0, то изначальный крайне маленький прирост
у предков человека мы можем считать нулевым, то есть S0 =
0, что значит, что производительность труда у предков человека была в
точности равна их минимальным потребностям: ![]() , что значит, что
, что значит, что
![]() . (36)
. (36)
можно оценить как «изначальный уровень технологии» и как константу в (31).
Нетрудно убедиться, что сделанные предположения, формулы (32)–(33), их решения и эмпирические данные по росту населения и ВВП не противоречат друг другу. Исходя из (31), (26), (35) и (36) получаем эмпирическое выражение
![]() , (37)
, (37)
которое одновременно удовлетворяет решению системы (32)–(33), дающему гиперболический рост населения мира и уровня технологии.
Следует также отметить, что при достаточно большой численности населения Земли линейным членом в (35) можно пренебречь и считать, что T ≈ S ~ N. В частности, в 2000 году T составляет порядка 6000 долларов на человека в год, в то время как m – всего порядка 200-300. В результате для современной эпохи соотношения G = γN2 и T = γN, выполняются c очень хорошей точностью.
Таким образом, понятие «уровень технологии», введенное как квазистационарная производительность труда, является хорошо операционализированной и относительно легко измеримой величиной, адекватной описанию глобального демографического процесса. Что важно, для этой величины удается найти эмпирическое подтверждение результатов модели (32)–(33).
Механизмы
демографического перехода
Предложенные нами объяснение и модель гиперболического роста населения Земли не отличаются кардинально от предлагаемых ранее моделей роста населения и технологии, отличие состоит в операционализации понятия «уровень технологии» и эмпирическом обосновании предложенных моделей.
Что же касается демографического перехода, то проведенный выше обзор концепций и моделей показывает, что исследователи гораздо менее едины во мнении относительно его причин и механизмов, и, хотя в большинстве своем, они связывают его не с ресурсными ограничениями, а с особенностями, заложенными в самом человеке, взгляд на эти особенности также сильно разнится. С.П. Капица связывает причину перехода с ограниченностью характерных времен развития человека и человечества, Кремер видит причину в уменьшении рождаемости в обеспеченных семьях, А.В. Подлазов связывает переход с неспособностью жизнесберегающих технологий увеличить продолжительность жизни свыше биологического предела. Видны также и различия на уровне подходов: если М. Кремер пытается описать реальный механизм перехода, то С.П. Капица и А.В. Подлазов скорее ищут не сам механизм снижения рождаемости, а причину смены режима глобального развития человечества, они пытаются объяснить, в чем состоит исключительность нынешнего состояния, почему демографический переход происходит именно сейчас за микроскопическое по историческим масштабам время и именно на том уровне развития, который достигнут на данный момент.
В предлагаемой нами ниже модели мы ставим задачей объяснить и микромеханизм перехода, и причину уникальности этого явления. Первое, с чем необходимо определиться – это с историческим диапазоном, в рамках которого модель претендует на описание действительности.
Достаточная проработанность демографической тематики и представительность оценок численности населения человечества, относящихся к глубокой древности, создает предпосылки для описания глобального демографического процесса, начиная с миллиона лет до н.э. по настоящее время.
Несмотря на заманчивость глобальных теорий, мы сознательно ограничим область рассмотрения. Поскольку кроме численности населения, для которой имеются удовлетворительные оценки на протяжении миллиона лет, мы используем и другие показатели (в частности мировой ВВП), значительно хуже представленные статистически, то область применимости модели естественным образом ограничена областью имеющихся статистических данных. Это не значит, что модель неприменима для более раннего времени, не представленного статистически, но в любом случае для обоснования этого требуются дополнительные исследования и оценки.
Более или менее достоверные имеющиеся данные по ВВП относятся к периоду с начала нашей эры по нынешнее время, причем начиная с 1970 года [40] они известны с большой точностью по каждому году. Таким образом, предлагаемая модель претендует на описание демографического и экономико-технологического роста за период с начала нашей эры по нынешнее время. Прогностические возможности модели также ограничиваются временами порядка столетия, о чем будет отдельно сказано ниже.
Как отмечалось в комментарии к рис. 1., уникальность нынешнего резкого спада темпов роста населения состоит в том, что он впервые за всю предыдущую историю человечества связан с резким снижением рождаемости в мировом масштабе. Все предыдущие спады происходили из-за увеличения смертности вследствие голода, войн и эпидемий. По сравнению со всем предыдущим этапом развития человечества именно наше время знаменует переход к качественно новому демографическому режиму.
Таким образом, модель демографического перехода должна выявить факторы, вызывающие этот переход, и, прежде всего, факторы резкого понижения рождаемости.
Грамотность
– основной фактор снижения рождаемости
Для определения основных факторов снижения рождаемости разумно обратиться к эмпирическим данным. Анализ большой статистической выборки убедительно показывает, что рост уровня образования населения в ходе модернизации, наряду с развитием медицинских технологий и системы социального обеспечения, является ведущим фактором снижения рождаемости [16], [17], [24], [32]. Сразу же отметим, что развитие медицинских технологий не только снижает рождаемость, но и, очевидно, смертность, однако это – отдельная тема, которая будет обсуждена ниже. По сравнению с обществами, уже завершившими демографический переход, к которым относится и Россия, влияние образования и здравоохранения на рождаемость особо велико для стран третьего мира. При этом появление и распространение новых медицинских технологий возможно только в результате развития сферы образования. Образование, с одной стороны, позволяет населению ознакомиться со средствами регуляции рождаемости, а с другой – меняет ценностные ориентации людей, что отражается и на репродуктивных установках.
Показатель грамотности, т.е. процент грамотных в обществе (стране, мире и т.д.) является хорошим интегральным показателем развития образовательных процессов. Дж. Бонгаартсом [17] было показано, что уровень грамотности женщин является надежным предиктором снижения рождаемости.
|
Таблица 1. Регрессионная модель факторов
рождаемости в мире в 1995 г. |
|
|
|
Нестандартизированный
коэффициент |
Стандартизированный коэффициент |
t |
Α |
|
|
Модель |
B |
Стандартная ошибка |
β |
||
|
Константа |
6,955 |
0,467 |
|
14,899 |
4×10-16 |
|
|
Грамотность
среди женщин, % |
- 0,038 |
0,007 |
- 0,600 |
- 5,139 |
0,00001 |
|
|
Кол-во врачей на
1000 чел. |
- 0,253 |
0,117 |
- 0,239 |
- 2,155 |
0,036 |
|
|
Урбанизация (%
населения, проживающего в городах) |
- 0,006 |
0,007 |
- 0,087 |
- 0,866 |
0,391 |
|
|
Примечание: R = 0,837; R2 = 0,701; α = 2×10‑11. |
Недостатком подхода Дж. Бонгаартса является то, что в ходе своего регрессионного теста он включил ожидаемую продолжительность жизни в ряд гипотетических факторов рождаемости, что несколько снизило объяснительную ценность его модели. В частности, согласно его результатам, большая продолжительность жизни понижала рождаемость. Безусловно, продолжительность жизни сама по себе может быть коррелятом, но никак не фактором снижения рождаемости. Проведем собственный кросс-национальный тест факторов рождаемости с помощью пошагового метода множественной регрессии (источник данных: [1]).
Пояснение к таблице 1:
Линейная регрессия позволяет представить зависимость между зависимой
(напр., Y) и независимой (напр., Х) переменной с
помощью линейного уравнения:
Y = A + B X,
где A – константа, а B – коэффициент, которые и вычисляются с помощью линейной
регрессии. В статистических пакетах множитель B, как правило,
обозначается как "Нестандартизированный
коэффициент".
Множественная регрессия – это разновидность, как правило, линейной
регрессии, направленная на изучение влияния нескольких независимых переменных
(факторов) на зависимую и позволяющая вывести уравнение вида: Y = A + B1X1 + B2X2 + B3X3 … .
При этом в уравнение вставляются только те переменные, которые
оказались значимыми предикторами зависимой переменной, т.е. те переменные,
показатель значимости α для которых меньше 0,05[1]. В нашем случае переменная "Урбанизация" оказалась незначимым
предиктором рождаемости, а переменные "Грамотность среди женщин" и
"Количество врачей на 1000 чел" – значимыми.
Для определения того, какой из статистически значимых
предикторов рождаемости является наиболее сильным, воспользуемся стандартизированным
коэффициентом β. Этот показатель указывает на важность независимых
переменных, вовлеченных в регрессионное уравнение. Он принимает значения от +1
до – 1. Значение + 1,0 означает полную ("функциональную") положительную
связь между признаками. В этом случае увеличение значения величины Х
сопровождается однозначно определенным увеличением значения величины У.
Значение – 1,0 означает полную ("функциональную") отрицательную
связь между зависимой и независимой переменными. В этом случае увеличение значения
величины Х сопровождается однозначно определенным уменьшением значения величины
У. В "мире людей" закономерности, описываемые функциональными
зависимостями, почти не встречаются. В данной регрессионной модели самым
сильным предиктором рождаемости является женская грамотность, т.к. коэффициент
β для нее самый высокий (-0,600). Коэффициент β для переменной
"Количество врачей на 1000 человек" боле, чем в два раза ниже (-
0,239).
Коэффициент R2 указывает на разброс
значений вокруг линии регрессии, т.е. на то, сколько процентов вариации данных
предсказывает регрессия. Данная трехфакторная модель объясняет более 70% всей
дисперсии данных.
Регрессионный анализ показывает, что женская грамотность является ведущим фактором снижения рождаемости в ходе модернизации (необходимо отметить, что женская, мужская и общая грамотность являются тесно связанными друг с другом параметрами). Другими важными, хотя и в меньшей степени, показателями являются количество врачей на душу населения и урбанизация. Очевидно при этом, что уровень здравоохранения серьезно зависит от уровня образования как с точки зрения обучения врачей, так и с точки зрения востребованности защиты здоровья населения (поскольку образование человека делает его более «дорогостоящим», то его жизнь, очевидно, требует большей защиты, что подталкивает развитие здравоохранения). Что касается урбанизации, то она, несомненно, является важным составляющим модернизации и, в частности, стимулирует рост грамотности в среде жителей городов, но в этом смысле она действует на снижение рождаемости опосредованно, а не напрямую. Поэтому можно считать показатель грамотности оптимальным интегральным показателем модернизационных процессов, являющихся факторами снижения рождаемости.
Снижение рождаемости, обусловленное грамотностью населения, избавлено от недостатков объяснения М. Кремера, считавшего, что высокие доходы понижают рождаемость. Не возникает противоречия между низким уровнем рождаемости в России и других постсоветских странах Восточной Европы и резким понижением их уровня жизни. С другой стороны, предложенное нами объяснение перехода является более широким, чем объяснение М. Кремера, в том смысле, что грамотные люди в среднем зарабатывают больше, чем неграмотные. Таким образом, объяснение М. Кремера работает только в период стабильности, в то время как объяснение низкой рождаемости через грамотность работает как в стабильные, так и в кризисные периоды.
В итоге для описания демографического перехода разработанная нами модель (32)–(33) должна быть расширена, чтобы учесть важнейший фактор понижения рождаемости – грамотность населения. В результате модификации модель (32)–(33) выглядит следующим образом:
![]() , (38)
, (38)
![]() , (33)
, (33)
![]() , (39)
, (39)
где L – доля грамотного населения, a, b, c – константы. Влияние грамотности на демографический переход выражается добавлением в (32) множителя (1 – L) и получении уравнения (38). Такое изменение имеет тот смысл, что даже несмотря на отсутствие ресурсного ограничения, рождаемость снижается с ростом грамотности. Что касается того факта, что смертность при модернизации также снижается, то уравнение (38) учитывает и этот факт, поскольку в (38) рассматривается именно прирост – разность между рождаемостью и смертностью, а при приближении грамотности к 100% нулевым становится именно прирост.
Введенное дополнительное уравнение для роста грамотности (39) имеет тот смысл, что рост уровня грамотности пропорционален доле грамотного населения L (потенциальные учителя), доле неграмотного населения (1 – L) (потенциальные ученики) и наличию излишков S, которые могут использоваться на образовательные программы (кроме того, S связано с уровнем технологий T, в том числе образовательных, увеличивающих скорость обучения). С математической точки зрения уравнение (39) аналогично логистическому уравнению [39], где насыщение достигается при уровне грамотности L = 1, а S отвечает за скорость выхода на этот потолок.
Несмотря на общую логичность модификации модели, ее вид (38)–(39) должен быть дополнительно обоснован. Поскольку очевидно, что при тех же логических заключениях о зависимости прироста населения от грамотности, увеличения грамотности при росте числа потенциальных учителей и т.п. модель может быть представлена в виде:
![]() ,
,
![]() ,
,
![]() ,
,
где φ1, φ2, φ3, φ4, φ5, φ6, φ7, φ8 – некоторые положительные степени, совсем не обязательно равные единице.
Что касается коэффициентов φ1, φ2, φ4, φ5, то в пользу того, что они могут быть положены единичными, говорит тот факт, что вдали от демографического перехода они удовлетворительно описывают гиперболический рост и хорошо ложатся на эмпирические данные (рис.3). В пользу определения остальных коэффициентов также должны сказать эмпирические данные.
Легко заметить, что в случае если φ1 = φ6 = 1, φ2 = φ7, φ3 = φ8, делением первого уравнения на третье получается уравнение
![]() ,
,
решение которого определяет связь между L и N в виде
![]() , (40)
, (40)
где λ – константа.
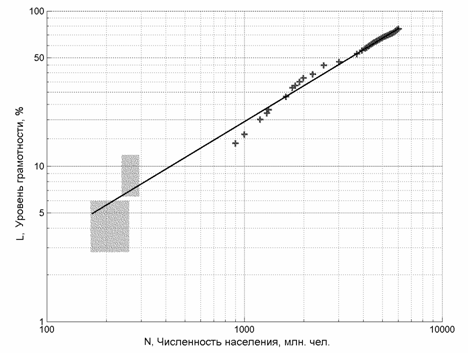
Для проверки данной гипотезы обратимся к историческим данным. На рис. 4 представлены данные по совместному росту грамотности и населения земли в двойном логарифмическом масштабе. В этом масштабе степенным зависимостям соответствуют прямые линии.
|
Рис.4. Уровень грамотности и численность населения Земли Прямоугольниками обозначены точки соответствующие 1 и 1000 н.э., для которых имеется разброс оценок |
Из графика видно, что степенная зависимость (40) достаточно хорошо описывает имеющиеся данные. Следует дополнительно отметить, что, к сожалению, исторических данных по уровню грамотности чрезвычайно мало и известны они с гораздо меньшей точностью, чем ВВП, и тем более численность населения. В частности, есть основания считать, что имеющиеся данные на 1 год н.э. занижены, а на 1000 год – несколько завышены. Тем не менее, с точки зрения оценки таких показателей, как образование и культура, по всей видимости, уровень грамотности – это единственный, хотя и плохо, но все-таки измеряемый исторический показатель. Его ведущая роль как фактора демографического перехода еще больше подчеркивает его важность и целесообразность использования в глобальных моделях наряду с данными по населению и ВВП. Безусловно, следует критически относиться к данным по грамотности не только из-за их малочисленности и низкой точности, но и потому что то, что мы понимаем под грамотностью сейчас и то, что считалось грамотностью тысячелетия назад, может быть не вполне сопоставимо. А потому их количественное использование в одной модели и вывод на один график, при том, что качество может быть отлично, не вполне адекватно. Тем не менее абсолютно такой же упрек с полным правом можно предъявить и к данным по численности населения, и к данным по ВВП. Поскольку количественное измерение в одной шкале современных людей и наших предков, живших миллион лет назад, или измерение стоимости современных высокотехнологичных продуктов и стоимости продукта, произведенного древними людьми, также не вполне адекватно.
В любом случае имеющиеся данные (рис.4) говорят в пользу использования соотношения (40), а следовательно, и в пользу положения φ1 = φ6 = 1, φ2 = φ7, φ3 = φ8, которое в свете того, что степень φ2 была ранее оценена как единица, может быть записано в виде: φ1 = φ6 = φ2 = φ7 = 1, φ3 = φ8. Что же касается равенства единице значения φ3, то в пользу этого говорит хорошее соответствие эмпирических данных с данными (рис.5 – 10), полученными при расчете модели (38)–(33)–(39). Конечно, более тонкая «подстройка» модели с помощью параметров φ1…8 могла бы улучшить соответствие, однако при той точности, которая доступна, «тонкая подстройка» теряет смысл, поскольку неизвестны точки, к которым следует подстраивать решение. В любом случае в такой общей модели следует стремиться сократить количество параметров, не улучшающих решение на качественном уровне.
Результаты расчета модели
(38)–(33)–(39) с параметрами: a = 1,085∙10-5
($×год)-1, b = 6,51 ∙10-12 (чел∙год)-1,
с = 8,2∙10-6
($∙год)-1, ![]() = 420 $ и с начальными
данными в 1 году н.э.: N0 = 170000000 чел, S0 = 17,47 $ , L0 = 0,052 , где L – безразмерная величина (от 0 до 1), знак «$» соответствует
международному доллару 1995 года., приведены на следующих графиках.
= 420 $ и с начальными
данными в 1 году н.э.: N0 = 170000000 чел, S0 = 17,47 $ , L0 = 0,052 , где L – безразмерная величина (от 0 до 1), знак «$» соответствует
международному доллару 1995 года., приведены на следующих графиках.
Полученные результаты (сплошная линия) по росту населения Земли хорошо описывают гиперболический рост и первую фазу демографического перехода к настоящему времени, что касается прогноза, то модель дает несколько отличные результаты по сравнению с прогнозами ООН (светло-серые маркеры). По результатам модели вторая фаза перехода будет проходить более резко, чем то предсказывает ООН. Более гладкого перехода можно было бы добиться введением φ3 = φ8 ≠ 1, однако, с одной стороны, прогноз ООН – это прогноз, опирающийся на свои модели, которые также огрубляют действительность, а с другой – представительность и точность имеющихся сейчас исторических данных не могут на должном уровне ни подтвердить, ни опровергнуть гипотезу φ3 = φ8 = 1. С появлением новых данных модель можно будет скорректировать.
Рост ВВП ярко демонстрирует еще более крутой рост, чем рост численности населения, и математически описывается формулой (35). Несмотря на то, что ВВП явно не входит в систему уравнений модели, на данном графике точки расчетной кривой вычисляются по формулам (31) и (26).
Графики в двойном логарифмическом масштабе «убирают» визуальную компоненту гиперболического роста и делают результаты более наглядными, хотя, конечно, и отклонения в этом масштабе выглядят более существенными, чем на графиках (рис.5 – 7).
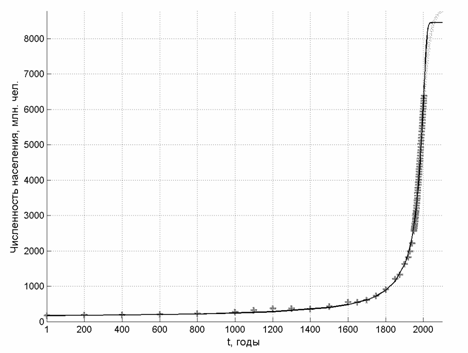
Рис. 5. Рост населения Земли
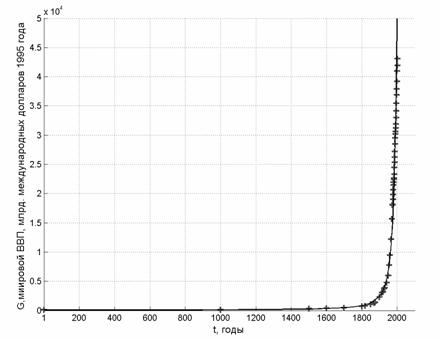
Рис.6. Рост мирового ВВП
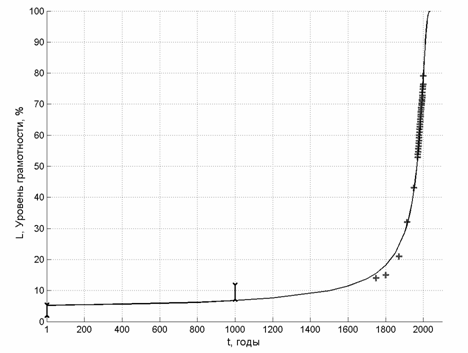
Рис.7. Рост уровня грамотности
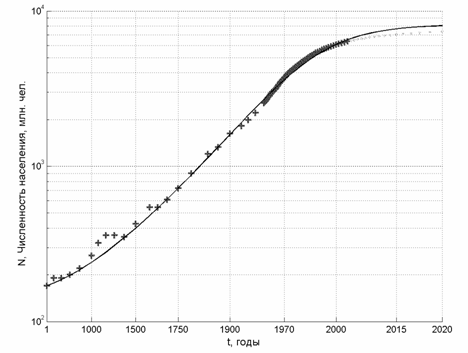
Рис.8. Рост населения Земли в двойном логарифмическом масштабе
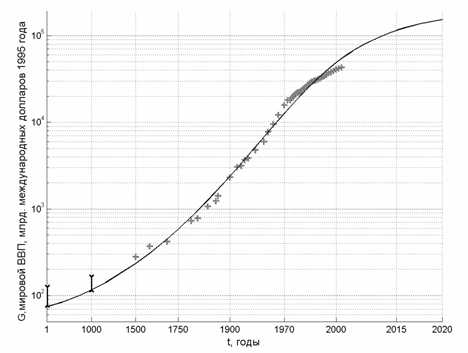
Рис.9. Рост мирового ВВП в двойном логарифмическом масштабе
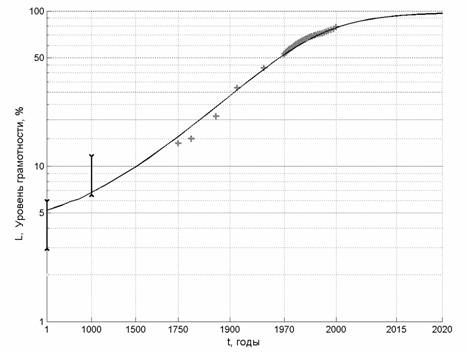
Рис.10. Рост уровня грамотности в двойном логарифмическом масштабе
Комментируя графики, нужно отметить, что, несмотря на локальные отклонения, модель (38)–(33)–(39) достаточно хорошо описывает имеющиеся эмпирические данные при том, что в нее входят всего три коэффициента. Причем масштабированием можно свести два из них к единицам – в этом случае в модель будет входить только один коэффициент, равный показателю степени в уравнении (40). Таким образом, несмотря на крайнюю простоту модели, она, тем не менее, с хорошим соответствием описывает совместную динамику сразу трех важнейших показателей глобального процесса развития человечества.
Заключение
В работе были проанализированы существующие математические концепции глобальной демографии. Первой и наиболее глубокой работой в этой области была работа С.П. Капицы, прекрасно описавшая и гиперболический рост, и демографический переход на феноменологическом уровне. С точки зрения поиска реальных механизмов гиперболического роста наиболее перспективным представляется подход, основанный на рассмотрении совместного роста населения Земли и технологии. С другой стороны, имеющиеся математические объяснения демографического перехода остаются на феноменологическом уровне. Объяснение М. Кремера с точки зрения экономики апеллирует к важному факту резкого снижения рождаемости, но видит корни в экономических причинах, что, как показывают примеры кризисов, являющихся хорошим тестом для выявления корреляций, не вполне адекватно.
В настоящей работе было проведено эмпирическое обоснование демографико-технологического подхода к описанию гиперболического роста населения Земли и была предложена модель демографического перехода, включающая три важных показателя – численность населения, уровень технологии и уровень грамотности. При ее простоте и малом количестве параметров модель с высокой точностью описывает совместную динамику всех трех показателей в рассматриваемом интервале с начала нашей эры по нынешнее время.
Литература
1. База данных "World 95". SPSS 2004. World95 Database. Chicago, IL: SPSS Inc.
2. Вольтерра В., Математическая теория борьбы за существование, М.Наука, 1976
3. Капица С. П. Математическая модель роста населения мира. Математическое моделирование 4/6: 65–79. 1992.
4. Капица С. П. Сколько людей жило, живет и будет жить на земле. М.: Наука. 1999.
5. Малков С.Ю. Математическое моделирование исторических процессов // Новое в синергетике: Взгляд в третье тысячелетие / Под ред. Г.Г.Малинецкого, С.П.Курдюмова. - М.: Наука, 2002. С.291-323.
6.
Мельянцев В. А. 1996. Восток и Запад во втором тысячелетии.
М.: МГУ.
7. Нефедов С.А. О демографических циклах в истории средневекового Египта [http://hist1.narod.ru/Science/Egipt/EgiptSV.htm]; О демографических циклах в истории Ирака и Ирана (VII-XIII вв.) [http://hist1.narod.ru/Science/Babilon/ Irak.htm] и др.
8. Подлазов А. В. Основное уравнение теоретической демографии и модель глобального демографического перехода. Препринт ИПМ им. М.В. Келдыша РАН, №88. 2001.
9. Подлазов А. В. Теоретическая демография как основа математической истории. Препринт ИПМ им. М.В. Келдыша РАН, №73. 2000.
10. Режимы с
обострением. Эволюция идеи: Законы коэволюции сложных структур. - М.:Наука,1999.- 255с.:
11. Ризниченко Г.Ю. Лекции по математическим моделям в биологии. Часть 1. Ижевск: НИЦ «Регулярная и хаотическая динамика», 2002
12. Тихонов А.Н. Системы дифференциальных уравнений, содержащие малые параметры при производных, Мат. Сб. т. 32, №3, 1952
13.
Aghion,
P., and P. Howitt. A model of Growth
through Creative Destruction. Econometrica 60: 323–52. 1992.
14.
Aghion,
P., and P. Howitt. Endogenous Growth
Theory. Cambridge, MA: MIT Press. 1998.
15.
Artzrouni,
M., and J. Komlos. Population Growth
through History and the Escape from Malthusian Trap: A Homeostatic Simulation
Model. Genus 41: 21–39. 1985.
16. Bongaarts, J. Completing the Fertility Transition in the Developing World: The Role of Educational Differences and Fertility Preferences. Population Studies 57: 321–35. 2003.
17. Bongaarts, J. The end of the fertility transition in the developing world. Policy
Research Division Working Paper no. 161. New York: Population Council. 2002.
18. Boserup, E. The Conditions for Agricultural Growth: The Economics of Agrarian Change under Population Pressure. Chicago, IL: Aldine. 1965.
19.
Braudel,
F. Capitalism
and Material Life, 1400–1800. New York, NY: Harper and Row. 1973.
20.
Cameron,
R. A Concise Economic History of World. New York, NY: Oxford University
Press. 1989.
21. Foerster, H. von, P. Mora, and L. Amiot. Doomsday: Friday, 13 November, A.D. 2026. Science 132:1291–5. 1960.
22.
Grossman,
G., and E. Helpman. Innovation and Growth
in the Global Economy. Cambridge, MA: MIT Press. 1991.
23. Habakkuk, H. J. English Population in the Eighteenth Century. Economic History Review 6: 117–33. 1953.
24. Hollingsworth, W. G. Ending the Explosion: Population Policies
and Ethics for a Humane Future. Santa Ana, CA:
Seven Locks Press; 1996.
25. Jones, C. R&D Based Models of Economic Growth,
unpublished, Massachusetts Institute of Technology, 1992.
26.
Komlos,
J., and S. Nefedov. A Compact
Macromodel of Pre-Industrial Population Growth. Historical Methods 35:92–4.
2002.
27. Kremer, M. Population Growth and Technological Change: One Million B.C. to 1990. The Quarterly Journal of Economics 108: 681–716. 1993.
28.
Kuznets,
S. Population Change and Aggregate
Output. in Demographic and Economic Change in Developed Countries. Princeton,
NJ: Princeton University Press. 1960.
29.
Maddison,
A. Monitoring the World Economy,
1820–1992. Paris: OECD. 1995.
30. Maddison, A. Monitoring the World Economy: A Millennial Perspective. Paris: OECD. 2001.
31.
Malthus,
T. Population: The First Essay. Ann
Arbor, MI: University of Michigan Press. 1978.
32. McMichael, T. Human Frontiers, Environments, and Desease. Past Patterns, Uncertain
Futures. Cambridge, UK: Cambridge University Press; 2001.
33. Nefedov, S. A. A Model of Demographic Cycles in Traditional Societies: The Case of Ancient China. Social Evolution & History 3(1): 69–80. 2004.
34. Podlazov A.V. Theory of the Global Demographic Process.
// proceedings of the international conference “Mathematical Modeling of Social
and Economical Dynamics”, Moscow, 2004.
35. Postan, M. M. Same Economic Evidence of Declining Population in the Later Middle Ages. Economic History Review. 2nd ser. 2:130–67. 1950.
36. Romer, P. Increasing Returns and Long-Run Growth,
Journal of Political Economy, XCIV (1986), 1002-37
37.
Simon,
J. The Economics of Population Growth. Princeton:
Princeton University Press. 1977.
38. Turchin, P.
Historical Dynamics: Why States Rise and Fall, Princeton University Press,
Princeton, NJ, 2003
39.
Verhulst,
P.F. Notice sur la loi que la population
suit dans son accroissement, Corr. Math. Et Phys. 10, 113-121, 1838
40.
World
Bank. World Development Indicators. Washington,
DC: World Bank. 2004.
[1] Статистическая значимость
(α) означает вероятность того, что
результаты данного теста могли появиться в результате случайности. Если,
например, статистическая значимость некой корреляции равна 0,01 (или что эта
корреляция значима на уровне 0,01), то вероятность того, что подобная
корреляция могла появиться в результате случайности, при отсутствии реальной
закономерной связи между признаками равна 0,01 (т.е., существует один шанс из
ста, что наблюдаемая корреляция является результатом случайности). В таком
случае вероятность довольно низка, и гипотеза о наличии связи между признаками
может считаться нашедшей подтверждение. Исторически сложилось, что в качестве порогового
уровня статистической значимости принимается 0,05 (~ 5% ~ 1 шанс из двадцати).
Т.е. если мы получили показатель значимости менее 0,05, то соответствующая
гипотеза считается успешно прошедшей статистическую проверку, если же этот
показатель более 0,05, то соответствующая гипотеза считается неподтвержденной.
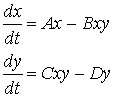 ,
,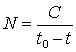 ,
,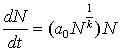 ,
,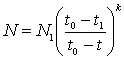 ,
, .
.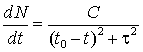 .
.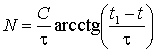 ,
,