Свойства логической энтропии

( Properties of logic entropy
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Брошкова Н.Л., Попов С.В.
(N.L.Broshkova, S.V.Popov)

ИПМ им. М.В.Келдыша РАН

Москва, 2005

Аннотация

Исследуются свойства логической энтропии, служащей мерой сложности информационных моделей. Демонстрируется отличие логической энтропии от энтропии Теории информации. Доказывается ряд соотношений, позволяющих оценивать энтропию информационных моделей в зависимости от энтропии предметных областей.

Abstract

There are researched the characteristic of logical entropy, described the measure of complicity information models. It is demonstrated difference of logical entropy from entropy of the Theories of information. It is proved correlation between entropy of the information model and entropy of the application domain.

Введение. Содержательное обоснование меры неопределенности информационных моделей было введено в [1]. В [2] приводится формальное определение логической энтропии, и обсуждаются некоторые ее свойства и их содержательные интерпретации. В этой работе продолжено исследование логической энтропии, как меры сложности информационных моделей.

1. О логической энтропии. Сформулируем и докажем ряд свойств логической энтропии.

Очевидна следующая теорема.

Теорема 1. Если для функции f(y, z) доли py(i) классов y-эквивалентности равны, то энтропия Hy равна логарифму от числа классов эквивалентности (или, что аналогично, от величины y-сечения).

Поэтому, если имеются только два класса с одинаковыми долями, то энтропия равна 1; если один класс, то энтропия равна 0.  

Основные свойства энтропии формулируются следующим образом.

Теорема 2. При фиксированном числе всех путей бинарной программы из истока в y-сечение, которое имеет k узлов, энтропия Hy максимальна, когда все доли py(i) одинаковы и равны k-1.

Доказательство этого свойства вытекает из того, что математическое ожидание М[log | ty(i)|] минимально при равных значениях py(i).

Теорема 3. Если Hy = k, то число узлов  y-сечения бинарной программы не менее 2k.

Доказательство. Пусть в y-сечении бинарной программы имеется h = 2n < 2k узлов. При фиксированном числе путей из истока в y-сечение энтропия Hy максимальна при равных долях py(i).                             Поэтому энтропия Hy не превосходит величины - å i =1,h  h-1 log h-1 = log h < k . Противоречие.

Теорема доказана.

Следствие. Чтобы функция f(y, z) обладала энтропией Hy = k, число переменных у должно быть не менее k.

Пример 1. Пусть y-сечение бинарной программы для функции f(y, z) имеет k узлов, а для функции g(y, z) – h узлов. Верхняя граница энтропии Hfy равна log k, а Hgy - log h. Эти значения достигаются в случае, когда py(i) = k-1 для функции f и py(i) = h-1 для g. Потому функция, обладающая большим y-сечением, имеет большую верхнюю границу энтропии. Это согласуется с содержательной интерпретацией логической энтропии как меры неопределенности вычислительного процесса. Действительно, чем больше сечение бинарной программы, тем больше неопределенность того, какой вычислитель осуществит вычисление при заданных входных значениях.

 

Пусть разложения функции f(y, z) по переменным y выглядят следующим образом: Úi=1,k [ysi] f(si1, z), а по переменным z так Új=1,h [z lj] f(y, lj1), где в квадратных скобках приведены дизъюнкты, определяемые одним классом эквивалентности, и si = {s1i, s2i, …, smi}, lj = {l1j, l2j, …, lnj}, i = 1, 2, …, k, j = 1, 2, …, h.

Разложение по переменным yz выглядит так:

f(y, z) = Úi=1,k j=1,h [ysiz lj] f(si1, lj1) = Úi=1,k j=1,h [ysiz lj] fij.

Здесь квадратными скобками [ysiz lj] обозначена конъюнкция дизъюнктов, соответствующих i-му y-классу и j-му z-классу, fij получена из f подстановкой y-набора si1 и z-набора lj1. Если f представляет всюду определенную вычислимую функцию, то среди fij, i = 1, 2, …, k, j = 1,2, .., h нет тождественно нулевых функций.

Справедлива следующая

Теорема 4. Если логическая функция f(y, z) представляет всюду определенную вычислимую функцию, то верно неравенство

Hyz £ Hy + Hz.

Доказательство. Обозначим py(i) долю y-наборов из i-го класса y-эквивалентности,  pz(j) – долю z-наборов из j-го класса z-эквивалентности, p(i, j) – долю yz-наборов, y-компоненты которых принадлежат i-му классу y-эквивалентности, а z-компоненты - j-му классу z-эквивалентности. Так как f представляет всюду определенную функцию, то для всех пар (i, j) справедливы равенства p(i, j) = py(i) pz(j) и å(i, j) p(i, j) = 1, где суммирование ведется по всем i = 1, 2, …, k, и j = 1, 2, …, h.

Пусть yz-сечение бинарной программы содержит m узлов и к множеству yz-наборов из q-го yz-класса Aq, q = 1, 2, …, m, относятся yz-наборы, характеризующиеся определенными значениями пар (i, j). Тогда pyz(q) есть доля yz-наборов, определяемых q-м yz-классом, и эта доля вычисляется как сумма

pyz(q) = å(i, j)ÎAq p(i, j).

Из равенства p(i, j) = py(i) pz(j) вытекает, что:

-åi, j p(i, j) log p(i, j) = -åi, j py(i) pz(j)log py(i) - åi, j py(i) pz(j)log pz(j) =

= -åi py(i) log py(i) - åj pz(j)log pz(j) = Hy + Hz.


Рассмотрим условную случайную величину x|Aq, которая принимает значения (i, j) из класса Aq с вероятностью P[x = (i, j)|(i, j) Î Aq]. По формуле условной вероятности имеем P[x = (i, j)|(i, j) Î Aq] = P[x = (i, j)]/P[(i, j)ÎAq] = p(i, j)/pyz(q). Энтропия этой случайной равна

-å(i, j)|(i, j)ÎAq p(i, j)/ pyz(q) log p(i, j)/ pyz (q).


Так как энтропия любой случайной величины не отрицательная, то

-å(i, j)|(i, j)ÎAq p(i, j)/ pyz(q) log p(i,j)/ pyz(q) ³ 0.


В силу того, что pyz(q) > 0 последнее неравенство можно переписать так:

-å(i, j)|(i, j)ÎAq p(i, j) log p(i, j)/ pyz(q) ³ 0.

Откуда вытекают соотношения:

-å(i, j)|(i, j)ÎAq p(i, j) log p(i, j) ³ -å(i, j)|(i, j)ÎAq p(i, j) log pyz(q) = - pyz(q) log pyz(q)


Суммируя обе части неравенства по всем классам yz-эквивалентности, получаем, что

-å(i, j) p(i, j) log p(i, j) ³ -åq pyz(q) log pyz(q).

То есть Hyz £ Hy + Hz.

Теорема доказана.

Докажем теперь утверждение, анонсированное в [2]. Оно касается соотношения между суммой H1 + H2 неопределенностей, характеризующих состояние уже спроектированной информационной системы и неопределенности H0 предметной области. В терминах бинарной программы и логической энтропии это выглядит следующим образом.

Пусть для логической функции f(y, z) переменные y определяют логическую энтропию Hy = -åi=1,k py(i) log py(i), и H0 есть двоичный логарифм от мощности множества T ее единичных означиваний. Введем для y-сечения бинарной программы новую величину H2, которую назовем остаточной энтропией: H2 = åi=1,k py(i) log Ti, где Ti есть мощность множества единичных означиваний функции, соответствующей i-му узлу y-сечения.

Справедлива

Лемма 5. Пусть a = b + c. Тогда верно неравенство

1+(1/2)(log b + log c) £ log a.

Доказательство. Пусть b £ c, и b = c – x для некоторого не отрицательного x. Искомое неравенство следует из неравенства 1+(log (c - x) + log c) £ 2 log (2c – x), которое вытекает из log 2(c - x) c £ log (2c – x)2. Последнее неравенство следует из легко проверяемого неравенства 2(c - x)c £ (2c – x)2.

Лемма доказана.

Справедлива

Теорема 6. Для логической функции f(y, z) имеет место неравенство

Hy + H2 £ H0.

Доказательство проведем индукцией по h - мощности множества переменных y.

Базис индукции, когда h = 0, элементарен, так как в этом случае Hy = 0 и  H2 = H0.

Индукционный переход. Пусть для y-сечения, когда множество y содержит h переменных, теорема верна, и мы продолжаем построение бинарной программы для f(y, z), означивая новую переменную z. Допустим, что в yz-сечении имеется в точности m узлов и Tj есть мощность множества единичных означиваний функции, приписанной его j-му узлу.

Допустим вначале, что такое продолжение не приводит к склейке узлов в yz-сечении. В этом случае для каждого узла j yz-сечения доля pyz(j) путей, ведущих из истока в этот узел, равна либо (1/2)py(i) либо py(i) для определенного узла i y-сечения. Это следует из определения бинарной программы.

Но тогда сумма

pyz(j)(- log pyz(j) + log Tj)

представима в виде двух сумм:

pyz(j)(- log pyz(j) + log Tj) и  pyz(j)(- log pyz(j) + log Tj).

Здесь первое суммирование осуществляется по тем узлам yz-сечения, для которых доли путей, ведущих в эти узлы, представляют собой половину от долей путей, ведущих в соответствующие узлы y-сечения. Второе - по тем узлам, для которых доли путей, ведущих в них, совпадают с долями путей, ведущих в соответствующие узлы y-сечения. Это позволяет перейти к суммированию по узлам y-сечения.

В результате первая сумма выглядит так:

py(i) - log (py(i)/2) + ½ py(i) log Tj1 + ½ py(i) log Tj2

Здесь j1 и j2 это те узлы yz-сечения, которые образованы из одного i-го узла y-сечения. Преобразуя эту сумму, получаем

py(i) (- log py(i) + 1 + ½(log Tj1 + log Tj2)).

По Лемме 5, 1 + ½(log Tj1 + log Tj2) £ log Ti, где Ti есть мощность множества единичных означиваний функции, приписанной i-узлу y-сечения. Следовательно, эта сумма не превосходит величины

py(i) (- log py(i) + log Ti),

где суммирование ведется по тем же узлам.

В силу того, что во второй сумме каждому узлу yz-сечения соответствует в точности один узел y-сечения, сумму

 pyz(j)(- log pyz(j) + log Tj)

можно представить так:

py(i)(- log py(i) + log Ti).

Здесь суммирование ведется по соответствующим узлам y-сечения, для каждого узла yz-сечения указывается в точности один соответствующий узел y-сечения.

Складывая py(i) (- log py(i) + log Ti) + py(i)(- log py(i) + log Ti), получим, что суммирование ведется по всем узлам y-сечения. Следовательно, эта сумма не превосходит величины H0. В частном случае теорема доказана.

Приведем теперь доказательство для общего случая.

Пусть при переходе к yz-сечению два различных узла i1 и i2 y-сечения порождают эквивалентные функции. В результате можно считать, что в yz-сечении склеились два узла j1 и j2, которые в итоге превратились в один узел j. Тогда соответствующая доля выглядит так: pyz(j) = pyz(j1) + pyz(j2). Мощности множеств единичных означиваний функций, соответствующих трем узлам j, j1 и j2, совпадают и пусть равны Tj.

Легко проверить неравенство

(pyz(j1)+pyz(j2))(-log(pyz(j1)+pyz(j1))+logTj) £


pyz(j1)(-logpyz(j1)+logTj)+pyz(j2))(-log(pyz(j2)+logTj).

Следовательно, склейка узлов yz-сечения не приводит к увеличению левой части искомого неравенства.

Теорема доказана.

В итоге на промежуточном этапе построения информационной модели наши знания, по сравнению с исходными, увеличились на величину

H0 – (Hy + H2).

Введем следующее обозначение для логической функции f(y, z).

При построении бинарной программы увеличение множества означиваемых переменных не всегда приводит к увеличению энтропии. Чтобы это показать, приведем следующие рассуждения.

Пусть q(i, j) – доля yz-наборов, таких, что одновременно их y-наборы принадлежат i-му классу y-эквивалентности, а сами они принадлежат j-му классу уz-эквивалентности. В терминах бинарной программы q(i, j) есть доля путей, проходящих из истока в j-й узел уz-сечения, одновременно проходя через i-й узел у-сечения. Справедливы равенства:

py(i) = å j=1,h q(i, j),  pyz(j) = å i=1,k q(i, j).

Энтропия Hy функции f(y, z) равна

-åi=1,k py(i) log py(i) =-åi=1,k (å j=1,h q(i, j)) log py(i) = -åi=1,k (å j=1,h q(i, j)log py(i))=

= -åi=1,k å j=1,h q(i, j) log py(i) = -åi=1,k  j=1,h q(i, j) log py(i).

Выразим энтропию Hyz.

-åj=1,h pyz(j)log pyz(j)=-åj=1,h (å i=1,k q(i, j))log pyz(j)=-åj=1,h (å i=1,k q(i, j)log pyz(j)) =

= -åi=1,k å j=1,h q(i, j) log pyz(j) = -åi=1,k  j=1,h q(i, j) log pyz(j).

Разность Hyz - Hy равна

åi=1,k  j=1,h q(i, j) log py(i) -åi=1,k  j=1,h q(i, j) log pyz(j) =

= åi=1,k  j=1,h q(i, j) (log py(i) - log pyz(j)) = åi=1,k  j=1,h q(i, j) log (py(i) / pyz(j)).

Величину log (py(i)/pyz(j)) можно рассматривать как случайную с распределением q(i, j). Тогда разность Hyz - Hy. есть ее среднее значение. Если она больше нуля, то эффективное yz-сечение больше эффективного y-сечения. Так как ширина эффективного сечения определяет сложность представления исходной функции через ее подфункции, то положительная разность обозначает, что функция выражается сложнее через переменные yz, чем от y.

2. Не зависимые переменные. В теории информации доказывается, что если система состоит из независимых подсистем, то ее энтропия представляет собой сумму энтропий ее подсистем. Аналогичным свойством обладает логическая энтропия: если логическая функция зависит от независимых аргументов, то суммарная энтропия этих аргументов равна сумме энтропий каждого из них.

Чтобы уточнить понятия независимости переменных логической функции, введем ряд определений и докажем несколько утверждений.

Будем говорить, что у функции f(y, z) переменные z не зависят от переменных y, если в разложении f(y, z) = Úi=1,k j=1,h [ysiz lj] каждая функция fij = ui Ù vj, i = 1, 2, …, k, j = 1, 2, …, h. В терминах матрицы Mf  (см. рис.1) независимость переменных z от y обозначает, что для каждого ее столбца (каждой строки) зафиксирована одна функция ui (vj), входящая в конъюнкцию на пересечении этой строки (столбца) со всеми другими столбцами (строками).

 

    z

у

 

l1

 

l2

 

l3

…

s1

u1 Ù v1

u1 Ù v2

u1 Ù v3

…

s2

u2 Ù v1

u2 Ù v2

u2 Ù v3

…

s3

u3 Ù v1

u3 Ù v2

u3 Ù v3

…

…

…

…

…

…

Рис. 1

 

Просто доказывается

Лемма 7. Если функция f(y, z) = f1(y) Ù f2(z), где f1(y) не содержит переменных z, а f2(z) - переменных y, то переменные z не зависят от y, и наоборот, переменные y не зависят от z.

Справедлива

Лемма 8. Если у функции f(y, z) переменные z не зависят от y, то она представима в виде конъюнкции f1(y) Ù f2(z), где f1(y) не содержит переменных z, а f2(z) - переменных y.

Доказательство. Представим функцию f(y, z) в таком виде:

Úi=1,k j=1,h [ysiz lj] fij.

В силу независимости переменных z от y получаем равенства:

f(y, z) = Úi=1,k [ysi] Ù (Új=1,h [z lj] (ui Ù vj)) =

= Úi=1,k [ysi] Ù ui Ù(Új=1,h [z lj] vj) = Úi=1,k [ysi] Ù ui Ù f2(z) =

= f2(z) Ù(Úi=1,k [ysi] Ù ui) = f1(y) Ù f2(z)

Лемма доказана.

Следствие. Если у функции f(y, z)  переменные z не зависят от y, то переменные y также не зависят от z.

Основываясь на этом, будем говорить просто о независимых переменных.

С другой стороны, верна

Теорема 9. Если у функции f(y, z) переменные y, z не зависимы, то ее нельзя представить в виде дизъюнкции g(y) Ú h(z), где g(y) не содержит переменных z, и h(z) - переменных y.

Доказательство. Так как переменные y и z не зависимы, то функция f(y, z) определяет матрицу Mf, как на рис. 1. Функция f(y, z) не тождественная константа. Поэтому все функции в клетках матрицы Mf попарно не эквивалентны. Пусть f(y, z) = g(y) Ú h(z), и g(y) не содержит переменных z, а h(z) - переменных y. Допустим, что функция g(y) истинна при некотором означивании sу ее переменных. Но тогда все yz–наборы вида sуsz, где sz все возможные z–наборы, принадлежат одному классу эквивалентности. Это обозначает, что в матрице Mf все функции в строке, характеризующейся одним y–набором sу, эквивалентны. Противоречие с условием о независимости переменных y и z.

Теорема доказана.

Отметим, что если функция f(y, z) представлена в к.н.ф., то независимые переменные y, z могут принадлежать одному дизъюнкту, но таких дизъюнктов должно быть, по меньшей мере, два. 

Теорема 10. Если у функции f(y, z) переменные y и z не зависимы, то Hyz = Hy + Hz.

Доказательство. Величина pyz|y(j | i) одинакова для каждого фиксированного i и всех узлов j, достижимых из i. Более того, pyz|y(j | i) = pz(j¢),  j, j¢ = 1, 2, …, k при определенном соответствии узлов j и j¢ yz-сечения и z-сечения. Но тогда pyz(j) = pz(j¢) py(i). Следовательно,

Hyz = åj pyz(j) log pyz(j) = åj,i py(i) pz(j¢) log py(i) pz(j¢) = Hy + Hz.

Теорема доказана.

Содержательная трактовка аддитивности энтропии достаточно понятна. Если два множества аргументов независимы, то они не влияют друг на друга, так как разложение по одному множеству аргументов никак не сказывается на наших знаниях о разложении по другому. Понятно, что в общем случае аддитивность энтропии места не имеет, так как не каждая пара (i, j) индексов матрицы Mf определяет в точности один класс yz-эквивалентности.

3. Условная энтропия. В этом разделе введем определение и рассмотрим свойства условной энтропии, которая определяется так же, как это делается в Теории информации.

Напомним обозначения, введенные при определении логической энтропии для функции f(y, z):

pyz|y(j½ i) есть доля путей, ведущих из i-го узла у-сечения в j-й узел уz-сечения среди всех путей из i-го узла у-сечения в уz-сечение;

py(i) – доля путей из истока в i-й узел у-сечения среди всех путей из истока в у-сечение;

pz(i) - доля путей из истока в i-й узел z-сечения среди всех путей из истока в z-сечение;

pyz(i) –доля путей из истока в i-й узел уz-сечения среди всех путей из истока в уz-сечение.

Пусть pyz(i, j) = pyz|y(j½ i) py(i). Это есть доля путей, проходящих из истока через i-й узел у-сечения, которые ведут в j-й узел уz-сечения.

Из этого определения следует равенство py(i) = åj pyz(i, j).

Аналогично вводятся соответствующие обозначения, когда рассматривается не бинарная программа, а означивания переменных.

Рассмотрим следующую задачу.

Пусть для функции f(y, z) необходимо установить класс yz-эквивалентности, которому принадлежит некоторый yz-набор. Если не пользоваться никакой дополнительной информацией, то неопределенность этого события вычисляется как энтропия аргументов yz. Допустим, теперь известно, каким y-классом порождается этот yz-набор. Поэтому при известном y-классе доли порождаемых им yz-классов отличаются от долей yz-классов всей функции. Эти доли могут рассматриваться как условные доли p(yz|y)  yz-классов, когда известно, каким y-классом они определяются. Эти рассуждения приводят к понятию условной энтропии:

Нyz|x(y) = i  = - Sj pyz|y(j | i) log pyz|y(j | i) и

Нyz|y = - S i, j py(i) pyz|y(j | i) log pyz|y(j | i) =  - S i, j pyz(i, j) log pyz|y(j | i).

Условная энтропия обладает такими свойствами.

Теорема 11. Нyz|y ≤ Нz.

Доказательство. Пусть i-ый класс y-эквивалентности порождает h классов yz-эквивалентности, которые занумеруем 1, 2, …, h. Очевидно, что h не больше числа H классов z-эквивалентности. В терминах матрицы Mf в ее i-ой строке одному классу yz-эквивалентности соответствует несколько клеток, в то время как одному классу z-эквивалентности соответствует в точности одна клетка. Но тогда энтропия Нyz|x(y) = i меньше, чем энтропия Нz, так как для некоторых классов j = 1, 2, …, h доли pyz|y(j | i) представляют собой суммарные доли нескольких классов z-эквивалентности.

Теорема доказана.

Теорема 12. Если аргументы y и z независимы, то Нyz|y = Нz.

Доказательство. При независимых аргументах y и z верны следующие равенства pyz|y(1| i) = pyz|y(2| i) =  … = pyz|y(h| i), i = 1, 2, …, k, так как доли путей в yz-сечение, проходящие через фиксированный i-ый узел y-сечения, не зависят от i. Поэтому pyz|y(j| i) = pz(j¢) при определенном соответствии между узлами yz-сечения и z-сечения. В этом случае

Нyz|x(y) = i = - Sj pyz|y(j | i) log pyz|y(j | i) = Нz   и  Нyz|y = Si py(i) Нz =  Нz.

Теорема доказана.

Таким образом, в случае независимых аргументов y и z условная энтропия Нzy|y совпадает с безусловной Нz. Поэтому знание о порождении набора определенным у-классом не влияет на наши знания о принадлежности yz-набора тому или иному yz-классу.

Справедлива

Лемма 13. Если ri, qi , i = 1, 2, …, n, – дискретные распределения случайных величин, то справедливо неравенство

Si = 1, n ri log (ri / qi) ³ 0.

Докажем следующее утверждение.

Теорема 14. Нyz|y ≤ Нyz.

Доказательство. Искомое неравенство преобразуется в следующее

- S i, j pyz(i, j) log pyz|y(j | i) ≤  - Sj pyz(j) log  pyz(j).

Для его доказательством воспользуемся неравенством из Леммы 11, положив

rj = pyz|y(j | i), qj = pyz(j). Тогда неравенство из Леммы 11 превращается в такое:

Sj = 1, n pyz|y(j | i) log (pyz|y(j | i) / pyz(j)) ³ 0.

Преобразуя, получаем

Sj = 1, n pyz|y(j | i) log pyz|y(j | i) ³ Sj = 1, n pyz|y(j | i) log  pyz(j)).

Так как неравенство справедливо для каждого i, то умножая на  py(i) и суммируя по i, получаем неравенство

Sj,i pyz|y(j | i)  py(i) log pyz|y(j | i) ³ Sj,i pyz|y(j | i) py(i) log  pyz(j)).

Используя равенство pyz(i, j) = pyz|y(j½ i) py(i), преобразуем левую часть неравенства в Sj,i pyz(i, j) log pyz|y(j | i). Используя равенство Si pyz|y(j | i) py(i) = pyz(j), правую часть неравенства преобразуем в Sj pyz(j) log  pyz(j)). Из этого следует искомое неравенство.

Теорема доказана. 

Пример 2. Верхняя граница энтропии Нyz|x(y) = i достижима и равна log k, если pyz|y(j | i) = k-1 при всех значениях j. Поэтому, если сравнивать верхние границы частной энтропии при одинаковых значениях долей pyz|y(j | i), то она тем больше, чем больше число узлов yz-сечения достижимо из i-го узла y-сечения. Это согласуется с содержательным представлением о неопределенности вычислительного процесса, представляемого бинарной программой. Действительно, число возможных продолжений вычисления из i-го узла y-сечения будет больше при большем числе достижимых вычислителей (т.е. узлов yz-сечения) из i-го узла y-сечения.

Пример 3. Из того, что математическое ожидание случайной величины увеличивается при увеличении ее значений и при одинаковом распределении следует, что условная энтропия Нyz|y возрастает при возрастании частных условных энтропий Нyz|x(y) = i. Это согласуется с содержательным представлением о неопределенности вычислительного процесса. Действительно, если число достижимых узлов yz-сечения из каждого узла y-сечения увеличивается, то при прочих равных условиях возрастает и усредненное значение

S i py(i) Нyz|x(y) = i.

Теорема 15. Верно неравенство Нyz ≤ Нy + Нyz|y.

Доказательство. Используя равенство pyz(i, j) = pyz|y(j| i) py(i), получаем

Нyz|y = - S i, j pyz (i, j) log  pyz (i, j) / py(i) = .

- S i, j pyz (i, j) log  pyz (i, j) + S i, j pyz (i, j) log  py(i).

Так как py(i) = åj pyz(i, j), то получаем

Нyz|y  = - S i, j pyz (i, j) log  pyz (i, j) + S i py (i) log  py(i) =

- S i, j pyz (i, j) log  pyz (i, j) - Нy.

Так как Si pyz(i, j) = Si pyz|y(j½ i) py(i) = pyz(j), то -Si pyz(i, j) log pyz(i, j) ³ - pyz(j) log pyz(j). Поэтому верно такое соотношение 

- Si,j pyz(i, j) log pyz(i, j) ³ - Sj pyz(j) log pyz(j) = Нyz

Отсюда получаем искомое неравенство 

Нyz|y ³ Нyz - Нy.

Теорема доказана.

4. Зависимые переменные. Следующим исследуемым классом функций будут так называемые функции с сильной зависимостью между переменными. Введем такое определение.

Назовем f(y, z) функцией с сильной зависимостью между переменными y и z (обозначим y ßà z), если в матрице Mf  не константные функции встречаются в точности по одной в каждой строке и в каждом столбце. Из этого вытекает, что для функции f(y, z) совпадают мощности фактор-множеств, определяемых у-эквивалентностью, z-эквивалентностью и yz-эквивалентностью. Кроме того, для каждого yz-класса, для которого результирующая функция не константа, его y-проекции однозначно определяют соответствующие z-проекции. В терминах матрицы Mf имеем, что все пары (i, j), где i – фиксированный номер столбца и j пробегает по всем номерам строк, определяют единственный класс yz-эквивалентности. Аналогично, если зафиксировать номер строки этой матрицы, то все ее столбцы также определяют единственный класс эквивалентности. Из этих рассуждений видно, что матрица Mf  квадратная.

Содержательно сильная зависимость трактуется, как взаимно-однозначная зависимость в следующем смысле. Каждый класс у-эквивалентности соответствует в точности одному классу z-эквивалентности и наоборот. Следовательно, каждый класс y-эквивалентности единственным образом определяет вычислитель, который перечисляет z-наборы лишь из одного класса z-эквивалентности. Очевидно, что верно и обратное.

Если f(y, z) есть функция с сильной зависимостью между переменными y и z, то ее разложение по переменным yz имеет вид Úi=1,k j=1,h [ysiz lj] fij, k = h и существует взаимно однозначное отображение j:{1, 2, ..., k} ® {1, 2, ..., h} такое, что для всякого i Î {1, 2, ..., k} не константа лишь функция fij(i). Разложив функцию f(y, z) по переменным y, получим Úi=1,k [ysi] f(s1i, z). В этом случае означивающие наборы для функции f(s1i, z) обладают таким свойством: лишь наборы, порожденные z-классом с номером j(i) не превращают f(s1i, z) в константу. Аналогично, разложив функцию f(y, z) по переменным z, получим Úi=1,h [zlj] f(y, l1j). И имеет место аналогичный факт: лишь наборы, порожденные y-классом с номером j-1(j) не превращают f(y, l1j) в константу. 

Следовательно, функция f(y, z) представима в виде Úi=1,k [ysiz lj(j)] fij(j)           или Ú j=1,h [ysj-1(j)z lj] fj-1(j)j.

Очевидна такая теорема.

Теорема 16. Если f(y, z) есть функция с сильной зависимостью y ßà z, то Нyz|y = 0.

Доказательство. Если pyz(i, j) есть доля путей из истока в уz-сечение, одновременно проходящие через i-й узел у-сечения и j-й узел уz-сечения, то pyz(i, j(i)) = py(i), а для остальных значений j pyz(i, j) = 0. Отсюда следует, что pyz|y(j(i) | i) = 1 и pyz|y(j | i) = 0 для остальных значений j. Теперь Нyz|y = - S i,j py(i) pyz|y(j | i) log pyz|y(j | i) = 0.

Следствие. Для функции f(y, z) с сильной зависимостью y ßà z, Нyz = Нy.

Можно несколько перефразировать отношение сильной зависимости следующим образом. Говорим, что два множества y и z переменных логической функции  f(y, z) обладают одинаковым распределением, если,

во-первых, существует взаимно-однозначное соответствие фактор-множеств, определяемых этими множествами переменных и,

во-вторых, доли наборов, порождаемых соответствующими классами, совпадают.

Это обозначает, что если y-эквивалентность известна, то дополнительное знание z-эквивалентности не увеличивает наших знаний о функции. Понятно, что для функции f(y, z) переменные y и z обладают одинаковым распределением тогда и только тогда, когда эти множества переменных сильно зависимы.

Будем говорить просто о зависимости переменных z от переменных y (обозначается y à z), если в каждой строке матрицы Mf в точности одна клетка не константная функция.

Из этого определения вытекает, что если f(y, z) есть функция с зависимостью y à z переменных, то для матрицы Mf выполняется неравенство  h £ k.

В этом случае между фактор-множествами, порождаемыми y-эквивалентностью и z-эквивалентностью, можно установить однозначное отображение j:{1, 2, ..., k} ® {1, 2, ..., h} такое, что для всякого i Î {1, 2, ..., k} не тождественная константа лишь функция fij(i). И наоборот, для каждого значения j Î {1, 2, ..., h} не тождественные константы  лишь  функции fj-1(j),j. Обратное отображение j-1 не однозначно, так как одному z-классу в общем случае соответствует несколько y-классов.

Зависимость y à z трактуется как функциональная в следующем смысле: каждый класс y-эквивалентности определяет в точности один класс z-эквивалентности. Обратное соотношение, в общем случае, неверно – несколько классов z-эквивалентности могут определяться одним классом y-эквивалентности.

Пусть f(y, z) есть логическая функция с зависимостью y à z ее аргументов, и ее разложение по y имеет вид f(y, z) = Úi=1,k [ysi] f(si1, z). В этом случае лишь z-наборы, образующие z-класс с номером j(i) не обращают функцию f(si1, z) в константу. Разложив функцию f(y, z) по переменным z, получим выражение f(y, z) = Új=1,h [zlj] f(y, lj1). В этом случае лишь y-наборы, образующие y-классы с номерами j-1(j), не обращают функцию f(z, lj1) в константу. Следовательно, f(y, z) = Úi=1,k [ysi ylj(i)] fi,j(i) и f(y, z) = Új=1,h [ysj-1(j)zlj] fj -1(j),j . 

Справедлива теорема.

Теорема 17. Пусть f(y, z) есть логическая функция с зависимостью y à z ее аргументов. Тогда Нyz|y = 0.

Доказательство. Пусть pyz(i, j) есть доля путей из истока в yz-сечение, одновременно проходя через i-ый узел y-сечения и j-ый узел yz-сечения. Отсюда следует, что pyz(i, j(i)) = py(i), а для остальных значений pyz(i, j) = 0. Отсюда следует, что pyz|y(j(i)|i) = 1 и pyz|y(j(i)|i) = 0 для остальных значений. Но тогда Нyz|y = åi,j py(i) pyz|y(j| i) log pyz|y(j| i) = 0.

Теорема доказана.

Следствие. Пусть f(y, z) есть логическая функция с зависимостью y à z ее аргументов. Тогда Нyz = Нy.

С другой стороны, если для функции f(y, z) имеется зависимость y à z, но отсутствует зависимость z à y, то Нzy|z > 0. Этот факт следует из того, что одному классу z-эквивалентности в общем случае соответствуют несколько классов y-эквивалентности. Поэтому доля путей из i-го узла y-сечения в j-ый узел yz-сечения при некоторых значениях  i, j отлична от 1 и нуля, так как из одного i-го узла могут вести пути в несколько узлов yz-сечения.

5. Свойства логической энтропии. Пусть функция f(y, z) представима в виде конъюнкции F(y) G(y, z) L(z), где функция F(y) не содержит переменных z, L(z) - переменных y и G(y, z) содержит оба множества y, z переменных. Для простоты пусть G(y, z)  не содержит иных переменных, кроме y, z. Назовем функцию G(y, z) сечением функции f(y, z). Разложим функции F(y), G(y, z) и L(z) по переменным соответственно y , yz и z. Результирующее выражение выглядит так:

Úi=1,k [ysi] Ù ui Ù (Úi, j  yaiz bj)Ù(Új=1,h [z lj] vj).

В разложении функции G(y, z) фигурируют конъюнкты yaiz bj, определенные бинарными кортежами ai и bj,  а не дизъюнкты, определяемые классами yz-эквивалентности.

Введем следующее определение.

Набор aibj из разложения функции G(y, z) является мостиком между классами si = {s1i, s2i, …, smi}, lj = {l1j, l2j, …, lnj} соответственно y-эквивалентности и z-эквивалентности для функций соответственно F(y) и L(z), если ai не ортогонален хотя бы одному набору из множества  {s1i, s2i, …, smi}, а bj – хотя бы одному набору из множества {l1j, l2j, …, lnj}. 

Справедлива следующая

Теорема 18. Если yz-набор aibj является мостиком между классами эквивалентности si и lj, то все наборы из si ´ lj не ортогональные набору aibj определяют один класс эквивалентности для функции f(y, z).

Доказательство. Означивание функции G(y, z) yz-набором aibj превращает ее в единицу. С другой стороны, каждый y-набор s1i, s2i, …, smi превращает функцию F(y) в ui , а z-набор l1j, l2j, …, lnj - функцию L(z) в vj. Отсюда вытекает, что каждый yz-набор из si ´ lj не ортогональный набору aibj превращает конъюнкцию F(y) G(y, z) L(z) в конъюнкцию ui Ù vj.

Теорема доказана.

С другой стороны, если yz-набор aibj не является мостиком между классами эквивалентности si и lj, то конъюнкция ui Ù vj не участвует в разложении функции f(y, z) по переменным y и z.

Таким образом, число классов yz-эквивалентности для функции f(y, z), определяется числом мостиков, соединяющих классы y-эквивалентности для функции F(y) и z-эквивалентности для L(z). Чем больше таких мостиков, тем ближе мощность фактор-множества yz-эквивалентности к kh. Если число мостиков меньше, то число классов yz-эквивалентности также уменьшается. В соответствии с этим меняется энтропия Нfyz по сравнению с суммой Нfy + Нfz. Содержательно это значит, что увеличение числа мостиков увеличивает независимость переменных y и z, уменьшение – приводит к их сильной зависимости.

Рассмотрим конъюнкцию F(y) L(z). Ее аргументы y и z не зависимые, поэтому HFLyz = HFLy + HFLz. Так как переменные z не встречаются в F(y), а переменные y – в L(z), то получаем равенства HFLy  = HFy и  HFLz = HLz. Отсюда HFLyz = HFy + HLz.

В общем случае для функции F(y) G(y, z) L(z) не каждая пара (i, j) определяет класс эквивалентности с той же долей, что и для функции F(y) L(z), так как некоторые функции ui Ù vj не встречаются в разложении в силу того, что i-ый и j–ый классы не соединяются ни одним мостиком. Поэтому в общем случае энтропия Hfyz не превосходит суммы Hfy + Hfz.

Справедлива следующая теорема.

Теорема 19. Пусть функция f(y, z) = F(y) G(y, z) L(z) и число переменных yz равно m. Тогда Hfyz £ m.

Доказательство. Энтропия Hfyz максимальная, когда доли наборов, определяемых каждым классом yz-эквивалентности одинаковы. Пусть d есть число путей бинарной программы, определяемой функцией f(y, z),  проходящих из истока в один узел yz-сечения. Тогда справедливо неравенство

 = log N/d.

где N есть число всех путей из истока в yz-сечение, и суммирование ведется по всем узлам yz-сечения.

Число узлов yz-сечения не более 2m. Так как d есть число путей, проходящих из истока в один узел yz-сечения, то N £ d 2m. Поэтому Hfyz £ m.

Теорема доказана.

Содержательно понятно, что если сечение функции содержит небольшое число переменных, то, означив эти переменные, мы получим небольшое сечение бинарной программы и  энтропия, определяемая этими переменными, не велика.

Справедлива

Теорема 20. Пусть у функции f(y, z) число переменных z равно m. Тогда Hyz - Hy £ m.   

Доказательство. Каждый узел у-сечения бинарной программы, определяемой функцией f(y, z), соединен путями не более, чем с 2m различными узлами yz-сечении. В результате вся совокупность Ny(i) путей, проходящих через i-ый узел у-сечения разбивается на не более, чем 2m не пересекающихся множеств путей, проходящих из истока в yz-сечение. Энтропия Hfyz будет максимальна, когда все доли путей, проходящих из истока в yz-сечение, одинаковы. Поэтому для любого i-го узла у-сечения имеем Ny(i)  £ 2m Nyz(j), где Nyz(j) – это число путей, проходящих через j-ый узел yz-сечения. Но тогда Ny(i) / Nyz(j) £ 2m. Отсюда следует утверждение теоремы.

Теорема доказана.

Исследование логической энтропии приводит к вопросу можно ли из функций с небольшой энтропией построить функцию с большой энтропией? Чтобы на него ответить докажем следующие теоремы.

Теорема 21. Для логических функций f(x, y) и g(x, y) имеет место неравенство

.

Доказательство. Построим для функции f(x, y)  g(x, y) бинарную программу . Узлы ее x-сечения, соответствующие не константным функциям, делятся на три типа, для которых выполняются условия соответственно: .

Рассмотрим бинарную программу для функции f(x, y), в которой порядок означивания переменных совпадает с порядком в . Узлы ее x-сечения, которые соответствуют не константным функциям, в программе  разделяются на два типа, в соответствии с выполнением условий: . Поэтому, каждому узлу  из x-сечения программы , для которого доля путей из истока составляет px(i) в x-сечении программы  соответствуют два узла  и  в той части x-сечения, для которой выполняется условие .

Оставив в программе  только пути, ведущие в эту часть x-сечения, получим подграф  бинарной программы . Если обозначить для  доли путей, ведущих в  и , соответственно  и , то получим равенство px(i) =  + . Отсюда вытекает неравенство , где есть энтропия x-сечения в выделенной из  части . Теперь сравним доли путей, ведущих в x-сечение, в графе  и всей программы . В графе  доли возрастают за счет исключения путей, ведущих в программе  в узлы x-сечения, которые удовлетворяют условию . Но так как доли в графе  возрастают по сравнению с долями аналогичных путей в , то энтропия меньше, чем энтропия . Отсюда следует неравенство .

Аналогично показывается, что имеют место неравенства , где есть энтропия x-сечения в части бинарной программы, которая включает пути ведущие в узлы x-сечения, выделяемые условиями . Следовательно, имеем неравенство .

Теорема доказана.

С другой стороны, верно утверждение.

Теорема 22. Для логических функций f(x, y) и g(x, y) имеет место неравенство

.

Доказательство. Построим для функции f(x, y) g(x, y) бинарную программу , в которой начальные отрезки всех путей из истока в сток получены означиванием переменных x, и программу , в которой порядок означивания переменных x совпадает с порядком в . Пусть пути, ведущие из истока в  x-сечение программы  (), образуют множество . Легко увидеть, что  . Более того, все пути из , ведущие в один узел  x-сечения, также ведут в один узел x-сечения программы . Назовем такие узлы соответствующими.

Отсюда следует, что число узлов x-сечения программы  не более числа узлов x-сечения программы , а доли путей, ведущих в один узел x-сечения программы  не меньше долей путей, ведущих в соответствующие узлы программы . Отсюда следует, что . Аналогично доказывается неравенство  . Отсюда вытекает заключение теоремы. 

Теорема доказана.

Последние два утверждения согласуются с содержательными представлениями. Объединение множеств событий влечет, по меньшей мере, не уменьшение неопределенности наших знаний об этих событиях (или фактах). С другой стороны, пересечение множеств подразумевает уточнение некоторых свойств или значений и поэтому – уменьшение неопределенности. Доказать аналогичные соотношения для дополнения множеств относительно простыми средствами не удается.

6. Энтропия суперпозиции функций. В этом разделе исследуем поведение энтропии логических функций, представляющих двоичные вычислимые функции. В частности рассмотрим, как зависит энтропия суперпозиции функций от энтропий образующих ее функций. Приведем сейчас лишь общие результаты. Более конкретно этот вопрос будет исследован на примере переписывающих алгоритмов.

Пусть логические функции f(x, y) и g(y, z) представляют вычислимые функции соответственно y =(x) и z = (y). Суперпозиция z = ((x)) представима конъюнкцией h(x, z) = f(x, y) g(y, z).

Рассмотрим xy-сечение бинарной программы  функции f при полном множестве Nx означиваний переменных x одинаковой длины. Пусть оно характеризуется энтропией  Особенность построения бинарной программы  состоит в том, что значения неподвижных переменных y однозначно определяются значениями аргумента x. Они не меняются при увеличении длины определяющего их x-набора. Каждый путь из истока в xy-сечение характеризуется некоторым x-набором  и определяемым им набором  значений неподвижных компонент y.

Рассмотрим xy-сечение бинарной программы  функции h, для которого означивания переменных x и y совпадают с означиваниями из бинарной программы . Число узлов xy-сечения программы  совпадает с числом узлов xy-сечения программы  и доли путей, ведущих в соответствующие узлы этих программ, также совпадают.

Продолжим построение бинарной программы  ниже i-го узла путем означивания переменных z. Так как g(y, z) представляет вычислимую функцию , неподвижные компоненты z однозначно определяются неподвижными компонентами y. Именно эти значения переменных z выберем в качестве z-наборов при продолжении построения программы . Если сравнить  с бинарной программой  для функции g(y, z), которая получается означиванием переменных y и z, как это сделано в , то имеет место следующее отношение включения.

Пусть в программе  из истока в i-ый узел xy-сечения ведет некоторое множество путей. Каждый из них характеризуется единственным x-набором и единственным значением неподвижных компонент y. Поэтому в i-ый узел xy-сечения мы попадаем из истока по путям, характеризующимся как различными, так и совпадающими y-наборами потому, что разные начальные x-наборы могут определять одинаковые значения неподвижных компонент y. При дальнейшем построении программы  ниже i-го узла означивания переменных z определяются неподвижными компонентами y, которые фиксируются функцией f(x, y). Поэтому число путей, ведущих из i-го узла xy-сечения в xyz-сечение, не превосходит числа различных y-наборов, которые встречаются в путях из истока в i-ый узел.

Часть программы , расположенная ниже i-го узла xy-сечения, представляет собой фрагмент программы , так как все пути программы  из истока в xyz-сечение проходящие через i-ый узел xy-сечения характеризуются множеством пар <,> y- и z-наборов, совпадающими с метками части путей из истока в yz-сечение программы . Если же рассматривать все пути программы  из истока в xyz-сечение, то они определяют все пары y- и z-означиваний, определяемые всеми путями программы .

Нам потребуются следующие определения.

Пусть Mx – некоторое множество начальных x-означиваний. Каждый x-набор  определяет единственный начальный y-набор  неподвижных компонент. Множество {(,)|  Mx} разбивается функцией f на классы эквивалентности, пусть K1, K2, …, Kl. Выделим из произвольного класса Ki все первые компоненты пар, обозначим это множество Kix и назовем x-проекцией класса Ki. Из того, что f представляет вычислимую функцию, вытекает, что |Kix| = |Ki| и Kix  Kjx =  при i j. В этом случае говорим, что функция f разбивает множество Mx на классы K1x, K2x, …, Klx и это разбиение порождает эквивалентность: тогда и только тогда, когда оба набора и  принадлежат одному классу из семейства K1x, K2x, …, Klx.

В точности так же можно выделить и y-проекцию Kiy класса Ki. Для нее выполняется неравенство |Kiy|  | Ki |.

Пусть теперь Mx = Nx и мы имеем совокупность y-проекций K1y, K2y, …, Kly. По каждому y-набору  Kiy функция g(y, z) определяет единственный z-набор  значений неподвижных компонент. Множество {(, ):  Kiy} таких пар функцией g(y, z) разбивается на классы эквивалентности. Таким образом, функция h разбивает множество {(,,)|  Nx,  - значения неподвижных компонент, определяемых по , и  - значения неподвижных компонент, определяемых по } на классы. В свою очередь функция f(x, y) разбивает множество {(,)|  Nx,  - значения неподвижных компонент, определяемых по } на классы. И распределения этих разбиений могут существенно различаться. В силу этого отличаются энтропии Hfxy и Hhxyz. Более конкретно значение энтропии функции h зависит от вида функций f и g.

Из этих рассуждений вытекают следующие утверждения.

Лемма 23. Число различных путей из xy-сечения в xyz-сечение программы  не превосходит числа путей из истока в xy-сечение.

Доказательство. Каждый путь из истока в xy-сечение определяет единственную y-проекцию, которая, в свою очередь, определяет единственное z-означивание. Следовательно, ниже всякого узла xy-сечения располагается не большее число путей, чем ведет в него из истока.

Лемма доказана.

Следовательно, все пути из истока в xyz-сечение задаются путями из истока в xy-сечение.

Лемма 24. Число путей из i-го узла xy-сечения в j-ый xyz-сечения программы  совпадает с числом путей из истока, проходящих через i-ый и j-ый узлы.

Доказательство. Пути из i-го узла xy-сечения в j-ый xyz-сечения представляют собой продолжение части путей из истока в i-ый узел. Но тогда путей из истока, проходящих через i-ый узел xy-сечения и j-ый xyz-сечения? будет столько же, сколько путей из i-го узла в j-ый.

Лемма доказана.

Отсюда вытекает, что число путей программы , выходящих из i-го узла xy-сечения и ведущих в xyz-сечение, не больше числа путей из истока в i-ый узел xy-сечения.

Действительно, все пути ниже i-го узла xy-сечения определяются y-проекциями, которые формируются путями из истока в i-ый узел.

Введем такое определение.

Пусть pz(j | i) есть доля путей программы , ведущих из i-го узла xy-сечения в j-ый узел xyz-сечения среди всех путей из i-го узла в xyz-сечение. Тогда частной условной энтропией, определяемой этим xyz-сечением относительно i-го узла, называется величина  Просто условной энтропией функции g относительно f назовем среднее частных условных энтропий .

Содержательно условная энтропия  характеризует сложность функции , где Kiy есть y-проекция i-го класса Ki эквивалентности, определяемой функцией f(x, y). Энтропия  описывает усредненную сложность функций , когда усредняющими  коэффициентами выступают доли pxy(i) путей бинарной программы  из истока в xy-сечение.

Теорема 25. Имеет место неравенство: .

(Энтропия конъюнкции логических функций, представляющей суперпозицию двух вычислимых функций, не превосходит суммы энтропий функции f и условной энтропии функции g относительно функции f).

Доказательство. = +=

=-  =. .  есть доля путей бинарной программы, проходящих одновременно через i-ый узел xy-сечения и j-ый узел xyz-сечения. Но тогда последняя сумма равна -.

, где . Тогда

=.

Искомое неравенство  переписывается следующим образом:   -. Это неравенство выполняется в случае, когда

  ,

что эквивалентно неравенству

 0.

Последнее неравенство очевидно, так как  1.

Лемма 26. Если {pi} и {qi}, i = 1, 2, …, k,  два множества не отрицательных чисел и , то верно неравенство

Доказательство вытекает из неравенства между средними арифметическим и геометрическим , при условии qi >0 и =1.

Лемма 27. Пусть h есть число узлов xyz-сечения, соединенных путями с i-м узлом xy-сечения. Тогда имеет место неравенство

--.

Доказательство. Искомое неравенство эквивалентно следующему

  .

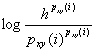
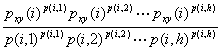
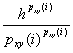
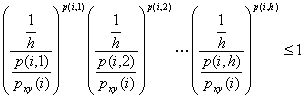Обозначим 1/h = p1 = p2 =…=ph, p(i, 1) = q1, p(i, 2) = q2, …, p(i, h) = qh. Очевидно, что . Тогда последнее неравенство переписывается так

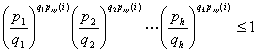
Лемма доказана.

Теорема 28. Пусть hi есть число узлов xyz-сечения, в которые ведут пути из i-го узла xy-сечения. Тогда верно неравенство

.

Доказательство. Имеют место следующие равенства.

 =

=+  =

+= -- .

Из леммы вытекает, что

-=.

Теорема доказана.

Таким образом, условная энтропия не превосходит среднего от логарифма мощности y-проекций классов эквивалентности, задаваемых функцией f при полном множестве Nx означиваний.

Исследуем, при каких условиях энтропия суперпозиции больше энтропии образующих их функций. Для этого введем следующее определение.

Функция g называется расширителем функции f, если выполняется неравенство , где x-означивания образуют полное множество Nx означиваний одинаковой длины, а y- и z-означивания определяются как при построении программы .

То, что g является расширителем для f, содержательно понимается следующим образом: функция  устроена сложнее, чем функция . Вопрос нахождения расширителей имеет существенное значение, так как именно к нему сводится задача построения сложных вычислимых функций из простых.

Справедлива

Теорема 29. Пусть для всякой пары i-го узла xy-сечения и j-го узла xyz-сечения программы , соединенных хотя бы одним путем, выполняется соотношение

Тогда g является расширителем f.

(Содержательно это обозначает, что доли путей, ведущих в i-ый узел xy-сечения, превосходит долю путей, ведущих в j-ый узел xyz-сечения. Следовательно, число путей, ведущих в i-ый узел больше числа путей, ведущих в j-ый узел.)

Доказательство.

 < -

- > 0

- > 0

-} > 0.

Имеет место равенство =1. Поэтому последнее неравенство эквивалентно

-} > 0

 > 0  > 0

 > 0.

Теорема доказана.

 

Литература

1.    Брошкова Н.Л., Попов С.В. Логическая энтропия. Препринт ИПМ им. М.В.Келдыше РАН, 2005.

2.    Брошкова Н.Л., Попов С.В. О проектировании информационных систем. Препринт ИПМ им. М.В.Келдыша РАН, 2005.

 

 

Архив

 

Т.25. Пусть  и  суть два начальных y-набора такие, что    и  определяет неподвижные z-компоненты  и - компоненты . Тогда выполняется включение   .

Доказательство. Набор  определяет функцию |, значения которой характеризуются неподвижными двоичными компонентами , которые присутствуют в каждом ее значении, в том числе когда аргумент имеет значение, начинающееся с . Следовательно, неподвижные компоненты функции | включают неподвижные компоненты функции |.

Теорема доказана.

 

Для дальнейшего нам требуется ввести обобщение понятия логической энтропии. Напомним, что при ее определении мы рассматривали так называемые бинарные программы, характеризующиеся линейным порядком означиваемых переменных. Говоря об y-сечении бинарной программы, где y = {y1, y2, …, ym} есть множество логических переменных, мы имели в виду, что порождение путей бинарных программ происходит означивания этих переменных в соответствии с определенным порядком. Поэтому, если в метках дуг путей, ведущих в y-сечение, рассматривать только индексы переменных, то все пути из истока в y-сечение характеризуются одинаковыми последовательностями.

Значение логической энтропии зависит лишь от долей путей из истока в y-сечение и при построении бинарной программы выше y-сечения не учитывает собственно способа означивания переменных. Поэтому можно расширить определение логической энтропии, рассматривая не однородные программы, а программы с произвольным порядком означивания переменных в путях из истока в y-сечение программы, сохраняя требование, чтобы каждый путь из истока в y-сечение определял означивания всех переменных y. Легко проверить, что при таком обобщении логической энтропии все полученные выше результаты остаются верными.

Наконец, ослабим последнее требование относительно означивания всех переменных y, задаваемых каждым путем.

По-прежнему будем рассматривать бинарную программу и ее сечение назовем y-сечением, где y = {y1, y2, …, ym} есть множество логических переменных, если имеется хотя бы один путь из истока в узел этого сечения, который определяет означивания всех переменных из y. Из определения бинарной программы вытекает справедливость следующего утверждения.

Лемма 23. Если i1, i2 суть узлы y-сечения и два пути, ведущие из истока в эти узлы определяют означивания соответственно  и   , где yi1, …, yih, yj1, …, yjm  переменные из  y и h  m, то при любом упорядочении первой последовательности путем перестановки ее членов она не может быть префиксом второй.

Доказательство вытекает из определения бинарной программы и того, что оба пути начинаются в истоке.

После этого определение логической энтропии формулируется, как и прежде.

Будем характеризовать каждый путь t, ведущий в y-сечение, множеством Var(t) переменных, для которых он определяет означивания. Каждый путь определяет свое множество означиваемых переменных и их означиваний. Но тогда y-сечение характеризуется парой <Max, Min> соответственно наибольшим и наименьшим множествами переменных, означивания которых приводит в y-сечение. Разность Max – Min назовем интервалом, порождаемым данным y-сечением бинарной программы. Очевидно, что пара <Max, Min> зависит от конкретного способа построения бинарной программы.

Инкрементом интервала = Max - Min (обозначается in()) назовем число всех означиваний переменных из интервала, которые принимают участие в построении y-сечения.

Рассмотрим классы так называемых локальных функций. А именно, локальной будем называть логическую функцию f(y, z), если все y-означивания порождают ограниченное число классов эквивалентности, определяемых лишь последними k компонентами этих означиваний.

Рассмотрим y-сечение бинарной программы для локальной функции.

Имеет место

Теорема 24. Пусть f(x, y) обобщенная функция и Hx – энтропия, определяемая переменными x , порядок означивания которых совпадает с естественным порядком переменные. Тогда определяющая окрестность для этих переменных имеет длину не менее Hx.