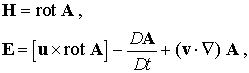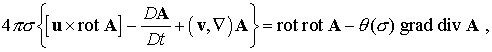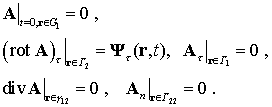Численное моделирование квазистационарных электромагнитных полей в многосвязных
областях и областях с изменяющимися во времени границами
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
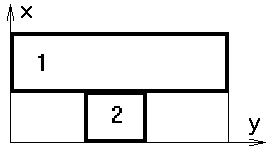
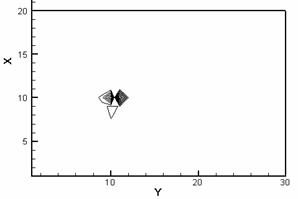
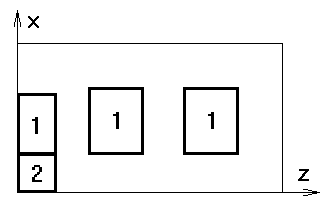
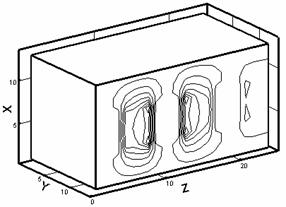
Рис. 1.1. Схема расчетной области.1 – рельс, 2 – якорь. |
Согласно [1, 4 – 6] при расчете
будем рассматривать не весь трехмерный ускоритель, а лишь его часть,
приходящуюся на область, жестко связанную с якорем и движущуюся вместе с ним.
Длина этой области (в направлении оси y) составляет несколько калибров
ускорителя в обе стороны от якоря (рис. 1.1) При таком подходе возникает
проблема задания граничных условий на передней и задней границах исследуемой
области. На боковых границах области этой проблемы нет, так как канал
рельсотрона обычно заключен в проводящий силовой бандаж. В силу геометрической
симметрии достаточно найти решение задачи в верхней половине области в
двумерном случае или в правой верхней четверти расчетной области в трехмерном случае.
При разработке модели использовано резкое различие длины ускорителя (по y)
и его поперечных размеров. Учтено также, что единственной заданной извне
электромагнитной величиной можно считать полный ток, определяемый источником
питания. Поэтому для постановки
граничных условий используется модель [4 – 6], в которой на торцах расчетной
области заданы тангенциальные компоненты магнитного поля, соответствующие
бесконечно длинной (вдоль оси y) системе проводников, для каждого из
которых задан полный ток. Решение же задачи во всей области получается путем
использования алгоритма [4 – 6] по заданным тангенциальным компонентам
магнитного поля.
Для расчета температурного поля в проводящей
области применим математическую модель[1] в СЭЛ переменных:
![]() .
.
Здесь w = u – v - относительная скорость вещества в движущемся со скоростью v объеме V, ρ – плотность
вещества, e - удельная внутренняя энергия, W = - k grad T – тепловой поток, k - коэффициент теплопроводности, T – температура, (j, E) – мощность тепловыделения за счет джоулева нагрева, удельную
энергию будем искать в виде 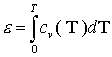 , cv – удельная теплоемкость. Расчет температурного поля ведется
параллельно с расчетом других полей (E, j, H, A).
, cv – удельная теплоемкость. Расчет температурного поля ведется
параллельно с расчетом других полей (E, j, H, A).
В задаче предполагается, что электропроводность
и другие параметры материалов зависят от температуры. В проводящей части
возможны фазовые переходы: плавление и кипение. Для построения разностных схем
в области вводится пространственная сетка. Дискретный аналог векторного
потенциала относится к ребрам ячеек сетки, напряженность магнитного поля - к их
граням. Подробности математической модели и вычислительного алгоритма
представлены в работах [1, 4 – 6]. Ниже используются обозначения, традиционные
для работ по моделированию электромагнитных явлений. Они совпадают с
используемыми в [1, 4 – 6]. Разностные схемы записываются для безразмерных
величин, как и (1.1).
При программной реализации для описания
расчетной области и постановки граничных условий рассчитывается набор
логических массивов, полностью определяющих область, ее границу и, тем самым,
матрицу системы линейных алгебраических уравнений (т.е. разностную схему) для
решаемой задачи [4, 7]. В данной работе используются разработанные в [8, 9]
новые алгоритмы формирования логических массивов на границах области,
позволяющие независимо от конфигурации получать значения внутренних и граничных
компонентов массивов. Согласно [4, 7] вокруг каждого ребра сетки могут
располагаться одна, две, три или четыре ячейки, принадлежащие расчетной
области. Это приводит к необходимости рассматривать шесть граничных плоскостей
расчетной области отдельно (для задания на них логических массивов). Введение в
[8, 9] виртуальных (используемых только при расчете логических массивов)
"ячеек", соответствующих граничным условиям первого или второго рода,
позволяет при формировании логических массивов учитывать соответствующие
граничные условия. То есть при использовании алгоритмов [8, 9] вокруг любого
(внутреннего или граничного) ребра разностной сетки располагаются 4 ячейки
(включая виртуальные "ячейки", "материал" которых
обозначает вид граничного условия), также 4 ячейки располагаются спереди ребра
(ребро "втыкается" в 4 ячейки) и 4 ячейки сзади. Это позволяет легко
рассчитывать логические массивы для любой конфигурации, без отдельного расчета
массивов на граничных плоскостях и ребрах области.
Для
решения возникающей системы линейных алгебраических уравнений используется
метод сопряженных градиентов совместно с неполным разложением Xолесского [10 –
13].
§ 2. Моделирование в случае
изменения границ областей при испарении материала
В
модели [1] в проводящих областях используются температурные зависимости
электропроводности, теплопроводности и теплоемкости материала с учетом фазовых
переходов. Такой способ моделирования позволяет определить временные границы
процессов плавления, кипения и определить момент начала испарения материала
проводника. В случае испарения материала ячейки электропроводность такой ячейки
должна резко измениться. В идеальном случае она должна стать равной нулю.
Однако при использовании алгоритма [1] в этом случае должна измениться и
разностная схема вследствие изменения границы раздела проводящих и непроводящих
подобластей. Ранее такой вариант (с изменением границ проводящих и
диэлектрических подобластей) не использовался. При моделировании испарения
проводника электропроводность в испарившейся части полагалась [1, 4 – 9] малой
("фоновой") величиной (на несколько порядков меньшей значения до
испарения), что обеспечивало соответствующее перераспределение тока. Но при
таком подходе образуются проводящие подобласти с малой электропроводностью,
которые должны соответствовать диэлектрическим. Использование для моделирования
диэлектрика проводника с малой электропроводностью может серьезно ухудшить
устойчивость решения по отношению к возмущениям правой части [1]. Например, в
случае однородной проводящей подобласти с малой электропроводностью зависимость
решения от правой части содержит малую электропроводность в знаменателе [1].
Если величина "фоновой" электропроводности берется большой, то
неверно считается тепловыделение и распределение токов. При малой величине
электропроводности решение становится сильно зависимым от малых изменений
правой части системы уравнений [1, 4 – 6], что неизбежно приводит к плохой сходимости
итераций и резкому уменьшению шага по времени.
Для
преодоления этих трудностей ниже предложена следующая модель: при превышении
температуры кипения в проводящей ячейке такая ячейка заменяется диэлектрической
с соответствующей перестройкой логических массивов [6, 7], используемых для
описания расчетной области и разностных схем, соответствующих дифференциальным
операторам.
Предложенный
алгоритм моделирования испарения перестраивает логические массивы,
предназначенные для подсчета джоулева тепла, приходящееся на каждое из ребер
разностной сетки. Логические массивы учитывают перераспределение тепла от
граничных с проводником ребер по ближайшим проводящим ячейкам. Пересчет
массивов позволяет избежать эффектов [3, 14], связанных с отнесением тепла к ячейкам
диэлектрика (с "фоновой" электропроводностью). В средах с малой
электропроводностью происходит наиболее интенсивный джоулев нагрев [14].
Появление в расчетной области подобластей (состоящих из одной или большего
числа ячеек) с малой электропроводностью ухудшает сходимость внешних итераций,
используемых для вычисления температуры, что уменьшает необходимый для
сходимости временной шаг.
Рассмотрим подробнее вопрос
устойчивости решения для различных способов моделирования испарения. Исследуем
обусловленность системы линейных алгебраических уравнений, получаемых при
разностной аппроксимации уравнений Максвелла. Для вычисления минимального и
максимального собственных значений будем использовать несколько видоизмененные
варианты методов [15]. В случае отсутствия движения матрица системы линейных
алгебраических уравнений разностной схемы [1, 4 – 6] является симметричной. В
этом случае число обусловленности есть частное от деления максимального и
минимального собственных чисел. Наличие движения делает матрицу несимметричной.
В этом случае число обусловленности есть корень квадратный из отношения
максимального и минимального собственных значений вспомогательной матрицы,
равной произведению матрицы системы на ее сопряженную [15].
Ниже приведены наибольшее и наименьшее
собственные значения системы линейных алгебраических уравнений, получаемых при
разностной аппроксимации задачи (1.3) для рассматриваемой задачи без движения.
Испарение в двумерном случае
Рассмотрим задачу в двумерном
приближении (используемый для нее алгоритм обобщается на трехмерный случай).
Область состоит из проводников и диэлектриков. Задача решается на разностной
сетке Nx = 20, Ny = 30 (здесь Nx, Ny
– количество ячеек сетки вдоль соответствующих осей).
Схема
модельной пространственной области, использованной в расчетах (в простейшем
двумерном случае), представлена на рис. 1.1. Якорь при этом движется в
положительном направлении оси у.
|
a б в |
|
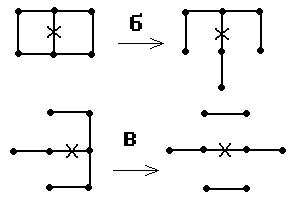
Рис. 2.1. Шаблоны разностных схем для оператора задачи в двумерном случае ( а – шаблон схемы в G1, б – шаблон схемы в G2, в – шаблон схемы на g12). |
Рассмотрим часть разностного
оператора без производной по времени и конвективных слагаемых в двумерной
постановке [1, 4 – 6]. В G1 шаблон разностной схемы для
оператора (rot rot) имеет вид, приведенный на рис. 2.1.а; в G2
оператор (rot rot – grad div) аппроксимируется на шаблоне рис. 2.1.б; вид
шаблона c учетом условий div A = 0 на g12 приведен
на рис. 2.1.в. С испарением ячеек меняются границы ¶ G1, ¶ G2, ¶ G12 и g12.
При отсутствии движения уравнение (1.3)
аппроксимируется на шаблонах, аналогичных шаблонам для оператора (rot rot –
grad div) в диэлектрике и (rot rot) в проводнике (рис. 2.1). В проводнике к
коэффициенту, соответствующему центральному ребру шаблона, добавляется
слагаемое, содержащее электропроводность и
связанное с производной по времени. При наличии в области движения в
шаблоны разностных схем, на которых аппроксимируются уравнения Максвелла,
добавляются конвективные слагаемые, что изменяет вид шаблонов в проводящей
подобласти.
Процессы
кипения и испарения проходят в двумерном приближении качественно сходно для
различных скоростей движения (то есть направления волн плавления и кипения не
зависят от скорости). Рассмотрим задачу с движением с перестроением шаблонов
разностных схем по предложенному алгоритму (при испарении материала). Якорь
движется в направлении оси y.
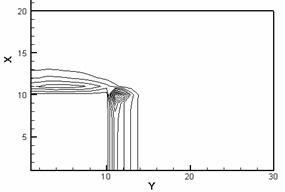
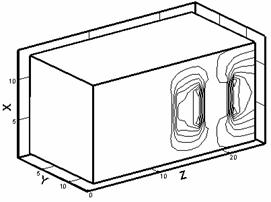
На
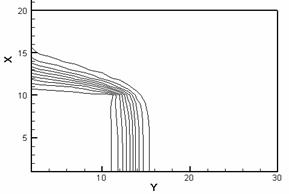
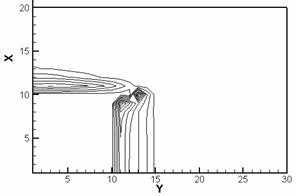
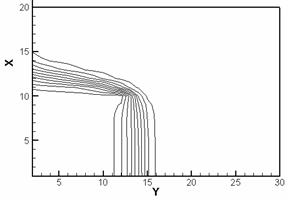
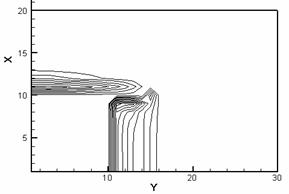
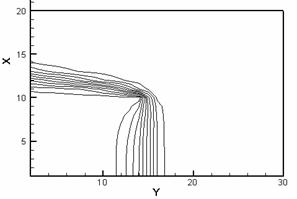
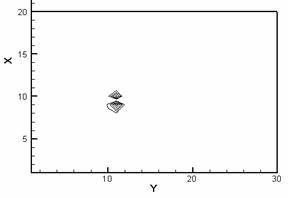
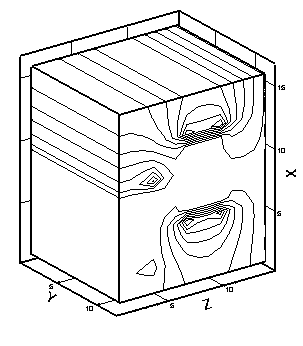
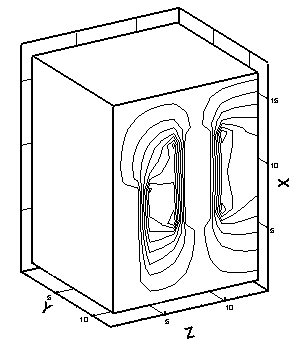
рис. 2.2 приведены полученные при численном моделировании картины изотерм
(слева) и линий уровня нормального компонента H для рассматриваемого
случая. Для удобства на рис. 2.2 по осям расположим номера ячеек (в ускоряемом
теле 10*10 ячеек, координаты ускоряемого тела по оси x (0 – 10), по оси y
(10 – 20)).
|
a |
|
|
|
б |
|
|
|
в |
|
|
|
г |
|
|
|
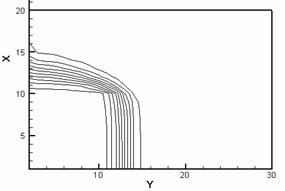
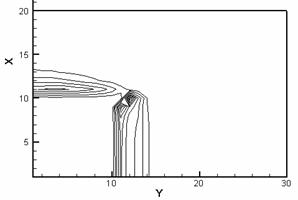
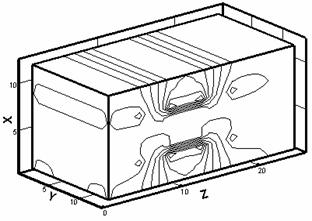
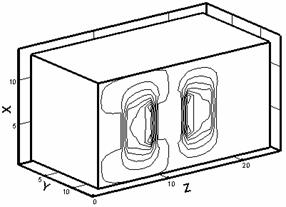
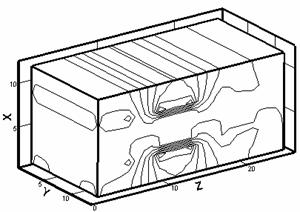
Рис. 2.2. Изотермы (слева) и картины распределения z - компонент вектора H (справа) в расчетной области: a – начало кипения, б – испарился материал одной ячейки, в – испарился материал двух ячеек, г – испарился материал четырех ячеек. |
||
Прежде
всего греется задняя граница ускоряемого тела (рис. 2.2.а) с наибольшим
значением температуры в угловой точке. Волна плавления и дальнейшего нагрева до
кипения движется вдоль границы g12 (в
направлении, противоположном направлению оси x). Волна испарения
движется (для данной конфигурации) преимущественно вдоль границы якоря и рельса
(в направлении оси y). В случае испарения ячеек картины перераспределения
вектора напряженности магнитного поля показывают наиболее интенсивную диффузию
магнитного поля в проводник вблизи области испарившегося материала (рис. 2.2).
Диффузия имеет место в средах с конечной электропроводностью, причем в средах с
малой электропроводностью интенсивность диффузии возрастает [14].
Рассмотрим
задачу без движения.
Исследуем устойчивость решения системы
линейных алгебраических уравнений, получаемых при разностной аппроксимации
уравнений Максвелла. При вычислении числа обусловленности будем использовать
комбинацию методов [15]: степенной метод с уточнением полученных собственных
значений и соответствующих им собственных векторов вариантами градиентного
метода.
Достижение в одной ячейке температуры
испарения при отсутствии движения не изменяет существенно обусловленности
системы, так как вид шаблона разностной схемы в задаче без движения для
диэлектрического или проводящего ребра сетки в случае испарения одной ячейки
без учета конвективных слагаемых остается неизменным.
Вычислим
собственные значения для различных методов моделирования кипения и испарения
материала. Рассмотрим несколько вариантов задачи: 1 – в области нет кипения; 2
– испаряются две крайние ячейки разностной сетки на границе якоря (параметры
задачи изменяются по традиционной схеме [1], вводится "фоновая"
электропроводность s0 = 10-5
при исходной s >1); 3 – температура испарения
достигается в двух крайних ячейках разностной сетки на границе якоря
("фоновая" электропроводность s0 = 10-10);
4 – две крайние ячейки разностной сетки на границе якоря становятся
диэлектрическими (материал испаряется и разностные схемы перестраиваются по
предложенному алгоритму).
В работе далее приведены наибольшее и
наименьшее собственные значения матрицы М системы линейных алгебраических уравнений,
получаемых при разностной аппроксимации уравнений Максвелла на разностной сетке
в рассматриваемой задаче без движения. При построении матрицы М для всех
вариантов в аппроксимации производной по времени шаг одинаков (t = 10-2). Итерации при вычислении собственных
значений выполнялись до тех пор, пока невязка ||M A – lA|| не становилась меньше 10-12 при ||A||
= 1 (M – матрица системы линейных алгебраических уравнений для аппроксимации
уравнений Максвелла на двумерной разностной сетке, A – собственный
вектор, который в данном случае имеет смысл векторного потенциала, l – собственное значение).
Таблица 1
Собственные
значения матрицы M для различных способов моделирования испарения материала в
двумерном случае
|
|
Наибольшее собственное значение |
Наименьшее собственное значение |
Число обусловленности |
|
Вариант 1 |
52.1784 |
1.6894·10-2 |
3.0885·103 |
|
Вариант 2 |
52.1784 |
2.5875·10-6 |
2.0165·107 |
|
Вариант 3 |
52.1784 |
2.5875·10-11 |
2.0165·1012 |
|
Вариант 4 |
52.1784 |
1.6398·10-2 |
3.1819·103 |
Из приведенных результатов (таблица
1) видно, что перестроение разностных схем при испарении материала позволяет
улучшить обусловленность матрицы решаемой системы на несколько порядков.
Отметим, что число обусловленности вариантов 2 и 3 определяется значением
"фоновой" электропроводности. Чем она меньше, тем больше число
обусловленности, стремящееся к бесконечности при стремлении "фоновой"
величины к нулю. При расчетах числа обусловленности для разных значений
"фоновой" электропроводности получены соответствующие результаты.
Наибольшее собственное значение практически не зависит от варианта модели. Для
случая с движением обусловленность системы изменяется аналогично, несмотря на
зависимость собственных значений от скорости движения якоря.
|
|
|
|
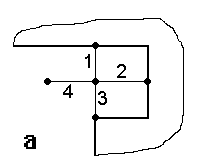
Рис. 2.3. а – расчетная область после испарения материала двух ячеек (испарился материал двух ячеек с общим ребром 2, в задаче нет движения), б – изменение шаблонов разностной схемы для ребер 1 – 3, в – изменение шаблона для ребра 4 (ребра, для описания которых изменяются шаблоны разностной схемы, обозначены символом Х). |
|
На
рис. 2.3 представлена часть расчетной области и разностной сетки в месте
испарения материала проводника. Ось x направлена вертикально, y -
горизонтально.
Согласно
предлагаемому алгоритму при испарении двух ячеек преобразуются разностные схемы
на ребрах 1 – 4 (рис. 2.3.б, в) (с учетом условия div A = 0 на g12). Без перестроения схем (в случае введения нулевой
электропроводности в испарившемся материале) образуется диэлектрическая
подобласть, в которой не выполняется условие div A = 0, что приводит к
неединственности решения. Без выполнения условия div A = 0 для
построения единственного решения необходимо, например, искать нормальное
решение, то есть обладающее минимальной нормой [1], что связано с дополнительными
вычислительными трудностями (подробнее см. § 3). Решение же, полученное после
перестроения разностных схем, само является нормальным (добавление в
испарившуюся подобласть условия div A = 0 дает нормальное решение). В
разностной задаче дискретный аналог условия div A = 0 относится к узлу
сетки (оно включает в себя 4 ребра, пересекающиеся в этом узле).
Преобразование
разностной схемы можно представить в матричной форме. Пусть матрица M – матрица
разностной схемы до преобразования шаблонов. MВ – матрица
после преобразования. Тогда MB = M + B, B – матрица преобразования.
Действие оператора (- grad
div) при испарении двух ячеек в
проводнике выражается во включении дискретного аналога оператора div с определенными коэффициентами (обозначим их а j) в четыре строки матрицы M
(изменяются четыре шаблона на ребрах 1 – 4 рис. 2.3). Дискретный аналог
оператора div обозначим b. Тогда матрица B имеет вид В = a
bT. Из симметричности используемых дискретных операторов
следует: a
bT = b
aT или a
bT b = b aT
b, то есть a = (a,b)/(b,b) b, В = с b
bT (c –
константа). При испарении материала в большем числе ячеек образуется большее
число узлов сетки с необходимостью выполнения условия div A = 0.Тогда
B = ![]() , где Bj
= сj
bj bjT – матрица с
четырьмя ненулевыми строчками - соответствует j - му узлу (из m) с
соответствующим условием. То есть ведение в (1.3) оператора ( - grad div)
эквивалентно требованию ортогональности решения векторам bj
в каждом внутреннем узле диэлектрической области
, где Bj
= сj
bj bjT – матрица с
четырьмя ненулевыми строчками - соответствует j - му узлу (из m) с
соответствующим условием. То есть ведение в (1.3) оператора ( - grad div)
эквивалентно требованию ортогональности решения векторам bj
в каждом внутреннем узле диэлектрической области
Решение
двумерной задачи на перестроенных схемах (при изменении границ проводящих и
диэлектрических подобластей), полученное методом сопряженных градиентов, в
различных вариантах задачи с достаточной точностью ортогонально собственным
векторам (соответствующим нулевому собственному значению) матрицы разностной
схемы без перестроения.
|
а |
б |
|
Рис. 2.4. а – x - компонент А0 , б – y - компонент А0. |
|
На
рис. 2.4 представлены компоненты вектора А0, соответствующего
наименьшему собственному значению, в случае нулевой электропроводности в
испарившемся материале (без перестроения схем). Значения обоих компонентов
собственного вектора имеют противоположный знак на ребрах, прилежащих к
испарившимся ячейкам (ребра 1 – 4 на рис. 2.3), то есть на ребрах
“недостающего” условия div A = 0.
В
рассматриваемой задаче (с движением) количество ячеек, в которых в данный
момент времени происходит кипение материала, зависит, прежде всего, от
количества ячеек сетки в ускоряемом теле. Рассмотрим далее часть границы g12 вдоль оси 0x в окрестности угловой точки, т.к.
процесс кипения начинается в угловой точке. Поскольку температура ячейки
представляет собой среднюю температуру в области, занимаемой ячейкой,
увеличение количества ячеек сетки приводит к кипению материала большего
количества ячеек.
Для исследования зависимости
количества ячеек сетки с кипящим материалом от общего количества ячеек сетки в
таблице 2 представлена зависимость температуры ячейки на границе g12 в якоре, ближайшей вдоль оси х к испарившейся
(в момент испарения), от количества ячеек вдоль оси 0х в якоре.
Таблицa
2
Зависимость температуры ячеек
ближайших к угловой точке (расположенных вдоль границы g12) от общего числа ячеек в ускоряемом теле
|
Количество ячеек по оси х в якоре |
Температура ячейки якоря, ближайшей вдоль оси 0х к испарившейся (К) |
|
10 |
1442 |
|
20 |
2376 |
|
40 |
2718.5 |
Испарение в трехмерном случае
Рассмотрим
вопрос об устойчивости решения для различных способов моделирования испарения в
трехмерном случае (для моделирования рассмотрим U - образный якорь [12, 13,
16]).
Вычислим собственные значения матрицы
разностного оператора для различных методов моделирования кипения и испарения
материала на трехмерной сетке (варианты задачи аналогичны двумерному случаю): 1
– в области нет кипения; 2 – испаряются две крайние ячейки разностной схемы на
ребре якоря (параметры задачи изменяются по традиционной схеме [1, 4 – 6],
вводится "фоновая" электропроводность); 3 – две крайние ячейки
разностной схемы на ребре якоря становятся диэлектрическими (материал
испаряется и разностные схемы перестраиваются по предложенному алгоритму). При
построении матрицы М для всех вариантов в аппроксимации производной по времени
шаг одинаков.
Итерации при вычислении собственных
значений выполнялись до тех пор, пока невязка ||M A – l A|| не становилась меньше 10-10 при ||A||
= 1 (M – матрица системы линейных алгебраических уравнений для аппроксимации
уравнения (1.3) на трехмерной разностной сетке, A – собственный вектор, l – собственное значение).
Таблица 3
Собственные
значения матрицы M для различных способов моделирования испарения материала в
трехмерном случае
|
|
Наибольшее собственное значение |
Наименьшее собственное значение |
Число обусловленности |
|
Вариант 1 |
20.457 |
5.331·10-5 |
3.837·105 |
|
Вариант 2 |
20.457 |
6.906·10-9 |
2.963·109 |
|
Вариант 3 |
20.457 |
5.326·10-5 |
3.840·105 |
Из приведенных результатов (таблица
3) видно, что перестроение разностных схем при испарении материала в трехмерном
случае также позволяет улучшить обусловленность решаемой системы на несколько порядков.
Улучшение обусловленности системы позволяет проводить расчет с большим шагом по
времени. Таким образом, при исследовании процессов в ускорителях
предпочтительной является модель с перестроением разностных схем и описателей
границ при испарении материала в ячейках разностной сетки, относящихся к
проводнику.
§ 3. Моделирование электромагнитных полей в многосвязных областях
В
[1, 4 – 6] исследовались способы построения единственного решения системы
уравнений Максвелла в квазистационарном приближении в неоднородных областях с
односвязной диэлектрической подобластью и связной границей g12. Связность g12 в случае
многосвязной проводящей подобласти дает единственное решение (такие случаи
исследовались в [17]).
Рассмотрим единственность решения
системы уравнений Максвелла в трехмерной области, в которой граница g12 несвязна. Несвязность g12 может
привести к неединственности решения задачи [1], т.е. ядро оператора задачи ker
M будет непустым.
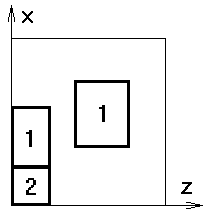
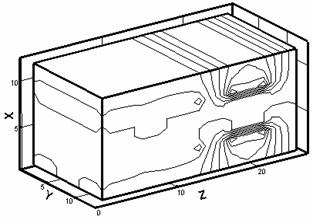
В качестве примера области с несвязной
границей g12 возьмем
область, соответствующую [18] (рис. 3.1). Рассматриваемая область состоит из
диэлектрической и проводящей подобластей. Часть границы ¶ G – граница g12 – не является связной. Она имеет два компонента
связности.
|
|
|
Рис. 3.1. Расчетная область. 1 - рельс, 2 - якорь. Сечение четверти трехмерной области плоскостью y = const. |
Для нахождения подпространства,
соответствующего ядру оператора M, используем два метода.
1)
Нахождение вектора, соответствующего разности двух решений системы уравнений Максвелла.
Согласно [1] решение системы уравнений
Максвелла в квазистационарном приближении в проводнике единственным образом
определяется граничными и начальными условиями.
Введение векторного потенциала H =
rot A в задаче без движения (при E = - DA/Dt) соответствует
второму и третьему уравнениям системы (1.1). Квазистационарность
рассматриваемых полей может привести к неединственности поля E в
диэлектрике, причем поле H определяется единственным образом во всей
области [1].
Допустим,
что у системы уравнений Максвелла существует два решения E1 и
E2. Обозначим их разность E = E1 – E2.
Для задачи (1.1) – (1.3), учитывая, что в диэлектрике E = - DA /
Dt (при v = 0), можно также рассмотреть разность решений А = А1
– А2 для векторного потенциала A.
Подставляя
разность решений А в исходную систему (1.3), учитывая единственность
решения в проводнике, получим задачу с нулевыми граничными условиями первого и
второго рода:
A = 0 в G1,
rot rot A
– grad div A = 0 в G2 , (3.1)
div
A = 0 на g12,
At = 0 на g12, (rot A)t = 0 на Г22,
An = 0 на Г22.
В
[19] показано наличие m
квазигармонических собственных функций оператора (rot rot), соответствующих
нулевому собственному значению (и отсутствие других, кроме квазигармонических),
представимых в виде градиентов многозначной функции в m - связной области,
обладающей либо m замкнутыми контурами, либо m поверхностями, несводимыми в точку, в случае различных
граничных условий (первого и второго рода). Согласно [20] в случае многосвязной
области, обладающей одновременно n несводимыми в точку контурами и m
поверхностями (с аналогичным свойством), собственные функции, соответствующие
контурами и поверхностями, могут быть линейно зависимы.
В
итоге анализа в соответствии с [19 – 21] (с учетом единственности магнитного
поля) вектор A можно представить как градиент некоторой функции A
= – grad f. Тогда задача (3.1) преобразуется
к виду:
div grad f = 0 в G2,
f = 0 на g121, f = 1 на g122, (3.2)
(grad f)n =
0 на Г22.
На
первом компоненте связности границы g12 (обозначим
его g121) задается нулевой потенциал, на
втором (обозначим его g122) -
единичный потенциал (аналогично [19, 20]).
Сопоставим полученной системе
разностную задачу и получим ее решение методом сопряженных градиентов с
декомпозицией по Холесскому [7 - 10]. Задача записывается в виде матричного
уравнения Lf = fL, где L – матрица,
аппроксимирующая оператор (div grad) (лапласиан), fL – правая часть
системы (содержащая граничные условия). Для повышения точности решения проведем
несколько циклов уточнения [7] (внешние итерации в задаче для нахождения f). В результате получим f (невязка
решения ||Lf – fL|| = 1.51·10-15)
и соответствующие А = – grad f.
|
а |
в |
|
б |
г |
|
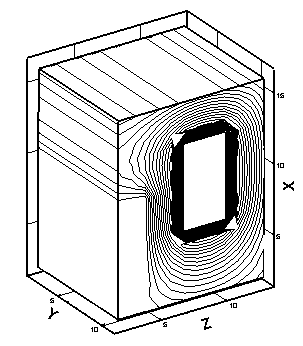
Рис. 3.2. Распределение f и А в рассматриваемой области: a – потенциал f, б – Ax , в – Aу, г – Az (по осям отложены номера ячеек пространственной сетки). |
|
На рис. 3.2.а представлено
распределение f в рассматриваемой области.
Распределения компонентов вектора A
также представлены на рис. 3.2. Рис. 3.2.б представляет составляющую градиента
потенциала по направлению оси x, рис. 3.2.г – по направлению оси z.
Вдоль оси у потенциал изменяется в наибольшей степени у границ
проводящего тела (рис. 3.2.в).
Поскольку матрица системы линейных
алгебраических уравнений, получаемых при аппроксимации системы уравнений
Максвелла, в случае неединственности решения является вырожденной, то для
нахождения ядра разностного оператора М в случае двусвязной границы g12 необходимо найти вектор, соответствующий нулевому
собственному значению матрицы.
2) Нахождение собственного вектора,
соответствующего минимальному собственному значению матрицы М численными
методами [15] (для той же сетки, на которой решалась задача для f).
При вычислении собственного значения с
невязкой, не превышающей 10-14
(||MA0 – lA0|| =
1.878·10-15), получим lmin = 1.386·10-18,
A0 – собственный вектор матрицы M, соответствующий lmin (||A0|| = 1). Полученный вектор
имеет ненулевые компоненты только в диэлектрике.
Для сравнения решения A,
полученного методом 1), с собственным вектором A0, полученным
методом 2), обозначим A1 = A/||A|| (при ||A0||
= 1). Далее вычислим норму ||A1 – A0|| =
3.89·10-13 (для случая h = const, здесь h – шаг сетки
по пространству). Норма разности векторов A1 и A0
много меньше норм векторов, то есть градиент решения задачи для потенциала
(3.2) является единственным собственным вектором, соответствующим нулевому
собственному значению разностной аппроксимации уравнений Максвелла в
квазистационарном случае (т.е. принадлежащим ядру оператора M).
Для построения
единственного решения системы с вырожденной матрицей целесообразно [1, 7]
искать нормальное решение задачи, то есть решение, обладающее минимальной
нормой. Это решение принадлежит пространству, ортогональному ядру оператора M.
В случае единственного собственного вектора матрицы М, соответствующего
нулевому собственному значению, множество решений системы представляет собой
прямую в гиперпространстве, параллельную вектору, порождающему ядро оператора
М.
При нахождении
ядра оператора M используем два подхода:
1)
Для построения матрицы системы, дающей единственное решение (такая матрица
нужна, если не удается получить какое-либо из решений системы из-за ее плохой
обусловленности), к системе из N уравнений MA = f добавим строчку
(A, A0) = 0 (условие ортогональности решения ядру
оператора M, норма A0 здесь не играет роли, примем ее равной
единице), в результате чего получаем неквадратную матрицу M0,
содержащую N столбцов и (N+1) строк. Для приведения матрицы, дающей
единственное нормальное решение, к квадратному виду размером N*N домножим ее на
транспонированную матрицу M0T [22] и получим нормальную
(в терминах [22]) систему M0TM0A = M0Tf
или (MTM + A0A0T)A
= MTf c симметричной квадратной матрицей размером N*N. Но
данная система обладает сильнозаполненной матрицей, что может усложнить ее
решение используемыми итерационными методами.
2)
В ряде случаев удается получить какое-либо из решений системы MA = f
(обозначим это решение A*). Тогда для построения нормального решения
проектируем полученное решение на пространство, ортогональное ядру оператора M,
домножением на проекционную матрицу (E - A0A0T),
A = (E - A0A0T)A*
(E – матрица c единичной
диагональю, здесь ||A0|| должна быть единичной). Такая
проекция является единственным решением нормальной системы (MTM + A0A0T)A
= MTf , то есть после подстановки этого решения в систему,
учитывая, что M A0 = 0 и A0TA0
= 1, получим:
(MTM + A0A0T)
(E – A0A0T)A* = (MTM
+ A0A0T – MTM A0A0T
– A0A0TA0A0T)A*
= (MTM + A0A0T – MT·0·A0T
– A0·1·A0T)A* = MTM
A* = MTf.
В случае m
собственных векторов, соответствующих нулевому собственному значению матрицы M
, для получения матрицы M0 к системе добавляется m строчек (A,
Aj) = 0, где j - номер собственного вектора (j=1,m). Тогда нормальная матрица M0TM0
примет вид (MTM + ). Для получения проекции полученного решения A* на
пространство, ортогональное ядру оператора M, последовательно домножим A*
на проекционные матрицы (E – AjAjT),
тогда проекционная матрица принимает вид
). Для получения проекции полученного решения A* на
пространство, ортогональное ядру оператора M, последовательно домножим A*
на проекционные матрицы (E – AjAjT),
тогда проекционная матрица принимает вид 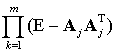 .
.
Для
получения матрицы менее сложного вида, дающей нормальное решение, рассмотрим
систему с матрицей M0 (неквадратная матрица размером N*(N+m), полученная после добавления в систему строчек (A,
A j) = 0, j = 1,m). Домножим систему M0A = f0
на матрицу E0T, (здесь E0 - матрица размером N*(N+m), составленная из матрицы с единичной диагональю (E) с добавленными строчками (A, A j)).
Тогда получим систему E0T M0A = E0T
f0 или (M +  )A = f с симметричной квадратной матрицей (если
M - симметрична).
)A = f с симметричной квадратной матрицей (если
M - симметрична).
Пусть
у матрицы M нулевому собственному значению соответствует несколько собственных
векторов. Если у M имеется m таких
собственных векторов, то после добавления (m – k) строчек и преобразования у матрицы (M + 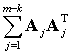 ) будет k собственных векторов, соответствующих нулевому
собственному значению. Тогда при поиске всех векторов, определяющих ядро
разностного оператора M, можно
использовать последовательное добавление к матрице слагаемых AjAjT. В результате, если А -
нормальное решение системы MA = f, то (M +
) будет k собственных векторов, соответствующих нулевому
собственному значению. Тогда при поиске всех векторов, определяющих ядро
разностного оператора M, можно
использовать последовательное добавление к матрице слагаемых AjAjT. В результате, если А -
нормальное решение системы MA = f, то (M +  )A = MA = f (это следует из
ортогональности решения А всем собственным векторам матрицы M). Если у матрицы M нулевое собственное значение
кратное и ему соответствуют вектора Ai, тогда для матрицы M нулевому собственному значению
соответствует любая линейная комбинация векторов Ai, а для матриц (M + AjAjT)
и (MTM + AjAjT)
нулевому собственному значению соответствует только линейная комбинация
векторов, ортогональная вектору Aj
)A = MA = f (это следует из
ортогональности решения А всем собственным векторам матрицы M). Если у матрицы M нулевое собственное значение
кратное и ему соответствуют вектора Ai, тогда для матрицы M нулевому собственному значению
соответствует любая линейная комбинация векторов Ai, а для матриц (M + AjAjT)
и (MTM + AjAjT)
нулевому собственному значению соответствует только линейная комбинация
векторов, ортогональная вектору Aj
Исследуем
применение предложенных методов к расчету нестационарной задачи.
Для решения системы уравнений Максвелла
при переходе с одного временного слоя на другой используются внешние и
внутренние итерации [1]. На каждой внутренней итерации методом сопряженных
градиентов [10 – 13] решается система линейных алгебраических уравнений MA =
f с симметричной матрицей. При этом слагаемые, связанные с конвективным
переносом, берутся с предыдущей внешней итерации и записываются в правую часть
системы f. Внешние итерации позволяют учесть конвективные слагаемые и
улучшить точность решения. На внешней итерации с учетом предыдущего приближения
A вычисляются новая скорость, новое приближение A (с учетом
конвективных слагаемых) и правая часть системы для следующей внутренней
итерации [1].
Для решения задачи в области с двумя
компонентами связности (рис. 3.1) вычислим минимальное собственное значение
матрицы М (в данной задаче рассмотрим сетку c неравномерным шагом по пространству): lmin = 7.08·10-18, ||MA0 - lA0|| = 6.12·10-11, ||A0||
= 1.
Невязка решения системы уравнений
Максвелла методом сопряженных градиентов на первой внешней итерации: ||MA*
- f|| = 9.981602·10-5 (A* - решение системы уравнений
Максвелла, ||A*|| = 33.30), (A*, A0) = - 1.967
, то есть полученное решение не является нормальным.
Строим проекцию A = (E - A0A0T)A*,
тогда (A, A0) = 3.54·10-15, невязка ||MA
- f|| = 9.981601·10-5, то есть нормальное решение является
решением системы.
На следующей (последней) внешней
итерации: ||MA* - f|| = 8.617·10-8, (A*, A0)
= - 2.08·10-7 , (A, A0) = - 2.03·10-14,
||MA - f|| = 8.617·10-8. То есть при использовании
проектирования на каждой внешней итерацией точность решения улучшается, а
решение приближается к нормальному.
Рассмотрим пример m-связной границы
g12. Предположим, что в конфигурации
рис. 3.1 есть (m – 1) внешних рельсов. Тогда в задаче о разности решений (3.1)
найдем несколько линейно независимых векторов, принадлежащих ядру разностного
оператора задачи. То есть рассмотрим систему функций fi [20], принимающих единичное значения поочередно на i-й
части границы g12 (i-м
рельсе).
|
|
|
Рис. 3.3. Расчетная область. 1 - рельс, 2 - якорь. |
Получим
решение задачи (3.1), (3.2) для границы g12 с тремя
компонентами связности (m = 3) рис. 3.3 (к области рис. 3.1 прибавим еще один
рельс, в реальности возможны и другие конструкции с многосвязными границами g12). Пусть f1 принимает
единичное значение на втором (по направлению оси z) рельсе (на остальной части границы g12 нулевое значение), f2 принимает
единичное значение на третьем рельсе.
Обозначим
А m1 = - grad f1 и А
m2 = - grad f2 . При
единичных нормах векторов А m1 и А m2 ( ||А
m1|| = ||А
m2|| = 1) ||M
А m1|| =
7.375·10-15, ||M А m2|| = 7.184·10-15, (А
m1, А
m2) = -
0.204, то есть векторы Аm1 и А
m2 линейно
независимы и являются собственными векторами матрицы M.
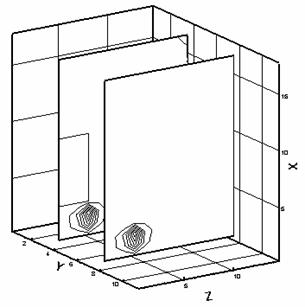
Распределения компонентов векторов Аm1 и Аm2
представлены на рис. 3.4.
Найдем
методами [15] один из собственных векторов матрицы М, соответствующих нулевому
собственному значению (с невязкой не превосходящей 10-15).
Обозначим этот вектор А m3.
Распределения компонентов вектора Аm3 представлены на рис. 3.5.
Рассмотрим вопрос о линейной
зависимости векторов Аm1, Аm2 и Аm3,
для чего проведем их ортогонализацию [22]. Пусть (||А m1|| = ||А
m2|| = ||А
m3|| = 1),
тогда после ортогонализации и нормирования векторов Аm1, Аm2
спроектируем вектор А m3 на пространство, ортогональное
векторам Аm1 орт., Аm2 орт. и получим ||Пр.
А m3||
=7.143·10-13. То есть вектор Аm3 есть линейная
комбинация векторов Аm1 и Аm2.
|
а |
в |
|
б |
г |
|
Рис. 3.4. Распределение компонентов векторов Аm1и Аm2 в рассматриваемой области: a – x-компонент Am1, б – z - компонент Am1 , в – x - компонент Am2, г – z - компонент Am2 (по осям отложены номера ячеек пространственной сетки). |
|
Заключение
Построены
новые алгоритмы для численного моделирования процессов, происходящих в областях
с изменяющимися границами проводников и диэлектриков. Предложены методы
улучшения устойчивости решения трехмерной задачи для квазистационарного
приближения уравнений Максвелла в случае высокотемпературного электрического
контакта. Построен алгоритм замены проводящих ячеек при превышении температуры
кипения диэлектрическими с соответствующей перестройкой логических массивов,
используемых для описания расчетной области и разностных схем, соответствующих
дифференциальным операторам.
|
а |
В |
|
Рис. 3.5. Распределение компонентов вектора Аm3 в рассматриваемой области: a – x-компонент Am3, б – z - компонент Am3 (по осям отложены номера ячеек пространственной сетки). |
|
Рассмотрен
вопрос об устойчивости решения для различных способов моделирования испарения.
Исследована обусловленность системы линейных алгебраических уравнений,
получаемых при разностной аппроксимации уравнений Максвелла в двумерном и
трехмерном случаях. Получены границы спектра разностного оператора для
различных способов моделирования. Из полученных результатов видно, что перестроение
разностных схем при испарении материала позволяет улучшить обусловленность
решаемой системы на несколько порядков по сравнению с ранее используемым
вариантом с "фоновой" электропроводностью. Предлагаемый алгоритм
позволяет получить нормальное решение задачи с нулевой "фоновой"
электропроводностью. Показано, что при исследовании процессов в ускорителях
предпочтительной является модель с перестроением разностных схем и описателей
границ при испарении материала проводника. Предлагаемый алгоритм позволяет избежать
эффектов, связанных с отнесением тепла к ячейкам диэлектрика (с
"фоновой" электропроводностью). Алгоритм обобщается и на другие
случаи изменения границ.
Разработаны
методы получения единственного квазистационарного решения системы уравнений
Максвелла в трехмерной области с многосвязными диэлектрическими и проводящими
подобластями. Для двусвязной и трехсвязной областей построены векторы,
определяющие подпространство, соответствующее ядру оператора квазистационарного
приближения уравнений Максвелла. При этом использовалось представление разности
решений уравнений Максвелла в виде градиента потенциала. Показано совпадение в
двусвязной области градиента потенциала с собственным вектором, соответствующим
минимальному собственному значению матрицы М, полученным численными методами.
Для построения единственного решения уравнений Максвелла представлены алгоритмы
получения нормального решения задачи, принадлежащего пространству,
ортогональному ядру оператора задачи (в m - связной области). Построена
преобразованная матрица, дающая единственное нормальное решение системы
уравнений Максвелла. В задачах, в которых удается получить какое-либо из
множества неединственных решений системы уравнений Максвелла, для нахождения
нормального решения построена проекция полученного решения на пространство,
ортогональное ядру разностного оператора M. Показано, что такая проекция
является нормальным решением системы. Предложенные алгоритмы можно применять
для нахождения нормального решения и в других случаях вырожденной матрицы M.
Алгоритмы решения системы уравнений Максвелла в многосвязной области,
позволяющие получить единственное решение, доведены до программной реализации.
Получены результаты расчета электромагнитных полей по построенным алгоритмам в
многосвязных областях в нестационарном случае.
Литература
1. Галанин М.П., Попов Ю.П. Квазистационарные электромагнитные поля в неоднородных средах: Математическое моделирование. М.: Наука, Физматлит, 1995, 320 с.
2. Материалы I Всесоюзного семинара по динамике сильноточного дугового разряда в магнитном поле (Новосибирск, 10-13 апреля 1990 г.). // Под ред. Жукова М.Ф. Новосибирск. Изд. Инст. Теплофизики СО АН СССР. 1990. 350 с.
3. Материалы II Всесоюзного семинара по динамике сильноточного дугового разряда в магнитном поле (Новосибирск, 4-6 декабря 1991г.). // Под ред. Накорякова В.Е. Новосибирск. Изд. Инст. Теплофизики СО РАН. 1992. 367 с.
4. Галанин М.П., Лотоцкий А.П., Попов Ю.П., Храмцовский С.С. Численное моделирование пространственно трехмерных явлений при электромагнитном ускорении проводящих макротел // Мат. моделирование. 1999. Т. 11, № 8. С. 3 - 22.
5. Галанин М.П. Компьютерное моделирование в задачах конвертирования электромагнитной и кинетической энергии. Задачи и модели. // Информационные технологии и вычислительные системы. 2002. № 4. С. 109 - 123.
6. Галанин М.П. Компьютерное моделирование в задачах конвертирования электромагнитной и кинетической энергии. Решение задач. // Информационные технологии и вычислительные системы. 2003. № 1 – 2. С. 112 - 127.
7. Галанин М.П., Храмцовский С.С. Организация расчета трехмерных квазистационарных электромагнитных полей в областях со сложной геометрией проводников и диэлектриков. // Препр. ИПМ им. М.В. Келдыша РАН. 1999. № 42. 18 с.
8. Галанин М.П., Лотоцкий А.П., Уразов С.С., Халимуллин Ю.А. Математическое моделирование эрозии металлических контактов в рельсотронном ускорителе // Препр. ИПМ им. М.В. Келдыша РАН. 2003. № 79. 28 с.
9. Галанин М.П., Лотоцкий А.П., Уразов С.С. Моделирование эрозии металлического контакта в ускорителе типа рельсотрон // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2004. № 4(15). С. 81-97.
10. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. М.: Наука. 1978. 592 с.
11. Kershaw D.S. The incomplete Cholessky -
Conjugate Gradient Method for the iterative solution of system of a linear
equations // J. Comput. Phys. 1978. Vol. 26. P.p. 43 - 65.
12. Джордж А., Лю Дж. Численное решение больших разреженных систем уравнений. М.: Мир. 1984. 333 с.
13. Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука. 1984. 320 с.
14. Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. М: Едиториал УРСС. 2004. 424 с.
15. Фадеев Д.К., Фадеева В.Н. Вычислительные методы линейной алгебры. М.: Физматгиз. 1963. 736 с.
16. Беляков Ю.И., Лотоцкий А.П., Савичев В.В., Халимуллин Ю.А. Исследование эрозии металлических контактов в рельсотронном ускорителе // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 1999. № 2. С. 46 - 60.
17. Галанин М.П., Уразов С.С.
Численное моделирование качественных особенностей распределений трехмерных
полей в неоднородных подобластях электродинамического ускорителя // Препр. ИПМ
им. М.В. Келдыша РАН. 2004. №27.
30 с.
18. Price
J.H., Yun H.D. et al. Discarding Armature and Barrel Optimization for a
Cannon Caliber Electromagnetic Launcher System // IEEE Transactions on
Magnetics. 1995. V. 31, N. 1. P.p. 225-230.
19. Никольский В.В. Вариационные методы для внутренних задач электродинамики. М.: Наука. 1967. 460 с.
20. Быховский Э.Б., Смирнов Н.В. Об ортогональном разложении пространства вектор-функций, квадратично суммируемых по заданной области, и операторах векторного анализа // Тр. МИАН СССР. - 1960. Т.59. С. 5 - 36.
21. Темам Р. Уравнения Навье-Стокса. Теория и численный анализ. М.: Мир. 1981. 408 c.
22. Канатников А.Н., Крищенко А.П. Линейная алгебра. М.: Изд-во МГТУ им Н.Э.Баумана. 2002. 336 с.