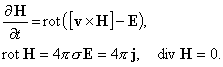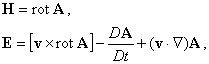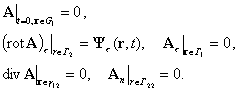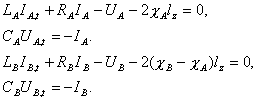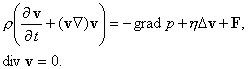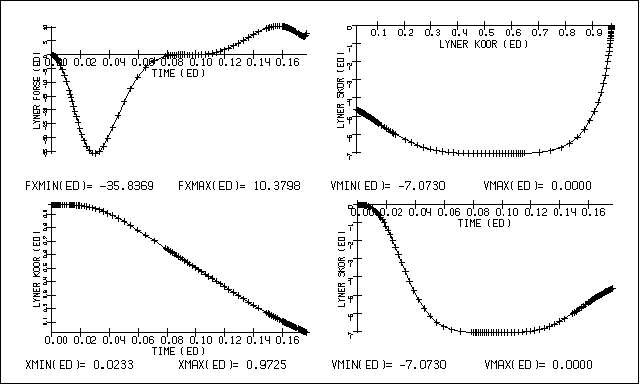Математическое моделирование электромагнитного ускорения проводящей пластины в компрессоре
потока
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Б |
|
Рис. 1.1. Эскиз основных деталей генератора тока и поперечное сечение собранного устройства: А - ускоряемая плоская лента с натяжным устройством и виток индуктора магнитного поля; Б - поперечное сечение генератора в собранном виде, указано направление протекания токов, направление ускорения и конфигурация ускоряющего магнитного поля. |
|
Как было
показано ранее [3], моделирование электродинамического разгона плоской (и
абсолютно жесткой) пластины лайнера имеет неплохое соответствие с результатами
экспериментов. Во всяком случае, в численных расчетах по простым моделям с
сосредоточенными параметрами (с учетом правильной зависимости поведения
индуктивности на базе разгона) удается определить величину скорости. Точность
расчетов скорости составляет 100 м/с при ее абсолютной величине V~ 1 км/с, а
время схождения пластин можно определить с точностью до 10 мкс при времени
ускорения 100-120 мкс для лайнеров с различной шириной (h = 21 -
Анализу
этого вопроса посвящена настоящая работа, к моменту написания которой уже
накоплен значительный объем данных. С точки зрения только что высказанного
желательно, чтобы амплитуда деформации пластины не превышала ее толщины. Однако
величина этой амплитуды будет определяться особенностями физического механизма
ускорения или, что более вероятно, неустойчивостями данного объекта пластины
или ленты, имеющего конечные размеры. Появление таких неустойчивостей обнаружено
экспериментально.
Работа выполнена
при частичной финансовой поддержке РФФИ (проект № 05-02-17737).
2. Экспериментальные результаты
|
|
|
|
|
|
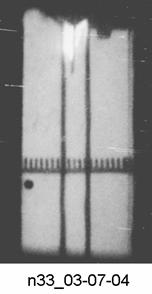
119 мкс |
127 мкс |
134 мкс |
137 мкс |
Рис.2.1. Кадры теневой киносъемки лайнера, разогнанного до V = 1 км/с.
Отметим,
что экспериментальные результаты, приведенные разработчиками МК в
опубликованных работах, например, в [3], показали удовлетворительное поведение
ленты при ускоряющих токах, близких к рабочим режимам 2.5-3 МА. Более того,
приведенные на рис. 2.1 фотографии теневой съемки лайнера показывают, что
профиль лайнера вплоть до момента сжатия магнитного потока остается
относительно тонким и его видимая толщина по оценке не превышает
Однако в
этой же работе [3] приведены данные об эффективной ширине лайнера, изменяющейся
во время ускорения. Эти данные получены по измерению «следов» пластины лайнера,
падающей на клиновые скосы, расположенные в зоне закрепления концов ленты (см.
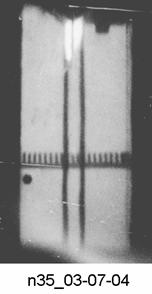
рис. 1.1Б). Фотография следов на развертке клиньев показана на рис. 2.2.
На
фотографии ясно видны границы деформируемой ленты в процессе ускорения, которые
заметно приближаются к средней плоскости витка по мере движения ленты.

Рис.2.2. Следы границы ленты, падающей на контактную наклонную поверхность в торце ускорителя с «пассивной» и «активной» схемами включения контура.
Как видно,
характер поведения пластины лайнера существенно отличен от простых
представлений ускорения проводящего листа с однородным распределением плотности
тока [4]. Хорошо известно [5], что распределение тока неоднородно по пластине с
конечной шириной. Подробно распределение токов в таких условиях исследовано в
[6]. В этом же убеждают результаты вычисления индуктивности ускорителя МК [3,
7], в которых отмечена резкая концентрация плотности тока на краях ленточного
лайнера. Однако вопрос о реальной картине деформации пластинчатого лайнера во
время ускорения до самого последнего времени оставался открытым.
В связи с
этим проведен специальный эксперимент, позволивший зафиксировать, по крайней
мере, начальную стадию процесса движения плоского лайнера. Для детальной
визуализации поведения ленты разработана схема скоростной фотографии,
приведенная на рис. 2.3. Для простоты проведения эксперимента применена схема с
«пассивным» короткозамкнутым лайнером при ограниченной величине ускоряющего
тока I = 2 МА.
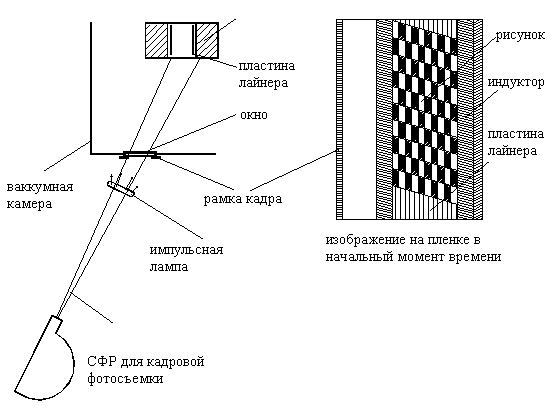
Рис. 2.3. Схема фотографирования плоскости лайнера
Скоростная
съемка (в отраженном свете) велась под углом к поверхности пластины, на
внутреннюю часть которой нанесен рисунок для идентификации участков
поверхности. Угол луча зрения составлял примерно 30 градусов к плоскости
симметрии витка и поверхности. На рис. 2.4 показаны характерные кадры
полученного фильма.
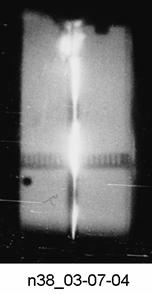
Видно, что
вначале (87 мкс) край ленты разворачивается, увеличивая угол к лучу зрения и
источнику света, а на следующем кадре (131 мкс) изображение края (нарисованных
клеток) становится уже. Либо имеет место разворот в обратном направлении, либо
край продолжает разворот внутрь зазора. Полный прогиб пластины на всем пролете
не превышал
3. Физическая модель
На рис. 3.1
приведена схема электромагнитного ускорителя проводящего лайнера. Показана одна
четверть сечения узла ускорения при z = const, аналогичного рис. 1.1 Б. Сечение узла ускорения при y = const
приведено на рис. 3.2. Показано присоединение соответствующих электрических
цепей индуктора и лайнера, которые могут коммутировать между собой. Здесь и
далее лайнер, индуктор и относящиеся к ним элементы и величины помечены соответствующими
индексами A и B.
|
|
|
|
6 мкс |
87 мкс |
|
|
|
|
131 мкс |
193 мкс |
Рис. 2.4. СФР-грамма съемки поверхности лайнера в процессе ускорения.
В начальный
момент времени конденсатор СВ в цепи индуктора заряжен до некоторого
начального напряжения. После замыкания цепи контактами КВ по
индуктору (и лайнеру) начинает течь разрядный ток. Созданное им в зазоре
ускорителя магнитное поле взаимодействует с протекающим по лайнеру током,
ускоряя лайнер вдоль оси х. В некоторый момент времени (вероятно, отличный от
момента начала ускорения) ключом КА замыкается цепь контура лайнера
с заряженным конденсатором СА. Соответствующий ток протекает по
лайнеру и создает внутри полости лайнера дополнительное магнитное поле.
Ускорившись, лайнер сжимает это поле, которое окончательно и выводится из системы
в виде импульса тока во внешней цепи лайнера. Требуется по начальным и
граничным данным, физическим характеристикам сред рассчитать их положение и
скорость, напряженность и давление магнитных полей в зазорах между пластинами ускорителя,
профиль их поверхностей, токи и напряжения во внешних электрических цепях.
Задача
рассматривается в пространственно двумерном приближении. Все величины считаются
зависящими только от координат x и y. В уравнениях производные по z
отсутствуют. Это означает формально бесконечную протяженность ускорительной системы
в данном направлении. При этом в модели учитывается «эффективная» длина системы
в z – направлении, в значительной степени определяющая процесс перекачки
энергии из внешней электрической цепи в кинетическую энергию лайнера.
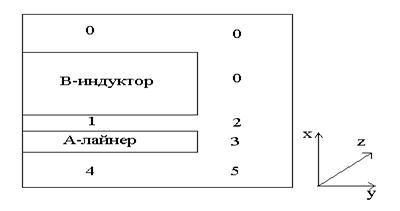
Рис. 3.1. Характерная схема
четверти сечения плоскостью z = const пространственной области, в
которой решается задача.
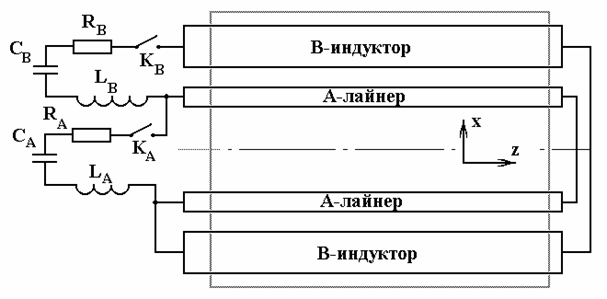
Рис. 3.2. Характерная схема сечения плоскостью y = const пространственной области, в которой решается задача (в рамке) и электротехнические цепи устройства.
Соответственно
у скоростей ненулевыми являются только x и y компоненты. Аналогично отличные от
нуля x и y компоненты имеет напряженность магнитного поля. Таким образом, эти
ненулевые векторы лежат в плоскости рис. 3.1. Векторы напряженности
электрического поля и плотности тока имеют по одной ненулевой z компоненте и
направлены перпендикулярно плоскости рис. 3.1.
Параметры
внешних электрических цепей предполагаются сосредоточенными, так что для
описания цепей можно применять уравнения Кирхгоффа [8-11]. Уравнения внешних
цепей обязаны быть выбраны в форме, которая бы обеспечивала сохранение энергии
в системе. Кроме того, математическая модель должна обеспечивать протекание
полного тока цепи через заданные сечения.
Индуктор предполагается
неподвижным, т.е. сила реакции крепежа соответствует действующей на индуктор
силе Лоренца и компенсирует ее. Его форма также является неизменной. Материал
индуктора является проводником.
На текущий момент существуют две модели, описывающие
материал лайнера: несжимаемая жидкость и упругое тело. В данной работе
сопоставляются результаты расчетов, выполненных с использованием этих двух
приближений. Далее приведены качественные (характер деформации лайнера) и
количественные (амплитудные значения и графики сосредоточенных величин)
характеристики процесса ускорения для различных наборов параметров (геометрия и
свойства материала лайнера).
4. Приближение лайнера электропроводной вязкой несжимаемой жидкостью
4.1.
Описание модели
4.1.1. Электродинамическая часть
Электродинамическая часть модели основана на системе
уравнений Максвелла в квазистационарном приближении (см. [9-11]):
|
|
(4.1) |
Здесь E и H – напряженности
электрического (в системе координат, где вещество покоится) и магнитного полей,
j – плотность тока, r = {x, y, z} – радиус-вектор, t – время, v – скорость
движения вещества (в данном случае движется лишь лайнер, скорость остальных
частиц в данной области равна нулю).
Для решения
задачи в рассматриваемой пространственной области вводим лагранжевые переменные
- начальные координаты точек данной области. Тогда D/Dt = ¶/¶t +
(v,Ñ), где ¶/¶t –
производная при фиксированных эйлеровых переменных, D/Dt – при фиксированных лагранжевых координатах, v – скорость движения частиц области.
После
введения векторного потенциала A задача
для определения полей внутри области принимает вид [9,10]:
|
|
(4.2) |
где А есть решение задачи:
|
|
(4.3) |
Здесь
учтена пространственная неоднородность параметров задачи: q(s) = 0 в G1 и q(s) = 1 в G2. В
(4.3) и далее используем индексы t для обозначения
тангенциальной (по отношению к границе) компоненты вектора, n – нормальной
компоненты. G = G1 È G2, G –
рассматриваемая область, G1 = {r
Î G: s > 0}, G2 = {r Î G: s = 0}, ¶G1 и ¶G2 – границы G1 и G2
соответственно, ¶G12 = ¶G1 ![]() ¶G2, Г1 – часть ¶G, на которой задано условие для
¶G2, Г1 – часть ¶G, на которой задано условие для ![]() , Г2 – часть ¶G, на которой задано условие
для Ht (
, Г2 – часть ¶G, на которой задано условие
для Ht (![]() – известная вектор-функция), ¶G = Г1 È Г2, Г12
= Г1
– известная вектор-функция), ¶G = Г1 È Г2, Г12
= Г1 ![]() ¶G2, g12 = ¶G12 È Г12.
¶G2, g12 = ¶G12 È Г12.
Вследствие
двумерности задачи и взаиморасположения проводников с током E = {0, 0, Ez},
H = {Hx, Hy,
0}, все производные по z в системе
(4.1) равны нулю, v = {vx, vy, 0}. Поэтому уравнение (4.3) преобразуется в
следующее:
|
|
(4.4) |
Нас
интересует решение (4.1) – (4.4), удовлетворяющее заданным начальным и
граничным условиям, а также обеспечивающее протекание заданного тока по каждому
из (вообще говоря, N)
проводников:
|
|
(4.5) |
Всем
необходимым условиям на границе раздела сред можно удовлетворить, если
допустить скачок Ez при
переходе через ![]() на величину ck(t), подлежащую определению. В итоге имеем:
на величину ck(t), подлежащую определению. В итоге имеем:
|
|
(4.6) |
Величина ck играет роль плотности
поверхностных магнитных токов. В рассматриваемом случае A = {0, 0, A}
ограниченность H сразу ведет к
условию непрерывности A при переходе
через ![]() . Отсюда следует, что для обеспечения скачка (4.6) необходимо
взять
. Отсюда следует, что для обеспечения скачка (4.6) необходимо
взять
Ez = ![]() внутри Sk.
внутри Sk.
А последнее условие (4.6) дает
|
|
(4.7) |
В результате вместо системы (4.4) имеем:
|
|
(4.8) |
|
DA = 0 в G2, |
|
|
с условиями |
(4.9) |
Параметры
внешних электрических цепей предполагаются сосредоточенными, так что для их
описания применены уравнения Кирхгоффа в следующем виде:
|
|
(4.10) |
Здесь
L, R, C, соответственно, -
индуктивность, сопротивление и емкость в цепи, I и U – сила тока и
напряжение на обкладках конденсатора. Величина χ дает скачок напряженности электрического поля, фигурирующий
в (4.6) - (4.7). В качестве Ik
в (4.7) стоят значения токов, протекающих по определенному проводнику. По
индуктору это IB, а по
лайнеру - (IA – IB) в соответствии с
электрической схемой. Индексами A и B помечены величины, относящиеся к лайнеру
и индуктору соответственно. Коэффициент 2 в уравнениях цепей появляется из-за
существования прямых и обратных направляющих для протекающего тока, lz - эффективная длина
системы в направлении оси z.
4.1.2. Гидродинамическая часть
Для
описания движения элементов сплошной среды в соответствии с принятой физической
моделью используем систему уравнений Навье-Стокса [12-15]:
|
|
(4.11) |
Здесь
ρ – плотность вещества, p – гидродинамическое давление, η = ρ ν – коэффициент динамической вязкости, ν – коэффициент кинематической
вязкости, v – вектор скорости,
F – вектор плотности силы Лоренца, F
= [j x H].
Согласно
сделанным предположениям, в данной системе происходит движение только лайнера.
Его границы являются свободными. Это дает следующие условия на границах лайнера
[15;13, с. 398]:
|
|
(4.12) |
(«равенство нулю нормальной
и смешанной компонент вязкого тензора давлений»). Здесь ![]() - компоненты тензора
вязких напряжений [12,13], n с
соответствующими индексами – компоненты вектора внешней нормали.
- компоненты тензора
вязких напряжений [12,13], n с
соответствующими индексами – компоненты вектора внешней нормали.
4.1.3. Энергетические соотношения
Протекание
электрического тока и движение вязкой жидкости сопровождаются выделением тепла,
которое распределяется по веществу с помощью процессов кинематического переноса
и теплопроводности. В качестве уравнения энергии в данном случае используется
уравнение теплопроводности следующего вида:
|
|
(4.13) |
Здесь
cv – удельная теплоемкость
вещества, κ – теплопроводность, ![]() – мощность выделения
энергии, включающая в себя джоулево тепло и источник тепла за счет вязкости, T - температура среды. В начальный
момент времени температура вещества считается заданной, на границах лайнера и
индуктора тепловой поток равен нулю.
– мощность выделения
энергии, включающая в себя джоулево тепло и источник тепла за счет вязкости, T - температура среды. В начальный
момент времени температура вещества считается заданной, на границах лайнера и
индуктора тепловой поток равен нулю.
4.2.
Физические параметры
Все расчеты проводятся в безразмерном виде. Для получения
размерной величины f
по безразмерной f* ее необходимо умножить на масштабный коэффициент f0. Соответственно для
получения безразмерной величины, задаваемой в программе, размерную величину
нужно поделить на масштаб f0. Всюду далее
звездочки у безразмерных величин опущены. Ниже даны масштабные коэффициенты для
основных физических величин.
x0 =
t0= 10-3 сек = 1 мс.
v0 = x0/ t0 = 104
см/сек = 0.1 км/сек = 100 м/сек.
ρ0 = 4 г/см3.
m0 =
T0 = 200 град К.
I0 = 2 106 а = 2 ма.
U0
= 20 в.
R0
= 10-5 ом.
C0 = 102 ф.
L0 = 10-8 гн.
F0 = 4 105 н.
Приведем физические параметры задачи, общие для всех
вариантов расчетов.
Начальная температура T = 1.45. Длина ускоряемого лайнера
по направлению z - lz = 8.0. Начальная скорость лайнера равна нулю.
Далее приведены размеры конструкции в соответствии с рис.
3.1 – 3.2. Высота индуктора равна 2.0, его полуширина – 1.25. Высота лайнера
равна 0.015. Расстояние между лайнером и индуктором по высоте в начальный
момент времени равно 0.02. Начальная высота нижней кромки лайнера равна 0.965.
Все расчеты проводятся для одной из двух геометрических
конфигураций, отличающихся полушириной лайнера: 1.05 ("узкий" лайнер)
либо 1.35 ("широкий" лайнер); для каждого варианта полуширина
указывается отдельно.
При расчете электромагнитных полей считается, что на
расстоянии 0.5 от краев лайнера или индуктора (в начальный момент времени)
находится идеально проводящий экран (в характере его электропроводности
возможны варианты).
Параметры материала индуктора взяты равными
соответствующим величинам стали: плотность ρ = 1.95, теплоемкость cv
= 9.21, теплопроводность κ = 1.998 10-5, электропроводность
σ = 52.9 при
Параметры материала лайнера взяты равными соответствующим
величинам алюминия: плотность ρ = 0.63525, теплоемкость cv =
18.037, теплопроводность κ = 1.035 10-4, электропроводность
σ = 40.66 при
Для всех материалов электропроводность взята в виде
функции температуры вида σ = σs / (1 + ασ T)
c соответствующими параметрами из [16].
Параметры электрической цепи индуктора составили:
индуктивность LB = 20.0, емкость СB = 3.1 10–5,
сопротивление RB = 1.2 102. Частота электромагнитных
колебаний в свободной цепи с такими параметрами ώ = 40.16, коэффициент
затухания ά = 3 (см. [11]). Начальное напряжение на обкладках конденсатора
взято равным 1800.0, начальный ток – нулевой. Во всех трех расчетах момент
замыкания цепи лайнера t0 = 106, относительно
прочих параметров это равнозначно тому, что цепь лайнера никогда не замыкается.
Число точек разностной сетки во всей пространственной
области составило 14063, при этом получено 27597 соответствующих треугольников.
Аналогичные числа для области лайнера – 1991/2555 и 3802/4902 (полуширина
лайнера 1.05/1.35).
4.3.
Выполненные расчеты
Ниже представлены 3 варианта расчета задачи, отличающиеся
некоторыми начальными параметрами.
4.3.1. Вариант 1
Полуширина лайнера 1.05 - на 0.2 меньше, чем у индуктора,
величина кинематической вязкости ![]() . Расчет продолжался до момента времени t = 0.1304, в который
скорость центра масс лайнера составила V = -7.945, координата центра масс x =
0.0598.
. Расчет продолжался до момента времени t = 0.1304, в который
скорость центра масс лайнера составила V = -7.945, координата центра масс x =
0.0598.
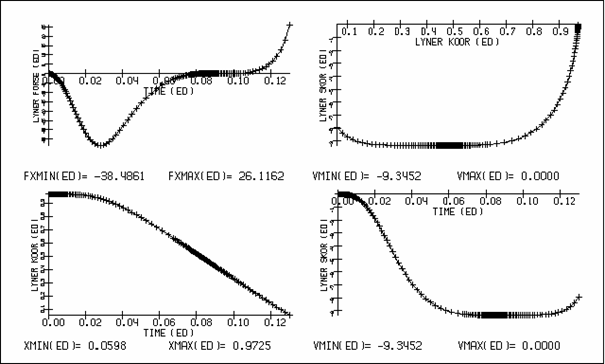
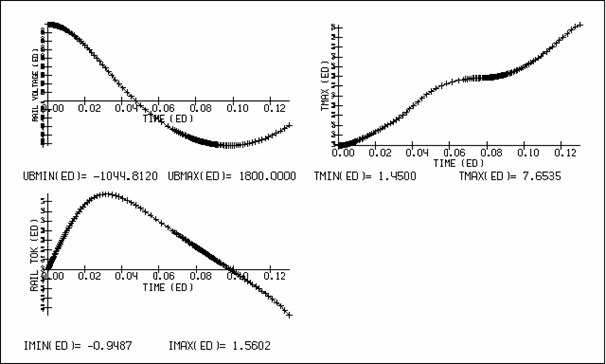
Максимальная (по модулю) величина скорости центра масс
лайнера за время ускорения составила V = -9.345, максимальная температура - T =
7.654, интегральная ускоряющая сила (в направлении x) изменялась от -38.49 до
26.12 (знак + соответствует торможению лайнера), ток в цепи индуктора изменялся
в пределах от -0.949 до 1.560, напряжение на обкладках конденсатора в цепи
индуктора менялось от -1044.81 до 1800.0. Динамику изменения сосредоточенных
величин можно проследить по графикам рис. 4.1.
К концу расчета форма лайнера искажается, он принимает
форму трапеции (отношение большего и меньшего основания - около 2.5). Правый
угол лайнера опережает центр. Рис. 4.2, 4.3 иллюстрируют эту ситуацию: в то
время как высота лайнера в центре (меньшее основание трапеции) остается
неизменной, правый край смещается к центру с соответствующим увеличением высоты
- чем ближе лайнер подлетает к нижней границе области, тем больше отношение
оснований трапеции. Данный эффект обусловлен переносом вещества с правого края
лайнера к центру - процессом, присущим всем вариантам расчетов с использованием
приближения вещества лайнера электропроводной жидкостью.
|
|
|
|
|
Рис. 4.1. Графики сосредоточенной информации для варианта 1. Справа налево, сверху вниз: интегральная сила от времени, скорость ц.м. лайнера от координаты ц.м. лайнера, координата ц.м. лайнера от времени, скорость ц.м. лайнера от времени, напряжение в цепи индуктора от времени, макс. температура в лайнере от времени, ток в цепи индуктора от времени. |
|
|
|
Рис. 4.2. Конечноэлементная сетка в области лайнера в момент времени t = 0.0943 |
|
|
|
Рис. 4.3. Конечноэлементная сетка в области лайнера в момент времени t = 0.1304 |
4.3.2. Вариант 2
Полуширина лайнера 1.35 - на 0.1 больше, чем у индуктора,
величина кинематической вязкости ![]() . Расчет продолжался до момента времени t = 0.1765, в который
скорость центра масс лайнера составила V = -4.639, координата центра масс x =
0.0233.
. Расчет продолжался до момента времени t = 0.1765, в который
скорость центра масс лайнера составила V = -4.639, координата центра масс x =
0.0233.
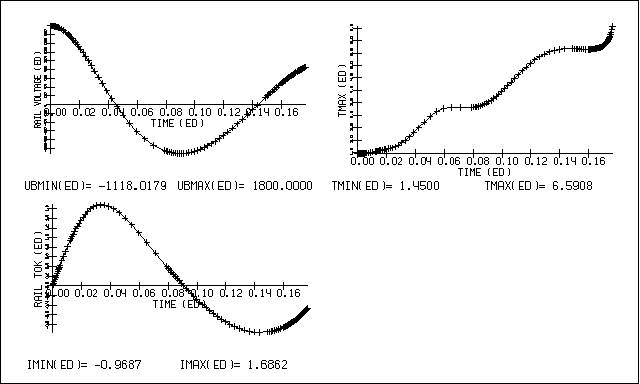
Максимальная (по модулю) величина скорости центра масс
лайнера за время ускорения составила V = -7.073, максимальная температура - T =
6.591, интегральная ускоряющая сила (в направлении x) изменялась от -35.84 до
10.38 (знак + соответствует торможению лайнера), ток в цепи индуктора изменялся
в пределах от -0.969 до 1.686, напряжение на обкладках конденсатора в цепи
индуктора менялось от -1118.02 до 1800.0. Динамику изменения сосредоточенных
величин можно проследить по графикам рис. 4.4.
|
|
|
|
|
Рис. 4.4. Графики сосредоточенной информации для варианта 2. Справа налево, сверху вниз: интегральная сила от времени, скорость ц.м. лайнера от координаты ц.м. лайнера, координата ц.м. лайнера от времени, скорость ц.м. лайнера от времени, напряжение в цепи индуктора от времени, макс. температура в лайнере от времени, ток в цепи индуктора от времени. |
Расчетная сетка в лайнере для трех различных моментов
времени показана на рис. 4.5-4.7. На них видно два основных отличия от
предыдущего случая. Во-первых, теперь лайнер выгибается в другую сторону.
Во-вторых, к моменту прекращения расчета лайнер принимает практически
горизонтальное положение (если рассматривать среднюю линию), последнее можно
объяснить тем, что расчет для "широкого" лайнера длился несколько
больше, чем расчет для "узкого" лайнера.
|
|
|
Рис. 4.5. Конечноэлементная сетка в области лайнера в момент времени t = 0.1479 |
|
|
|
Рис. 4.6. Конечноэлементная сетка в области лайнера в момент времени t = 0.1609 |
|
|
|
Рис. 4.7. Конечноэлементная сетка в области лайнера в момент времени t = 0.1761 |
4.3.3. Вариант 3
|
|
|
|
Рис. 4.8. Правый край лайнера, ν = 0.1, t = 0.0781 |
Рис. 4.9. Правый край лайнера, ν = 0.025, t = 0.0785 |
|
|
|
|
Рис. 4.10. Правый край лайнера, ν = 0.1, t = 0.1139 |
Рис. 4.11. Правый край лайнера, ν = 0.025, t = 0.1116 |
|
|
|
|
Рис. 4.12. Правый край лайнера, ν = 0.1, t = 0.1469 |
Рис. 4.13. Правый край лайнера, ν = 0.025, t = 0.1409 |
|
|
|
|
Рис. 4.14. Правый край лайнера, ν = 0.1, t = 0.1512 |
Рис. 4.15. Правый край лайнера, ν = 0.025, t = 0.1504 |
В данном варианте кинематическая вязкость уменьшена до ![]() . Это сделано, чтобы вызвать большие деформации лайнера (с
целью изучения их динамики). Расчет продолжался до момента времени t = 0.1504,
в который скорость центра масс лайнера составила V = -5.981, координата центра
масс x = 0.1598.
. Это сделано, чтобы вызвать большие деформации лайнера (с
целью изучения их динамики). Расчет продолжался до момента времени t = 0.1504,
в который скорость центра масс лайнера составила V = -5.981, координата центра
масс x = 0.1598.
Максимальная (по модулю) величина скорости центра масс
лайнера за время ускорения составила V = -7.086, максимальная температура - T =
5.582, интегральная ускоряющая сила (в направлении x) изменялась от -35.43 до
10.07 (знак + соответствует торможению лайнера), ток в цепи индуктора изменялся
в пределах от -0.959 до 1.675, напряжение на обкладках конденсатора в цепи
индуктора менялось от -1114.99 до 1800.0.
На рис. 4.8 - 4.15 сопоставлена динамика деформации
правого края для вариантов 2 и 3, отличающихся вязкостью (в целом, лайнеры
деформируются одинаково, основные отличия - на правом крае). Прослеживаются две
закономерности. Во-первых, большая высота правого края при тех же временах в
варианте 3 (вполне объяснимо: с уменьшением вязкости поведение материала
лайнера стремится к поведению газа, а не жидкости, в котором связи между
частицами намного слабее). Во-вторых, при вязкости ν = 0.025 на границе правого края укладывается в два раза
больше полуволн, чем при вязкости ν = 0.1 (особенно отчетливо видно на рис. 4.14 - 4.15).
5. Приближение лайнера электропроводным упругим телом
5.1.
Описание модели
В данной модели электродинамическая часть
описывается так же, как в приближении электропроводной вязкой жидкостью.
Принципиальным отличием является представление материала лайнера в форме
упругого электропроводного твердого тела. Этим вызваны изменения модели,
приведенные ниже.
Используемая математическая модель представляет
собой систему уравнений нелинейной теории упругости в перемещениях. При этом
описание упругих движений ведется в лагранжевых переменных. В качестве
начальной модели выбрана модель упругого тела с квадратичной зависимостью
упругой энергии от напряжений, но тензор деформации является нелинейным по
перемещениям. Используемая модель получена в соответствии с теорией [12-14]. Мы
непосредственно следуем [14].
Пусть
ρ и ρ0 – текущая и начальная плотность материала лайнера,
xi и ai – эйлеровые и лагранжевые переменные – координаты
частицы текущая и начальная, ui = xi - ai –
смещения, ![]() - скорость частицы (i
= 1, 2, 3 в общем случае, в нашем – до 2: x1 = x, x2 =
y). Производная по времени
- скорость частицы (i
= 1, 2, 3 в общем случае, в нашем – до 2: x1 = x, x2 =
y). Производная по времени ![]() является
субстанциональной производной – производной по времени вдоль траектории
движения частицы.
является
субстанциональной производной – производной по времени вдоль траектории
движения частицы.
Тогда
(всюду далее предполагается суммирование по повторяющимся индексам) тензор
деформаций и два его первых инварианта имеют вид:
![]() (5.1)
(5.1)
Уравнение
движения, записанное через эйлеровы переменные, включая эйлеровы производные и
эйлеров тензор напряжений σij, записывается в обычном виде:
![]() (5.2)
(5.2)
Здесь Fi
– соответствующая компонента силы Лоренца F = [j x H]. От уравнений движения
(5.2) в форме Эйлера перейдем к уравнениям в форме Лагранжа:
![]() (5.3)
(5.3)
При
преобразованиях существенно используется якобиан перехода от эйлеровых
координат к лагранжевым ![]() . В (5.3) Lij – лагранжев тензор напряжений. Он
связан с эйлеровым тензором следующим образом:
. В (5.3) Lij – лагранжев тензор напряжений. Он
связан с эйлеровым тензором следующим образом:
![]() (5.4)
(5.4)
Тензор
напряжений в форме Лагранжа следующим образом зависит от внутренней энергии U
(на единицу массы) упругого тела:
![]() (5.5)
(5.5)
Для
описания состояния упругого тела в качестве первого приближения возьмем следующую
модель состояния упругого тела:
 (5.6)
(5.6)
Тогда
выражение (5.5) дает:
![]() (5.7)
(5.7)
В
выражениях (5.6), (5.7) λ и μ – коэффициенты Ламе, β = (3 λ
+ 2 μ) αT, αT - коэффициент теплового
расширения, cγ – удельная теплоемкость при постоянной деформации.
Аналогично
получению уравнений движения имеем уравнение энергии в следующей форме:
![]() (5.8)
(5.8)
Использование
термодинамических соотношений в конце концов дает уравнение теплопроводности в
следующем виде:
![]() (5.9)
(5.9)
В правой
части (5.8), (5.9) стоит мощность джоулева нагрева.
Заметим,
что в правых частях уравнений движения (5.3) и теплопроводности (5.8), (5.9)
стоит сомножитель (якобиан преобразования координат) ![]() , который существенно облегчает интегрирование уравнений по
лагранжевым ячейкам при численных расчетах.
, который существенно облегчает интегрирование уравнений по
лагранжевым ячейкам при численных расчетах.
Согласно
сделанным предположениям, в данной системе происходит движение только лайнера.
Его границы, как и в предыдущих работах, являются свободными.
Выписанная
модель является нелинейной. Нелинейность связана с конечностью перемещений.
Предположение их малости даст уравнения обычной линейной теории упругости.
5.2.
Физические параметры
В связи с переходом к модели упругого тела возникают три
новых параметра, определяющие упругие свойства материала лайнера: коэффициенты
Ламэ и коэффициент теплового расширения. Их значения таковы: λ = 1097.5,
μ = 672.75, β = 21.6. Им соответствуют скорости распространения
продольных и поперечных упругих волн: 62.014 и 32.543 соответственно.
Замыкание цепи лайнера происходит в момент времени t0
= 6 10-2. Параметры электрической цепи лайнера составляют:
индуктивность LA = 2.5, емкость СA = 103, сопротивление
RA = 10-5. Частота электромагнитных колебаний в свободной
цепи с такими параметрами ώ = 0.02, коэффициент затухания ά = 2 10–6.
Начальное напряжение на обкладках конденсатора - нулевое, начальный ток –
нулевой.
5.3.
Выполненные расчеты
5.3.1. Вариант 4
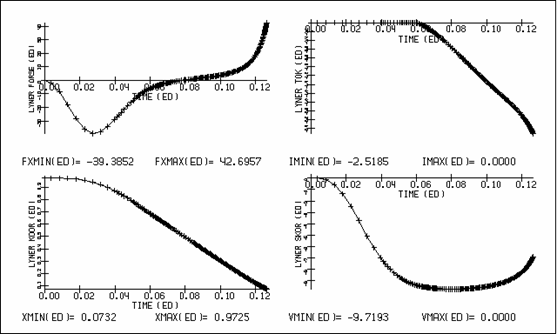
Полуширина лайнера 1.05. Расчет продолжался до момента
времени t = 0.1265, в который скорость центра масс лайнера составила V =
-6.874, координата центра масс x = 0.0732.
Максимальная (по модулю) величина скорости центра масс
лайнера за время ускорения составила V = -9.719, максимальная температура - T =
4.757, интегральная ускоряющая сила (в направлении x) изменялась от -39.39 до
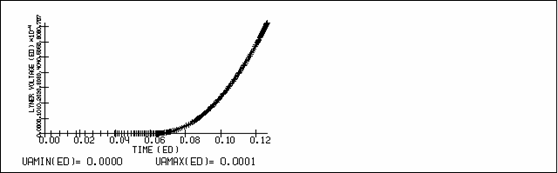
42.70 (знак + соответствует торможению лайнера), ток в цепи лайнера изменялся в
пределах от -2.519 до 0.0, напряжение на обкладках конденсатора в цепи лайнера
менялось от 0.0 до 0.0001. Ток в цепи индуктора изменялся в пределах от -0.966
до 1.585, напряжение на обкладках конденсатора в цепи индуктора менялось от
-986.92 до 1800.0. Динамику изменения сосредоточенных величин можно проследить
по графикам рис. 5.4.
|
|
|
Рис. 5.1.
Конечноэлементная сетка в области лайнера в момент времени t = 0.0780 |
|
|
|
Рис. 5.2.
Конечноэлементная сетка в области лайнера в момент времени t = 0.1150 |
|
|
|
Рис. 5.3.
Конечноэлементная сетка в области лайнера в момент времени t = 0.1265 |
На рисунках 5.1-5.3 изображена расчетная сетка в лайнере
в данном варианте. Видно, как в отличие от модели вариантов 1-3 лайнер
сохраняет свою прямоугольную форму на протяжении всего расчета. Аналогично
варианту 1 правый край лайнера в данном варианте опережает центр - т.е. такое
поведение является характерным для данной ширины лайнера (а именно, когда она
меньше ширины индуктора) и не зависит от используемой модели. В момент
прекращения расчета положение лайнера явно отлично от горизонтального (сравн. с
вариантом 1), что связано с меньшим временем расчета - лайнер не успел
выпрямиться.
5.3.2. Вариант 5
Полуширина лайнера 1.35. Расчет продолжался до момента
времени t = 0.1690, в который скорость центра масс лайнера составила V =
-1.518, координата центра масс x = 0.0211.
|
|
|
|
|
|
|
Рис. 5.4. Графики
сосредоточенной информации для варианта 4. Справа налево, сверху вниз:
интегральная сила от времени, ток в цепи лайнера от времени, координата ц.м.
лайнера от времени, скорость ц.м. лайнера от времени, скорость ц.м. лайнера
от координаты ц.м. лайнера, макс. температура в лайнере от времени, ток в
цепи индуктора от времени, напряжение в цепи индуктора от времени, напряжение
в цепи лайнера от времени. |
Максимальная (по модулю) величина скорости центра масс
лайнера за время ускорения составила V = -7.355, максимальная температура - T =
3.524, интегральная ускоряющая сила (в направлении x) изменялась от -33.45 до
120.22 (знак + соответствует торможению лайнера), ток в цепи лайнера изменялся
в пределах от -2.447 до 0.0, напряжение на обкладках конденсатора в цепи
лайнера менялось от 0.0 до 0.0001. Ток в цепи индуктора изменялся в пределах от
-1.161 до 1.698, напряжение на обкладках конденсатора в цепи индуктора менялось
от -1113.67 до 1800.0.
Расчетная сетка в лайнере для пяти последовательных
моментов времени приведена на рис. 5.5-5.9. Данный вариант особо интересен тем,
что в процессе расчета наблюдается как опережение правого края лайнера его
центром, так и обратная ситуация. Первое (расположение, характерное для
"широкого" лайнера - см. вариант 2) имеет место до момента времени t
= 0.16741, в этот момент (рис. 5.7) наступает перегиб, после чего (рис.
5.8-5.9) правый край лайнера начинает опережать центр (как в случае "узкого"
лайнера).
|
|
|
Рис. 5.5.
Конечноэлементная сетка в области лайнера в момент времени t = 0.16251 |
|
|
|
Рис. 5.6.
Конечноэлементная сетка в области лайнера в момент времени t = 0.16633 |
|
|
|
Рис. 5.7.
Конечноэлементная сетка в области лайнера в момент времени t = 0.16741 |
|
|
|
Рис. 5.8.
Конечноэлементная сетка в области лайнера в момент времени t = 0.16850 |
|
|
|
Рис. 5.9.
Конечноэлементная сетка в области лайнера в момент времени t = 0.16896 |
6. Анализ полученных результатов
6.1.
Эффект стабилизации изгибных неустойчивостей в вязком лайнере
Представим обоснование эффекту, препятствующему образованию
изгибных конфигураций в вязком лайнере. Рассмотрим рис. 6.1, на котором
изображена поверхность края лайнера, внутренняя область которого заполнена проводящей
жидкостью. Натяжение магнитных силовых линий приводит к течению вещества вдоль
плоских поверхностей, что сопровождается перераспределением «погонной» массы
между элементами – трубками тока. В том случае, если основное направление
ускорения на рис. 6.1 направлено по оси Y, определим соответствующую компоненту
ускоряющей силы, как скорость изменения импульса Fy = d/dt (mVy),
где m – плотность распределенной массы по пластине в поперечном направлении.
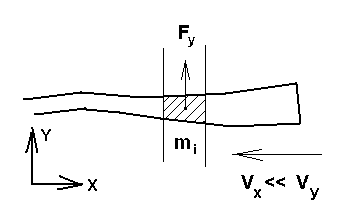
Рис. 6.1. Элемент dx
пластины ускоряемого лайнера.
Распишем выражение для силы, которая в простом
приближении тонкого лайнера определена текущей геометрией (конфигурацией) и
величиной полного тока ускорителя:
Fi = mi dvi/dt + vi dmi/dt.
Отсюда получим:
dvi/dt = 1/mi
(Fi - vi dmi/dt).
Таким образом, поперечное течение вещества в пределах
контура пластины приводит к появлению «тормозящей» силы, препятствующей
убеганию кромок пластины по оси Y под действием местного усиленного магнитного
давления.
В принципе, аналогичный механизм «стабилизации» скоростей
Vyi должен работать всегда, независимо от того, как сгребается
вещество лайнера вдоль пластины, однако наиболее ярко это видно на модели
квазижидкого лайнера с малым коэффициентом вязкости. Для примера на рис. 6.2
показана форма лайнера, расчетная сетка и поле скоростей Vх в пределах сечения
лайнера.
На рисунке видно, что скорость средней линии пластины на
краю лайнера уменьшается по сравнению со скоростью ее в средней части, а
перемещение внутренней кромки (справа вверху) отстает от величины перемещения
средней части лайнера.
6.2.
Влияние скорости распространения возмущений по пластине на ее деформацию
В работах [21, 22] было объяснение другому явлению,
наблюдаемому с самого начала экспериментальных исследований. Встречные пластины
лайнера, которые при разгоне и перемещении должны неминуемо растягиваться в
продольном направлении, удивительным образом сохраняют прямолинейность и
взаимную параллельность. Хотя обычно растяжение ленты предполагает продольную
равнонагруженность, показано, что продольное течение материала и инерциальные
силы при характерных скоростях лайнера приводят к возбуждению низкоскоростной
волны пластической деформации. Скорость этой волны недостаточна, чтобы
оторваться от точки контакта лайнера и клиновой подложки на рис. 1.1, поэтому
область пластического растяжения не затрагивает пластины лайнера в зоне сжатия
магнитного потока.
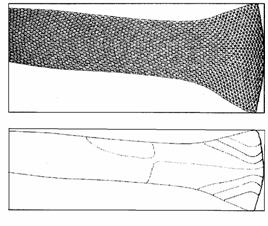
Рис.6.2. Расчетная сетка,
форма сечения и изолинии поля равных скоростей Vx для расчета ускорения лайнера
с малой вязкостью (коэфф. динамич. вязкости 0,001). Момент времени t=63 мкс от
начала процесса. Скопировано из [20].
По - видимому, это имеет непосредственное отношение и к
деформации лайнера в поперечном сечении. На рис. 6.1 показана кривая разрушения
пластины алюминия АД-0, полученная на разрывной машине.
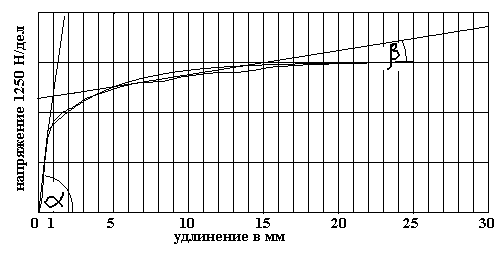
Рис. 6.1 Данные испытаний
материала AД-0 для лайнеров МК. (АД-0) неровная кривая – результат испытаний,
гладкая кривая – моделирующая функция: [на графике 450 точек на оси x и 200
точек по оси y, моделирование по точкам]
Начальный участок σ < σт кривой,
описывающей зависимость напряжения в материале от величины удлинения
(относительного удлинения Δl/l) - область упругости. Угол α ее
наклона – пропорционален модулю Юнга Е, определяющему скорость звука в металле
Vзв~(E/ρ)1/2. Условно считая график прямой также и
за точкой σт, определим ее наклон через угол β. Тогда по
аналогии получим скорость распространения волны пластической деформации Vпл
<< Vзв. Поскольку постановка задачи упруго -
пластического течения материала лайнера в ускорителе МК вызывает значительные
трудности, то можно предположить пробную модель упругого тела, исключающего из
рассмотрения реальную область упругости. Характерное давление магнитного поля
при величине индукции ускоряющего поля B = m0 I / h = 4 p
10‑7 Гн/м 2 МА /
|
|
|
Рис. 6.2.
Конечноэлементная сетка в области лайнера в момент времени t = 0.0165 |
|
|
|
Рис. 6.3.
Конечноэлементная сетка в области лайнера в момент времени t = 0.0252 |
|
|
|
Рис. 6.4.
Конечноэлементная сетка в области лайнера в момент времени t = 0.0339 |
|
|
|
Рис. 6.5.
Конечноэлементная сетка в области лайнера в момент времени t = 0.0404 |
|
|
|
Рис. 6.6.
Конечноэлементная сетка в области лайнера в момент времени t = 0.0456 |
Отметим, что показана только начальная фаза деформации
края пластины, которая, как нам представляется, отвечает реальному случаю
появления изгиба на краю пластины. При дальнейшем расчете должны продолжиться
упругие колебания, не ограниченные диссипацией энергии за счет внутреннего
трения в материале.
Отметим еще один экспериментальный факт, непосредственно
связанный с предметом исследований. Если анализировать теневые фотографии лайнеров,
разгоняемых при различной токовой загрузке (разные напряжения на питающей
батарее) наблюдается следующая закономерность. Толщина тени пластины (реально
это величина стрелы прогиба пластины) больше в тех экспериментах, где меньше
амплитуда тока I. Из общих соображений можно предположить, что в данном случае
велика роль скорости нагружения лайнера, пропорциональная величине I2.
То есть при достижении в материале предела текучести область, захваченная
деформацией, будет тем меньше, чем меньшее время прошло с начала процесса. Это
соображение укладывается в рамки обсуждаемой версии о конечной скорости
распространения возмущений в реальном лайнере, величина которой существенно
меньше, чем скорость звука Vзв.
7. Заключение
В работе сделана попытка обобщить накопленный материал по результатам расчетно - теоретического моделирования динамики течений материала пластинчатого лайнера в процессе его ускорения в магнитном компрессоре. Приведены достаточно подробные данные отдельных экспериментов. Цель такой демонстрации - показать особенности поведения поперечного сечения лайнера с током в ускоряющем самосогласованном магнитном поле, которые пока не воспроизводятся достоверно при использовании модели вязкого тела или модели упругой пластины. В относительно длительном процессе ускорения лайнера (10-4 с) электротехнические характеристики процесса слабо зависят от выбранной модели, учитывающей нелинейную проводимость. Это объясняется относительно малой базой разгона по сравнению с пролетным расстоянием пластин до встречи, и, соответственно, небольшими деформациями сечения за время основного разгона. В этой фазе развитие различных возмущений можно описывать различными моделями, составив кусочно-достоверную картину процесса. В фазе быстрой кумуляции магнитного потока это будет затруднительно хотя бы потому, что к этому моменту времени возмущения профиля лайнера вырастают за пролетное время и достигают максимальной величины. Однако существует и более важный момент, побуждающий интенсифицировать разработку достоверной модели. Он заключается в том, что объем экспериментальной информации, полученный в фазе схлопывания лайнера, будет более скудным, нежели приведенный выше для фазы разгона. Тому есть чисто технические причины, связанные с использованием известных датчиков в экстремальных условиях.
Авторы выражают благодарность В.П. Бахтину, Н.М. Умрихину и Д.А. Топоркову за полезные обсуждения результатов и представление иллюстраций к экспериментальным данным.
8. Литература
2. G.M. Fowler, D.R. Peterson, J.P. Kerrisk et al. Explosive Flux - Compression Strip Generation. // В кн. Сверхсильные магнитные поля. Физика, техника, применение. Под ред. В.М. Титова и Г.А. Швецова. М., Наука. 1984. 415 с. С. 282 - 291.
3. V.P. Baktin, E.V.Grabovsky, A.M.Zhiluchin, V.F.Levashov, A.P.Lototsky, Y.P.Melnikov, K.F.Pashkovsky, V.P.Smirnov, D.A.Toporkov, N.M.Umrikhin. Power Peaker Based on Plate MC-Generator Driven by Electrical Current. MEGAGAUSS-9. Proceeding of Ninth Int. Conf. On Megagauss Magnetic Field Generation and Related Topics (Moscow-St.Peterburg, Iuly 7-14,2002) Sarov. VNIIEF. 2004. P. 324 - 330.
4. Г.А. Кнопфель. Сверхсильные магнитные поля. – М. Мир. 1972. 392 с.
5. П.Л. Калантаров, Л.А. Цейтлин. Расчет индуктивностей. Лен – д. Энергоатомиздат. 1986. 488 с.
6. Г.А. Шнеерсон. Поля и переходные процессы в аппаратуре сверхсильных токов. М. Энергоатомиздат. 1992. 414 с.
7. В.П. Бахтин, Е.В. Грабовский, А.М. Житлухин, А.П. Лотоцкий, В.Ф. Левашов, Н.М. Умрихин, Д.А. Топорков. Динамика пластинчатого лайнера и сжатие магнитного поля в схеме с перехватом магнитного потока из ускорительного контура. Теоретические и экспериментальные исследования, выполненные в 2003г. ТРИНИТИ. Сборник трудов. Отделение Физики токамаков – реакторов. Троицк. 2004г. С.с. 171 – 175.
8. В.В. Никольский, Т.И. Никольская. Электродинамика и распространение радиоволн. М. Наука. 1989. 544 с.
9. М.П. Галанин, Ю.П. Попов. Квазистационарные электромагнитные поля в неоднородных средах. Математическое моделирование. М., Наука. Физматлит. 1995. 320 с.
10. Дж.А. Стрэттон. Теория электромагнетизма. М. - Л. - д. ОГИЗ, Гос. изд-во техн. - теорет. лит-ры. 1948. 540 с.
11. И.Е. Тамм. Основы теории электричества. М. Наука. 1989. 504 с.
12. Н.Е. Кочин, И.А. Кибель, Н.В. Розе. Теоретическая гидромеханика. Часть 1. М., Гос. Изд. Физматлит. 1963. 584 с.
13. Н.Е. Кочин, И.А. Кибель, Н.В. Розе. Теоретическая гидромеханика. Часть 2. М., Гос. Изд. Физматлит. 1963. 728 с.
14. Д. Поттер. Вычислительные методы в физике. М. Мир. 1975. 392 с.
15. Г.В. Логвинович. Гидродинамика течений со свободными границами. Киев. Наукова думка. 1969. 216 с.
16. Физические величины. Справочник. Под ред. И.С. Григорьева, Е.З. Мейлахова. М. Энергоатомиздат, 1991, 1232 с.
17. В.С. Зарубин, Г.Н. Кувыркин. Математические модели термомеханики. М. Физматлит. 2002. 168 с.
18. И.И. Гольденблат. Нелинейные проблемы теории упругости. М. Наука. 1969. 336 с.
19. Д. Бленд. Нелинейная динамическая теория упругости. М. Мир. 1972. 184 с.
20.
М.П. Галанин, А.П. Лотоцкий, В.Ф. Левашов.
Расчет электродинамического ускорения плоских пластин в лабораторном
магнитокумулятивном генераторе. // Препринт ИПМ им. М.В. Келдыша РАН. 2001. № 3. 30 с.
21. M.P. Galanin, A.P. Lototsky. The Mathematical Modelling of a Strip Liner Accelerated by Pulsed Magnetic Field Produced By Longitudinal Current. MEGAGAUSS-9. Proceeding of Ninth Int. Conf. On Megagauss Magnetic Field Generation and Related Topics (Moscow - St. Peterburg, Iuly 7-14. 2002). Sarov. VNIIEF. 2004. P.p. 537 - 544.
22.
В. Бахтин, Е.
Грабовский, А. Житлухин, А. Лотоцкий, Н. Умрихин, Д. Топорков. Течение пластин
лайнера в концевых точках, ограничивающих длину подвижной части Магнитного
компрессора. Сборник трудов ТРИНИТИ, вып.4. Троицк. 2005г. С.с. 120 - 123.
 А
А