, Tmelt
is melting temperature of Ni.
Fluctuation stage is very short-range. Its duration is approximately 10-4
sec. But this stage is defined determinates all following peculiarities of
blistering [1-8].
Stochastic simulation of nano-scale surface and near surface region modification:
high-temperature blistering and thin films formation
|
Development of high-temperature blistering under the
influence of plasma or ion beams on solid surface.
Introduction.
Understanding of processes of interaction between
solids surfaces and plasma has significance for development technologies which
have concern with cosmophysics, controlled thermonuclear fusion,
nanotechnologies. Such problems as blistering, flaking and physical processes,
which take place under irradiation of solids surfaces by ions beams. All these
processes result in solids properties change, plasma pollution and plasma properties
change. Computer simulation of interaction between plasma and solids surfaces
takes on special significance in connection with high price, labor-consuming
and complexity of laboratory experiments with plasma.
Fluctuation stage of high-temperature blistering is examined in this
work. Formation of gas-vacancy pores, which were named blisters, into Ni crystal lattice under the influence
of He ions is discussed. He ions have energy from 10 keV to 100
MeV, radiation dose is from 1016 to 1019 ions/sm2,
the temperature of sample material T is , Tmelt
is melting temperature of Ni.
Fluctuation stage is very short-range. Its duration is approximately 10-4
sec. But this stage is defined determinates all following peculiarities of
blistering [1-8].
Model of blistering. Kinetic
and stochastic equations of model.
Stochastic model of fluctuation stage
of high-temperature blistering has been suggested. The model under discussion
is based on Brownian motion model. Blistering is considered as first-order
phase transition on its fluctuation stage. Bubbles have size approximately of
several angstorm and this kind of defects is considered Brownian particle with
sphere form and variable mass. Blisters can interact with each other, with
solid lattice and with solid surface. Let us use scheme of splitting on
physical processes: bubbles formation and its stochastic motion. The evolution
of bubbles presented as a superposition of the stochastic processes of size
increase and bubbles stochastic motion in crystalline lattice. It is possible
since processes of bubble size increase and bubble migration in lattice have
appreciably different time scales. Characteristic time for blisters size
increasing is 10-9 sec, typical time for its migration in lattice is
10-8 sec. Kinetic equations of Brownian motion model can be solved
by the method of stochastic analog.
The
main idea of the method is change of kinetic equations its stochastic analogs
and solve stochastic differential equations [9]. Authors apply not only
splitting on physical processes but splitting on coordinate too [1-8], because
we have taken into account the interaction of all defects with surface.
Received kinetic equation and its stochastic analogs display below. Let us
present our model by the system of two kinetic partial differential equations
of Fokker-Planck-Kolmogorov and Smoluchovskiy-Kramers kinds.
The
first equation under consideration (Kinetic Fokker-Planck-Kolmogorov equation
for evaluation of blister size) is follow:
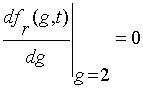
g is number of He atoms in
bubble, 
is distribution
function, 
is diffusion
coefficient in phase space of all possible bubble sizes, 
is Gibbs potential of
bubble (cluster) formation.
The
equation Ito in Stratonovich form, which is equation of stochastic analog of
Fokker-Planck-Kolmogorov equation, is presented below
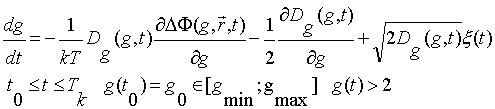
Tk is
full time of computation, 
is stochastic
function, 
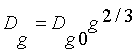. The same equation can be formulated for vacancies into
lattice, but we are examined only He atoms for simplicity of presentation.
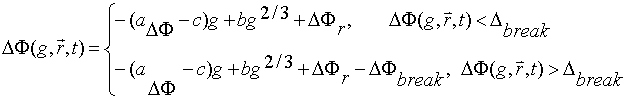
We
have taken into account the difference between chemical potentials of two phase
(
), surface tension on bubble –metal surface (b), elastic force of lattice reaction (c) [3-8], inequality between
locations in lattice points and internodes (
), relcases in crystalline lattice (
) [3-8]. Nbr
is number single relcases, 
is energy of single
relcase, 
is binding energy in
lattice. 
, gcr is
critical size of bubble, 
, 
. The choosen of initial state of clusterization depends on
fluctuation instability of system.
The
Gibbs potential has form which is presented on figure below.
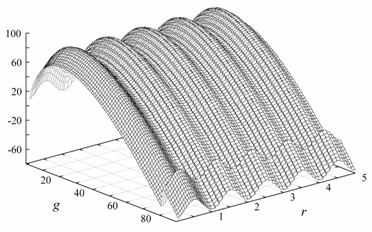
The dependence of Gibbs potential (Joule/atom)
from the both blister size (g) and position in crystal lattice (r). Blister
size is measured in number of helium atoms in bubble. r is measured in lattice parameter of
Ni (lattice parameter of Ni a=3.5 Å).
The break on g »80 corresponds the first break of
due to increasing of blister size.
Fig.2
One-dimensional
Gibbs energy versus cluster size. This figure illustrated the region of
instability of
DF for fluctuation-dependent stochastic process
{g(t), t
³
0}.
Cluster
migration into lattice can be modelized by 3-dimentional Brownian motion. The
kinetic equation for motion of blisters is following
, 
.
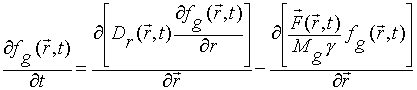
We
consider that blister comes out surface and dies on it if z£ z2.
Fig.
3 presents examined region schematically.
x,y,z are measured in
lattice parameter, zmin is surface, zmax = 2 Rp,
Rp is middle depth of projection run, origin of coordinates is in point {x=0, y=0, z=0}, 
is kinetic
distribution function, 
is diffusion
coefficient in lattice space, Mg is mass of blister, 
is dissipative factor,
is
potential of indirect interaction between bubbles by way of acoustic phonons
and Friedel oscillation of electron density in the case of metal substrate
[10].
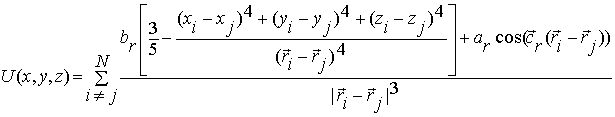where ar, br, cr are fitting coefficient
of model.
The
stochastic analog of the kinetic equation for one coordinate is following:
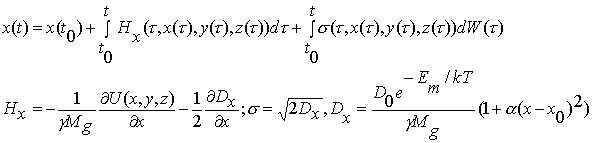
Em
is energy of migration, dW is
increment of Wiener stochastic process. For z
coordinate U=Ubb+Ubs,
Ubb is potential of interaction between bubbles and Ubz is interaction potential
between bubble and surface.
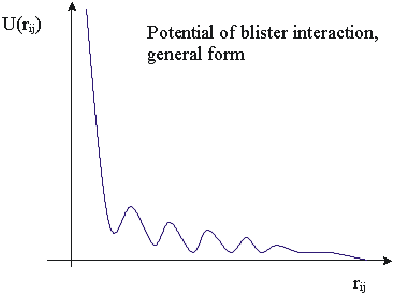
Fig.4
The fusion of blister is considered in model under discussion. The
fusion of two bubbles is made approximately. Two bubbles interflow if following
condition is realized: distance between centers of mass bubbles is less than
sum of blisters radiuses and some model parameter Df. 0 £ Df £a, a is lattice parameter [3-8].
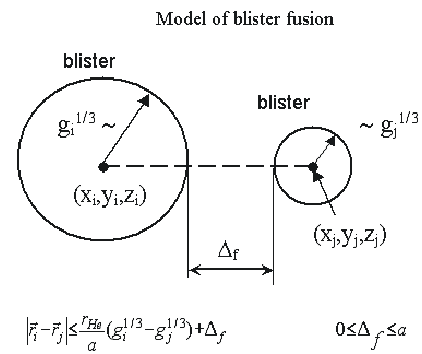
Fig.
5
Used
model allows to find the distribution functions of bubbles from size and
pozition in lattice at different moment of time.
Such
characteristics as middle size of bubbles, porosity of layers, tension in
layers, number of blasted blisters and dependence of these values from time can
be find as a result of processing of these distribution functions.
The modified Artem’ev method [11, 3-8] has been used for solution of
stochastic differential equations.
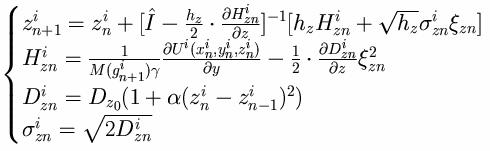
The numerical scheme is presented below:
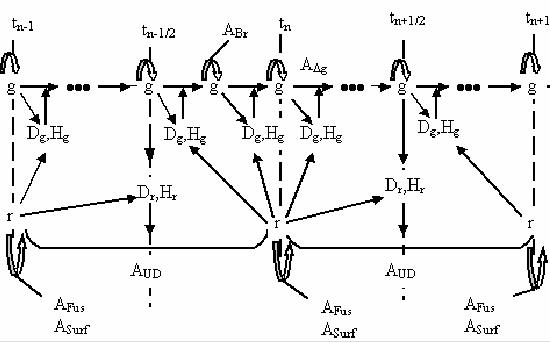
Fig.6
here ADg –operator of size change; ABr
–operator of lattice broken; AUD- operator of diffusion, bubbles
interaction and interaction between bubble and surface; AFus-
operator of fusion; ASurf – operator of exit on surface, reflection
from it or destruction on it.
We used 106 trajectories of
stochastic process for receiving of physical results, which are presented
below.
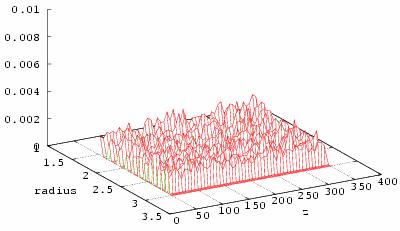
Two
dimensional distribution function, initial time Blister radius, Å Distance from surface, lattice parameter
Fig.7
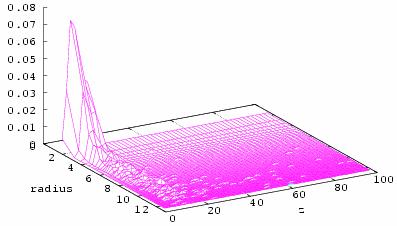
Two dimensional distribution function, moment of finish of calculation Blister radius, Å Distance from surface, lattice parameter
Fig.8
Dispersion of blister size N-number of trajectories Fig.9 Time, step of algorithm Fig. 10 Time, step of algorithm
Distance from surface to center of blister, lattice parameter Fig. 11 Time, step of algorithm
blister with number i belongs to j-layerwhere V is volume of all sample, Vj is volume of layer with number j, gi
is size of blister at examined time moment, g0 is size of blister at
initial time, f(g,z,t) is distribution function at examined time, f(g) is
distribution function at initial time, z is distance between surface and centre of
blister, z is measured in lattice parameter, z=0 is surface under irradiation.
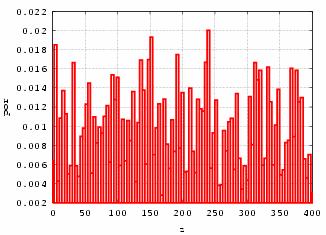
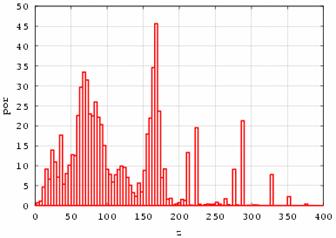
initial time
moment of time finish of calculation
Fig. 12
Fig.
13
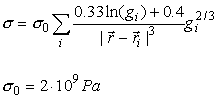
The dependence of stress from layer
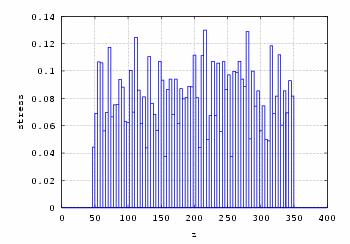
Fig. 14
Stress, s0
Stress, s0 initial
time
time of finish of
calculation
Fig. 15
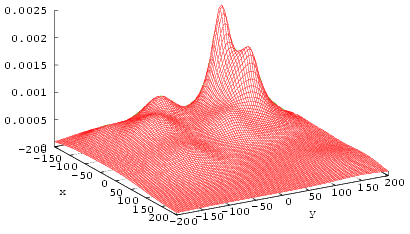
Stress, s0 zÎ[0;0.25 Rp] t=0.25 Tfinish
coordinate y, lattice parameter coordinate
х, lattice
parameter
Fig. 16
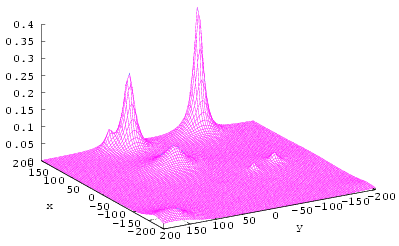
Stress, s0 zÎ[0;0.25 Rp] t=Tfinish coordinate
х, lattice
parameter y
coordinate, lattice parameter Fig. 17
The dependence of blister size at finish of calculation from different
temperatures
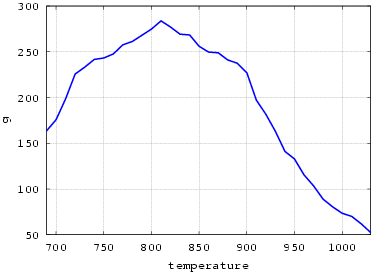
Blister size, Number of He atoms in blister
Temperature, К
Fig. 18
Blister size
Change of themperature during calculation
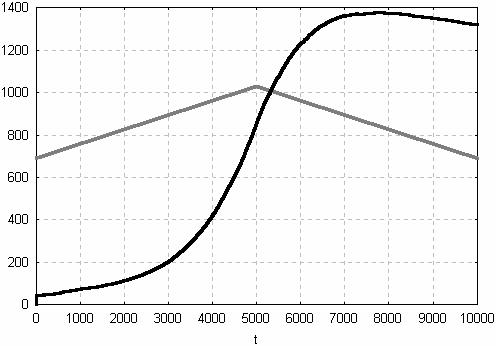
Fig. 19
Conclusions.
The
most interesting results of these experiments are:
1.
the new kinetic and
stochastic model of fluctuation stage of blistering are created;
2.
the Artem’ev method is
modified for solution of system of stochastic equation with
functional-coefficients;
3.
the complex of programs for
simulation of fluctuation stage of blistering is elaborated;
4.
distribution functions of
bubbles from sizes and coordinates are nonequilibrium during fluctuation stage;
5.
blisters chains are formed
athwart to incident flux of ions;
6.
quasi-lattice of bubbles is
observed;
7.
blister size can reach 12
Å during fluctuation stage, decrease of growth rate after bubble size 10
Å is connected with increase of crystal lattice damage;
8.
bubbles size reaches maximum
when relation of solid temperature to melting temperature of materials is 0.47;
9.
the bubbles migration into
the direction of surface under irradiation if bubble radius is less than
10.
the greatest porosity and
greatest tensions are observed on depths of ~ 0.85 Rp and ~
0.35Rp, Rp is middle depth of projection run;
11.
approximately 15% of
blisters destroyed on solid surface during fluctuating stage.
Thin films formation under the influence of plasma or
ion beams on solid surface.
Introduction.
Numerical
simulation of adatoms clusterization of solids surfaces under plasma influence
is interesting for creation of thin films and covers with necessary behaviour.
Release coatings, anticorrosion covers, nano-functional, resistant to pollution
and ultrahydrophobic coverings are examples of coatings with defined
properties. The study of nano-capsules and ions implantation into near surface
layers, interstitial atoms and formed clusters migrations from solids to
surface is very important for creation of self-repair materials and coves. The
fluctuation stage of thin films formation is examined in this paper.
Model, kinetic and
stochastic equations of model.
The
modified by ions substrate is choosen metal W. Let us consider this problem
using stochastic approach, similar has been used in blistering model, which had
been presented in [1-8]. The surface of metal substrate has been contacted with
vapour of Ni. For example the thin film material can be examined liquid Ni
metal. Thin films behaviour differs from behaviour of solids consisting from
same material. Cover formation includes adsorption, creation of new phase
islands, increase/decrease of them sizes, motion of new phase islands on
surface and others processes. The initial fluctuating stage of thin films
formation is of great important, parameters of processes during this stage
determine the behaviour of covers in many respects. The duration of this stage
is approximately 10-4 sec. The island of new phase (cluster of
adatoms) consists of deposited atoms of evaporated material predominantly and
small number of implanted atoms which went on surface as result as diffusion on
material lattice. Increasing or decreasing of island (i.e. cluster of adatoms)
depends on fluctuations during its sizes stochastic changes and jump-like
fusion of clusters. Initial stage of cover formation has been considered as the
geterogeneous first-order phase transformation (from vapour to liquid on the
substrate), here have not be examined chemical reactions during fluctuation
stage of this phase transition. Let us model the stochastic diffusion of
islands on the surface as a brownian motion adapted for flat coordinate
configuration. Following previous experience of computer simulation [1-8] we
can use stochastic analog approach as well physical processes splitting. The
sizes of islands formation and stochastic migration of islands processes have
the different time of development. So, typical time for change of island size
10-8 sec and for migration on substrate surface 10-7
sec. The moving of clusters on surface is realizes under
exposure of surface potential and long-range indirect potentials of interaction
of clusters each with other.
The
phase transition on the surface can be formulated using fundamental Leontovich
equation, which is presented by the system of two kinetic equations of
Kolmogorov-Feller and Smolukhovskii-Kramers kinds (which have been received
after splitting procedure of problem):
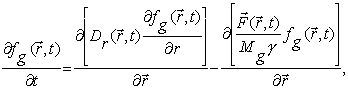
where
S
a
is source of vapour which generats ion with fa
- maxwell ion function, which is characterized by
temperature 2500 K, g is the number
of atoms which is consisted in island-clusters, 
is the diffusion
coefficient in the space of cluster sizes; 
is the bubble size
distribution function – the probability to find the cluster with size g in interval of values of g [g,g+Dg], 
is the Gibbs energy, Mg is the cluster mass, g is constant of friction, distribution function 
is the islands space
function 
is the position
of cluster mass centre in orthogonal coordinates system: 
= -200, 
= 200, 
= -200, 
= 200,
is the potential of
long-range clusters interaction between them through phonons and oscillation of
electron density. The form of potential is similar [3-8], firstly this
interaction had been formulated by [10] in problem of light defect
clusterization into lattice.
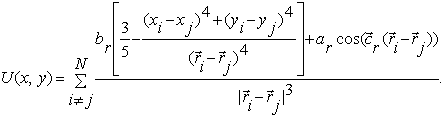
ar, br,
cr is model
parameters.
The non-linear functional coefficient of equation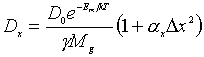 
is stochastic
diffusion coefficient of islands on surface, D0 is coefficient diffusion of adatom on surface, Em is bonding energy of
adatom with surface, 
is parameter of model.
The Gibbs energy looks like following:
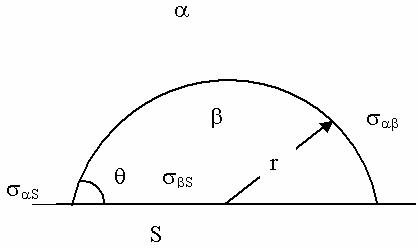
Fig.
20 The scheme of new phase island on solid surface.
where
, 
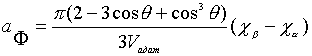is difference of
chemical potential of phases (vapor and liquid), 
, 
are surface
tension between Ni vapour-liquid Ni in island, liquid Ni island-W, Ni vapour-W,
c is coefficient of elastic lattice
reaction, 
is the energy required
for breaking of a single bond with lattice, in our case it is value from
laboratory experiment, 
is the bond energy in
lattice, 
, Nb is
number of broken bonds. 
shows influence of
substrate lattice and the fact that influence of substrate lattice decreases
when cluster size increases, when cluster locates in point (x,y) 
, here ax
and ay are lattice
parameter on x and y axes, in our case ax=ay=a, a
is lattice parameter of W. Y is model function which is depended on islands sizes, also the
dislocation of the lattice. If cluster locates in point (x,y) then 
~ 
, otherwise Y~1, the dislocation can be simulated by Y decreasing in same times. All parameters are non-dimensional, it is
traditional for kinetic theory. The 
and 
are nonlinear
functional-coefficients which dependence on clusters sizes.
Gibbs
energy includes difference of chemical potential of vapour and liquid phases,
interface tensions on surfaces of condensate- vapour, condensate- substrate,
substrate- vapour, elastic force of lattice and possibility of relcases of part
of connections in lattice, non-equivalence of islands positions on surface. The
heterogeneous condensation is considered on substrate and on clusters surfaces.
Joul/atom
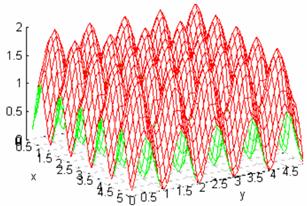
Fig. 21. The 
without
cluster and dislocation is presented in this figure.
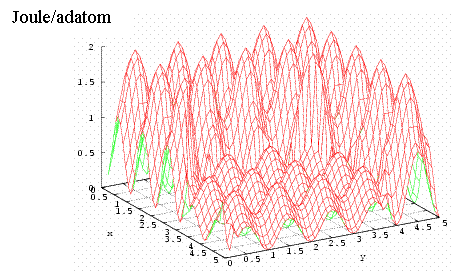
Fig. 22. This figure presents
when the cluster has size equated two lattice parameters and
located in place with coordinates (3;2). x
and y measured in lattice parameters
of W.
Joule/adatom
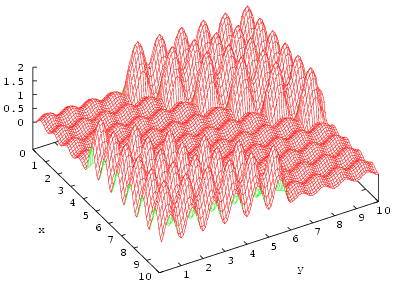
Fig. 23 This figure presents
near dislocation which
placement can be described by equation y=x
For
solve these kinetic equations authors used original computational method of
stochastic simulation [9, 12, 1-8]. The main idea of this method is using the
fundamental qualities of partial differential equations Fokker-Planck kind, which give us possibility to present
physical problem by set Ito-Stratonovich equations with functional-
coefficients. SDE are equivalent to kinetic problem formulated with Fokker-Planck formalism. We replace of kinetic
equation by these stochastic analogs – stochastic differential stochastic
Ito-Stratonovich equations /SDE/. The SDE (analogue of equation for fr(g,t)) looks like
following:
where Tk
is duration of fluctuating stage, x is stochastic function related with increment of
Wiener process, g0 is initial cluster size, gmin and gmax
are borders of unstable region of initial size of cluster which calculated from
, T is temperature
of cluster, 
, gcr is critical size.
For solve of systems of stochastic equations authors
modified Artemiev’s method [11]; it is a second-order accuracy method, with
infinite domain of stability. For all i=1,2,...106 trajectories of
Wiener stochastic process we can use the following determination of the
function 
, where a1 и
a2 are random numbers evenly distributed in
region (0,1).
Fig. 24 presents of calculation scheme.
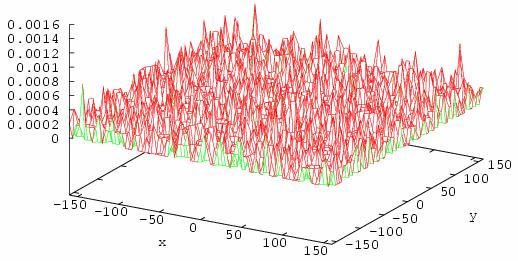
Fig. 25. The distribution function of islands from x
and y coordinate at initial time moment is shown on this figure. The
distribution function is normalize on 1.
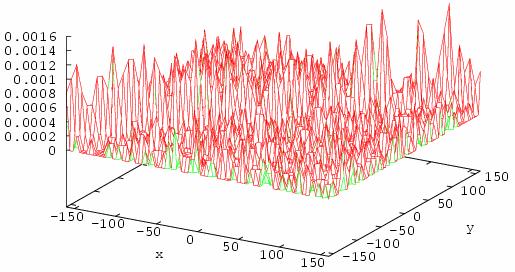
Fig. 26. The distribution function of islands from x
and y coordinate at finish moment of time is presented on this figure.
finish moment of time initial time moment
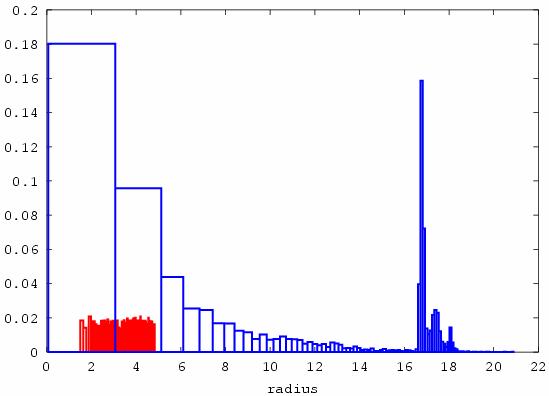
Fig. 27. This figure presents distribution function of
clusters from size at initial and finish moments of time. The radius in lattice
parameters of W is shown on abscissa axis.
Fig. 28. The snap of surface at finish moment of time
is presented in this figure.
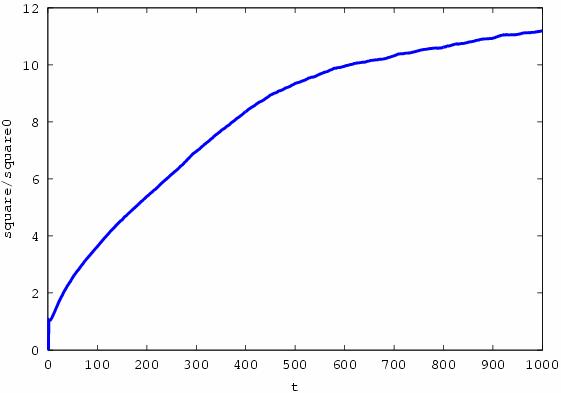
Fig. 29. The ratio of total islands square from total
islands square at initial time moment is shown. The time in txy
is put off on abscissa axis.
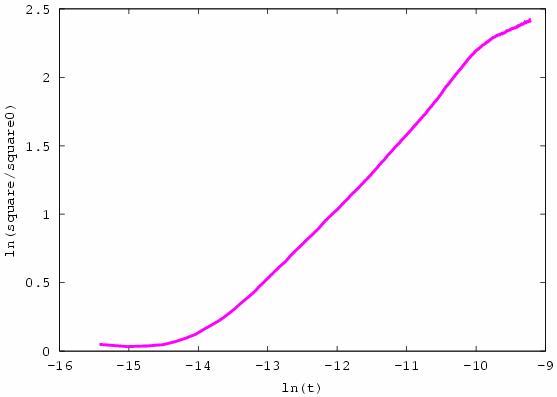
Fig. 30. This figure describes change of logarithm of
the ratio of total islands square from total islands square at initial time
moment depend on logarithm of time. Time is supposed in sec.
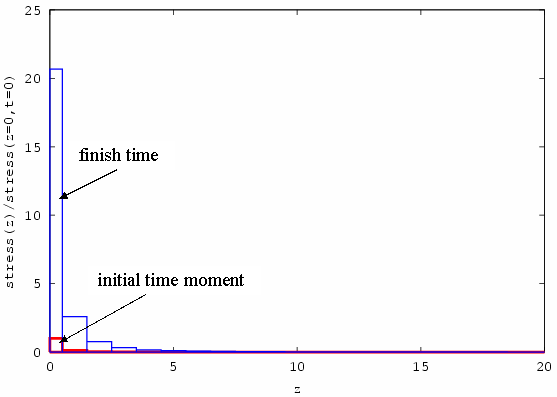
Fig. 31. presents the dependence of rate of stress in
layer at finish time to stress on surface at initial time moment from layer
depth. Z is layer depth measured in lattice parameter of W.
Conclusions
As we can see from presented pictures, radius of
islands distribute uniformly from 5.31 Å to 17.7 Å at initial time
moment. From 10-4 sec form of distribution function shows that two
most probably radiuses exist. The first size (~ 16 Å) is similar to critical size and
corresponds to newly form clusters, second size (~ 61 Å) corresponds to islands which grow
including at the expense of fusions during calculation.
The number of islands placed near linear dislocation
is more than clusters number far from it approximately at 8 times. So, the thin
films formation begins on defects of surface such as dislocations.
Three stage of cover formation during fluctuation
stage are discovered. The first stage lasts from 0 to 8×10-7 sec, it is stage of slow development.
The second stage continues from 8×10-7 sec to 5×10-5 sec and it is stage of quick growth of
thin film. The third stage lasts from 5×10-5 sec to 10-4 sec and it is
notable for deceleration of growth velocity. At that, cover square increases at
11 times approximately with respect to cover square at initial moment of time.
The calculations confirm that influence of cover
reaches on depth of 5 lattice parameters approximately. At the same time,
stress on surface and near surface layers caused by thin film formation does
not exceed the stress caused by blisters development. The stress on surface
connected with cover growth increase at 21 times during fluctuating stage.
Acknowledgments
The
work is partially supported by Russian Science Support Foundation, RFBR grant
02-01-01004, the program "Nanoparticles and nanotechnology" by
Department of Mathematical Sciences RAS 3.5 and scientific school 1388.2003.2.
References.
1.
Bondareva A.L., Zmievskaya
G.I.// Mathematical Models of Non-Linear Excitations, Transfer, Dynamics and
Control in Condensed Systems and Other Media / Ed. L. Uvarova. ¾ N. Y.: Plenum Publ. Co. 1998. P 241-250.
2.
Bondareva A.L., Zmievskaya
G.I. // Proceeding. XXV ICPIG, 2001,
3.
Bondareva A.L., Zmievskaya
G.I. //
4.
Bondareva A.L., Zmievskaya
G.I.//
5.
Bondareva A.L., Zmievskaya
G.I. // Thermophysics and Aeromechanics, Vol. 10, No. 2, 2003, pp. 255-265
6.
Bondareva A.L., Zmievskaya
G.I.// Proc. of ICPIG XXVI July 15-20
2003
7.
Bondareva A.L., Zmievskaya
G.I.// Proc. of 16th International Symposium on Plasma Chemistry.
8.
Bondareva A.L. Stochastic
simulation of fluctuating stage of high-temperature blistering, Ph.D. thesis,
9.
Zmievskaya G.I.// Plasma
Physics Reports, 1997. Vol. 23, No. 4, P. 45.
10.
Morozov A.I., Ovchankov
P.A., Sigov A.S. in: Coll. of Research Papers, ed. by Yu.S. Sigov, Moscow,
Keldysh IAM AS
11.
Artemiev S.S., Averina T.A.
Numerical analysis of systems of ordinary and stochastic differential
equations.-Utrecht, The Netherlands. 1997. P. 176
12.
Zmievskaya G.I. // Rarefied
Gas Dynamics, AIAA edited by Shizgal, B.D. and Weaver, D.P. Vol. 159
Washington, DC, 1994, pp. 371-383