Аннотация
Работа посвящена решению задачи магнитной ориентации малого осесимметричного спутника,
стабилизируемого собственным вращением. Управление скоростью вращения и ориентацией оси
вращения производится токовыми катушками, взаимодействующими с магнитным полем Земли. В работе
рассматриваются два автономных алгоритма управления токовыми катушками. Для работы магнитной
системы ориентации с использованием первого алгоритма необходимо оценивать вектор угловой
скорости спутника. Второй алгоритм не требует оценки угловой скорости. В работе также
анализируется энергопотребление магнитной системы ориентации в зависимости от выбора
требуемого направления оси вращения спутника. Приводятся результаты моделирования движения
спутника относительно центра масс при использовании предлагаемых алгоритмов управления.
Abstract
A preprint is devoted to an orientation problem of the small axisymmetrical spin-stabilized
satellite. The magnetic coils interacting with the magnetic field of the Earth implement
spin-rate control and the spin-axis attitude control. Two autonomous coil control algorithms
are considered. For functioning of magnetic attitude control system with the first algorithm
it is necessary to estimate a vector of the angular velocity of the satellite. The second
algorithm does not demand an estimation of angular velocity. The power consumption of the
magnetic attitude control system is analyzed for different required directions of the
spin-axis of the satellite. The numerical simulation results of the satellite attitude
motion with considered algorithms are represented.
1. Введение
Настоящая
работа продолжает исследования, начатые в работе [1], по обеспечению ориентации
спутника, стабилизируемого собственным вращением. Стабилизация спутника в
инерциальном пространстве за счет его закрутки вокруг оси с наибольшим моментом
инерции является одним из наиболее простых и часто используемых способов
обеспечения заданного углового движения спутника [2]. Для обеспечения
требуемого направления оси вращения и требуемой скорости собственного вращения
спутника можно использовать магнитную систему. Такое сочетание использовалось
еще в 60-х и 70-х годах для ориентации метеорологических спутников серии
"TIROS" [3-5]. Сейчас аналогичный способ ориентации используется на
Европейских метеорологических спутниках серии “Meteosat”. Результаты настоящей
работы, а также работы [1], могут быть использованы при разработке системы
ориентации наноспутника ТНС-1 (ФГУП РНИИ КП) [6].
Исполнительными
элементами магнитной системы ориентации, рассматриваемой в работе, являются три
взаимно ортогональные катушки. Для управления направлением оси вращения
используется катушка, расположенная параллельно оси симметрии спутника. Для
управления скоростью вращения спутника используются две другие катушки, лежащие
в экваториальной плоскости спутника.
Ранее на
практике использовались различные способы управления. Частичный обзор
результатов этих работ приведен в [1]. Способ управления, предложенный в
работах [7, 8], основан на анализе величины рассогласования
между номинальным (расчетным) и текущим кинетическим моментом спутника. Этот
алгоритм в настоящее время используется для ориентации американского малого
спутника LionSat [9]. В настоящей работе также используются этот
подход для управления ориентацией и скоростью вращения спутника. Алгоритмы
управления ориентацией и скоростью вращения являются частями автономного
алгоритма управления угловым движением спутника, использующего информацию об
угловой скорости спутника.
Работа [1]
посвящена исследованию, основанному на асимптотических и численных методах,
магнитной системы ориентации для спутника, стабилизируемого собственным
вращением. В ней аналитически
оценивается минимально необходимый дипольный момент спутника, требуемый
для поддержания некоторого наперед выбранного направления оси вращения в
инерциальном пространстве при наличии возмущающего гравитационного момента.
Аналитически описано возникновение эффекта перерегулирования при управлении
ориентацией спутника. Описано использование на спутнике пассивного нутационного
демпфера.
В настоящей работе
предлагаются два автономных алгоритма магнитной ориентации спутника.
Автономность алгоритмов подразумевает, что каждый из алгоритмов содержит
алгоритм управления ориентацией, алгоритм управления скоростью вращения
спутника и алгоритм гашения нутационного движения. Различие между двумя
рассматриваемыми алгоритмами состоит в составе информации, необходимой для
выбора управляющего дипольного момента, который создавается магнитными
катушками. Для первого алгоритма необходимы: измерения магнитного поля, угловой
скорости спутника и требуемого направления оси вращения. (В случае спутника
ТНС-1 требуемым направлением является направление на Солнце и определяется с
помощью солнечного датчика). Для второго алгоритма достаточно измерений
магнитного поля и требуемого направления оси вращения спутника. Этот алгоритм
получается из предыдущего алгоритма как предельный случай, когда спутник быстро
вращается вокруг оси симметрии – случай, так называемого, спутника-гироскопа.
Второй алгоритм, не требуя измерений угловой скорости, лучше подходит для
использования в системе ориентации ТНС-1. Однако этот алгоритм обеспечивает меньшую
точность ориентации.
Для двух
предлагаемых алгоритмов проведено компьютерное моделирование работы магнитной
системы ориентации с параметрами, соответствующими наноспутнику ТНС-1. Для
первого алгоритма, требующего измерения
угловой скорости спутника, предложено вычислять угловую скорость путем
дифференцирования матрицы перехода между инерциальной и связанной системами
координат. Матрица перехода в этом случае вычисляется локальным методом по
измерениям двух неколлинеарных векторов: вектора индукции геомагнитного поля и
вектора направления на Солнце.
2. Уравнения движения спутника
Для анализа
алгоритмов управления вращательным движением спутника разработана модель движения
и соответствующее программное обеспечение, позволяющие имитировать его движение
с разными алгоритмами управления. Траектория движения центра масс спутника
является кеплеровой и задается шестью оскулирующими элементами.
Для описания
вращательного движения спутника используются связанная с Землей инерциальная система координат (ИСК) 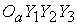 и связанная со спутником система координат (ССК) и связанная со спутником система координат (ССК) 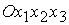 . Определим ИСК так. Ее начало . Определим ИСК так. Ее начало 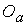 совпадает с центром
масс Земли. Ось совпадает с центром
масс Земли. Ось 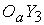 направлена в Северный
Полюс Мира. Оси направлена в Северный
Полюс Мира. Оси 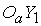 и и 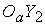 лежат в экваториальной
плоскости Земли, причем ось лежат в экваториальной
плоскости Земли, причем ось 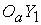 направлена в точку
Весеннего равноденствия. Начало направлена в точку
Весеннего равноденствия. Начало 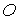 ССК помещено в центр
масс спутника, а оси совпадают с его главными осями инерции. Для определенности
будем считать, что требуется обеспечить ориентацию оси ССК помещено в центр
масс спутника, а оси совпадают с его главными осями инерции. Для определенности
будем считать, что требуется обеспечить ориентацию оси 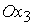 . Обозначим . Обозначим 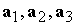 ‑ орты
соответствующих осей связанной системы координат, причем, орт ‑ орты
соответствующих осей связанной системы координат, причем, орт 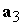 направлен вдоль оси
симметрии спутника, направлен вдоль оси
симметрии спутника, 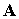 ‑ матрица
перехода из ССК в ИСК, то есть ‑ матрица
перехода из ССК в ИСК, то есть 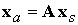 . Матрицу перехода можно представить в виде . Матрицу перехода можно представить в виде 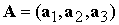 . Выберем векторы . Выберем векторы 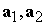 в качестве позиционных
переменными; тогда для вектора в качестве позиционных
переменными; тогда для вектора 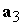 можно записать можно записать 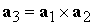 . .
Вращательное
движение спутника описывается системой уравнений
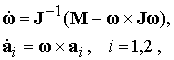 (2.1) (2.1)
где  ‑ тензор инерции
спутника, ‑ тензор инерции
спутника,  ‑ вектор
абсолютной угловой скорости спутника в проекциях на оси ССК, ‑ вектор
абсолютной угловой скорости спутника в проекциях на оси ССК, 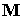 ‑ вращательный
момент в проекциях на оси ССК. Точкой обозначено дифференцирование по времени ‑ вращательный
момент в проекциях на оси ССК. Точкой обозначено дифференцирование по времени 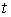 . Поскольку векторы . Поскольку векторы 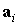 задаются своими
проекциями на оси ИСК, то и вектор задаются своими
проекциями на оси ИСК, то и вектор  , заданный в первом уравнении в ССК, во втором уравнении
должен быть преобразован в ИСК. Это можно сделать, умножив его на матрицу , заданный в первом уравнении в ССК, во втором уравнении
должен быть преобразован в ИСК. Это можно сделать, умножив его на матрицу 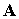 . Вращательный момент . Вращательный момент 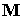 есть сумма моментов
сил разной природы. Учитываются гравитационный момент в виде есть сумма моментов
сил разной природы. Учитываются гравитационный момент в виде
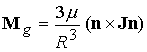 , (2.2) , (2.2)
где 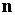 ‑ орт местной
вертикали в проекциях на оси ССК, ‑ орт местной
вертикали в проекциях на оси ССК, 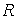 ‑ расстояние
между центрами масс спутника и Земли, ‑ расстояние
между центрами масс спутника и Земли, 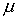 ‑ гравитационный
параметр Земли и магнитный момент от взаимодействия дипольного магнитного
момента спутника с геомагнитным полем ‑ гравитационный
параметр Земли и магнитный момент от взаимодействия дипольного магнитного
момента спутника с геомагнитным полем
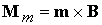 ,
(2.3) ,
(2.3)
где  ‑ магнитный
дипольный ‑ магнитный
дипольный  момент спутника, момент спутника, 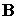 ‑ индукция
геомагнитного поля в точке расположения центра масс спутника. Магнитный момент
рассматривается далее как управляющий момент. ‑ индукция
геомагнитного поля в точке расположения центра масс спутника. Магнитный момент
рассматривается далее как управляющий момент.
Рассмотрим
последовательно два автономных алгоритма магнитной ориентации: первый алгоритм,
требующий измерения угловой скорости спутника и второй алгоритм, не требующий
информации об угловой скорости.
3. Алгоритм управления магнитными катушками, требующий измерения
угловой скорости спутника (первый алгоритм)
Изложенный в
настоящем разделе автономный алгоритм отличается от алгоритма, приведенного в
[1], наличием алгоритма гашения нутационного движения спутника.
Согласно
основному уравнению динамики твердого тела изменение его кинетического момента 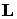 определяется главным
моментом сил, приложенных к телу. Пусть на тело действует только управляющий
магнитный момент, тогда можно записать определяется главным
моментом сил, приложенных к телу. Пусть на тело действует только управляющий
магнитный момент, тогда можно записать
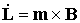 .
(3.1) .
(3.1)
Предположим,
что на спутнике установлены три взаимно перпендикулярные магнитные (токовые)
катушки. Током через каждую из них можно управлять независимо. Будем считать,
что катушка с дипольным моментом 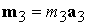 , создающая момент вдоль оси симметрии спутника с ортом , создающая момент вдоль оси симметрии спутника с ортом 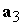 , управляет положением этой оси в пространстве. Катушки с
дипольными моментами , управляет положением этой оси в пространстве. Катушки с
дипольными моментами 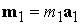 , , 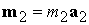 используются для
управления скоростью вращения спутника, несмотря на то, что механический
магнитный момент, создаваемый этими катушками, будет также влиять и на положение
в пространстве оси симметрии спутника. Это влияние будем рассматривать как
возмущение положения оси симметрии спутника наряду с эффектом от действия
гравитационного момента. используются для
управления скоростью вращения спутника, несмотря на то, что механический
магнитный момент, создаваемый этими катушками, будет также влиять и на положение
в пространстве оси симметрии спутника. Это влияние будем рассматривать как
возмущение положения оси симметрии спутника наряду с эффектом от действия
гравитационного момента.
Величина
дипольного момента каждой катушки может принимать лишь три фиксированных
значения: 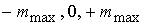 . Тем не менее, чтобы избежать эффекта перерегулирования на
этапе окончательного приведения спутника к номинальному движению, может
потребоваться поэтапное уменьшение дипольного момента катушек. Обычно дипольный
момент катушки формируется подачей следующих друг за другом прямоугольных
импульсов напряжения равной продолжительности. Тогда, пропуская нужное
количество импульсов в единицу времени, можно обеспечить требуемое уменьшение
среднего за период формирования момента до нужной величины. Это, так
называемая, широтно-импульсная модуляция. . Тем не менее, чтобы избежать эффекта перерегулирования на
этапе окончательного приведения спутника к номинальному движению, может
потребоваться поэтапное уменьшение дипольного момента катушек. Обычно дипольный
момент катушки формируется подачей следующих друг за другом прямоугольных
импульсов напряжения равной продолжительности. Тогда, пропуская нужное
количество импульсов в единицу времени, можно обеспечить требуемое уменьшение
среднего за период формирования момента до нужной величины. Это, так
называемая, широтно-импульсная модуляция.
Изложенный далее алгоритм
управления ориентацией и алгоритм управления скоростью вращения спутника
производится в соответствии с [1].
3.1. Управление ориентацией оси вращения спутника
Введем рассогласование 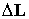 между требуемым
(номинальным) кинетическим моментом между требуемым
(номинальным) кинетическим моментом 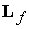 и фактическим на
текущий момент времени кинетическим моментом и фактическим на
текущий момент времени кинетическим моментом 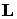 следующим образом: следующим образом:
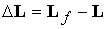 . (3.2) . (3.2)
Управление
величиной дипольного момента 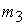 будем выполнять так,
чтобы минимизировать величину рассогласования по кинетическому моменту будем выполнять так,
чтобы минимизировать величину рассогласования по кинетическому моменту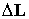
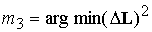 . .
Квадрат рассогласования
выбирается вместо модуля в силу дифференцируемости этой функции при любом
значении 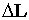 . .
Полагая 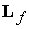 неизменным в инерциальном пространстве,
запишем производную квадрата неизменным в инерциальном пространстве,
запишем производную квадрата 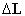 по времени в силу
уравнения (3.1) по времени в силу
уравнения (3.1)
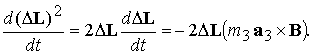
Отсюда, требуя для
производной 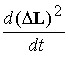 отрицательного
значения, получаем выражения для искомого дипольного момента отрицательного
значения, получаем выражения для искомого дипольного момента 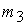 , ,
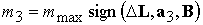 ,
(3.3) ,
(3.3)
где 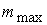 ‑ максимальный
магнитный момент, создаваемый катушками ( ‑ максимальный
магнитный момент, создаваемый катушками (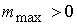 ), ), 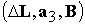 ‑ смешанное
произведение векторов: ‑ смешанное
произведение векторов: 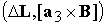 . .
Теперь
получим закон управления скоростью осевого вращения спутника.
3.2. Управление скоростью вращения спутника
Аналогично
предыдущему случаю рассмотрим величину рассогласования кинетического момента 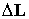 , ,
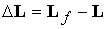 . .
В качестве
номинального магнитного момента зададим момент, который имел бы спутник, если
бы он вращался вокруг оси симметрии с требуемой угловой скоростью, а ось
симметрии ориентировалась так, как она ориентирована в текущий момент времени
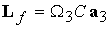 . (3.4) . (3.4)
Здесь 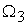 ‑ требуемая
скорость вращения, ‑ требуемая
скорость вращения, 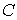 ‑ момент инерции
спутника вдоль оси симметрии. Такой выбор позволяет рассмотреть только
отличие текущей закрутки спутника от номинальной. Рассмотрим, как и в предыдущем
случае, производную
квадрата ‑ момент инерции
спутника вдоль оси симметрии. Такой выбор позволяет рассмотреть только
отличие текущей закрутки спутника от номинальной. Рассмотрим, как и в предыдущем
случае, производную
квадрата 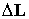 по времени по времени
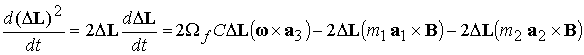 . .
Требуя, чтобы
производная квадрата величины рассогласования кинетического момента спутника 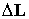 была минимальна,
получаем, что дипольные магнитные моменты, необходимые для управления скоростью
вращения, должны удовлетворять выражениям была минимальна,
получаем, что дипольные магнитные моменты, необходимые для управления скоростью
вращения, должны удовлетворять выражениям
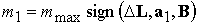 , , 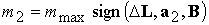 . (3.5) . (3.5)
Теперь
рассмотрим алгоритм гашения нутационного движения спутника, который не
использовался в [1].
3.3. Алгоритм
гашения нутационного движения спутника
В настоящем разделе
описывается алгоритм гашения нутационного движения спутника, использующий
оценку угловой скорости спутника. Этот алгоритм можно использовать попеременно
с алгоритмами управления ориентацией и скоростью вращения спутника. При
движении спутника с использованием описываемого алгоритма создается эффект,
схожий с действием нутационного демпфера. Воспользуемся динамическими
уравнениями Эйлера для описания движения спутника
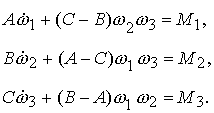 (3.6)
(3.6)
Здесь 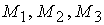 ‑ проекции
механического момента и ‑ проекции
механического момента и 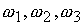 ‑ проекции
вектора ‑ проекции
вектора  на связанные оси.
Будем рассматривать динамически осесимметричный спутник, движущийся в магнитном
поле. В этом случае уравнения (3.6) переписываются в виде на связанные оси.
Будем рассматривать динамически осесимметричный спутник, движущийся в магнитном
поле. В этом случае уравнения (3.6) переписываются в виде
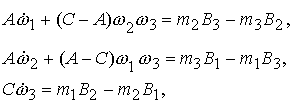 (3.7)
(3.7)
где 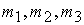 ‑ проекции
дипольного магнитного момента спутника на связанные оси, ‑ проекции
дипольного магнитного момента спутника на связанные оси, 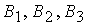 ‑ вектор индукции
магнитного поля Земли в проекциях на связанные оси. Под гашением нутационного
движения будем понимать уменьшение компонент ‑ вектор индукции
магнитного поля Земли в проекциях на связанные оси. Под гашением нутационного
движения будем понимать уменьшение компонент  и и 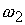 угловой скорости.
Умножая первое уравнение системы (3.7) на угловой скорости.
Умножая первое уравнение системы (3.7) на  , а второе уравнение на , а второе уравнение на 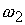 и складывая полученные
выражения, имеем и складывая полученные
выражения, имеем
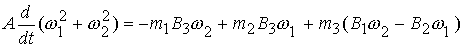 . (3.8) . (3.8)
Для
уменьшения величины 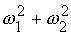 при неизменной
величине закрутке спутника при неизменной
величине закрутке спутника 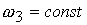 необходимо найти необходимо найти 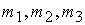 , удовлетворяющие следующим условиям: , удовлетворяющие следующим условиям:
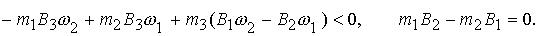 (3.9) (3.9)
Решение системы (6.4) удобно
искать, записав эту систему в векторном виде
 (3.10) (3.10)
где 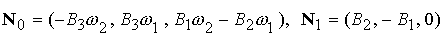 . Решением системы (3.10) будут все точки . Решением системы (3.10) будут все точки  , принадлежащие плоскости , принадлежащие плоскости  , которые лежат в полупространстве , которые лежат в полупространстве 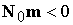 . Линию пересечения плоскостей . Линию пересечения плоскостей 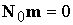 и и 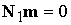 , перпендикулярную их нормалям, можно задать вектором , перпендикулярную их нормалям, можно задать вектором 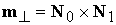 . В качестве решения системы (3.10) возьмем вектор . В качестве решения системы (3.10) возьмем вектор 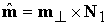 . Легко видеть, что вектор . Легко видеть, что вектор 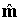 есть действительно
частное решение системы (3.9’): есть действительно
частное решение системы (3.9’):
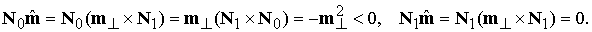
На основании частного
решения 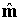 из условий нормировки
получим вектор управления из условий нормировки
получим вектор управления
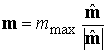 ,
(3.11) ,
(3.11)
где 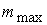 ‑ максимально
допустимая величина момента реальных исполнительных органов управления. ‑ максимально
допустимая величина момента реальных исполнительных органов управления.
Подставляя
управление (3.11) в выражение (3.8), получим
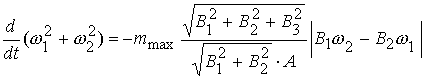 . (3.12) . (3.12)
Знак «минус» правой части
выражения (3.12) обеспечивает отрицательное значение производной величины 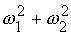 , а, следовательно, и уменьшение этой величины, что и нужно
для функционирования алгоритма гашения нутационного движения спутника. , а, следовательно, и уменьшение этой величины, что и нужно
для функционирования алгоритма гашения нутационного движения спутника.
Теперь
перейдем к описанию второго автономного алгоритма, не требующего измерения
угловой скорости спутника.
4. Алгоритм управления магнитными катушками, не требующий измерения
угловой скорости спутника (второй алгоритм)
Будем рассматривать действие
на спутник только управляющего магнитного момента. Пусть на спутнике имеется
катушка с дипольным моментом 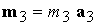 , направленным вдоль оси симметрии спутника с ортом , направленным вдоль оси симметрии спутника с ортом 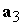 . Как и в предыдущем случае, эта катушка управляет положением
продольной оси в пространстве. Катушки с дипольными моментами . Как и в предыдущем случае, эта катушка управляет положением
продольной оси в пространстве. Катушки с дипольными моментами 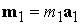 , , 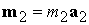 используются для
управления скоростью вращения спутника. используются для
управления скоростью вращения спутника.
Предлагаемый в этом разделе
алгоритм для своего функционирования не требует информации о векторе угловой
скорости спутника. Однако такой алгоритм может быть применен только для быстро
вращающегося вокруг оси симметрии спутника – спутника-гироскопа.
Рассматриваемый алгоритм будет приведен как предельный случай вышеописанного
алгоритма, когда спутник быстро вращается.
Кинетический момент 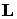 осесимметричного спутника
представим в виде осесимметричного спутника
представим в виде
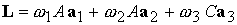 , ,
где 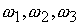 ‑ проекции
вектора угловой скорости спутника на связанные оси, ‑ проекции
вектора угловой скорости спутника на связанные оси, 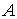 , ,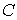 ‑ главные моменты инерции спутника. Предположим, что
спутник быстро вращается вокруг оси симметрии с моментом инерции ‑ главные моменты инерции спутника. Предположим, что
спутник быстро вращается вокруг оси симметрии с моментом инерции 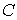 , то есть , то есть 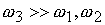 . Тогда текущий кинетический момент спутника . Тогда текущий кинетический момент спутника 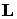 можно приближенно
представить в виде можно приближенно
представить в виде
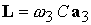 . (4.1) . (4.1)
Выражение для кинетического
момента (4.1) будет использовано далее для получения алгоритмов управления
ориентацией и скоростью вращения спутника. Эти алгоритмы будут получены
предельным переходом от алгоритмов, описанных в разделах 3.1 и 3.2, при этом
выражение (4.1) является тем самым предельным предположением.
Перейдем к изложению способа
управления ориентацией оси вращения спутника.
4.1. Управление ориентацией оси вращения спутника
Пусть требуемый кинетический
момент спутника 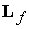 записывается в виде записывается в виде
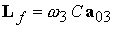 ,
(4.2) ,
(4.2)
где 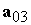 ‑ требуемое
направление оси симметрии спутника. Тогда, подставляя выражения (4.1) и (4.2) в
закон управления (3.3), получим ‑ требуемое
направление оси симметрии спутника. Тогда, подставляя выражения (4.1) и (4.2) в
закон управления (3.3), получим
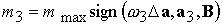 , ,  (4.3) (4.3)
где 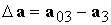 . Этот закон управления можно переписать и в следующем виде: . Этот закон управления можно переписать и в следующем виде:
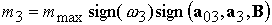 .
(4.4) .
(4.4)
Эффективность такого
управления будет наибольшая, если создаваемый механический магнитный момент
лежит в плоскости, содержащей векторы 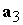 и и 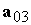 . Если же создаваемый момент перпендикулярен плоскости,
содержащей векторы . Если же создаваемый момент перпендикулярен плоскости,
содержащей векторы 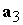 и и 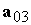 , то эффективность управления будет нулевой. Численные
эксперименты показали, что в этом случае также происходит увеличение
нутационных колебаний спутника. Поэтому имеет смысл в процессе работы алгоритма
ориентации вычислять проекцию создаваемого механического магнитного момента на
плоскость, содержащую векторы , то эффективность управления будет нулевой. Численные
эксперименты показали, что в этом случае также происходит увеличение
нутационных колебаний спутника. Поэтому имеет смысл в процессе работы алгоритма
ориентации вычислять проекцию создаваемого механического магнитного момента на
плоскость, содержащую векторы 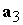 и и 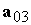 , и если данная проекция становится мала, то на некоторое
время отключать управляющий момент. Этот период времени авторы настоящей работы
назвали большой паузой. Численные эксперименты показали, что, например,
для находящегося на орбите высотой 650 км спутника ТНС-1 с учетом предъявленных
требований на систему ориентации длительность большой паузы следует задавать
около 200 с. Нормаль к плоскости, содержащей векторы , и если данная проекция становится мала, то на некоторое
время отключать управляющий момент. Этот период времени авторы настоящей работы
назвали большой паузой. Численные эксперименты показали, что, например,
для находящегося на орбите высотой 650 км спутника ТНС-1 с учетом предъявленных
требований на систему ориентации длительность большой паузы следует задавать
около 200 с. Нормаль к плоскости, содержащей векторы 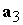 и и 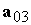 , вычисляется по формуле , вычисляется по формуле
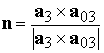 .
(4.5) .
(4.5)
Вектор, имеющей направление создаваемого механического
магнитного момента, записывается так:
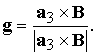 (4.6)
(4.6)
Проекция вектора 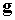 на плоскость,
содержащую векторы на плоскость,
содержащую векторы 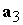 и и 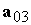 , вычисляется по формуле , вычисляется по формуле
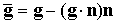 .
(4.7) .
(4.7)
Большая пауза, в течение которой управляющий
магнитный момент следует выключать, должна начаться, если
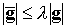 , (4.8) , (4.8)
где 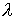 ‑ некоторый
параметр, величина которого выбирается опытным путем. Численные эксперименты,
проведенные для наноспутника ТНС-1, показывают, что этот параметр следует
полагать приблизительно равным 0.2-0.3. ‑ некоторый
параметр, величина которого выбирается опытным путем. Численные эксперименты,
проведенные для наноспутника ТНС-1, показывают, что этот параметр следует
полагать приблизительно равным 0.2-0.3.
Изложим способ управления скоростью вращения спутника.
4.2. Управление скоростью вращения спутника
Пусть текущий кинетический
момент спутника 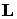 записывается формулой
(4.1), а требуемый кинетический момент записывается формулой
(4.1), а требуемый кинетический момент 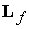 задан выражением (3.4).
Подставляя эти выражения в закон управления (3.5) получаем задан выражением (3.4).
Подставляя эти выражения в закон управления (3.5) получаем
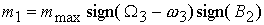 , , 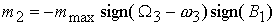 , (4.9) , (4.9)
где 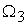 ‑ требуемая
скорость вращения; ‑ требуемая
скорость вращения; 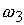 ‑ проекция
вектора угловой скорости на орт связанной системы координат ‑ проекция
вектора угловой скорости на орт связанной системы координат 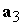 ; ; 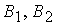 ‑ проекции на
связанные оси вектора индукции магнитного поля Земли, ‑ проекции на
связанные оси вектора индукции магнитного поля Земли, 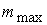 ‑ максимальный
магнитный момент, создаваемый катушками. ‑ максимальный
магнитный момент, создаваемый катушками.
Как и в предыдущем
случае укажем область, где полученное управление (4.9) наиболее эффективно. Вне
этой области включение управления приводит к неоправданному увеличению
нутационного движения. Упомянутая область описывается двойным неравенством
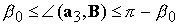 , ,  (4.10) (4.10)
где 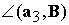 ‑ угол между
ортом ‑ угол между
ортом 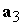 и вектором индукции и вектором индукции 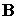 магнитного поля Земли, магнитного поля Земли,
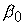 ‑ параметр,
величина которого выбирается опытным путем. Численные эксперименты, проведенные
для спутника ТНС-1, показывают, что этот угол следует полагать приблизительно
равным ‑ параметр,
величина которого выбирается опытным путем. Численные эксперименты, проведенные
для спутника ТНС-1, показывают, что этот угол следует полагать приблизительно
равным 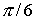 . .
Перейдем к описанию алгоритма гашения нутационного движения спутника.
4.3.
Алгоритм гашения нутационного движения спутника
Опишем
алгоритм гашения нутационного движения спутника, для которого в отличие от
алгоритма, описанного в 3.3, требуется только информация о знаке производной
составляющей магнитного поля Земли вдоль оси симметрии спутника, а не ее
величине. В этом алгоритме уменьшение угловых скоростей  и и 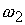 выполняется с помощью
одной катушки, направленной по оси симметрии спутника с ортом выполняется с помощью
одной катушки, направленной по оси симметрии спутника с ортом 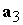 . Дипольный магнитный момент . Дипольный магнитный момент 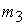 формируется по закону формируется по закону
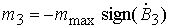 . (4.11) . (4.11)
Здесь 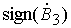 ‑ знак
производной составляющей магнитного поля Земли вдоль оси симметрии спутника.
Для реального рабочего алгоритма следует определять знак производной сравнением
показаний магнитометра, измеряющего составляющую магнитного поля вдоль оси
симметрии спутника, по двум соседним моментам времени. ‑ знак
производной составляющей магнитного поля Земли вдоль оси симметрии спутника.
Для реального рабочего алгоритма следует определять знак производной сравнением
показаний магнитометра, измеряющего составляющую магнитного поля вдоль оси
симметрии спутника, по двум соседним моментам времени.
Идея
предложенного закона управления величиной магнитного момента катушки состоит в
имитации работы нутационного демпфера, построенного на использовании на
спутнике элемента из магнитомягкого материала [10]. Перемагничивание
магнитомягкого элемента вызывает рассеяние энергии движения спутника
относительно центра масс. Предложенный загон управления имитирует магнитный
момент идеализированного гистерезисного стержня с прямоугольной петлей
гистерезиса.
4.4. Определение скорости вращения спутника на основании измерений
магнитометров
Как видно из закона управления
ориентацией (4.4) и закона управления скоростью вращения спутника (4.9) для
функционирования этих алгоритмов требуется оценка компоненты угловой скорости 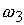 , то есть фактически - скорости вращения спутника вокруг оси
симметрии. При условии, что спутник быстро вращается, скорость вращения
спутника можно довольно просто определить с помощью двухосного магнитометра,
оси которого расположены в экваториальной плоскости спутника. В случае быстрого
вращения спутника изменением вектора индукции магнитного поля вследствие
движения спутника по орбите можно пренебречь и считать, что проекция вектора
индукции на экваториальную плоскость спутника изменяется только из-за вращения
спутника. Тогда , то есть фактически - скорости вращения спутника вокруг оси
симметрии. При условии, что спутник быстро вращается, скорость вращения
спутника можно довольно просто определить с помощью двухосного магнитометра,
оси которого расположены в экваториальной плоскости спутника. В случае быстрого
вращения спутника изменением вектора индукции магнитного поля вследствие
движения спутника по орбите можно пренебречь и считать, что проекция вектора
индукции на экваториальную плоскость спутника изменяется только из-за вращения
спутника. Тогда
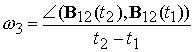 , (4.12) , (4.12)
где 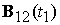 , , 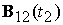 ‑ проекции
вектора индукции магнитного поля Земли на экваториальную плоскость спутника в
моменты времени ‑ проекции
вектора индукции магнитного поля Земли на экваториальную плоскость спутника в
моменты времени 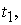 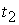 , обозначение , обозначение 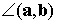 означает угол между
векторами означает угол между
векторами 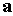 , , 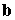 . Использование формулы (4.12) предполагает, что интервал
времени . Использование формулы (4.12) предполагает, что интервал
времени 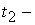 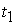 выбран достаточно
малым, что бы за это время спутник не успел повернуться на угол более, чем выбран достаточно
малым, что бы за это время спутник не успел повернуться на угол более, чем 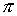 . .
5. Программный комплекс для
моделирования движения спутника
относительно центра масс
Для
моделирования динамики спутника и верификации предложенных алгоритмов
управления разработан программный комплекс на ПЭВМ с использованием среды
MATLAB. Интерфейс программного комплекса приведен на рис.5.1. Для упрощения
визуализации собственного вращения спутник изображен в виде многоугольника.
Выходными
данными программного комплекса являются графики зависимости компонент вектора
текущей угловой скорости и матрицы направляющих косинусов, графики угла 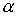 между осью вращения и
заданным направлением в инерциальном пространстве (например, нормаль к
плоскости орбиты или направление на Солнце), энергопотребление магнитной
системы ориентации, а также анимационная картина вращательного движения
спутника. Приведенные в настоящей работе результаты компьютерного моделирования
были получены с помощью этого программного комплекса. между осью вращения и
заданным направлением в инерциальном пространстве (например, нормаль к
плоскости орбиты или направление на Солнце), энергопотребление магнитной
системы ориентации, а также анимационная картина вращательного движения
спутника. Приведенные в настоящей работе результаты компьютерного моделирования
были получены с помощью этого программного комплекса.
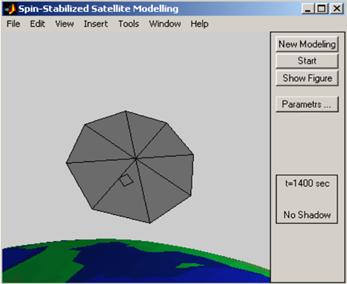
Рис.5.1. Интерфейс
программного комплекса предназначенного для моделирования вращательного
движения спутника
6.
Моделирование вращательного движения спутника c магнитной системой
ориентации, использующей первый алгоритм
Для
проверки работоспособности алгоритмов ориентации на начальном этапе было
проведено моделирование одновременного использования алгоритмов: приведения оси
вращения к направлению нормали к плоскости орбиты по формуле (3.3) и алгоритма
управления скоростью вращения по формулам (3.5). Эффект перерегулирования был
первоначально обнаружен при проведении численных экспериментов моделирования
динамики спутника с использованием алгоритмов управления ориентацией. В
работе [1] возникновение этого эффекта было показано аналитически. Чтобы
исключить эффект перерегулирования, при уменьшении угла отклонения оси
симметрии от требуемого направления величина создаваемого дипольного момента 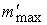 уменьшалась в
соответствии со следующими формулами: уменьшалась в
соответствии со следующими формулами:
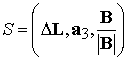 , (6.1) , (6.1)
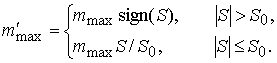 (6.2)
(6.2)
Здесь 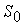 является подстроечным
параметром, величина которого выбиралась из интервала является подстроечным
параметром, величина которого выбиралась из интервала 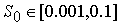 . Формулы (6.1) и (6.2) являются эмпирическими. . Формулы (6.1) и (6.2) являются эмпирическими.
Результаты
моделирования, приведенные далее, выполнены для идеального случая, когда в
каждый момент времени известна ориентация и угловая скорость спутника. При
моделировании задавались следующие значения оскулирующих элементов орбиты:
долгота восходящего узла 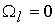 , наклонение орбиты , наклонение орбиты 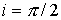 , параметр , параметр 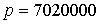 м (соответствует высоте орбиты 650 км), эксцентриситет м (соответствует высоте орбиты 650 км), эксцентриситет 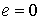 . Параметры моделируемого спутника соответствуют наноспутнику
ТНС-1: максимальный дипольный момент, создаваемый каждой катушкой . Параметры моделируемого спутника соответствуют наноспутнику
ТНС-1: максимальный дипольный момент, создаваемый каждой катушкой 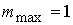 A×м A×м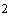 , тензор инерции спутника , тензор инерции спутника 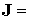 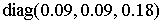 кг×м кг×м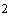 , требуемая ориентация оси вращения спутника – по нормали к
плоскости орбиты. Также задаются начальная ориентация спутника и начальная
абсолютная угловая скорость. , требуемая ориентация оси вращения спутника – по нормали к
плоскости орбиты. Также задаются начальная ориентация спутника и начальная
абсолютная угловая скорость.
На
рис.6.1 изображены зависимости от времени отклонение спутника относительно
нормали к плоскости орбиты (рис.6.1а) и компоненты угловой скорости (рис.6.1б)
при следующих начальных условиях движения спутника относительно его центра
масс: ось симметрии спутника лежит в плоскости орбиты, начальная абсолютная
угловая скорость 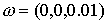 . Скорость измеряется в рад/с. Рис.6.2а и рис.6.2б
представляют результат моделирования при тех же параметрах орбиты и спутника,
но отличающийся начальной угловой скоростью . Скорость измеряется в рад/с. Рис.6.2а и рис.6.2б
представляют результат моделирования при тех же параметрах орбиты и спутника,
но отличающийся начальной угловой скоростью
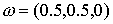 с-1.
Управление осуществляется непрерывно.
с-1.
Управление осуществляется непрерывно.
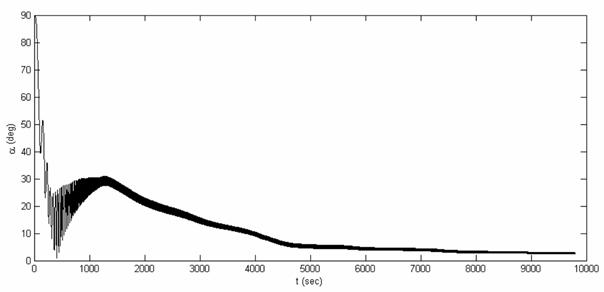
Рис.6.1а.
Моделирование вращательного движения спутника при использовании магнитной
ориентации: зависимость от времени угла отклонения 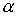 от нормали к плоскости
орбиты. Начальное вращение отсутствует от нормали к плоскости
орбиты. Начальное вращение отсутствует

Рис.6.1б.
Моделирование вращательного движения спутника при использовании магнитной
ориентации: зависимость от времени компонент вектора угловой скорости спутника.
Начальное вращение отсутствует
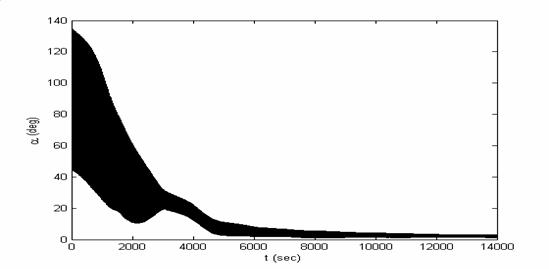
Рис.6.2a.
Моделирование вращательного движения спутника при использовании магнитной
ориентации: зависимость от времени угла отклонения 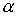 от нормали к плоскости
орбиты при начальной абсолютной угловой скорости от нормали к плоскости
орбиты при начальной абсолютной угловой скорости 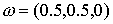 с-1 с-1
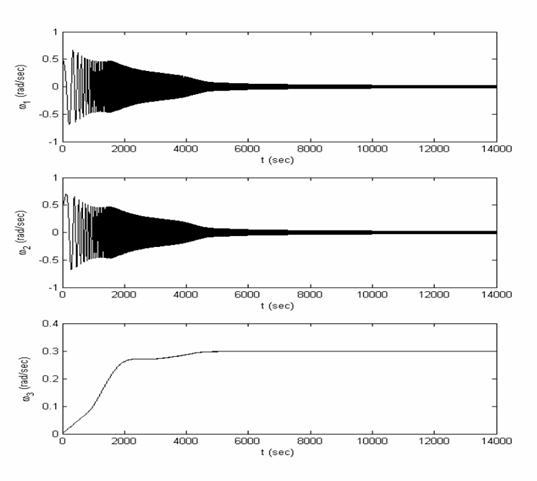
Рис.6.2б.
Моделирование вращательного движения спутника при использовании магнитной
ориентации: зависимость от времени компонент вектора угловой скорости спутника
при начальной абсолютной угловой скорости 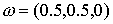 с-1 с-1
Моделирование
динамики спутника проведено при попеременном использовании алгоритмов
ориентации спутника, описываемого формулами (3.3) и (3.5), и алгоритма гашения
нутационного движения, описываемого формулой (3.10). Попеременное использование
двух алгоритмов осуществлялась следующим образом: сначала в течение определенного
интервала времени работал алгоритм ориентации спутника, а потом в течении
другого интервала времени работал алгоритм гашения нутационного движения.
Интервалы попеременной работы разных алгоритмов выбирались порядка нескольких
секунд. Уменьшение величины дипольного магнитного момента, создаваемого
спутником для управления, при уменьшении угла отклонения оси спутника от
требуемого направления производилось также в соответствии с формулами
(6.1)-(6.2). Параметры орбиты и спутника выбирались те же, что для предыдущего
случая, приведенные на стр.14. Требуемая ориентация спутника – по нормали к
плоскости орбиты. На рис.6.3 изображены зависимости отклонения оси спутника от
нормали к плоскости орбиты (рис.6.3а) и компонент угловой скорости от времени
(рис.6.3б) при следующих начальных условиях: ось симметрии спутника лежит в
плоскости орбиты, начальная абсолютная угловая скорость 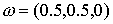 рад/с. рад/с.
Приведенные
результаты моделирования относятся к случаю ориентации спутника по нормали к
плоскости орбиты. Для ориентации спутника по направлению на Солнце, то есть под
углом к плоскости орбиты, графики переходных процессов получаются похожими за
исключением режима поддержания выбранной ориентации. Отличие заключается в том,
что в случае ориентации на Солнце возникает периодическое возмущение,
создаваемое гравитационным моментом. На рис.6.4 изображена зависимость
отклонения спутника от направления на Солнце, которое было выбрано отклоненным
от нормали к плоскости орбиты на 45 градусов. Начальные условия движения
спутника относительно его центра масс выбирались следующими: ось симметрии
спутника лежит в плоскости орбиты, начальная абсолютная угловая скорость 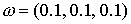 с-1. Рис.6.5 иллюстрирует режим поддержания
ориентации на Солнце. с-1. Рис.6.5 иллюстрирует режим поддержания
ориентации на Солнце.
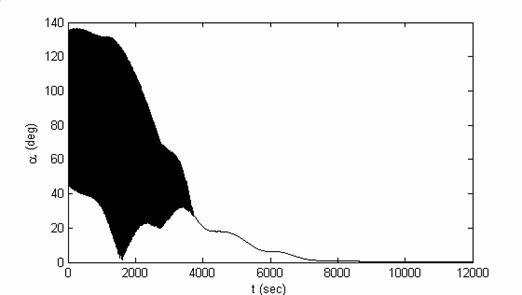
Рис.6.3a.
Моделирование вращательного движения спутника при использовании магнитной
ориентации с алгоритмом гашения нутационного движения: зависимость от времени
угла отклонения 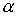 от нормали к плоскости
орбиты при начальной абсолютной угловой скорости от нормали к плоскости
орбиты при начальной абсолютной угловой скорости 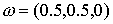 с-1 с-1
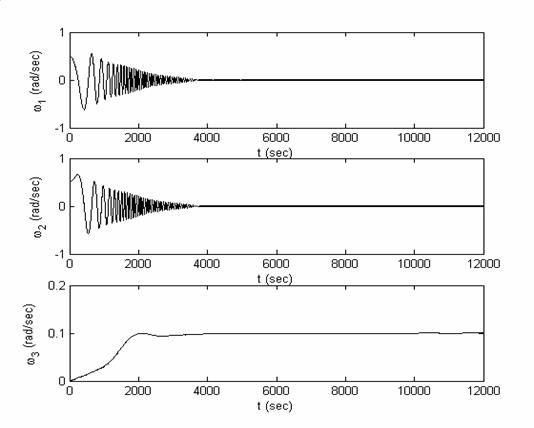
Рис.6.3б.
Моделирование вращательного движения спутника при использовании магнитной
ориентации с алгоритмом гашения нутационного движения: зависимость от времени
компонент вектора угловой скорости спутника при начальной абсолютной угловой
скорости 

Рис.6.4.
Зависимость отклонения спутника от направления на Солнце, которое отклонено от
нормали к плоскости орбиты на 45 градусов.
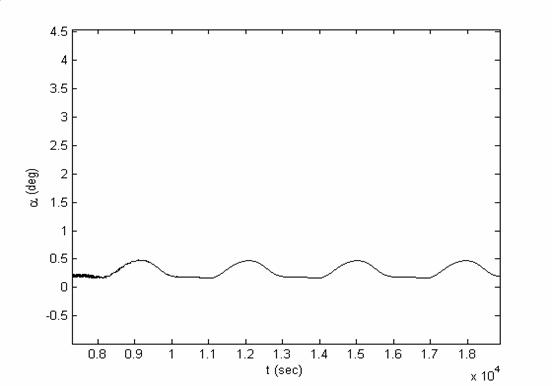
Рис.6.5.
Режим поддержания ориентации на Солнце. Изображена зависимость отклонения
спутника от направления на Солнце, которое составляет с нормали к плоскости
орбиты угол 45 градусов
Рассмотрим
энергопотребление спутника при ориентации его по нормали к плоскости орбиты и
по направлению на Солнце. В качестве величины, характеризующей потребляемую
энергию, будем использовать интеграл от квадрата величины магнитного дипольного
момента по времени
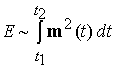 , (6.3) , (6.3)
исходя из того, что
дипольный момент катушки пропорционален току, по ней протекающему, а
рассеиваемая и, значит, потребляемая мощность пропорциональна квадрату тока. На
рис.6.6 и рис.6.7 представлен расход «энергии», то есть изменение величины
(6.3), для режима поддержания ориентации по нормали к плоскости орбиты и по
направлению на Солнце. Направление на Солнце в данном примере составляет угол в
45 градусов к нормали к плоскости орбиты. Для удобства сравнения графики
приведены при одном и том же изменении значений по «энергии» и по времени, то
есть разность между максимальным и минимальным значениями этих величин для двух
графиков одно и тоже, несмотря на различие их абсолютных значений. Из графиков
видно, что в случае поддержания ориентации на Солнце требуется непрерывно
затрачивать энергию, в отличие от случая поддержания ориентации по нормали к
плоскости орбиты. Величину затрачиваемой энергии в этом случае надо учитывать
при выборе режима ориентации оси вращения спутника.
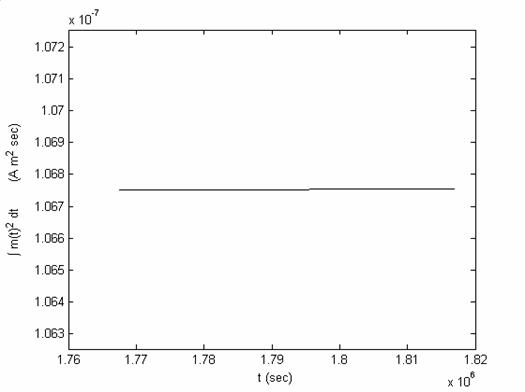
Рис.6.6.
Расход энергии для режима поддержания ориентации по нормали к плоскости орбиты
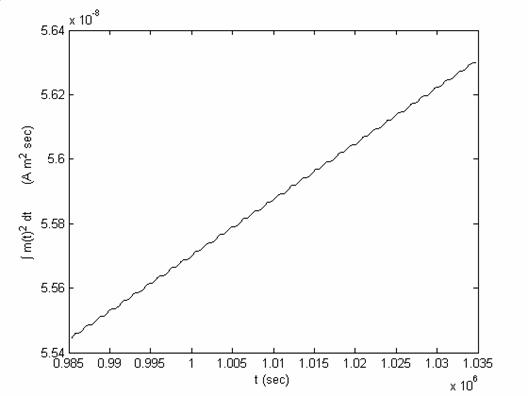
Рис.6.7.
Расход энергии для режима поддержания ориентации направления на Солнце, которое
отклонено от нормали к плоскости орбиты на 45 градусов
7.
Использование первого алгоритма при вычислении
ориентации и угловой скорости спутника с помощью магнитометра и солнечного
датчика
Результаты
моделирования, приведенные до этого, выполнены для идеального случая, когда в
каждый момент времени известна ориентация и угловая скорость спутника. На
практике ориентацию и угловую скорость спутника следует определять перед каждым
сеансом управления. Рассмотрим далее случай, когда эти величины необходимо
определять на основании измерений солнечного датчика и магнитометров.
7.1. Определение ориентации и угловой скорости
спутника локальным методом с помощью магнитометра и солнечного датчика
Локальный
метод позволяет определить угловое положение спутника в отдельной точке орбиты
при наличие пары известных неколлинеарных векторов, полученных измерениями в
связанной со спутником системе координат и вычисленных в некоторой базовой (в
нашем случае ‑ инерциальной) системе координат [11]. В нашем случае такой
парой векторов будут вектор напряженности геомагнитного поля 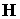 и вектор направления
на Солнце и вектор направления
на Солнце 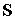 . .
Пусть на
борту спутника установлены датчики, позволяющие в определенные моменты времени
измерять векторы напряженности магнитного поля Земли 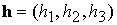 и единичный вектор и единичный вектор 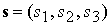 направления на Солнце,
задаваемые своими проекциями на оси связанной системы координат. В те же
моменты времени рассчитываем компоненты векторов направления на Солнце,
задаваемые своими проекциями на оси связанной системы координат. В те же
моменты времени рассчитываем компоненты векторов 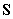 и и 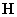 в инерциальной системе
координат: в инерциальной системе
координат: 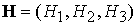 , , 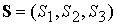 . Естественно для проведения таких расчетов необходимо знать
положение центра масс спутника в пространстве. Для тех моментов, когда спутник
находится в тени Земли или Солнце не попадает в поле зрения солнечного датчика,
локальный метод не работает. . Естественно для проведения таких расчетов необходимо знать
положение центра масс спутника в пространстве. Для тех моментов, когда спутник
находится в тени Земли или Солнце не попадает в поле зрения солнечного датчика,
локальный метод не работает.
Пусть матрица
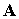 с элементами с элементами 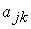 ( (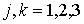 ) описывает переход от связанной со спутником к инерциальной
системе координат. Тогда можно записать четыре матричных соотношения ) описывает переход от связанной со спутником к инерциальной
системе координат. Тогда можно записать четыре матричных соотношения
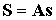 , , 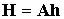 , , 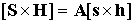 , , 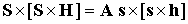 (7.1) (7.1)
Составим матрицу из трех
взаимно ортогональных единичных векторов и запишем связь между измеренными и
вычисленными векторами с помощью этой матрицы
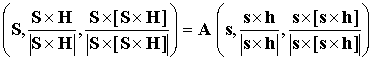 . (7.2) . (7.2)
Из этого выражения следует,
что матрицу 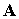 можно вычислить по
формуле можно вычислить по
формуле
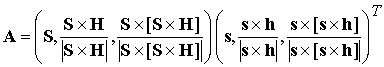 . (7.3) . (7.3)
Угловую
скорость спутника определим методом конечных разностей, используя вычисленные
по вышеприведенным формулам значения матрицы направляющих косинусов, по формуле
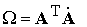 . (7.4) . (7.4)
Воспользуемся формулой 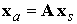 раздела 2. Пусть раздела 2. Пусть 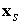 ‑ радиус-вектор точки твердого тела. Тогда
распределение скоростей в теле относительно ИСК выражается через угловую
скорость тела по формуле Эйлера ‑ радиус-вектор точки твердого тела. Тогда
распределение скоростей в теле относительно ИСК выражается через угловую
скорость тела по формуле Эйлера 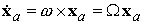 . Здесь матрица . Здесь матрица
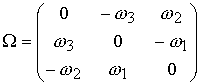 . (7.5) . (7.5)
выражается через проекции
вектора абсолютной угловой скорости спутника на неподвижные оси. С другой
стороны, дифференцируя формулу 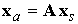 по времени, имеем по времени, имеем 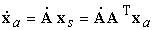 . Подставляя в левую часть выражение для . Подставляя в левую часть выражение для 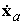 из формулы Эйлера,
разрешая полученное выражение относительно матрицы угловых скоростей и приводя
матрицу к осям, связанным с телом путем ее умножения справа на матрицу A, а слева на AT, получим выписанное выше выражение для матрицы W через проекции вектора абсолютной угловой
скорости спутника на связанные с телом оси. Для повышения точности выбирается
среднее по двум соответствующим элементам значение компоненты угловой скорости
(назовем эту операцию - усреднение по двухточечной схеме). Производная из формулы Эйлера,
разрешая полученное выражение относительно матрицы угловых скоростей и приводя
матрицу к осям, связанным с телом путем ее умножения справа на матрицу A, а слева на AT, получим выписанное выше выражение для матрицы W через проекции вектора абсолютной угловой
скорости спутника на связанные с телом оси. Для повышения точности выбирается
среднее по двум соответствующим элементам значение компоненты угловой скорости
(назовем эту операцию - усреднение по двухточечной схеме). Производная 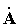 матрицы матрицы 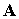 в момент времени в момент времени 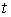 вычислялась так: вычислялась так:
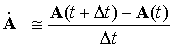 . (7.6) . (7.6)
Интервал времени 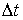 подбирается
эмпирически, исходя из возможной скорости осевого вращения спутника. Результаты
моделирования для различных интервалов подбирается
эмпирически, исходя из возможной скорости осевого вращения спутника. Результаты
моделирования для различных интервалов 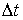 приведены на рис.7.1,
7.2 и 7.3. На графиках показаны для сравнения проекции вектора приведены на рис.7.1,
7.2 и 7.3. На графиках показаны для сравнения проекции вектора 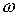 (сплошные линии) и
эти же проекции, вычисленные по методу конечных разностей (пунктирные линии),
на разных интервалов времени равных (сплошные линии) и
эти же проекции, вычисленные по методу конечных разностей (пунктирные линии),
на разных интервалов времени равных 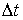 = 1, 3 и 5 сек. В приведенных примерах считается,
что определение ориентации спутника в требуемые моменты времени производилось
без ошибок. Результаты моделирования работы системы ориентации при наличии
ошибок измерения солнечного датчика будет представлено в последующем разделе. = 1, 3 и 5 сек. В приведенных примерах считается,
что определение ориентации спутника в требуемые моменты времени производилось
без ошибок. Результаты моделирования работы системы ориентации при наличии
ошибок измерения солнечного датчика будет представлено в последующем разделе.
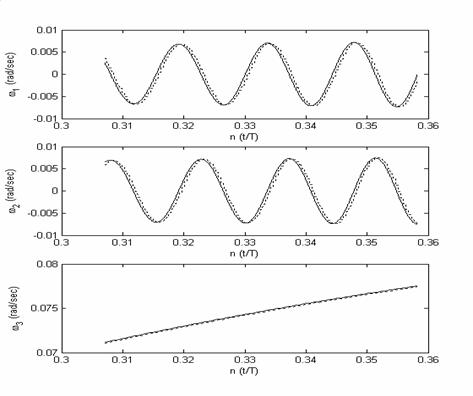
Рис.7.1.
Результат моделирования построения оценки угловой скорости  , вычисленной по методу конечных разностей при интервале
времени между двумя измерениями , вычисленной по методу конечных разностей при интервале
времени между двумя измерениями  = 1 сек. = 1 сек.
Рис.7.2.
Результат моделирования построения оценки угловой скорости  , вычисленной по методу конечных разностей при интервале
времени между двумя измерениями , вычисленной по методу конечных разностей при интервале
времени между двумя измерениями 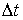 = 3 сек = 3 сек
Рис.7.3.
Результат моделирования построения оценки угловой скорости  , вычисленной по методу конечных разностей при интервале
времени между двумя измерениями , вычисленной по методу конечных разностей при интервале
времени между двумя измерениями  = 5 сек = 5 сек
7.2.
Моделирование вращательного движения спутника c магнитной системы
ориентации, использующей первый алгоритм, при вычислении угловой скорости с
помощью показаний магнитометров и солнечного датчика
Для
моделирования вращательного движения спутника рабочее время разбивалось на
несколько интервалов, в течение которых производились следующие действия:
1. моделирование первого измерения солнечного
датчика и магнитометров
2. пауза в течение времени 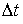
3. моделирование второго измерения солнечного
датчика и магнитометров
4. оценка ориентации и угловой скорости
спутника на основании измерений, сделанных в два разные моменты времени
5. моделирование управляющего магнитного
момента для управления ориентацией спутника
6. моделирование управляющего магнитного
момента для гашения нутационного движения спутника
Приведенная выше
последовательность действий повторялась циклически.
Чтобы
исключить эффект перерегулирования, при гашении нутационных колебаний так же,
как это было сделано при управлении ориентацией спутника, производилось
уменьшение величины создаваемого дипольного момента 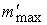 в соответствии со
следующими формулами: в соответствии со
следующими формулами:
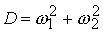 ,
(7.7) ,
(7.7)
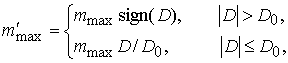 (7.8)
(7.8)
где 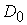 является подстроечным
параметром, величина которого выбиралась равной является подстроечным
параметром, величина которого выбиралась равной 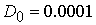 . .
При
моделировании вращательного движения использовались оскулирующие элементы
орбиты и параметры спутника, приведенные на стр.14. Начальная ориентация
спутника: ось симметрии лежит в плоскости экватора и отклонена от нормали к
плоскости орбиты на 90 градусов. Начальная угловая скорость спутника 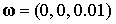 . .
На
рис.7.4 - 7.7 представлены результаты моделирования вращательного
движения спутника при использовании магнитной ориентации с построением оценки
ориентации и угловой скорости спутника на основании двух измерений, сделанных в
разные моменты времени. На рисунках изображена зависимость от времени угла
отклонения 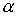 либо от нормали к плоскости
орбиты, либо от направления на Солнце, которое отклонено от нормали к плоскости
орбиты на 45 градусов. Интервал между измерениями был выбран равный либо от нормали к плоскости
орбиты, либо от направления на Солнце, которое отклонено от нормали к плоскости
орбиты на 45 градусов. Интервал между измерениями был выбран равный 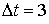 сек для всех представленных случаев. На рис. 7.4,
7.5 изображены результаты, полученные при моделировании измерений магнитометра
и солнечного датчика без погрешностей. Из графиков видно, что если измерения не
зашумлены, то движение спутника мало чем отличается от случая, когда ориентация
и угловая скорость спутника известны. На рис. 7.6, 7.7 изображены результаты,
полученные при моделировании измерений солнечного датчика с ошибкой. Для
моделирования ошибки измерения солнечного датчика использовалась случайная
величина, имеющая нормальное распределение с нулевым математическим ожиданием и
со среднеквадратичном отклонением в 3 градуса. Измерения моделируемого
магнитометра были не зашумлены. сек для всех представленных случаев. На рис. 7.4,
7.5 изображены результаты, полученные при моделировании измерений магнитометра
и солнечного датчика без погрешностей. Из графиков видно, что если измерения не
зашумлены, то движение спутника мало чем отличается от случая, когда ориентация
и угловая скорость спутника известны. На рис. 7.6, 7.7 изображены результаты,
полученные при моделировании измерений солнечного датчика с ошибкой. Для
моделирования ошибки измерения солнечного датчика использовалась случайная
величина, имеющая нормальное распределение с нулевым математическим ожиданием и
со среднеквадратичном отклонением в 3 градуса. Измерения моделируемого
магнитометра были не зашумлены.

Рис.7.4.
Моделирование вращательного движения спутника при использовании магнитной
ориентации с построением оценки ориентации и угловой скорости спутника.
Изображена зависимость от времени угла отклонения 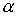 от нормали к плоскости
орбиты от нормали к плоскости
орбиты
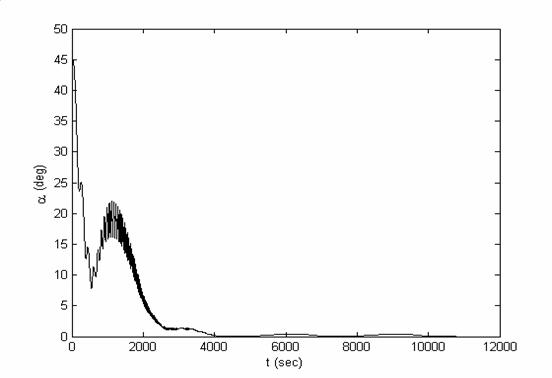
Рис.7.5.
Моделирование вращательного движения спутника при использовании магнитной
ориентации с построением оценки ориентации и угловой скорости спутника.
Изображена зависимость от времени угла отклонения 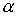 от направления на
Солнце, которое отклонено от нормали к плоскости орбиты на 45 градусов от направления на
Солнце, которое отклонено от нормали к плоскости орбиты на 45 градусов
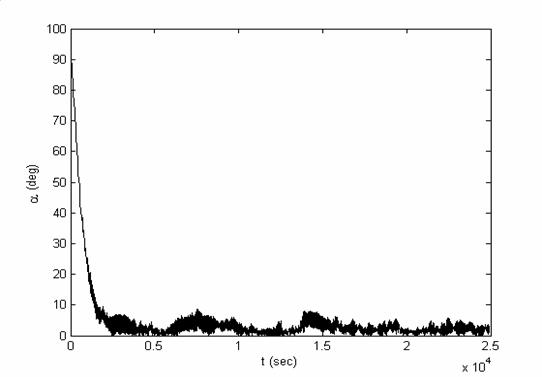
Рис.7.6.
Моделирование вращательного движения спутника при использовании магнитной
ориентации с построением оценки ориентации и угловой скорости спутника по
зашумленным измерениям. Изображена зависимость от времени угла отклонения 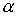 от нормали к плоскости
орбиты от нормали к плоскости
орбиты
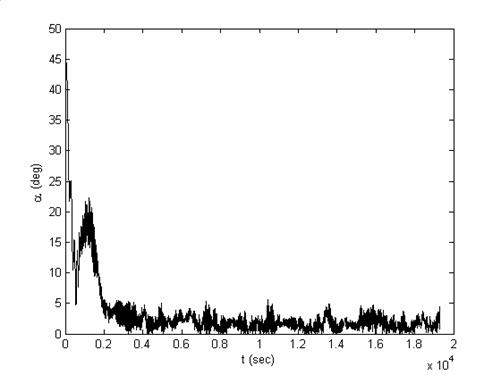
Рис.7.7.
Моделирование вращательного движения спутника при использовании магнитной
ориентации с построением оценки ориентации и угловой скорости спутника по
зашумленным измерениям. Изображена зависимость от времени угла отклонения 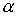 от направления на
Солнце, которое отклонено от нормали к плоскости орбиты на 45 градусов от направления на
Солнце, которое отклонено от нормали к плоскости орбиты на 45 градусов
8.
Моделирование вращательного движения спутника c магнитной системой
ориентации, использующей второй алгоритм
Было
проведено компьютерное моделирование вращательного движения спутника с
использованием рассматриваемого алгоритма ориентации. Для моделирования
вращательного движения использовались оскулирующие элементы орбиты и параметры
спутника, приведенные в разделе 6, за исключением мощности магнитных катушек. В
настоящем примере моделировалась работа четырех катушек установленных на
спутнике: две взаимно перпендикулярные катушки в экваториальной плоскости
спутника мощностью 0.1 А×м и две катушки (большая и малая) расположенные
вдоль оси симметрии спутника мощностью 0.8 А×м и две катушки (большая и малая) расположенные
вдоль оси симметрии спутника мощностью 0.8 А×м и 0.2 А
×
м
и 0.2 А
×
м
 . .
Ориентация
спутника рассматриваемым методом осуществляется в три этапа. На первом этапе
длительностью 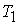 с помощью большой и
малой катушки, направленной вдоль оси симметрии спутника, по закону управления
(4.11) производится гашение компонент с помощью большой и
малой катушки, направленной вдоль оси симметрии спутника, по закону управления
(4.11) производится гашение компонент  и и 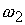 угловой скорости,
приобретенной спутником после отделения от ракеты-носителя. угловой скорости,
приобретенной спутником после отделения от ракеты-носителя.
На втором
этапе длительностью 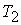 производится закрутка
спутника с помощью катушек расположенных в экваториальной плоскости спутника по
закону управления (4.9). Оценка скорости закрутки производится на основании
формулы (4.12). При этом малая катушка используется также для гашения
нутационного движения. Большая катушка выключена. производится закрутка
спутника с помощью катушек расположенных в экваториальной плоскости спутника по
закону управления (4.9). Оценка скорости закрутки производится на основании
формулы (4.12). При этом малая катушка используется также для гашения
нутационного движения. Большая катушка выключена.
Третий этап
продолжается в течение всего времени функционирования спутника. На этом этапе
осуществляется ориентация спутника с помощью большой катушки на основании
закона управления (4.4). Малая катушка используется для гашения нутационного
движения спутника. Также при необходимости с помощью катушек расположенных в
экваториальной плоскости спутника осуществляется поддержание заданной скорости
вращения.
На рис.8.1
изображены зависимости от времени отклонения спутника от направления на Солнце
(рис.8.1а) и компоненты угловой скорости (рис.8.1б). В приведенном примере
направление на Солнце отклонено от нормали к плоскости орбиты на 45 градусов и
лежит в плоскости экватора. Начальные условия: ось симметрии спутника лежит в
плоскости орбиты, начальная абсолютная угловая скорость 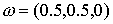 рад/с. Длительность
первого и второго этапов алгоритма ориентации в приведенном случае выбирались
следующим образом рад/с. Длительность
первого и второго этапов алгоритма ориентации в приведенном случае выбирались
следующим образом 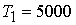 с, с, 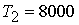 с. с.
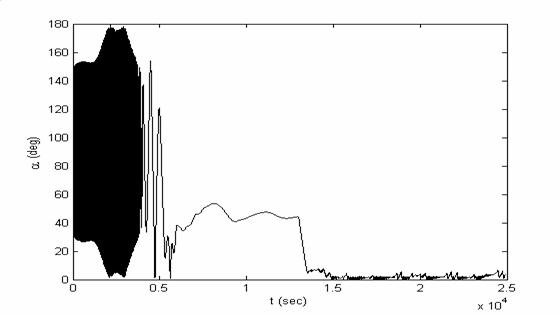
Рис.8.1а.
Моделирование вращательного движения спутника при использовании магнитной
ориентации: зависимость от времени угла отклонения 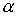 от направления на
Солнце от направления на
Солнце
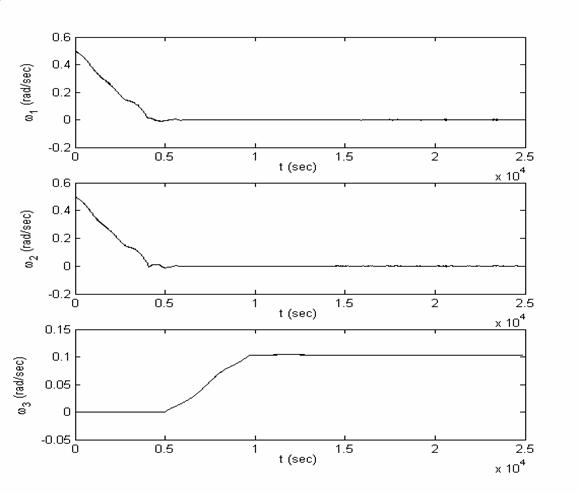
Рис.8.1б.
Моделирование вращательного движения спутника при использовании магнитной
ориентации: зависимость от времени компонент вектора угловой скорости спутника.
9.
Заключение
Проведено детальное численное моделирование вращательного движения
спутника, стабилизируемого собственным вращением, с магнитной системой
ориентации для двух различных автономных алгоритмов управления токовыми
катушками. Показано, что для спутника с параметрами, соответствующими
наноспутнику ТНС-1, снабженного трехосным магнитометром и солнечным датчиком,
целесообразно применять второй алгоритм, не использующий измерения угловой
скорости спутника.
10. Благодарности
Работа
выполнена при финансовой поддержке Российского фонда фундаментальных
исследований (грант № 03-01-00652), Государственного контракта с Федеральным
Агенством по науке и инновациям (№ 02.700.12.050), контракта с РНИИ КП,
Программы Президента Российской Федерации для поддержки молодых российских
ученых и ведущих научных школ (грант № НШ-2003.2003.1) и гранта Landan Network Centro Volta
(2005 г.).
Литература
1. Ильин А.А.,
Овчинников М.Ю., Пеньков В.И., Обеспечение
ориентации малого спутника, стабилизируемого собственным вращением, М.: Препринт ИПМ
им.М.В.Келдыша РАН, 2004, N 83.
2. Фишелл Р.Э., Стабилизация вращения спутников, Автоматическое
управления космическими летательными аппаратами (Труды I Международного
симпозиума ИФАК по автоматическому управлению в мирном использовании
космического пространства) М.: «Наука», 1968.
3. Мангер В. П., Управления пространственным
положением метеоро-логических спутников "Тирос". Автоматическое
управления космическими летательными аппаратами (Труды I Международного
симпозиума ИФАК по автоматическому управлению в мирном использовании
космического пространства) М. «Наука» 1968.
4. Гехт Е., Менджер У.П., Магнитная система
управления угловым положением спутников серии "Тайрос". Проблемы
ориентации искусственных спутников Земли. М. «Наука» 1966.
5. Кейглер Дж. Е., Точная система ориентации
для усовершенствованного варианта ИСЗ "Тирос". Управления
космическими аппаратами и кораблями (Труды II Международного симпозиума ИФАК по
автоматическому управлению в мирном использовании космического пространства) М.
Наука 1971.
6. Ю.М.Урличич, А.С.Селиванов, Ю.М.Тучин. Проект
технологического наноспутника ТНС-1 для дистанционного зондирования Земли.
Доклад на научно-практической конференции «Авиакосмические системы на базе
микротехнологий», С.-Петербург, 9-11 июня 2003г.
7. Шегехара М., Выбор законов управления
угловым положением вращающихся спутников, Управление в пространстве, (Труды V
Международного симпозиума ИФАК по автоматическому управлению в пространстве),
т.1, М.: «Наука», 1975.
8. Shigehara
M, Geomagnetic Attitude Control of an Axisymmetric Spinning Satellite, J. of
Spacecraft and Rocket, June 1972, v.9, N6, pp 391-398.
9. Hur Ph.,
Melton R., Spencer D., Meeting Science Requirements For Attitude Determination аnd
Control in а Low-Power, Spinning Nanosatellite Paper IAC-04-IAF-A.4.05 at the
55th Congress IAF, 4-8 Oct., 2004, Vancouver,
Canada.
10. Нохрина Е.Е. Исследование возможности демпфирования
колебаний спутника. В сб.: Обработка информации и моделирование М., МФТИ, 2002,
с.119-122.
11. Барабаш С.В., Кирюшкин И.Ю., Норберг У.,
Овчинников М.Ю., Пеньков В.И., Методы определения углового движения
наноспутника Munin, М.: Препринт ИПМ им.М.В.Келдыша РАН, 2003, N 24.
|