Введение

Основной целью данной работы является обзор принципов построения динамических моделей в экологии, а также представление локально-экологического подхода к моделированию экосистем и приложение его принципов к исследованию и прогнозу развития среднеширотного двувидового леса. Основной акцент делается на построение принципиальных взаимодействий динамической системы ресурс – двувидовой лес – окружающая среда на основании экспериментально полученных данных и закономерностей. Приводятся предварительные результаты компьютерного моделирования.

В последнее время для решения практических задач все шире применяется моделирование динамики развития экосистем на основе дифференциальных и интегро-дифференциальных уравнений. Данный подход широко используется для моделирования разнообразных биологических сообществ и, в частности, лесных массивов [1,2].

Модели развития экосистем можно разделить на два больших класса:

·                              непрерывные (на основе обыкновенных дифференциальных уравнений для сосредоточенных моделей и дифференциальных уравнений в частных производных для пространственно-распределенных систем)

·                              дискретные (на основе систем алгебраических уравнений, которые в большинстве случаев можно получить путем дискретизации дифференциальных уравнений; в пространственно-распределенном случае это характерные модели, называемые клеточными автоматами).

Разумеется, перед применением как непрерывных, так и дискретных, моделей необходимо доказать их адекватность. Для этого используются хорошо известные методики [1], в частности, ретроспективный анализ. В разработку модели мы включаем следующие позиции.

·                              Биологическую  формулировку модели  и области  ее применимости (основные концепции, обоснование структуры, априорная оценка возможностей прогнозирования, перечень моделируемых воздействий и т.д.)

·                              Математическую формулировку (применяемый математический аппарат, организация вычислений, программные средства и т.д.)

·                              Адекватность моделей, т.е. их соответствие реальному объекту, куда входят  способы оценки адекватности (по  асимптотическому поведению, путем сравнения с  наблюдениями).  Здесь же надо выяснить вопросы  непрерывной зависимости от начальных данных, параметров системы, допустимые области их задания и другие вопросы.

В данной работе мы постарались привести обзор классических моделей в экологии, завершая его построением своей собственной модели, относящейся к вычислительной экологии лесов.

ЧАСТЬ.1 КЛАССИЧЕСКИЕ МОДЕЛИ

1.1. Логистическая модель: развитие отдельной популяции

Наиболее простым описанием динамики отдельно взятой популяции может служить так называемая логистическая модель, предложенная П.Ферхлюстом в прошлом веке для описания динамики человеческого населения и Р.Пёрлом уже в 20-ые годы нашего столетия применительно к биологическим сообществам. Согласно ей, динамика численности популяции (либо плотности биомассы) u описывается обыкновенным дифференциальным уравнением [2]:

,                                                                                                   (1)                

где a=const представляет собой максимальную удельную скорость роста популяции, коэффициент b=const описывает внутривидовую конкурентную борьбу. Коэффициент a представляет собой разность между естественным приростом С и смертностью D в популяции: a=С–D. Вообще говоря, численность популяции может изменяться в результате всего четырёх факторов: рождаемости, смертности, эмиграции и иммиграции. Если рассматриваются сосредоточенные модели, то учитываются только первые два из них; если требуется построить пространственно-распределённую модель, то необходимо учитывать все четыре фактора. 

При малых u (т.е. когда можно положить bu²<<au) логистическое уравнение  описывает экспоненциальное увеличение плотности биомассы: . Такой быстрый рост соответствует, например, развитию молодой популяции, повсеместно наблюдаемому в природе. Кроме того, экспоненциальный рост часто наблюдается на отдельных промежутках времени при стечении благоприятных факторов развития популяции.

Следует сразу заметить, что прирост биомассы, согласно (1), пропорционален первой степени u. Это характерно для лесных популяций,  для которых общий прирост биомассы деревьев, например за год, приблизительно пропорционален общему количеству биомассы). В других случаях необходимо учитывать специфику той или иной популяции. Если в основе размножение лежит скрещивание, предполагающее встречи между разнополыми особями, то прирост будет пропорционален u² [2].

Очевидно, что неограниченное возрастание биомассы невозможно. Начиная с некоторого момента, оно будет тормозиться в результате недостатка ресурса, конкуренции внутри популяции, передачи инфекции из-за тесноты и т.п. Поэтому многие популяции, попав в новое место обитания, обнаруживают так называемый S-образный рост численности. Т.е. кривая временной зависимости численности имеет ярко выраженную S-образную форму[3]. Нетрудно видеть, что логистическое уравнение (1) описывает все эти основные свойства развития отдельной популяции. Его аналитическое решение даётся формулой логистической функции

,                                                                          (2)

где равновесное значение биомассы u^max=a/b. График (2), изображённый на рис.1, имеет S-образную форму.

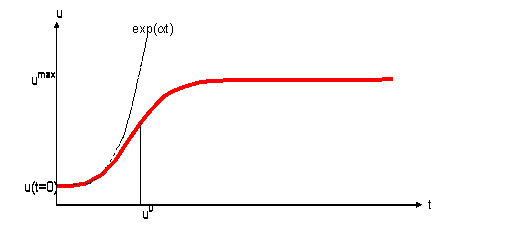Рис.1. Логистическая функция (1).

В природе, как правило, максимальная плотность любой популяции, которая может устойчиво существовать в данной экосистеме, ограничена сверху определённой величиной u^max, называемой ёмкостью среды. Известно огромное количество экспериментальных подтверждений логистической модели [2]. Развитие разнообразных популяций, как простейших микроорганизмов, так и высших животных и растений укладывается в эту схему. А именно, при малой исходной плотности биомассы u(t=t­­­_{0­­­­­­}), начальный рост популяции будет почти экспоненциальный с показателем экспоненты a. Поэтому его иногда называют «биотическим потенциалом» популяции, т.е. максимальными возможностями роста численности при самых благоприятных внешних условиях. Экспоненциальный рост означает, что вначале популяция растёт медленно (du/dt мало), но по мере увеличения размеров скорость роста увеличивается (с ростом u).

Пока плотность биомассы достаточно мала, отдельные представители популяции не оказывают друг на друга значительного виляния. Однако при некоторой плотности биомассы (приблизительно равной u⁰ на рис.1) начинают сказываться тормозящие эффекты (конкуренция и прочее), рост популяции замедляется, стремясь к асимптотическому значению u^max, определяемому внешними условиями существования. Применительно к лесным популяциям, основными тормозящими факторами являются взаимное затемнение деревьями друг друга и конкурентная борьба за водные и почвенные ресурсы. Плодородие лесной почвы определяет в итоге максимальную равновесную плотность биомассы u^max.

Даже такое простое описание логистической моделью (1) имеет важное значение для биологического прогноза развития популяции, подвергаемой промыслу. Зная основные параметры модели (биотический потенциал и ёмкость среды), можно с достаточной точностью предсказать оптимальную плотность биомассы, которую необходимо поддерживать в культивируемой популяции для сохранения устойчивой возможности воспроизводства.

С физической точки зрения, объяснить значение коэффициентов логистической модели (1) удобно посредством введения нелинейного (зависящего от u)  коэффициента естественного прироста С(u, u₀).

                                                                                          (3)

Разумно предположить, что при малых значениях u отдельные особи не оказывают друг на друга никакого влияния, и поправочный коэффициент может быть взят равным 1. При очень больших (выше некоторого порогового u_tr) рост прекращается вовсе (коэффициент близок к 0), а при средних значениях u он плавно уменьшается от 1 до 0 при росте u. Два из возможных вариантов поправочной функции С(u, u₀) приведены на рис.2, причем кусочно-линейная функция (с наклонным участком) как раз и соответствует логистической модели (1).

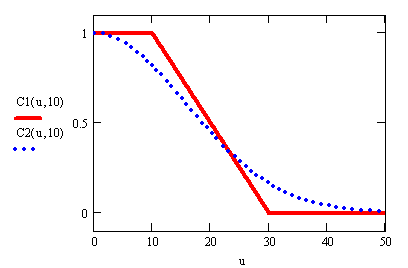
Рис.2. Поправочные коэффициенты естественного прироста

Рис.3. Решения логистического уравнения

Решения задачи Коши для дифференциального уравнения (3), с приведенными на рис.2 коэффициентами, показаны на рис.3. Из их сравнения видно, что выбор конкретного вида С(u, u₀) не влияет на качественное поведение решения, а адекватные параметры модели (скорость экспоненциального роста и емкость среды) могут быть найдены путем ретроспективного анализа данных эксперимента, например, при помощи построения регрессии.

Основная роль, отводимая логистическому уравнению в настоящей работе, следующая. Очевидно, что при наличии благоприятных внешних условий (при некоторой плотности ресурса) свободно развивающаяся популяция деревьев одного вида должна следовать логистическому росту. Значит, более сложные модели должны в этом случае давать результаты, сходные с (2). С другой стороны это означает, что основные параметры (биотический потенциал и ёмкость среды для деревьев данного вида) могут быть, для конкретизации общей модели, взяты из анализа упрощённой логистической модели. Как правило, данные о логистическом росте тех или иных пород, известны достаточно точно по результатам полевых наблюдений за посадками леса и характеристиками почвы.

1.2. Основные межвидовые взаимодействия

Модели отдельной популяции, наиболее простой из которых является модель (3), могут достаточно точно описывать динамику популяции  и в случае её взаимодействия с другими участниками биоценоза. Для этого в уравнение включаются соответствующие члены, выражающие влияние на численность данной популяции со стороны тех или иных видов. В действительности же лесной биоценоз включает в себя конкурирующие между собой деревья   разных пород, изменяющиеся водные и почвенные ресурсы. Уже в случае двух сосуществующих видов динамика популяций значительно усложняется, и появляется необходимость применять новые подходы для анализа и прогнозирования развития экосистемы.

Наиболее общие принципы построения математических моделей были сформулированы Вольтерра в начале нашего века [4]. Им были рассмотрены модели экосистем, состоящих из нескольких видов и запаса потребляемого ими ресурса. Гипотеза Вольтерра состоит в следующем. Доля ресурса, потребляемого каждым видом в единицу времени, пропорциональна плотности биомассы этого вида, взятой с некоторым коэффициентом, выражающим межвидовую конкуренцию. Если вид питается пищей, имеющейся в ограниченном количестве, то прирост его биомассы пропорционален количеству съеденной пищи; если количество ресурса не ограничено, то прирост пропорционален величине биомассы. В каждую единицу времени отмирает постоянная доля существующих особей, эта доля или коэффициент естественной смертности зависит от вида. Если рассматриваются система «хищник–жертва», то скорость как размножения хищника, так и гибели жертв, пропорциональна вероятности встреч особей хищника и жертвы.

В настоящее время для классификации возможных взаимодействий в экосистемах предлагается следующая формальная процедура [2]: каждой паре видов сопоставляется три символа: либо «плюс» (когда изменение численности одного вида вызывает аналогичное изменение численности другого), либо «нуль» (при отсутствии влияния), либо «минусом» (когда изменение численности одного вида вызывает обратное  изменение численности другого). Эти категории биотических взаимодействий приведены в таблице 1.

Таблица 1.

При таком описании межвидовых отношений в лесном биоценозе  к конкуренции  можно отнести любые взаимодействия между деревьями разных видов:  соперничество за свет, влагу или минеральное питание.

Общая двухвидовая модель, которую мы будем обсуждать во 2-й части работы, включает элементы  указанных  взаимодействий. Поэтому остановимся подробно  на трёх из шести типах взаимодействия.

Мутуализм (симбиоз). Это типичный пример взаимодействия зелёных растений – главных производителей  органического вещества – с азотофиксирующими прокариотами и микоризообразующими грибами. Ниже, при построении моделей леса  мы будем использовать обобщённый показатель плодородия почвы р,  который  определяет рост биомассы u. При симбиозе увеличение плодородия почвы за счёт переработки ежегодного опада и отмершей биомассы превышает истощение почвы вследствие  питания растений.

В системе уравнений (4) плодородие  р    пропорционально биомассе микрофлоры. Поэтому  скорость роста р пропорциональна самому плодородию (т.е. биомассе микрофлоры), а также биомассе деревьев, которые в результате опада и отмирания дают пищу для  микроорганизмов почвы. В уравнениях  это последнее слагаемое. Отрицательные члены - это внутривидовая конкуренция:

                                                                  (4)

     Эта система имеет ограниченное решение только при единственном условии:

 В последнем несложно убедиться, если перейти к рассмотрению  системы на фазовой плоскости.   Главные изоклины обоих уравнений пересекаются только при этом условии.   Легко получить и  нашу  прямоугольную область  устойчивости, так как  система допускает траектории u=0  и p=0.  Две другие стороны, параллельные координатным осям, должны окаймлять прямоугольник содержащий точку пересечения изоклин.  Через стороны этого прямоугольника траектории системы могут только входить. Одно из требований адекватности выполнено. Точек покоя  здесь   четыре (рис. 4): неустойчивый узел в нуле,  седловая точка на оси ординат и седловая точка на оси абсцисс, а также четвертая точка —  устойчивый узел координаты которой получаются в результате приравнивания нулю правых частей системы (4). Соответствующий фазовый портрет для узла дан на рис. 5.

Рис.4. Точки покоя системы уравнений симбиоза

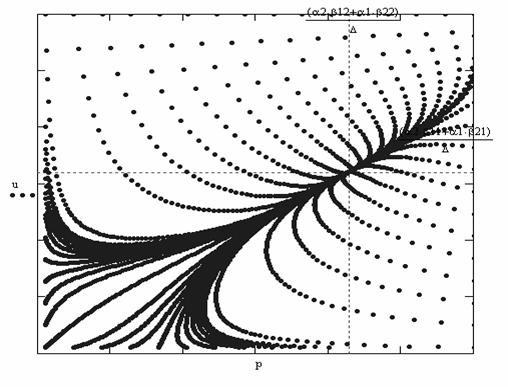
           Рис.5. Фазовый портрет системы уравнений симбиоза

Может возникнуть вопрос, как ведут себя траектории, когда устойчивости нет.   В этом случае из точек покоя в первой четверти исчезает точка пересечения изоклин   Р1(u,p)=0 и R1(u,p)=0.  Два седла и неустойчивый узел остаются.  Однако получить фазовый портрет  для произвольного времени не удается, так как решение за конечный промежуток времени уходит на бесконечность. Из приведенного на рис.6 фазового портрета видно, что в этом случае  из любой точки плоскости  мы попадем на  бесконечность.

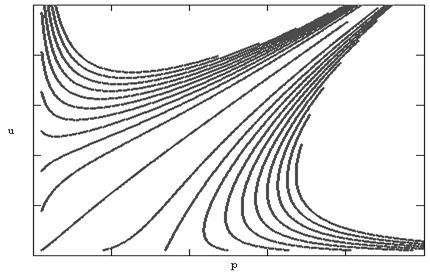
 Рис.6. Фазовый портрет модели симбиоза (неустойчивость)

Может возникнуть вопрос,  можно ли для  расчетов реальных систем пользоваться  неустойчивыми моделями. Из рисунка 6 видно, что траектории для некоторого, очень малого,  значения времени могут рассчитываться достаточно успешно. Ситуация здесь вполне аналогична использованию  моделей экспоненциального роста для начального  периода в логистической модели. Другими словами, применение неустойчивых моделей можно рассматривать как  приближенный метод.

Конкуренция.   Система, описывающая конкуренцию между двумя видами с плотностью биомассы u1, u2, базируется на обобщении логистического уравнения (1)

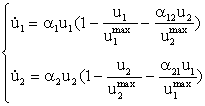,                                                (5)      

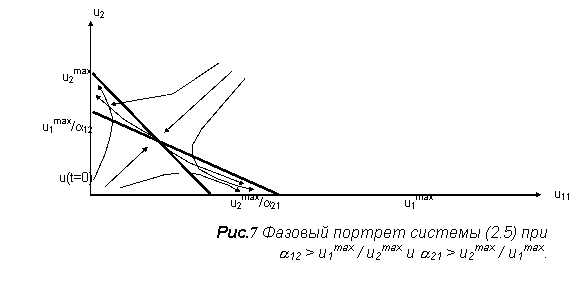
Её поведение может быть охарактеризовано с помощью фазового портрета на плоскости с координатами (u1, u2) [2]. Здесь же содержится несколько вероятных сценариев эволюции, в зависимости от начального значения плотности биомассы. На рис.7 изображён один из четырёх возможных путей развития двувидовой системы с конкуренцией, описываемой системой (5).

Эта система похожа на разобранную систему симбиоза, за исключением знаков перед коэффициентами.   Из рис.7 видно, что изоклины могут пересекаться  в 1 четверти в двух вариантах: когда точка пересечения с осью ординат изоклины для   первого уравнения,  выше  аналогичной точки  изоклины второго уравнения и  наоборот.

Также возможны два случая, когда  изоклины не пересекаются в первой четверти (один вариант - первая изоклина  выше, второй вариант - наоборот). По виду правых частей ясно, что   для всех четырех вариантов  можно построить для переменных  модели прямоугольную область «адекватности». Значит, все четыре случая дают устойчивые модели. 

Эти комбинации также можно получить из рис.7: если a12 < 1 и a21 >1, то конкурентную борьбу со временем выигрывает первый вид, если a12 >1 и a21 < 1, то побеждает второй. При a12 < 1 и a21 < 1, реализуется устойчивое сосуществование видов, а в последнем случае (представленном на рисунке)     исход конкуренции определяется начальным соотношением численностей [2].

Хищник—жертва. Классическая модель Вольтерра [4] хищника (u) и жертвы (Р),описывается системой:

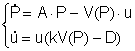                                                                                                     (6)           

где V(P) – монотонно возрастающая функция Р (называемая трофической), равная биомассе жертв, потребляемой хищником в единицу времени, причём на воспроизводство хищником тратится часть полученной от «поедания» жертвы  биомассы.

При малых Р: V(P)=P/P0 Вольтерра показал, что система (6) имеет интеграл вида

,        где                                        (7)             

Этот результат можно получить, если провести  разделение переменных.  Приведенный интеграл в неявном виде задает траектории системы. Польза от этого  интеграла невелика, так как по его виду  не так просто получить траектории системы.

       Однако с помощью процедуры линеаризации системы можно определить точки покоя. Одна точка (0,0)-  седло,   вторая ( чисто мнимые  характеристические числа)  центр . Система негрубая.  Точки покоя и фазовый портрет приведены на рис.8. Негрубая  модель " жертва-хищник "   очень нравится биологам, так как она дает волны  биомасс жертв и хищников, которые действительно наблюдаются на опыте.

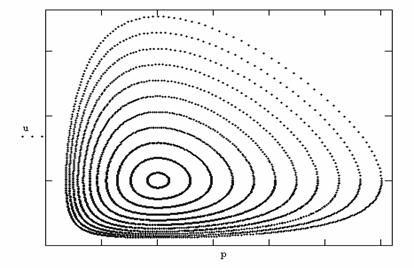
Рис8. Фазовый портрет модели  Хищник­-жертва

 Рис.9. Модель  Хищник­-жертва  с конкуренцией среди жертв

Поскольку негрубые модели  не адекватны, то  возникло стремление подправить модель так, чтобы негрубость ушла, а волны остались.  Одна из таких попыток - добавить в уравнение для жертвы учет конкурентной внутривидовой  борьбы. Эта добавка- отрицательный квадратичный член в уравнении для жертвы Негрубость модели может быть устранена путём введения внутривидовой конкуренции среди жертв путем добавления в первое уравнение слагаемого (-gР²). К сожалению,  эти попытки приводят к  волнам, но экспоненциальным, т.е. очень быстро затухающим, что на практике не наблюдается (рис. 9).

Таким образом, видно, что введение в уравнение для жертв конкуренции  лишь частично спасает положение:  модель становится  грубой, но остается  не «адекватной».   Это обстоятельство наталкивают на мысль еще раз пересмотреть модель. В  подправленной модели не учтена конкуренция  среди хищников, что, конечно же, при  увеличении плотности последних имеет место.  Поэтому необходимо ввести такую конкуренцию. В работе [5] соответствующие исследования были проведены.   

1.3. Пространственно – распределённые модели

Миграция особей. В работе [6] для описания пространственно-распределённой системы выделено три типа моделей: камерные, диффузионные и интегральные.

Камерные модели имеют вид:

,                                                         (8)

где u_i(t) – cостояние i - го узла в момент времени t, m_ij(t) – поток миграции, сумма по всем узлам , но что самое главное, на рождаемость и смертность в данном узле не влияет состояние соседних узлов.

В диффузионных моделях поток биомассы определяется градиентом концентрации ресурса в узле и химическим потенциалом узла (на языке экономических моделей – «привлекательностью»).

В [7] показано, что уже для простейшей модели, дополненной диффузионным слагаемым, можно получить решение в виде распространяющейся волны. Пусть

                                                                                                       (9)

Здесь F(u) – группа членов типа правой части логистической модели (3). Если в начальный момент времени t=o u(r,0)=u₀q(r), то решением (9) будет распространяющаяся влево волна

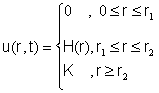,                                                                                            (10)

причём её скорость стремится снизу к , а форма – к функции u₀(r+Vt), где u₀(r) – решение уравнения

.                                                                                    (11)

В интегральных моделях первое слагаемое в (8) заменяется на функцию от числа частиц в окрестности клетки, покрывающей несколько узлов:

                                                           (12)

 S(u_i) – окрестность u_i.

В типичных интегральных моделях прирост биомассы описывается выражением

,                                                                             (13)

где q₁ – прирост биомассы имеющихся деревьев, q₂ – новые ростки; а интенсивность конкурентных отношений выражением

.                                                                            (14)

Интегральное слагаемое с ядром b(x,y) соответствует нелокальной конкуренции.

Интегральные модели намного сложнее с вычислительной точки зрения. В уже упомянутой работе [6] предложен критерий применимости камерных и диффузионных моделей. Они корректны, если расстояние миграции особи данного вида за время одного шага расчёта меньше диаметра узла, а размеры характерных неоднородностей всегда больше 4D, где D  – максимальный размер особи.

Восстановление возобновляемого ресурса. В логистической модели (1) и в более сложных многовидовых и простраственно-распределённых моделях борьба за ресурсы учитывается только введением коэффициентов конкуренции, при этом состояние и запасы ресурса (пищи автотрофов или «жертв») считаются неизменными, или по крайней мере эти изменения не задаются явно. В то же время в ряде случаев очень важно учесть состояние ресурса в данный момент. Особенно это важно при описании растительных сообществ, где плодородие почвы – одна из важнейших характеристик биогеоценоза.

Теории с возобновляемым ресурсом предсказывают намного более разнообразное поведение систем, чем теории без восстановления. Наиболее простой и часто используемый их вариант – введение постоянной скорости роста запасов ресурса.

В нашем подходе скорость восстановления ресурса полностью определяется состоянием леса. Однако, и у нас  есть элементы теории с постоянной скоростью роста запасов ресурса. Прежде всего, это разболачивание почвы, где ресурсу сопоставляется толщина слоя подповерхностных вод, взятая с обратным знаком. Чем меньше плотность биомассы, тем быстрее идёт заболачивание [5]. Волны заболачивания напоминают периодические волны в системе «ресурс–потребитель», описанные в работе [7]. В ней использовались уравнения

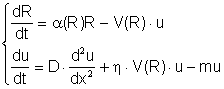,                                                                           (12)

где R – концентрация питательного ресурса, u – плотность биомассы, D – коэффициент диффузии, m – естественная смертность, h – коэффициент усвояемости ресурса, a(R)=1 – R/R₀ – коэффициент, ограничивающий рост ресурса значением R₀. Функция V(R) может быть взята в виде V(R)=V₀R/(k+R). Постоянная k называется константой Микаэлиса; чем она меньше, тем меньшая плотность ресурса необходима для того, чтобы затраты на поиски ресурса становились пренебрежимо малыми, и скорость его выедания определялась только скоростью переработки ресурса биомассой. Типичные волновые решения в системе «ресурс–потребитель», приведены на рис.10. При k =3 (трудные условия) наблюдаются затухающие колебания (рис. 10, слева), а при k =0.6 – периодические волны (рис. 10, справа).

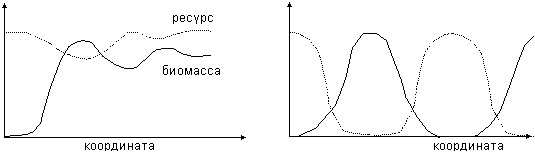
Рис.10. Волновые решения в системе ресурс-потребитель

ЧАСТЬ 2. МОДЕЛИРОВАНИЕ РАЗВИТИЯ ЛЕСА

2.1. Локально-экологический подход.

Сущность применяемого нами подхода состоит, в основном, в следующем:

·           Моделирование нацелено на практическое применение, в основном, на региональное  экологическое прогнозирование.

·           Рассматривается не обязательно биоценоз как единое целое. Задача, поскольку относится к определённой территории, ставится, в общем случае,  в виде интегро-дифференциальных (или разностных) уравнений с соответствующими граничными условиями. При этом необходима возможность постоянной коррекции начальных условий в соответствии с происходящими в системе реальными изменениями.

·           Особая роль должна уделяться построению сценариев развития экосистемы при том или ином внешнем (антропогенном или природном) воздействии. Этот принцип отвечает основной задаче прикладной экологии – оценить последствия техногенных проектов, меняющих условия существования биоценоза и дать соответствующие рекомендации по осуществлению одних действий и по запрещению других.

·           Моделирование нацелено на краткосрочный и среднесрочный прогноз. Поэтому в отличие от задач  глобальной экологии, возможно, и даже представляет особый интерес, неустойчивых и нефизичных состояний динамической системы (например, неограниченный рост популяции). Здесь надо иметь в виду, что система с данными набором параметров существует очень небольшой промежуток времени, и параметры, определяющие фазовый портрет системы, непрерывно меняются.

Локально-экологическая модель должна быть реальной с точки зрения экологических взаимодействий и не должна противоречить опытным данным. Это означает, что она, во-первых, она должна правильно описывать основные взаимодействия и, во-вторых, предусматривала возможность качественного изменения биоценоза при определённом значении некоторого определяющего параметра (например, вымирание популяции при увеличении среднего возраста выше некоторой критической отметки). С математической точки зрения это означает соответствующий анализ фазового портрета модельной системы, поиск бифуркаций и т.п.

В то же время модель должна быть относительно простой и не перегружена большим количеством параметров (как внутренних, так и внешних). Известно, что, применяя очень сложную модель, можно (якобы) объяснить любые эффекты. Однако практической пользы от такой модели немного, поскольку верный прогноз она выдать, как правило, не в состоянии.

2.2. Базовая модель.

Обратимся теперь к реализации изложенных локально-экологических принципов и рассмотрим в качестве первого (и основного в рамках данной работы) шага упрощённую модель развития двувидового леса, описывающую эволюцию популяции как единого целого, не учитывающую ни пространственного распределения, ни миграции особей. На этом этапе, по сути, выражающем глобально-экологические требования, необходимо адекватно определить характер основных взаимодействий.  Будем характеризовать популяцию вектором  плотности биомассы , i=л (лиственные породы), х(хвойные). Ограничимся двухуровневой системой трофических взаимодействий типа «ресурс - потребитель»: почва - конкурирующий между собой двувидовой лес. Состояние почвы характеризуем третьей переменной - обобщённым показателем плодородия Р(t). Динамическая система, использованная нами для описания данной сосредоточенной модели, выглядит следующим образом:

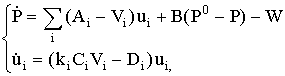       i = {х, л}                                        (13)

·           P – обобщённый показатель плодородия – плотность ресурса (кг/м²);

·           u_л – плотность биомассы лиственных пород  (кг/м²);

·           u_х – плотность биомассы хвойных пород  (кг/м²);

·           А_i – коэффициент восстановления почвы за счёт опада i-ой породы (1/год);

·           В – коэффициент самовосстановления почвы (1/год);

·           Р⁰ – асимптотическое значение плодородия в отсутствие леса  (кг/м²);

·           V_i – скорость потребления ресурса (трофическая функция) (1/год);

·           с­_i – поправочный множитель, описывающий конкуренцию;

·           k_i – коэффициент роста i–ой породы;

·           D_i – коэффициент естественной смертности деревьев (1/год);

·           W – влияние внешних факторов, чаще пагубное, поэтому с отрицательным знаком, (кг/(год×м²))

·           t₀ – среднее время взросления молодого леса (год)

Данная система, как нетрудно видеть, является обобщением классической модели Вольтерра [4]. Распишем теперь коэффициенты A_i¼D_i (все они могут быть зависеть как от плотности биомассы, так и от плодородия), входящие в систему (1), и выясним их смысл. Будем в первом приближении считать, что эти коэффициенты являются комбинацией экспериментально установленной константы (определяющей развитие популяции в нормальных условиях) и некоторой поправочной функции, выражающей степень отклонения от этих нормальных условий. Здесь важно, чтобы выраженные таким образом коэффициенты правильно (с практической точки зрения) описывали эволюцию леса в зависимости от введённых параметров (возраста, освещённости, заболоченности и т.п.). 

Во-первых, будем считать скорость потребления лесом ресурса прямо пропорциональной плотности ресурса:

                                                                                         (14)

(при не слишком большом плодородии почвы).

Во-вторых учтём, что коэффициент естественной смертности существенно зависит от среднего возраста популяции

.                                                                                                      (15)

В-третьих, учтём, что увеличение обобщённого показателя плодородия происходит благодаря переработке ежегодного опада (пропорционального биомассе i-й породы) и отмершей биомассы, т.е. сумме

                                                                                       (16)

В четвёртых, положим B = const ~ 0, что соответствует медленному экспоненциальному самовосстановлению ресурса при отсутствии леса.

В пятых, степень воздействия (недостаточной или избыточной) освещённости, заболоченности и количества осадков на i-ю породу учтём в виде поправочной функции, входящей в коэффициент рождаемости:

                                                                   (17)

Функция Sun(u) отражает тот факт, что лиственные породы сильнее страдают от затенения, чем хвойные, а хвойные, в свою очередь, не любят излишней освещённости. Слагаемое Rain(u, N) описывает поправку к годовому приросту биомассы с учётом засухи. Оно является функцией общего количества выпавших за год осадков N(t) и учитывает необходимые затраты данной породы на испарение и внутреннее потребление воды (десукцию и транспирацию). Считается, что лиственным породам для нормальной жизни без роста необходимо большее количество влаги, чем хвойным.­­ Функция Bog зависит от общего количества избыточной влаги N^tot, скопившейся за всё время и становится равной нулю при превышении N^tot границы полного заболачивания.

Фазовый портрет системы (13) в случае оптимального увлажнения включает в себя несколько стационарных точек (узлов), соответствующих монокультурному лесу. Если использовать явный вид поправочных функций (14-17), то эти состояния являются устойчивыми, при условии  (т.е. не слишком высокой смертности). Стационарная плотность биомассы хвойного равна u⁰×(10/3-k_хA_х/D_х), лиственного – u⁰×(3-k_лA_л/D_л). Здесь u⁰ – характерная плотность биомассы, при которой не происходит взаимного затенения растений. Стационарное значение биомассы как хвойного, так и лиственного леса, примерно вдвое превышает параметр u⁰, что отвечает экспериментальным сведениям. Кроме того, существует ещё одно устойчивое состояние, соответствующее редкому хвойному лесу с плотностью биомассы u⁰×(3D_х/k_хA_х-1). Плотность ресурса составляет P=A/V⁰.

    Sun (u)                                                                           Bog(N^tot)

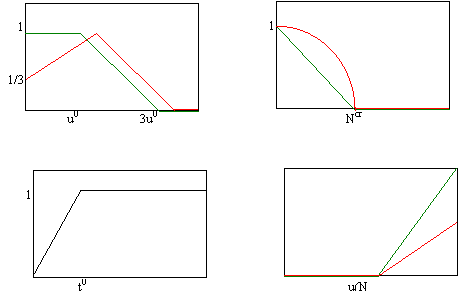
       Age(t)                                                                           Rain(u)

Рис.11. Явный вид поправочных функций в сосредоточенной модели.

Состояние густого хвойного леса является глобально устойчивым, а лиственного – устойчивым при условии u_х = 0. Понятно, что при отсутствии ростков хвойных пород, лиственный лес останется устойчивым и будет существовать (в рамках рассматриваемых простых условий) неограниченно долго. Если же в него проникнут семена хвойных, то со временем они вытеснят лиственных (такая смена и происходит периодически  в природе).

Кроме того, существует седловая точка, соответствующая нулевой биомассе (отсутствию леса).  Такое состояние также биологически оправдано: при посадке леса на пустое пространство, плотность биомассы начинает монотонно возрастать, и малые отклонения от нулевой плотности выводят систему из равновесия (по Р она, разумеется, устойчива, и находится в состоянии P=P⁰). Однако, если D>kV⁰P⁰, то нулевое состояние становится устойчивым (это может соответствовать либо низкой продуктивности почвы – посаженный лес не развивается, а чахнет, либо высокому коэффициенту естественной смертности – этот случай описывает вымирание зрелого леса с большим средним возрастом деревьев. Именно таков глобальный сценарий развития леса: лиственный лес – хвойный – старение и вымирание хвойного леса). При определённом соотношении параметров возможно также устойчивое сосуществование смешанного леса.

Некоторые результаты расчётов согласно изложенной модели приведены на рис.12-13.

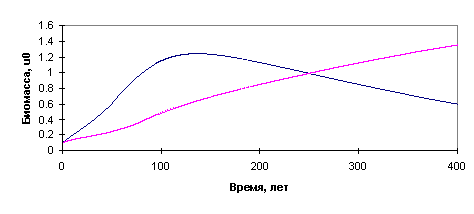
Рис.12. Результаты расчётов: замена лиственного леса хвойным

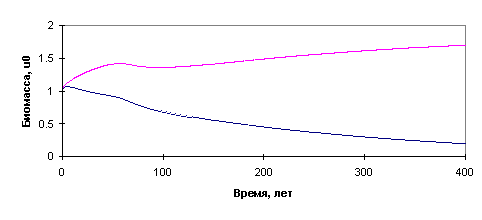
Рис.13. Результаты: вымирание хвойного леса при недостатке влаги

2.3. Развитие модели: эффекты возраста и пространственного распределения леса.

Возрастную структуру популяции, в рамках сосредоточенной модели, можно описать, переходя от плотности биомассы i-й породы u_i к вектору , состоящему из M элементов, каждый из которых равен плотности биомассы определённой возрастной группы. Например, 0-й элемент равен плотности биомассы деревьев от 0 до 10 лет, 1-й – от 10 до 20 лет и т.д. Модификация системы (13) состоит в том, что количество уравнений увеличивается с (2+1) до (М+1), а все коэффициенты заменяются соответствующими массивами (описывающими смертность и т.д. в каждой из возрастной групп). Кроме того, в правую часть уравнений для плотности биомассы  вводятся дополнительные слагаемые, выражающие приток биомассы из младшей возрастной группы и сток в старшую группу (за счёт взросления деревьев). Подробно модель, учитывающая возраст, проанализирована в [5].

Обобщение на пространственно-распределённый случай вводится путём добавления зависимости плотностей биомассы и ресурса от пространственных координат [5,8]. В этом случае система (13) записывается для каждого узла сетки (на которую разбивается изучаемая территория). Связь между узлами осуществляется как локально (перенос семян и вегетативное размножение), так и нелокально (перетекание воды с учётом рельефа местности).

     Сформулируем основные особенности обобщённой пространственно-распределённой модели  среднеширотного двувидового (смешанного) леса:

·      в модели присутствуют конкурентные отношения между видами, выражающиеся в борьбе за ресурсы, например, за воду в условиях недостаточного увлажнения. Подобные зависимости носят нелинейный, пороговый характер, воды начинает не хватать только если уровень осадков падает ниже критического;

·      в модели присутствуют конкурентные отношения. Например, борьба за водные ресурсы, различное отношение лиственных и хвойных пород к заболоченности, взаимодействие свето- и тенелюбивых растений. В последнем случае (конкуренция за световые ресурсы), чем больше тенелюбивых (хвойных) растений, тем хуже условия развития светолюбивых (лиственных);

·      учитывается возрастная структура леса. В размножении участвуют только деревья с возрастом больше порогового возраста взросления. Поэтому коэффициент размножения зависит не от полной плотности биомассы, но от плотности биомассы взрослых растений;

·      перенос  биомассы между узлами сетки вводится не при помощи диффузионного члена, пропорционального второй производной от концентрации, а при помощи экспоненциально убывающего переноса семян: вероятность рождения нового растения в некоторой точке пропорциональна расстоянию между ней и всеми возможными источниками семян;

·      учитывается «эффект опушки»: вероятность экспансии леса через границу зависит от соответствующей поправочной функции – «функции опушки», отражающей тот факт, что растения, с одной стороны, легко завоёвывают такие пространства, как вырубки, а с другой, не могут проникнуть в урбанизированную местность или перебраться через различные (к примеру, водные) преграды;

·      модель сильно нелинейна, большинство коэффициентов имеют немонотонный или пороговый характер. Например, коэффициент рождения новых деревьев пропорционален биомассе зрелых деревьев только в неплотных насаждениях. В плотных насаждениях концентрация рассеянных семян достигает критического значения, густота подроста определяется уже ограниченностью ресурсов, и зависимость от плотности биомассы взрослых деревьев исчезает;

·      плодородие почвы рассматривается как возобновляемый ресурс, скорость его возобновления пропорциональна плотности  отмершей биомассы деревьев, так как при этом в почву возвращаются питательные вещества. Однако рост биомассы вызывает истощение почвы, и между состояниями почвы и биомассы наблюдается отрицательная обратная связь: повышение плодородия влечёт за собой бурный рост леса и последующее истощение, а понижение плодородия влечёт умирание леса и восстановление почвы. Такая отрицательная обратная связь позволяет повысить устойчивость системы, а в ряде случаев получить интересные периодические решения. Однако данное взаимодействие почвы и леса не единственно. Мы учитываем возможность заболачивания, проявляющуюся в том, что суммарный сток и испарение с облесённой поверхности меньше чем с открытой, и во влажном климате почва может заболотиться. При этом если продуктивность падает, лес вымирает, испарение повышается, и почва восстанавливается. Уравнения, описывающие эти явления, схожи с уравнениями «хищник-жертва» (или «ресурс-потребитель»), где в роли хищника выступает лес. В то же время, поскольку восстановление ресурса происходит благодаря отмиранию биомассы, в отношениях лес – почва доминируют симбиотические отношения.  Взаимодействие двух описанных механизмов и нелинейность позволяют получить разнообразное поведение модели [5].

·      Кроме всего перечисленного в уравнения входит «внешняя сила», зависящая от времени и непосредственно влияющая на продуктивность почвы и/или количество растений того или другого вида. «Внешняя сила» может быть введена в виде нескольких функций, входящих в уравнения как аддитивно (для моделирования, например, низового пожара, полностью уничтожающего подрост), так и мультипликативно (например, для моделирования нашествия  вредителей).

Переход к пространственно-распределённой модели иллюстрирует применимость локально-экологического подхода: задаётся базовая модель экологических взаимодействий (сосредоточенная модель, учитывающая возраст популяции), характеристики территории (границы, функции опушки на границах, рельеф местности и прочие параметры) и начальные условия, полученные экспериментально для данной территории. Апробация модели на событиях прошлых лет и розыгрыш возможных сценариев будущего системы составляет основную цель экологического анализа и прогнозирования. В настоящее время продолжается работа над пользовательской версией программы, позволяющего исследовать поведение лесного биоценоза на изложенных принципах.

Литература.

[1] Свирежев Ю.М., Логофет Д.О. Устойчивость биологических сообществ. М., Наука, 1978.

[2]  Фёдоров В.Д., Гильманов Т.Г. Экология. М., Изд. МГУ, 1980.

[3] Уильямсон М. Анализ биологических популяций. М.: Мир, 1975.

[4] Вольтерра В. Математическая теория борьбы за существование. М.: Наука, 1976.

[5] В.И. Кузнецов «Математическая модель эволюции леса», диссертация на соискание ученой степени кандидата физ-мат наук, М, 1998

[6] Тузинкевич А.В. Интегральные модели пространственно-временной динамики экосистем. Владивосток: ДВО АН СССР, 1989

[7]  Гигаури  А.А., Свирижев Ю.М. Распространение волны в системе ресурс – потребитель. ДАН СССР, т.258 (1981), №5, с.1274–1278

[8] Козлов Н.И., Кузнецов В.И. Численное моделирование динамики лесных покровов. Препринт ИПМ РАН №59 М., 1991.
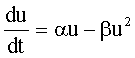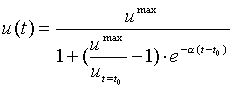