Аннотация
Уравнения состояния предполагаются заданными в форме табличной зависимости давления и внутренней
энергии от температуры и плотности. Проведено исследование работоспособности аппроксимирующих их
формул, удовлетворяющих требованию термодинамического согласования. Существенной оказалась
роль якобиана уравнения состояния. Сформулированы условия, которые необходимо проверять для
обеспечения его невырождения.
Рассмотрены вопросы контроля самих таблиц, задающих исходные данные, и вопросы практической
реализации предлагаемых алгоритмов.
Abstract
EQSs are assumed to be presented in form of table dependence of pressure and inner energy
from temperature and density. A investigation of robustness of approximation formulas is
carried out. The role of Jacobean of EQS turns out to be significant. The conditions that
should be proved to provide its nonsingularity are formulated.
The problems of control of tables which present initial data and issues of practical
realization suggested algorithms are considered.
Содержание
стр.
Введение
………………………………………………………….. 3
§ 1. Постановка задачи
о работоспособности алгоритма……… 4
§ 2. Обеспечение
невырожденности якобиана уравнения
состояния…………………………………………………….. 7
§ 3. Реконструкция
базиса………………………………………. 9
§ 4. Еще раз о
контроле якобиана уравнения состояния ………
13
§ 5. "Блеск и
нищета" билинейной аппроксимации.…………… 15
§ 6. О контроле
исходных табличных данных….……………… 21
§ 7. О численной
реализации …………………………………… 24
Заключение
………………………………………………………….
27
Литература
………………………………………………………….
28
Введение
Настоящая работа представляет
непосредственное продолжение работы автора
[1]. Она была посвящена конструированию аналитических формул для
уравнений состояния, заданных в форме двух таблиц, описывающих зависимость
давления p и внутренней удельной
энергии e от температуры Т и плотности r.
Как известно, такая форма предполагает, что функции 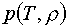 и и 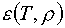 удовлетворяют
некоторому дифференциальному уравнению (условию термодинамического согласования). удовлетворяют
некоторому дифференциальному уравнению (условию термодинамического согласования).
Автор [2] воспользовался билинейной
аппроксимацией табличных данных, пренебрегающей этим условием. Для исправления
этого недостатка, который представляется принципиальным, в [1] было предложено
конструировать уравнение состояния в отдельной табличной ячейке как линейную
комбинацию частных решений упомянутого дифференциального уравнения. Чтобы такая
комбинация обеспечивала нужные табличные значения двух функций 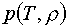 и и 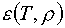 в четырех углах
ячейки, она должна содержать 8 свободных параметров. Эти параметры однозначно
определяются как решение соответствующей системы 8 линейных уравнений. При
удачном выборе базисных частных решений для вычисления параметров удается
получить явные формулы. в четырех углах
ячейки, она должна содержать 8 свободных параметров. Эти параметры однозначно
определяются как решение соответствующей системы 8 линейных уравнений. При
удачном выборе базисных частных решений для вычисления параметров удается
получить явные формулы.
В [1] были рассмотрены также вопросы
практического применения получаемых аппроксимационных формул при численном
решении газодинамических задач.
Работа [1] заканчивалась констатацией того факта,
что вопрос о работоспособности предложенного алгоритма (с учетом его возможного
усовершенствования) остался открытым и должен стать предметом специальных
исследований. Настроение самого автора удивительным образом совпало с
высказыванием академика В.И.Вернадского (см. [3], стр.712, №4340): "Я
вполне сознаю, что могу увлечься ложным, обманчивым, пойти по пути, который
заведет меня в дебри; но я не могу не идти по нему…"
Выбор
этого пути обусловлен стремлением автора сделать "критику"
использования билинейной аппроксимации в [2] конструктивной, предложив подход,
позволяющий преодолеть ее принципиальные недостатки.
§ 1. Постановка задачи о работоспособности алгоритма.
Рассматривается случай, когда
уравнение состояния задается или конструируется по табличным данным в виде:
(1.1) 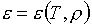 , , 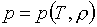 . .
Условие
термодинамического согласования требует, чтобы они удовлетворяли уравнению:
(1.2)
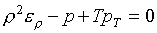
Пару
функций  , , 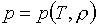 можно считать неявной
формой задания функции р=Р(r,e), посредством которой происходит замыкание
системы дифференциальных уравнений газовой динамики. можно считать неявной
формой задания функции р=Р(r,e), посредством которой происходит замыкание
системы дифференциальных уравнений газовой динамики.
Как
уже отмечалось в [1] на С.17, специфика разностной схемы С.К.Годунова для
расчета газодинамических задач (см., напр., [4]) состоит в том, что уравнение
состояния привлекается в такой момент расчета, когда плотность r
можно считать известной. Поэтому необходимая для практической реализации
алгоритма [1] температура Т должна
определяться из уравнений:
(1.3)
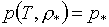 или или 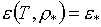 , ,
где 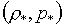 или или 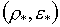 - заданные значения. - заданные значения.
В роли 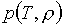 , , 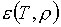 будут фигурировать
"агрегаты": будут фигурировать
"агрегаты":
(1.4) 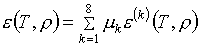 , , 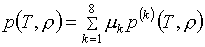 , ,
представляющие
линейные комбинации выбранных базисных функций e(k), p(k)
с вычисленными значениями параметров mk.
Первый аспект работоспособности
обсуждаемого алгоритма связан с вопросом о существовании
и единственности решения соответствующих уравнений (1.3).
Заметим, что для
корректности численного решения газодинамической задачи и, в частности, задачи
о распаде разрыва, требуется большее:
существование и единственность решения системы
двух уравнений:
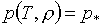 и и 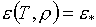 . .
Это соответствует
положению о том, что среди термодинамических величин, описывающих состояние
среды, только две могут быть выбраны в качестве независимых, остальные же можно
вычислить с помощью уравнения состояния.
Как известно из курсов математического
анализа, определяющим условием для этого является необращение в нуль
соответствующего якобиана:
(1.5) 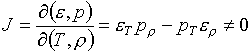
Будем называть J
якобианом уравнения
состояния.
Как и в работе [2], будем
предполагать, что табличные данные таковы: таблица 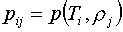 монотонно возрастает
по обоим индексам, а таблица монотонно возрастает
по обоим индексам, а таблица 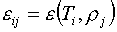 монотонно возрастает
по первому индексу, т.е. выполнены условия: монотонно возрастает
по первому индексу, т.е. выполнены условия:
(1.6) 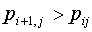 , , 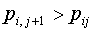 , , 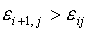 . .
Тогда при
конструировании аппроксимационных формул (1.4) для отдельной табличной ячейки
естественно требовать, чтобы были выполнены условия:
(1.7) 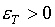 , , 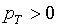 , , 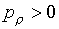
Отсутствие среди (1.7) условия на
производную er
не случайно.
В силу условия
термодинамического согласования (1.2)
(1.8) 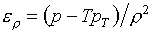 , ,
т.е. не является
независимой и "уж какой получится".
Например,
для идеального газа
(1.9) 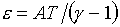 , , 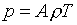
будем иметь 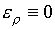 . .
Подставляя (1.8) в формулу (1.5) для
якобиана, получаем:
(1.10)
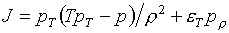
С
учетом (1.7) дополнительное условие
(1.11) 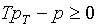 , или , или 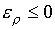 , ,
обеспечивает получение
J>0.
В
частности, для двучленного уравнения
состояния:
(1.12) 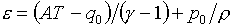 , , 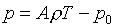
будем иметь:
(1.13) 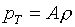 , , 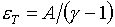 , , 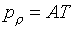 , , 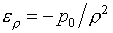
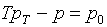 , , 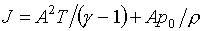
О
его параметрах обычно предполагается, что
(1.14) 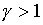 , , 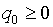 , , 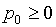 . .
Тогда можно корректно определить
скорость звука:
(1.15)
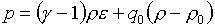
(1.16)
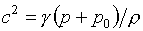 , , 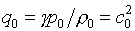 . .
Следовательно,
как отмечается, напр., в [5] на с.148, двучленное уравнение состояния позволяет
рассматривать "растяжение" среды до некоторого допустимого уровня
отрицательных давлений: 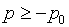 . Если величина отрицательного давления такова, что
превосходится предел прочности материала, то может начаться процесс его
разрушения. Идеальный газ (1.9) представляет частный случай двучлена при q0=p0=0. . Если величина отрицательного давления такова, что
превосходится предел прочности материала, то может начаться процесс его
разрушения. Идеальный газ (1.9) представляет частный случай двучлена при q0=p0=0.
Таким образом, первоочередной аспект
обеспечения работоспособности обсуждаемого алгоритма сводится к выполнению достаточных условий (1.7) и (1.11):
(1.17) 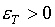 , , 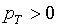 , , 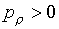 , , 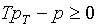
для аппроксимационных
формул (1.4). Он будет обсуждаться в §2.
Второй аспект обеспечения
работоспособности, отмеченный в §5 работы [1], связан с тем обстоятельством,
что при расчетах со сложными уравнениями состояния (в частности, при решении
задачи о распаде разрыва, которая является основным структурным элементом при
использовании схемы С.К.Годунова) в качестве одного из апробированных на
практике методов применяется локальная
аппроксимация двучленным уравнением состояния. Его эффективные параметры
определяются формулами, предложенными А.В.Забродиным (см., напр., [5], с.177).
В рассматриваемом случае параметрического задания уравнения состояния в виде
(1.1) эти формулы приобретают вид (см.[6], с.51):
(1.18) 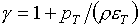 , , 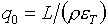 , , 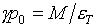 , ,
где 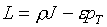 , , 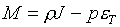 . .
Тогда ограничения на
параметры (1.14) сводятся к обеспечению условий L³0 , M³0 , т.е.
(1.19) 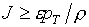 , , 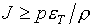 . .
Легко проверить, что это достигается
при дополнении (1.17) требованиями:
(1.20) 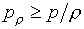 , , 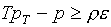 . .
Выполнение таких достаточных условий гарантировало бы возможность использования
упомянутого приема локальной аппроксимации двучленным уравнением состояния. Мы
сосредоточим внимание на вопросе о выполнении требований (1.17), являющихся
достаточными для обеспечения J>0,
т.е. невырождения якобиана уравнения состояния. К обсуждению ситуации с
параметрами q0,
p0
вернемся в конце §4.
§ 2. Обеспечение невырожденности якобиана уравнения
состояния
Начнем с анализа конкретной ситуации,
возникающей в случае использования базисных функций, которые в [1] были названы
"квадратичным" базисом. Тогда аппроксимационные формулы (1.4) имеют
вид:
(2.1) 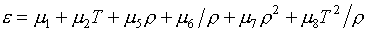
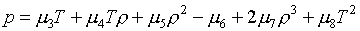
Конкретные значения
коэффициентов mk вычисляются по табличным значениям функций 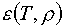 , , 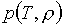 в четырех углах
табличной ячейки: в четырех углах
табличной ячейки:
(2.2) 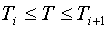 , , 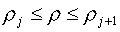 . .
Процесс вычисления и расчетные формулы
для mk
подробно рассматривались в §3 работы [1]. Ввиду громоздкости мы их приводить не
будем. Выражения для производных в условиях (1.17) в случае (2.1) имеют
следующий вид:
(2.3) 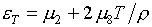
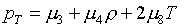
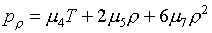
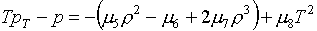
Чтобы убедиться в том,
что для всех значений (T,r) в ячейке (2.2)
выполнены первые два условия eТ>0 и рТ>0, достаточно вычислить по формулам (2.3)
значения функций eТ, рТ в четырех угловых точках ячейки и проверить,
что все они положительны. Можно было бы сделать это и экономнее, выписав
конкретные формулы, зависящие от знаков коэффициентов m4
и m8.
Но мы этого сознательно делать не будем в интересах дальнейшего изложения.
Проверка выполнения третьего условия рr>0 несколько
сложнее. В случае, если:
(2.5) 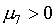 , , 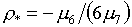 , , 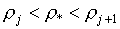 , ,
минимальное значение
функции рr
для табличной ячейки может достигаться не в одной из четырех угловых точек, а в
точке с координатами:
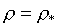 , , 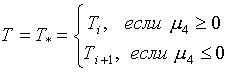
Аналогично, для
проверки выполнения последнего условия 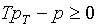 необходимо найти точку
минимума функции необходимо найти точку
минимума функции
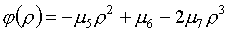
На это может претендовать
корень уравнения
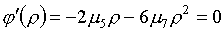 , ,
а именно точка с
координатами:
(2.6) 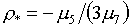 , если , если 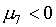 и и 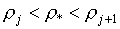 , ,
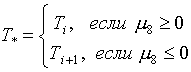
В остальных случаях
минимальное значение ТpТ-р будет достигаться в
одной из четырех угловых точек ячейки.
Если в результате (или в процессе)
описанной проверки окажется, что хотя бы одно из условий (1.17) не выполнено,
пока (до конца §4) будем считать, что "квадратичный" базис дает
неудовлетворительный результат (несмотря на то, что речь идет о проверке достаточных, а не необходимых условий).
Обсуждение вопроса о дальнейших действиях отложим до следующего §3.
Если же все условия (1.17) выполнены, принимаем
функции (2.1) в качестве аппроксимирующих для уравнения состояния в
рассматриваемой табличной ячейке.
Обратимся к уравнениям (1.3), из
которых должна определяться температура Т
при заданных значениях 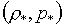 или или 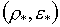 . Условия . Условия 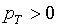 , , 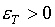 , означающие монотонное возрастание функций по аргументу Т, гарантируют существование и единственность решений уравнений (1.3) в том
случае, если значения p* (или e*) удовлетворяют условиям: , означающие монотонное возрастание функций по аргументу Т, гарантируют существование и единственность решений уравнений (1.3) в том
случае, если значения p* (или e*) удовлетворяют условиям:
(2.7) 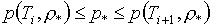 или или 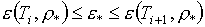
И вот здесь мы можем
столкнуться с явлением, которое назовем "эффектом
лоскутного покрытия". Суть его такова.
Для каждой табличной ячейки
конструирование аппроксима-ционных формул (1.4) осуществляется независимо.
Поэтому в окрестности общей границы двух соседних ячеек с точки зрения величин 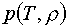 , , 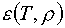 может возникать либо
"двойное покрытие", либо незаполненный "зазор". В последнем
случае при попадании точки (r*,р*)
или (r*,e*) в зону такого "зазора" (а это
формально возможно ввиду того, что вычисление r* осуществляется заранее) нужное из условий (2.7) не будет выполнено. И тогда
решение уравнения (1.3) искать не имеет смысла. может возникать либо
"двойное покрытие", либо незаполненный "зазор". В последнем
случае при попадании точки (r*,р*)
или (r*,e*) в зону такого "зазора" (а это
формально возможно ввиду того, что вычисление r* осуществляется заранее) нужное из условий (2.7) не будет выполнено. И тогда
решение уравнения (1.3) искать не имеет смысла.
Следовательно, прежде, чем приступить к решению (1.3), следует проверить (2.7). В
случае его невыполнения необходимо принимать какое-то "волевое"
решение по назначению корня Т. Более
подробно обсуждать это и формулировать практические рекомендации не хотелось
бы, не располагая соответствующим экспериментальным материалом.
Если проверки (2.7) не производить, а
приступить к решению нужного из уравнений (1.3), которые в рассматриваемом
варианте (2.1) будут квадратными, то в случае невыполнения (2.7) эти уравнения либо дадут два корня, лежащие
вне отрезка [Ti,Ti+1], либо эти корни
будут комплексными. В обоих случаях они не могут быть признаны приемлемым
решением.
§ 3. Реконструкция базиса
Перейдем теперь к обсуждению вопроса,
что делать, если в результате описанной в §2 проверки обнаружится, что для
решения (2.1) в конкретной табличной ячейке не удалось обосновать невырождение
якобиана. Такая ситуация предполагается вполне возможной, и в [1] гипотетически
обсуждались различные способы ее преодоления. В основном они ориентировались на
замену базисных функций, в надежде, что удается добиться приемлемого
результата. Как это реализовать практически?
Чтобы избежать громоздких повторов,
будем предполагать, что читатель располагает текстом работы [1], и будем делать
на него конкретные прямые ссылки.
Прежде всего отметим, что
конструирование базиса - процедура тонкая и капризная. Сошлемся, например, на
рассуждение о "сбалансированности" базиса (см. [1], с.8). Замена любой функции в базисе
ведет к необходимости пересчета всех искомых коэффициентов mk
, хотя, возможно, при сохранении значительной части расчетных формул (см.[1],
с.17).
Начнем с анализа ситуации, связанной с
возможной заменой последней базисной пары функций e(8), р(8). Во-первых, именно с
нее начинается процесс последовательного вычисления коэффициентов mk
, и это упрощает анализ. Во-вторых, уже
из формул (2.3) видна существенная (может быть, даже определяющая) роль вклада
этих функций (вместе с коэффициентом m8) в величины eТ, рТ, ТрТ-р
и, следовательно, влияния на якобиан
уравнения состояния.
Как следует из системы уравнений (3.6)
на стр.13 работы [1], для рассматриваемой системы базисных функций m8
определяется формулой:
(3.1)
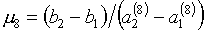 , ,
где 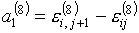 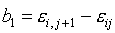
(3.2) 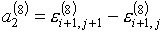 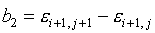
Если используется
степенное решение уравнения (1.2)
(3.3) 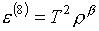 , ,  , ,
то (3.1) принимает
вид:
(3.4)
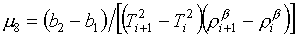
Если b2-b1>0 , то для
получения m8>0 необходимо b>0.
Если b2-b1<0
, то m8>0 при b<0. В случае b2-b1=0
получаем m8=0 , т.е. можно обойтись вообще без функций
e(8), р(8).
Для базисной пары (3.3) формулы
производных имеют вид:
(3.5) 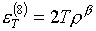 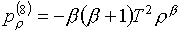
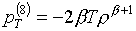 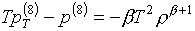
В случае
"квадратичного" базиса используется b=
-1, что и приводит к формулам (2.3). Если
b2-b1<0 , использование таких функций представляется
естественным, поскольку m8>0 и вклад базисных функций e(8), р(8)
будет положительным.
Из формул (3.5) видно, что такая
ситуация в случае b2-b1<0
сохранится и при использовании степеней -1<b<0.
Однако заметим, что после замены в (2.3) вклада таких функций (со своим, заново
рассчитанным, коэффициентом m8>0 и формулами (3.5)), описанная в §2
процедура контроля якобиана уравнения состояния вычислительно существенно
усложнится. Поэтому (по крайней мере, пока) от их использования воздержимся.
Обратимся теперь к случаю b2-b1>0. Из
формул (3.4) и (3.5) нетрудно видеть, что
при b>0 будем иметь m8>0 и получается отрицательным вклад 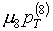 , а в случае b<0 -
m8<0 и, следовательно, отрицателен вклад , а в случае b<0 -
m8<0 и, следовательно, отрицателен вклад 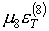 . Таким образом, в
случае b2-b1>0 использование базисной пары (3.3)
представляется нецелесообразным. . Таким образом, в
случае b2-b1>0 использование базисной пары (3.3)
представляется нецелесообразным.
В работе [1] рассматривался вариант
использования в качестве базисной пары e(8), р(8) функций
(3.6) 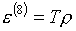 , , 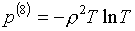 , ,
В этом случае
коэффициент m8 определяется
формулой:
(3.7)
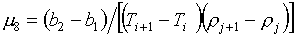 , ,
т.е. m8>0 в случае b2-b1>0. Однако
для функций (3.6) производные определяются формулами:
(3.8) 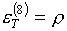 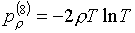
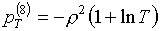 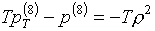
Легко видеть, что
ввиду "разнобоя" знаков в этих формулах замена в (2.3) слагаемых с
коэффициентом m8 на (3.7)-(3.8) ничего
определенного не сулит. Поэтому использование
базисных функций (3.6) представляется нецелесообразным.
В поисках выхода для случая b2-b1>0 после
двойной описанной неудачи автор пришел к функциям вида:
(3.9) 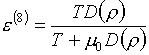 , , 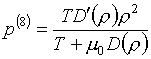 . .
Здесь D(r)>0 - некоторая,
пока произвольная функция r,
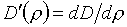 , m0>0 - свободный параметр (нужный с точки
зрения размерности и полезный с точки зрения возможного использования в
качестве управляющего). , m0>0 - свободный параметр (нужный с точки
зрения размерности и полезный с точки зрения возможного использования в
качестве управляющего).
Для функций (3.9) будем иметь:
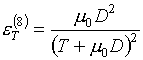 , , 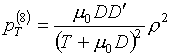
(3.10) 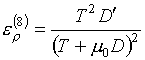 , , 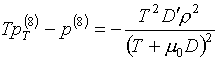
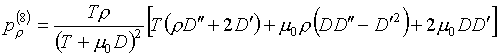
Следовательно, функции
(3.9) удовлетворяют условию (1.2) термодинамического согласования и могут быть
использованы в качестве базисных. Получающийся базис условно назовем "дробно-линейным". Вычисление
по формуле (3.1) коэффициента m8 дает следующий
результат:
(3.11) 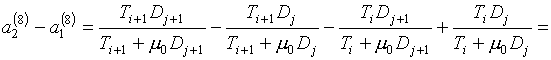
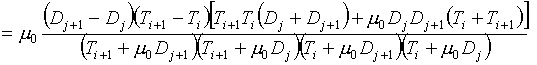
Следовательно, m8>0 в случае, если
b2-b1>0, Dj+1-Dj>0.
В
качестве наиболее простого варианта естественно выбрать
(3.12) 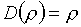 , , 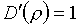 . .
Формулы (3.10) заново
выписывать не будем, за исключением последней, которая заметно упрощается:
(3.13)
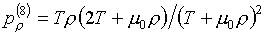 . .
Итак, в случае b2-b1>0
желаемая цель "воздействия" на функции eТ, рТ, рr
достигается, если 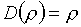 . "Нежелательный" отрицательный вклад в функцию ТрТ-р может быть, с точки
зрения якобиана, "компенсирован" - см. формулу (1.10). . "Нежелательный" отрицательный вклад в функцию ТрТ-р может быть, с точки
зрения якобиана, "компенсирован" - см. формулу (1.10).
Отметим, что возможности использования
базисных функций (3.9) не ограничиваются рассмотренным случаем. Не исключено,
что существенную роль может сыграть и вариация свободного параметра m0.
Функции (3.9) вносят определенный
элемент новизны в вопрос о решении уравнений (1.3). Теперь они приобретают вид:
(3.14) 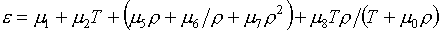
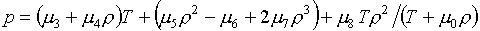 , ,
где r=r*, e=e* (или p=p*)
- заданные величины. Это снова квадратные
уравнения относительно Т, но их
коэффициенты формируются совсем иначе, чем в (2.1).
Еще одна интересная возможность
реконструкции базиса связана с назначением вместо функций 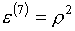 , , 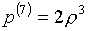 пары функций пары функций
(3.15) 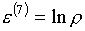 , , 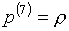
Такая возможность описывалась в [1] в
рамках "логарифмического" базиса. Ввиду отмеченного выше отказа от
использования функций (3.6), рассмотрим назначение (3.15) в
"квадратичном" и "дробно-линейном" базисе. Тогда
аппроксимационные формулы (1.4) имеют вид:
(3.16) 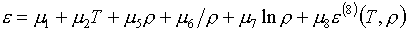
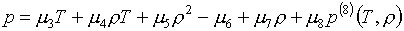
Здесь e(8), р(8)
назначаются либо как в (2.1), либо как в (3.14). Для краткости сохраним
название "логарифмический" для первого случая и назовем базис "смешанным" - во втором.
Расчетные формулы для параметров mk в случае
"логарифмического" и "смешанного" базиса аналогичны тем,
которые были получены в §4 работы [1] для "логарифмического". Отличия
- такие же, как были перечислены на стр.17 в [1] при переходе от
"квадратичного" базиса к "логарифмическому" и вполне
очевидны. Главное из них состоит в том, что для формул (4.4) и (4.5) на стр.16
работы [1] в случае "квадратичного" и "логарифмического"
базиса полагаем g1=h1, g2=h2, g3=h3,
которые определены формулами (3.10) на стр. 13 работы [1]. В случае
"дробно-линейного" и "смешанного" базиса
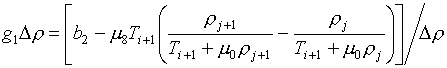
(3.17) 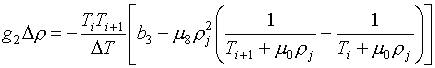
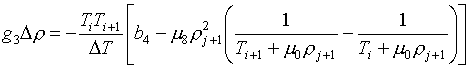
Очевидно, что с точки
зрения решения уравнений (3.16) для определения Т при заданных 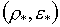 или или 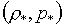 замена (3.15) никаких
новых трудностей не порождает - это снова квадратные
уравнения. замена (3.15) никаких
новых трудностей не порождает - это снова квадратные
уравнения.
§ 4. Еще раз о контроле якобиана уравнения состояния
Ввиду появления новых ситуаций,
вызванных описанными в §3 заменами базисных функций, возникает необходимость
проанализировать их с точки зрения контроля невырожденности якобиана уравнения
состояния.
Начнем с реконструкции
"квадратичного" базиса введением функций (3.15) 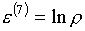 , , 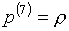 , названной "логарифмическим" базисом. Тогда в
формулах (2.3) сохраняются eТ, рТ, а две последние
заменяются на следующие: , названной "логарифмическим" базисом. Тогда в
формулах (2.3) сохраняются eТ, рТ, а две последние
заменяются на следующие:
(4.1) 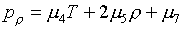
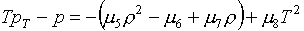
Для контроля рr
будет достаточно вычисления ее в четырех угловых точках ячейки, как для eТ
и рТ. Для проверки условия 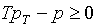 аналогично (2.6)
достаточно дополнительно включить точку с координатами: аналогично (2.6)
достаточно дополнительно включить точку с координатами:
(4.2) 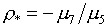 , если , если 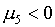 и и 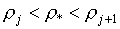
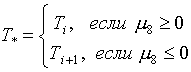
Процедура контроля
якобиана полностью аналогична описанной в §2 для "квадратичного"
базиса.
Теперь обратимся к случаю
"дробно-линейного" базиса. Для формул (3.14) выражения для
производных получаются из (2.3) после замены функциональных коэффициентов при m8
на их выражения (3.10). Позволим себе выписать новые формулы:
(4.3) 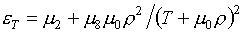
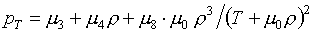
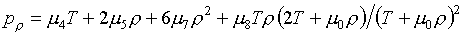
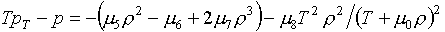
Аналогичные формулы
для (3.16) в случае использования 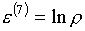 , , 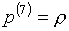 в
"смешанном" базисе сохраняют этот вид для eТ и рТ
(ввиду отсутствия слагаемых с коэффициентом m7), а для рr
и в
"смешанном" базисе сохраняют этот вид для eТ и рТ
(ввиду отсутствия слагаемых с коэффициентом m7), а для рr
и 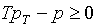 нужно в (4.3) заменить
слагаемые с коэффициентом m7 на нужно в (4.3) заменить
слагаемые с коэффициентом m7 на 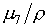 и m7r
соответственно. и m7r
соответственно.
Легко видеть, что получение условий,
аналогичных выписанным в (2.5), (2.6) и (4.2) для "квадратичного" и
"логарифмического" базиса, в случае (4.3) для
"дробно-линейного" и "смешанного" представляется весьма
затруднительным. Проверка (вместе с проверкой угловых точек ячейки) и
выполнение таких условий гарантировали бы невырождение якобиана уравнения
состояния на всей "территории" табличной ячейки (2.2).
"Экзотический" вид условий
(2.5), (2.6) и (4.2) создает впечатление малой вероятности ситуаций, при
которых именно их роль оказалась бы определяющей. (Заметим, что это проверяется
численным экспериментом в случае "квадратичного" базиса (2.1) и его
"логарифмической" модификации с 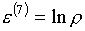 , , 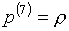 ). Поэтому напрашивается естественное практическое разрешение возникающих трудностей: ограничиться контролем четырех угловых точек
и центральной точки ячейки (вместо возможной точки минимума внутри ячейки). ). Поэтому напрашивается естественное практическое разрешение возникающих трудностей: ограничиться контролем четырех угловых точек
и центральной точки ячейки (вместо возможной точки минимума внутри ячейки).
Более
того, целесообразно заменить контроль последних двух достаточных условий (рr>0
и 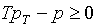 ) прямым контролем
положительности значений якобиана в этих пяти точках. ) прямым контролем
положительности значений якобиана в этих пяти точках.
Отметим далее, что можно этот контроль усилить проверкой выполнения
условий (1.19) вместо проверки условия J>0. В случае их
выполнения формулы (1.18) гарантируют (1.14) и, следовательно, корректность процедуры локальной
аппроксимации двучленным уравнением состояния.
Впрочем, даже, если "запас
положительности" якобиана J недостаточен для обеспечения условий
(1.19), в этом нет ничего "страшного". В монографии [5] на стр.177 можно
прочесть, что в случае получения значения параметра g<1
следует назначить g=1+d, где d>0
- достаточно малая величина. Важно только, чтобы к такой процедуре
регуляризации не приходилось прибегать слишком часто.
В
рассматриваемой нами ситуации с параметром g
как раз все в порядке, поскольку выполнения условий eТ>0, рТ>0 мы добиваемся, и
формула (1.18) дает для g "хорошее" значение. При получении
значений L<0
или М<0 вполне может оказаться,
что при работе в пределах рассматриваемой табличной ячейки (а только в ней и
применимы сконструированные формулы) двучленное уравнение (1.15) и скорость
звука (1.16) не теряют смысла и при фактически вычисленных значениях параметров
q0, p0.
Если это не так, то можно "волевым" решением назначить L=0
или М=0. Важно только, как уже
упомянуто выше, чтобы применение такого приема не стало систематическим. Тогда
лучше позаботиться о другой аппроксимации уравнения состояния.
Во избежание недоразумений отметим,
что описанный выше контроль по пяти точкам не дает "стопроцентной"
гарантии, т.е. может пропускать
некоторые случаи с вырождением якобиана внутри ячейки. Тогда квадратные
уравнения (3.14) или (3.16) могут иметь два корня на отрезке [Ti,Ti+1].
Для одного из них якобиан отрицателен, а для другого - положителен. Его и следует
отбирать.
§ 5. "Блеск и нищета" билинейной аппроксимации
Проведенные исследования, выявившие
относительную громоздкость предлагаемого алгоритма конструирования
термодинами-чески согласованного уравнения состояния, вызывают желание снова
обратиться к "забракованной" нами процедуре билинейной аппроксимации,
эффективно использовавшейся в работе [2].
Этот интерес усиливается тем
замечательным обстоятельством, что отмеченный в §2 "эффект лоскутного покрытия" не возникает в единственном
(если не считать случайных совпадений) случае,
когда аппроксимационные формулы представляют билинейные функции. Тогда на общей
границе соседних ячеек две "соседние" линейные функции, совпадающие в
двух угловых точках ячейки, создают примыкание соответствующих "зон
влияния" при отсутствии "зазора".
Проведем анализ формул билинейной
аппроксимации с точки зрения невырожденности якобиана уравнения состояния.
Выпишем эти формулы в том виде,
который использовался в работе [2], изменив только обозначения для
коэффициентов:
(5.1)
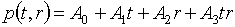 , ,
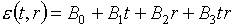 . .
В них введены
следующие обозначения:
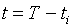 , , 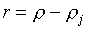 , , 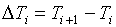 , , 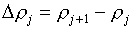
(5.2) 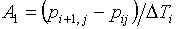 , , 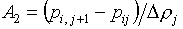
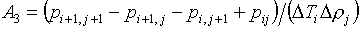 , , 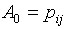
и аналогично для
коэффициентов В0, В1,
В2, В3 с заменой
pij на eij
.
В силу требований
монотонности (1.6) заданных таблиц будем иметь:
(5.3) A1 >0, A2
>0, B1 >0.
Что касается А3, В2, В3 , то их положительность не
гарантируется, и это будет играть существенную роль в дальнейшем. Легко видеть,
что
(5.4) 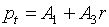 , , 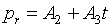 , ,
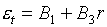 , , 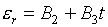 , ,
и для якобиана
уравнения состояния (5.1) получаем:
(5.5) 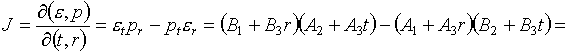
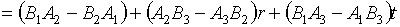
Условий (5.3) явно
недостаточно для обеспечения невырожденности
J.
В
качестве примера приведем следующий:
(5.6) 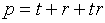 , , 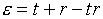
на единичном квадрате:
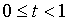 , , 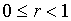 . .
Для
формул (5.6) будем иметь:
(5.7) 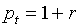 , , 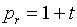 , ,
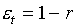 , , 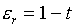 , , 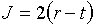 . .
Следовательно,
якобиан J=0
на всей диагонали квадрата r=t,
положителен по одну сторону от нее (r>t)
и отрицателен по другую (r<t).
Таблицы для функций (5.6) на единичном квадрате
удовлетворяют всем предъявленным требованиям монотонности, т.е. внешне по
таблицам ничего "плохого" мы не увидим. Аппроксимационные формулы
(5.1) точно воспроизводят значения
этих функций и, следовательно, будут выдавать результат (5.6) на произвольной сетке.
Вырождение
якобиана J приводит к следующему. Каждое из двух
уравнений (5.6) однозначно разрешимо и относительно t
и относительно r (поскольку они линейны). Но система двух
уравнений (5.6) имеет не одно, а два решения при заданных p=p*, e=e*. Как легко видеть,
если t=t*, r=r* - решение, то t=r*, r=t* - тоже будет решением (в силу полной
симметрии переменных t,r). Одно из них - выше
диагонали (в зоне J>0),
второе - ниже диагонали (в зоне J<0).
Такая
неоднозначность недопустима для задачи о распаде разрыва или численном решении
газодинамических задач. (Какое из двух возможных решений мы собираемся получить
и как гарантировать сходимость итерационных процессов?).
Далее,
в случае, если А3<0 или
В3<0, из формул (5.4)
очевидно возникают ограничения на размеры табличной ячейки 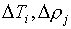 . Но в примере (5.6) и эти ограничения не спасают, поскольку
якобиан J вырождается на всей диагонали,
т.е. при сколь угодно мелкой сетке.
Поэтому требование невырожденности
якобиана уравнения состояния является необходимым условием, предъявляемым в
(5.1). В силу линейности формулы (5.5) для якобиана очевидно, что для этого
необходимо и достаточно, чтобы в четырех
угловых точках табличной ячейки якобиан
J
имел одинаковые знаки (в условиях монотонно возрастающих
таблиц - положителен). . Но в примере (5.6) и эти ограничения не спасают, поскольку
якобиан J вырождается на всей диагонали,
т.е. при сколь угодно мелкой сетке.
Поэтому требование невырожденности
якобиана уравнения состояния является необходимым условием, предъявляемым в
(5.1). В силу линейности формулы (5.5) для якобиана очевидно, что для этого
необходимо и достаточно, чтобы в четырех
угловых точках табличной ячейки якобиан
J
имел одинаковые знаки (в условиях монотонно возрастающих
таблиц - положителен).
Автор
высказывает предположение, что именно
нарушение этого требования стало первопричиной
тех численных эффектов, которые отмечались во введении к работе [1] при
цитировании работы [2]. Это могло быть вызвано стремлением к "повышению
эффективности алгоритма в случае не
слишком подробных таблиц". Но при этом нельзя "увлекаться",
а руководствоваться требованием не
слишком больших шагов сетки, чтобы не допустить вырождения якобиана.
Как
практически определить эту допустимую границу? Представляется естественным
следующий рецепт.
В
четырех угловых точках ячейки вычисляем значения якобиана J.
Если все 4 значения положительны, все в порядке: якобиан не вырождается на всей
"территории" табличной ячейки. Если одна пара значений 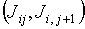 или или 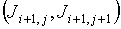 положительна, а другая
- отрицательна, напрашивается вывод, что шаг положительна, а другая
- отрицательна, напрашивается вывод, что шаг 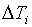 завышен. Если
положительна одна из пар завышен. Если
положительна одна из пар 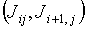 или или 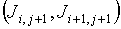 , а другая отрицательна, то завышен шаг , а другая отрицательна, то завышен шаг 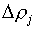 . В оставшихся ситуациях могут быть завышены оба шага . В оставшихся ситуациях могут быть завышены оба шага 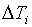 и и 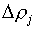 или один из них. или один из них.
Вообще
говоря, есть надежда, что исправить ситуацию можно путем "уплотнения"
таблиц. Хотя, как показывает пример (5.6), такая надежда оправдывается не
всегда.
Важно
заметить, что для уменьшения погрешности аппроксимации исправление ситуации посредством
"уплотнения" таблиц целесообразно осуществлять при использовании дополнительных значений "настоящих"
табулируемых функций. Попытка сделать это путем досчета дополнительных
узлов по формулам билинейной интерполяции может не дать результата: в силу
единственности решения будут сохраняться коэффициенты аппроксимации, а,
следовательно, (в части узлов) и значения производных и якобиана. Поэтому уже
полученное билинейное решение можно использовать только для определения минимального участка таблиц, который
нуждается в "уплотнении", и предварительной
оценки шагов "уплотненных" таблиц
для этого участка.
Допустим,
что заданные две таблицы 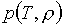 , , 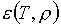 для
"настоящего" (реального) уравнения состояния таковы, что гарантируют
невырождение якобиана (5.5). Однако при этом могут быть не выполнены более
жесткие ограничения (1.19), которые позволили бы корректно применять процедуру локальной аппроксимации двучленным
уравнением состояния. Автор [2] во введении на стр.782 отмечает, что этим
приемом "с успехом пользовался в течение ряда лет. Трудность возникала
только при наличии областей, где среда находится в состоянии фазового перехода
между жидкостью и газом (кипящая жидкость)". И вдруг автору [2]
понадобилось развить другой подход для случая задания уравнения состояния в табличной форме. По-видимому, именно
описанная выше ситуация стала основной причиной для этого: если не
гарантирована даже положительность якобиана, то не приходится говорить о
"запасе положительности", необходимом для условий (1.19). для
"настоящего" (реального) уравнения состояния таковы, что гарантируют
невырождение якобиана (5.5). Однако при этом могут быть не выполнены более
жесткие ограничения (1.19), которые позволили бы корректно применять процедуру локальной аппроксимации двучленным
уравнением состояния. Автор [2] во введении на стр.782 отмечает, что этим
приемом "с успехом пользовался в течение ряда лет. Трудность возникала
только при наличии областей, где среда находится в состоянии фазового перехода
между жидкостью и газом (кипящая жидкость)". И вдруг автору [2]
понадобилось развить другой подход для случая задания уравнения состояния в табличной форме. По-видимому, именно
описанная выше ситуация стала основной причиной для этого: если не
гарантирована даже положительность якобиана, то не приходится говорить о
"запасе положительности", необходимом для условий (1.19).
Согласимся
с этим другим подходом и теперь напомним о требовании термодинамической согласованности функций p(T,r), e(T,r), которое не выполнено для билинейной
аппроксимации (что и послужило исходным стимулом для выполнения работы автора
[1] и настоящей).
Потенциальная опасность
термодинамической несогласован-ности обсуждалась в [1] и состоит в том, что в
случае билинейной аппроксимации "изо-фи-линия" 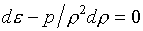 может существенно
отличаться от "настоящей" изэнтропы. При "не слишком
подробных" таблицах уравнения состояния это может увести далеко от истины.
Конечно, такая потенциальная
опасность не обязательно реализуется в практических расчетах. Но, по крайней
мере, в контроле (например, посредством сравнительных расчетов) несомненно
нуждается. может существенно
отличаться от "настоящей" изэнтропы. При "не слишком
подробных" таблицах уравнения состояния это может увести далеко от истины.
Конечно, такая потенциальная
опасность не обязательно реализуется в практических расчетах. Но, по крайней
мере, в контроле (например, посредством сравнительных расчетов) несомненно
нуждается.
А
с формальной точки зрения следует, во избежание недоразумений, в случае
использования билинейной аппроксимации исключить
употребление термина "энтропия", поскольку она не существует.
Энтропия
S
существует только для термодинамически согласованных функций. Одним из путей,
обеспечивающих их получение, является использование термодинамических потенциалов (см., напр., [7], с.60-67). В случае
выбора в качестве независимых переменных T и r
в роли термодинамического потенциала выступает свободная энергия:
(5.8) 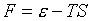 , , 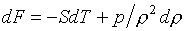
Тогда для остальных
термодинамических величин получаем формулы:
(5.9) 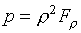 , , 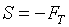 , , 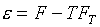 
Одна таблица для функции F(T,r)
полностью задает уравнение состояния.
Казалось бы совершенно естественным при аппроксимации такой таблицы
использовать для табличной ячейки билинейные функции вида:
(5.10)
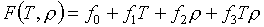
В пользу такого
решения работают, по крайней мере, два аргумента. Во-первых, четыре свободных
коэффициента f0 , f1 , f2 , f3 однозначно определяются по 4 значениям
функции F(T,r) в четырех угловых
точках ячейки, причем по очень простым формулам, аналогичным (5.2). Во-вторых,
- отсутствием для таких формул "эффекта лоскутного покрытия", как
отмечено в начале этого параграфа.
Формулы (5.9) дают в случае (5.10)
такой результат:
(5.11) 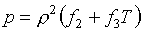 , , 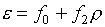
Для их производных
будем иметь:
(5.12) 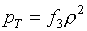 , , 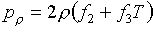 , ,
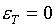 , , 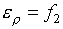 , , 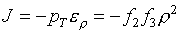
Следовательно, для
невырождения якобиана J такого уравнения состояния необходимо и
достаточно, чтобы
(5.13) 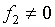 , , 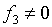
Кроме
возможного невыполнения этих условий, гораздо хуже, что 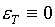 . Вследствие этого соответствующее уравнение (1.3) для
внутренней энергии e
просто не позволяет определить температуру Т.
Таким образом, билинейную форму (5.10) приходится признать непригодной для
аппроксимации термодинамического потенциала F с точки зрения рассматриваемого нами
подхода, несмотря на приведенные выше аргументы в пользу такого решения. . Вследствие этого соответствующее уравнение (1.3) для
внутренней энергии e
просто не позволяет определить температуру Т.
Таким образом, билинейную форму (5.10) приходится признать непригодной для
аппроксимации термодинамического потенциала F с точки зрения рассматриваемого нами
подхода, несмотря на приведенные выше аргументы в пользу такого решения.
Легко
проверить, что аналогичная ситуация будет наблюдаться и в случае попытки
использования билинейной аппроксимации для термодинамического потенциала 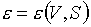 . Поэтому обусловленное приведенными выше
"естественными" аргументами высказывание автора на стр.26 работы [1], что "билинейная аппроксимация -
как раз то, что нужно", является опрометчивым и ошибочным. . Поэтому обусловленное приведенными выше
"естественными" аргументами высказывание автора на стр.26 работы [1], что "билинейная аппроксимация -
как раз то, что нужно", является опрометчивым и ошибочным.
В
связи с упоминанием о термодинамическом потенциале 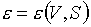 уместно отметить еще
следующее. Из соответствующего ему термодинамического тождества уместно отметить еще
следующее. Из соответствующего ему термодинамического тождества
(5.14)
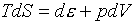 , или , или 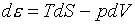 , ,
следует что
(5.15) 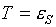 , , 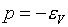
Требования,
предъявляемые к уравнениям состояния, описанные в [4] на с.104-105,
формулируются в виде неравенств:
(5.16) 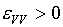 , , 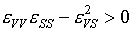
С учетом (5.15) они
могут быть записаны в виде:
(5.17) 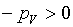 , , 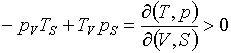
Последнее есть не что
иное, как требование невырожденности якобиана в случае независимых переменных V,S, аналогичное рассматриваемому в
настоящей работе применительно к независимым переменным T,r.
Легко проверить, что второе из условий
(5.16), а, следовательно, и (5.17), не выполнено для билинейной аппроксимации
термодинамического потенциала 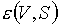 , что и приводит к ситуации, отмеченной выше. , что и приводит к ситуации, отмеченной выше.
Слова "блеск и нищета" в
названии настоящего параграфа имеют благую цель привлечь внимание к вопросам, в
которые билинейная интерполяция благодаря простоте и прозрачности используемых
формул вносит определенную четкость и ясность.
§ 6. О контроле исходных табличных данных
При ознакомлении с публикациями по
уравнениям состояния в переменных Т,r
(или 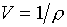 ) автор обнаружил, в
частности, следующее. ) автор обнаружил, в
частности, следующее.
В работе [9]
при конструировании модельного уравнения состояния, описывающего термодинамику
веществ при высоких концентрациях энергии, (среди других более сложных
примеров) для ионной компоненты используется термодинамический потенциал
(6.1) 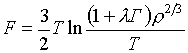 , , 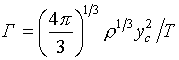
Здесь 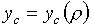 - степень ионизации при
Тe=0, - степень ионизации при
Тe=0,
l
- числовой параметр (свободная постоянная).
Из (6.1), в
соответствии с (5.9), вытекают следующие выражения для давления и внутренней
энергии ионной компоненты:
(6.2) 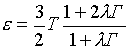 , ,
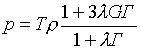 , ,
где
(6.3)
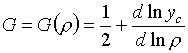
Можно проверить, что
формулы (6.2) записываются в виде:
(6.4) 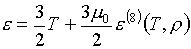 , , 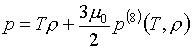 , ,
где функции e(8),
р(8) совпадают с (3.9), если полагать
(6.5) 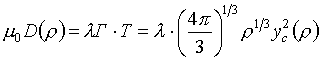
В более ранней работе [8], на которую
ссылается [9], представлены формы
уравнения состояния, учитывающие уменьшение теплоемкости и коэффициента
Грюнайзена с ростом температуры при ударном сжатии пористых веществ. Эти
уравнения привлекают (в качестве отдельных слагаемых) функции вида (см.,[8],
с.687):
(6.6) 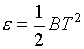 , , 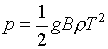 , ,
где В=В(r) - коэффициент
электронной теплоемкости,
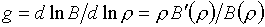 . .
В формулах (6.6)
усматривается явная связь с формулами (3.3). Правда, подстановка (6.6) в
условие (1.2) обнаруживает, что в формуле для g неправильный знак (если это не
опечатка): должно быть
(6.7)
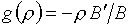 . .
В качестве
"холодных" упругих составляющих используются функции:
(6.8) 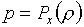 , , 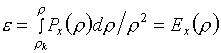
В функциях (6.8)
просматривается аналогия с теми слагаемыми в (2.1), которые не зависят от Т. В
сугубо иллюстративных целях позволим себе, сохранив обозначения, привести
гораздо более громоздкие формулы со стр.696 работы [8]:
(6.9) 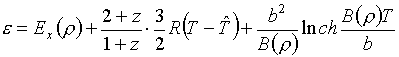
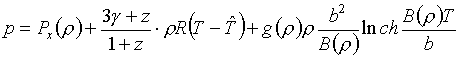
В этих формулах
участвуют:
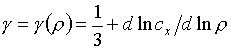 , ,
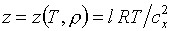 , , 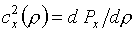 , ,
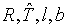 - постоянные
(абсолютные и экспериментальные). - постоянные
(абсолютные и экспериментальные).
Отметим, что, в отличие от (6.2),
приведенных в [9] со ссылкой на [8], при конструировании формул (6.9)
использовались не только термодинамические потенциалы, но и соображения
полуэмпирического характера, имеющие целью получить удовлетворительное согласие
с экспериментальными данными. Проверка (6.9) на выполнение условия (1.2)
термодинамического согласования обнаруживает, что в некоторых деталях оно не
выполнено.
Наконец, в качестве просто случайного
примера упомянем непосредственно соседствующую с [9] статью [10]. В ней на основе уравнения состояния
бинарной смеси вода-пар получены формулы для уравнения состояния тернарной
системы вода-пар-газ (связь между e,
р, V,
a, где a - массовая
концентрация) с температурой Т в качестве параметра. При этом вопрос о
термодинамической согласованности даже не обсуждается, и ее, естественно, нет.
Задача конструирования реальных
уравнений состояния, конечно же, гораздо сложнее, чем аппроксимация готовых
табличных данных. Поэтому естественно при решении последней стремиться к
наиболее простым базисным функциям. Этим объясняется, в частности,
использование в §4 в качестве D(r) простейшей
функции D(r)=r. Тем не менее,
тот факт, что в качестве базисных в
случае необходимости могут использоваться те же функции, которые участвуют
при конструировании реальных уравнений состояния (если они являются
термодинамически согласованными), можно рассматривать как косвенное
свидетельство правильности избранного подхода.
Осмыслим саму процедуру составления и
использования таблиц. Если табулируемые функции удовлетворяют условиям
термодинамического согласования, то при
достаточно мелком шаге таблиц им можно доверять и, по-видимому, произвольные процедуры интерполяции (даже
типа простейших билинейных) не должны вызывать беспокойства.
Однако такая благополучная ситуация
наблюдается далеко не всегда, и описываемые
в литературе формулы для уравнений состояния условию термодинамического
согласования могут и не удовлетворять. Представленные выше примеры имели
целью, прежде всего, проиллюстрировать это обстоятельство.
В такой ситуации аппроксимация табличных данных с использованием термодинамически согласованных функций
представляется последним "форпостом", необходимым для корректности математической постановки
газодинамической задачи. Кроме того, как следует из изложенного выше, не менее
важным является обеспечение
невырожденности якобиана уравнения состояния.
В связи с изложенным вспоминается, как
К.И.Бабенко, еще не будучи членом-корреспондентом АН, неоднократно, по
различным поводам говорил: "Мы же все-таки математики, а не холодные
сапожники!"
В работе [1] на стр.26 автор счел
логичным отметить, что следует осторожно относиться к самим задаваемым
таблицам. Не исключено, что они могут содержать скрытые погрешности (внутренние
противоречия). Это могут быть и просто ошибки или опечатки.
В качестве одного из конкретных
практических способов их обнаружения предлагается следующий. Построенные для
конкретного базиса аппроксимационные формулы (1.4) позволяют определить и
соответствующий термодинамический потенциал F.
Вычислим его значения в угловых точках табличной ячейки. Естественно, что
аналогичное вычисление F в соседних ячейках дает в общих узлах
различающиеся результаты. Если эти различия невелики, ситуация может считаться
нормальной. Получение же больших относительных различий является поводом для
беспокойства и "подозрений", которые могут иметь вполне конкретный "адрес",
причину и стать поводом для поиска способа устранения.
Следует также в случае неблагоприятной
ситуации с вырождением якобиана упомянуть о возможности "уплотнения"
заданных таблиц (уменьшения шагов DTi
или Drj)
в определенных конкретных местах. Эта возможность может быть реализована
аналогично описанному в §5 для билинейной аппроксимации и с теми же оговорками,
предусматривающими использование дополнительных значений "настоящих
функций".
Ограничимся таким
"расплывчатым" описанием до получения результатов численных
экспериментов на "живом" табличном материале. В качестве такого
можно, например, привлечь те же табличные данные, которые использовались в
работе [2] и упомянуты на стр.783. Это позволило бы осуществить те
сравнительные расчеты, о которых сказано в предыдущем §5.
§ 7. О численной реализации
Рассмотрим некоторые вопросы,
связанные с вычислительной реализацией предлагаемых алгоритмов.
Прежде всего следует отметить (см.,
напр., [9], с.483), что при численном моделировании широкого класса как
прикладных, так и теоретических задач (например, в астрофизике, при
моделировании термоядерных мишеней) уравнение состояния может использоваться в
очень широком диапазоне изменения температур и плотностей. Поэтому с
вычислительной точки зрения некоторые из полученных расчетных формул возможно
понадобится преобразовать.
Центральное место в обсуждаемом
алгоритме занимает решение системы из восьми линейных уравнений, хотя оно и
реализуется по явным расчетным формулам для коэффициентов mk. Главной
характеристикой решаемой системы является величина, называемая числом обусловленности m(А) ее матрицы А. Оно определяется формулой
(7.1) 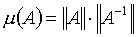 , ,
где 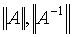 - нормы матрицы
системы и обратной к ней. - нормы матрицы
системы и обратной к ней.
В качестве нормы проще всего выбрать
евклидову матричную норму, равную квадратному корню из суммы квадратов всех
элементов матрицы. Ее называют также нормой Фробениуса или нормой Шура. Эта
норма эквивалентна спектральной норме матрицы (см., напр., [11], с.21).
Заметим, что полученные явные формулы
для решения позволяют (после их преобразования) выписать элементы обратной
матрицы А-1.
Следовательно, число обусловленности m(А) может быть вычислено без затруднений.
Устойчивый алгоритм решения системы
линейных уравнений с квадратной матрицей начинается с масштабирования ее элементов и вектора правых частей (см. [11], с.91).
Из уравнения (1.2) термодинамического
согласования очевидно, что оно сохраняется, если в табличной ячейке ввести
новые переменные:
(7.2) 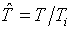 , , 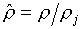 , , 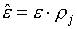
Тогда ячейка
приобретает "новые" размеры:
(7.3) 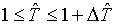 , , 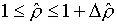 , , 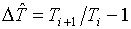 , , 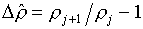
Заметим, что величина 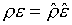 при этом сохраняется.
Можно было бы аналогичной нормировке подвергнуть величины р и re.
Однако в силу линейности (1.2) относительно этих величин можно этого и не
делать. при этом сохраняется.
Можно было бы аналогичной нормировке подвергнуть величины р и re.
Однако в силу линейности (1.2) относительно этих величин можно этого и не
делать.
Поскольку масштабирование в каждой
табличной ячейке выполняется независимо, то естественно, что после завершения
расчета в ней следует вернуться к "обычным" величинам.
Заметим, что масштабирование не влияет
на величину числа обусловленности матрицы (7.1). Весьма существенное влияние на
его значение оказывает присутствие в расчетных формулах малых величин шагов
"локально масштабированной" сетки 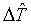 , , 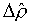 . .
В работе [1] решение системы 8
линейных уравнений реализуется как процесс последовательного вычисления величин
mk
(k=1,…,8)
в порядке убывания их номеров. В этом процессе стоит отметить вычисление
величин m7, m6, m5 как решений систем
трех линейных уравнений, которые приведены в [1] под номерами (3.10) и (4.3) на
стр.13 и 15. Вместо выписанных там рекуррентных формул для вычисления m7, m6, m5 могут быть
использованы известные формулы Крамера. Для системы 3-го порядка они
записываются вполне компактно (но и не компактнее представленных для
рекуррентного процесса) и, конечно, в силу единственности решения, дадут тот же
результат. Их возможное преимущество может заключаться в том, что явно
выписанная форма зависимости от величин b1, b2, b3, b4,
представляющих входные табличные данные, может подсказать рекомендации по
выбору самих расчетных формул. Аналогичная, но более простая ситуация была
описана в §3 в связи с параметром m8. Кроме того, такие формулы позволят
выписать часть элементов обратной матрицы системы А-1.
Пока предполагается, что могут быть
использованы оба варианта описанных в [1] расчетных формул, условно названных "квадратичным" и "логарифмическим".
Единственное изменение по сравнению с [1] состоит, как описано выше в §3, в
отказе от использования в качестве пары e(8), р(8) функций (3.6) и
замене их функциями (3.9) с D(r)=r. Вопрос о том, какому из вариантов отдавать
предпочтение (в случаях, когда работоспособны и те и другие), может решаться,
например, исходя из величин числа обусловленности (7.1).
Читателю может показаться чрезмерным
столь подробное обсуждение вопроса о расчетных формулах. Однако следует иметь в виду, что речь идет о массовой операции, которая может
применяться не один раз в ходе
итерационного процесса для решения задачи о распаде разрыва со сложными
уравнениями состояния (поскольку при этом может происходить переход в другую табличную ячейку). В
свою очередь, как уже отмечалось, распад разрыва является массовым структурным
элементом разностной схемы С.К.Годунова.
В
момент решения конкретной "производственной" задачи нужно уже
располагать четкой информационной базой по поводу выбора тех или иных расчетных
формул.
Вопросы о поиске подходящих базисных функций (для конкретных табличных
уравнений состояния и применительно к конкретной табличной ячейке) должны
решаться до и независимо от решения
"производственных" задач, и результат поиска должен быть отражен в
упомянутой информационной базе. Эта информация может меняться по мере ее
накопления и в ходе возможного совершенствования алгоритмов.
По аналогии с примером (5.6) для
билинейной интерполяции автор не сомневается в том, что для каждого конкретного
выбранного базиса из частных решений (1.2) может быть специально построен
пример "плохой" табличной ячейки. Она будет удовлетворять требованиям
монотонности (1.6) и при этом давать такие параметры mk, что соответствующие
аппроксимационные формулы (1.4) будут иметь вырождающийся в ячейке якобиан
уравнения состояния (1.5).
Вообще говоря, нельзя полностью
исключить и существование примера, для которого базис, обеспечивающий
невырождение якобиана, не удастся найти в ограниченном
наборе рассматриваемых возможностей. В такой ситуации уместно вспомнить шутку:
"Трудно поймать черную кошку в темной комнате, особенно, если ее там
нет". Более того, автор был свидетелем высказывания Р.П.Федоренко:
"Любой метод можно загубить специально придуманным тестом".
Но
при этом следует иметь в виду, что такие примеры могут носить искусственный
("патологический") характер и быть весьма далекими от реальности.
Поэтому будем исходить из того, что проведенное исследование позволяет
надеяться на следующее. Арсенала расчетных формул, возникающих из четырех
описанных в §2 и §3 вариантов базисных функций, связанных с вариацией e(7), р(7)
и e(8), р(8), располагающих еще и свободным параметром m0,
как правило, достаточно для получения
в табличной ячейке решения с невырожденным якобианом. Напомним также, что в качестве
дополнительного "резерва" может быть использовано уменьшение шагов
таблицы, т.е. ее "уплотнение", в конкретном месте.
Подтверждение
(или опровержение) этого предположения может дать только численный эксперимент
с реальными табличными уравнениями состояния. В неблагоприятных ситуациях в
нашем распоряжении есть и другие возможности назначения базисных функций,
описанные в работе [1] и §3 настоящей. Они могут быть и еще более расширены,
но, чтобы не загромождать изложения, ограничимся сказанным.
Заключение
В
настоящей работе проведено исследование работоспособности формул для уравнений
состояния, аппроксимирующих задаваемые в табличной форме зависимости давления и
удельной внутренней энергии от температуры и плотности. При этом весьма
существенной оказалась роль якобиана уравнения состояния. Сформулированы
условия, которые необходимо проверять после получения конкретных расчетных
формул для аппроксимирующих функций в отдельной табличной ячейке.
Поскольку
сами табулируемые функции могут не удовлетворять условию термодинамического
согласования, представляется необходимым требовать этого от аппроксимирующих
функций. Поэтому они конструируются как линейные комбинации базисных решений
соответствующего дифференциального уравнения.
Рассмотрены
вопросы контроля самих таблиц, задающих
исходные данные, и вопросы практической реализации предлагаемых алгоритмов.
Точка
зрения автора на билинейную аппроксимацию отражена в §5 и §6. Если заданные
таблицы уравнения состояния получены на основе функций, которые удовлетворяют
условию термодинамического согласования, и шаги таблиц таковы, что гарантируют
невырождение соответствующих якобианов для табличных ячеек, то использование
билинейных формул, по-видимому, можно считать вполне приемлемым. Отсутствие
"эффекта лоскутного покрытия", описанного в конце §2, является их
несомненным достоинством, наряду с относительной простотой реализации.
Автор выражает благодарность
М.С.Гавреевой за помощь в оформлении работы.
Литература
1. Прокопов
Г.П. Аппроксимация табличных уравнений состояния для расчета газодинамических
задач.// Препринт ИПМ им.М.В.Келдыша РАН, М., 2004, №66, 28 стр.
2. Чарахчьян
А.А. Об алгоритмах расчета распада разрыва для схем С.К.Годунова.// Ж. вычисл.
матем. и матем. физики, 2000, 40, №5, С.782-796.
3. Мудрость
тысячелетий. Энциклопедия.// М., ОЛМА-ПРЕСС, 2005, 848с.
4.
Численное решение многомерных задач
газовой динамики. Под общей ред.
С.К.Годунова// М., «Наука», 1976, 400 С.
5. Куликовский
А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения
гиперболических систем уравнений.// М.: ФИЗМАТЛИТ, 2001, 608 С.
6. Прокопов
Г.П. О задании уравнений состояния при моделировании неполностью ионизованной
плазмы.// Вопросы атомной науки и техники. Сер.: Матем. моделир. физ.
процессов, 2000, вып.3, С.45-63.
7. Зоммерфельд
А. Термодинамика и статистическая физика.// М., Изд-во иностр. литер., 1955,
480 С.
8. Кормер
С.Б., Фунтиков А.И., Урлин В.Д., Колесникова А.Н. Динамическое сжатие пористых
металлов и уравнение состояния с переменной теплоемкостью при высоких
температурах.//Ж. эксперим. и теор. физ., 1962, т.42, вып.3, с.686-702.
9. Баско
М.М. Уравнение состояния металлов в приближении среднего иона.// Теплофизика
высоких температур, 1985, 23, №3, с.483-491.
10. Кузнецов
Н.М., Тимофеев Е.И. Уравнение состояния, ударные адиабаты, скорость звука в
тернарной системе вода-пар-газ.// Там же, с.477-482.
11. Малышев
А.Н. Введение в вычислительную линейную алгебру.// Новосибирск, Наука,
Сибирское отделение, 1991, 232с.
|