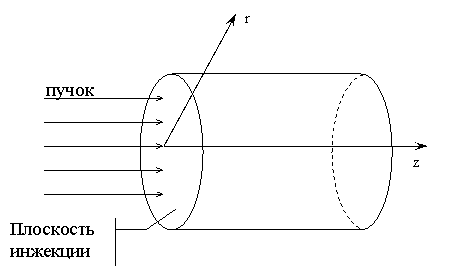
Численное моделирование возбуждения электромагнитных полей в цилиндрической полости потоком релятивистских электронов
( Numerical Simulation of Electromagnetic Fields Generation in the Cylindrical Cavity by Relativistic Electron Flux
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Введение

Возбуждение электромагнитных полей в полостях технологических объектов, находящихся под воздействием гамма-излучения, определяется комптоновской ионизацией материалов. В результате ионизации возникает поток комптоновских электронов высоких энергий, который, в свою очередь, взаимодействует с молекулами нейтрального газа, заполняющего полости, и образует потоки вторичных электронов. Возникающие при этом электромагнитные колебания влияют на функционирование электронной аппаратуры объектов.

Разработка адекватной математической модели указанных физических процессов и построение вычислительных алгоритмов в сложной геометрии является нетривиальной задачей. В связи с этим актуальными становятся разработка и исследование математических моделей конкретных физических экспериментов, построение численных методик расчёта электромагнитных полей и проведение на их основе численного эксперимента. Численный эксперимент позволит более детально изучать отдельные этапы эволюции физических процессов и путём сравнения с результатами физических экспериментов выбрать адекватную математическую модель.

В настоящей работе рассматривается эксперимент, в котором аксиально-симметричный поток гамма-квантов проникает сквозь торец в цилиндрическую камеру (материал – Fe), заполненную воздушной средой. Ось потока совпадает с осью камеры. Процесс взаимодействия гамма-квантов с торцом камеры и образование потока комптоновских релятивистских электронов моделируется методом Монте – Карло [1], его описание выходит за рамки настоящей работы. В работе этот поток считается заданным, т. е. в камеру инжектируется аксиально-симметричный пучок релятивистских электронов.

Математическая модель рассматриваемого эксперимента включает три взаимосвязанные подзадачи.

1.     Задача для двумерных нестационарных уравнений Максвелла в цилиндрических координатах с граничными и начальными условиями.

2.     Вычисление проводимости воздушной среды в камере.

3.     Моделирование потока релятивистских электронов методом крупных частиц.

При численной реализации модели были решены следующие проблемы.

Во-первых, в зависимости от интенсивности потока релятивистских электронов возможны процесс лавинной ионизации воздушной среды в камере и, как следствие, большая проводимость. Поэтому численные методики интегрирования уравнений Максвелла и уравнений для вычисления проводимости должны быть адаптированы к этим процессам. В настоящей работе для этой цели используется идеология метода квазианалитической интерполяции [2].

Во-вторых, стандартные процедуры вычисления плотности тока в методе крупных частиц не обеспечивают сохранение заряда в ячейках, что в случае малой проводимости воздушной среды может привести к накоплению фиктивного заряда в расчётной области и заметному искажению электрического поля [3]. Поэтому в работе предлагается методика расчёта плотности тока, основанная на законе сохранения заряда в ячейках.

В-третьих, в силу цилиндрической симметрии расчётной сетки возникает проблема со взвешиванием заряда частиц вблизи оси симметрии. Стандартные процедуры взвешивания не дают удовлетворительного результата в осевых ячейках. Простая интерполяция из соседних не осевых ячеек не годится, так как требуется выполнение закона сохранения заряда в ячейках. В работе предлагается процедура взвешивания, дающая правильный результат в осевых ячейках.

В-четвёртых, предложен и реализован подход к распараллеливанию вычислительного алгоритма, который принципиально отличается от геометрического распараллеливания и использует тот факт, что моделирование крупных частиц занимает основное расчётное время.

§1. Математическая модель

Рассматривается эксперимент, в котором аксиально-симметричный пучок релятивистских электронов инжектируется в цилиндрическую камеру, заполненную нейтральной воздушной средой (рис.1). Ось пучка совпадает с осью камеры. Давление в камере Р=1атм. Математическая модель эксперимента включает следующие взаимосвязанные подзадачи.

рис. 1

1. Уравнения Максвелла  в цилиндрических координатах с граничными и начальными условиями:

,

,

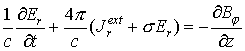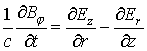,                                                                                 (1)

.

2. Уравнения движения релятивистских электронов

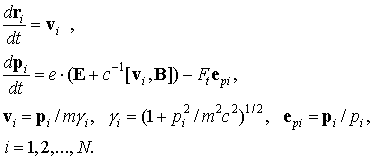                                     (2)

Начальные координаты электронов распределены в плоскости инжекции (z = 0) равномерно по сечению. Начальные скорости отвечают энергетическому спектру электронов в пучке. Сила ионизационного торможения F_t описывается формулой Бета – Блоха:

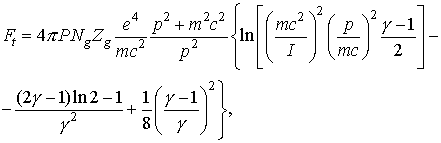                              (3)

где Р – давление в атм., . Плотность внешнего тока , входящая в уравнения (1), вычисляется по координатам и скоростям электронов  методом крупных частиц.

3. Уравнения для вычисления проводимости воздушной среды в камере:

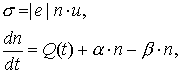                                                                           (4)

где n – концентрация электронов проводимости, Q(t) – источник вторичной ионизации (вычисляется с использованием метода крупных частиц), u(P,E) – подвижность электронов проводимости, a(P,E) – скорость вторичной ионизации (значения величин u(P,E) и a(P,E) посчитаны по методике, изложенной в работе [4], и содержатся в таблицах),

.

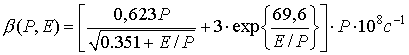§2. Численное интегрирование уравнений Максвелла и уравнения для вычисления проводимости воздушной среды

Для разностной аппроксимации системы уравнений (1) используется вариант явной схемы «крест». Вводится равномерная сетка по времени  и равномерная прямоугольная пространственная сетка , . Взаимное расположение на пространственной сетке компонент поля и плотности тока показано на рис.2. Электрическое поле определено в целые моменты времени , магнитное поле и плотность тока – в полуцелые моменты времени .

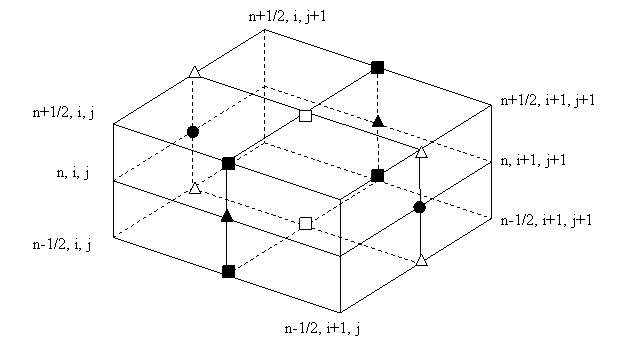
Рис. 2

Пространственные производные заменяются центрально-симметричными разностными соотношениями

,

,

,

.

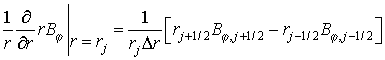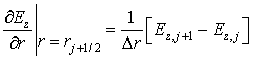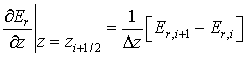При интегрировании по времени используется идеология метода квазианалитической интерполяции [2]. Для аппроксимации дифференциального уравнения с начальным условием

,

вводится вспомогательная функция  так, что:

,

- точное решение вспомогательной задачи:

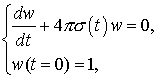
решив которую получим

.

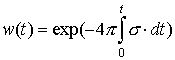Тогда  есть решение задачи Коши:

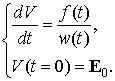
Интегрируя это уравнение и аппроксимируя интеграл по времени, получим разностную запись исходного уравнения

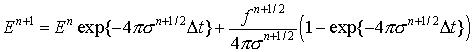.               (5)

Такой метод обеспечивает первый порядок аппроксимации по Dt в пределе . Большая проводимость характерна для задач о распространении сильноточных релятивистских пучков в плотных газах (P > 1атм.). При малой проводимости  используется аппроксимация

.

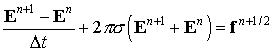Была рассчитана следующая тестовая задача:

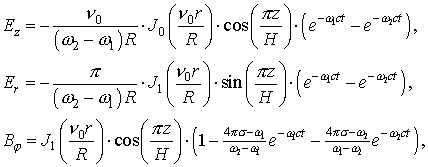
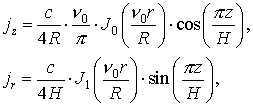
где

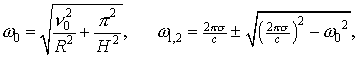
– наименьший положительный нуль функции Бесселя.

Метод квазианалитической интерполяции используется также при интегрировании уравнения (4):

.

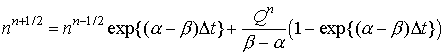Необходимость в использовании квазианалитической интерполяции диктуется тем обстоятельством, что при E > 100 СГСЕ значение a велико.

§3. Моделирование потока релятивистских электронов методом крупных частиц

Численное интегрирование уравнений движения (2) проводится по методу, аналогичному методу Бориса [5]:

,

,

,

,

,          ,

.

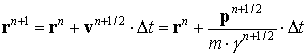Здесь компоненты поля билинейно интерполированы с узлов пространственной сетки на координаты частиц. В алгоритме на каждом шаге по времени проводится проверка неравенства

.

В случае нарушения этого неравенства электрон считается поглотившимся и его дальнейшее движение не рассматривается. Метод Бориса был выбран в связи с тем, что он полностью учитывает тот факт, что магнитное поле изменяет направление движения электрона, но не изменяет его энергию.

Метод крупных частиц, использованный для вычисления плотности тока, входящей в уравнения (1), имеет несколько особенностей.

3.1. Расчёт плотности тока в узлах расчётной сетки базируется на законе сохранения заряда в ячейках и основывается на методике работы [3]. Соблюдение закона сохранения заряда в ячейках особенно важно обеспечить в случае малой проводимости воздушной среды. В этом случае метод крупных частиц, не обеспечивающий сохранение заряда в ячейках, может привести к накоплению фиктивного заряда в расчётной области и заметному искажению электрического поля.

Стандартные процедуры вычисления плотности тока в узлах  пространственной сетки имеют следующий вид:

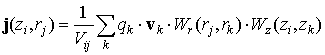,                                             (6)

где  – объём ячейки;  – заряд и скорость частицы с номером k;  – координаты k-й частицы;  – форм-факторы, которые представляют собой долю заряда или объёма частицы, переданную ячейке  по каждому из двух направлений z и r.

.                                                                (7)

Эти процедуры не обеспечивают сохранение заряда в ячейках.

В работе предлагается другой алгоритм вычисления плотности тока, аналогичный алгоритму из [3]. В этом алгоритме производится подсчёт заряда, перенесённого каждой частицей через границу пространственной ячейки за один шаг по времени. Полученные значения суммируются по частицам, делятся на площадь границы и приравниваются к плотности тока в узле расчётной сетки на границе ячейки.

Подсчёт заряда, перенесённого одной частицей через границу ячейки за один шаг по времени, проводится следующим образом. Предположим, что частица находится в ячейке , как показано на рис.3. Размеры частицы не превышают размеров ячейки, поэтому заряд частицы передаётся только ячейке  и соседним с ней ячейкам. Предположим также, что частица не может пройти за один шаг по времени больше половины ячейки  (). Тогда в предыдущий момент времени заряд частицы распределялся между теми же 9 ячейками с индексами , , , , , , , , . Пусть  – форм-факторы рассматриваемой частицы в ячейке  в момент времени . Тогда заряд, вынесенный частицей из ячейки  через верхнюю или нижнюю границу, суть

;

заряд, вынесенный из ячейки  через правую или левую границу, есть

.

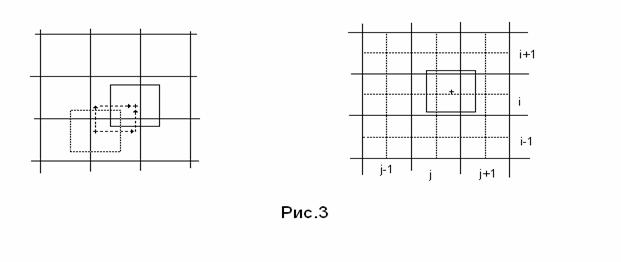
         Предложенные формулы расчёта не являются единственно возможными. Они представляют собой полусумму результатов, полученных для двух вариантов движения частицы: смещение сначала параллельно оси z, а затем вдоль радиального направления до конечного положения частицы; смещение сначала вдоль радиального направления, а затем параллельно оси z (см. рис.3).

Для сглаживания электромагнитных шумов предложенный алгоритм вычисления плотности тока необходимо дополнить процедурой усреднения тока по характерному промежутку времени пролёта частицей пространственной ячейки [3]:

,

где  – усреднённая плотность тока на предыдущем шаге по времени, , h – характерный размер пространственной ячейки,  – характерная скорость движения частиц (для релятивистских электронов ).

3.2. В силу цилиндрической симметрии возникает трудность, связанная с распределением заряда частиц вблизи оси. Кроме требования сохранения заряда частицы (7) форм-факторы должны обеспечивать правильный расчёт плотности тока в плоскости инжекции :

,                                                      (8)

где  – плотность входного тока в плоскости инжекции;  – площадь сечения j-й ячейки плоскостью ; суммирование ведётся по частицам, инжектируемым в камеру в момент времени .

Начальные координаты электронов распределены в плоскости инжекции равномерно по r. Поэтому заряды инжектируемых частиц вычисляются по формуле:

,

где N – число частиц, инжектируемых в одну ячейку за один шаг по времени. В пределе при  заряд частицы имеет вид

,

и в соотношении (8) суммирование заменяется интегрированием:

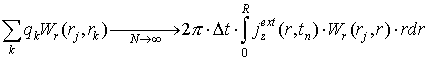.                        (9)

В предположении, что в пределах ячейки , из (8) и (9) получается необходимое условие

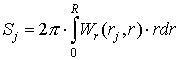,                                                                          (10)

которому должна удовлетворять неотрицательная функция .

Рассмотрим два стандартных форм-фактора.

1. Взвешивание по модели CIC с равномерно заряженными крупными частицами.

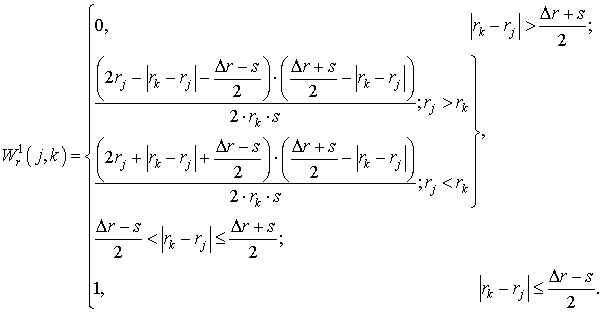
2. Линейное взвешивание.

Здесь s – размер частицы. Функции  и  удовлетворяют условиям (7) и (10) для ненулевых ячеек, независимо от размера частиц. Эти условия линейные, поэтому линейная комбинация  и  также будет удовлетворять им. Для нулевой ячейки отношение интеграла в условии (10) к площади ячейки имеет вид:

,             .

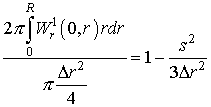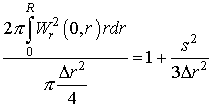Из этих уравнений видно, что если в качестве искомой функции взять , то условия (7) и (10) будут выполнены для всех ячеек.

Ниже приведены расчетные данные для плоскопараллельного пучка (частицы движутся в направлении оси z).

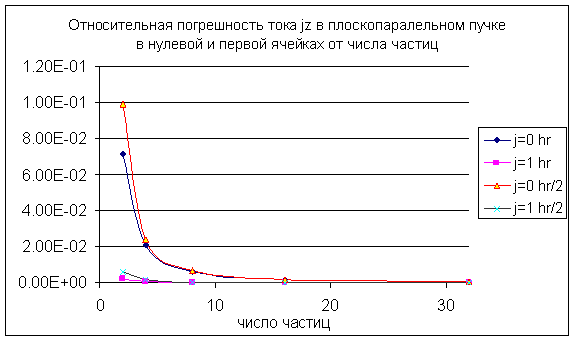
Использовались частицы размера hr и hr/2, , в плоскопараллельном пучке. Как видно из графика относительной погрешности, точность модели зависит не только от числа частиц, но и от координат ячейки и размеров частиц. При удалении от оси симметрии, относительная погрешность быстро падет. Уменьшение размера частиц приводит к возрастанию погрешности во всех ячейках.

2.3. Для сглаживания флуктуаций плотности тока, вызванных дискретной структурой пучка, целесообразно распределять начальные координаты и скорости частиц с использованием последовательности точек, равномерно распределённых в трёхмерном единичном кубе. При этом обычные случайные числа не годятся из-за их большой дисперсии при малой выборке. Удовлетворительные результаты даёт использование обращённых двоичных, троичных и пятеричных дробей  [6].

Последовательность точек  равномерно заполняет трёхмер-ный куб; последовательность точек  равномерно заполняет квадрат.

Опишем подробно процедуру инжекции крупных частиц в камеру в момент времени  .

Пусть J – число ячеек в плоскости инжекции . Ячейки и частицы имеют кольцевую форму (см. рис.4). Координаты частиц в плоскости инжекции распределены равномерно по r:

,

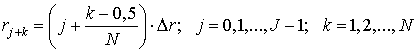где N – число точек в пределах одной j-й ячейки. Число инжектируемых частиц увеличивается пропорционально номеру ячейки, т. е. с координатой  стартует j+1 частиц. Таким образом, в j-й ячейке стартует  частиц. Линейное относительно j увеличение числа частиц в j-й ячейке отвечает цилиндрической симметрии задачи и связано с пропорциональным j увеличением площади ячейки кольцевой формы (см. рис.4).

Начальные энергии и направления вылета электронов в j-й ячейке разыгрываются с использованием чисел . Косинус полярного угла вылета  является решением уравнения

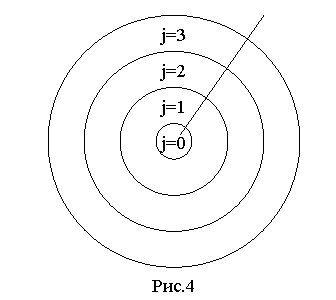
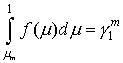,                 (11)

где  – нормированная плотность распределения электронов по . Азимутальный угол вылета электрона считается равномерно распределённым:

.

Начальная энергия электрона находится в результате решения уравнения:

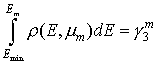,                                                                            (12)

где  – нормированная плотность распределения электронов по E при фиксированном . Здесь

,

P – число шагов по времени между повторами в последовательности точек . Интегральные уравнения (11), (12) решаются независимо методом Ньютона и составляются таблицы  и , которые многократно используются в алгоритме при задании начальных энергий и направлений вылета электронов.

В связи с тем, что скорости электронов имели три компоненты, уравнения движения (2) интегрировались в декартовых координатах. Для расчёта плотности тока производился переход в цилиндрическую систему координат  (в силу аксиальной симметрии угловая координата не использовалась). Начальные координаты электронов в декартовой системе координат имели вид:

,

т. е. все частицы стартовали с одного луча. Такое описание применимо в аксиальной симметрии, когда точки на окружности  равноправны.

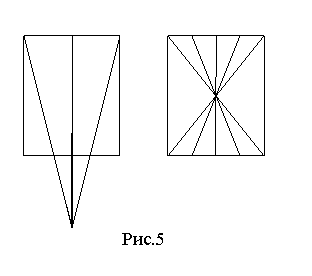Алгоритм по численному моделированию потока релятивистских электронов методом крупных частиц исследовался на следующих тестах: свободное движение (в отсутствие поля) однородного плоскопараллельного потока; пучок, расходящийся из точки, и пучок, сходящийся в точке (рис.5); деформация однородного плоскопараллельного потока электронов с фиксированными энергиями в заданном электромагнитном поле без учёта самосогласования (требование постоянства энергий электронов позволяет аналитически решить уравнения движения частиц и получить точную картину деформации пучка); свободное движение моноэнергетического пучка частиц, направления движения которых имеют распределение, равномерное по заданному телесному углу . В тестовых расчётах были получены достаточно точные (<1%) результаты вычисления плотности тока при приемлемых значениях параметров дискретизации .

§4. Параллельная реализация вычислительного алгоритма на многопроцессорной вычислительной системе с распределённой памятью

Рассматриваемая в настоящей работе численная методика, реализующая метод крупных частиц, включает два основных блока:

1)     решение уравнений Максвелла (1) сеточным методом и расчёт проводимости (4);

2)     решение уравнений движения крупных частиц (2) (электронов пучка) и вычисление плотности тока пучка .

В процессе работы программы на каждом временном шаге блоки обмениваются данными. Этими данными являются массивы значений компонент электромагнитного поля, заполняемые в первом блоке и используемые во втором для решения уравнений движения электронов пучка, и плотность тока пучка , вычисляемая во втором блоке и используемая в первом для решения уравнений Максвелла.

Просматриваются два основных подхода к распараллеливанию численной методики.

Первый подход – традиционное геометрическое распараллеливание. Расчётная область разбивается на подобласти, в каждой из которых за исключением границ задача решается самостоятельно. Эффективность распараллеливания существенно зависит от равномерности загрузки процессоров, обслуживающих разные подобласти. В связи с этим при реализации этого подхода возникает следующая трудность. Двум основным блокам численной методики требуются разные затраты временных ресурсов, которые отличаются на порядки. А именно, на моделирование движения частиц и их взвешивание на сетке требуется значительно больше времени, чем на разностное решение уравнений Максвелла. Это объясняется тем, что число крупных частиц много больше числа узлов пространственной расчётной сетки. В связи с этим равномерность загрузки процессоров жёстко связана с равномерностью распределения крупных частиц пучка в расчётной области. Однако в практических задачах ситуация усложняется тем, что пучок далеко не всегда занимает всю расчётную область. Он может находиться в некоторой её части и изменяться в пространстве и во времени (расширяться, сжиматься, деформироваться и т.п.).

Авторами настоящего препринта реализован второй подход к распараллеливанию численной методики, который использует тот факт, что моделирование крупных частиц занимает основное расчётное время. Число крупных частиц, приходящееся на одну пространственную ячейку, является дополнительной размерностью задачи. Поэтому если это число составляет сотни или тысячи единиц, то распараллеливание резонно проводить «по частицам», т.е. разделить всю совокупность крупных частиц на списки и распределить их по процессорам. Фактически это означает распараллеливание только второго блока численной методики, отвечающего за вычисление плотности тока пучка . При таком распараллеливании равномерность загрузки процессоров обеспечивается подобием списков частиц. Каждый процессор вычисляет плотность тока пучка во всей расчётной области, опираясь на свой список крупных частиц. Подобие списков достигается тем, что все процессоры решают одну и ту же задачу с одинаковыми функциями начальных распределений и источников крупных частиц.

Организация обменных операций при распараллеливании «по частицам» принципиально отличается от геометрического распараллеливания. В геометрическом распараллеливании обмены осуществляются между двумя процессорами, обслуживающими соседние пространственные подобласти. В распараллеливании «по частицам» используются коллективные обмены.

Опишем схему организации обменов во втором подходе более детально. Пусть M – число процессоров, пронумерованных от 0 до (M – 1). 0-ой процессор назовём головным (root). В головном процессоре реализуется первый блок численной методики, отвечающий за решение уравнений Максвелла. Выходными данными первого блока являются компоненты электромагнитного поля в узлах пространственной сетки, которые после вычисления на данном временном шаге распределяются по всем процессорам. Второй блок численной методики реализуется во всех процессорах, включая головной. Полный список крупных частиц пучка заранее разделён на M подобных списков, пучок расслаивается при этом на M одинаковых пучков. Процессор с номером i вычисляет плотность тока , созданную i-м пучком. После вычисления производится сбор и суммирование результатов в головном процессоре:

.

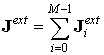Затем происходит переход на следующий временной слой и алгоритм повторяется. Следует отметить, что такая схема организации обменов возможна благодаря тому, что частицы взаимодействуют друг с другом только на макро-уровне – через поле. Столкновения частиц не учитываются.

§5. Исходные данные и результаты расчётов

Результаты вычислительного эксперимента получены при следующих значениях исходных данных. Цилиндрическая камера (см. рис.1) имеет высоту H = 50 см и радиус R = 12,5 см. Плотность входного тока в плоскости инжекции z = 0 имеет вид:

,

где  = 0,0525 СГСЕ/нс – амплитуда; график функции  изображён на рис.6;  = 12 см;  – функция Хевисайда. Нормированная плотность распределения электронов по косинусу полярного угла вылета  в любой точке плоскости инжекции имеет вид, изображённый на рис.7. Табличным способом задана нормированная плотность распределения  инжектируемых электронов по энергии при фиксированном значении . В качестве примера на рис.8 приведены графики функции  при трёх различных значениях параметра . Крестики соответствуют , треугольники – , квадратики – .

Основной расчёт проводился на 64 процессорах многопроцессорной вычислительной системы МВС-1000М и занял 220 мин. При этом на хранение текущей информации о координатах, импульсах и зарядах крупных частиц потребовалось по 150 Мбайт оперативной памяти на каждом процессоре. Таким образом, если бы тот же расчёт целиком проводить на одном процессоре, то потребовалось бы около 10 Гбайт оперативной памяти. Такой объём оперативной памяти не мог быть выделен одному процессору. Для оценки эффективности распараллеливания вычислительного алгоритма был проведён расчёт задачи на 32 процессорах. Общее время вычислений оказалось равным 410 мин, что указывает на то, что эффективность распараллеливания вычислений не менее 90%.

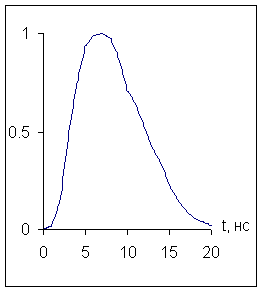
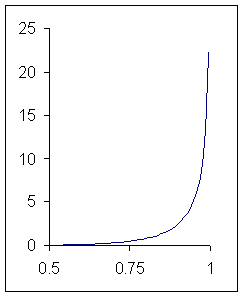
Рис.8

Рис.7

Рис.6

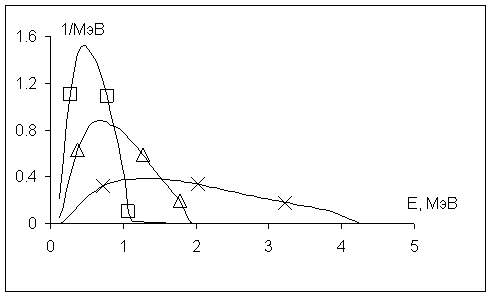
На рис.9 показаны линии уровня максимального по времени модуля z-компоненты напряжённости электрического поля . Видно, что на оси z есть два локальных максимума этой величины. Один из них достигается в плоскости инжекции , другой – на противоположном торце камеры . На боковой поверхности камеры, т.е. при , имеем .

Рис.9

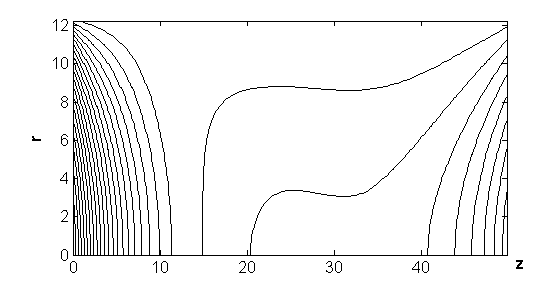
Рис.10

         

На рис.10 изображены зависимости от времени z-компоненты напряжённости электрического поля  в двух указанных точках экстремума величины . Наибольшее значение  достигается в точке . Качественно эти зависимости представляют собой наложение «мелких» высокочастотных собственных резонаторных колебаний поля в камере на импульс, порождённый действием внешнего тока (см. рис.6). В других точках камеры зависимость от времени имеет тот же качественный вид, причём с увеличением z от 0 до H величина импульса уменьшается от положительного значения до отрицательного.

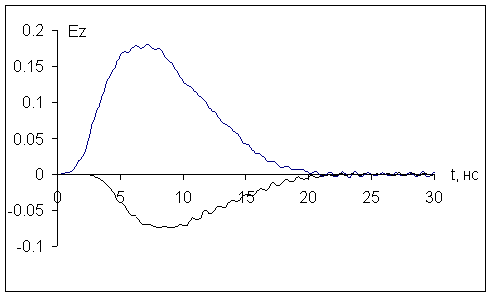
Рис.11

На рис.11 показаны линии уровня максимального по времени модуля напряжённости магнитного поля . Здесь в плоскости инжекции  в окрестности см имеется одна точка максимума этой величины. Значения  монотонно убывают до 0 вдоль любой кривой, пересекающей каждую линию уровня в одной точке и соединяющей точку максимума с любой точкой на оси камеры .

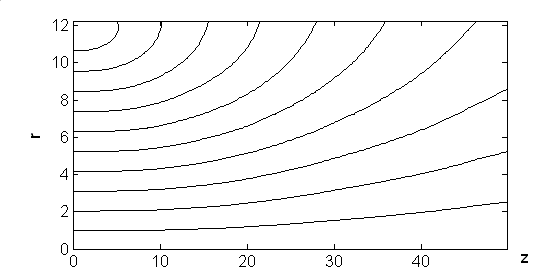
Рис.12

         

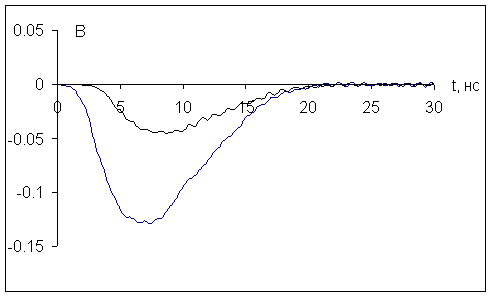
На рис.12 приведены зависимости от времени напряжённости магнитного поля в двух точках  и . В других точках камеры зависимость от времени этой величины имеет тот же качественный вид: наложение «мелких» высокочастотных собственных резонаторных колебаний поля в камере на импульс, порождённый действием внешнего тока (см. рис.6). При этом величина импульса во всех точках камеры отрицательна, как изображено на рис.12.

Приведённые результаты вычислительного эксперимента сравнивались с предварительными результатами физического эксперимента. Сравнение показало на удовлетворительное совпадение амплитуд электрического поля, полученных в физическом эксперименте, с результатами численных расчётов.

Авторы выражают признательность к. ф.-м. н. М. Е. Жуковскому за предоставленные исходные данные для вычислительного эксперимента, постоянное внимание и помощь в работе.

Литература

1.     М.Е.Жуковский, С.В.Подоляко, Р.В.Усков. Алгоритм расчёта простран-ственного и спектрального распределений электронов, порождённых при взаимодействии проникающего излучения с объектами. М.: Ин. прикл. матем. им. М.В.Келдыша РАН, 2004, препр. №89, 16с.

2.     В.Я.Арсенин, Г.Д.Васильков. О разностных схемах для дифференциаль-ных уравнений с диссипативными членами. – М.: Ин. прикл. матем. им. М.В.Келдыша АН СССР, 1981, препр. №17, 20с.

3.     М.В.Скачков. О проблеме шумов и сохранения заряда в методе крупных частиц. // Матем. моделирование, 2000, т.12, №9, с.96-108.

4.     А.В.Березин и др. О математических моделях вторичной ионизации. М.: Ин. прикл. матем. им. М.В.Келдыша РАН, 2002, препр. №29, 20с.

5.     J.P.Boris. Relativistic Plasma Simulation-Optimization of a Hybrid Code // Proc. Fourth. Conf. Num. Sim. Plasmas, Naval Res. Lab., Wash D.C., 2-3 November 1970, p.3-67.

6.     Ч.Бэдсэл, А.Ленгдон. Физика плазмы и численное моделирование. М.: Электроатомиздат, 1989, 455с.