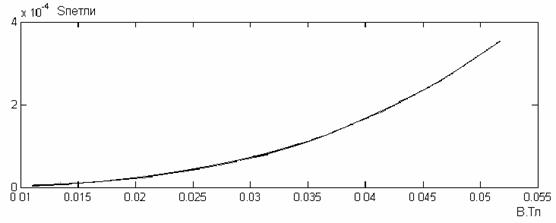
Определение параметров стенда для наземного тестирования магнитного гистерезисного демпфера
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
μ = μнач + αR
H, |
(1.1) |
где μ – проницаемость на кривой
намагничения при напряженности поля H, ![]() – начальная проницаемость,
– начальная проницаемость, ![]() – постоянная Релея, равная dμ/dH. Для большинства
ферромагнетиков эта кривая при индукциях внешнего магнитного поля порядка 0.1
– постоянная Релея, равная dμ/dH. Для большинства
ферромагнетиков эта кривая при индукциях внешнего магнитного поля порядка 0.1![]() представляет собой прямую,
представляет собой прямую, ![]() – индукция насыщения
стержня. Закон Релея можно записать в виде
– индукция насыщения
стержня. Закон Релея можно записать в виде
|
B
= μнач H
+ αR H2. |
(1.2) |
Эта зависимость индукции от
Н представлена кривой M на рис.3.
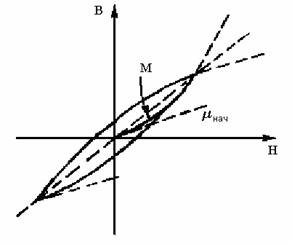
|
Рис.3. Вид петли гистерезиса в модели Релея |
Релей
установил также закон изменения B в интервале B = ± ![]() при изменении H
при изменении H![]() в пределах ±
в пределах ±![]() (то есть для ветвей петли гистерезиса). Восходящая и
нисходящая ветви петли гистерезиса, согласно Релею, представляют собой параболы
(то есть для ветвей петли гистерезиса). Восходящая и
нисходящая ветви петли гистерезиса, согласно Релею, представляют собой параболы
|
|
(1.3) |
где μ =![]() . Тангенс угла наклона для нисходящей ветви в вершине петли
равен начальной проницаемости основной кривой (
. Тангенс угла наклона для нисходящей ветви в вершине петли
равен начальной проницаемости основной кривой (![]() ) [6]. Уравнения (1.1-1.3) записаны в гауссовой системе
единиц.
) [6]. Уравнения (1.1-1.3) записаны в гауссовой системе
единиц.
Переходя в
систему СИ, получим следующее выражение для намагниченности стержня:
|
|
(1.4) |
Это уравнение достаточно
точно описывает намагниченность стержня при условии |![]() | <
| < ![]() , где
, где ![]() – коэрцитивная сила
данного материала, и симметричном перемагнивании.
– коэрцитивная сила
данного материала, и симметричном перемагнивании.
1.2. Модель «параллелограмма»
При значениях
проекции напряженности внешнего магнитного поля ![]() , удовлетворяющих условиям
, удовлетворяющих условиям ![]() , намагниченность стержня может быть описана моделью
«параллелограмма»,
, намагниченность стержня может быть описана моделью
«параллелограмма», ![]() – значение проекции
напряженности внешнего магнитного поля, при которой наступает насыщение
материала. Намагниченность стержня в модели «параллелограмма» имеет следующий
вид:
– значение проекции
напряженности внешнего магнитного поля, при которой наступает насыщение
материала. Намагниченность стержня в модели «параллелограмма» имеет следующий
вид:
|
|
(1.5) |
|
|
|
|
|
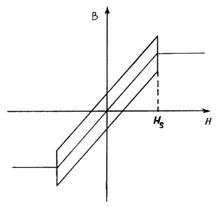
Рис.4.
Вид петли гистерезиса в модели «параллелограмма» |
||
Коэффициент k найдём из
условия непрерывности функции, описывающей потери на гистерезис, при ![]() (H
(H![]() – коэрцитивная сила). Для этого приравняем площади петли
Релея и параллелограмма при
– коэрцитивная сила). Для этого приравняем площади петли
Релея и параллелограмма при ![]()
|
|
Интегрируем
обе части и выполним необходимые преобразования:
|
Þ Þ Þ |
Таким
образом, получим выражение для намагниченности стержня
|
|
(1.6) |
1.3. Модель «насыщения»
Когда![]() , демпфирования нет. То есть I =
, демпфирования нет. То есть I = ![]() = const, где
= const, где ![]() - индукция насыщения.
- индукция насыщения.
2. Исследование колебаний
намагниченного спутника в подвесе
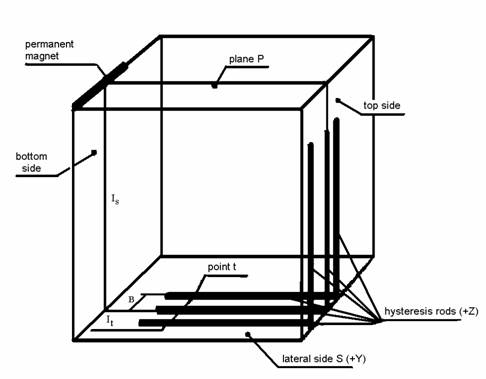
В качестве
модели спутника будем рассматривать твердое тело, подвешенное на упругой нити (условно
показанное в виде пластины на рис.5). На нем расположен постоянный магнит,
который необходим для создания восстанавливающего момента, возвращающего
спутник в положение равновесия подобно стрелке компаса. Под углом ![]() к постоянному магниту
расположен магнитомягкий стержень.
к постоянному магниту
расположен магнитомягкий стержень.

Рис.5. Модель спутника
Введем
обозначения: ![]()
![]() индукция внешнего
магнитного поля, создаваемого катушками;
индукция внешнего
магнитного поля, создаваемого катушками; ![]()
![]() магнитный дипольный момент
постоянного магнита;
магнитный дипольный момент
постоянного магнита; ![]()
![]() магнитный дипольный момент
гистерезисного стержня;
магнитный дипольный момент
гистерезисного стержня; ![]()
![]() механический момент,
создаваемый магнитными силами;
механический момент,
создаваемый магнитными силами; ![]()
![]() угол между осями
стержня и постоянного магнита (рис.6);
угол между осями
стержня и постоянного магнита (рис.6); ![]()
![]() угол между осью
постоянного магнита и направлением вектора
угол между осью
постоянного магнита и направлением вектора ![]() ;
; ![]()
![]() положение равновесия
подвеса, то есть значение угла
положение равновесия
подвеса, то есть значение угла ![]() , когда подвес находится в положении равновесия;
, когда подвес находится в положении равновесия; ![]()
![]() коэффициент вязкого
трения;
коэффициент вязкого
трения; ![]()
![]() коэффициент упругости
подвеса; J
коэффициент упругости
подвеса; J
![]() момент инерции
спутника.
момент инерции
спутника.
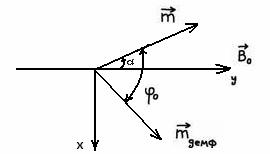
Рис.6. Углы между введенными векторами
Запишем
уравнение движения спутника
|
|
(2.1) |
|
|
(2.2) |
где V – объем стержня, ![]()
![]() намагниченность стержня.
намагниченность стержня.
2.1. Уравнение движения спутника в подвесе
Рассмотрим
уравнение (2.1). Поскольку демпфирующий и восстанавливающий механические
моменты направлены по одной оси, то справедливо равенство
|
|
Тогда
уравнение движения (2.1) запишется в виде
|
|
(2.3) |
Положим ![]() в уравнении (2.3), тогда получим
в уравнении (2.3), тогда получим
|
|
(2.4) |
Выразим ![]() через
через ![]() , где
, где ![]() – проекция
напряженности
– проекция
напряженности ![]() внешнего магнитного
поля на ось стержня,
внешнего магнитного
поля на ось стержня,
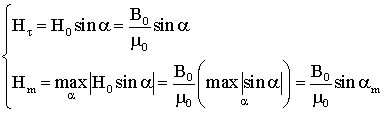
В уравнение
(2.4) подставим выражение (1.3) для модели Релея
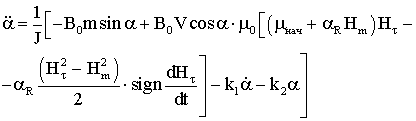
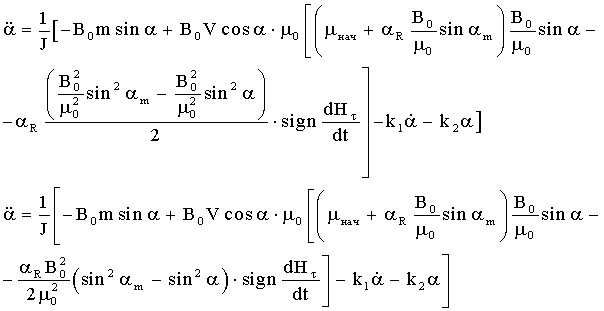
А также для модели параллелограмма
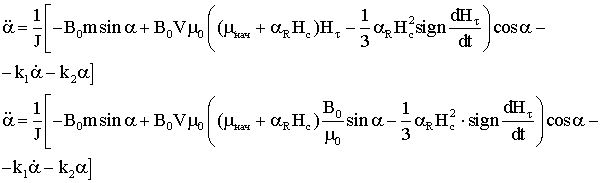
От размерной переменной t перейдем к безразмерной переменной ![]() по формуле
по формуле ![]() , где
, где ![]() , Т
, Т![]() характерное время. Чтобы сделать эту замену, найдем
характерное время. Чтобы сделать эту замену, найдем ![]() . За характерное время Т возьмем период гармонических
колебаний спутника, на котором установлен только постоянный магнит. Для того,
чтобы найти частоту колебаний, запишем уравнение свободных колебаний спутника
. За характерное время Т возьмем период гармонических
колебаний спутника, на котором установлен только постоянный магнит. Для того,
чтобы найти частоту колебаний, запишем уравнение свободных колебаний спутника
![]()
Делаем замену при помощи
вспомогательных выражений
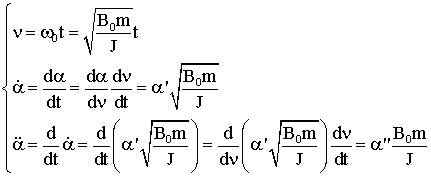
После замены
переменных уравнение движения запишется в следующем виде:
1) для модели Релея:
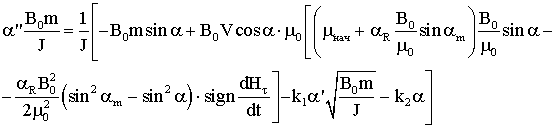
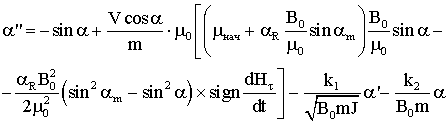
2) для модели параллелограмма:
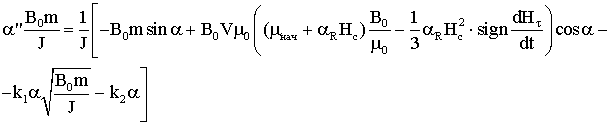
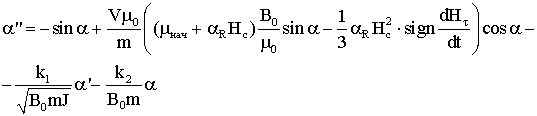
Упростим
полученные выражения:
1) для модели Релея:
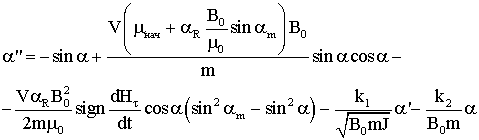
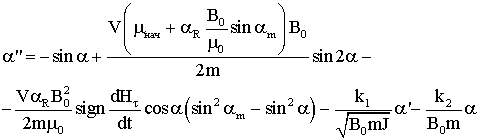
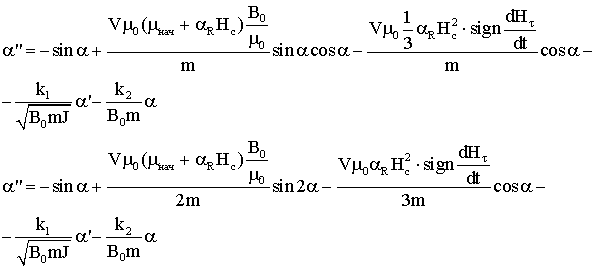
2) для модели «параллелограмма»:
2.2. Исследование модели Релея
Введем
безразмерные параметры
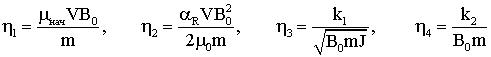 ,
,
тогда получим уравнение движения
в безразмерном виде
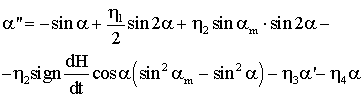
Приведем
подобные члены
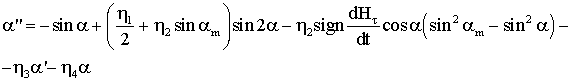
Считая
колебания малыми, разложим тригонометрические функции в окрестности ![]()
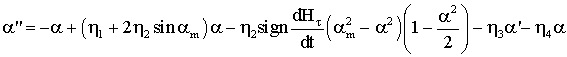 .
.
Раскроем
скобки
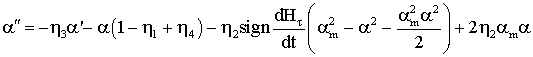 (2.5)
(2.5)
Запишем
уравнение (2.5) в стандартном виде[1]
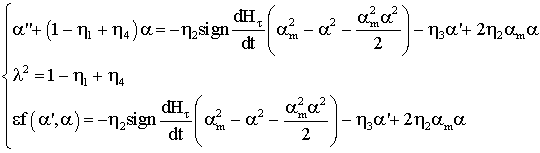 (2.6)
(2.6)
2.3.
Исследование модели «параллелограмма»
Введем
безразмерные параметры
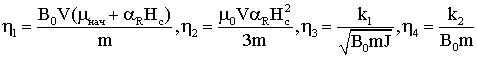 ,
,
отличные от
введенных в разделе 2.2, но имеющих те же обозначения. Тогда получим уравнение движения
в безразмерном виде
![]() .
.
Считая
колебания малыми, разложим тригонометрические функции в окрестности ![]()
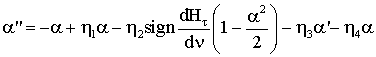 .
.
Пренебрежем
членами порядка выше первого и запишем оставшиеся члены
|
|
(2.7) |
Перепишем
уравнение (2.7) в стандартном виде
|
|
(2.8) |
2.4. Решение
уравнений движения (2.6) и (2.8)
В этом
параграфе для решения уравнения движения, записанном в стандартном виде, будем
использовать метод Ван-дер-Поля [4].
Сделаем замену
![]() . В результате для правой части уравнения в рамках модели Релея получим выражение
. В результате для правой части уравнения в рамках модели Релея получим выражение
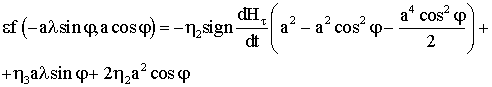
Членом ![]() можно пренебречь.
можно пренебречь.
Чтобы найти
зависимость амплитуды колебаний от времени, подставим это уравнение в уравнение
для поиска усредненных величин
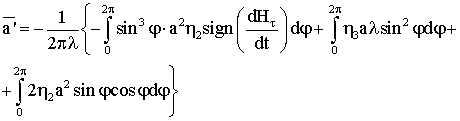
Вычислим входящие
сюда интегралы
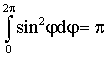 ,
, 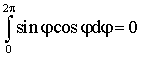 .
.
Рассмотрим значения sign на
периоде от 0 до 2π. Из замены видно, что при увеличении φ от 0 до
π угол уменьшается от a до –a, а из введенной системы координат
следует, что мы «находимся» на верхней ветви петли Релея. Получается добавка к I,
следовательно, ![]() . Аналогично, при изменении φ от π до 2π
поллучаем, что
. Аналогично, при изменении φ от π до 2π
поллучаем, что ![]() , тогда справедлива цепочка равенств
, тогда справедлива цепочка равенств
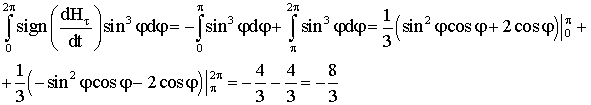
Таким образом,
получили уравнение
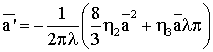 ,
, ![]() .
.
Его решение
запишем в виде
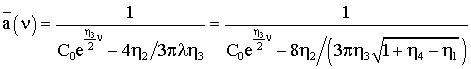 .
.
Найдем
постоянную C![]() . Пусть
. Пусть ![]() , тогда, подставляя эти начальные условия, получаем
, тогда, подставляя эти начальные условия, получаем
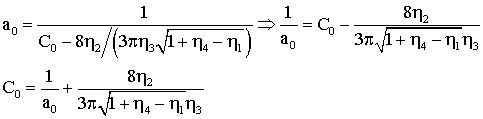 .
.
Итак, имеем
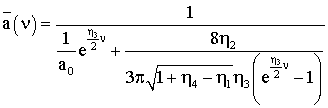
Возвращаясь к
переменной t, получаем
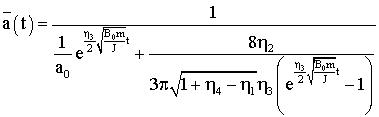
Проведем
аналогичные выкладки для модели
«параллелограмма». Правая часть уравнения в стандартном виде выглядит
следующим образом:
![]()
Чтобы найти зависимость
амплитуды колебаний от времени, подставим это выражение в усредненное уравнение
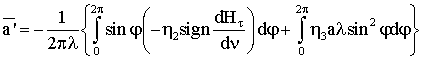
Вычислим интегралы входящие
сюда квадратуры. Второй интеграл имеет вид 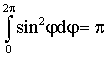 . Рассмотрим значения sign на периоде от 0 до 2π. Из
замены видно, что при увеличении φ от 0 до π угол уменьшается от a до
–a, а из введенной системы координат следует, что мы «находимся» на верхней
ветви петли Релея. Получается добавка к I, следовательно
. Рассмотрим значения sign на периоде от 0 до 2π. Из
замены видно, что при увеличении φ от 0 до π угол уменьшается от a до
–a, а из введенной системы координат следует, что мы «находимся» на верхней
ветви петли Релея. Получается добавка к I, следовательно ![]() . Аналогично, при изменении φ от π до 2π:
. Аналогично, при изменении φ от π до 2π: ![]() .
.
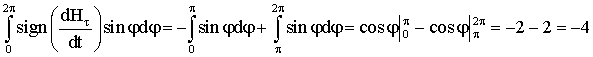
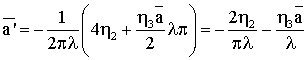
Решение этого
уравнения запишется в виде
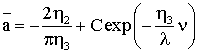
Найдем C.
Пусть ![]() , подставляем начальные значения
, подставляем начальные значения
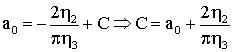
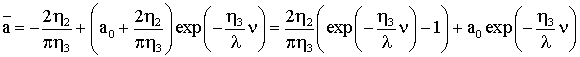
Возвращаясь к
переменной t, получаем окончательно
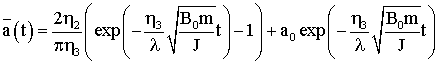
2.5. Анализ решения уравнения движения
Теперь, когда
получено уравнение движения, нужно разобраться, как влияет демпфирующий
стержень на движение спутника и какое магнитное поле нужно создать, чтобы
влияние стержня было достаточно заметным. За затухание колебаний за счет
гистерезиса в нашем уравнении отвечает параметр ![]() .
.
Будем
исследовать отношение амплитуд ![]() в момент
в момент ![]() без затухания на
гистерезис (в числителе) и с затуханием (в знаменателе) для модели Релея. После подстановки
выражений для амплитуд получаем
без затухания на
гистерезис (в числителе) и с затуханием (в знаменателе) для модели Релея. После подстановки
выражений для амплитуд получаем
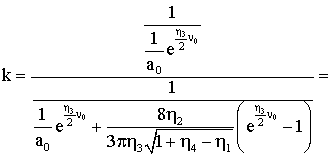
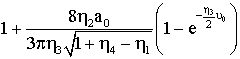
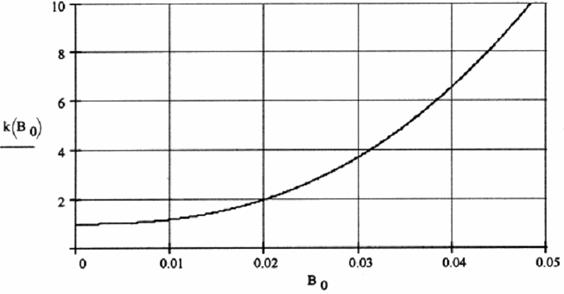
Построим
график зависимости k от индукции магнитного поля, подставив численные значения
параметров для реальной модели и взяв ![]() за переменную (рис.7).
за переменную (рис.7).
Коэффициент
упругости подвеса найдем из условия - пусть период колебаний диска диаметром 30
см и массой 200 г равен 1 мин. Запишем уравнение колебаний диска ![]() . С другой стороны
. С другой стороны ![]() . Отсюда можем найти коэффициент упругости
. Отсюда можем найти коэффициент упругости
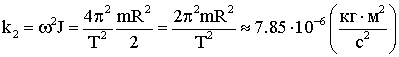 .
.
Коэффициент
вязкого трения о воздух найдем, зная, что колебания того же диска затухают за 1
час (возьмем начальную амплитуду 180°, конечную 1°):
|
|
Значения для
остальных параметров возьмем такие, чтобы они соответствовали реальному спутнику
типа MUNIN,
|
|
|
|
|
Перед построением графика
вспомним, что безразмерные параметры также являются функциями индукции
магнитного поля |
||
|
|
||
|
|
||
Рис.7. График зависимости k от индукции магнитного поля
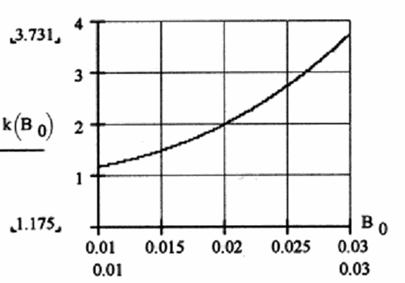
Приведем детальный
график в окрестности k=2 (рис.8).
|
|
Рис.8. График
зависимости k от индукции ![]() в окрестности значений
k=2
в окрестности значений
k=2
k(0.01)=1.175; k(0.02)=1.991; k(0.03)=3.731
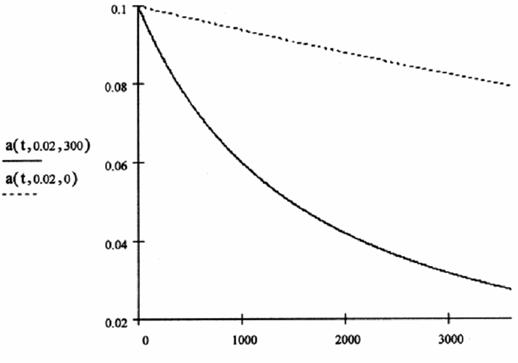
Посмотрим, как
меняется амплитуда колебаний при B![]() =0.02 Тл, когда есть затухание за счет гистерезиса (
=0.02 Тл, когда есть затухание за счет гистерезиса (![]() =300) и когда его нет (
=300) и когда его нет (![]() =0), то есть когда затухание происходит только за счет
вязкого трения (рис.9).
=0), то есть когда затухание происходит только за счет
вязкого трения (рис.9).
|
|
Рис.9.
Зависимость амплитуды колебаний при B![]() =0.02 Тл с затуханием и без затухания
=0.02 Тл с затуханием и без затухания
Из приведенных графиков
видно, что при индукции магнитного поля порядка ![]() Тл и более влияние гистерезиса на затухание колебаний
становится достаточно заметным. Это говорит о том, что для испытаний на Земле
необходимо искусственно создавать магнитное поле, поскольку значение индукции
магнитного поля Земли имеет порядок
Тл и более влияние гистерезиса на затухание колебаний
становится достаточно заметным. Это говорит о том, что для испытаний на Земле
необходимо искусственно создавать магнитное поле, поскольку значение индукции
магнитного поля Земли имеет порядок ![]() Тл.
Тл.
3. Исследование движения
намагниченного стержня в подвесе
3.1. Объект исследования
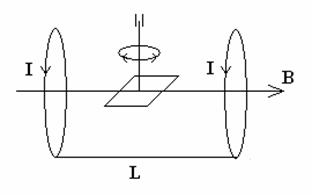
Будем
рассматривать стержень из магнитомягкого материала, находящийся на упругом
подвесе во внешнем магнитном поле (рис.10). Считаем, что вектор индукции
внешнего магнитного поля направлен перпендикулярно оси подвеса. В положении
равновесия подвеса ось стержня перпендикулярна вектору напряженности магнитного
поля. Считается, что стержень совершает колебания в плоскости, перпендикулярной
оси подвеса.
|
|
|
|
Рис.10. Стержень, закрепленный на упругой нити во внешнем магнитном поле |
||
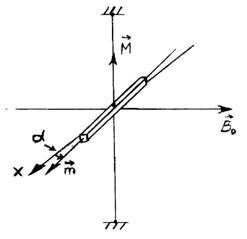
Рассмотрим
следующую систему осей: направление оси ![]() совпадает с
направлением вектора индукции внешнего магнитного поля; ось M направлена вверх
вдоль оси подвеса; ось x перпендикулярна осям
совпадает с
направлением вектора индукции внешнего магнитного поля; ось M направлена вверх
вдоль оси подвеса; ось x перпендикулярна осям ![]() и M, направлена вдоль
оси стержня в положении равновесия и, соответственно дополняет оси
и M, направлена вдоль
оси стержня в положении равновесия и, соответственно дополняет оси ![]() и M до правой тройки. Запишем
уравнение движения стержня
и M до правой тройки. Запишем
уравнение движения стержня
|
|
(3.1) |
где M – вектор,
удовлетворяющий условию |M|=J![]() ; J – экваториальный момент инерции стержня; α –
угол между осью x и вектором магнитного момента стержня;
; J – экваториальный момент инерции стержня; α –
угол между осью x и вектором магнитного момента стержня; ![]() – индукция внешнего
магнитного поля; m(α) – магнитный момент стержня;
– индукция внешнего
магнитного поля; m(α) – магнитный момент стержня; ![]() – коэффициент вязкого
трения;
– коэффициент вязкого
трения; ![]() – коэффициент
упругости подвеса.
– коэффициент
упругости подвеса.
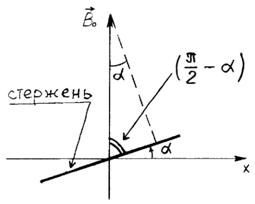
Перепишем
уравнение (3.1) в проекциях на оси x, ![]() , M в соответствии с рис.10 и рис.11
, M в соответствии с рис.10 и рис.11
|
|
(3.2) |
|||
|
|
|
||
|
Рис.11. Расположение стержня при отклонении от положения равновесия на угол α |
|
|||
Учитывая, что
магнитный момент выражается через объем и намагниченность стержня по формуле
(2.2), получим уравнение
|
|
(3.3) |
Намагниченность
стержня I является функцией от угла α и зависит от выбранной модели
гистерезиса, ![]() , где
, где ![]() – проекция
– проекция ![]() (напряженности
внешнего магнитного поля) на ось стержня:
(напряженности
внешнего магнитного поля) на ось стержня: ![]() или
или ![]() , где
, где ![]() – магнитная
проницаемость вакуума.
– магнитная
проницаемость вакуума.
3.2. Исследование уравнений
движения в рамках различных моделей гистерезиса
3.2.1.
Уравнения движения в безразмерном виде
Вернемся к
уравнению движения стержня (3.3). За характерное время возьмем период колебаний
стержня при наличии только упругого подвеса (то есть без воздуха и магнитного
поля), которые описываются уравнением ![]() . Для этого уравнения
. Для этого уравнения ![]() . Перейдем к безразмерному времени по формуле
. Перейдем к безразмерному времени по формуле
|
|
(3.4) |
тогда ![]() ,
, ![]() .
.
Уравнение
движения (3.3), выраженное через безразмерное время по формуле (3.4), запишется
так:
|
|
(3.5) |
Подставляя в
уравнение (3.5) выражения для намагниченности стержня вначале в модели Релея
(1.4), а затем в модели «параллелограмма» (1.6), получим уравнения движения,
выраженные через проекцию на стержень вектора напряженности внешнего магнитного
поля ![]() :
:
1) для модели Релея
|
|
(3.6) |
2) для модели «параллелограмма»
|
|
(3.7) |
3.2.2.
Исследование уравнения движения в рамках модели Релея
Продолжим
решение уравнения (3.6) для модели Релея. Подставляя ![]() (см. раздел 2) и
(см. раздел 2) и ![]() , где
, где ![]() – амплитуда колебаний, получим
– амплитуда колебаний, получим
|
|
Преобразуем
это уравнение к более удобному для дальнейшей работы виду
|
|
(3.8) |
Введем
безразмерные параметры
|
|
(3.9) |
и запишем
уравнение (3.8) в безразмерном виде
|
|
(3.10) |
Будем считать
параметры ![]() , тогда есть основание полагать, что уравнение (3.10) может
допускать решение при |α|<<1. Разложим тригонометрические функции в
уравнении (3.10) в окрестности α=0 и получим
, тогда есть основание полагать, что уравнение (3.10) может
допускать решение при |α|<<1. Разложим тригонометрические функции в
уравнении (3.10) в окрестности α=0 и получим
|
|
(3.11) |
Проанализируем
получившееся уравнение.
-
Член ![]() зависит от начальной
магнитной проницаемости материала стержня. Он создает опрокидывающий момент,
следовательно, необходимо задать некоторые ограничения на параметры модели,
поскольку, например, если опрокидывающий момент будет больше или равен
восстанавливающему, то система не вернется в состояние с α=0.
зависит от начальной
магнитной проницаемости материала стержня. Он создает опрокидывающий момент,
следовательно, необходимо задать некоторые ограничения на параметры модели,
поскольку, например, если опрокидывающий момент будет больше или равен
восстанавливающему, то система не вернется в состояние с α=0.
-
Член ![]() зависит от постоянной
Релея и также создает опрокидывающий момент (добавка, связанная с увеличением
магнитной проницаемости материала по мере увеличения
зависит от постоянной
Релея и также создает опрокидывающий момент (добавка, связанная с увеличением
магнитной проницаемости материала по мере увеличения ![]() , описывает увеличение наклона петли Релея – см. (1.1).
, описывает увеличение наклона петли Релея – см. (1.1).
-
Член 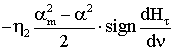 также зависит от
постоянной Релея (добавка или уменьшение магнитной проницаемости в зависимости
от того, по какой ветви петли Релея (нисходящей или восходящей), мы «движемся»
в данный момент) – отвечает за затухание колебаний из-за гистерезиса.
также зависит от
постоянной Релея (добавка или уменьшение магнитной проницаемости в зависимости
от того, по какой ветви петли Релея (нисходящей или восходящей), мы «движемся»
в данный момент) – отвечает за затухание колебаний из-за гистерезиса.
-
Член ![]() зависит от вязкости
воздуха, отвечает за затухание колебаний, вызванное вязким трением (в
результате работы мы должны оценить допустимый коэффициент вязкости воздуха,
при котором будет заметен эффект затухания колебаний за счет гистерезисного
стержня).
зависит от вязкости
воздуха, отвечает за затухание колебаний, вызванное вязким трением (в
результате работы мы должны оценить допустимый коэффициент вязкости воздуха,
при котором будет заметен эффект затухания колебаний за счет гистерезисного
стержня).
-
Член –α создает восстанавливающий момент, вызванный действием
упругого подвеса.
-
3.2.3.
Некоторые ограничения в модели Релея
Рассмотрим
возникающие ограничения в модели Релея на амплитуду угла α и
упругость подвеса.
1)
Амплитуда угла α. Поскольку минимальная
напряженность внешнего магнитного поля – это напряженность магнитного поля
Земли ![]() ≈ 20 А/м, то, учитывая, что
≈ 20 А/м, то, учитывая, что ![]() , и коэрцитивная сила, например, 4-79-пермаллоя
, и коэрцитивная сила, например, 4-79-пермаллоя ![]() ≈ 4 А/м (см. Приложение), получим ограничение на угол α:
≈ 4 А/м (см. Приложение), получим ограничение на угол α:
![]() . Таким образом, получаем, что для материала 4-79-пермаллой
при амплитудах
. Таким образом, получаем, что для материала 4-79-пермаллой
при амплитудах ![]() модель Релея
становится неприменимой. Если мы создаем искусственное магнитное поле
(например, с помощью катушек Гельмгольца) такое, что, к примеру, напряженность
суммарного поля в 10 раз больше поля Земли, то максимальная амплитуда угла
отклонения, при которой модель Релея будет применима, становится в 10 раз
меньше (в случае 4-79-пермаллоя – около 1˚).
модель Релея
становится неприменимой. Если мы создаем искусственное магнитное поле
(например, с помощью катушек Гельмгольца) такое, что, к примеру, напряженность
суммарного поля в 10 раз больше поля Земли, то максимальная амплитуда угла
отклонения, при которой модель Релея будет применима, становится в 10 раз
меньше (в случае 4-79-пермаллоя – около 1˚).
2) Упругость подвеса и объем стержня. Ограничение
на упругость подвеса вытекает из условия малости опрокидывающего момента,
который в уравнении (3.10) описан членами, содержащими параметры ![]() . Рассмотрим параметр
. Рассмотрим параметр ![]() :
:
|
|
Подставим в
соотношение для ![]() следующие значения
параметров:
следующие значения
параметров: ![]() (см. Приложение);
(см. Приложение); ![]() (
(![]() ,
, ![]() ,
, ![]() ); V вычислим, полагая размеры стержня l = 20 см, d = 1 мм [5]:
); V вычислим, полагая размеры стержня l = 20 см, d = 1 мм [5]: ![]() . Получим, что при напряженности магнитного поля, равной
напряженности магнитного поля Земли,
. Получим, что при напряженности магнитного поля, равной
напряженности магнитного поля Земли, ![]() . Из вышеизложенного видно, что при увеличении напряженности
внешнего магнитного поля в 10 (100) раз, упругость подвеса необходимо
увеличивать в 100 (10000) раз. Из выражения для параметра
. Из вышеизложенного видно, что при увеличении напряженности
внешнего магнитного поля в 10 (100) раз, упругость подвеса необходимо
увеличивать в 100 (10000) раз. Из выражения для параметра ![]() также видно, что
вместо увеличения в 100 (10000) коэффициента упругости подвеса можно,
соответственно в 100 (10000) раз уменьшать объем стержня.
также видно, что
вместо увеличения в 100 (10000) коэффициента упругости подвеса можно,
соответственно в 100 (10000) раз уменьшать объем стержня.
Теперь
проанализируем параметр ![]()
|
|
Здесь ![]() (см. Приложение);
(см. Приложение); ![]() ,
, ![]() ,
, ![]() . Получим, что при напряженности магнитного поля, равной
напряженности магнитного поля Земли,
. Получим, что при напряженности магнитного поля, равной
напряженности магнитного поля Земли, ![]() .
.
Поскольку в выражение
для параметра ![]() входит индукция
внешнего магнитного поля в третьей степени (а не во второй, как в
входит индукция
внешнего магнитного поля в третьей степени (а не во второй, как в ![]() ), то при изменении напряженности поля на один порядок,
придется менять значения упругости или объема стержня на три порядка.
), то при изменении напряженности поля на один порядок,
придется менять значения упругости или объема стержня на три порядка.
3.2.4. Дальнейшее
исследование уравнения движения в рамках модели Релея
Продолжим
исследование уравнения движения в рамках модели Релея. Перейдем к исследованию
уравнения движения, записанного в безразмерном виде (3.11), методом
Ван-дер-Поля. Для этого необходимо уравнение (3.11) переписать в стандартном виде
![]() , где |
, где |![]() |<<1. В результате получим
|<<1. В результате получим
|
|
(3.12) |
Здесь члены ![]() и
и ![]() находятся в правой
части. Ниже при интегрировании по периоду они дают нуль. Это значит, что
опрокидывающий момент полагается малым. Если мы не хотим пренебрегать
опрокидывающим моментом, то эти два члена нужно перенести в левую часть. Тогда
находятся в правой
части. Ниже при интегрировании по периоду они дают нуль. Это значит, что
опрокидывающий момент полагается малым. Если мы не хотим пренебрегать
опрокидывающим моментом, то эти два члена нужно перенести в левую часть. Тогда ![]() ниже в уравнении
(3.15) войдет в член
ниже в уравнении
(3.15) войдет в член ![]() следующим образом:
следующим образом: ![]() (при амплитудах
порядка 1° и значениях
(при амплитудах
порядка 1° и значениях ![]() и
и ![]() , оцененных выше, это дает поправку около 2%, при амплитудах
порядка 10° – 5%).
, оцененных выше, это дает поправку около 2%, при амплитудах
порядка 10° – 5%).
Для решения
системы (3.12) нужно решить уравнение
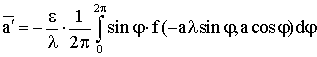
Введем
стандартную замену переменных из метода Ван-дер-Поля: ![]() , где a,φ – новые переменные
, где a,φ – новые переменные ![]() функции времени. После
такой замены переменных получаем
функции времени. После
такой замены переменных получаем
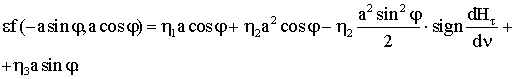
Тогда
уравнение для усредненной по быстрой фазе амплитуды на периоде запишется так:
|
|
(3.13) |
Рассмотрим
значения sign на периоде от 0 до 2π. Из замены видно, что при увеличении
φ от 0 до π угол уменьшается от a до –a, а из введенной системы
координат следует, что мы «находимся» на верхней ветви петли Релея. Получается
добавка к I, следовательно ![]() . Аналогично, при изменении φ от π до 2π:
. Аналогично, при изменении φ от π до 2π: ![]() . После интегрирования правой части уравнения (3.13) получим
. После интегрирования правой части уравнения (3.13) получим
|
|
(3.14) |
Решая
уравнение (3.14), получаем выражение для амплитуды
|
|
(3.15) |
где ![]() – константа, зависящая от начальной амплитуды. Подставляем
начальную амплитуду
– константа, зависящая от начальной амплитуды. Подставляем
начальную амплитуду ![]() . Тогда
. Тогда ![]() . Следовательно,
. Следовательно,
|
|
(3.16) |
Если в (3.16)
разложить экспоненты до первой степени аргумента включительно, то получим
следующую зависимость:
|
или
|
(3.17) |
Из уравнения
(3.14) следует ограничение на вязкость воздуха. Чтобы демпфирование от
гистерезиса было заметно по сравнению с вязким трением, необходимо выполнение
следующего условия:
|
|
Таким образом,
для вязкого трения получаем ![]() . Оценим
. Оценим ![]() , подставляя следующие значения параметров: a = 0.2 (10°);
, подставляя следующие значения параметров: a = 0.2 (10°); ![]() (см. ограничения
выше);
(см. ограничения
выше); ![]() ;
; ![]() . Тогда для вязкого трения получаем
. Тогда для вязкого трения получаем ![]() .
.
3.2.5. Исследование
уравнения движения в рамках модели «параллелограмма»
Рассмотрим
ограничение на амплитуду колебаний для модели «параллелограмма». Аналогично
тому, как это было сделано для модели Релея, вычислим амплитуду колебаний
стержня, больше которой модель «параллелограмма» будет применима. Подставляя
значения для геомагнитного поля ![]() и напряженности поля,
при которой происходит насыщение 4-79-пермаллоя
и напряженности поля,
при которой происходит насыщение 4-79-пермаллоя ![]() (см. Приложение), в
выражение
(см. Приложение), в
выражение ![]() , получим ограничение на угол α
, получим ограничение на угол α ![]() . Таким образом, получаем, что для материала 4-79-пермаллой
при амплитудах
. Таким образом, получаем, что для материала 4-79-пермаллой
при амплитудах ![]() модель
«параллелограмма» становится неприменимой.
модель
«параллелограмма» становится неприменимой.
Продолжим
решение уравнения движения в рамках модели «параллелограмма» (3.7)
|
|
Подставляя в
это уравнение ![]() , получим
, получим
|
|
(3.18) |
Введем
безразмерные параметры
|
|
(3.19) |
Запишем
уравнение (3.18) в безразмерном виде
|
|
(3.20) |
Будем считать параметры ![]() . Тогда есть основание полагать, что уравнение (3.20) допускает
решение при |α|<<1. Разложив тригонометрические функции в уравнении
(3.20) в окрестности α=0, получим
. Тогда есть основание полагать, что уравнение (3.20) допускает
решение при |α|<<1. Разложив тригонометрические функции в уравнении
(3.20) в окрестности α=0, получим
|
|
(3.21) |
Перейдем к
исследованию уравнения движения, записанного в безразмерном виде (3.21),
методом Ван-дер-Поля. Записываем уравнение (3.21) в стандартном виде
|
|
(3.22) |
При усреднении
период разбивается на несколько частей:
при |α| >
![]() таких, что |
таких, что |![]() | >
| > ![]() , используем модель, описанную уравнениями (3.18 – 3.22), то
есть в качестве модели гистерезиса берем параллелограмм (рис. 4);
, используем модель, описанную уравнениями (3.18 – 3.22), то
есть в качестве модели гистерезиса берем параллелограмм (рис. 4);
при |α| <
![]() таких, что |
таких, что |![]() | <
| < ![]() , используем модель Релея (рис. 3).
, используем модель Релея (рис. 3).
при |![]() | =
| = ![]() , разрыва нет, поскольку при выборе коэффициента k перед
знаком sign в модели «параллелограмма» использовалась связка через равенство
потерь энергии на гистерезис в рамках моделей Релея и «параллелограмма».
, разрыва нет, поскольку при выборе коэффициента k перед
знаком sign в модели «параллелограмма» использовалась связка через равенство
потерь энергии на гистерезис в рамках моделей Релея и «параллелограмма».
|
|
|
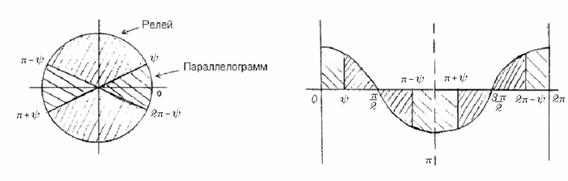
Рис.12.
Точки перехода от модели Релея к модели «параллелограмма» на интервале
|
При изменении
фазы φ от 0 до 2π получаются точки ψ, где заменяем модель (рис.
12):
при ![]() используется модель
«параллелограмма»;
используется модель
«параллелограмма»;
при ![]() – модель Релея.
– модель Релея.
Чтобы не
путать безразмерные параметры в моделях Релея и «параллелограмма», параметрам в
модели Релея будет приписывать сверху индекс R. Уравнение для усреднения по
быстрой фазе запишется следующим образом:
|
|
Интегралы,
содержащие произведение синуса на косинус на ![]() и
и ![]() обращаются в нуль.
Тогда имеем
обращаются в нуль.
Тогда имеем
|
|
![]() (
(![]() см. выше в ограничениях на модель Релея). После
интегрирования получаем
см. выше в ограничениях на модель Релея). После
интегрирования получаем
|
|
(3.23) |
где ![]() находится следующим
образом
находится следующим
образом ![]() .
. ![]() .
.
Из уравнения (3.23)
видно, что если ψ = 0, то есть амплитуда ![]() (точка перехода с
одной модели на другую), то уравнение (3.23) преобразуется к виду (3.13), то
есть совпадает с уравнением для амплитуды в модели Релея.
(точка перехода с
одной модели на другую), то уравнение (3.23) преобразуется к виду (3.13), то
есть совпадает с уравнением для амплитуды в модели Релея.
Из уравнения
(3.23) следует ограничение на вязкость воздуха. Чтобы демпфирование от
гистерезиса было заметно по сравнению с вязким трением, необходимо выполнение
следующего условия:
|
|
(3.24) |
Подставим сюда следующие
значения параметров: a = 0.5 (30°); ![]() (см. выше);
(см. выше); ![]() (см. выше);
(см. выше); ![]() ;
; ![]() = 350000 (см.
Приложение);
= 350000 (см.
Приложение); ![]() ;
; ![]() . Получаем
. Получаем ![]() ~ 0.033. Тогда для
вязкого трения имеем следующую оценку:
~ 0.033. Тогда для
вязкого трения имеем следующую оценку: ![]() .
.
3.2.6. Исследование уравнения движения в рамках модели насыщения
В случае
модели «насыщения» период, на котором происходит интегрирование, разбивается на
множества следующим образом:
при ![]() – модель
«параллелограмма»;
– модель
«параллелограмма»;
при ![]() – модель Релея.
– модель Релея.
Тогда
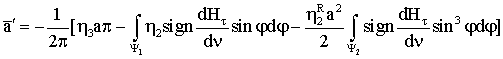 (3.25)
(3.25)
Подставим пределы
интегрирования в первый интеграл из (3.25), получим
|
|
После
интегрирования получаем уравнение для амплитуды
|
|
(3.26) |
Здесь ![]() , где
, где ![]() – угол, при котором
происходит переход от модели «параллелограмма» к модели Релея;
– угол, при котором
происходит переход от модели «параллелограмма» к модели Релея; ![]() – угол, при котором
происходит переход от состояния насыщения к модели «параллелограмма».
– угол, при котором
происходит переход от состояния насыщения к модели «параллелограмма».
Из уравнения
(3.25) следует ограничение на вязкость воздуха в рамках модели «насыщения».
Чтобы демпфирование от гистерезиса было заметно по сравнению с вязким трением,
необходимо выполнение следующего условия:
|
|
(3.27) |
Произведем
оценку допустимого коэффициента вязкого трения, когда напряженность внешнего
магнитного поля равна напряженности геомагнитного поля. Подставим в (3.26)
следующие значения параметров: a = 0.7 (30°); ![]() = 0.1 (см. выше);
= 0.1 (см. выше); ![]() (см. выше);
(см. выше); ![]() ;
; ![]() = 350000 (см.
Приложение);
= 350000 (см.
Приложение); ![]() ;
; ![]() ;
; ![]() . Получаем
. Получаем ![]() ~0.031. Тогда для вязкого трения имеем
~0.031. Тогда для вязкого трения имеем ![]() .
.
Проведем
сравнение коэффициентов вязкого трения и упругости нити, полученных выше в
результате оценки в рамках моделей Релея, «параллелограмма» и «насыщения», с
коэффициентами вязкого трения и упругости нити, вычисленных на основании
экспериментальных данных.
Рассмотрим
пример: диск диаметром 30 см и массой 200 г подвешен на упругой нити. Период
колебаний диска равен 10 сек. Колебания диска затухают от ![]() до
до ![]() за t=10 мин.
за t=10 мин.
Коэффициент
упругости нити найдем, зная, что ![]() для уравнения
колебаний
для уравнения
колебаний ![]() . С другой стороны
. С другой стороны ![]() . Момент инерции диска вычислим по формуле
. Момент инерции диска вычислим по формуле ![]() . Тогда получим
. Тогда получим
![]()
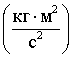 .
.
Запишем
уравнения затухающих колебаний ![]() . Его решение имеет следующий вид
. Его решение имеет следующий вид ![]() . Из этой формулы получается соотношение для начальной и
конечной амплитуды
. Из этой формулы получается соотношение для начальной и
конечной амплитуды ![]() . Отсюда находим коэффициент вязкого трения
. Отсюда находим коэффициент вязкого трения

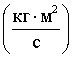 .
.
Если
полученный коэффициент вязкого трения считать сравнимым с коэффициентом вязкого
трения о воздух для стержня, то в рамках наших предположений достаточно создать
разрежение в несколько раз меньше атмосферного, чтобы было заметно затухание
колебаний стержня за счет гистерезисных потерь в стержне при напряженности
внешнего магнитного поля, равной напряженности геомагнитного поля.
3.3. Алгоритм
для вычисления допустимого коэффициента вязкого трения воздуха по заданной
напряженности внешнего магнитного поля
Ограничение на
вязкость воздуха следует последовательно рассматривать в рамках моделей Релея и
«параллелограмма». В рамках модели «насыщения» это делать необязательно,
поскольку данная модель отличается от модели «параллелограмма» только тем, что
здесь есть участок петли гистерезиса, на котором не происходит демпфирования.
Сначала
необходимо обратиться к модели Релея. Ограничение на вязкость воздуха следует
из уравнения (3.14)
|
|
Чтобы демпфирование было
заметно по сравнению с вязким трением, необходимо выполнение следующего
условия:
|
|
Таким образом,
для вязкого трения получаем: ![]() .
.
Прежде, чем
подставлять в это соотношение значения для ![]() и
и ![]() , необходимо обратиться к ограничениям на упругость подвеса и
объем стержня. Коэффициент
, необходимо обратиться к ограничениям на упругость подвеса и
объем стержня. Коэффициент ![]() необходимо взять
таким, чтобы он удовлетворял оценкам, полученным путем анализа малых параметров
необходимо взять
таким, чтобы он удовлетворял оценкам, полученным путем анализа малых параметров
![]() и
и ![]() . Амплитуда а вычисляется из соотношения
. Амплитуда а вычисляется из соотношения ![]() , где
, где ![]() - коэрцитивная сила
для данного материала.
- коэрцитивная сила
для данного материала.
После
получения допустимого коэффициента вязкого трения в рамках модели Релея,
обратимся к модели «параллелограмма». Ограничение на вязкость воздуха в рамках
модели «параллелограмма» следует из уравнения (3.23)
|
|
Чтобы демпфирование было
заметно по сравнению с вязким трением, необходимо выполнение условия (3.24)
|
|
Таким образом, учитывая, что
![]() , для вязкого трения получаем следующую оценку:
, для вязкого трения получаем следующую оценку:
|
|
Амплитуда а должна удовлетворять соотношению ![]() , где
, где ![]() – напряженность
внешнего магнитного поля, при которой происходит насыщение данного материала. Коэффициент
– напряженность
внешнего магнитного поля, при которой происходит насыщение данного материала. Коэффициент
![]() необходимо взять
таким, чтобы он удовлетворял оценкам, полученным путем анализа малых параметров
необходимо взять
таким, чтобы он удовлетворял оценкам, полученным путем анализа малых параметров
![]() и
и ![]() .
.
После
получения оценок для коэффициента вязкого трения в рамках модели Релея и модели
«параллелограмма» достаточно выбрать наибольшую из них.
4. Анализ решения уравнения движения с помощью улучшенной модели
Известно, что
при линейном увеличении амплитуды напряженности внешнего поля площадь петли
гистерезиса растет нелинейно, и в какой то момент выходит на постоянную
величину. Площадь петли гистерезиса за один период равна потери энергии на
перемагничивание на том же интервале времени.
Заметим, что
площадь петли и коэффициент ![]() оба пропорциональны
кубу напряженности внешнего поля. То есть
оба пропорциональны
кубу напряженности внешнего поля. То есть ![]() . Тогда формула для отношения амплитуд будет выглядеть
следующим образом:
. Тогда формула для отношения амплитуд будет выглядеть
следующим образом: ![]() .
.
Чтобы
полностью исключить влияние атмосферы на затухание положим k=10, то есть S по
сравнению с предыдущими вычислениями (в районе 0.02 Тл) выросло в 9 раз.
|
OutX , Тл |
OutY, |
|
0.0110 |
0.0027 |
|
0.0161 |
0.0109 |
|
0.0212 |
0.0247 |
|
0.0263 |
0.0469 |
|
0.0314 |
0.0796 |
|
0.0365 |
0.1246 |
|
0.0416 |
0.1840 |
|
0.0467 |
0.2598 |
|
0.0518 |
0.3541 |
Табл.1. Зависимость площади петли гистерезиса от амплитуды внешнего магнитного поля
|
|
Рис.12. Зависимость площади петли от амплитуды магнитного поля
Из приведенных
табл.1 и рис.12 видно, что достаточно взять значение индукции поля, равное 0.04
Тл.
Заключение
В работе
рассмотрена механическая система, состоящая из постоянного магнита и
гистерезисного стержня из магнитомягкого материала, размещенных на плоском диске,
который подвешен на упругой нити во внешнем магнитном поле. В положении
равновесия ось стержня перпендикулярна вектору напряженности магнитного поля. Проведен
анализ уравнения движения стержня в рамках трех моделей гистерезиса: модели
Релея, модели «параллелограмма», модели «насыщения». Численно оценены
допустимые параметры модели. Для вычислений в качестве примера использованы
данные для 4-79-пермаллоя. Получен искомый алгоритм, позволяющий вычислять
допустимый коэффициент вязкого трения воздуха по заданной напряженности
внешнего магнитного поля и наоборот. Показано, что подходящем выбором напряженности
внешнего магнитного поля можно обеспечить превалирование гистерезисного
демпфирования со стороны стержня над демпфированием за счет вязкого трения
диска о воздух и, тем самым, провести анализ динамики спутника в лабораторных
условиях.
Приложение
|
Состав |
79% Ni, 17%
Fe, 4% Mo |
|
Начальная
магнитная проницаемость |
20000 |
|
Максимальная
магнитная проницаемость |
100000 |
|
Коэрцитивная
сила |
0.05 Эрстед
(3.98 А/м) |
|
Напряженность
магнитного поля, при которой наступает насыщение, |
|
|
Точка Кюри |
460°C |
|
Потери на
гистерезис при насыщении |
|
|
Электрическое
сопротивление |
55 мком·см |
|
Плотность
ρ |
|
|
Постоянная
Релея |
350000 |
Табл.2. Характеристики материала 4-79-пермаллой
Литература
1. Бозорт Р. Ферромагнетизм. –
М.: Издательство иностранной литературы, 1956. – 784 с.
2. Голик И.В. Некоторые условия
наземного тестирования пассивной магнитной системы ориентации. – Выпускная
квалификационная работа на степень магистра. – М.: МФТИ, 2001. – 27 с.
3. Калашников С.Г.
Электричество. – М.: Наука, 1989.
4. Моисеев Н.Н. Асимптотические
методы нелинейной механики. – 2-е изд., перераб. – М.: Наука. Главная редакция
физико-математической литературы, 1981. – 400 с.
5. Овчинников М.Ю., Пеньков В.И.
Пассивная магнитная система ориентации наноспутника, Космические исследования,
2002, т.40, N 2, с.156-170.
6. Сивухин Д.В. Общий курс
физики, т. III. – М.: Наука, 1986.
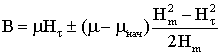 ,
,
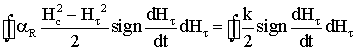 .
.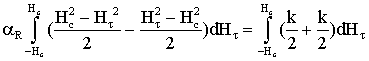
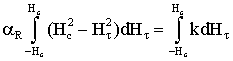
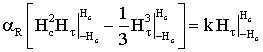
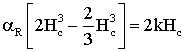
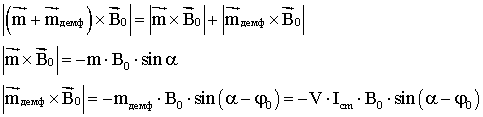
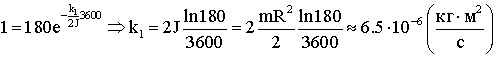
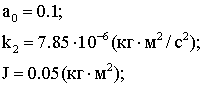
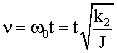 ,
, .
.
 .
.
 .
.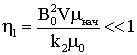
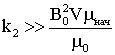 .
.
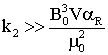 .
.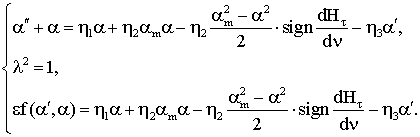
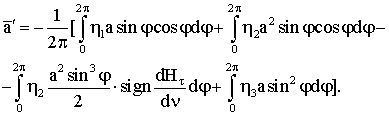
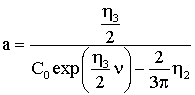 ,
,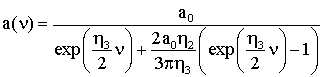 .
.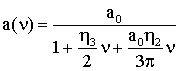
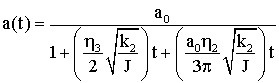 .
.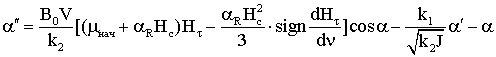 .
.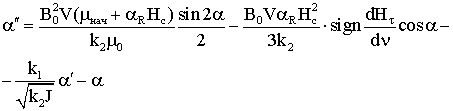 .
.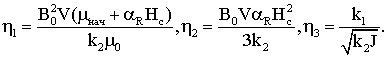
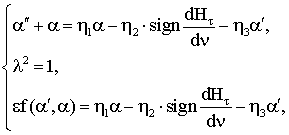
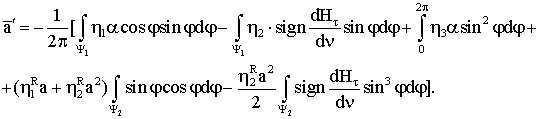
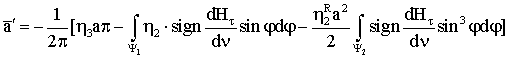 ,
, ,
, .
.
 .
. .
. .
.