Пассивная магнитная система ориентации первого российского наноспутника ТНС-0
|
|
Начальная магнитная
проницаемость |
Максимальная магнитная
проницаемость |
Коэрцитивная сила |
Индукция насыщения |
|
60 000 |
164 000 |
0.96 |
0.74 |
На спутнике можно
разместить восемь гистерезисных стержней (по четыре в двух взаимно
перпендикулярных направлениях, параллельных верхней крышке спутника). Параметры
стержней указаны в табл.2.
Табл. 2. Параметры гистерезисных стержней
|
Начальная магнитная
проницаемость |
Максимальная магнитная
проницаемость |
Коэрцитивная сила |
Индукция насыщения |
|
25 000 |
180 000 |
1.6 |
0.74 |
В рамках дипольной
модели геомагнитного поля его средняя напряженность на круговой орбите высотой ![]() .
.
![]()
Вводя
начальную угловую скорость ω(0), запишем его решение
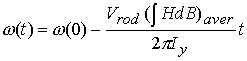
Откуда
следует, что скорость вращения затухает за конечное время
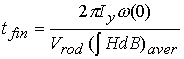
Для стержней из
материала 79НМ сечением 0.1см×0.2см
и максимальной допустимой длине стержней 15см
получаем объем одного стержня V=0.3см². Тогда при объеме Vrod~1.2см² в каждом наборе и начальной угловой скорости ω(0)~180°/с получаем оценку времени
переходного процесса – tfin~200 часов. Сразу следует
отметить, что это очень оптимистичная оценка, скорее оценка ``снизу'' - здесь
не учитывается реальная площадь петли, на которую сильно влияет близость
сильного магнита и других намагниченных элементов спутника и приборов к
стержням; взаимное положение стержней; осевое вращение спутника, сильно
затрудняющее рассеяние его кинетической энергии вращательного движения;
переходный процесс при колебательном относительно вектора H движении спутника и так далее.
5. Расположение
гистерезисных стержней в теле спутника
При установке стержней
нужно учитывать влияние поля постоянного магнита, из-за которого возможен сдвиг
рабочей точки стержня и, как следствие, потеря эффективности его демпфирующих
свойств. Для уменьшения этого эффекта стержни следует располагать в плоскости,
перпендикулярной оси магнита и проходящей через его центр, или в параллельных
ей плоскостях.
На спутнике
установлены два набора гистерезисных стержней, по четыре стержня в каждом (
1–ый набор – стержни № 1 – 4, 2–ой набор – стержни № 5 – 8 ). Стержни
располагаются на верхней крышке спутника (рис.4).
Известно [7], что при
расстоянии между параллельными идентичными стержнями более 0.3-0.4 их длины, их взаимным влиянием можно пренебречь. Это
влияние сказывается во взаимном размагничивании стержней и, как следствие,
снижении эффективности. При расстоянии, равном 0.02 длины, два стержня эквивалентны одному. При расстоянии, равном
0.2 длины, эффективность падает на 12.5%. Это значит, что вместо двух
стержней будут работать как бы 1.75
стержня.
Влиянием
стержней из разных наборов можно пренебречь, так как они располагаются
перпендикулярно друг другу. Очевидно, что из-за близкого расположения
уменьшиться эффективность работы следующих пар стержней: № 2 – № 3, № 7 – № 8
примерно на 12.5%, № 5 – № 6 на 25 %. Как это скажется на общей
эффективности более подробно будет рассмотрено при описании численной модели
гистерезиса. Стержни заглублены в крышку и приклеены по краям (см. рис.1а).
Расположение системы ориентации на верхней крышке спутника показано на рис.5.
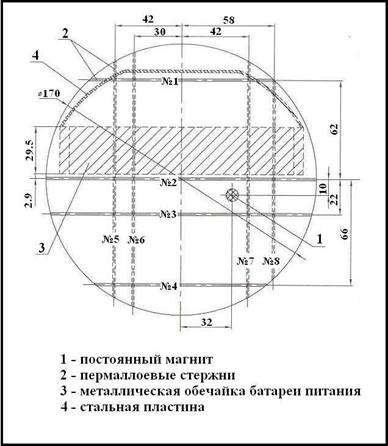
Рис. 4. Расположение гистерезисных стержней
на верхней крышке спутника (чертеж РНИИ КП)

Рис. 5. Размещение
системы ориентации на верхней крышке спутника (фото РНИИ КП)
6. О влиянии
постоянного магнита на эффективность гистерезисных стержней
Если гистерезисный стержень расположен в плоскости, не
проходящей через центр магнита, или вектор дипольного момента не совпадает с
направлением геометрической оси симметрии магнита, то вдоль стержня возникает
постоянная составляющая магнитного поля Hs .
Это приводит к смещению рабочей точки гистерезисного стержня. Для демонстрации
этой ситуации воспользуемся моделью параллелограмма. В силу того, что
максимальная индукция внешнего поля B=0.27
T не превосходит индукцию насыщения Bs=0.74 T
возможны два варианта:
• Перемагничивание без смещения рабочей точки идет по
главной петле гистерезиса до среднего значения напряженности внешнего
магнитного поля. Смещение рабочей точки таково, что перемагничивание пойдет по
петле, равной начальной. Это означает, что данное смещение не приводит к потере
эффективности стержней (рис.6).
• Смещение рабочей точки приводит к снижению
эффективности стержней. Площадь петли перемагничивания уменьшилась при сдвиге
рабочей точки (рис.7).
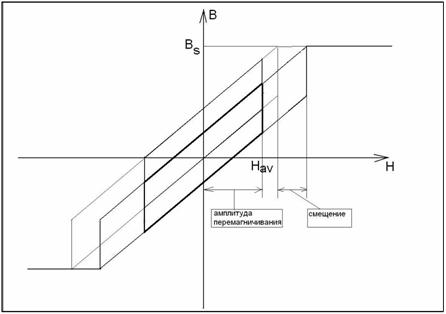
Рис. 6. Смещение рабочей точки гистерезисного стержня
без потери эффективности
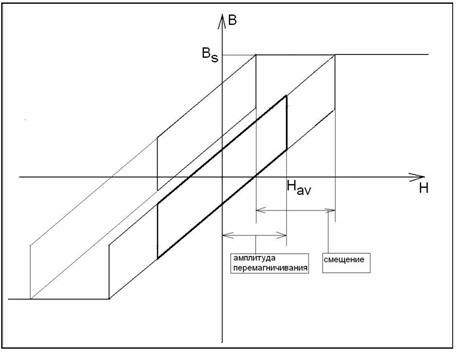
Рис. 7. Смещение рабочей точки гистерезисного
стержня, приведшее к потере эффективности
Получим выражение для составляющей ![]() вектора
вектора ![]() вдоль стержня. Введем обозначения (см. рис.8):
вдоль стержня. Введем обозначения (см. рис.8):
O – центр магнита;
P – точка
стержня, в которой анализируем составляющую поля вдоль стержня;
OH (ls) – перпендикуляр
к проекции стержня на плоскость, перпендикулярную оси постоянного магнита и
проходящую через его центр;
HS (s) – расстояние
от стержня до этой плоскости;
lt – расстояние
SP.
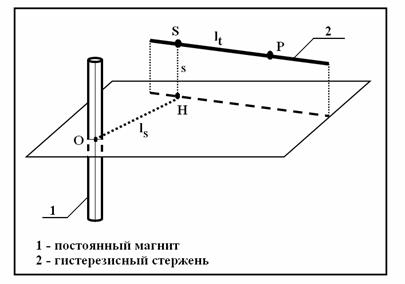
Рис. 8. К вычислению составляющей магнитного
поля постоянного магнита вдоль гистерезисного стержня
Отметим,
что по разные стороны от точки S составляющая магнитного поля будет иметь
разный знак. Таким образом, если бы стержень был симметричен относительно S, то
эта составляющая компенсировалась бы за счет разных знаков. В нашем же случае
происходит не полная компенсация. На рисунках 9, 10, 11 рассмотрены случаи для
различных расстояний ls, для стержней № 1, 7 и 8. Магнитное поле диполя
считается по известной формуле
 ,
,
где
![]() – радиус вектор,
проведенный из центра магнита к рассматриваемой точке (P). В наших
обозначениях модуль составляющей магнитного поля вдоль стержня находится по
формуле
– радиус вектор,
проведенный из центра магнита к рассматриваемой точке (P). В наших
обозначениях модуль составляющей магнитного поля вдоль стержня находится по
формуле
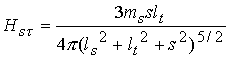 .
.
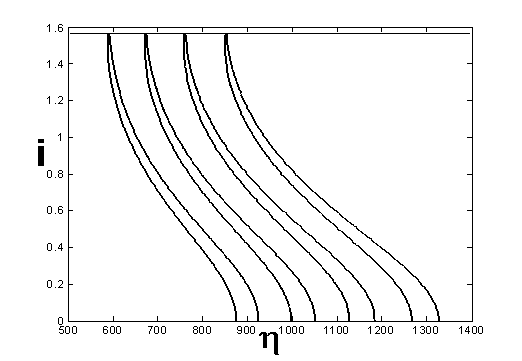
Отметим, что s для стержней первого набора составляет
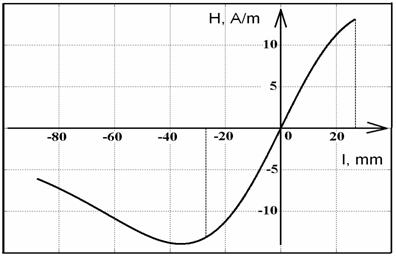
Рис. 9. Составляющая
магнитного поля вдоль стержня №1, расстояние до магнита
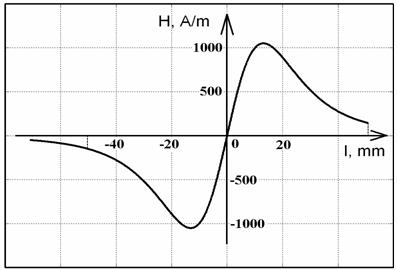
Рис. 10. Составляющая магнитного поля вдоль
стержня №8, расстояние до магнита
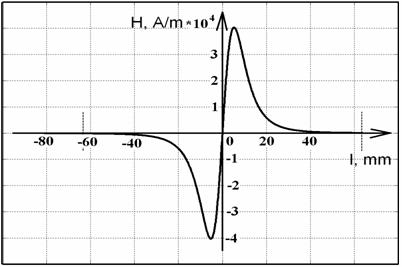
Рис. 11. Составляющая поля постоянного
магнита вдоль гистерезисного стержня №7, расстояние до магнита
7. О влиянии
температуры среды на магнитные свойства гистерезисных стержней
Способность
ферромагнетиков намагничиваться различна при разных температурах, тем самым
можно говорить о зависимости магнитной восприимчивости от температуры. Она
уменьшается с увеличением температуры. Падают значения их магнитной
восприимчивости и проницаемости при любом значении магнитного поля, ослабляется
гистерезис и уменьшается намагничивание насыщения. При некоторой температуре TK,
называемой температурой Кюри,
ферромагнитные свойства исчезают совсем. Температура Кюри различается для
разных ферромагнетиков. Для наиболее широко используемых при демпфировании
движений спутника магнитомягких материалов значения температуры Кюри приведены
в табл.3. Выбранный в качестве материала стержней молибденовый пермаллой 79НМ
сохраняет магнитные свойства в разумных пределах изменения температуры на
посадочных местах стержней.
Табл. 3. Температура Кюри для магнитомягких материалов
|
Марка материала |
Основной состав, % |
|
|
79HM |
79 Ni, 4 Mo,
остальное Fe |
450 |
|
50H |
50 Ni,
остальное Fe |
500 |
8. Результаты
численных расчетов
Попытки использовать простые модели типа модели
параллелограмма или модели Релея приводят к результатам, которые носят или
качественный характер (модель параллелограмма), или допускают использование
лишь в окрестности начала координат (модель Релея) при симметричном
перемагничивании. Сложный характер эффекта гистерезиса требует применения
модели, реализованной на ЭВМ. Используемая в настоящей работе модель,
имитирующая работающий на растяжение однородный стержень, который находится под
действием переменной нагрузки и трется боковой поверхностью о неподвижное основание,
подробно описана в [8]. Параметры модели в нашем случае следующие:
![]() – параметр,
определяющий ширину петли гистерезиса;
– параметр,
определяющий ширину петли гистерезиса;
![]() – параметр,
определяющий магнитную восприимчивость стержня (здесь приведено некоторое
среднее значение по всем стержням);
– параметр,
определяющий магнитную восприимчивость стержня (здесь приведено некоторое
среднее значение по всем стержням);
![]() ,
, ![]() – параметры, связанные
с эффективностью работы стержней первого и второго набора соответсвенно (здесь
приведены значения этих параметров с учетом взаимного влияния стержней и
влияния магнита).
– параметры, связанные
с эффективностью работы стержней первого и второго набора соответсвенно (здесь
приведены значения этих параметров с учетом взаимного влияния стержней и
влияния магнита).
Для сравнения в табл.4 приведены значения параметров ![]() для тех же самых
наборов стержней без учета влияний.
для тех же самых
наборов стержней без учета влияний.
Табл. 4. Взаимное влияние стержней и влияние поля постоянного магнита
|
|
Без учета влияний |
С учетом влияния поля постоянного магнита |
С учетом взаимного влияния и влияния магнита |
|
|
12.93 |
7.60 |
6.94 |
|
|
13.28 |
11.66 |
9.43 |
Требуется выяснить влияние на характеристики
установившегося и переходного движений начальной скорости вращения. Приведем
результаты расчетов для спутника с тензором инерции
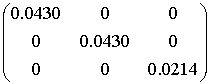 [кг×м2],
[кг×м2],
постоянным магнитом с
моментом mS=2.2A·м2
и наклонением орбиты 51.6 °.
Серия расчетов, проведенных с использование уточненной
численной модели гистерезиса, реализованной на языке FORTRAN, показала, что
наиболее существенным фактором, влияющим на длительность переходного движения и
на точность ориентации в течение длительного времени, является начальная
угловая скорость вращения спутника.
Пример переходного процесса с начальной угловой
скоростью 300![]() (
(![]() - угловая скорость орбитального движения спутника) вокруг
одной из осей, перпендикулярной оси симметрии, и по 5
- угловая скорость орбитального движения спутника) вокруг
одной из осей, перпендикулярной оси симметрии, и по 5![]() вокруг остальных двух осей и параметрами модели, описанными
выше, приведен на рис.12 и рис.13 (θ
угол отклонения оси ориентации спутника от вектора H) и рис.14, рис.15, рис.16 (проекции ω1, ω2, ω3 вектора
абсолютной угловой скорости на главные оси инерции спутника) в зависимости от
безразмерного времени
вокруг остальных двух осей и параметрами модели, описанными
выше, приведен на рис.12 и рис.13 (θ
угол отклонения оси ориентации спутника от вектора H) и рис.14, рис.15, рис.16 (проекции ω1, ω2, ω3 вектора
абсолютной угловой скорости на главные оси инерции спутника) в зависимости от
безразмерного времени ![]() . На всех последующих рисунках по оси абсцисс указано
безразмерное время τ, которое
изменяется на 2π за один оборот
спутника по орбите, ω3
– проекция вектора абсолютной угловой скорости на ориентируемую ось. Для этих
параметров графики угла θ и
проекций ω1, ω2,
ω3 на одном витке приведены на рис.17 и рис.18, рис.19,
рис.20 соответственно.
. На всех последующих рисунках по оси абсцисс указано
безразмерное время τ, которое
изменяется на 2π за один оборот
спутника по орбите, ω3
– проекция вектора абсолютной угловой скорости на ориентируемую ось. Для этих
параметров графики угла θ и
проекций ω1, ω2,
ω3 на одном витке приведены на рис.17 и рис.18, рис.19,
рис.20 соответственно.
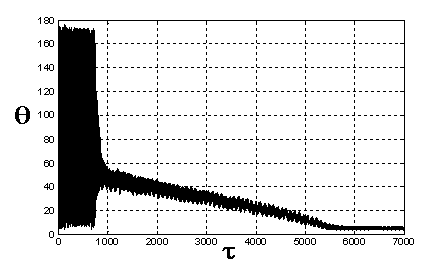
Рис. 12. Угол θ
отклонения оси ориентации спутника от вектора H.
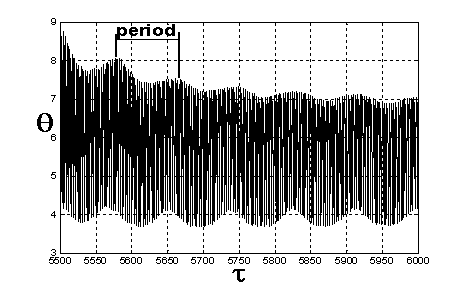
Рис. 13. Угол θ
отклонения оси ориентации спутника от вектора H после выхода на стационарное движение
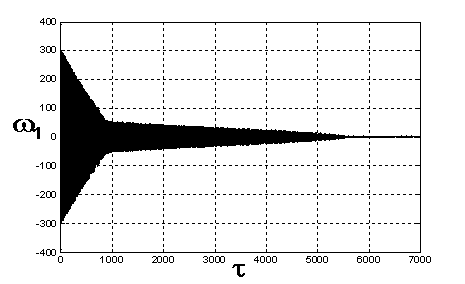
Рис. 14. Проекция
ω1 вектора абсолютной скорости на главные оси инерции спутника
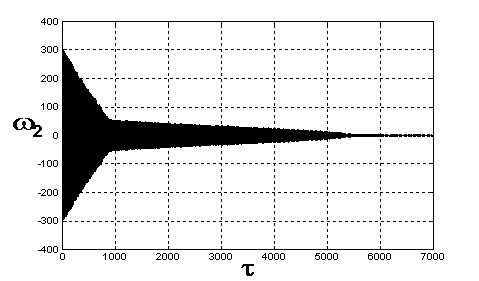
Рис. 15. Проекция
ω2 вектора абсолютной скорости на главные оси инерции спутника
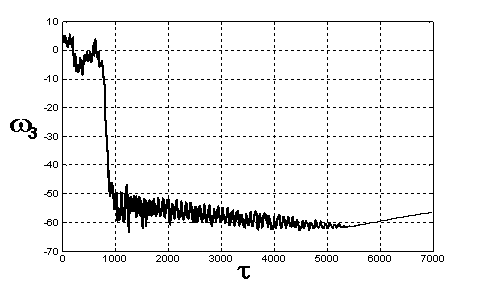
Рис. 16. Проекция
ω3 вектора абсолютной скорости на главные оси инерции спутника
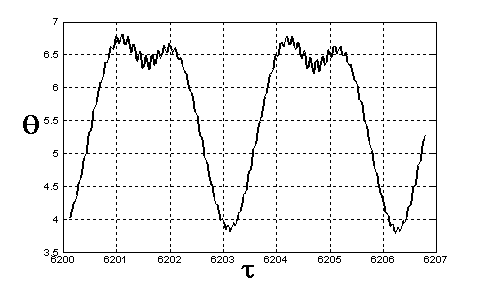
Рис. 17. Зависимость
угла θ на 971-ом витке

Рис. 18. Зависимость
проекции ω1 на 971-ом витке
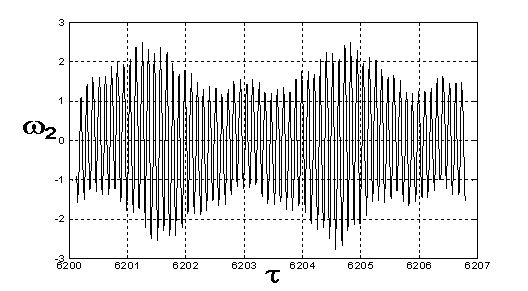
Рис. 19. Зависимость
проекции ω2 на 971-ом витке
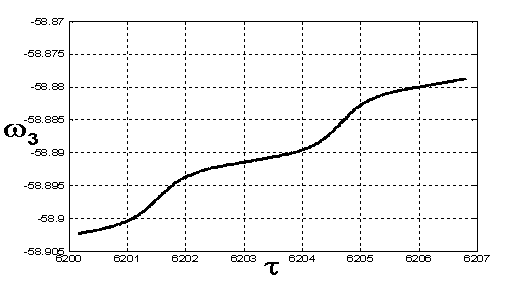
Рис. 20. Зависимость
проекции ω3 на 971-ом витке
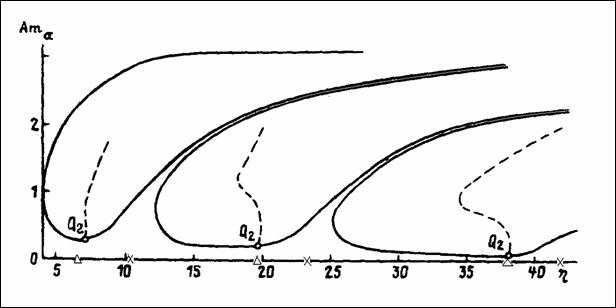
Медленное убывание амплитуды обусловлено чрезвычайно
медленным демпфированием скорости вращения спутника вокруг ориентируемой оси,
что вызвано перемагничиванием стержней по частным петлям, имеющим весьма малую
площадь. Этот факт отмечался также в [9]. На графике для угла θ ясно видны наложенные на
медленные, почти периодические с периодом в пол-витка по орбите вынужденные
колебания с частотой, близкой частоте собственных колебаний спутника.
8.1. Суточное вращение Земли
Результаты, приведенные выше, были получены в рамках модели наклонного диполя, согласно
которой геомагнитное поле аппроксимируется полем диполя, наклоненного к оси
вращения Земли под углом 11.5°, и,
тем самым, учитывается суточное вращение Земли. Модель наклонного диполя
получается как первое приближение в Гауссовом разложении потенциала
геомагнитного поля. В результате суточного вращения Земли угол между диполем и
его проекцией на плоскость орбиты непрерывно меняется [10]. Эффект от ее
вращения хорошо виден на рис.13. Результаты расчетов, проведенные по
стандартной модели Гаусса, мало отличаются от представленных.
В отсутствие гистерезиса коэффициенты уравнений
движения спутника, полученные в рамках модели
прямого диполя, зависят периодически от времени с периодом, равным половине
периода обращения спутника по орбите. Решения этих уравнений построены в виде
формальных рядов по степеням малого параметра ![]() [5]. По сути – это
огибающие быстро осциллирующих вынужденных колебаний оси ориентации спутника с
частотой собственных колебаний, наиболее близкой частоте вынуждающей силы
(порядка
[5]. По сути – это
огибающие быстро осциллирующих вынужденных колебаний оси ориентации спутника с
частотой собственных колебаний, наиболее близкой частоте вынуждающей силы
(порядка![]() ). При наличии гистерезиса система уравнений не допускает
периодических решений и приходится строить предельные режимы интегрированием на
достаточно больших интервалах времени.
). При наличии гистерезиса система уравнений не допускает
периодических решений и приходится строить предельные режимы интегрированием на
достаточно больших интервалах времени.
Благодарности
Работа выполнена при поддержке ФГУП ``Российский
научно-исследовательский институт космического приборостроения'' и Российского
фонда фундаментальных исследований (грант N 03-01-00652), а также Федерального агенства по науке
и инновациям Российской Федерации.
Заключение
В
результате проведенных исследований были определены:
•Состав магнитной системы ориентации. Постоянный
магнит с дипольным моментом 2.2 A·м2
ориентирует спутник вдоль местного вектора напряженности поля Земли. В качестве
демпфирующего устройства выбраны 8 гистерезисных стержней из магнитомягкого
материала – молибденового пермаллоя марки 79HM.
•Параметры
и расположение гистерезисных стержней.
•Выделены и учтены основные возмущающие факторы.
Расчеты проводились с использованием модели, учитывающей суточное вращение
Земли; эффекты, связанные с этим процессом особенно четко видны на рис.13.
•Проведено моделирование движения спутника
относительно своего центра масс в рамках улучшенной модели гистерезиса (см.
раздел “Результаты численных расчетов”), которое показало приемлемые точности и
времена переходных процессов.
Спутник был успешно
выведен на почти круговую орбиту вручную российским космонавтом с борта
Международной космической станции 28-го марта 2005 года. Параметры орбиты следующие:
высота ![]() °, эксцентриситет
°, эксцентриситет ![]() . Запуск спутника показан на рис.21.
. Запуск спутника показан на рис.21.

Рис. 21. Запуск наноспутника ТНС-0 (фото с экрана ТВ)
Литература
[1]
Научно – технический отчет. Исследование динамики и определение параметров
системы ориентации наноспутника ТНС–0. М.: ИПМ им.М.В.Келдыша РАН, 2004.
[2]
Ю.М.Урличич, А.С.Селиванов, Ю.М.Тучин, О.Е.Хромов, И.В.Никушкин.
Технологический наноспутник минимальной комплектации ТНС-0. Аннотации докладов
на III Конференции ``Микротехнологии в авиации и космонавтике'',
Санкт-Петербург, 8-9 июня,
[3]
“Исследование динамики и определение параметров системы ориентации наноспутника
ТНС-
[4]
В.В.Белецкий. Движение искусственных спутников относительно центра масс. М.:
Наука, 1966.
[5]
В.А.Сарычев. М.Ю.Овчинников. Магнитные системы ориентации искусственных
спутников Земли. Итоги науки и техники. Сер.: Исследование
космического пространства. М.: ВИНИТИ, 1985. Т.23. - 106с.
[6] Ovchinnikov M.Yu., Methods
to Obtain the Principal Parameters of Simple ACS for Small Satellites, Acta
Astronautica, March 1998, V.43, Issue 11-12, pp.597-605.
[7]
А.П.Коваленко. Магнитные системы управления космическими летательными
аппаратами. М., Машиностроение, 1975. – 248 с.
[8]
В.А.Сарычев, В.И.Пеньков, М.Ю.Овчинников. Математическая модель гистерезиса,
основанная на магнитомеханической аналогии. Математическое моделирование, 1989,
т.1, N 4, с.122-133.
[9] G.Horn, S.Regenberg, Zur stabilisierung eines
satelliten mit hilfe des erdmagnetfeifdes. Z.Flugwiss.,
1966, v.14, N 9, pp.398-413.
[10] B.V.Rauschenbakh,
M.Yu.Ovchinnikov and S.McKenna Lawlor, Essential Spaceflight Dynamics and
Magnetospherics, Kluwer & Microcosm Publ., 2002, 416p.
[11]
Б.В.Раушенбах. М.Ю.Овчинников. Лекции по динамике космического полета. М.:
МФТИ, 1997. - 188с.


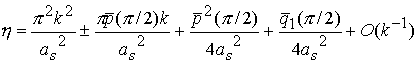
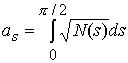 ,
, 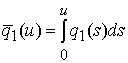 ,
, 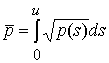 .
.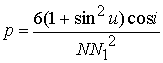 ,
, 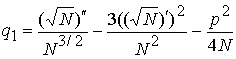 ,
,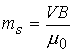 , где
, где