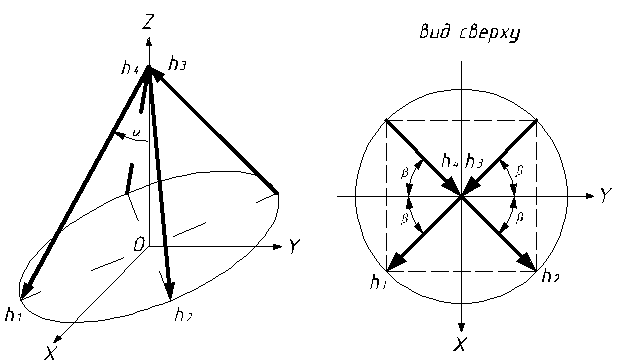
Анализ динамических возможностей систем управления малым космическим аппаратом, построенных на базе двигателей-маховиков

( The Analysis of Dynamic Capabilities of the Control Systems by the Spacecraft Built on the Basis of the Reaction Wheels
Preprint, Inst. Appl. Math., the Russian Academy of Science)

1. Электромеханические исполнительные органы систем управления малыми космическими аппаратами.

         Электромеханические исполнительные органы (ЭМИО) систем управле­ния (СУ) космических аппаратов (КА) предназначены для создания управляющих моментов. Во многих случаях, при создании длительно сущест­вующих КА с высокими требованиями к динамике и точности ориентации использованию ЭМИО в составе СУ нет альтернативы. В то же время ЭМИО являются наиболее массивными и энергопотребляющими устройствами СУ, постоянно задействованными в процессе функционирования КА. В связи с этим задачи выбора типа ЭМИО и оптимизации их характеристик являются актуальными.

         Для больших КА и орбитальных станций целесообразность применения силовых гироскопических комплексов на основе силовых гироскопов с посто­янным значением кинетического момента во многих случаях очевидна. Для малых КА выбор типа ЭМИО для СУ является не тривиальной задачей.

ЭМИО для малых КА могут быть построены на базе:

- силовых гироскопических комплексов (СГК) различного типа,

- трехстепенных силовых стабилизаторов с управляемым значением  кинети­ческого момента,

- управляющих маховиков.

         Между областями применения перечисленных устройств нельзя про­вести резких границ. Соответственно динамические требования к СУ, вклю­чающей в свой состав ЭМИО, во многом определяются множеством требуе­мых значений кинетического момента . Множество  является областью изменения в связанной с КА системе координат значения вектора суммарного кинетического момента ЭМИО. Изменение этого вектора в указанной области в соответствии с реализуемыми в системе законами должно обеспечивать требуемое управление параметрами движения относительно центра масс КА. Естественно множество  должно содержаться внутри множества создавае­мых ЭМИО значений кинетического момента .

         Таким образом, для всех вариантов построения ЭМИО должно быть обес­печено выполнение условия:

                                                            .                                                    (1.1)

         При выполнении условия (1.1) можно утверждать, что величина суммар­ного кинетического момента создаваемого двигателями маховиками, будет достаточна, для обеспечения требуемой угловой скорости вращения КА.

Введем связанную с КА правую декартову систему координат , на­ча­ло координат точка  совпадает с центром масс КА, а оси совпадают с главными центральными осями инерции КА. Обычно область множества  ограничена эллипсоидом:

                                            ,                                (1.2)

где  - проекции суммарного вектора требуемого кинетического момента ЭМИО на оси системы координат ,  - моменты инер­ции КА в связанной системе координат ,     - проекции макси-маль­ной требуемой угловой скорости КА на оси системы координат .

         Построение области множества создаваемых ЭМИО значений кинетиче­ского момента  задача более сложная. В зависимости от располо­жения ЭМИО относительно главных осей КА, возможно подобрать форму области кинетического момента , наиболее соответствующую заданным моментам инерции КА.

В данной работе рассматривается решение такой задачи для двух раз­личных конфигураций системы ЭМИО, построенных на базе маховиков, ос­новными преимуществами которых по сравнению с другими типами ЭМИО являются относительная дешевизна, конструктивная простота и простота алгоритмов управления.

Следует отметить, что рассмотренный ниже способ построения облас­тей вариации кинетического момента пригоден и для построения областей механического момента, создаваемого маховиками.

2. Конфигурация системы маховиков «четырехгранная пирамида».

2.1. Область возможных значений кинетического момента. Рассмот­рим систему маховиков, оси которых расположены параллельно боковым ребрам четырехгранной пирамиды (рис. 1).

Рис. 1

Орты   осей маховиков имеют в системе координат  компо­ненты:

,      ,

,        .

Здесь  - угол между осью маховика и осью ,  - угол определяющий по­ложение и форму основания пирамиды в плоскости , при  основа­ние представляет собой квадрат; при  <  <  основание является прямо­угольником с большей стороной расположенной параллельно оси ; при   <  <  основание является прямоугольником с большей стороной распо­ло­женной параллельно оси . Углы  и  - параметры системы. Сум­марный кинетический момент маховиков выражается формулой

                                             ,                                         (2.1)

в которой  - значение кинетического момента маховика с номером . Махо­вики считаем одинаковыми. В этом случае  ≤  ≤  , где  - абсолютная величина предельного значения кинетического момента отдель­ного маховика. Величина  - еще один параметр системы. Скалярная за­пись векторного выражения (2.1):

,           ,

.

Здесь  компоненты  в системе координат . Выражение (2.1)  для краткости будем записывать в виде . Кроме того, будем ис­пользовать обычное представление вектора , указывая в круг­лых скобках его компоненты в системе координат . Не ограни­чивая общности, положим .

         Рассмотрим область  пространства , заполняемую кон­цами векторов (2.1) при  ≤ . Эта область является областью возможных значений кинетического момента системы маховиков и представляет собой выпуклый многогранник, обладающий центральной симметрией относи­тельно начала координат. Перечислим вершины, ребра и грани этого много­гранника. Координаты каждой вершины многогранника соответствуют коор­динатам конца вектора суммарного кинетического момента составленного из определенной комбинации максимальных значений кинетических моментов маховиков , из чего следует, что общее число вершин не может быть более 16 = 2⁴. Однако существуют комбинации, при которых суммарный вектор  лежит внутри области , что зависит от взаимного расположения маховиков относительно связанной системы координат . В данном слу­чае многогранник  имеет 14 вершин, поскольку  и . Обозначим их  и  . При каждом  вер­шины  и  расположены центрально симметрично относительно точки . Вер­шины характеризуются соотношениями:

1)  :                                           

2)  :                  

3)  :                 

4)  :                 

5)  :                

6)  :                                    

7)  :                                           

8)  :                                            

9)  :                                     

10)  :         

11)  :        

12)  :        

13)  :       

14)  :                              

Здесь в фигурных скобках указаны орты ребер, выходящих из каждой вер­шины. Многогранник  имеет 24 ребра. Ребра будем задавать, указывая соеди­няемые ими вершины и параметризации соответствующих отрезков. Имеем:

1):           9):                17):

2):           10):              18):

3):           11):              19):

4):           12):              20):

5):         13):                 21):

6):        14):                22):

7):         15):                 23):

8):         16):                 24):

Здесь  ≤  ≤ . Первая вершина ребра получается при , последняя – при .         Многогранник  имеет 12 граней, которые обозначим  и  . При каждом  грани  и  расположены центрально симметрично относи­тельно точки . Грани будем задавать списком принадлежащих им ребер и параметризацией:

1) ,                ,

2) ,                ,

3) ,                ,

4) ,                ,

5) ,                ,

6) ,                ,

7) ,                ,

8) ,                ,

9) ,                ,

10) ,               ,

11) ,              ,

12) ,              .

Здесь принято, что обозначения вида  и  задают одно и тоже ребро, но при разном выборе первой и последней вершин. Таким образом, много­гран­ник  имеет 14 вершин, 12 граней и 24 ребра, что соответствует значению Эйлеровой характеристики (14 + 12 – 24 = 2), которое постоянно для всех вы­пуклых многогранников. В табл. 1 приведены значения координат вершин многогранника  в декартовой системе координат  при значении углов  и  (способ, применявшийся для определения значений углов  и , описан в п. 2.3).

Таблица 1.

Вид многогранника  в декартовой системе координат  приведен на рис. 2.

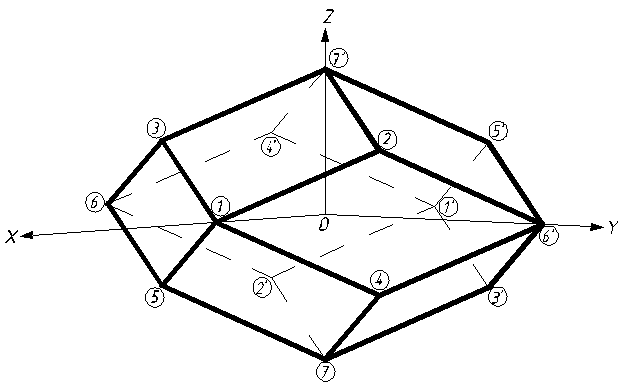
Рис. 2

На рис. 3 изображены проекции многогранника  на координатные плос­кости системы .

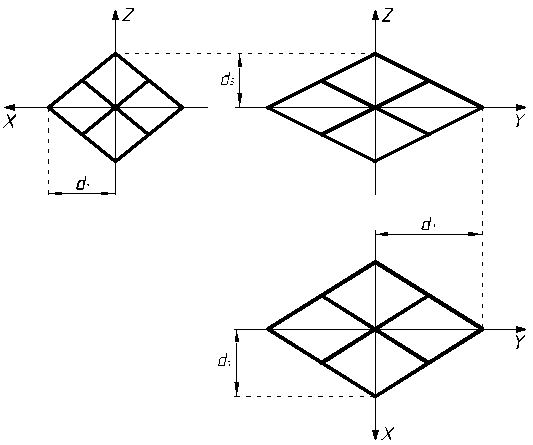
Рис. 3

Многогранник  допускает ряд преобразований симметрии. Он перехо­дит в себя при повороте вокруг осей , ,  на угол кратный  (в част­ном случае при значении угла  многогранник  переходит в себя при повороте вокруг оси  на угол кратный ). Координатные плоскости системы  являются его плоскостями симметрии.

         Приведем некоторые метрические характеристики многогранника . Все его ребра имеют длину 2. Следовательно, все грани – ромбы. Вершины  и  находятся на расстоянии  от начала координат - точки , вершины  и  отстоят от этой точки на расстояние , а вер­шины  и  на расстояние . Расстояния до вершин , , ,  и , , ,  от точки  равны . Равенство  имеет место при , равенство  достигается при одновременном выполне­нии условий  и .

Таким образом, соотношения между расстояниями , ,  выража­ются неравенствами, приведенными в табл. 2.

Таблица 2.

В табл. 3 указаны зависимости, позволяющие определить расстояние от начала координат  до каждой грани многогранника .

Таблица 3.

2.2. Возможности системы при отключении одного из маховиков. Оценим возможности рассматриваемой системы в случае, когда один из ма­ховиков отключен (вышел из строя). Без ограничения общности можно счи­тать, что отключен маховик с осью, параллельной орту . Суммарный кине­тический момент такой усеченной системы выражается векторной формулой

                                               ,                                          (2.2)

скалярная запись которой имеет вид

,                ;

.

Выражение (2.2) для краткости будем записывать в виде . Здесь по-прежнему  ≤  ≤  . Не ограничивая общности, положим . Область пространства, заполняемая концами векторов (2.2) при ≤, – область возможных значений кинетического момента системы  маховиков – представляет собой параллелепипед . Перечислим вершины, ребра и грани этого параллелепипеда. Вершины (их у параллелепипеда 8) обозначим  и  . При каждом  вершины  и  расположены центрально сим­мет­рично относительно точки . Вершины характеризуются соотношениями:

1)  :              

2)  :                

3)  :              

4)  :             

5)  :        

6)  :        

7)  :        

8)  :       

Здесь в фигурных скобках указаны орты ребер, выходящих из каждой вер­шины. Параллелепипед имеет 12 ребер. Ребра параллелепипеда  будем за­давать, указывая соединяемые ими вершины и параметризации соответст­вующих отрезков. Имеем:

1):,             5):,          9):,

2):,             6):,          10):,

3):,            7):,         11):,

4):,          8):,        12):.       

Здесь  ≤  ≤ . Первая вершина ребра получается при , последняя – при .  Как и всякий параллелепипед  имеет 6 граней, которые обозна­чим  и  . При каждом  грани  и  расположены центрально симмет­рично относительно точки . Грани будем задавать списком принадле­жащих им ребер и параметризацией:

1) ,                ,

2) ,                ,

3) ,                ,

4) ,                ,

5) ,                ,

6) ,                .

Здесь принято, что обозначения вида  и  задают одно и тоже ребро, но при разном выборе первой и последней вершин. В табл. 4 приведены зна­че­ния координат вершин параллелепипеда  в декартовой системе координат  при значении углов  и  с учетом отказа одного маховика.

Таблица 4.

Вид параллелепипеда  в декартовой системе координат  приве­ден на рис. 4.

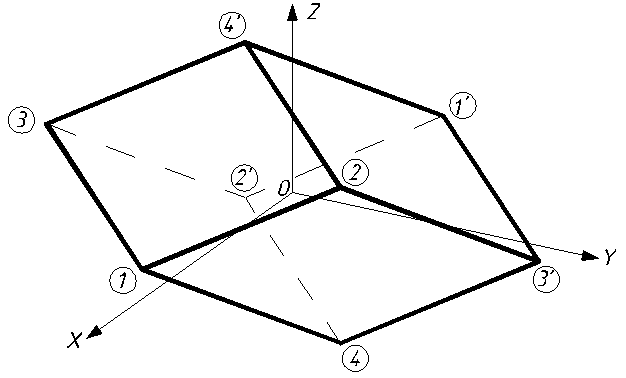
Рис. 4

На рис. 5 изображены проекции параллелепипеда  на координатные плоскости системы .

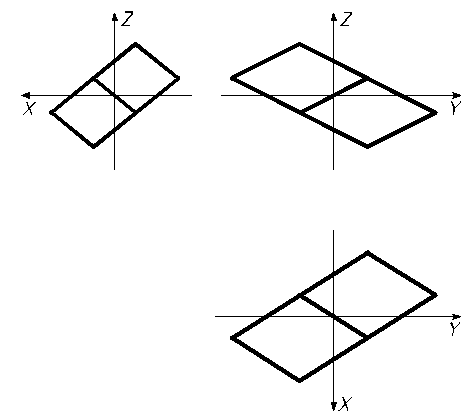
Рис. 5

Параллелепипед  представляет собой многогранник  с длиной ребер  , , , , ,  равной нулю,  поскольку именно эти ребра парал­лельны орту  и, соответственно, оси отключенного маховика. Таким обра­зом, в декартовой системе координат , координаты вершин , , , , ,  параллелепипеда  совпадают с координатами середин ребер , , , , ,  многогранника  соответственно. Приведем некото­рые метрические характеристики многогранника . Его ребра имеют длину 2. Следовательно, все грани – ромбы. Вершины  и  находятся на расстоя­нии  от начала координат - точки , вершины  и  от­стоят от этой точки на расстояние , а вершины  и  на расстояние . Расстояния до вершин  и  от точки  равны . Равенство  имеет место при , равенство  достигается при одновременном выполнении условий  и .

Таким образом, соотношения между расстояниями , ,  выража­ются неравенствами, приведенными в табл. 2.

В табл. 5 указаны зависимости, позволяющие определить расстояние от начала координат  до каждой грани параллелепипеда .

Таблица 5.

2.3. Расположение маховиков на космическом аппарате. Рассмотрим вопрос, как следует расположить описанную в п. 2.1 систему из четырех ма­ховиков на КА и как лучше всего выбрать значения углов  и , чтобы обес­печить достаточно широкие возможности управления угловой скоростью ап­парата.

         Моменты инерции относительно главных центральных осей инерции КА, т.е. осей , ,  обозначим соответственно , , . Примем зна­чения этих моментов равными: , , . Поскольку система управления ориентацией космического аппарата должна быть достаточно универсальной, естественно потребовать, чтобы максималь­ные абсолютные значения реализуемых ею угловых скоростей вращения во­круг каждой из осей ,  и  были одинаковы. Предполо­жим, что пол­ный кинетический момент КА - сумма кинетических моментов несущего тела и маховиков - равен нулю. Тогда имеют место соотношения:

,              ,                .

Здесь , ,  и , ,  - проекции абсолютной угловой скорости несу­щего тела и собственного кинетического момента системы маховиков на оси  ,  и  соответственно. Разрешая последние соотношения относи­тельно угловых скоростей, получим

                      ,                 ,                     .                 (2.3)

Исходя из требуемого условия  и c учетом соотношений     , , , определим значение угла . , , откуда получаем . Зная значение угла  определяем значение угла . , , откуда получаем , .

Таким образом, при полученных значениях углов  и , максимальные значе­ния абсолютных величин компонент угловой скорости КА в системе  составляют , где  - абсолютная вели­чина предель­ного значения кинетического момента отдельного маховика. Если по какой-либо оси реализуется отвечающее ей максимальное значение, то компоненты угловой скорости по двум другим осям равны нулю. Указан­ные максималь­ные значения компонент угловой скорости характеризуют предельные воз­можности системы маховиков для разворотов КА вокруг его главных цен­тральных осей инерции. При произвольном выборе направления вектора уг­ловой скорости в системе  максимальное значение модуля этого век­тора будет меньше. Область допустимых значений угловой скорости аппарата представляет собой многогранник , получающийся из многогран­ника  преобразованием подобия, задаваемым формулами (2.3). Указанные выше предельные значения угловых скоростей реализуются на вершинах этого многогранника.

3. Конфигурация системы маховиков «шестигранная пирамида».

3.1. Область возможных значений кинетического момента. Рассмот­рим систему маховиков, оси которых расположены параллельно боковым ребрам правильной шестигранной пирамиды (рис. 6).

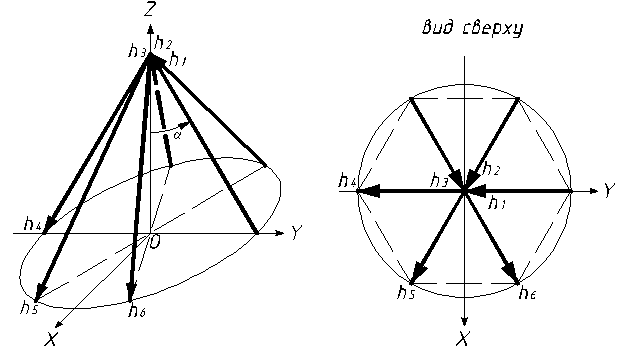
Рис. 6

Орты   осей маховиков имеют в системе координат  компо­ненты:

,                           ,

,                ,

,            .

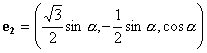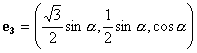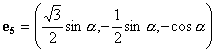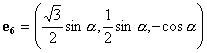Здесь  - угол между осью маховика и осью . Угол  - параметр системы.  Суммарный кинетический момент маховиков выражается формулой:

                                    ,                          (3.1)

в которой  - значение кинетического момента маховика с номером . Махо­вики считаем одинаковыми. В этом случае  ≤  ≤  , где  - абсолютная величина предельного значения кинетического момента отдель­ного маховика. Величина  - еще один параметр системы. Скалярная за­пись векторного выражения (3.1)

,   ,

.

Здесь , ,  компоненты  в системе координат . Выражение (3.1)  для краткости будем записывать в виде . Кроме того, будем использовать обычное представление вектора , указы­вая в круглых скобках его компоненты в системе координат . Не ограничивая общности, положим .

Рассмотрим область  пространства , заполняемую концами векторов (3.1) при  ≤ . Эта область является областью возможных значе­ний кинетического момента системы маховиков и представляет собой выпук­лый многогранник, обладающий центральной симметрией относительно на­чала координат. Перечислим вершины, ребра и грани этого многогранника. Координаты каждой вершины многогранника соответствуют координатам конца вектора суммарного кинетического момента составленного из опреде­ленной комбинации максимальных значений кинетических моментов махови­ков , из чего следует, что общее число вершин не может быть более 64 = 2⁶. В данном случае существуют 2 комбинации, при которых сум­марный вектор  равен нулю ( и ), и 30 комби­наций, когда суммарный вектор  лежит внутри области , что за­висит от взаимного расположения маховиков относительно связанной сис­темы коор­динат . Оставшиеся 32 комбинации соответствуют вершинам многогран­ника. Обозначим их  и  . При каждом  вершины  и  расположены центрально симметрично относительно точки . Вершины характеризуются соотношениями:

1)  :                              

2)  :                    

3)  :           

4)  :                  

5)  :                        

6)  :                    

7)  :                            

8)  :              

9)  :        

10)  :         

11)  :        

12)  :              

13)  :                     

14)  :                  

15)  :                         

16)  :         

17)  :                      

18)  :                                     

19)  :           

20)  :         

21)  :    

22)  :         

23)  :                   

24)  :             

25)  :      

26)  :                          

27)  :                          

28)  :                 

29)  :              

30)  :            

31)  :                   

32)  :                          

Здесь в фигурных скобках указаны орты ребер, выходящих из каждой вер­шины. Многогранник  имеет 60 ребер. Ребра будем задавать, указывая соединяемые ими вершины и параметризации соответствующих отрезков. Имеем :

1):                   31):                 

2):                   32):          

3):                     33):                   

4):                 34):                 

5):                  35):              

6):                36):                

7):                   37):           

8):                      38):           

9):                      39):          

10):                   40):                

11):              41):
          12):             42):    

13):                43):        

14):                   44):            

15):                      45):          

16):              46):  

17):          47):    

18):                48):        

19):                   49):

20):                       50):

21):                   51):                

22):                  52):               

23):              53):    

24):              54):                

25):                  55):           

26):                   56):            

27):                     57):                   

28):                 58):                

29):                 59):                   

30):                   60):

Здесь  ≤  ≤ . Первая вершина ребра получается при , последняя – при .         Многогранник  имеет 30 граней, которые обозначим  и  . При каждом  грани  и  расположены центрально симмет­рично относи­тельно точки . Грани будем задавать списком принадлежащих им ребер и параметризацией:

1) ,                ,

2) ,                ,

3) ,                ,

4) ,                ,

5) ,              ,

6) ,              ,

7) ,              ,

8) ,              ,

9) ,              ,

10) ,             ,

11) ,            ,

12) ,            ,

13) ,           ,

14) ,           ,

15) ,             ,

16) ,             ,

17) ,           ,

18) ,           ,

19) ,         ,

20) ,         ,

21) ,         ,

22) ,         ,

23) ,         ,

24) ,         ,

25) ,       ,

26) ,       ,

27) ,         ,

28) ,         ,

29) ,         ,

30) ,         .

Здесь принято, что обозначения вида  и  задают одно и тоже ребро, но при разном выборе первой и последней вершин. Таким образом, много­гран­ник  имеет 32 вершины, 30 граней и 60 ребер. В табл. 6 приведены зна­чения координат вершин многогранника  в декартовой системе координат  при значении угла (способ, применявшийся для определения значе­ния угла  , описан в п. 3.3).

Таблица 6.

Вид многогранника  в декартовой системе координат  приведен на рис. 7.

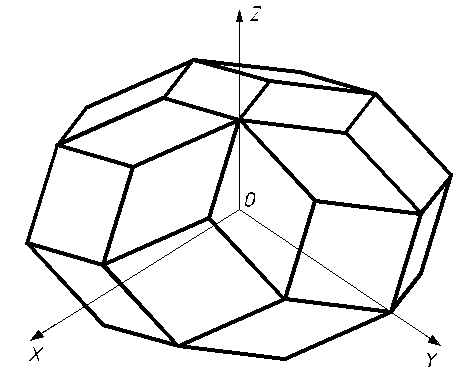
Рис. 7

На рис. 8 изображены проекции многогранника  на координатные плос­кости системы .

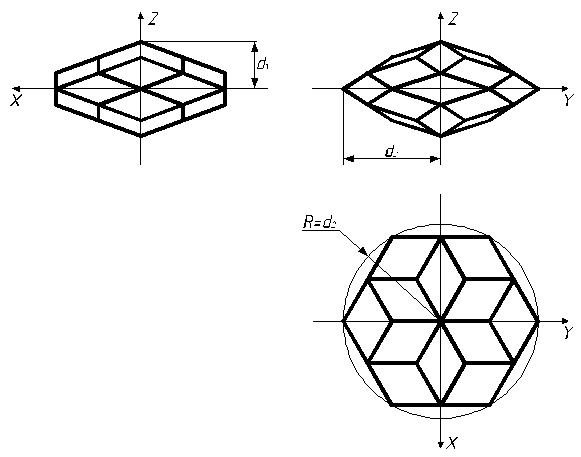
Рис. 8

На рис. 9 изображены проекции многогранника  на координатную плос­кость   и обозначены вершины многогранника.

Рис. 9

Многогранник  допускает ряд преобразований симметрии. Он перехо­дит в себя при повороте вокруг осей , ,  на угол кратный . Коорди­натные плоскости системы  являются его плоскостями симметрии.

         Приведем некоторые метрические характеристики многогранника . Все его ребра имеют длину 2. Следовательно, все грани – ромбы. Вер­шины  и  находятся на расстоянии  от начала координат - точки , вершины , , ,  и ,  отстоят от этой точки на расстояние , а вершины , , , , , , , , ,  и ,  на расстоя­ние . Расстояния до вершин , , , , , , , , ,  и ,  от точки  равны . Соотношения между расстоя­ниями , , ,  выражаются неравенствами, приведенными в табл. 7.

                              Таблица 7.

В табл. 8 указаны зависимости, позволяющие определить расстояние от начала координат  до каждой грани многогранника .

       Таблица 8.

3.2 Возможности системы при отключении одного из маховиков. Оценим возможности рассматриваемой системы в случае, когда один из ма­ховиков отключен (вышел из строя). Без ограничения общности можно счи­тать, что отключен маховик с осью, параллельной орту . Суммарный кине­тический момент такой усеченной системы выражается векторной формулой

                                        ,                                (3.2)

скалярная запись которой имеет вид

,                  ,

.

Выражение (3.2) для краткости будем записывать в виде . Здесь по-прежнему  ≤  ≤  . Не ограничивая общности, положим . Область пространства, заполняемая концами векторов (3.2) при  ≤  – область возможных значений кинетического момента системы  маховиков – представляет собой многогранник . Перечислим вершины, ребра и грани этого многогранника. Вершины (в данном случае их 22) обо­значим  и  . При каждом  вершины  и  расположены цен­трально симметрично относительно точки . Вершины характеризуются соот­ношениями:

1)  :                         

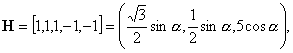
2)  :                      

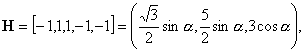
3)  :                    

4)  :                  

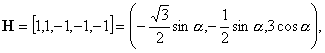
5)  :                         

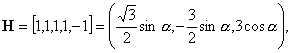
6)  :                                  

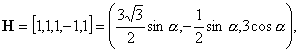
7)  :                        

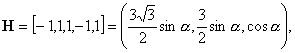
8)  :                  

9)  :                  

10)  :                  

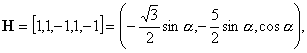
11)  :                        

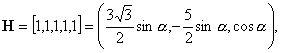
12)  :           

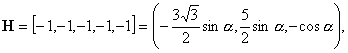
13)  :                   

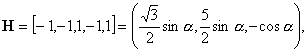
14)  :                         

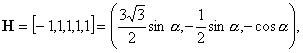
15)  :                           

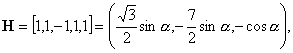
16)  :                    

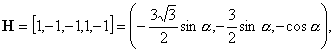
17)  :               

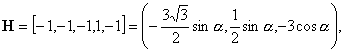
18)  :              

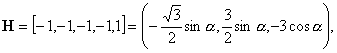
19)  :                    

20)  :                           

21)  :                 

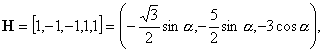
22)  :              

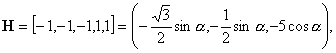
Здесь в фигурных скобках указаны орты ребер, выходящих из каждой вер­шины. Параллелепипед имеет 40 ребер. Ребра многогранника  будем зада­вать, указывая соединяемые ими вершины и параметризации соответствую­щих отрезков. Имеем:

1):     15):    29):         

2):     16):      30):

3):       17):   31):

4):   18):     32):

5):   19):   33):

6):    20):    34):      

7):        21):     35):      

8):        22):     36):       

9):    23):     37):

10):   24):       38):      

11):   25):       39):

12):    26):  40):

13):     27):    

14):   28):

Здесь  ≤  ≤ . Первая вершина ребра получается при , последняя – при . Многогранник  имеет 20 граней, которые обозначим  и  . При каждом  грани  и  расположены центрально симмет­рично относительно точки . Грани будем задавать списком принадлежащих им ре­бер и параметризацией:

1) ,                ,

2) ,                ,

3) ,                ,

4) ,                ,

5) ,                ,

6) ,                ,

7) ,              ,

8) ,              ,

9) ,               ,

10) ,             ,

11) ,            ,

12) ,            ,

13) ,            ,

14) ,            ,

15) ,           ,

16) ,          ,

17) ,             ,

18) ,             ,

19) ,           ,

20) ,           .

Здесь принято, что обозначения вида  и  задают одно и тоже ребро, но при разном выборе первой и последней вершин. В табл. 9 приведены зна­че­ния координат вершин многогранника  в декартовой системе координат  при значении угла  с учетом отказа одного маховика.

Таблица 9.

Вид многогранника  в декартовой системе координат  приведен на рис. 10.

Рис. 10

На рис. 11 изображены проекции многогранника  на координатные плоскости системы .

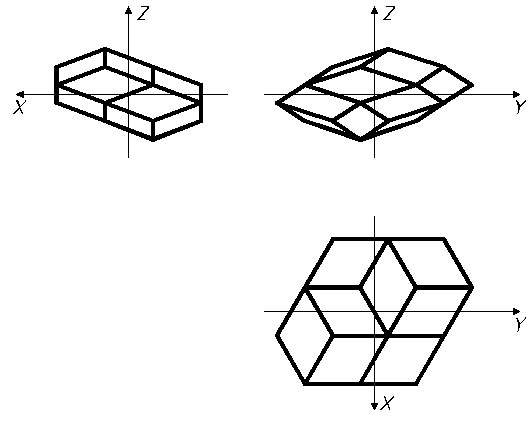
Рис. 11

На рис. 12 изображены проекции многогранника  на координатную плоскость  и обозначены вершины многогранника.

Рис. 12

Многогранник  представляет собой многогранник  с длиной ребер  , , , , , , , , ,  равной нулю,  поскольку именно эти ребра параллельны орту  и, соответственно, оси от­ключенного маховика. Таким образом, в декартовой системе координат , координаты вершин , , , , , , , , ,  многогран­ника  совпадают с координатами середин ребер , , , , , , , , ,  многогранника  соответственно. Приве­дем некоторые метрические характеристики многогранника . Его ребра имеют длину 2. Сле­довательно, все грани – ромбы. Зависимости, определяю­щие расстояния от начала координат (точки ), до вершин многогранника  представлены в табл. 10.

       Таблица 10.

В табл. 11 указаны зависимости, позволяющие определить расстояние от начала координат  до каждой грани многогранника .

           Таблица 11.

Приведенные выше геометрические построения областей возможных значений ки­нетических моментов маховиков позволяют сделать вывод, что схема, состоящая из большего количества маховиков, менее чувствительна к отказам и имеет область возможных значений кинетического момента, более прибли­женную к эллипсоиду, что дает более широкие возможности управле­ния уг­ловой скоростью КА.

3.3. Расположение маховиков на космическом аппарате. Рассмотрим вопрос, как следует расположить описанную в п. 3.1 систему из шести махо­виков на КА и как лучше всего выбрать значения угла , чтобы обеспечить достаточно широкие возможности управления угловой скоростью КА.

         Также как в п. 2.3 моменты инерции КА относительно главных цен­траль­ных осей инерции , ,  обозначим соответственно , ,  и примем значения этих моментов равными: , , . Исходя из условия  и c учетом соотношений  , , , определим значение угла . , , откуда получаем . Здесь , ,  и , ,  - проекции абсолютной угловой скорости несу­щего тела и собственного кине­тического момента системы маховиков на оси  ,  и  соответственно. Поскольку  >  и пирамида, по ребрам кото­рой располагаются маховики, является правильной, то рациональнее ее рас­положить таким образом, чтобы вектора  и  лежали в плоскости . Таким образом, при полученном зна­чении угла , максимальные значения аб­солютных величин компонент угло­вой скорости аппарата в системе  составляют , , где  - абсолютная величина предельного значе­ния кинетического момента отдельного маховика.

Литература

1.       Белецкий В.В. Движение искусственного спутника относительно

центра масс. М., Наука, 1965.

2.       Раушенбах Б.В., Токарь Е.Н. Управление ориентацией космических аппа­ратов. М., Наука, 1974.

3.       Барбашин Е.А. Функции Ляпунова. М., Наука, 1970.