Метод конечных элементов с базисными функциями специального вида для задач на собственные значения
( Finite elements method with special basic functions for eigenvalue problems
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Оглавление:

I.    Введение. 4

II.   Постановка задачи и метод RFB для задач на собственные значения. 4

III. Базисные функции специального вида. 6

IV.  Одномерный случай.. 8

IV.1.       Простейшая задача на собственные значения для оператора второй производной с постоянным коэффициентом. 8

IV.2.       Задача на собственные значения для оператора второй производной с переменным коэффициентом   12

V.   Двумерный случай. 17

V.1.        Общая теория. 17

V.2.        Задача для оператора Лапласа в квадрате. 19

V.3.        Задача для оператора Лапласа в L-образной области. 21

VI.  Методы решения матричных задач на собственные значения с нелинейным вхождением собственного числа.. 23

VI.1.       Метод обратных итераций для матричных задач на собственные значения с нелинейным вхождением собственного числа. 23

VI.2.       Метод Дэвиса. 24

VI.3.       Комбинация двух методов. 26

VII.       Заключение. 27

Список литературы... 28

I.        Введение.

Целью данной работы является применение метода, известного в англоязычной литературе как RFB (residual-free bubbles)[1,4,5] к решению задач на собственные значения. Рассматриваются задачи для эллиптического оператора в одномерной и двумерной области. Суть метода RFB для задач на собственные значения излагается в главе 0.

Важной частью работы является доказательство того, что указанный метод эквивалентен методу конечных элементов с базисными функциями, которые выбраны специальным образом, т.е. можно выбрать базисные функции в методе конечных элементов таким образом, что получается та же разностная задача, что и в методе RFB. Именно этим фактом объясняется название работы.  Этому вопросу посвящена глава III.  В главе IV приводятся два примера применения описываемого метода в одномерном случае. И, наконец, в главе V рассматриваются двумерные задачи для оператора Лапласа.

Отметим, что в результате применения метода RFB для задач на собственные значения (в отличие от краевых задач) возникает матричная  задача на собственные значения с нелинейным вхождением собственного числа. Поэтому встает вопрос о методах решения подобных задач. В качестве таких методов в данной работе выбраны модифицированный метод обратных итераций и метод Дэвиса, описываемые в главе VI. Кроме того,  рассматривается вопрос применения комбинации указанных методов.

II.      Постановка задачи и метод RFB для задач на собственные значения.

Рассмотрим абстрактную задачу на собственные значения в области :

где L – некоторый эллиптический оператор, , а  - двумерная или одномерная область.

Ей соответствует обобщенная задача:

Здесь  и  - билинейные формы. Заметим, что , а  если  - классическое решение задачи (1), то билинейная форма   имеет вид:

где  - скалярное произведение в .

Пусть  - разбиение области  на подобласти.

Классический метод конечных элементов заключается в замене исходного Гильбертова пространства в обобщенной задаче на его конечномерное подпространство . В качестве пространства  обычно выбирается пространство непрерывных кусочно-полиномиальных функций, обычно – кусочно-линейных. Тогда обобщенная задача (2) будет выглядеть следующим образом:

При этом основная идея метода RFB состоит в расширении пространства кусочно-полиномиальных функций специальными функциями, которые обращаются в ноль на границе элементов сетки и построены таким образом, что получаемое решение удовлетворяет дифференциальной задаче внутри каждого элемента сетки (bubble functions). Идея подобного подхода тесно связана с так называемыми стабилизированными методами (stabilized methods). [1,4,5] Стабилизированные методы возникли в связи с тем, что применение традиционного метода конечных элементов к некоторым задачам, особенно задачам конвекции-диффузии не давало удовлетворительных результатов. При этом стабилизированные методы дают повышение точности в таких задачах за счет устранения осцилляций решения.  Метод RFB возник в результате попытки подвести теоретическую основу под идеи стабилизированных методов и является одним из практических способов построения стабилизированных методов. Кроме того, существует другой способ построения стабилизированных методов, связанный с использованием функций Грина для дифференциальной задачи на каждом элементе сетки. Однако было доказано, что эти два способа получения стабилизированных методов эквивалентны[1].

В методе RFB [1,3,4,5] рассматривается пространство , которое представляется как сумма подпространств , где  - пространство непрерывных кусочно-линейных функций, линейных на каждом элементе сетки, а  - некоторое, возможно бесконечномерное, замкнутое пространство, состоящее из функций, обращающихся в ноль на границе элементов сетки. Таким образом, по сравнению  с традиционным методом производится расширение пространства, в котором ставится обобщенная задача. Здесь важно, что  - пространство именно кусочно-линейных, а не кусочно-полиномиальных функций более высокого порядка. Многие факты, приводимые далее в общем случае для кусочно-полиномиальных функций неверны.

Примечание 1: В частности  может включать в себя все функции, обращающиеся в ноль на границе элементов сетки. При этом в одномерном случае  (в пространствах большей размерности это неверно). Кроме того,  в одномерном случае  фактически будет представлять собой точное решение задачи (4), a  будет линейным интерполянтом . Однако в этом случае полученная задача (4) будет совпадать с исходной.

Из разложения  следует, что любая функция  из  однозначно представляется в виде суммы:

Тогда  задачу (4) можно переписать в следующем виде:

Учитывая, что любая функция из  обращается в ноль на границе элементов сетки,  можно представить в виде:

Здесь  прямая сумма по всем элементам сетки К, а  - это сужение пространства  на элементе К.

Тогда любая функция из  однозначно представляется в виде суммы:

Следовательно, второе уравнение системы (6) можно записать отдельно для каждого элемента сетки, и система принимает вид:

где индекс K у билинейных форм означает интегрирование по K-му элементу сетки.

Далее, согласно методу RFB, из второго уравнения системы (9) аналитически выражается , при этом  рассматривается как параметр, и фактически  ищется отдельно на каждом элементе сетки K как решение краевой задачи, а не задачи на собственные значения, что значительно проще. Если же решить второе уравнение системы (9) не удается, то можно рассмотреть более простую задачу, например полученную заменой переменных коэффициентов, входящих в оператор L их кусочно-постоянным приближением. 

III.    Базисные функции специального вида.

Обратимся ко второму уравнению системы (9):

Используя линейность форм  и  по первому аргументу, можно записать:

Заметим, что функция  является линейной на любом элементе сетки К. Следовательно, учитывая (3), а также то, что  на границе элемента, билинейную форму  можно записать в виде . Далее, учитывая, что , получаем следующее уравнение:

Теперь  может быть представлено как решение этой задачи, зависящее от   и , для любого :

где  – некоторый линейный ограниченный оператор, зависящий от параметра ,  действующий из пространства  в пространство  и определенный для каждого элемента сетки K[1].

Обратимся теперь к первому уравнению системы (9), учитывая (8):

Далее уравнение (10) можно записать в следующем виде:

Уравнения (10) и (15) эквивалентны, так как в суммах  и  на каждом элементе сетки K, остается лишь одно слагаемое, соответствующее данному элементу сетки.

Складывая (14) и (15), получим:

И, наконец, учтем равенства , а . Подставляя их в равенство (16), получим:

Обозначим  для любого . Обозначим пространство всех  через . Отметим, что пространство  является линейным, так как пространства  и  - линейны.

Используя новые обозначения, из уравнения (17) получаем следующую обобщенную задачу:

Таким образом, мы получили обобщенную задачу, которая соответствует методу конечных элементов с модифицированными базисными функциями . Важно отметить, что пространство  конечномерно (это следует из конечномерности пространства ).  Следовательно, задача (6), которая была получена из традиционного метода конечных элементов расширением исходного пространства пространством  (возможно бесконечномерным), эквивалентна задаче (18), полученной модификацией исходного пространства без увеличения размерности. Имеется в виду, что разностные задачи, получаемые указанными двумя способами совпадают.

Будем считать, что функции  достаточно гладкие и на них можно подействовать оператором L. Тогда (12) можно записать в следующем виде:

Так как последнее равенство верно для любого , то можно перейти к операторному уравнению:

Пусть размерность пространства  равняется N. Введем в нем базис . Тогда на каждом элементе сетки K базисные функции пространства  представляются в виде . Подставляя это разложение в (20), и учитывая что  обращается в ноль на границе элементов сетки, получаем следующую краевую задачу на каждом элементе сетки K:

Таким образом, базисные функции пространства  в задаче (18) могут быть получены как решение этой краевой задачи. Это дает практический способ получения базисных функций . При этом в качестве кусочно-линейных базисных функций  выбираются так называемые “функции-домики”. Еще раз отметим, что описанный способ получения базисных функций  может использоваться, только если функции из   достаточно гладкие.

IV.  Одномерный случай

IV.1.                  Простейшая задача на собственные значения для оператора второй производной с постоянным коэффициентом.

В качестве первого примера рассмотрим следующую простейшую краевую задачу на собственные значения:

Введем равномерную сетку: . Определим финитные функции ,  отличные от нуля на отрезке , в соответствии с (21) как решение краевых задач на отрезках и :

Нетрудно убедиться, что функции, удовлетворяющие системам (23) для данной задачи, будут иметь вид:

На рис. 1 и 2 приведены графики функции  при N=10 для собственных значений  и  соответственно.

Рисунок 1

Рисунок 2

Рассмотрим теперь обобщенную постановку задачи (22). Пусть  -конечномерное пространство функций с базисом . Будем искать приближенное решение в виде разложения по базису :

Тогда обобщенная постановка задачи (22) выглядит следующим образом:

где билинейные формы  и  имеют вид:

Подставляя (25) в (26), получим:

Получаем матричную задачу на собственные значения с трехдиагональной матрицей. Учитывая, что базисные функции  по построению являются точным решением уравнения  на соответствующих отрезках сетки, можно найти коэффициенты системы следующим образом:

Аналогично:

Таким образом, находя производные базисных функций :

мы получаем следующую нелинейную задачу на собственные значения:

где  матрица   имеет вид:

Методы, позволяющие решить задачу (32), описаны в главе VI.

Нетрудно получить точное решение задачи (22):

Интересно отметить, что исходная задача (22) имеет счетное множество решений (собственных значений и собственных функций). При этом получаемая разностная схема за счет специального выбора базисных функций является точной в точках сетки при заданном  (см. Примечание 1 в главе 0). Отсюда следует, что получаемая с помощью метода конечных элементов с модифицированным базисом дискретная задача также имеет счетное множество решений. При этом, решая задачу (32), можно получить любое решение исходной задачи.

На рис. 3 и 4 представлены результаты расчетов для различных начальных приближений к собственным значениям (n=5 и n=20 в (34) соответственно). Из рис. 4 видно, что описанный метод применим даже для больших собственных значений и малого числа точек. Нужно отметить, что данный пример носит исключительно иллюстративный характер, и высокая точность объясняется использованием, информации о точном решении.

Рисунок 3

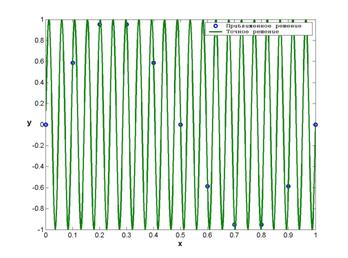
Рисунок 4

Замечание: сетка с постоянным шагом была выбрана в данном примере исключительно для простоты изложения. Описанный метод может быть применен и в случае сетки с переменным шагом.

IV.2.                  Задача на собственные значения для оператора второй производной с переменным коэффициентом

Рассмотрим следующую краевую задачу на собственные значения:

Известно, что данная задача имеет непрерывный спектр . Представляет интерес вопрос нахождения нижней границы спектра подобных задач.

Попытаемся найти точное решение уравнения  на отрезке сетки. Для этого преобразуем левую часть уравнения по формуле дифференцирования произведения. В результате получим:

Полученное уравнение сводится к линейному дифференциальному уравнению с постоянными коэффициентами заменой переменных .

Обозначим . Тогда общее решение уравнения (36) имеет вид:

Как видно полученная функция имеет особенность в нуле. Поэтому выбирать базис для метода конечных элементов в виде функций (37) нельзя. Чтобы избавиться от особенности в нуле сдвинем левую границу отрезка на  и устремим затем  к нулю. Таким образом, мы переходим к новой задаче на собственные значения:

Исследуем спектр этой задачи. Будем искать собственные функции  в виде (37). Из граничных условий получаем:

Из второго условия получаем уравнение относительно q:

Откуда приближенно (при ):

И следовательно:

Таким образом, задача (38) будет иметь дискретный спектр и нижняя граница спектра задачи стремится к 0.25 (т.е. к нижней границе спектра задачи (35)) при .

Оценка (42) может быть использована также как начальное приближение при численном решении задачи итерационным методом.

Введем равномерную сетку: .

В соответствии с (21) будем искать базисные функции  как решение следующих краевых задач на отрезках и :

Рассмотрим теперь обобщенную постановку задачи (38). Пусть, как и ранее,  - конечномерное пространство функций с базисом . Будем искать приближенное решение в виде разложения по базису :

Тогда в обобщенной постановке задача выглядит следующим образом:

где a(u,v), b(u,v) – билинейные формы, которые имеют вид:

Зная точное решение (37), можно найти базисные функции, удовлетворяющие  условиям (43):

где

Важно отметить, что здесь, в отличие от предыдущего примера, функции  различны на разных отрезках сетки. На рисунке 5 изображены графики функций  при N=10, i=1,2,3,4.

Рисунок 5

Аналогично предыдущей задаче вычисляем коэффициенты матрицы :

Для  получаем следующие выражения:

На рис. 6 и 7 представлены результаты решения задачи при  для первого и третьего собственных значений. Для сравнения на рис. 8 и 9 приведены результаты решения задачи с теми же параметрами методом конечных элементов с традиционным кусочно-линейным базисом.

Рисунок 6

Рисунок 7

Рисунок 8

Рисунок 9

V.   Двумерный случай.

V.1. Общая теория.

Рассмотрим задачу (1) в двумерной области . Пусть  - разбиение области  на треугольные подобласти. Согласно изложенному в главе III методу требуется решить краевую задачу (21), зависящую от параметра , для каждого элемента сетки K:

Здесь  - базисные функции пространства , линейные на каждом элементе сетки K.

Даже в простейшем случае, когда L – это оператор Лапласа с постоянными коэффициентами, аналитическое решение подобной задачи в треугольнике произвольной формы представляет сложность. Поэтому мы не можем выбрать в качестве пространства  на каждом элементе сетки K пространство всех функций из , обращающихся в ноль на границе элемента. Вместо этого введем на каждом элементе сетки К треугольную подсетку и в качестве пространства  рассмотрим пространство функций, которые являются кусочно-линейными внутри элемента сетки и линейными на каждом элементе подсетки.

Обозначим N – число внутренних точек сетки области , T – число треугольников в триангуляции области , M – число внутренних точек подсетки на каждом треугольнике глобальной сетки. Будем считать, что число внутренних точек на каждом треугольнике одинаково. Это делается исключительно для простоты дальнейшего изложения. 

Пусть  - базис пространства , а  - базис пространства  для каждого треугольника сетки k=1..T. Обращаем внимание, что в данном случае пространство  будет конечномерным. Тогда любая функция  из пространства  раскладывается по базису:

Подставляя разложение (52) в систему (9), получим следующую систему линейных алгебраических уравнений относительно коэффициентов  и :

Следует отметить, что полученная система имеет большую размерность. Однако ее можно не решать непосредственно, а свести к системе относительно только коэффициентов .

Изучим структуру матрицы системы (53). Размерность этой системы равна . Систему (53) можно записать в матричном виде:

где  - вектор-столбец неизвестных, соответствующих узлам глобальной сетки ;  - векторы-столбцы неизвестных, соответствующих узлам на подсетках ;  - квадратная матрица, зависящая от  и от ;  и   - прямоугольные матрицы, зависящие от ,   и от ;  - квадратные матрицы, зависящие от  и от .

Заметим, что, если оператор L – самосопряженный, то матрица системы (53) симметричная, и следовательно:

Кроме того, нетрудно видеть, что матрицы  имеют только три ненулевых строки, соответствующие вершинам k-го треугольника (соответственно матрицы  имеют только три ненулевых столбца).

Покажем, что описываемый  в данной главе метод соответствует общему методу, изложенному в главе III. Для этого достаточно определить вид оператора  для любого элемента сетки K, действующего из пространства  в пространство :

Из уравнений  системы (54)  формально выражается через :

Последнее соотношение фактически задает оператор , действующий из пространства  в пространство , и матрица этого оператора есть .

На практике наиболее эффективным методом решения системы (54) является исключение переменных из векторов  из матричного уравнения . Причем это можно сделать независимо для каждого k. В результате получим систему:

Где матрица  представляется в виде . При этом для самосопряженного оператора L из симметричности матрицы  и соотношений (55) следует, что матрица  также является симметричной.

Таким образом, задача свелась к решению задачи на собственные значения с матрицей прядка порядка N.

V.2. Задача для оператора Лапласа в квадрате

Рассмотрим сначала задачу для оператора Лапласа в квадрате:

где область  - единичный квадрат .

В этом случае билинейные формы  и  представляются в виде:

Тогда задача (9) принимает вид:

Известно точное решение задачи (59):

На рис. 10 и 11 приведены результаты решения задачи (зависимость погрешности нахождения собственного числа от 1/N, где N – число точек сетки) для старшего собственного числа () для стандартного метода конечных элементов с кусочно-линейным базисом и описанного выше модифицированного метода  соответственно. При этом в модифицированном методе число треугольников на подсетке было взято равным 64.

Рисунок 10

Рисунок 11

На рисунке 12 приведена зависимость  от 1/M, где  - собственное число, найденное с помощью обычного метода конечных элементов с кусочно-линейным базисом,   - собственное число, найденное с помощью модифицированного метода на той же сетке(с введением подсетки), а M – число точек подсетки.

Рисунок 12

Как видно из рис. 10, 11 и 12  описанный метод, в отличие от одномерного случая, в двумерных задачах (в отличие от одномерных) хотя и дает повышение точности по сравнению со обычным методом, но незначительное. В чем же принципиальное отличие двумерного случая от одномерного для данного метода?

Напомним, что мы выбирали пространство, в котором ищется решение в виде , где  - пространство непрерывных кусочно-линейных функций, а  - некоторое, возможно бесконечномерное, замкнутое пространство функций, обращающихся в ноль на границе элементов сетки. В идеале  может включать в себя все функции, обращающиеся в ноль на границе элементов сетки. Тогда, как отмечено в Примечании 1 главы 0, в одномерном случае , а   фактически будет представлять собой точное решение. Конечно, в реальных задачах в качестве  выбирается некоторое подпространство пространства всех функций, обращающиеся в ноль на границе элементов сетки, однако при хорошем выборе можно получить решение близкое к точному. Принципиальное отличие двумерных задач в том, что даже если выбрать в качестве  пространство всех функции, обращающихся в ноль на границе элементов сетки, мы не получим равенства . Действительно, нетрудно видеть, что на ребрах треугольников сетки функции из  всегда будут линейными. Это является принципиальным отличием задач в областях более высокой размерности от одномерных. И, как показывает приведенный пример, это оказывается существенным. Следовательно, единственный возможный путь улучшения метода – это модификация базисных функций не только внутри элементов сетки, но и на их границе. Отметим, что вопрос о том, как это сделать, пока не решен.

V.3. Задача для оператора Лапласа в L-образной области

Рассмотрим сначала задачу для оператора Лапласа в L-образной области:

где  -область, изображенная на рис. 13.

Рисунок 13

Покажем, что собственная функция, отвечающая старшему собственному числу, имеет особенность в точке . Представим собственную функцию в окрестности этой точки в полярных координатах:

Здесь  - это угол относительно оси , а  - расстояние от точки . Тогда, записывая уравнение системы (63) в полярных координатах, получим:

Из последнего равенства после очевидных преобразований получаем:

Из краевого условия системы (63) нетрудно получить, то . Тогда учитывая, что в окрестности точки   стремится к нулю, получаем . Отсюда и следует, что собственная функция будет иметь особенность в точке .

Введем билинейные формы  и  также, как и в предыдущей задаче, т.е. в виде (60) (но, естественно, на другой области ). Тогда обобщенная задача будет иметь вид (61).

На рис. 14 и 15 приведены результаты решения задачи описанным выше модифицированным методом для старшего собственного числа. При этом  число треугольников на подсетке было взято равным 64. На рис. 14 приведена зависимость погрешности нахождения собственного числа от 1/N, где N – число точек сетки (в качестве “точного” было взято значение ) . На рис. 15 изображена собственная функция, соответствующая старшему собственному числу.

Рисунок 14

VI. Методы решения матричных задач на собственные значения с нелинейным вхождением собственного числа

VI.1.                  Метод обратных итераций для матричных задач на собственные значения с нелинейным вхождением собственного числа.

Рассмотрим следующую нелинейную задачу на собственные значения:

где - квадратная матрица с нелинейным вхождением .

Рассмотрим итерационный метод решения таких задач[6]. Пусть заданы два начальных приближения для собственного значения:  и , а также начальное приближение для собственного вектора – x₀. Два начальных приближения для собственного значения требуется для численного нахождения производной матрицы А.

Обозначим через  разностную производную матрицы А, вычисляемую на n-й итерации по формуле:

Это матричное выражение вычисляется поэлементно.

Метод состоит из двух вложенных циклов. Во внутреннем цикле проводятся итерации по к. На каждой итерации находится новое приближение к собственному вектору –x_k+1 и новое приближение к поправке на собственное значение -  по формулам:

где норма  определяется следующим образом: . В результате внутренних итераций по индексу k находится поправка на собственное значение - . Во внешнем цикле проводятся итерации по индексу n, на каждой итерации после внутреннего цикла перевычисляется приближение к собственному значению по формуле:

Описанный метод фактически является комбинацией метода обратных итераций для линейных задач и метода Ньютона. Как известно, метод Ньютона сходится, если начальное приближение для  достаточно близко к точному корню.

VI.2.                  Метод Дэвиса

Данный метод [2] предназначен для поиска всех нулей аналитической функции в заданной ограниченной области на комплексной плоскости.

Пусть   -  аналитическая функция в области,  ограниченной контуром C.

Тогда интегралы

содержат в себе информацию обо всех нулях аналитической функции, лежащих в области, ограниченной контуром C. Здесь N – число корней в рассматриваемой области.

В качестве области будем рассматривать единичный круг  с центром в начале координат. При этом фактически можно решать задачу в любой ограниченной области, которую можно конформно отобразить в единичный круг.

Первым шагом метода является определение числа корней. Число корней N в области определяется по принципу аргумента:

где  - изменение аргумента при обходе точкой z полного контура в положительном направлении.

Пусть  - точки равномерно распределенные по контуру.

В работе [2] предлагаются следующие неравенства, которые гарантируют надежное определение числа нулей по принципу аргумента:

где  - максимальное изменение аргумента от точки к точке.

Очевидно, что всегда можно добиться выполнения этих неравенств, увеличивая число точек m на контуре.

Вычисление интегралов (71) по квадратурным формулам непосредственно осложнено тем, что в выражение явно входит производная . Для того, чтобы избавиться от явного вхождения производной производится интегрирование по частям:

Так как рассматриваемая область является единичным кругом, удобно перейти к полярным координатам:

Тогда интегралы  представляются в виде:

Полученные интегралы аппроксимируются квадратурными формулами в точках  по методу трапеций:

Из формул (76) приближенно вычисляются значения .

Следующий шаг – определение значений  - нулей функции  в рассматриваемой области. Как известно, интегралы  обладают свойством:

При этом, если у функции  есть кратные нули, то они входят соответствующее число раз в сумму (77).

Будем искать нули  как корни полинома:

Соотношение между коэффициентами  и суммами  известно из линейной алгебры:

Отсюда, зная , можно рекуррентно вычислить коэффициенты . Таким образом, задача нахождения нулей  свелась к задаче нахождения нулей полинома N-й степени. Кроме того, известно, что все нули этого полинома лежат внутри единичного круга. Задача нахождения этих нулей является простой, для этого может быть использован метод Ньютона.

В приведенных выше выкладках предполагалось, что в качестве рассматриваемой области выбран единичный круг  с центром в начале координат. Однако фактически может использоваться любая ограниченная область, которую конформным отображением можно перевести в единичный круг. Действительно, пусть  - функция, заданная в некоторой области, а  - конформное отображение единичного круга в данную область, тогда описанный метод можно применить к функции, заданной в единичном круге .

В данной работе применялся вариант изложенного метода для круга произвольного радиуса с произвольным центром на комплексной плоскости. Метод использовался для решения матричной задачи на собственные значения с нелинейным вхождением собственного числа, для чего в качестве функции выбирался определитель матрицы: .

В работе [2] приведена оценка погрешности вычисления сумм . Пусть функция  аналитическая в круге , где ,  - нули функции внутри круга ,   - нули функции в области . Тогда справедлива оценка:

где  - некоторая аналитическая функция в рассматриваемой области.

Из приведенной оценки следует, что наибольшую погрешность вносят нули расположенные близко к контуру. Кроме того, погрешность зависит от числа нулей в выбранной области и снаружи в близи границы области. Поэтому метод Дэвиса может использоваться для нахождения нулей с приемлемой точностью лишь при не очень большом их числе в выбранной области. При практическом использовании метода зависимость погрешности от числа точек интегрирования наблюдалась лишь при малом числе точек. Связано это, по всей видимости, с тем, что погрешность от приближенного вычисления интегралов мала по сравнению с погрешностью вычисления определителя матрицы (для вычисления определителя использовалось LU-разложение). 

VI.3.                  Комбинация двух методов.

Достоинством метода Дэвиса является то, что он включает в себя способ определения числа корней в заданной области, что не всегда известно заранее. Недостатком метода является то, что он не позволяет определить собственные вектора и невысокая точность при большом числе корней и неудачном выборе области.

Используемый итерационный метод дает значительное более точное решение, чем метод Дэвиса и позволяет определить не только собственные числа, но и собственные векторы, однако требует достаточно хорошего начального приближения к собственному значению.

Исходя из изложенного, наиболее эффективной представляется комбинация двух методов, в которой сначала используется метод Дэвиса в рассматриваемой области для определения количества собственных значений и их приближенных значений, а затем полученные значения используются как начальные приближения для итерационного метода. В результате собственные значения определяются с большей точностью и имеется возможность определить собственные вектора.

VII.           Заключение.

В данной работе рассмотрен вопрос применения метода RFB к решению задач на собственные значения. Указанный метод рассматривается для эллиптического оператора в одномерной или двумерной области. Кроме того, доказано, что указанный метод эквивалентен методу конечных элементов с базисными функциями, выбранными специальным образом. А именно, показано, что можно выбрать базисные функции в методе конечных элементов таким образом, что в результате получается та же разностная задача, что и в методе RFB.

Приведены примеры применения описываемого метода для двух одномерных задач и для двух  двумерных. Приводятся результаты решения указанных задач и сравнение точности метода с обычным методом конечных элементов с кусочно-линейным базисом. При этом показывается, что в рассматриваемых одномерных задачах модифицированный метод дает более точное решение. Однако в двумерном случае в рассматриваемых задачах описываемый метод не дает существенного улучшения точности по сравнению со стандартным методом конечных элементов с кусочно-линейным базисом. Связано это с тем, что в двумерном случае, в отличие от одномерного, требуется модификация базисных функций не только внутри элементов сетки, но и на их границе. Отметим, что вопрос о том, как это сделать, пока не решен.

В результате применения метода RFB для задач на собственные значения возникает матричная задача на собственные значения с нелинейным вхождением собственного числа. Рассмотрены методы решения таких задач: модифицированный метод обратных итераций и метод Дэвиса. А также рассмотрен вопрос применения их в комбинации друг с другом.

Все программные модули, используемые для расчетов, в том числе работа с матрицами, работа с треугольными сетками, реализация изложенных выше методов решения нелинейных задач на собственные значения, реализация методов RFB и конечных элементов, выполнены на языке C++ в среде С++Builder 5.0. Для создания иллюстраций к работе были использованы средства Matlab 6.5 и Tecplot 9.0.

Список литературы

1.          Brezzi F., Franca L.P., Hughes T.J.R., Russo A. . Comput. Methods Appl. Mech. Engrg. 145, 329-339, 1997.

2.          Davies B., Locating zeros of an analytic function, Journal of Computational Physics 66, 36, 1986.

3.          Franca L.P., Nesliturk A., Stynes M., On the stability of residual-free bubbles for convection-diffusion problems and their approximation by a two-level finite element method. Comput. Methods Appl. Mech. Engrg. 166, 35-49, 1998.

4.          Hughes T.J.R. Multiscale phenomena: Green’s functions, The Dirichlet-to-Neumann formulation, subgrid scale models, bubbles, and the origins of stabilized methods. Comput. Methods Appl. Mech. Engrg. 127, 387-401, 1995.

5.          Hughes T.J.R., Feijoo G.R., Mazzei L., Quincy J.B. The variational multiscale method – a paradigm for computational mechanics. Comput. Methods Appl. Mech. Engrg. 166, 3-24, 1998.

6.          Дроздова О.М. О сходимости одного итерационного метода решения нелинейной спектральной задачи. Дифференциальные уравнения. Том XXII, № 7, 1263-1265, 1986.