Об обтекании пластины вязкой несжимаемой жидкостью
( On the Viscous Incompressible Fluid Flow around a Plate
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Брюно А.Д., Шадрина Т.В.
(A.D.Bruno, T.V.Shadrina)

ИПМ им. М.В.Келдыша РАН

Москва, 2005
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 05-01-00050)

Аннотация

Методами степенной геометрии изучается классическая задача о пограничном слое при обтекании полубесконечной пластины потоком вязкой несжимаемой жидкости. Такой поток описывается системой трех уравнений Навье-Стокса в частных производных. Асимптотика потока при стремлении к бесконечности вдоль пластины удовлетворяет укороченной системе, которая в автомодельных координатах сводится к обыкновенному дифференциальному уравнению Блазиуса. Детальное исследование его решений позволяет описать асимптотику потока. Дан также обзор известных результатов. Работа носит методический характер, но в ней также получены новые результаты.

Abstract

By methods of Power Geometry, we study the classical problem of the boundary layer in the viscous incompressible fluid flow around a semi-infinite plate. The flow is described by the Navier-Stocks system of three partial differential equations. When one tends to infinity along the plate, the asymptotics of the flow satisfies to a truncated system, which is reduced in self-similar coordinates to the ordinary differential Blasius equation. A detailed study of its solutions allows to describe the asymptotics of the flow. We give a survey of know results as well. The paper is mostly methodological, but it contains also some new results.


E-mails: bruno@keldysh.ru, shadrina@aport.ru
Введение
В книге [3] изложены общие концепции степенной геометрии. В препринтах [4-6] разработаны методы применения степенной геометрии к задачам гидромеханики. В них эти методы были применены к задачам погранслоя на полубесконечной игле для двух вариантов: течение жидкости и течение газа. Здесь эти методы применяются к классической задаче погранслоя на пластине [1,2]. Эта работа имеет определенный методический характер, но в ней также получены новые результаты. В работе показано как на простейшей задаче применяются эти методы степенной геометрии. Другой вариант применения методов степенной геометрии к изучению погранслоя на пластине имеется в книге [3]. Однако, методы, используемые здесь, существенно продвинуты, по сравнению с тем, что использовано в книге, и носят более универсальный характер.
В этой работе рассматривается стационарный поток вязкой несжимаемой жидкости, набегающий на полубесконечную пластину. Такой поток описывается системой уравнений Навье-Стокса, которая сводится к системе двух уравнений в частных производных с двумя независимыми переменными x, y (являющимися декартовыми координатами), для двух зависимых переменных: функции тока y и давления p. Пластина задается как x і 0, y=0. Цель работы - найти при x®+Ґ асимптотики решений для зависимых переменных, удовлетворяющие всем граничным условиям.
Для этого используются методы степенной геометрии. Из полной системы методами пространственной степенной геометрии выделяется укороченная система, которая является первым приближением полной системы при x®+Ґ вблизи пластины. И, кроме того, решения этой укороченной системы удовлетворяют граничным условиям в бесконечности. После этого, методами плоской степенной геометрии анализируются автомодельные решения полученной укороченной системы, которая сводится к одному обыкновенному дифференциальному уравнению (уравнению Блазиуса). Методами плоской степенной геометрии анализируется уравнение Блазиуса и находятся асимптотики его решений при стремлении его независимой переменной к нулю и к бесконечности. Вычисляется само решение Блазиуса с б\'ольшей точностью, чем раньше, и предлагается его новое асимптотическое разложение.
§ 1. Преобразование системы уравнений Навье-Стокса
Рассмотрим систему уравнений Навье-Стокса [8, гл. VIII, § 76; 9, гл. 3, п. 3.3], описывающую стационарный поток вязкой несжимаемой жидкости

u  u
x
 +v  u
y
 +  1
r
  p
x
 =n ж
и 		 2 u
x2
 +  2 u
y2
 ц
ш 		,

u  v
x
 +v  v
y
 +  1
r
  p
y
 =n ж
и 		 2 v
x2
 +  2 v
y2
 ц
ш 		,
(1.1)

 u
x
 +  v
y
 =0.
Здесь x и y - прямоугольные координаты; u и v - компоненты вектора скорости потока соответственно по осям x и y; p - давление; r - плотность; n - кинематический коэффициент вязкости; r, n = const № 0.
Используя третье уравнение системы (1.1), введем функцию тока y по формулам
u=  y
y
 ,  v=-  y
x
 .
(1.4)
Тогда система (1.1) принимает вид
f1    def
=
 
    й
л 		 y
y
  2y
xy
 -  y
x
  2y
y2
 щ
ы 		+  1
r
  p
x
 -n ж
и 		 3y
x2y
 +  3y
y3
 ц
ш 		=0,
(1.5)

f2    def
=
 
    й
л 		-  y
y
  2y
x2
 +  y
x
  2y
xy
 щ
ы 		+  1
r
  p
y
 +n ж
и 		 3y
x3
 +  3y
xy2
 ц
ш 		=0.
В обозначениях степенной геометрии [4] здесь
x1=x,  x2=y,  x3 = y,  x4 = p.
§ 2. Первые приближения решения в бесконечности вдоль пластины
Рассмотрим теперь обтекание полубесконечной пластины, которая описывается как x і 0, y=0, стационарным потоком вязкой несжимаемой жидкости в положительном направлении оси x. Такое обтекание описывается системой уравнений Навье-Стокса (1.1) с граничными условиями
u=uҐ,  v=0,  p=p0 при x=-Ґ,  uҐ,p0=const № 0;
u=v=0 при x і 0,  y=0.
(2.1)
Согласно (1.4) это обтекание также описывается системой (1.5) с граничными условиями в бесконечности и на пластине
y = uҐ y,  p=p0 при x=-Ґ;  uҐ,p0 = const № 0;
(2.3)

 y
x
 =  y
y
 =0 при x і 0,  y=0.
(2.4)
Заменой координат y = n[(y)\tilde], p=[(p)\tilde] uҐ2, x=n[(x)\tilde]/uҐ, y=n[(y)\tilde]/uҐ эта задача сводится к задаче с uҐ = 1, n = 1 и с новым p0= const № 0, которая рассматривается ниже.
Лемма 1. Граничные условия
y = y,  p=p0  при y®+Ґ;  p0=const
(2.5)
имеют место для x О (-Ґ,+Ґ).
Доказательство. Заметим, что функции y = y, p=p0 аннулируют каждый из членов в уравнениях (1.5). Следовательно, функции (2.5) являются решением любой укороченной системы для системы (1.5). В [3, гл. VI, § 6, п. 2] описано как двигаясь по укороченным системам, имеющимся при y®Ґ и -Ґ < x < 0, можно перенести граничное условие (2.3) на случай x > 0, y®Ґ, т.е. получить условие (2.5). Для этого для системы (1.5) рассмотрим все ее укороченные системы, соответствующие граничным условиям (2.5).
Таблица 1. Выделение укороченной системы.
Здесь Dk[(   def) || ( = )]  б[(P)\tilde],[(Q)\tilde]kс.
ikQk[(Q)\tilde]kDkT
11-1,  -2,  2,  0-1,  0-2+
2-1,  0,  0,  1-1,  0-2+
3-2,  -1,  1,  0-2,  0-4
40,  -3,  1,  00,  -2-2+
25-2,  -1,  2,  0-2,  1-3
60,  -1,  0,  10,  -1-1+
7-3,  0,  1,  0-3,  1-5
8-1,  -2,  1,  0-1,  -1-3
Носители уравнений системы (1.5) представлены в таблице 1. Ее первый столбец содержит номер i уравнения fi=0, второй столбец содержит номер k точки Qk носителя, третий столбец содержит сами точки Qk носителей S(fi). В уравнениях системы (1.5) в квадратные скобки объединены члены с одним и тем же векторным показателем степени Qk.
Из граничного условия (2.5) видно, что при y®+Ґ имеются граничные условия вида [4]
f3    def
=
 
   y-y=0,

f4    def
=
 
   p-p0=0.
Каждому из них соответствует носитель, состоящий из двух точек. А именно: S(f3) состоит из точек Q9=(0,0,1,0) и Q10=(0,1,0,0); S(f4) состоит из точек Q11=(0,0,0,1) и Q12=(0,0,0,0). Согласно теореме 2 [4] вектор P=(p1,p2,p3,p4) должен удовлетворять условиям бQ9,Pс = бQ10,Pс и бQ11,Pс = бQ12,Pс, т.е.
p3=p2,  p4=0.
(2.6)
Согласно полученным на вектор P условиям (2.6), векторы Qk можно спроецировать на плоскость [(Q)\tilde]=([(q)\tilde]1,[(q)\tilde]2) по формулам [(q)\tilde]1=q1, [(q)\tilde]2=q2+q3, а значением q4 мы пренебрегаем. Четвертый столбец таблицы 1 содержит проекции [(Q)\tilde]k = (q1,q2+q3) векторов Qk. Проекции [S\tilde] (f1) и [S\tilde] (f2) носителей уравнений системы (1.5), их выпуклые оболочки [(G)\tilde]1, [(G)\tilde]2 и их нормальные конусы представлены на рис. 1.
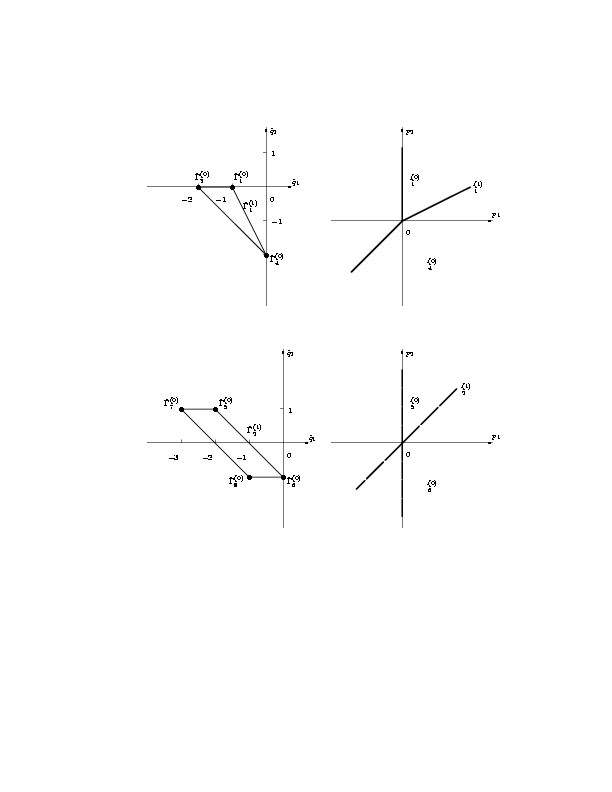
Рис. 1. Проекции носителей уравнений системы (1.5) (a)
и нормальные конусы проекций (б).
Каждому вектору [(P)\tilde]=(p1,p2) соответствует укороченная система
^
f
 
i[(P)\tilde] 
 (X)=0, i=1,2
(2.7)
системы (1.5), где [^(f)]i[(P)\tilde](X) содержит те члены из S(fi), для которых скалярное произведение б[(P)\tilde], [(Q)\tilde]с имеет наибольшее значение при этом i. Граничному условию (2.3) с x®-Ґ отвечают вектор [(P)\tilde]=(1,0) и соответствующая укороченная система (2.7). Согласно рис. 1 эта же укороченная система соответствует векторам [(P)\tilde]=(p1, p2) с p1 > p2/2 > 0, т.е. значениям x < 0 с ln|x| > (1/2)lny > 0 при y®Ґ. Следовательно, граничные условия (2.5) выполнены при этих x и y. При y®Ґ движению по x от -Ґ до 0 соответствует поворот вектора [(P)\tilde] в положительном направлении от (1, 0) до (0,1). Двигаясь по соответствующим укороченным системам (2.7) переносим условие (2.5) на значения x О (-Ґ, 0). Двигаясь по тем же укороченным системам в обратном направлении, т.е. от вектора [(P)\tilde]=(0,1) к вектору [(P)\tilde]=(2,1), перенесем условие (2.5) на x О [0,+Ґ). Лемма доказана.
Традиционно граничные условия на внешней границе пограничного слоя берутся из потока, невозмущенного обтекаемым препятствием (в данном случае пластиной). Следовательно, граничные условия (2.3) продлеваются до граничных условий (2.5). Но эта процедура основана на физических соображениях. В лемме 1 это сделано чисто математически.
Лемма 2. Для системы (1.5) укороченная система, соответствующая пограничному слою на игле и граничным условиям (2.5), единственна. Она имеет нормальный вектор P=(2,1,1,0) и есть
^
f
 
1 
    def
=
 
    й
л 		 y
y
  2y
xy
 -  y
x
  2y
y2
 щ
ы 		+  1
r
  p
x
 -  3y
y3
 =0,
(2.8)

^
f
 
2 
    def
=
 
     1
r
  p
y
 =0,
(2.9)
а автомодельные координаты x, h(x) и p(x) для задачи (2.4), (2.5), (2.8), (2.9) суть
x = y/Цx,  h(x)=y/Цx,  p(x)=p.
(2.10)
Доказательство. Пластина описывается как x і 0, y=0. Вблизи пластины, при x®+Ґ и y® 0, имеем p1 > 0, p2 < 0. Следовательно, игле соответствует IV квадрант плоскости (p1,p2). Граничные условия (2.5) при x®+Ґ и y®+Ґ означают, что p1,p2 > 0, т.е. им соответствуют точки из I квадранта плоскости (p1,p2). Нас интересуют такие грани проекций [(G)\tilde]1 и [(G)\tilde]2, расширенные нормальные конусы которых содержат как IV квадрант, так и точки из I квадранта плоскости (p1,p2). Совмещение рисунков нормальных конусов проекций показано на рис. 2. Из него видно, что IV квадрант и точки из I квадранта содержаться только в расширенном нормальном конусе системы \check UJD = \checkU1(1)З\checkU6(0). Направляющий вектор нормального конуса [U\tilde]1(1) это вектор [(P)\tilde]=(2,1). По вектору [(P)\tilde]=(p1,p2) восстанавливаем вектор P=(p1, p2,p3,p4) согласно равенствам (2.6) и получаем в исходных координатах (p1, p2,p3,p4) вектор P=(2,1,1,0). Полученному вектору P соответствуют грани носителей S(f1) и S(f2), содержащие точки Q1, Q3, Q4, Q6. Этим точкам соответствует укороченная система (2.8), (2.9).
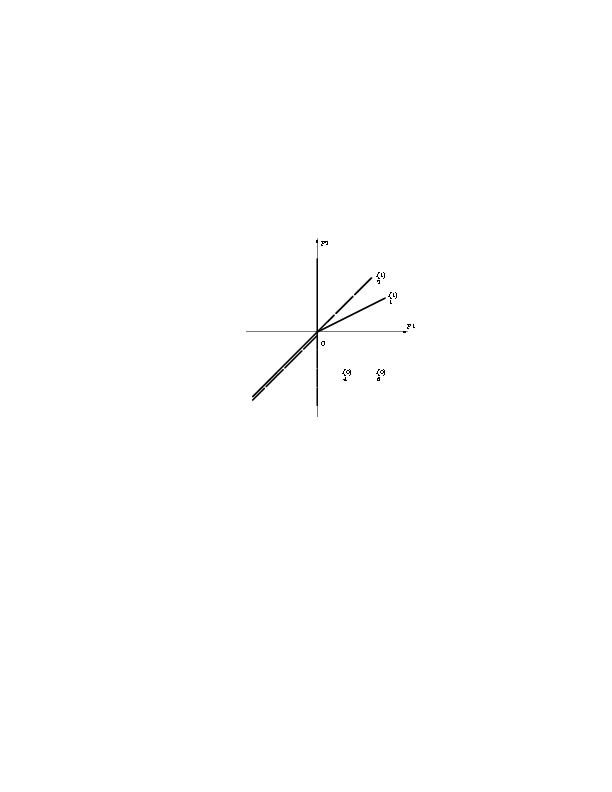
Рис. 2. Совмещенные нормальные конусы проекций
носителей уравнений системы (1.5).
Пятый столбец таблицы 1 содержит значения скалярных произведений Dk=б[(P)\tilde],[(Q)\tilde]kс = бP, Qkс для [(P)\tilde]=(2,1), P=(2,1,1,0). В шестом столбце (T) знак "+" отмечает максимальные значения б[(P)\tilde],[(Q)\tilde]kс для данного i, соответствующие им члены суммы fi включены в укорочение [^(f)]i1(di) в (2.8), (2.9).
Полученный вектор P=(Pў,P"), т.е. Pў=(p1,p2)=(2,1). Кроме того, вектор B1ў=(-1/2,1) составляет базис в пространстве векторов Qў=(q1,q2), удовлетворяющих условию бPў,Qўс = 0. Тогда согласно теореме 3 [4], T3ў=(1,0), T4ў=(0,0) и автомодельные координаты x, h, p имеют вид
x = y/Цx,  x3    def
=
 
   y = Цxh(x),  x4    def
=
 
   p = p(x),  
что соответствует (2.10). Лемма 2 доказана.
§ 3. Уравнение и решение Блазиуса
3.1. Вывод уравнения Блазиуса. В автомодельных координатах (2.10) система уравнений (2.8), (2.9) принимает вид
^
f
 
1 
    def
=
 
    -  2
x
 (hh"+2 h"ў+  1
r
 xpў)=0,
(3.1)

^
f
 
2 
    def
=
 
     1
y
 (  1
r
 xpў)=0,
(3.2)
где ў=d/dx. Из уравнения (3.2) следует, что
 1
r
 xpў=0,
следовательно, из уравнения (3.1) получаем
j(x,h)    def
=
 
   hh"+2 h"ў=0.
(3.3)
Это уравнение Блазиуса [2,13]. Для полученной системы (3.1), (3.2) граничные условия (2.4), (2.5) в автомодельных координатах (2.10) имеют вид
h=x,  p=p0 при x®+Ґ,
(3.4)

h=hў=0 при x = 0.
(3.5)
Из (3.1) и (3.4) следует, что
p=const=p0 при x № 0.
Таким образом, получили уравнение (3.3) с граничными условиями (3.5) и
hў=1 при x®+Ґ.
(3.6)
Итак, доказана
Лемма 3. В автомодельных координатах (2.10) задача (2.4)-(2.7) сводится к задаче (3.1), (3.2), (3.4), (3.5), которая, после исключения p, сводится к задаче (3.3), (3.5), (3.6).
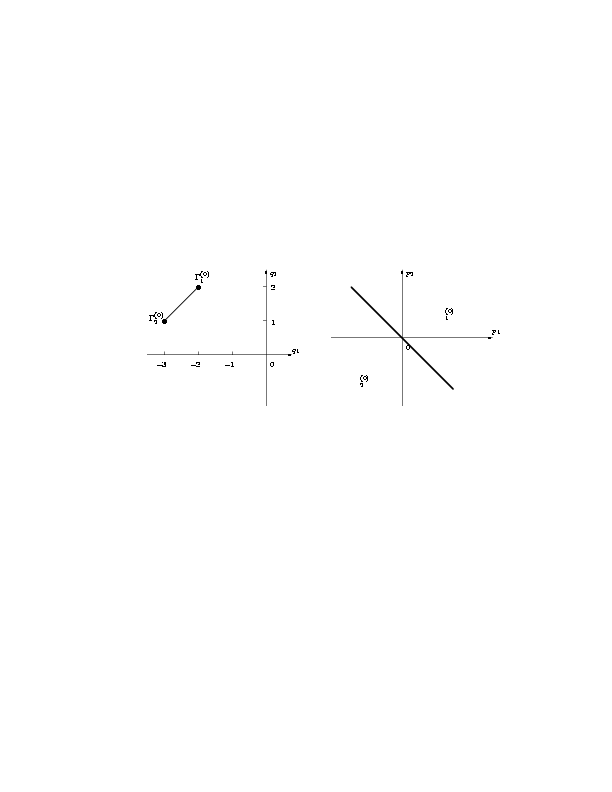
Рис. 3. Носитель уравнения (3.3) (a)
и его нормальные конусы (б).
Носитель S(j) уравнения (3.3) состоит из двух точек Q1=(-2,2) и Q2=(-3,1) (рис. 3). Изучим его решения, используя методы из [7].
3.2. Уравнение Блазиуса вблизи нуля [2, 10]. При x® 0 конус задачи есть p1 Ј 0 и из граничных условий (3.5) имеем p2 Ј 0. Эта область, т.е. третий квадрант, содержится в нормальном конусе U2(0), которому соответствует вершина G2(0). Ей соответствует укороченное уравнение [^(j)]2(0)[(   def) || ( = )]  2h"ў=0, все решения которого имеют вид h=c0+c1x+[(c)\tilde]x2. Из граничного условия (3.5) следует, что c0=c1=0. Следовательно, при x® 0 укороченное решение уравнения (3.3) есть h=[(c)\tilde] x2. Найдем теперь его критические числа [7, § 1, п. 1.4]. Первая вариация d[^(j)]2(0)/dh=2d3/dx3, следовательно, L(x)=2d3/dx3 и характеристический многочлен есть n(k)=k(k-1)(k-2). Его корни k Ј 2=r, следовательно, наше укороченное решение не имеет критических чисел. Найдем теперь носитель разложения решения. Все точки сдвинутого носителя S(j)-G2(0) можно представить в виде mR1, где вектор R1=(1,1) и целое m і 0. Тогда r1[(   def) || ( = )]  б(1,2),R1с = 3 и носитель разложения решения K={s=2+3l, целое l > 0}. Таким образом при x® 0 получено разложение решения
h=
~
c
 
   x2+ Ґ
е
l=1 
 cl  x2+3l,
(3.7)
где [(c)\tilde] - произвольная постоянная, все cl однозначно определяются. Коэффициенты cl этого разложения легко определяются, в [2, 10] приведены рекурентные формулы для их получения
cl=(-1)l  
2 Cl 
~
c
 
   l+1
 
(2+3l) !
 ,
где первые пять коэффициентов Cl имеют следующие значения
C1=1,  C2=11,  C3=375,  C4=27 897,  C5=3 817 137.
Например, c1=-[(c)\tilde]  2/60 и c2=11 [(c)\tilde]  3/20160. Легко находятся и дальнейшие коэффициенты подстановкой (3.7) в уравнение (3.3), например,
C6=865 874 115,  C7=303 083 960 103.
3.3. Уравнение Блазиуса вблизи бесконечности. При x®Ґ конус задачи есть p1 і 0 и p2 і 0, т.е. лежит целиком в нормальном конусе U1(0). Вершине G1(0) соответствует укороченное уравнение [^(j)]1(0)[(   def) || ( = )]  hh"=0. Все его нетривиальные решения имеют вид h=c0+c1x; из граничного условия (3.6) получаем c1=1. Сделаем в уравнении (3.3) замену h = c0+x, h=h+h1, получим уравнение
f(h,h)    def
=
 
   hh1"+h1h1"+2h1"ў=0.
(3.8)
Носитель S(f) уравнения (3.8) состоит из трех точек Q1=(-1,1), Q2=(-2,2) и Q3=(-3,1) (рис. 4). При h®Ґ конус задачи p1 і 0, p2 Ј 0. В него попадают нормальные конусы U1(0) и U1(1). Вершине G1(0) соответствует укороченное уравнение hh1"=0, его решение после возврата к переменным h и x совпадает с полученным укороченным решением.
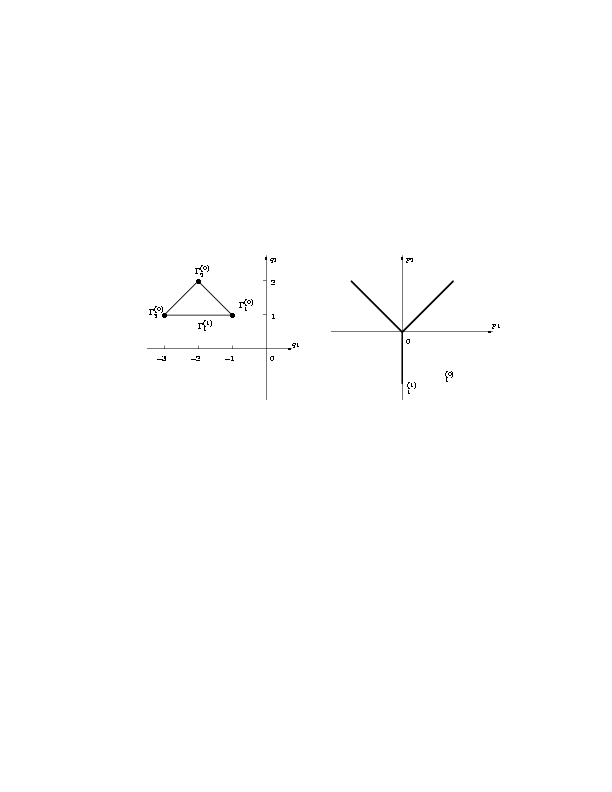
Рис. 4. Носитель уравнения (3.8) (a)
и его нормальные конусы (б).
Ребру G1(1) соответствует укороченное уравнение
^
f
 
 (1)
1 
    def
=
 
   hh1"+2h1"ў=0.
(3.9)
Так как ребро G1(1) является горизонтальным, сделаем логарифмическое преобразование [7, § 5, п. 5.4]
g=  dlnh1
dh
 ,
(3.10)
тогда
h1"=gўh1+g2h1,  h1"ў=g"h1+3ggўh1+g3h1,
и уравнение (3.8) после сокращения на h1 принимает вид
hgў+hg2+2g"+6ggў+2g3=0.
(3.11)
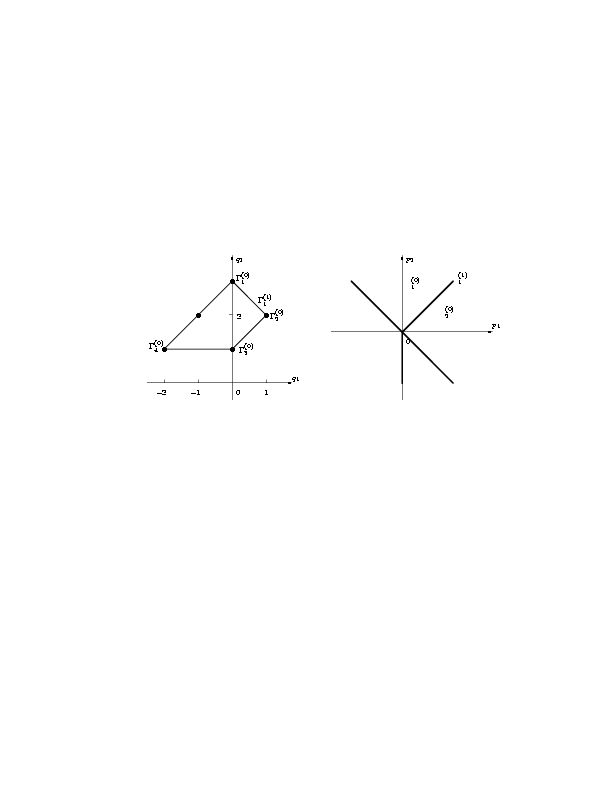
Рис. 5. Носитель уравнения (3.11) (a)
и его нормальные конусы (б).
Носитель уравнения (3.11) состоит из 5 точек Q1=(0,3), Q2=(1,2), Q3=(0,1), Q4=(-2,1) и Q5=(-1,2) (рис. 5). Конус задачи p1 + p2 і 0, с ним пересекаются нормальные конусы U1(0), U2(0) и U1(1). Укороченные уравнения, соответствующие вершинам G1(0) и G2(0) имеют только тривиальные решения. Ребру G1(1) соответствует укороченное уравнение hg2+2g3=0, его нетривиальное решение
g=-h/2.
(3.12)
Сдвинутый носитель уравнения (3.11) расположен в решетке с базисом M1=(1,1), M2=(2,0). Сдвинутый носитель решения (3.12) - это вектор (1, -1), который лежит в решетке с базисом M1, M2. Поэтому решетка, соответствующая уравнению (3.11) и решению (3.12) та же самая, т.е. состоит из точек Q=lM1+mM2=(l+2m, l), l и m - целые. На прямую q2=-1 попадают точки с l=-1, т.е. с q1=-1+2m. Поскольку конус задачи K={s < 1}, то носитель разложения решения K={s=1-2k, целое k і 0} и решение имеет вид
g=-  1
2
 h+ Ґ
е
k=1 
 bk  h1-2k.
Все постоянные bk однозначно определяются. В частности,
b1=-2,  b2=12,  b3=-168,  b4=3 312,  b5=-80 928.
Следовательно,
g=-  1
2
 h-2h-1+12h-3-168h-5+3312h-7-80928h-9+ Ґ
е
k=6 
 bkh1-2k.
Из (3.10) получаем
lnh1=-  1
4
 h2-2lnh-6h-2+42h-4-552h-6+10116h-8- Ґ
е
k=5 
  bk
2k
 h-2k+
~
c
 
1 
 ,
где [(c)\tilde]1 - произвольная постоянная. Следовательно, при h®Ґ решение уравнения (3.9) есть
h1=
~
c
 
2 
 h-2exp й
л 		-  1
4
 h2-6h-2+42h-4-552h-6+10116h-8- Ґ
е
k=5 
  bk
2k
 h-2k щ
ы 		,
где [(c)\tilde]2 - произвольная постоянная. Так как экспонента разлагается в ряд ex=1+x+x2/2+x3/3!+x4/4!+..., то
h1=
~
c
 
2 
 h-2e-h2/4 й
л 		1+ Ґ
е
k=1 
  ak
h2k
 щ
ы 		,
(3.13)
где коэффициенты ak однозначно определяются. В частности, a1=-6, a2=60, a3=-840, a4=15 120. Также эти коэффициенты можно вычислить, подставив (3.13) в уравнение (3.9). Таким образом были определены дальнейшие коэффициенты разложения (3.13), а именно, a5=-332  640, a6=8 648 640.
Итак, при x® Ґ получена нестепенная асимптотика решений уравнения (3.3)
h ~ x+c0+
~
c
 
2 
 (x+c0)-2 й
л 		1+ Ґ
е
k=1 
  ak
(x+c0)2k
 щ
ы 		exp[-(x+c0)2/4].
(3.14)
Укороченное уравнение (3.9) можно записать так:
(lnh1")ў=-h/2,
откуда
h1"=gexp[-h2/4],
где g - произвольная постоянная. Следовательно,
h1=g h
у
х
Ґ 
 h
у
х
Ґ 
 exp[-h2/4] dh dh.
Поэтому при x® Ґ асимптотику (3.14) можно выписать в явном виде через двойной интеграл [1, 10, 13]
h ~ x+c0+g x
у
х
Ґ 
 x
у
х
Ґ 
 exp[-(x+c0)2/4] dxdx,
(3.15)
где g = [(c)\tilde]2/4, что легко проверить.
3.4. Уравнение Блазиуса вблизи точки x0 > 0.
Лемма 4. В любой точке x = x0=const, h=h0=const с x0 О (0,Ґ), h0 № 0 производная hў(x) решения h(x) уравнения Блазиуса (3.3) либо монотонна, либо постоянна.
Доказательство. Перепишем уравнение (3.3) в виде
h"ў=-  1
2
 hh".
(3.16)
Согласно теореме Коши в любой точке x = x0=const, h=h0=const, hў=hў0=const, h"=h"0=const с x0 О (0,Ґ), h0 № 0 решение h(x) уравнения (3.3) аналитично и единственно. Следовательно, производная hў(x) решения также аналитична. Она имеет в этой точке экстремум, только если h"0=0. Но, согласно (3.16), тогда в этой точке h"ў=0. Дифференцируя уравнение (3.16), получаем, что в этой точке и все дальнейшие производные h(k) равны нулю. Аналитическая функция hў(x), у которой в некоторой точке все дальнейшие производные равны нулю, является постоянной. Доказательство окончено.
Лемма 4 аналогична лемме 4 из [6]. Из леммы 4 следует, что производная hў(x) решения уравнения (3.3) может быть трех видов
а. Постоянная hў(x)=const=0. В этом случае все производные h(k)(x)=0 и, следовательно, решение h(x) постоянно.
б. Постоянная hў(x)=const № 0. В этом случае решение h(x) уравнения (3.3) является прямой с некоторым постоянным наклоном, следовательно, решение h(x) монотонно.
в. Функция hў(x) монотонна. В этом случае, исходя из граничных условий (3.5), (3.6), она монотонно возрастает от 0 до 1 при увеличении x. Это значит, что в любой точке x = x0=const, x0 О (0,Ґ) производная hў=hў0 не равна нулю. Следовательно, решение hў(x) не имеет экстремума в этой точке. В этом случае решение уравнения (3.3), удовлетворяющее граничным условиям (3.5), (3.6), монотонно.
Итак, получена
Лемма 5. В любой точке x = x0=const, h=h0=const с x0 О (0,Ґ), h0 № 0 непостоянное решение h(x) уравнения (3.3), удовлетворяющее граничным условиям (3.5), (3.6), монотонно.
Для дальнейшего исследования, в уравнении (3.3) сделаем замену
x = x0+
~
x
 
 ,
где x0=const > 0. Тогда уравнение (3.3) перейдет в себя
hh"+2 h"ў=0.
(3.17)
Его носитель и нормальные конусы показаны на рис. 3. Нас интересуют решения, у которых [(x)\tilde]® 0 и h®Ґ, т.е. конус задачи есть p1 Ј 0, p2 і 0. С ним пересекаются все нормальные конусы. Рассмотрим соответствующие укороченные уравнения.
Вершине G1(0) соответствует укороченное уравнение
hh"=0.
Все его решения имеют вид h=c0+c1[(x)\tilde], т.е. при [(x)\tilde]® 0 решения h® c0 и не уходят в бесконечность.
Вершине G2(0) соответствует укороченное уравнение
2h"ў=0.
Все его решения имеют вид h=c0+c1[(x)\tilde]+c2[(x)\tilde]2, т.е. при [(x)\tilde]® 0 решения h® c0 и также не уходят в бесконечность.
Ребру G1(1) соответствует все уравнение (3.17). Для нахождения решения воспользуемся методами из [7, § 1, п. 1.3]. Нормальный конус U1(1) является прямой {l(-1,1)}. Нормальный конус u решения пересекается с U1(1) только если вектор (1,r) О U1(1), т.е. r=-1 и решение имеет вид h=cr[(x)\tilde]-1. Подставив его в уравнение (3.17) и сократив на [(x)\tilde]-4, получим уравнение для постоянной cr
2cr2-12cr=0,
отсюда получаем, что cr=6. Следовательно, решение имеет вид h=6[(x)\tilde]-1. При [(x)\tilde]® 0 решения h® +Ґ. Однако, из граничных условий (3.6) следует, что при x® +Ґ для решения должно быть h® +Ґ. Если в точке x = x0 > 0 также h® +Ґ, то в точке x = x1 > x0 решение h(x) имеет экстремум, что противоречит лемме 5. Следовательно, решения, уходящие в бесконечность не удовлетворяют граничным условиям (3.5), (3.6).
Следовательно, вблизи точки x = x0 > 0 решения уравнения Блазиуса (3.3), удовлетворяющие граичным условиям (3.5), (3.6), не уходят на бесконечность и не приходят из бесконечности.
3.5. Вычисление функции Блазиуса. Уравнение Блазиуса (3.3) является квазиоднородным. Его решение, удовлетворяющее граничным условиям (3.5), (3.6), называется функцией Блазиуса. Оно существует и единственно. Следовательно, можно применить теорему 7 [11] и свести граничную задачу (3.3), (3.5), (3.6) на двух концах интервала к двум граничным задачам на одном конце [12, гл. 16]. Сначала решается задача
FF"+2F"ў=0;  F(0)=Fў(0)=0,  F"(0)=1,
(3.18)
а затем
hh"+2h"ў=0;  h(0)=hў(0)=0,  h"(0)=(Fў(Ґ))-3/2.
(3.19)
Для численного решения задачи (3.18) берем значение постоянной c=1/2 и по формуле (3.7) находим для малого значения x = x0 начальные данные F(x0)[(   def) || ( = )]  h(x0), Fў(x0)[(   def) || ( = )]  hў(x0) и F"(x0)[(   def) || ( = )]  h"(x0). В результате численного решения задачи (3.18) получаем
c=(FўN)-3/2/2,
(3.20)
где FўN=Fў(xN) - значение производной, полученное для некоторого большого значения x = xN. На рис. 6 показано как изменяется значение c в зависимости от того, какое берется значение xN, обозначенное там x.
С полученным значением c из (3.20) находим для малого значения x = x0 по формуле (3.7) начальные данные h(x0), hў(x0) и h"(x0). После численного решения задачи (3.19) находим значения постоянных c0 и [(c)\tilde]2. Постоянную c0 находим из формулы (3.14)
c0=hN-xN,
(3.21)
где hN=h(xN) - полученное численно значение h при некотором большом значении x = xN. График зависимости получаемого значения c0 от взятого xN показан на рис. 7, где x=xN.
Постоянную [(c)\tilde]2 находим по формуле
~
c
 
2 
 =  1
4
 (h1-x1-c0) ж
и 		x1
у
х
Ґ 
 x
у
х
Ґ 
 exp[-(x+c0)2/4]dxdx ц
ш 		-1
 
 ,
(3.22)
где h1=h(x1) - значение, полученное численно в точке x1. Двойной интеграл в точке x1 вычисляется численно. В формуле (3.22) вместо двойного интеграла можно взять ряд из (3.14), домноженный на 4, ибо
(x1+c0)2 x1
у
х
Ґ 
 x
у
х
Ґ 
 exp[-(x+c0)2/4]dxdx =

= 4 й
л 		1+ Ґ
е
k=1 
  ak
(x1+c0)2k
 щ
ы 		exp[-(x1+c0)2/4],
где все постоянные ak однозначно определяются и начальные ak выписаны в п. 3.3. Однако, в отличие от постоянных c и c0, вычисление постоянной [(c)\tilde]2 вызывает некоторую сложность, связанную с тем, что значение двойного интеграла при увеличении x1 очень быстро уменьшается и выходит за пределы погрешности вычислений. На рис. 8, где x1=x, видно, что в данных вычислениях при x1 > 8 происходит "срыв" счета и при дальнейшем увеличении x1 получаемые значения [(c)\tilde]2 становятся произвольными (большими положительными и отрицательными). Таким образом, для получения [(c)\tilde]2 нужно брать значения интеграла и разложения при небольших x1, т.е. при x1 Ј 8.
Были получены следующие значения для постоянных в формулах (3.7) и (3.14)
c = 0.166028668,  c0 = -1.720787605,  
~
c
 
2 
 = 0.93307.  
(3.23)
Такие же, чуть менее точные, значения были получены и в [2,13] и уточнены в [10].
§ 4. Возвращение к исходной задаче
Для решения Блазиуса h=b(x) получены разложения при x® 0
b(x)=
~
c
 
   x2+ Ґ
е
l=1 
 cl  x2+3l
(4.1)
и при x®Ґ
b(x) ~ x+c0+
~
c
 
2 
 (x+c0)-2 й
л 		1+ Ґ
е
k=1 
  ak
(x+c0)2k
 щ
ы 		exp[-(x+c0)2/4]
(4.2)
с постоянными (3.23). Сделав преобразования, обратные к (2.10), получим в погранслое вблизи пластины
y ~ x1/2b(y/Цx).
Оценим точность этой асимптотики при x®Ґ, используя замечание 1 из [4]. Согласно лемме 2 укороченная система (2.8), (2.9) имеет нормальный вектор P=(2,1,1,0). Чтобы применить замечание 1 из [4] при x®Ґ, надо иметь нормальный вектор N с единичной первой координатой, т.е. N=P/2=(1,1/2,1/2,0). Тогда бN,Qс = бP,Qс/2. Согласно табл. 1 для бN,Qс имеем
a1=-1,    b1=-2,

a2=-1/2,    b2=-3/2.
Следовательно, min |ai-bi|=1. Согласно замечанию 1 из [4] имеем e0=1. Итак,
y = x1/2[b(y/Цx)+O(x-e)],
где 0 < e < 1=e0.
В лемме 2 для укороченной системы (2.8), (2.9) были предложены автомодельные координаты (2.10). С их помощью было найдено автомодельное решение Блазиуса системы (2.8), (2.9). Если согласно (2.9) положить p=const, то уравнение (2.8) принимает вид
 y
y
  2y
xy
 -  y
x
  2y
y2
 -  3y
y3
 =0
с граничными условиями (2.4), (2.5). В [14, § 7.6] показано, что имеются еще и другие неавтомодельные решения этой задачи. В [15] получено второе приближение решения в пограничном слое. Оно содержит члены с lnx. В [16, § 8] построена теория дальнейших приближений, которые содержат члены со степенями lnx.
Список литературы
  1. Prandtl L. Über Flüssigkeitsbewegung bei sehr kleiner Reibung // Verhandlungen des III. Internat. Math.-Kongr., Heidelberg, 1904. Leipzig: Teubner, 1905. S. 484-491.

  2. Blasius H. Grenzschichten in Flüssigkeiten mit kleiner Reibung // Zeit. für Math. und Phys. 1908. B. 56. S. 1-37.

  3. Брюно А.Д. Степенная геометрия в алгебраических и дифференциальных уравнениях. М.: Физматлит, 1998. 288 с.

  4. Брюно А.Д., Шадрина Т.В. Методы исследования погранслоя на игле. Препринт N 35, М.: ИПМ им. М.В. Келдыша, 2004. 27 с.

  5. Брюно А.Д., Шадрина Т.В. О несжимаемом погранслое на игле. Препринт N 36, М.: ИПМ им. М.В. Келдыша, 2004. 21 с.

  6. Брюно А.Д., Шадрина Т.В. Сжимаемый теплопроводный погранслой на игле. Препринт N 37, М.: ИПМ им. М.В. Келдыша, 2004. 32 с.

  7. Брюно А.Д. Асимптотики и разложения решений обыкновенного дифференциального уравнения // УМН, 2004, т. 59, N 3, с. 31-80.

  8. Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1978. 736 с.

  9. Бэтчелор Дж. Введение в динамику жидкости. М: Мир, 1973. 758 с.

  10. Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидродинамика. Ч. II. М.: Гостехиздат, 1948, 612 с.

  11. Брюно А.Д. Автомодельные решения и степенная геометрия // УМН, 2000, т. 55, N 1, с. 3-44.

  12. Ibragimov N.H. (Ed.) Lie Group Analysis of Differential Equations. V.1. Boca Ration, FL: CRC Press, 1994.

  13. Прандтль Л. Механика вязких жидкостей // В книге : Аэродинамика (ред. Дюрэнд), пер. с англ., том III, М.-Л.: 1939. Оборонгиз. С. 47-327, § 14.

  14. Ван-Дайк М. Методы возмущений в механике жидкости // Пер. с англ. М.: Мир, 1967. 311 с.

  15. Imai I. Second approximation to the laminar boundary-layer flow over a flat plate // J. of Aeronautical Sci. 1957, v. 24, p. 155-156.

  16. Goldstein S. Lectures on fluid mechanics. N.-Y., Wiley, 1960.

File translated from TEX by TTH, version 3.40.
On 01 Sep 2005, 15:59.