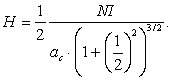Проектирование имитатора геомагнитного поля в составе лабораторного стенда
для отработки способов управления ориентацией микроспутников
|
|
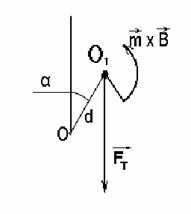
Рис.1. Удержание центра масс макета выше точки опоры |
Макета, O1 – его центр масс (рис.1). Пусть точка O1 смещена относительно O на расстояние d. Тогда момент силы тяжести составит:
где α – угол между OM и вертикалью, M – масса макета, g – ускорение свободного падения. Этому моменту должен противодействовать механический момент, действующий со стороны магнитного поля:
где m – магнитный момент макета спутника, |
B – индукция магнитного поля. Следовательно, необходимо потребовать выполнение неравенства
![]()
Пусть d=1 мм, M=1 кг, α=45º, m=1 А·м2. Тогда получаем, что индукция магнитного поля должна быть более 7·10-3 Тл, что соответствует напряженности 5500 А/м (см. раздел 3.1. Несостоятельность варианта приподнятого центра масс»). Здесь и далее напряженность этого поля обозначаем Hsup. При меньших значениях напряженности поля центр масс макета будет неминуемо опускаться ниже точки опоры.
2.2. Однородность поля
Поле должно быть однородным в той
области пространства, где находятся магнитные элементы системы управления
макетом спутника. Предполагается, что области пространства, ограниченной сферой
радиусом
Следуя [2], назовем степенью неоднородности модуля напряженности поля отношение отклонения модуля напряженности от номинального значения к номинальному значению
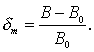
Назовем степенью неоднородности направления поля угол между вектором напряженности номинального поля и действительного поля в точке:
![]()
Достаточно, чтобы в рабочей области пространства выполнялись неравенства δm < 1% и δa<0.5˚. Неоднородность поля не имеет смысл делать меньше, так как указанные величины сравнимы с погрешностями типовых магнитометров.
2.3. Дополнительные ограничения
Управление полем должно осуществляться компьютером по заданной программе. Наиболее простой, если не единственно возможный, вариант реализации источника магнитного поля - это использование трех пар катушек с током со взаимно перпендикулярными осями.
Время непрерывной работы стенда должно быть 1 - 2 часов. В случае большого тепловыделения катушками они могут перегреться, что нежелательно. В дальнейшем (см. раздел 3.1), будет показано, что вариант с поднятым центром масс не удовлетворяет разумным требованиям рассеиваемой мощности. Кроме того, электрические параметры катушек определяют требования, выдвигаемые к электронному блоку, управляющему током.
2.4. Выбор конструкции имитатора
Имитирующее поле, которое удовлетворяет выше изложенным требованиям, проще всего создать, используя катушки с током. Сердечники использовать нецелесообразно. Хотя они и дают выигрыш в однородности и напряженности поля, они создают неудобства при изменении поля, так как приходиться учитывать эффект гистерезиса. Кроме того, диаметр сердечника должен быть больше диаметра области однородного поля, что делает очень дорогим создание стенда.
В литературе [2] рассмотрены следующие варианты геометрических конфигураций катушек:
· три пары одинаковых круглых колец (рис.2а),
· три пары одинаковых квадратных колец (рис.2б),
· три пары кратного двум количества колец (рис.2в и рис.2г).
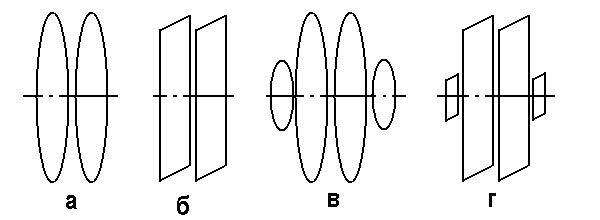
Рис.2. Различные геометрические конфигурации колец
В [2] показано, что в случае кратных колец оптимальной с точки зрения потребляемой мощности и однородности создаваемого поля конфигурацией является та, для которой все кольца имеют одинаковый размер и пространственно совпадают, образуя первую или вторую конфигурацию. Там же показано, что существует оптимальная геометрическая конфигурация у круглых колец. При этой конфигурации круглые катушки имеют меньшие габариты по сравнению с квадратными, если объемы создаваемых ими однородных полей совпадают. С точки зрения энергетики, круглые кольца в такой конфигурации также являются оптимальными. Таким образом, наилучшей геометрической конфигурацией среди всех возможных является конфигурация с круглыми некратными кольцами (рис.3). Стоит отметить, что если руководствоваться иными критериями однородности поля, можно показать, что квадратные кольца лучше круглых [3]. С учетом того, что для круглых колец были в наличии почти готовые каркасы, выбор пал именно на круглые кольца.
Обозначим радиус катушки через ac, расстояние между центрами катушек - dc. Примем dc/ac=1.116, это соответствует оптимальной геометрической конфигурации [2]. Номинальное поле для одной пары катушек – это создаваемое ими поле на их оси посередине между их центрами. Его напряженность выражается следующей формулой:
|
|
(1) |
где NI – число ампер-витков в каждой из катушек [4].
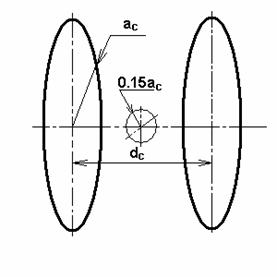
Рис.3. Круговые кольца
Габариты
установки определим из следующий соображений. В [2] показано, что указанная
выше степень неоднородности поля выполняется в объеме, ограниченном сферой
радиусом r=0.15ac. В этот объем должна уместиться часть макета
спутника, взаимодействующая с внешним магнитным полем. Ее габариты
предполагаются порядка
Рис.4. Пространственная конфигурация катушек
Из (1) получаем, что число ампер-витков для Hsub и Hsup при ас=0.6 м и dc/ac=1.116 составит NIsub=216 А и NIsup= 4960 А соответственно.
3. Расчет электрических параметров
Пусть задано число ампер витков NI и диаметр катушек ac. Необходимо выбрать число витков N катушки (или ток I), а также диаметр и материал провода. При этом надо минимизировать потребляемую мощность и массу катушки.
Сопротивление каждой катушки составляет
|
|
(2) |
Напряжение, необходимое для поддержания нужного числа ампер витков, определяется формулой
|
|
(3) |
где R – сопротивление обмотки, S0 – площадь поперечного сечения проводящей жилы обмоточного провода (то есть без учета изоляции), ρ – удельное сопротивление материала провода.
Мощность, рассеиваемая обмоткой, определяется формулой
|
|
(4) |
Варьируемыми параметрами при выбранном материале провода являются площадь проводящего сечения провода S0 и число витков N или ток I.
Преобразуем формулы (3) и (4). Пусть S – диаметр обмотки, тогда число витков N будет равно kS/S0. Коэффициент пропорциональности k определяется способом намотки и толщиной изоляции провода. Он равен отношению проводящей площади сечения обмотки к полной площади. Подставляя выражение для N в (3) и (4), получаем
|
|
(5) |
|
|
(6) |
Масса катушки определяется цепочкой формул
|
|
(7) |
где λ – плотность обмоточного провода. Следовательно, если заданы NI, ac, материал провода и способ намотки (k=const), то, с одной стороны,
· рассеиваемая мощность обратно пропорциональна площади обмотки и больше ни от чего не зависит,
· напряжение питания пропорционально количеству витков и обратно пропорционально площади обмотки.
С другой стороны, масса пропорциональна площади обмотки.
3.1. Несостоятельность варианта приподнятого центра масс
Покажем, что вариант с приподнятым центром масс на практике неосуществим. Пусть обмоточным проводом служит медь с ρ=1.78·10-8 Ом·м и сечение обмотки – круг диаметром D=5 см. Коэффициент k в лучшем случае равен 1. Тогда, согласно (6), потребляемая мощность составит
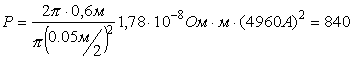 Вт.
Вт.
Этой мощности хватает, чтобы вскипятить литр воды за 5 мин.
То есть без специальной системы охлаждения установка просто сгорит. Уже при
таком диаметре обмотки масса одной катушки будет около
3.2. Расчет электрических и энергетических параметров катушек в случае опущенного центра масс
Выполним расчет в случае медного
обмоточного провода ПЭТВ-2 с диаметром медной жилы
При выборе числа витков следует
учитывать технологические возможности намотки катушек большого диаметра.
Большинство существующих намоточных станков позволяет создавать катушки с
диаметром до
Для того, чтобы обеспечить NIsub ампер×витков, необходим ток I=NIsub/N=216/150=1.4 ампера. Напряжение питания катушек U=IR=33 В. Выделяемая мощность P=UI=47 Вт. Определим массу провода без учета изоляции, используя формулу (7),
![]() .
.
Определим индуктивность катушки. В радиотехнической литературе (например, [5]) приведены эмпирические формулы для расчета индуктивностей катушек различных геометрических конфигураций. В случае, если катушка представляет собой кольцо, ее индуктивность L можно сравнительно просто найти численными методами. Пусть ток в катушке равен I. По определению индуктивности, Ф=LI, где Ф - создаваемый этим током магнитный поток через катушку. С другой стороны, магнитный поток через поверхность есть интеграл по этой поверхности от индукции магнитного поля. В качестве поверхности можно взять круг, границей которого является само кольцо. Индукция поля определяется согласно закону Био-Савара-Лапласа. Задавшись определенной величиной тока I и вычислив соответствующий ему поток Ф, можно определить индуктивность кольца. Применяя этот метод, получаем, что индуктивность катушки составляет 7·10-4 Гн.
Для сравнения вычислим параметры катушек, создающих требуемое магнитное поле, при различных диаметрах ac. Считаем, что катушки намотаны тем же проводом и содержат то же число витков. Диаметры катушек возьмем равными внутренним диаметрам обручей, выпускаемых промышленностью, так как именно обручи рассматривались как возможные каркасы для намотки катушек. Данные, полученные по формулам (1), (2), (7), сведены в таблице 1. В первой колонке указан диаметр 2·ас катушки. Во второй - диаметр 2r сферы с магнитным полем требуемой степени однородности. Далее указаны сопротивление R катушки, число ампер-витков NI, ток через катушку I, напряжение U, рассеиваемая мощность P и масса M катушки. Здесь, как и прежде, I=NI/150, U=IR, P=UI. Из таблицы видно, что при увеличении диаметра катушки резко растет рассеиваемая мощность. Это и так можно понять: поскольку I~ac и R~ac, то P=I2R~ac3. Так как создание управляемого источника питания большой мощности может оказаться сложной задачей, то диаметр катушки надо выбирать как можно меньше.
Таблица 1. Параметры катушек различных диаметров
|
2·ас, мм |
2·r, мм |
R, Ом |
NI, А |
I, А |
U, В |
P, Вт |
M, кг |
|
540 |
81 |
10.3 |
97.3 |
0.65 |
6.6 |
4.3 |
1 |
|
650 |
98 |
12.3 |
117 |
0.78 |
9.6 |
7.5 |
1.2 |
|
750 |
113 |
14.2 |
135 |
0.90 |
13 |
12 |
1.4 |
|
900 |
135 |
17.1 |
162 |
1.1 |
18 |
20 |
1.7 |
|
1200 |
180 |
22.8 |
216 |
1.4 |
33 |
47 |
2.2 |
3.3. Требования к источнику питания
Напомним, что предлагаемая геометрическая конфигурация катушек состоит из трех пар катушек со взаимно перпендикулярными осями. Чтобы изменять направление и модуль напряженности поля, в случае идеальных катушек достаточно управлять каждой парой катушек в отдельности. Это приводит к блок-схеме управления катушками, показанной на рис.5. Ток в каждой из трех пар катушек определяется блоком управления (БУ). Каждая пара катушек с блоком управления образуют независимый канал. Все три канала подключены к одному и тому же источнику питания (ИП).
Стоит отметить, что токи в катушках даже в пределах одного канала должны быть разными, в силу того, что катушки никогда не будут идеальны и абсолютно идентичны. Это не дает возможности включать катушки последовательно или параллельно. Все шесть катушек должны управляться независимо друг от друга. Можно лишь заранее сказать, что токи в катушках в пределах одной пары близки по величине, а в идеальном случае равны.
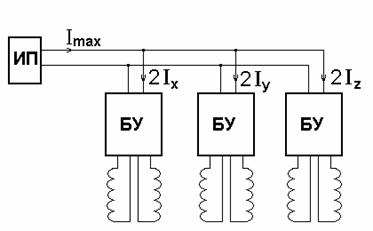
Рис.5.
Блок-схема управления катушками
Рассмотрим идеальный случай, когда все катушки одинаковы. Оценим суммарный ток Imax, потребляемый всеми шестью катушками, с учетом того, что максимальное значение суммарного поля не превышает Hsub, а направление поля может быть любым. Пусть проекции вектора напряженности магнитного поля на взаимно перпендикулярные оси пар катушек задаются следующими выражениями:
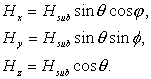
Так как все катушки имеют одинаковую конфигурацию, то ток в каждой из пар катушек пропорционален соответствующей проекции вектора H, причем коэффициент пропорциональности η для всех катушек один и тот же. Пусть Ix – ток в каждой катушке из пары, создающей компоненту Hx поля. Аналогично определим Iy и Iz, при этом Ix=ηHx, Iy= ηHy, Iz= ηHz. Задача о нахождении максимума суммарного потребляемого тока сводится к нахождению максимума суммы 2·Ix+2·Iy+2·Iz по всем возможным углам θ и φ:
![]()
![]()
Пусть при токе I, текущем через одну пару колец, и нулевом токе через две другие пары колец, напряженность поля равна Hsub. Этот ток задается выражением I=ηHsub. Подставляя отсюда коэффициент η в выражение для Imax, находим, что
![]()
В нашем случае I=1.4 А, Imax=4.8 А. Для удобства сведем вместе полученные данные:
· Максимальный ток на одну катушку – 1.4 А.
· Максимальное требуемое напряжение на одну катушку - 50 В
· Суммарный максимальный ток всех катушек – 4.8 А.
4. Конструкция имитатора магнитного поля
Главным фактором при проектировании конструкции имитатора поля является его простота и возможность быстрой модификации конструкции в будущем. Приведем описание спроектированной конструкции и соответствующие схематические рисунки.
На материалы, используемые в предлагаемой конструкции, наложены следующие условия:
· они должны быть немагнитными, чтобы не искажать поле;
·
прочными, чтобы выдержать катушки массой до
· простыми в обработке;
· дешевыми и доступными;
· долговечными.
Этим требованиям лучше всего удовлетворяют алюминий, фанера и пластмассы. Именно они использовались при создании стенда.
Каждая из
шести катушек намотана на алюминиевом каркасе. Каркасом служит обруч (тор)
внутренним диаметром
Имея только одну точку опоры, катушки под действием собственного веса заметно деформируются. Для увеличения жесткости вертикальные катушки крепятся при помощи хомутов в П-образной обойме каждая, сделанной из проката алюминия профиля «уголок». Обойма крепится к массивному фанерному основанию при помощи уголков. Такая конструкция является статически неопределенной (см. [6]), что увеличивает ее жесткость. Использование хомутов позволяет легко извлечь катушку из обоймы в случае необходимости.
Две пары
параллельных обойм с катушками устанавливаются перпендикулярно друг другу (см.
рис.7 и рис.8). Важно отметить, что отношение радиуса катушки к расстоянию
между катушками, работающими в паре, не может быть одинаковым для всех трех пар
катушек, в частности, идеальным (dc/ac=1.116). Иначе бы
катушки пространственно пересекались. За основу принято отношение dc/ac=1,
но оно меняется в пределах удвоенного диаметра сечения обруча при переходе от
одной пары к другой. Это изменение составляет порядка
Для крепления горизонтальных катушек в раме устанавливаются восемь несущих металлических балок, сделанных из алюминия того же профиля, что и обоймы. Катушки на них фиксируются при помощи хомутов.
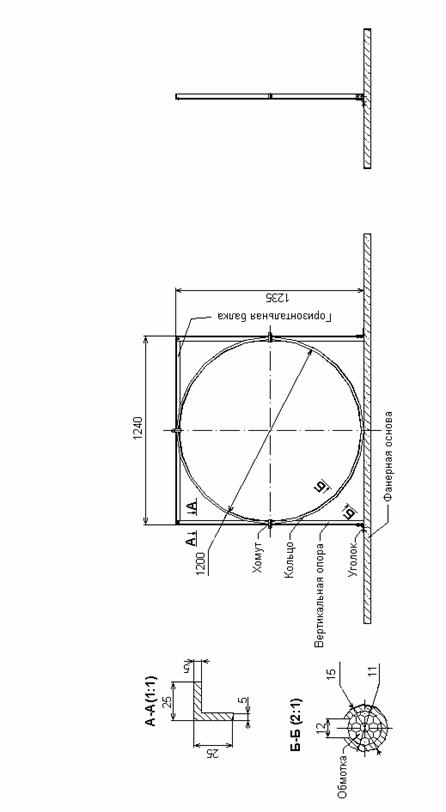
Рис.6. Обойма с катушкой
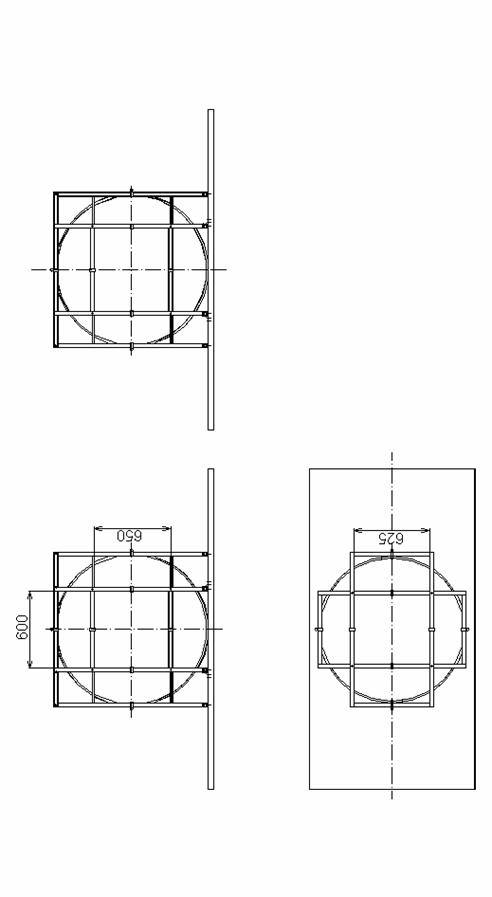
Рис.7. Рама (габариты и общий вид)
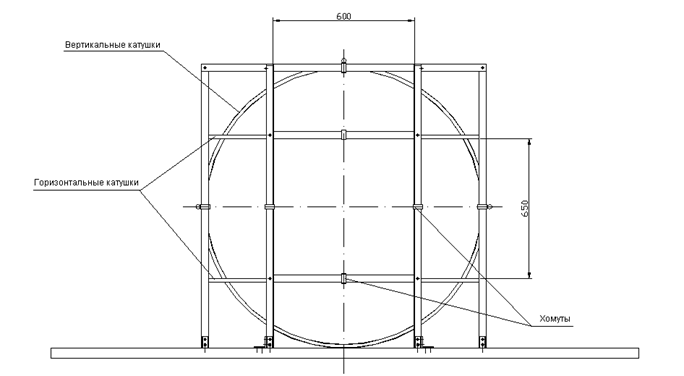
Рис.8. Рама (вид спереди)
5. Экспериментальный образец имитатора магнитного поля
Согласно предложенной выше схеме был создан экспериментальный образец имитатора поля (рис.9). По чисто технологическим причинам расчетные параметры отличаются от параметров, которыми обладает образец. Во-первых, сложно выдержать плоскости катушек, работающих в паре, параллельными, а плоскости остальных катушек перпендикулярными им. Это существенно влияет на параметры магнитного поля. Во-вторых, следует учесть принципиальную невозможность выдержать равными расстояния между центрами катушек, работающих в парах. При равных расстояниях катушки должны будут пространственно пересекаться. В-третьих, из-за того, что внутренние поверхности обручей, куда проводилась укладка провода, отличались друг от друга, все катушки получились разными по количеству витков. Оно изменяется от 128 до 150. Это следует учесть при управлении током в катушках.
Расчетная индуктивность катушек в случае 128 витков составляет 5.8·10-4 Гн, в случае 150 витков – 6.9·10-4 Гн (погрешность 5%, вызвана тем, что обмотка имеет конечное сечение).
Измеренные сопротивления катушек лежат в интервале от 22 до 28 Ом, причем для каждой из катушек погрешность измерения сопротивления составляет ±1 Ом. Такая погрешность может быть вызвана изменением внутренних механических напряжений в обмотках. Эти напряжения меняются, если деформировать катушку, например, наклонить. От таких деформаций катушки предохраняют обоймы, в которых они находятся.
Напомним, что все шесть катушек должны управляться независимо друг от друга. Кроме того, это дает возможность сделать поправку на различие в числе витков, различие в сопротивлении подводящих проводов и другие неблагоприятные факторы. Также для учета этих факторов примем коэффициент запаса по напряжению равным 1.5. Тогда максимально требуемое напряжение составит Umax=50 В. С учетом того, что минимальное число витков равно 128, максимальный ток через каждую из катушек равен 1,7 А. Чтобы поддерживать поле в пределах его максимального значения, необходим суммарный ток на все катушки 6А. Мощность, рассеиваемая одной катушкой при максимальном токе – 85 Вт.
Следует упомянуть про механические характеристики фанерной основы. Любая ее деформация, даже самая незначительная, сказывается на геометрии всех катушек. Для ее предотвращения требуются ребра жесткости.

Рис.9. Экспериментальный образец
5.1. Требования эксплуатации
При работе следует делать поправку на геомагнитное поле, которое не является постоянным. Оно существенно искажается железобетонными конструкциями (которые намагничиваются в нем) и другими крупными телами. В пределах одной комнаты магнитный фон может меняться в несколько раз.
Для создания поля нужной величины необходимо пользоваться заранее построенными калибровочными кривыми (зависимость напряженности поля от тока через катушки). Не рекомендуется пользоваться расчетными значениями, ибо далеко не все отклонения от идеальной геометрии могут быть в них учтены. Калибровка выполняется по отдельности для каждой пары катушек. Необходимо учитывать помимо напряженности поля еще и его направление. После калибровки и учета всех поправок не рекомендуется передвигать экспериментальный образец.
5.2. Расчет управляющих токов
Рассмотрим геометрическую конфигурацию колец, отличающуюся от идеальной только отношением dc/ac. Примем это отношение равным отношению, заложенному в конструкции имитатора поля, то есть примем dc/ac=1. Напомним, что для оптимальной конфигурации колец dc/ac=1.116 [2]. Определим, какие токи надо поддерживать в катушках, чтобы создать поле заданной величины. Напряженность H кругового витка с током на оси задается формулой
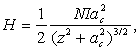
где NI - число ампер-витков, ac - радиус витка, z - расстояние от центра витка до интересуемой точки. В нашем случае z=0.5ac. Тогда
|
|
(8) |
Также понятно, что если у двух разных катушек одинаковое число ампер-витков, то они создают абсолютно одинаковые поля в пространстве. Следовательно, для создания поля в центре между двумя разными катушками надо чтобы каждая из них создавала в центре половину от требуемого поля. В этом случае поле во всем остальном пространстве не будет отличаться от поля, созданного двумя идентичными катушками. Из (8) получаем формулу для определения тока катушки через требуемое поле и число витков:
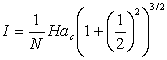 .
.
В таблице 2 приведены значения управляющих токов и соответствующие им значения расчетного магнитного поля посередине между катушками на их общей оси при ac=0.6 м. Значения при других полях находятся линейной интерполяцией. Первая строка - требуемая напряженность поля, создаваемая парой катушек, выраженная в А/м. Первый столбец - число витков рассматриваемой катушки из этой пары. На пересечении строки и столбца - необходимый ток для этой катушки, выраженный в амперах.
Таблица 2. Зависимость напряженности поля от тока
|
|
10 |
20 |
30 |
40 |
50 |
60 |
100 |
150 |
200 |
250 |
|
128 |
0.066 |
0.131 |
0.197 |
0.262 |
0.328 |
0.393 |
0.655 |
0.983 |
1.31 |
1.638 |
|
144 |
0.058 |
0.116 |
0.175 |
0.233 |
0.291 |
0.349 |
0.582 |
0.873 |
1.165 |
1.456 |
|
150 |
0.056 |
0.112 |
0.168 |
0.224 |
0.28 |
0.335 |
0.559 |
0.839 |
1.118 |
1.398 |
Напомним,
что расстояние между катушками в парах не может быть одинаковым. Разброс
составляет порядка
6. Уравнения движения макета спутника
6.1. Анализ сил и моментов, действующих на макет
На макет спутника действуют следующие основные силы и моменты сил:
· сопротивление движению со стороны воздуха;
· реакция шарнира (опоры), которая состоит из момента реакции и силы реакции, приложенной к точке опоры;
· сила тяжести;
· механический момент, действующий со стороны магнитного поля на исполняющие катушки макета.
Сопротивление воздуха не поддается простому описанию, тем более что оно зависит от аэродинамических характеристик самого макета. Из-за малых линейных скоростей точек макета пренебрегаем им.
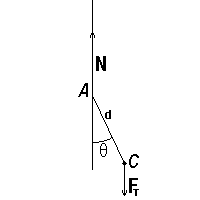
Рассмотрим два варианта: когда макет спутника опирается на острие иглы, и когда макет подвешен на длинной нити. В первом случае сравним момент реакции шарнира с механическим моментом, действующим со стороны магнитного поля. Для этого оценим минимальный диаметр d острия иглы или струны подвеса.
Механическое напряжение не должно превышать напряжение σт текучести материала опоры или подвеса с коэффициентом запаса n, то есть
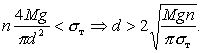
Здесь M – опять масса макета. Примем M=1 кг и
коэффициент запаса 1.5. В случае стали (σт= 200 МПа) диаметр
составит d>
Момент реакции шарнира в случае его реализации как опоры на острие иглы определяется силой трения. Оценим его. Пусть R - радиус острия иглы, k - коэффициент трения, равный 0.1, p=Mg/S - давление на острие, S=πR2 - площадь острия. Тогда максимальный механический момент, действующий со стороны острия на макет, составляет
![]()
В случае стали Lf>1.1·10-4 Н·м, для титана Lf>5.6·10-5 Н·м. Максимальный момент, действующий со стороны магнитного поля, при m=1 A*м2, H=250 А/м составляет
![]()
Таким образом, в случае опоры на острие иглы нельзя пренебрегать моментом сил сопротивления. Учет этих сил - весьма сложная задача. Выход может быть найден, если сухое трение заменить на жидкое, поддающееся сравнительно простому математическому описанию.
Определим момент реакции шарнира в случае подвеса как упругий момент закрученной нити. Погонный угол закрутки φ=2πk/L, где k - число оборотов нити, L - ее длина. Механический момент составит (см. [6])
|
|
(9) |
где G=8·1010 Па - модуль Юнга второго рода для стали, Ip=πD4/32 - полярный момент инерции круглого стрежня. При L=3 м и числе оборотов k=20 крутящий момент будет равен 2.8·10-4 Н·м, что сравнимо с максимально возможным управляющим моментом. Следовательно, необходимо в конструкции подвеса предусмотреть механизм, защищающий струну от перекручивания. Этим механизмом может быть вертлюг, но стоит отметить, что при использовании вертлюга необходимо, как и в первом случае, учитывать силы трения, возникающие внутри него. Лучше всего, если в этом механизме вместо сухого трения опять же присутствует жидкое трение.
Отметим, что если не предусмотреть такого механизма и потребовать, чтобы при работе со стендом число оборотов k нити было небольшим, то сильно ограничиваются возможности стенда. Например, закрутка макета спутника вокруг какой-либо оси будет практически неосуществима.
Примем модель тела на подвесе (струне). Причем упругий момент, препятствующий перекручиванию нити подвеса, будем считать пренебрежимо малым. Уравнения движения тела с опорой в одной неподвижной точке описаны, например, в [7] и [8].
6.2. Вывод уравнений движения тела на струне
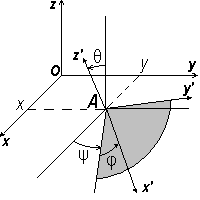
Сделаем предположение, что струна бесконечно длинная. Как следствие этого считаем, что точка подвеса всегда находится в одной и той же горизонтальной плоскости. Таким образом, положение точки подвеса A можно задать двумя переменными x и y (рис.10) в неподвижной системе координат Oxyz. Еще три переменные (углы Эйлера φ, ψ и θ) задают ориентацию макета. Свяжем с макетом систему координат Ax`y`z` как показано на рисунке. Пусть центр масс макета лежит на оси z` и смещен вниз на расстояние d от точки подвеса. Его координаты в системе координат Ax`y`z` - (0,0,-d).
Из сделанного предположения также вытекает, что упругий момент, возникающий при закручивании нити, равен нулю. Действительно, если принять длину подвеса равной бесконечности, то погонный угол закрутки будет равен нулю. И, согласно (9), крутящий момент тоже будет равен нулю.
К центру масс C тела приложена сила тяжести Fт (рис.11). Из сделанного предположения следует также, что струна всегда вертикальна. Следовательно, сила реакции N подвеса направлена всегда вверх. Так как точка A подвеса всегда лежит в одной и той же горизонтальной плоскости, то сила реакции N не совершает работы.
Обозначим массу тела опять M, моменты инерции вокруг главных осей - A, B и C. Пусть, для простоты, эти оси направлены параллельно осям координат x`, y` и z`.
|
Рис.10. Системы координат |
Рис.11. Силы, действующие на тело |
Составим уравнения Лагранжа второго рода. Кинетическая энергия тела складывается из энергии поступательного движения центра масс и энергии вращения вокруг центра масс. Найдем скорость движения центра масс. Она складывается из переносной скорости движения точки подвеса и относительной скорости движения центра масс вокруг точки подвеса. В проекциях на оси x, y, z
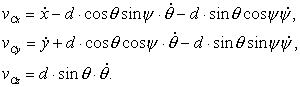
Кинетическая энергия, согласно теореме Кенига, запишется в виде
![]()
где p, q, r - проекции угловой скорости вращения макета на его главные оси инерции, вычисляемые по формулам
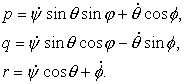
Потенциальная энергия складывается из потенциальной энергии макета в поле силы тяжести и потенциальной энергии закрученной струны. Последняя, в силу конструктивных особенностей, пренебрежимо мала по сравнению с первой. Таким образом, можно записать
![]() .
.
Лагранжиан системы L=T-П. Уравнения Лагранжа второго рода запишутся в виде
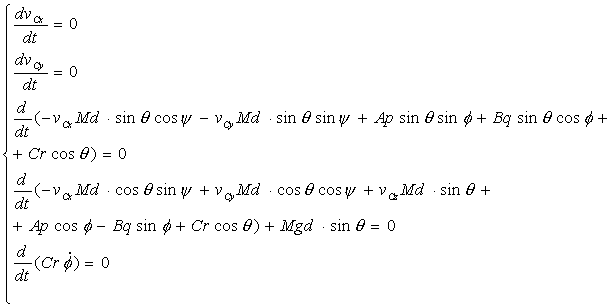 Очевидно, что vCx и vCy
являются первыми интегралами системы, они выражают закон сохранения импульса.
Преобразуем систему к виду
Очевидно, что vCx и vCy
являются первыми интегралами системы, они выражают закон сохранения импульса.
Преобразуем систему к виду
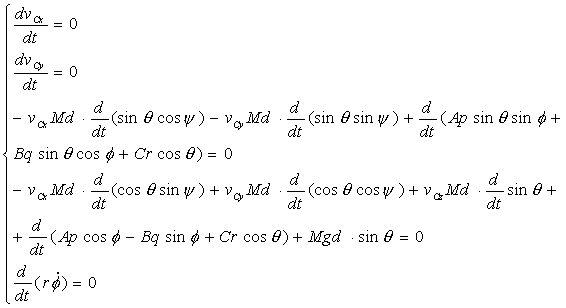
Полученную систему уравнений можно привести к нормальному виду. Для этого можно сделать следующую замену переменных:
![]()
![]()
![]()
![]()
![]()
При этом получится система десяти дифференциальных уравнений с десятью неизвестными.
В случае активной системы управления в правую часть уравнений Лагранжа добавляются механические моменты взаимодействия магнитного поля с катушками. В случае, если внешнее магнитное поле постоянно и равно B0 и на макете спутника находится постоянный магнит с моментом m, достаточно в выражение потенциальной энергии добавить энергию взаимодействия магнита с полем
|
|
(10) |
В качестве примера проинтегрируем численными методами систему уравнений Лагранжа с потенциальной энергией (10). Пусть магнитное поле постоянно и направлено вдоль оси, совпадающей с z’ при θ=θ0, ψ=ψ0. Пусть магнитный момент постоянного магнита направлен вдоль оси z`. Тогда потенциальная энергия взаимодействия магнита с полем запишется в виде
![]()
Зададимся параметрами макета спутника, начальными условиями и параметрами магнитного поля
M=1 кг, А=0.15 кг∙м2, B=0.2 кг∙м2, С=0.2 кг∙м2, d=1 мм, m=1 А∙м2
![]()
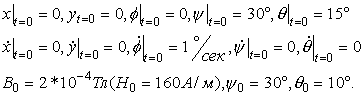
Графики изменения координат при движении системы, соответствующем этим данным, представлены на рис.12 - рис.16.
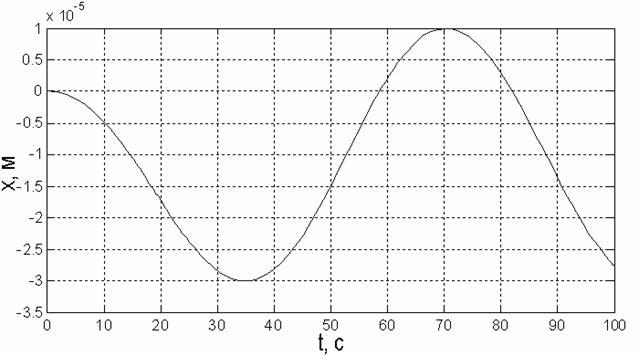
Рис.12. Зависимость координаты x от времени
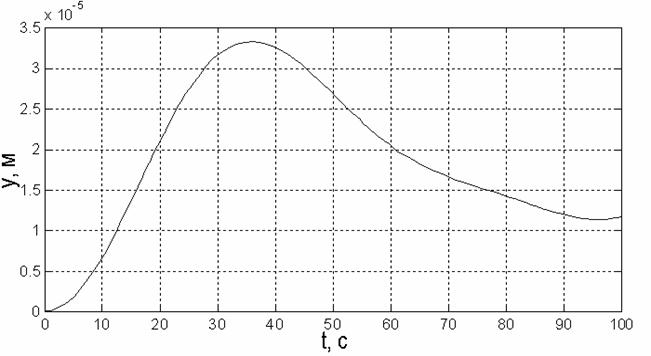
Рис.13. Зависимость координаты y от времени
Рис.14. Зависимость координаты φ от времени
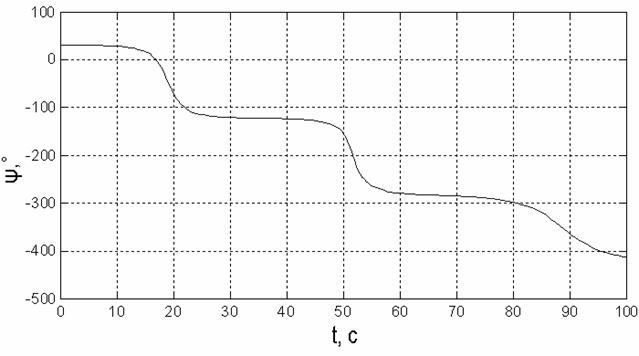
Рис.15. Зависимость координаты ψ от времени
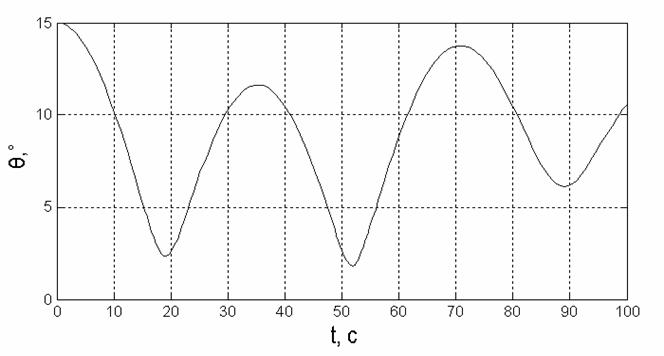
Рис.16. Зависимость координаты θ от времени
Литература
1.
А.М.Яновский. Земной магнетизм. Л.: Издательство ЛГУ,
2. M.Pastena and M.Grassi, Optimum
Design of a three-axis Magnetic Field Simulator, IEEE Transaction on Aerospace
and Electronic Systems, Vol.38, No.2, April 2002, pp.488-501.
3. E. di Sotto, Un simulatore magnetico
per l’analisi del dipolo di bordo di un veicolo spaziale, Quaderni di
Astrodinamica, n. 4, 2005.
4.
Д.В.Сивухин. Общий курс физики. Учебное пособие: для
вузов. В 5 т. Т.III. Электричество. 4-е изд.,
стереот. М.: Физматлит; Издательство МФТИ,
5.
П.Л.Калантаров, Л.А.Цейтлин. Расчет индуктивностей:
Справочная книга. 3-е изд., переработанное и дополненное. Л.: Энергоатомиздат,
Ленинградское отделение,
6.
В.И.Феодосьев. Сопротивление материалов. 9-е изд.,
переработанное. М.: Наука,
7.
К.Магнус. Гироскоп. Теория и применение. Перевод с
немецкого Г.Д.Блюмина и др. Под редакцией Г. Д. Блюмина. М.: Мир,
8.
Ю.Ф.Голубев. Основы теоретической механики: Учебник.
2-е изд., переработанное и дополненное. М.: Издательство МГУ,
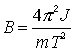
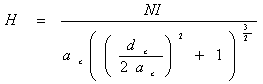 ,
,