Аннотация
Предложен и обоснован метод конечных суперэлементов (МКСЭ) для решения бигармонического
уравнения в ограниченной области. Метод основан на разбиении области на суперэлементы
с последующим решением в них ряда вспомогательных задач, каждая из которых представляет
собой краевую задачу для бигармонического уравнения с граничными условиями, являющимися
базисом для интерполяции искомого решения на границах суперэлементов. Решение исходной
задачи далее ищется в виде разложения по построенной системе функций. Показано, что искомое
решение можно восстановить, используя найденные выше функции и следы. Получены оценки
погрешности для одного варианта МКСЭ.
Abstract
In this work finite superelements method (FSEM) for solution of biharmonical equation
in bounded domains is proposed and developed. The method is based on splitting of domain
into subdomains with the solution of a number of intermediary problems, every of which
is boundary value problem for biharmonical equation with boundary condition, being basis
for interpolation of searching solution on a superlements boundaries. The initial problem
solution is found as an expansion on the constructed function system. It is shown that
solution of general problem can be recovered using functions and traces found above.
Error estimates for one case of FSEM are obtained.
Содержание
Введение 3
1. Основные обозначения и положения. 5
2. Классическая слабая постановка. 7
3. Специальная слабая постановка. 8
4. Эквивалентность постановок. 10
5. Построение вариационного уравнения . 11
5.1. Общие построения. 11
5.2. Вариационное уравнение для бигармонического
уравнения 15
6. Построение аппроксимаций МКСЭ. 17
7. Оценки ошибок для метода Бубнова-Галёркина. 18
8. Примеры. 22
Заключение 25
Литература 25
Введение.
Существует
широкий класс задач, решение которых содержит резкие неоднородности,
проявляющиеся на мелких по отношению к размеру области пространственных
масштабах. Численное решение таких задач требует специальных сеток для
разрешения особенностей. Для этого необходимо использовать либо адаптивные к
решению сетки, сгущающиеся в окрестности особенностей, либо достаточно мелкие
сетки с равномерным шагом 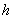 и огромным количеством
точек. Первый вариант требует применения специальных алгоритмов, второй –
соответствующей памяти ЭВМ. В то же время проявления особенностей зачастую
являются локальными, сосредоточенными в мелкомасштабных подобластях.
Подтверждением тому является характерный вид функций Грина [1] и типичных
решений многих задач математической физики [2], а также физические эффекты
такие, как принцип Сен-Венана в теории упругости [3] и другие. Наличие областей
сосредоточения особенностей позволяет ввести сетку с размером и огромным количеством
точек. Первый вариант требует применения специальных алгоритмов, второй –
соответствующей памяти ЭВМ. В то же время проявления особенностей зачастую
являются локальными, сосредоточенными в мелкомасштабных подобластях.
Подтверждением тому является характерный вид функций Грина [1] и типичных
решений многих задач математической физики [2], а также физические эффекты
такие, как принцип Сен-Венана в теории упругости [3] и другие. Наличие областей
сосредоточения особенностей позволяет ввести сетку с размером 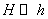 , узлы и соединяющие линии которой проходят по участкам
относительной гладкости решения. При этом сетка размером , узлы и соединяющие линии которой проходят по участкам
относительной гладкости решения. При этом сетка размером 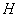 заведомо не позволяет
разрешить особенности при использовании обычных численных методов, но зато
число её узлов достаточно мало. заведомо не позволяет
разрешить особенности при использовании обычных численных методов, но зато
число её узлов достаточно мало.
Для
решения подобных задач Л.Г. Страховской и Р.П. Федоренко [4–7] предложен метод
конечных суперэлементов (МКСЭ). Метод появился более 25 лет назад и
использовался при решении ряда сложных задач диффузии, теории упругости,
кинетики ядерных реакторов и других.
Метод
конечных элементов (МКЭ) основан на представлении решения задачи в виде
разложения по системе базисных функций, имеющих конечный носитель. При этом
мера таких носителей предполагается малой (сетка 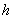 ) и стремящейся к нулю. Базисные функции в МКЭ берутся
относительно простой структуры, как правило, полиномиальной. ) и стремящейся к нулю. Базисные функции в МКЭ берутся
относительно простой структуры, как правило, полиномиальной.
МКСЭ
также основан на представлении решения задачи в виде разложения по системе
базисных функций, имеющих конечный носитель. Однако в МКСЭ мера таких носителей
(сетка 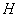 ) не предполагается стремящейся к нулю и столь велика, что
она заведомо не позволяет (при использовании МКЭ) передать особенности решения.
Другое отличие касается построения базисных функций. В МКСЭ базисные функции
строятся для данной рассматриваемой задачи специальным образом так, чтобы в них
самих содержалась значительная информация о решении задачи. Именно специальный,
под задачу, выбор базисных функций и позволяет с помощью очень грубого
разбиения исходной области получить хорошее численное решение. ) не предполагается стремящейся к нулю и столь велика, что
она заведомо не позволяет (при использовании МКЭ) передать особенности решения.
Другое отличие касается построения базисных функций. В МКСЭ базисные функции
строятся для данной рассматриваемой задачи специальным образом так, чтобы в них
самих содержалась значительная информация о решении задачи. Именно специальный,
под задачу, выбор базисных функций и позволяет с помощью очень грубого
разбиения исходной области получить хорошее численное решение.
Обоснование
варианта метода было предложено в работах [8,9].
Другой
подход к исследованию МКСЭ с использованием операторов Пуанкаре-Стеклова и
вариационных уравнений для следов функций на границах СЭ приведён в работах
[10–12] для ряда таких задач, как задача о скважине для уравнения Лапласа,
задача теории упругости, задача о скоростном скин-слое. В этих работах
рассматривались дифференциальные задачи 2-го порядка по пространству.
В
настоящей работе развит и обоснован вариант МКСЭ для решения бигармонического уравнения
с одним вариантом граничных условий. Построена вариационная постановка задачи
для следов. Доказаны существование и единственность решения, сходимость
приближённого решения к точному. Рассмотрен ряд численных примеров.
Работа
выполнена при частичной финансовой поддержке Российского фонда фундаментальных
исследований (проект РФФИ № 03 - 01 - 00461).
1.
Основные обозначения и положения.
Пусть
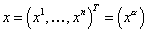 – координаты точки из области – координаты точки из области 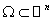 , , 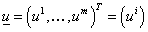 – вектор из – вектор из 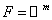 , где , где 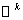 – – 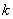 -мерное евклидово пространство. Для всех тензорных величин во
введённых в рассмотрение пространствах используется суммирование по дважды
повторяющимся индексам. В случае, когда суммирование не требуется, будем
ставить под индексом дугу, например -мерное евклидово пространство. Для всех тензорных величин во
введённых в рассмотрение пространствах используется суммирование по дважды
повторяющимся индексам. В случае, когда суммирование не требуется, будем
ставить под индексом дугу, например 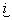 . Для производной некоторой величины . Для производной некоторой величины 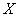 по координате по координате 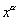 будем использовать
обозначение будем использовать
обозначение 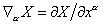 . .
Пусть
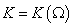 – некоторый класс
функций – некоторый класс
функций 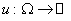 над некоторым
множеством над некоторым
множеством 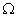 . Будем говорить, что . Будем говорить, что 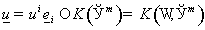 , , 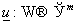 , если , если 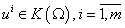 . То есть можно считать, что . То есть можно считать, что 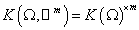 (декартова степень)
или (декартова степень)
или  . Здесь . Здесь 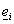 – вектора стандартного
базиса в – вектора стандартного
базиса в 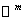 . .
Рассмотрим
следующую краевую задачу:
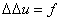 в в 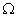 , ,
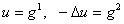 на на 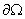 . (1) . (1)
Эта
задача эквивалентна (в случае классического решения (1)) системе уравнений
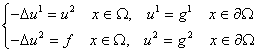 , ,
которую мы
запишем в векторном виде
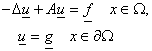 , (2) , (2)
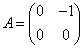 . .
Здесь и далее 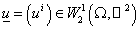 , , 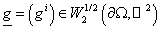 , , 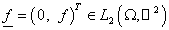 ; через ; через 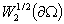 обозначено
пространство следов функций из обозначено
пространство следов функций из 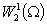 на на 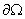 [13–15]. [13–15].
Введём
скалярные произведения в некоторых представленных выше пространствах:
в 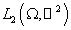 : : 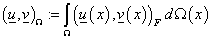 (далее зависимость от (далее зависимость от 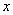 опускается), опускается),
в 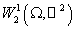 : : 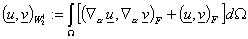 , ,
в 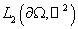 : : 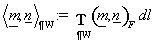 . .
Также
рассмотрим в 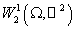 подпространство подпространство 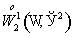 , являющееся замыканием , являющееся замыканием 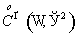 в в 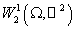 , с нормой , с нормой
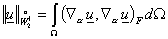 . .
Здесь 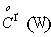 – пространство бесконечно дифференцируемых функций,
обращающихся в нуль на границе области – пространство бесконечно дифференцируемых функций,
обращающихся в нуль на границе области 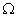 . .
В
пространстве 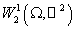 введём билинейные
формы введём билинейные
формы
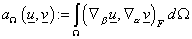 , ,
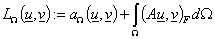 . .
Система
(2) строго эллиптична в области 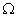 [14, с. 88]. В общем
случае это означает, что найдутся такие положительные константы [14, с. 88]. В общем
случае это означает, что найдутся такие положительные константы 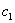 и и 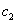 , что выполняется неравенство , что выполняется неравенство
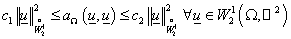 . .
Оператор
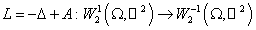 является формально
порождённым билинейной формой является формально
порождённым билинейной формой 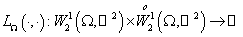 , то есть , то есть
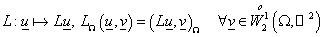 . (3) . (3)
Введём
область определения оператора 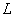
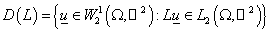 . .
Предполагаем,
что выполняется условие единственности решения задач (1) и (2).
Последнее означает, что задача с нулевыми правой частью и граничными условиями
имеет только тривиальное решение.
2.
Классическая слабая постановка.
Поскольку
уравнение (2) выполняется тождественно (если 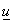 – классическое
решение), то можно обе части уравнения скалярно умножить на некоторую функцию – классическое
решение), то можно обе части уравнения скалярно умножить на некоторую функцию 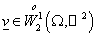 : :
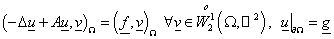 . (4) . (4)
Применим
формально к левой части формулы (4) процедуру интегрирования по частям:
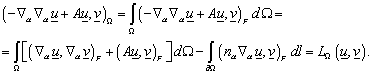
Слагаемое 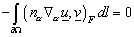 , так как , так как 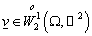 . .
Получаем
в новой записи:
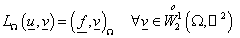 . (5) . (5)
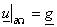 , (6) , (6)
где 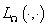 определена выше. определена выше.
Если
область имеет липшицеву границу, то верна
Теорема 1. Существует единственный оператор 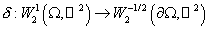 такой, что выполняется
равенство такой, что выполняется
равенство 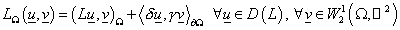 . .
Здесь 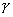 – оператор взятия следа – оператор взятия следа 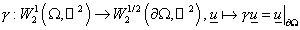 . .
Доказательство
общего случая приведено в [16, с. 188]. Равенство, приведённое в условии
теоремы, называют абстрактной формулой Грина.
В нашем случае для областей с кусочно-гладкой границей и функции 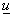 из из 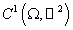 верна следующая формула: верна следующая формула:
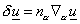 , где , где 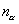 – компоненты внешней нормали. – компоненты внешней нормали.
3.
Специальная слабая постановка.
Предположим,
что область  можно представить в
виде объединения можно представить в
виде объединения 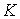 подобластей подобластей 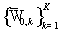 , , 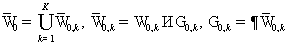 . .
Будем
считать, что области 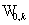 – многогранники,
образующие правильное разбиение области – многогранники,
образующие правильное разбиение области 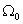 (т.е. любые два
многогранника либо не пересекаются, либо пересекаются по многограннику меньшей
размерности). Пусть (т.е. любые два
многогранника либо не пересекаются, либо пересекаются по многограннику меньшей
размерности). Пусть 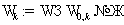 . Тогда . Тогда 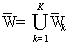 . .
Границу
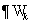 области области 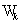 представим в виде представим в виде 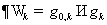 , где , где 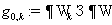 , , 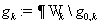 . Области . Области 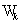 будем называть суперэлементами.
Т.к. все участвующие в разбиении области являются многогранниками, то на их
границе почти всюду существует внешняя нормаль. будем называть суперэлементами.
Т.к. все участвующие в разбиении области являются многогранниками, то на их
границе почти всюду существует внешняя нормаль.
Определим
пространства 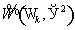 следующим образом: следующим образом:
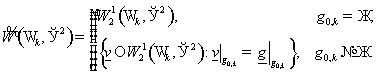
Пусть
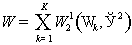 , , 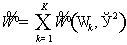 . .
Элемент
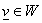 представляет собой
набор из представляет собой
набор из 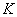 функций функций 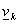 : :
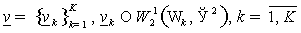 . .
Существует
каноническое вложение пространства 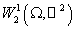 в пространство в пространство 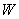 : :
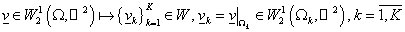 , ,
и пространства 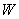 в пространство в пространство 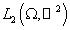 . .
Будем далее пользоваться обобщением
следующей леммы [10, с. 10]
Лемма 2. Функция 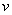 из из 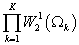 принадлежит пространству принадлежит пространству 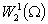 тогда и только тогда, когда тогда и только тогда, когда
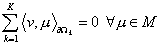 , ,
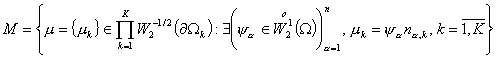 , ,
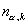 – компоненты внешней нормали к границе – компоненты внешней нормали к границе 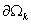 области области 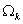 . .
Следствие 2.1. Функция 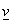 из из 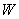 принадлежит пространству принадлежит пространству 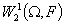 тогда и только тогда,
когда тогда и только тогда,
когда
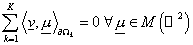 , ,
где 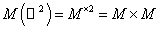 – декартова степень множества – декартова степень множества 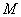 из условия леммы 2. из условия леммы 2.
Доказательство. В силу
определения принадлежности классу 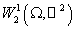 получаем, что получаем, что 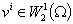 , где , где 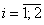 . Следовательно, в силу леммы 2 для произвольных функций . Следовательно, в силу леммы 2 для произвольных функций 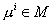 выполняются следующие
равенства (нет суммирования по индексу выполняются следующие
равенства (нет суммирования по индексу  ) )
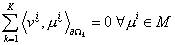 . .
В силу
произвольности выбора 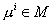 заключаем, что эти
равенства можно просуммировать по индексу заключаем, что эти
равенства можно просуммировать по индексу  , после чего получим эквивалентное равенство. Используя
определение скалярного произведения на границе, получаем требуемое в условии
леммы равенство с элементом , после чего получим эквивалентное равенство. Используя
определение скалярного произведения на границе, получаем требуемое в условии
леммы равенство с элементом 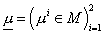 . Следствие доказано. . Следствие доказано.
В
дальнейшем нам понадобится следующая обобщённая постановка задачи (2):
определить 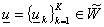 : (7) : (7)
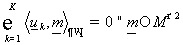 , (8) , (8)
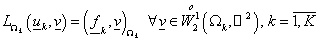 , (9) , (9)
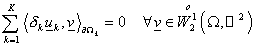 . (10) . (10)
Здесь
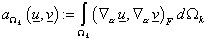 , (11) , (11)
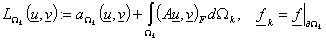 , (12) , (12)
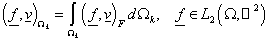 , (13) , (13)
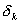 – введённый выше
оператор – введённый выше
оператор 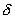 для области для области 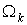 . .
4.
Эквивалентность постановок.
Лемма 3. Постановки (5)–(6) и (7)–(10) эквивалентны в том смысле,
что 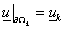 . .
Доказательство. Докажем
сначала, что если вектор-функция 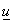 является решением
задачи (5)–(6), то она удовлетворяет соотношениям (7)–(10). Для этого
рассмотрим является решением
задачи (5)–(6), то она удовлетворяет соотношениям (7)–(10). Для этого
рассмотрим 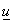 как элемент
пространства как элемент
пространства 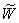 . Тогда условие (7) удовлетворяется по построению
пространства . Тогда условие (7) удовлетворяется по построению
пространства 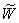 , условие (8) – в силу следствия 2.1. , условие (8) – в силу следствия 2.1.
Для
доказательства выполнения условия (9) рассмотрим произвольную функцию 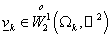 . Продолжив её нулём на . Продолжив её нулём на 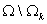 , получим функцию , получим функцию 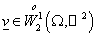 в силу следствия 2.1.
Подставив в силу следствия 2.1.
Подставив 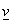 в (5), получим (9). в (5), получим (9).
Запишем
правую часть (5) в виде
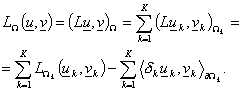
Отсюда, учитывая
свойство аддитивности интеграла Лебега, получим (10).
Докажем
обратное утверждение.
В
силу условий (7) и (8), следствия 2.1 и определения пространства 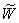 получаем, что получаем, что 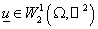 и и 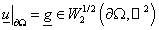 . .
Условие
(9) равносильно тому, что 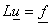 в в 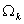 . Тогда для . Тогда для 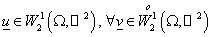 имеем имеем
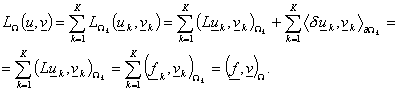
Лемма доказана.
5.
Построение вариационного уравнения.
5.1.
Общие построения.
Введём
оператор 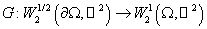 , сопоставляющий функции , сопоставляющий функции 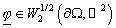 функцию функцию 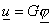 , являющуюся решением задачи , являющуюся решением задачи
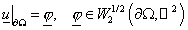 , (14) , (14)
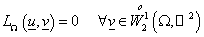 . (15) . (15)
Используя
абстрактную формулу Грина и тот факт, что в
силу (15) из эквивалентности постановок верно 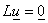 , получаем , получаем
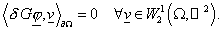 (16) (16)
Введём
оператор Пуанкаре-Стеклова [10]: 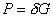 . Запишем (16) в виде . Запишем (16) в виде
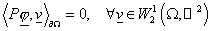 . (17) . (17)
Известно
[17], что операторы 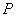 и и 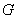 являются линейными и
непрерывными. являются линейными и
непрерывными.
Далее
удобно будет представлять операторы 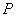 и и 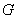 в матричном виде: в матричном виде: 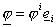 , , 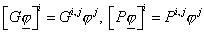 , где , где 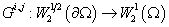 , , 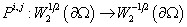 – линейные непрерывные
операторы. Ввёдённые операторы – ограничения операторов – линейные непрерывные
операторы. Ввёдённые операторы – ограничения операторов 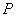 и и 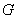 на подпространства,
порождённые функциями вида на подпространства,
порождённые функциями вида 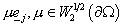 и умноженные скалярно
на и умноженные скалярно
на 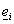 , то есть , то есть 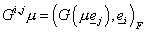 . По построению эти операторы являются непрерывными. Здесь . По построению эти операторы являются непрерывными. Здесь 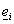 – вектора стандартного базиса в – вектора стандартного базиса в 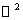 . .
Рассмотрим
построенную выше систему соотношений (7)-(10). Представим 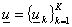 в виде в виде 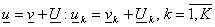 , где , где 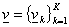 – такая функция, что – такая функция, что
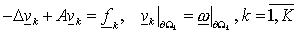 , (18) , (18)
где 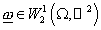 , , 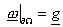 – произвольная функция
данного класса, удовлетворяющая на – произвольная функция
данного класса, удовлетворяющая на 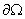 главным граничным
условиям. Предполагается, что каждая краевая задача из (18) имеет единственное
решение. главным граничным
условиям. Предполагается, что каждая краевая задача из (18) имеет единственное
решение.
Построенная
таким образом функция 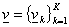 будет принадлежать
пространству будет принадлежать
пространству 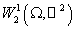 , удовлетворять на , удовлетворять на 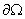 главным граничным
условиям и в каждой подобласти главным граничным
условиям и в каждой подобласти 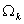 являться решением
исходного уравнения. Смысл представления функции являться решением
исходного уравнения. Смысл представления функции 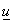 в таком виде – свести
задачу (5)–(6) к задаче с однородными граничными условиями на в таком виде – свести
задачу (5)–(6) к задаче с однородными граничными условиями на 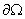 . .
Подставив
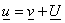 в соотношения (5)–(6),
получим уравнения для в соотношения (5)–(6),
получим уравнения для
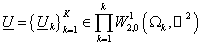 : :
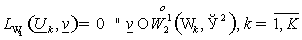 , (19) , (19)
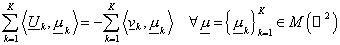 , (20) , (20)
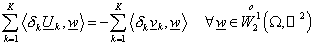 , (21) , (21)
где
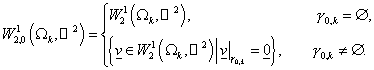
Используя
оператор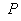 , перепишем соотношения (19), (21) в виде: , перепишем соотношения (19), (21) в виде:
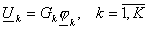 , (22) , (22)
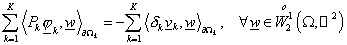 . (23) . (23)
Здесь
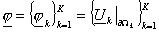 – набор следов искомой
функции – набор следов искомой
функции 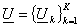 на на 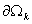 , ,  – операторы – операторы 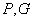 , соответствующие подобластям , соответствующие подобластям 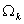 . .
Таким
образом, формально задача может решаться в два этапа:
1.
По соотношениям (23) определяем функцию 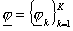 – след неизвестного решения на границах подобластей – след неизвестного решения на границах подобластей 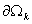 . .
2.
По известным функциям 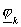 согласно (22)
восстанавливаем решения согласно (22)
восстанавливаем решения 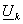 в подобластях в подобластях 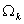 , решая в , решая в 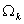 соответствующие
краевые задачи. соответствующие
краевые задачи.
Рассмотрим
гильбертово пространство 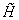 , определённое следующим образом: , определённое следующим образом:
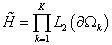 . .
Скалярное
произведение и норму в 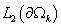 введём обычным
образом: введём обычным
образом:
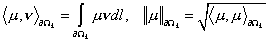 . .
В пространстве 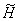 введём скалярное
произведение и норму прямого произведения: введём скалярное
произведение и норму прямого произведения: 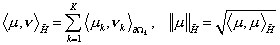 . .
Рассмотрим
вложенные в 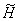 подпространства подпространства 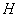 и и 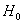 , определённые следующим образом: , определённые следующим образом:
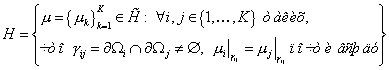 , ,
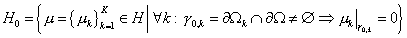 . .
Аналогично
введём пространство
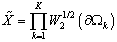 , , 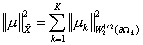 . .
В пространстве 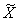 рассмотрим
подпространства рассмотрим
подпространства
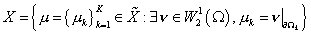 , ,
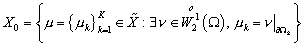 . .
В качестве
пространства, двойственного к 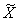 , будем рассматривать пространство , будем рассматривать пространство
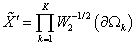 . .
Во всех введённых выше пространствах
функции являются скалярными. Пусть 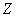 означает любое из
введённых выше пространств, тогда положим означает любое из
введённых выше пространств, тогда положим 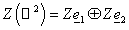 . В этом пространстве определим скалярное произведение и
норму прямой суммы. . В этом пространстве определим скалярное произведение и
норму прямой суммы.
Так как
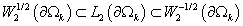 , ,
то верны
вложения
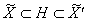 , , 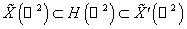 . .
Отметим, что 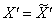 , , 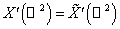 . .
В пространствах 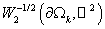 и и 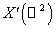 будем рассматривать
обычные нормы двойственного пространства: будем рассматривать
обычные нормы двойственного пространства:
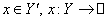 , , 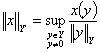 , ,
где 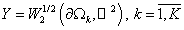 или или 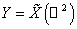 . .
Рассмотрим
определённые выше линейные операторы 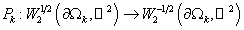 и определим билинейную
форму и определим билинейную
форму
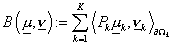 , ,
определённую для
всех 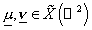 . Из непрерывности операторов Пуанкаре-Стеклова следует
непрерывность введённой билинейной формы. С помощью этой формы, используя
введённое выше пространство . Из непрерывности операторов Пуанкаре-Стеклова следует
непрерывность введённой билинейной формы. С помощью этой формы, используя
введённое выше пространство 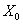 , запишем уравнение (23) в виде , запишем уравнение (23) в виде
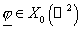 : : 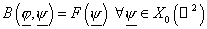 , ,
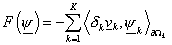 . (24) . (24)
Отметим, что построенные выше
соотношения верны для любой функциональной матрицы 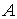 при условии, что все
вспомогательные задачи имеют единственные решения. при условии, что все
вспомогательные задачи имеют единственные решения.
5.2. Вариационное уравнение
для бигармонического уравнения.
В
дальнейшем будем рассматривать основной случай, соответствующий задаче (2). Это
необходимо для получения оценок погрешности.
Так
как форма 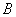 билинейна, её можно
записать в виде: билинейна, её можно
записать в виде:
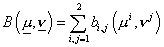 , , 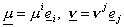 , ,
где 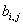 – билинейные формы,
определённые на – билинейные формы,
определённые на 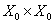 следующим образом: следующим образом: 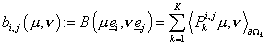 . Введённые билинейные формы являются непрерывными. . Введённые билинейные формы являются непрерывными.
В
силу того, что при решении задачи (14)–(15) граничные условия вида 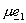 дают дают 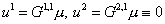 , получаем , получаем 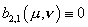 . Отсюда следует, что соотношения (24) в нашем случае можно
записать в виде: . Отсюда следует, что соотношения (24) в нашем случае можно
записать в виде:
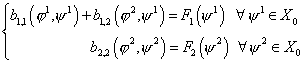 . (25) . (25)
Здесь 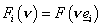 , где , где 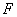 – линейный функционал, определённый в (24). – линейный функционал, определённый в (24).
Очевидно,
задачу (25) можно решать последовательно. Дополнительно отметим, что 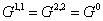 – оператор Грина для
уравнения Лапласа. Отсюда следует, что – оператор Грина для
уравнения Лапласа. Отсюда следует, что 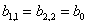 , , 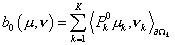 , где , где 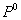 – оператор Пуанкаре-Стеклова
для уравнения Лапласа. Нам понадобится доказанная в [10] – оператор Пуанкаре-Стеклова
для уравнения Лапласа. Нам понадобится доказанная в [10]
Теорема 5. Билинейная форма 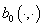 является непрерывной,
симметричной и коэрцитивной в пространстве является непрерывной,
симметричной и коэрцитивной в пространстве 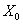 , т.е. , т.е.
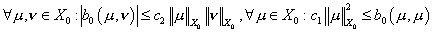 . .
Из
эквивалентности постановок следует, что каждая из задач (7)–(10) и (24) имеет
единственное решение. Справедлива
Теорема 6. Пусть
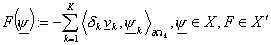 , ,
где 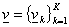 – такая функция, что – такая функция, что
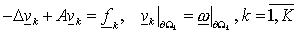 , ,
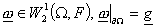 – произвольная функция, удовлетворяющая на – произвольная функция, удовлетворяющая на 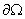 главным граничным
условиям. главным граничным
условиям.
Тогда
решение 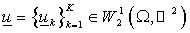 исходной задачи в
суперэлементе имеет вид исходной задачи в
суперэлементе имеет вид 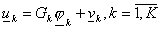 , где , где 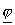 – решение задачи (24)
с указанным – решение задачи (24)
с указанным 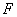 . .
Отметим,
что существование и единственность решения задачи (24) можно получить, решая
эквивалентную ей систему (25) последовательно и используя результаты теоремы 5
и леммы Лакса-Мильграма [14] для каждого уравнения.
6.
Построение аппроксимаций МКСЭ.
Метод конечных суперэлементов
является проекционным (проекционно-сеточным) методом решения уравнения (24).
Предположим что функционал 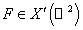 , определённый в (24), принадлежит пространству , определённый в (24), принадлежит пространству 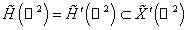 . Тогда уравнение (24) будет справедливо для любого . Тогда уравнение (24) будет справедливо для любого  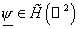 . .
Для
аппроксимации задачи (24) выберем некоторое конечномерное подпространство 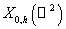 пространства пространства 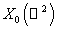 , являющееся линейной оболочкой системы функций , являющееся линейной оболочкой системы функций 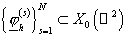 , и подпространство , и подпространство 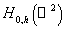 пространства пространства 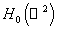 , являющееся линейной оболочкой системы функций , являющееся линейной оболочкой системы функций 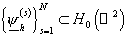 . Приближённое решение . Приближённое решение 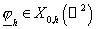 задачи (18) будем
искать в виде задачи (18) будем
искать в виде
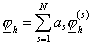 . (26) . (26)
Приближённым
решением задачи (24) будем считать решение следующей конечномерной задачи:
Определить
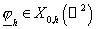 : : 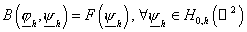 . (27) . (27)
Выбирая
различным образом пространства 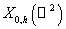 и и 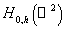 , можно получить различные варианты МКСЭ. Расчёт во всех
случаях будем проводить по следующей схеме: , можно получить различные варианты МКСЭ. Расчёт во всех
случаях будем проводить по следующей схеме:
1.
Для каждой функции 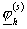 вычислим и запомним
функции вычислим и запомним
функции
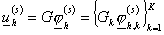
и
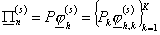 . .
2.
Сформировав и решив конечномерную задачу (20), получим приближённое решение 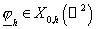 задачи (18). Тогда
приближённое решение исходной краевой задачи (2) будет иметь вид задачи (18). Тогда
приближённое решение исходной краевой задачи (2) будет иметь вид
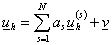 . .
Одним
из вариантов выбора базисных функций может быть МКСЭ Бубнова-Галёркина. Введём
на множестве  систему узлов систему узлов 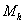 , состоящую из вершин прямоугольников , состоящую из вершин прямоугольников 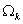 . Каждому узлу . Каждому узлу 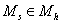 сопоставим скалярную базисную
функцию сопоставим скалярную базисную
функцию 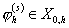 , определённую следующим образом: в узле , определённую следующим образом: в узле 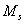 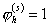 , в остальных узлах она равна нулю, на внешние границы
суперэлементов продолжена линейно, на всех внутренних границах суперэлементов , в остальных узлах она равна нулю, на внешние границы
суперэлементов продолжена линейно, на всех внутренних границах суперэлементов 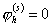 . Выберем также . Выберем также 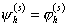 . .
Будем
выбирать векторные базисные функции так, чтобы только одна из их компонент не
равнялась нулю; введём двухиндексную запись:
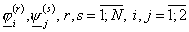 , , 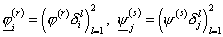 . (28) . (28)
7. Оценки ошибок для метода Бубнова-Галёркина.
Используя
допущения предыдущего параграфа, будем решать систему (25) последовательно.
Выпишем второе уравнение системы (25)
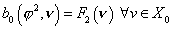 (29) (29)
и его
конечномерную аппроксимацию
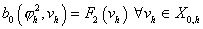 . (30) . (30)
Так как форма 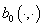 является коэрцитивной
и непрерывной, выполняются условия леммы Сеа [14, 16]. Отсюда следует оценка: является коэрцитивной
и непрерывной, выполняются условия леммы Сеа [14, 16]. Отсюда следует оценка:
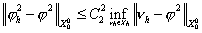 . .
Аналогично,
выпишем первое уравнение
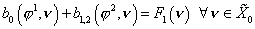 , (31) , (31)
и его
аппроксимацию
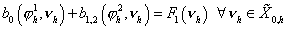 . (32) . (32)
Дополнительно
рассмотрим решение следующей задачи:
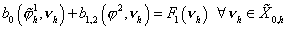 . (33) . (33)
От предыдущей
задачи она отличается видом второго слагаемого в левой части равенства. Чтобы
оценить 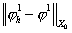 , воспользуемся неравенством треугольника: , воспользуемся неравенством треугольника:
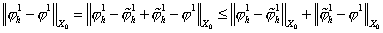 . .
Второе
слагаемое оценим с помощью леммы Сеа:
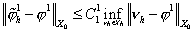 . .
Для
оценки первого слагаемого вычтем (32) из (33) и подставим в полученное
соотношение 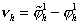 : :
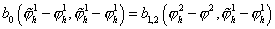 . .
Отсюда
получаем, что верна цепочка неравенств
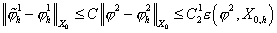 , ,
где 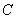 означает константу, не
зависящую от означает константу, не
зависящую от 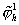 , , 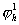 и и 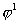 . Здесь мы использовали коэрцитивность формы . Здесь мы использовали коэрцитивность формы 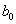 , непрерывность билинейной формы , непрерывность билинейной формы 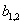 и лемму Сеа. и лемму Сеа.
Таким образом, верны следующие оценки:
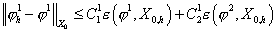 , , 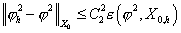 , ,
где 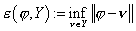 – расстояние от
элемента – расстояние от
элемента 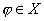 до подпространства до подпространства 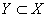 . В данном случае . В данном случае  . .
Аналогично [10,12] получим оценку
сверху для 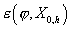 в случае двухмерной
пространственной задачи, когда в случае двухмерной
пространственной задачи, когда  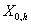 порождено непрерывными
кусочно-линейными функциями на границах суперэлементов. Будем считать, что порождено непрерывными
кусочно-линейными функциями на границах суперэлементов. Будем считать, что
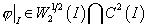 , ,
где 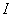 – произвольное ребро
одного из суперэлементов. Пусть на этом ребре c натуральным параметром – произвольное ребро
одного из суперэлементов. Пусть на этом ребре c натуральным параметром 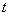 задана сетка задана сетка 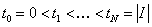 , характеризующая пространство , характеризующая пространство 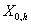 . .
Для любого 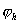 верно неравенство верно неравенство
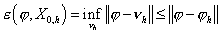 . .
Выберем
в качестве 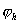 кусочно-линейный
интерполянт функции кусочно-линейный
интерполянт функции 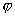 . .
Определим следующие нормы в
пространствах следов
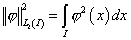 , ,
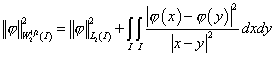
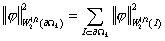 , ,
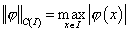 . .
Возьмём интерполянт 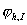 функции функции 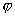 на ребре на ребре 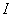 относительно заданной
сетки. Используя формулу конечных приращений Лагранжа, можно показать, что
верны неравенства относительно заданной
сетки. Используя формулу конечных приращений Лагранжа, можно показать, что
верны неравенства
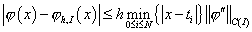 , ,
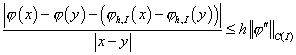 . .
Здесь 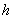 – максимальный шаг
сетки по всем границам суперэлементов. – максимальный шаг
сетки по всем границам суперэлементов.
Используя данные неравенства,
получим
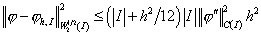 . .
Определим функции 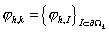 – интерполянты функции – интерполянты функции
 на границах
суперэлементов на границах
суперэлементов  . Из неравенства . Из неравенства
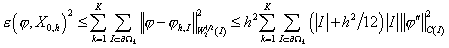 , ,
следует
оценка 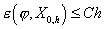 , где , где 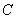 – константа, не
зависящая от шага сетки. – константа, не
зависящая от шага сетки.
Оценки погрешности принимают вид
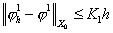 , , 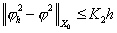 , ,
где
константы 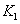 и и 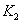 зависят от области и
её разбиения области на суперэлементы, но не зависят от зависят от области и
её разбиения области на суперэлементы, но не зависят от 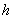 . .
8.
Примеры.
Приведём
несколько примеров тестовых расчётов.
В качестве
точного решения задачи (1) возьмём функцию вида
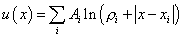 , , 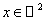 (34) (34)
которую для
удобства будем задавать набором 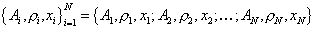 . Исходя из решаемой системы (2), определим соответствующие
граничные условия и правую часть. Будем сравнивать решение численной задачи с
исходной функцией. . Исходя из решаемой системы (2), определим соответствующие
граничные условия и правую часть. Будем сравнивать решение численной задачи с
исходной функцией.
Зададим
область
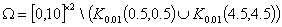 (35) (35)
и функцию (34),
заданную следующим набором параметров 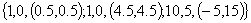 . В формуле (35) символ . В формуле (35) символ 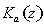 означает круг радиуса означает круг радиуса 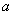 с центром в точке с центром в точке 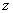 . Первые два слагаемых функции (34), соответствующей данному
набору параметров, являются гармоническими в области (35). . Первые два слагаемых функции (34), соответствующей данному
набору параметров, являются гармоническими в области (35).
Область
разбивалась на 100 суперэлементов, которые представляли собой квадраты со
стороной 1. На рисунках 1, 2 приведены карты линий уровня численного решения
для функций 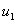 и и 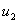 . На рисунке 3 приведён график сечения диагональю . На рисунке 3 приведён график сечения диагональю 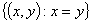 численного решения,
соответствующего функции численного решения,
соответствующего функции 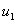 . Нормы в . Нормы в 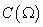 ошибок численного
решения для ошибок численного
решения для 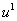 и и 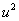 равны равны 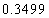 и и 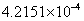 соответственно.
Отметим, что максимальные значения ошибка для соответственно.
Отметим, что максимальные значения ошибка для 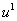 достигает в
окрестностях скважин. достигает в
окрестностях скважин.
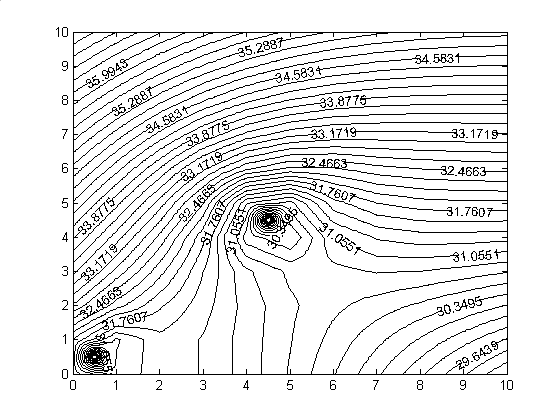
Рис. 1. График численного
решения для функции 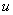 . .
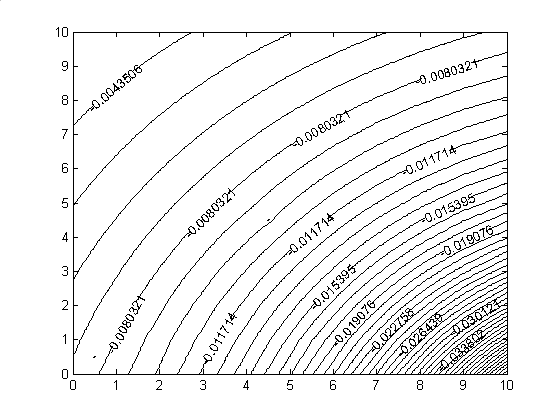
Рис. 2. График численного
решения для функции 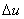 . .
Рис. 3. Сечение плоскостью 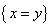 графика функции графика функции 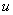 . .
В
качестве второго тестового примера рассмотрим задачу в той же самой области, но
с точным решением вида 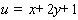 . Эта функция является гармонической в области . Эта функция является гармонической в области 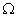 . .
Область
разбивалась на 16 суперэлементов, которые представляли собой квадраты со
стороной 2.5. Нормы в 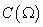 ошибок численного
решения для ошибок численного
решения для 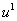 и и 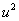 имеют порядок имеют порядок 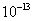 и и 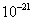 , соответственно. Такая высокая точность связана с тем, что
решение является линейной функцией – её следы аппроксимируются точно. , соответственно. Такая высокая точность связана с тем, что
решение является линейной функцией – её следы аппроксимируются точно.
Отметим,
что в этих примерах в каждом суперэлементе решался следующий ряд задач:
определение функции 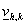 и функций и функций 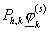 , где , где 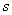 пробегает все
суперузлы, лежащие на границе пробегает все
суперузлы, лежащие на границе 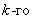 суперэлемента. Затем
рассчитывались коэффициенты и правая часть системы уравнений для определения
решения в суперузлах. суперэлемента. Затем
рассчитывались коэффициенты и правая часть системы уравнений для определения
решения в суперузлах.
Заключение.
В работе
предложен и обоснован вариант МКСЭ для решения бигармонического уравнения в
ограниченной области. Построена специальная слабая постановка для определения
следов решения на границах СЭ. Показана её эквивалентность исходной задаче. На
основе разработанного формального подхода построена расчётная схема. Для одного
варианта метода получена оценка ошибок приближённого решения. При решении ряда
тестовых задач метод показал свою эффективность. Получено хорошее
количественное совпадение с точным решением. Анализ метода показывает, что при
численном решении бигармонического уравнения МКСЭ может быть наиболее
эффективно использован при проведении параллельных вычислений с целью
существенного сокращения затрат машинного времени.
Литература.
1.
Бутковский А.Г. Характеристики систем с распределёнными параметрами. М.: Наука,
1979. 224 с.
2. Тихонов А.Н., Самарский А.А.
Уравнения математической физики. М.: Наука, 1972. 736 с.
3. Сен-Венана принцип. Физическая
энциклопедия. Т.4, М.: Большая Российская энциклопедия, 1994. с. 486.
4. Страховская Л.Г., Федоренко Р.П. Об
одном варианте метода конечных элементов // ЖВМиМФ. 1979. Т. 19. № 4. с.
950–960.
5. Страховская Л.Г., Федоренко Р.П.
Расчёт диффузии в многосвязной области методом конечных суперэлементов //
Препринт ИПМ АН СССР. М., 1987. № 171.
6. Страховская Л.Г., Федоренко Р.П.
Расчёт напряжений в композитном теле методом конечных суперэлементов //
Препринт ИПМ АН СССР. М., 1994. № 97.
7. Федоренко Р.П. Введение в
вычислительную физику. М.: Издательство МФТИ, 1994. 528 с.
8. Репях В.В. Применение одного
варианта метода конечных суперэлементов к решению задач теории упругости //
ЖВМиМФ. 1986. Т. 26, № 11. с. 1643–1653.
9.
Репях В.В. Анализ ошибок метода приближённых суперэлементов // ЖВМиМФ, 1989, Т.
30, № 7. с. 963–983.
10.
Галанин М.П., Савенков Е.Б. О связи метода конечных суперэлементов Федоренко и
проекционных методов. // Препр. Инст. Прикл. Матем. им. М.В. Келдыша РАН, 2001,
№ 67. 36 с
11.
Галанин М.П., Савенков Е.Б., Темис Ю.М. Метод конечных суперэлементов Федоренко
для решения задач теории упругости. // Препр. Инст. Прикл. Матем. им. М.В.
Келдыша РАН, 2004, № 38. 38 с
12.
Галанин М.П., Савенков Е.Б. Совместное использование метода конечных
суперэлементов и метода конечных элементов. // Препр. Инст. Прикл. Матем. им.
М.В. Келдыша РАН, 2004, № 13. 36 с
13.
Соболев С.Л. Некоторые применения функционального анализа в математической
физике.– 3-е изд., перераб. и доп./Под ред. О.А. Олейник.– М.: Наука Гл. Ред.
физ.-мат. лит., 1988. 336 с.
14.
Гилбарг Д., Трудингер Н. Эллиптические дифференциальные уравнения с частными
производными второго порядка: Пер. с англ./ Под ред. А.К. Гущина.– М.:Наука,
Гл.ред. физ.-мат. лит. 1989. 464 с.
15. Яковлев Г.Н. О следах функций
из 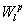 на кусочно-гладких
поверхностях.// Матем. сборник. 1967. Т. 74 (116). № 4. с. 526–543. на кусочно-гладких
поверхностях.// Матем. сборник. 1967. Т. 74 (116). № 4. с. 526–543.
16.
Обэн Ж.-П. Приближённое решение эллиптических краевых задач. М.: Мир, 1977. 384
с.
17.
Лебедев В.И., Агошков В.И. Операторы Пуанкаре-Стеклова и их приложение в
анализе. М.: ОВМ АН СССР, 1983.
|