Аннотация
Представлены результаты численного моделирования осесимметричных течений плазмы, возникающих
в коаксиальном ускорителе в присутствии продольного магнитного поля. Исследования проведены
на основе двумерной одножидкостной МГД-модели динамики плазмы в общем случае трехкомпонентного
магнитного поля. Стационарные течения получены методом установления в процессе решения
нестационарной МГД-задачи. Результаты расчетов установившихся трансзвуковых потоков
сопоставляются с решениями, полученными ранее в рамках аналитической модели двумерных течений
плазмы в каналах ускорителей. Выявлены основные закономерности плазмодинамических процессов.
Наблюдается возникновение токовых слоев в потоке плазмы при сравнительно больших значениях
продольного поля.
Abstract
Computations of axisymmetric plasma flows in coaxial accelerator with longitudinal magnetic
field are considered. The investigations are carried out within the framework of
two-dimensional one-component MHD-model in case of three-component magnetic field.
The steady-state flows are calculated by the relaxation method for time-dependent MHD-equations.
The numerical and analytical solutions are compared with reference to steady-state transonic
two-dimensional plasma flows in accelerator channels. The features of the plasma-dynamic
processes are exposed. It is found that the current layers are appeared in plasma flows in
case of respective large longitudinal magnetic field.
В в е д е н и е
В
работе обсуждаются качественные особенности плазмодинамики, обусловленные
наличием продольного магнитного поля и вращения плазмы в каналах ускорителей.
Дополнительное продольное поле 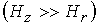 помимо
традиционного для данных систем азимутального магнитного поля помимо
традиционного для данных систем азимутального магнитного поля 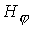 дает новые
возможности для управления динамическими процессами и реализации трансзвуковых
течений. дает новые
возможности для управления динамическими процессами и реализации трансзвуковых
течений.
Плазменный
ускоритель [1] схематично состоит из двух коаксиальных электродов,
подсоединенных к соответствующей электрической цепи. Между электродами в плазме
протекает ток 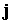 , имеющий преимущественно радиальное направление. В свою
очередь ток, проходящий по внутреннему электроду, порождает азимутальное
магнитное поле , имеющий преимущественно радиальное направление. В свою
очередь ток, проходящий по внутреннему электроду, порождает азимутальное
магнитное поле 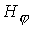 . За счет силы Ампера . За счет силы Ампера 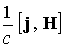 плазма ускоряется
вдоль оси системы. Аналогично газодинамическому соплу в канале плазменного
ускорителя при правильной организации процесса реализуется трансзвуковое
течение так, что в средней наиболее узкой части канала происходит переход
скорости потока через скорость быстрой магнитозвуковой волны. плазма ускоряется
вдоль оси системы. Аналогично газодинамическому соплу в канале плазменного
ускорителя при правильной организации процесса реализуется трансзвуковое
течение так, что в средней наиболее узкой части канала происходит переход
скорости потока через скорость быстрой магнитозвуковой волны.
Явление
кризиса тока [1, 2] ограничивает достижение больших скоростей в таких
квазистационарных плазменных ускорителях, как торцевой сильноточный ускоритель,
торцевой холловский ускоритель, коаксиальный плазменный ускоритель с
непроницаемыми, сплошными электродами и в целом ряде других устройств.
Преодоление кризиса тока возможно в системах типа квазистационарного
плазменного ускорителя (КСПУ) и стационарного плазменного двигателя (СПД)
[1,3]. В настоящее время СПД является наиболее продвинутой разработкой. На
протяжении десятилетий с его помощью осуществляется коррекция орбит спутников.
В двухступенчатом КСПУ для достаточно плотной
плазмы осуществляется режим ионного токопереноса с проницаемыми электродами. На
данных установках [4,5,6,7] были получены мощные плазменные потоки (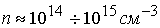 , , 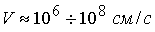 ). При этом,
отмечалась высокая степень устойчивости и азимутальной симметризации движущейся
плазмы. Такие возможности ускорителей обуславливают перспективность
использования их модификаций в космической технике в качестве электрореактивных
плазменных двигателей, а также в различных приложениях, включая термоядерные. ). При этом,
отмечалась высокая степень устойчивости и азимутальной симметризации движущейся
плазмы. Такие возможности ускорителей обуславливают перспективность
использования их модификаций в космической технике в качестве электрореактивных
плазменных двигателей, а также в различных приложениях, включая термоядерные.
Основам
теории аксиально-симметричных течений плазмы посвящены обзор [8] и монография
[1]. Заметная роль в разработке квазистационарного плазменного ускорителя и
понимании происходящих процессов отводится математическим моделям [9].
Численным исследованиям динамики плазмы и
ионизующегося газа в каналах ускорителей посвящены также обзор [10] и
целый ряд других публикаций (см., например, [11,12]). Теоретические и численные
исследования процессов в ускорителях для достаточно плотной плазмы проводятся в
рамках МГД-уравнений. В отличие от плазменных ускорителей в стационарных
плазменных двигателях используется иной механизм ускорения разреженной плазмы (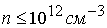 ) и исследуются решения кинетических уравнений для функции
распределения [1,13-15]. ) и исследуются решения кинетических уравнений для функции
распределения [1,13-15].
Наличие
продольного магнитного поля в плазменных ускорителях, с одной стороны,
усложняет течение, в частности, приводит к вращению, с другой - позволяет
исследовать динамику плазмы во всем многообразии процессов. Предшествующие
двумерные численные исследования следует рассматривать как частный случай в
отсутствии вращения.
В работе [16] аналитически выявлено влияние продольного
магнитного поля на двумерные осесимметричные потоки двухкомпонентной плазмы.
Исследования проведены в рамках
приближения плавного канала для уравнений идеальной магнитной гидродинамики.
Анализ важнейших свойств потоков в этом случае показал, что благодаря
продольному полю можно существенно уменьшить влияние эффекта Холла. Некоторые вопросы
МГД-течений в соплах с продольным магнитным полем затронуты в работе [17], где
представлены примеры течений в квазиодномерном приближении.
Иерархия численных моделей предполагает на первом этапе
исследования динамики плазмы в рамках одножидкостной модели на основе
МГД-уравнений с учетом конечной проводимости среды и в частном случае идеально
проводящей плазмы. В данной работе представлена такая модель. Она позволяет
изучить основные свойства течений плазмы в присутствии продольного магнитного
поля. Некоторые аспекты постановки задачи и результаты первых численных
экспериментов представлены в [18-20]. Эффект Холла, зависимость проводимости
плазмы от направления магнитного поля и 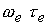 обусловлены поправками
к локально максвелловской функции распределения. На гладких решениях эти факторы не оказывают
значительного влияния на динамику плазмы в целом. Их можно учесть в дальнейшем на основе
двухжидкостных МГД-моделей. Соответствующие коэффициенты переноса найдены в
явном виде [21] для простой, классической, низкотемпературной плазмы.
Экспериментальные исследования [4-7,22] и оценки параметров в рассматриваемом диапазоне
указывают на то, что использование классических коэффициентов переноса в
известной степени оправдано при решении не только данной, но и большого числа
самых разнообразных плазмодинамических задач (см., например, [23]). обусловлены поправками
к локально максвелловской функции распределения. На гладких решениях эти факторы не оказывают
значительного влияния на динамику плазмы в целом. Их можно учесть в дальнейшем на основе
двухжидкостных МГД-моделей. Соответствующие коэффициенты переноса найдены в
явном виде [21] для простой, классической, низкотемпературной плазмы.
Экспериментальные исследования [4-7,22] и оценки параметров в рассматриваемом диапазоне
указывают на то, что использование классических коэффициентов переноса в
известной степени оправдано при решении не только данной, но и большого числа
самых разнообразных плазмодинамических задач (см., например, [23]).
1. Модель течений плазмы
Рассмотрим двумерное осесимметричное течение плазмы в
канале между двумя коаксиальными профилированными электродами (Рис. 1). В
предыдущих численных моделях [10-11] движение плазмы предполагалось зависящим
от одной азимутальной компоненты магнитного поля 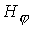 и двух компонент
скорости и двух компонент
скорости 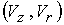 . При наличии продольного магнитного поля и
возникающего вращения в задаче участвуют все три компоненты магнитного поля и
скорости . При наличии продольного магнитного поля и
возникающего вращения в задаче участвуют все три компоненты магнитного поля и
скорости 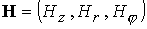 , , 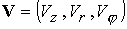 . .
Для достаточно плотной среды можно считать плазму
квазинейтральной 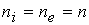 и пренебречь
инерцией электронов ( и пренебречь
инерцией электронов (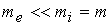 ). В рамках одножидкостной модели ). В рамках одножидкостной модели 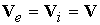 постановка задачи
включает традиционные уравнения магнитной газодинамики с учетом конечной
проводимости среды постановка задачи
включает традиционные уравнения магнитной газодинамики с учетом конечной
проводимости среды
 ; ; 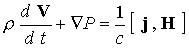
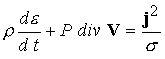 ; ; 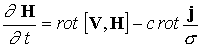 (1) (1)
где все
переменные имеют обычный смысл 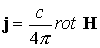 ; ; 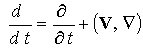
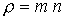 ; ; 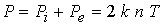 ; ; 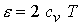 ; ; 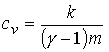
В данной системе уравнений
пренебрегаем вязкостью компонент плазмы и тепловыми потоками в силу малости
соответствующих диссипативных членов по сравнению с другими слагаемыми. В
рассматриваемом диапазоне параметров задачи стандартные оценки передачи тепла и
характерного времени обмена энергией между компонентами показывают, что 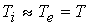 . Результаты численных экспериментов демонстрируют тот факт,
что на уравнение энергии не ложится сколько-нибудь существенной нагрузки в
общей картине динамики плазмы. Разница между температурами электронной и ионной
компонент может быть учтена в
последующих исследованиях. Кроме того, ограничимся исследованием динамики
водородной плазмы ( . Результаты численных экспериментов демонстрируют тот факт,
что на уравнение энергии не ложится сколько-нибудь существенной нагрузки в
общей картине динамики плазмы. Разница между температурами электронной и ионной
компонент может быть учтена в
последующих исследованиях. Кроме того, ограничимся исследованием динамики
водородной плазмы (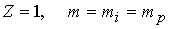 ), часто используемой в экспериментах. ), часто используемой в экспериментах.
Согласно закону Ома электрическое поле
определяется соотношением
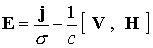 (2) (2)
где 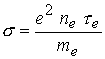 - электропроводность среды. - электропроводность среды.
При численном интегрировании
многомерной МГД-задачи должно быть выполнено условие бездивергентности
магнитного поля (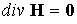 ). Существует несколько подходов для обеспечения
соленоидальности магнитного поля (см., например, [24]). Самый простой способ состоит в том, чтобы переписать
уравнения с учетом векторного потенциала ). Существует несколько подходов для обеспечения
соленоидальности магнитного поля (см., например, [24]). Самый простой способ состоит в том, чтобы переписать
уравнения с учетом векторного потенциала
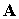 (
(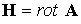 ). Такой подход становится особенно очевидным, если решается
осесимметричная задача ( ). Такой подход становится особенно очевидным, если решается
осесимметричная задача (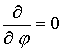 ). Действительно, в цилиндрической системе координат имеем ). Действительно, в цилиндрической системе координат имеем
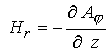 ; ; 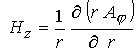 (3) (3)
где 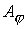 - тороидальная компонента векторного потенциала - тороидальная компонента векторного потенциала 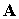 . Соотношения (3) в
аксиально-симметричном случае обеспечивают точное выполнение условия . Соотношения (3) в
аксиально-симметричном случае обеспечивают точное выполнение условия 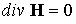 . Правда, в уравнениях импульсов следует аппроксимировать
вторые производные векторного потенциала. Как показали результаты численного
моделирования, в расчетах не наблюдается выбросов в распределении вторых
производных и разворотов тока . Правда, в уравнениях импульсов следует аппроксимировать
вторые производные векторного потенциала. Как показали результаты численного
моделирования, в расчетах не наблюдается выбросов в распределении вторых
производных и разворотов тока 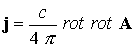 , что свидетельствует об адекватном описании процессов. , что свидетельствует об адекватном описании процессов.
Физическая
картина процессов определяется не абсолютными значениями тех или иных
параметров в определенной системе единиц измерения, а так называемыми
безразмерными параметрами. В качестве единиц измерения выберем размерные
константы: 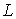 - длина канала; - длина канала; 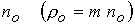 , , 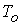 , , 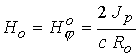 - характерные значения
концентрации, температуры и азимутальной составляющей магнитного поля на входе
в канал, где - характерные значения
концентрации, температуры и азимутальной составляющей магнитного поля на входе
в канал, где 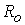 - радиус внешнего
электрода, - радиус внешнего
электрода, 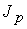 - разрядный ток в системе. С помощью
перечисленных величин формируются единицы: давления - - разрядный ток в системе. С помощью
перечисленных величин формируются единицы: давления - 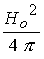 , скорости – , скорости – 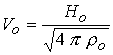 (характерная
альфвеновская скорость), времени - (характерная
альфвеновская скорость), времени - 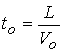 (’’пролетное” время).
Связь исходных размерных величин с безразмерными параметрами, участвующими в
задаче, определяется следующим образом: (’’пролетное” время).
Связь исходных размерных величин с безразмерными параметрами, участвующими в
задаче, определяется следующим образом: 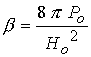 - отношение газового и
магнитного давлений на входе, где - отношение газового и
магнитного давлений на входе, где 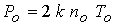 ; ; 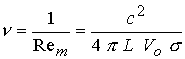 - магнитная вязкость, обратно пропорциональная
магнитному числу Рейнольдса для спитцеровской проводимости - магнитная вязкость, обратно пропорциональная
магнитному числу Рейнольдса для спитцеровской проводимости 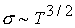 . .
С учетом сделанных выше замечаний в
осесимметричном случае уравнения (1) в безразмерной форме можно записать в
терминах 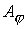 -компоненты векторного потенциала и -компоненты векторного потенциала и 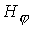 -компоненты магнитного поля
: -компоненты магнитного поля
:
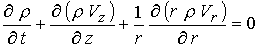 (4) (4)
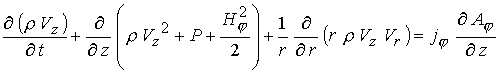 (5) (5)
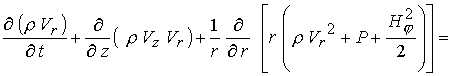
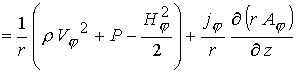 (6) (6)
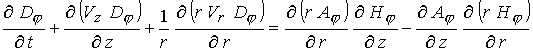 (7) (7)
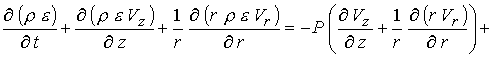
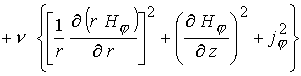 (8) (8)
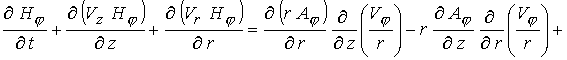
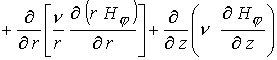 (9) (9)
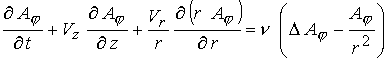 (10) (10)
В этих
уравнениях дополнительно введены следующие обозначения:
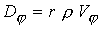 , , 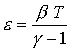 , , 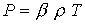 , , 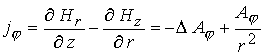 - тороидальная компонента тока, где - тороидальная компонента тока, где 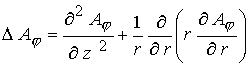 . В итоге имеем семь уравнений для переменных . В итоге имеем семь уравнений для переменных 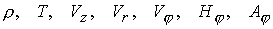 . .
Численное
интегрирование уравнений (4)-(10) ведется в области переменных 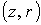 , соответствующей форме канала, изображенного на рис.1,3,4. , соответствующей форме канала, изображенного на рис.1,3,4.
Уравнения и условия на границах определяют динамику потока.
На входе в канале 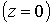 полагаем, что плазма
подается с известными значениями
плотности и температуры полагаем, что плазма
подается с известными значениями
плотности и температуры 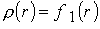 , , 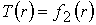 . .
Если не рассматривается дополнительное
уравнение электрической цепи, считаем, что ток поддерживается постоянным и
поступает в систему только через электроды, т.е. 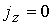 при при 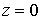 или или 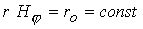 ( (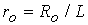 ) . ) .
Естественно
предположить, что подача плазмы осуществляется вдоль определенного направления,
например, вдоль координатных линий.
Данные
граничные условия являются традиционными для численных моделей динамики плазмы
в каналах в отсутствии продольного магнитного поля. При его наличии необходимы
граничные условия для 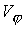 и и 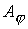 . .
Считаем,
что плазма во входном сечении 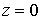 не вращается и
азимутальная скорость равна нулю не вращается и
азимутальная скорость равна нулю 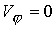 . .
Кроме
того, зададим на входе 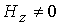 . Следуя [16], воспользуемся уравнением радиального
равновесия . Следуя [16], воспользуемся уравнением радиального
равновесия
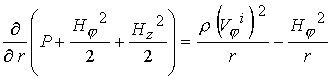 (11) (11)
На входе в
канал при условии 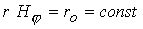 и и 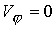 из (11) получим,
что из (11) получим,
что
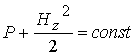 (12) (12)
В случае
холодной плазмы (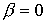 ) при ) при 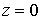 имеем имеем 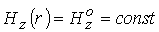 . Интегрируя (3), найдем . Интегрируя (3), найдем
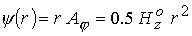 (13) (13)
В общем
случае 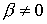 необходимы
дополнительные согласования граничных условий. Соотношение (12) отвечает
уравновешенному в радиальном направлении потоку плазмы на входе. Это возможно,
в частности, для двух очевидных способов подачи. Во-первых, традиционные в
численных моделях условия на входе необходимы
дополнительные согласования граничных условий. Соотношение (12) отвечает
уравновешенному в радиальном направлении потоку плазмы на входе. Это возможно,
в частности, для двух очевидных способов подачи. Во-первых, традиционные в
численных моделях условия на входе 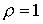 и и 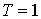 при любом при любом 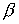 приводят в случае
радиального равновесия к приводят в случае
радиального равновесия к 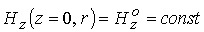 и соотношению (13).
Во-вторых, если и соотношению (13).
Во-вторых, если 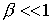 , возможна произвольная подача, в том числе в соответствии с
аналитической моделью [16], где , возможна произвольная подача, в том числе в соответствии с
аналитической моделью [16], где 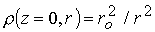 и плотность у
центрального электрода существенно выше. При этом, можно осуществить
сопоставление с аналитическим решением. Заметим, что в экспериментах [5]
наблюдается улучшение характеристик плазменного потока и работы ускорителя в
целом при неравномерной подаче плазмы, когда ее концентрация на входе во вторую
ступень КСПУ больше в окрестности внутреннего электрода. и плотность у
центрального электрода существенно выше. При этом, можно осуществить
сопоставление с аналитическим решением. Заметим, что в экспериментах [5]
наблюдается улучшение характеристик плазменного потока и работы ускорителя в
целом при неравномерной подаче плазмы, когда ее концентрация на входе во вторую
ступень КСПУ больше в окрестности внутреннего электрода.
На
выходе ( 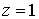 ) для исследуемых
трансзвуковых потоков предполагается свободное ( сверхзвуковое ) вытекание
плазмы. ) для исследуемых
трансзвуковых потоков предполагается свободное ( сверхзвуковое ) вытекание
плазмы.
Рассмотрим
граничные условия на электродах. Динамика плазмы в ускорителях исследуется в разных режимах токопереноса. В режиме
электронного токопереноса линии тока ионной компоненты плазмы лежат на поверхности непроницаемых электродов:
катода и анода, а сами электроды не являются эквипотенциальными. Наоборот, в
режиме ионного токопереноса электроды
представляют собой эквипотенциальные поверхности и должны быть
прозрачными для плазмы. Случай самосогласованного протекания плазмы через
электроды обусловлен исключительно эффектом Холла. Пренебрегая им (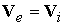 ), приходим к режиму непроницаемых сплошных эквипотенциальных
электродов, который в реальной физической практике ( ), приходим к режиму непроницаемых сплошных эквипотенциальных
электродов, который в реальной физической практике (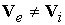 ) является вырожденным. ) является вырожденным.
В
одножидкостной модели эффект Холла не учитывается и полярность электродов не
различается. Поэтому модель пригодна для качественного описания указанных
режимов, но в большей степени отвечает
случаю непроницаемых сплошных эквипотенциальных электродов.
В
данной работе граничные условия на электродах
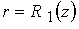 и и 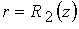 , образующих стенки канала, предполагают эквипотенциальность
электродов ( , образующих стенки канала, предполагают эквипотенциальность
электродов (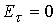 ) и непроницаемость поверхности для плазмы ( ) и непроницаемость поверхности для плазмы (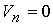 ). При наличии продольного магнитного поля необходимо
дополнительное соотношение. В плазмодинамике ). При наличии продольного магнитного поля необходимо
дополнительное соотношение. В плазмодинамике 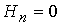 является типичным и
естественным условием, связывающим компоненты магнитного поля на границе плазма
– проводник. Оно приводит, в частности, к сохранению магнитного потока вдоль
канала. Таким образом, на электродах, ограничивающих исследуемый плазменный
объем, выполнены следующие условия: является типичным и
естественным условием, связывающим компоненты магнитного поля на границе плазма
– проводник. Оно приводит, в частности, к сохранению магнитного потока вдоль
канала. Таким образом, на электродах, ограничивающих исследуемый плазменный
объем, выполнены следующие условия:
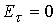 ; ; 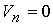 и и 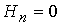
В
случае плазмы конечной проводимости при 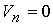 соотношение соотношение 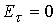 , где , где 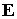 определяется с помощью
(2), дает определяется с помощью
(2), дает 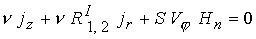 . Здесь . Здесь 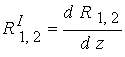 ; ; 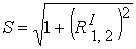 . Равенство . Равенство 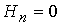 на самом деле можно
заменить более точным соотношением на самом деле можно
заменить более точным соотношением 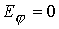 , которое при , которое при 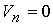 позволяет найти позволяет найти 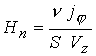 . Видно, что в случае идеально проводящей плазмы (магнитная
вязкость . Видно, что в случае идеально проводящей плазмы (магнитная
вязкость 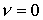 ) из ) из 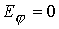 следует общепринятое
условие следует общепринятое
условие 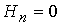 . В представленных далее численных экспериментах . В представленных далее численных экспериментах 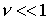 и и 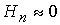 . .
В МГД-моделях течений плазмы в каналах
со сплошными электродами возможна постановка более содержательных граничных
условий, отражающих сложные процессы в тонких приэлектродных слоях и на границе
с диэлектриком. С этой целью проводились исследования внутренней структуры
слоев [25,26]. Кроме того, ведутся работы по изучению взаимодействия плазмы с
поверхностью различных материалов и их эрозии (см., например, [27]).
Методика численного интегрирования
детально изложена в [18]. Поскольку речь идет об исследовании процессов на
качественном уровне, достаточно ограничиться набором методов, хорошо
зарекомендовавших себя, часто используемых и вполне апробированных на
рассматриваемом классе явлений. Конкретный выбор алгоритмов обусловлен
спецификой задачи.
В
представленной модели вращающихся осесимметричных потоков
проводится расщепление по физическим факторам и координатам 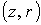 . В расчете
переноса с коррекцией потоков использован алгоритм [28], разработанный для
интегрирования обобщенного . В расчете
переноса с коррекцией потоков использован алгоритм [28], разработанный для
интегрирования обобщенного одномерного уравнения переноса и адоптированный с учетом
расщепления для решения системы уравнений (4)-(9). Уравнение переноса (10) для
величины одномерного уравнения переноса и адоптированный с учетом
расщепления для решения системы уравнений (4)-(9). Уравнение переноса (10) для
величины 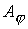 решается с помощью
одного из характеристических методов [29]. решается с помощью
одного из характеристических методов [29].
Конечная
проводимость, как функция температуры, присутствует в правых частях уравнений (9), (10) для величин 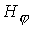 и и 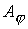 . Влияние диссипативных факторов вычисляется на основе
неявной схемы. В данном случае применяется потоковый вариант метода прогонки
[30]. . Влияние диссипативных факторов вычисляется на основе
неявной схемы. В данном случае применяется потоковый вариант метода прогонки
[30].
2. Результаты
моделирования
На основе представленной модели
проведена серия численных экспериментов. В численной модели можно произвольно
выбрать значения концентрации 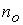 , температуры , температуры 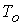 , разрядного тока , разрядного тока 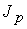 и длины канала и длины канала 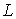 . В данном случае эти параметры соответствуют экспериментам
по программе КСПУ [4-7]. Например, для
величин . В данном случае эти параметры соответствуют экспериментам
по программе КСПУ [4-7]. Например, для
величин 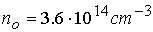 , , 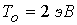 , , 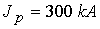 , , 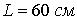 безразмерные
параметры задачи равны безразмерные
параметры задачи равны 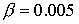 , , 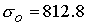 . Магнитное число Рейнольдса отвечает спитцеровской
зависимости проводимости от температуры: . Магнитное число Рейнольдса отвечает спитцеровской
зависимости проводимости от температуры: 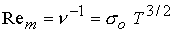 . Кроме того, зададим величину продольного магнитного поля на
входе в канал, например, . Кроме того, зададим величину продольного магнитного поля на
входе в канал, например, 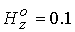 . Напомним, что единицей магнитного поля является значение . Напомним, что единицей магнитного поля является значение 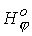 . Такая достаточно малая величина . Такая достаточно малая величина 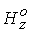 позволяет реализовать
трансзвуковое течение согласно аналитической модели [16], на основе которой
осуществим верификацию данной численной модели.
Геометрия канала (рис. 1, 3, 4)
также отвечает аналитическим исследованиям двумерных течений плазмы. При
этом, плотность на входе в канал меняется по закону позволяет реализовать
трансзвуковое течение согласно аналитической модели [16], на основе которой
осуществим верификацию данной численной модели.
Геометрия канала (рис. 1, 3, 4)
также отвечает аналитическим исследованиям двумерных течений плазмы. При
этом, плотность на входе в канал меняется по закону 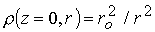 . Предполагая изэнтропичность (энтропия . Предполагая изэнтропичность (энтропия 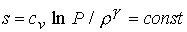 ) поступающей плазмы, имеем ) поступающей плазмы, имеем 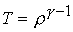 при при 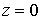 . .
Численное решение исходной
нестационарной задачи осуществляется до установления течения. Время
установления по порядку величины равно единице 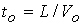 или характерному
“пролетному” времени. Это составляет несколько сот шагов в численной модели,
где временной шаг ограничен условием
Куранта. При условии установления потока картина распределения искомых величин
не меняется в процессе вычислений.
Дальнейший расчет для любого промежутка времени дает среднеквадратичное
отклонение всех переменных не превышающее одного процента в следующем
примере. или характерному
“пролетному” времени. Это составляет несколько сот шагов в численной модели,
где временной шаг ограничен условием
Куранта. При условии установления потока картина распределения искомых величин
не меняется в процессе вычислений.
Дальнейший расчет для любого промежутка времени дает среднеквадратичное
отклонение всех переменных не превышающее одного процента в следующем
примере.
На рис.1 для указанных выше параметров
представлено трансзвуковое течение в присутствии продольного магнитного поля.
Для определенности выберем направление электрического тока (линии уровня функции 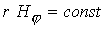 ) на рис. 1б
так, что внешний электрод является анодом. Длина векторов на рис.
1д (в сантиметрах) равна безразмерному
значению скорости в данной точке. ) на рис. 1б
так, что внешний электрод является анодом. Длина векторов на рис.
1д (в сантиметрах) равна безразмерному
значению скорости в данной точке.
На
рис. 1а (пунктир) видно, что в середине канала скорость потока переходит через
местную скорость быстрой магнитозвуковой волны 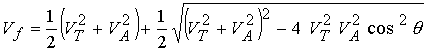 . Здесь . Здесь 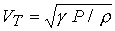 - газодинамическая
тепловая скорость звука, - газодинамическая
тепловая скорость звука, 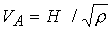 , , 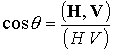 . .
Наблюдаются особенности в
распределении продольного магнитного поля 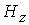 (рис. 1б). Оно
увеличивается с ростом (рис. 1б). Оно
увеличивается с ростом 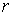 и достигает
максимального значения на поверхности
внешнего электрода в средней наиболее узкой части канала ускорителя и достигает
максимального значения на поверхности
внешнего электрода в средней наиболее узкой части канала ускорителя 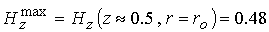 . Плазма как бы “выталкивает” продольное поле в область с
меньшей концентрацией, если не учитывать локальные процессы вблизи самого
электрода. . Плазма как бы “выталкивает” продольное поле в область с
меньшей концентрацией, если не учитывать локальные процессы вблизи самого
электрода.
Азимутальная скорость 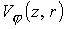 (рис. 1в) увеличивается в радиальном и осевом
направлениях. Иначе говоря, небольшое продольное поле приводит к возрастающему
вращению плазмы, которое достигает максимального значения в окрестности
внешнего электрода на выходе из канала ускорителя (рис. 1в) увеличивается в радиальном и осевом
направлениях. Иначе говоря, небольшое продольное поле приводит к возрастающему
вращению плазмы, которое достигает максимального значения в окрестности
внешнего электрода на выходе из канала ускорителя 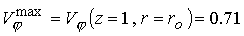 . Тем не менее, при . Тем не менее, при 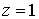 доля доля 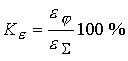 кинетической энергии,
обусловленной вращением кинетической энергии,
обусловленной вращением 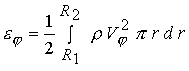 , составляет небольшую
часть от всей кинетической энергии вытекающего потока , составляет небольшую
часть от всей кинетической энергии вытекающего потока 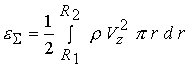 . В расчете эта
величина равна . В расчете эта
величина равна 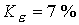 . .
Поведение
плотности 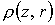 (сплошные кривые на
рис. 1г) в окрестности внешнего электрода обусловлено продольным магнитным
полем. Случаю (сплошные кривые на
рис. 1г) в окрестности внешнего электрода обусловлено продольным магнитным
полем. Случаю 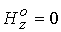 отвечают штрих
пунктирные кривые на рис. 1г и 1б. При наличии отвечают штрих
пунктирные кривые на рис. 1г и 1б. При наличии 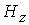 вблизи внешнего
электрода меняется наклон линий уровня функции вблизи внешнего
электрода меняется наклон линий уровня функции 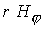 (электрический ток) и
одновременно здесь же происходит увеличение плотности, связанное с вращением
плазмы. Рис. 2 более отчетливо иллюстрирует данный эффект. Здесь изображены
зависимости плотности (электрический ток) и
одновременно здесь же происходит увеличение плотности, связанное с вращением
плазмы. Рис. 2 более отчетливо иллюстрирует данный эффект. Здесь изображены
зависимости плотности 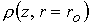 от координаты от координаты 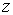 вдоль внешнего
электрода при различных значениях вдоль внешнего
электрода при различных значениях 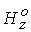 . Сплошные кривые 1
и 2 отвечают расчетам при . Сплошные кривые 1
и 2 отвечают расчетам при 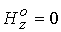 и и 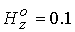 соответственно. На
выходе из ускорителя ( соответственно. На
выходе из ускорителя (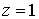 , , 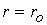 ) плотность увеличивается от значения ) плотность увеличивается от значения 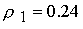 в отсутствии
продольного поля до величины в отсутствии
продольного поля до величины 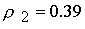 при его наличии.
Коэффициент увеличения плотности в присутствии продольного поля, определяемый
как отношение при его наличии.
Коэффициент увеличения плотности в присутствии продольного поля, определяемый
как отношение 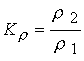 , при данном значении , при данном значении 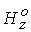 равен равен 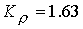 . В отсутствии продольного поля . В отсутствии продольного поля 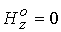 согласно экспериментам
в окрестности непроницаемого внешнего электрода (анода) ближе к выходу за счет
эффекта Холла возникает недостаток ионов. Как правило, это приводит к явлению
кризиса тока и срыву процесса ускорения. Можно предположить, что решение этой
проблемы, полное или частичное,
возможно, в частности, путем введения в систему небольшого продольного
поля, благодаря возникающему вращению и “отжатию” плазмы к внешнему электроду. согласно экспериментам
в окрестности непроницаемого внешнего электрода (анода) ближе к выходу за счет
эффекта Холла возникает недостаток ионов. Как правило, это приводит к явлению
кризиса тока и срыву процесса ускорения. Можно предположить, что решение этой
проблемы, полное или частичное,
возможно, в частности, путем введения в систему небольшого продольного
поля, благодаря возникающему вращению и “отжатию” плазмы к внешнему электроду.
Далее сопоставим результаты расчета
установившегося течения плазмы с аналитическим решением. Эти решения не обязаны
совпадать, поскольку аналитическая модель [16] построена в приближении плавного
канала для МГД-уравнений идеально проводящей холодной плазмы ( 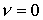 , , 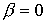 ). Наиболее заметные
отличия аналитической модели характеризуются на рис. 1в, 1г и 2 штриховыми кривыми, соответствующими ближайшим
сплошным линиям в полной МГД-модели. Количественной характеристикой
сопоставления двух моделей может служить разница двух решений в норме ). Наиболее заметные
отличия аналитической модели характеризуются на рис. 1в, 1г и 2 штриховыми кривыми, соответствующими ближайшим
сплошным линиям в полной МГД-модели. Количественной характеристикой
сопоставления двух моделей может служить разница двух решений в норме 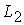 . Среднеквадратичные отклонения для переменных . Среднеквадратичные отклонения для переменных 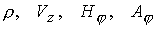 не превышают 10%. Для
радиальной компоненты не превышают 10%. Для
радиальной компоненты 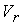 и и 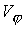 эти отклонения
несколько выше, что представляется вполне закономерным, поскольку в
аналитической модели использовано приближение плавного канала. Таким образом,
принципиальных качественных отличий двух решений не наблюдается, а идеального
количественного совпадения и не должно быть. эти отклонения
несколько выше, что представляется вполне закономерным, поскольку в
аналитической модели использовано приближение плавного канала. Таким образом,
принципиальных качественных отличий двух решений не наблюдается, а идеального
количественного совпадения и не должно быть.
Дальнейшие исследования на основе
полной МГД-модели позволили выявить следующие закономерности. Увеличение
продольного магнитного поля очевидным образом приводит к росту плотности в
окрестности внешнего электрода. Кривые 3 и 4 на рис. 2 отвечают соответственно
значениям 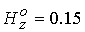 и и 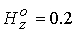 . С усилением продольного поля возрастает доля энергии
вращения и значение коэффициента роста плотности. В случае . С усилением продольного поля возрастает доля энергии
вращения и значение коэффициента роста плотности. В случае 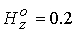 имеем имеем 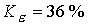 ; ; 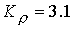 ; ; 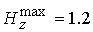 ; ; 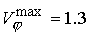 . Начиная с некоторого
критического значения продольного поля, происходит качественное изменение
картины течения. Величина критического поля зависит от параметров задачи и
условий подачи плазмы на входе. Если . Начиная с некоторого
критического значения продольного поля, происходит качественное изменение
картины течения. Величина критического поля зависит от параметров задачи и
условий подачи плазмы на входе. Если 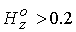 в рассматриваемом
примере, вблизи внешнего электрода, где продольное поле имеет максимальные
значения, в движущейся плазме формируется токовый слой и область практически
равномерного течения с постоянной скоростью.
Эта область ограничена снаружи эквипотенциальным электродом. Внутри
канала область отделена от основного потока тонким токовым слоем, изображенным
на рис. 3 для в рассматриваемом
примере, вблизи внешнего электрода, где продольное поле имеет максимальные
значения, в движущейся плазме формируется токовый слой и область практически
равномерного течения с постоянной скоростью.
Эта область ограничена снаружи эквипотенциальным электродом. Внутри
канала область отделена от основного потока тонким токовым слоем, изображенным
на рис. 3 для 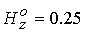 . Пунктир на данном
рисунке отвечает . Пунктир на данном
рисунке отвечает 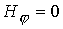 . Такое замыкание электрического тока на внешнем электроде
указывает на возможное образование привязок тока в случае достаточно больших
значений . Такое замыкание электрического тока на внешнем электроде
указывает на возможное образование привязок тока в случае достаточно больших
значений 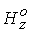 . В аналитическое модели также существует критическое
продольное поле. При значениях . В аналитическое модели также существует критическое
продольное поле. При значениях 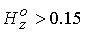 аналитическое решение
[16], отвечающие трансзвуковому течению плазмы, не было найдено. аналитическое решение
[16], отвечающие трансзвуковому течению плазмы, не было найдено.
Равномерную подачу плазмы на входе ( 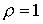 , , 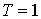 при при 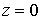 ) иллюстрирует рис. 4. На этом рисунке изображено
соответствующие трансзвуковое течение в присутствии продольного магнитного поля
( ) иллюстрирует рис. 4. На этом рисунке изображено
соответствующие трансзвуковое течение в присутствии продольного магнитного поля
(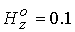 ) и тех же значений ) и тех же значений 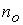 , , 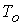 , , 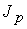 , , 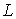 и соответственно и соответственно 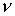 , , 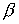 . (см. для сравнения
рис. 1в, г, д ) . Распределения функции . (см. для сравнения
рис. 1в, г, д ) . Распределения функции 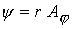 , электрического тока , электрического тока 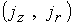 и векторного поля и векторного поля 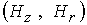 качественно не
отличаются и очень близки к тем, что представлены на рис. 1а и 1б при условии неравномерной подачи. В
случае равномерной подачи продольное магнитное поле более плавно меняется в
радиальном направлении и соответственно меньше его максимальное значение качественно не
отличаются и очень близки к тем, что представлены на рис. 1а и 1б при условии неравномерной подачи. В
случае равномерной подачи продольное магнитное поле более плавно меняется в
радиальном направлении и соответственно меньше его максимальное значение 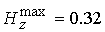 при при 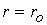 и и 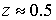 . Нарастание
азимутальной скорости . Нарастание
азимутальной скорости 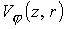 (сплошные кривые на
рис. 4а) не столь значительно и не так
велико ее значение (сплошные кривые на
рис. 4а) не столь значительно и не так
велико ее значение 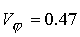 в точке в точке 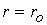 и и 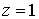 . Максимум . Максимум 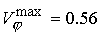 достигается при достигается при 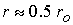 и и 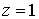 . В то же время доля
энергии вращения на выходе практически не меняется . В то же время доля
энергии вращения на выходе практически не меняется 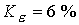 . Введение в систему
продольного поля при равномерной подаче не приводит к качественно иному
поведению плотности в окрестности внешнего электрода. Распределения плотности
и температуры в объеме канала (сплошные кривые на рис. 4 б, в) подобны
тем, что получены в случае . Введение в систему
продольного поля при равномерной подаче не приводит к качественно иному
поведению плотности в окрестности внешнего электрода. Распределения плотности
и температуры в объеме канала (сплошные кривые на рис. 4 б, в) подобны
тем, что получены в случае 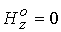 . Они естественным образом отличаются оттого, что
представлено на рис. 1 г,
д, поскольку теперь на входе . Они естественным образом отличаются оттого, что
представлено на рис. 1 г,
д, поскольку теперь на входе 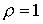 и и 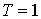 . Коэффициент увеличения плотности при . Коэффициент увеличения плотности при 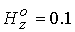 равен равен 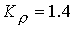 . Сравнивая векторное поле скоростей . Сравнивая векторное поле скоростей 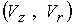 (рис. 1д и
4б), можно отметить, что в случае
неравномерной подачи продольная скорость плазмы практически не зависит от
радиуса (рис. 1д и
4б), можно отметить, что в случае
неравномерной подачи продольная скорость плазмы практически не зависит от
радиуса 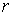 . Ее монотонный рост в
направлении оси . Ее монотонный рост в
направлении оси 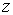 очевиден и обусловлен
ускорением плазмы. В данном случае продольная скорость зависит от радиуса и
имеет более высокие значения в окрестности внутреннего электрода.
Соответственно плотность здесь меньше. очевиден и обусловлен
ускорением плазмы. В данном случае продольная скорость зависит от радиуса и
имеет более высокие значения в окрестности внутреннего электрода.
Соответственно плотность здесь меньше.
Независимо
от способа подачи плазмы на входе распределения температуры 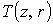 на рис. 1д, 4в за счет
выделяемого тепла (слагаемое на рис. 1д, 4в за счет
выделяемого тепла (слагаемое 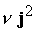 в уравнении (8) ) отличаются
от тех, что можно получить в случае изоэнтропического течения ( в уравнении (8) ) отличаются
от тех, что можно получить в случае изоэнтропического течения (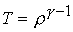 во всем объеме канала), даже при малых значениях магнитной
вязкости во всем объеме канала), даже при малых значениях магнитной
вязкости 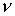 или большой
проводимости. Поэтому, в частности,
модель идеальной магнитной газодинамики считают более грубой. Хотя в целом ряде
случаев ( или большой
проводимости. Поэтому, в частности,
модель идеальной магнитной газодинамики считают более грубой. Хотя в целом ряде
случаев (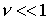 , , 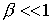 ) она позволяет получить значения искомых величин, за
исключением температуры,
практически совпадающие с
результатами расчетов в МГД-модели с учетом конечной проводимости среды. Это подтверждают вычисления, проведенные по
двум моделям. Для указанных выше
параметров они дают очень близкие результаты, не связанные с распределением
температуры. Кроме того, численные эксперименты показали, что при малых
значениях ) она позволяет получить значения искомых величин, за
исключением температуры,
практически совпадающие с
результатами расчетов в МГД-модели с учетом конечной проводимости среды. Это подтверждают вычисления, проведенные по
двум моделям. Для указанных выше
параметров они дают очень близкие результаты, не связанные с распределением
температуры. Кроме того, численные эксперименты показали, что при малых
значениях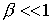 , характерных для плазменных ускорителей, температурный фон
не оказывает заметного влияния на динамику плазмы в целом. Поэтому учет
переноса излучения в данной модели не является элементом первой необходимости и
может быть осуществлен в дальнейших исследованиях. , характерных для плазменных ускорителей, температурный фон
не оказывает заметного влияния на динамику плазмы в целом. Поэтому учет
переноса излучения в данной модели не является элементом первой необходимости и
может быть осуществлен в дальнейших исследованиях.
Аналогично
случаю неравномерной подачи усиление продольного поля увеличивает долю энергии
вращения, коэффициент 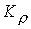 , , 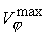 и и 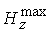 . Так, для . Так, для 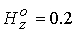 имеем имеем 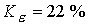 и и 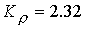 . При достаточно большой величине . При достаточно большой величине 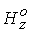 также наблюдаются
качественные изменения картины течения и формирование токового слоя. В данном
случае перестройка течения происходит
при более высоких значениях продольного поля также наблюдаются
качественные изменения картины течения и формирование токового слоя. В данном
случае перестройка течения происходит
при более высоких значениях продольного поля 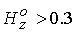 . .
Варьирование
таких параметров задачи, как 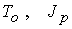 , не приводит к принципиальным изменениям описанных выше
процессов. Увеличение характерной температуры до , не приводит к принципиальным изменениям описанных выше
процессов. Увеличение характерной температуры до 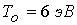 ( (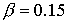 , , 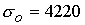 ) сопровождается уменьшением значения критического
продольного поля, связанного с образованием токового слоя ) сопровождается уменьшением значения критического
продольного поля, связанного с образованием токового слоя 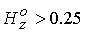 . В то же время возрастают значения коэффициентов . В то же время возрастают значения коэффициентов
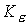 и и 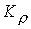 в сравнении с
расчетами при в сравнении с
расчетами при 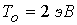 . Например, при . Например, при 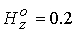 имеем имеем 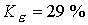 и и 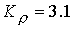 . Подобные тенденции наблюдаются при увеличении разрядного тока. Если . Подобные тенденции наблюдаются при увеличении разрядного тока. Если 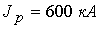 ( (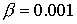 , , 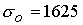 ), то получим ), то получим 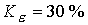 и и 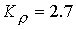 для критического
значения для критического
значения 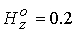 . .
Для
более плотной плазмы 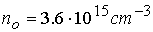 ( (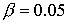 , , 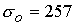 ) расширяется диапазон значений продольного поля, отвечающих
ламинарному течению ) расширяется диапазон значений продольного поля, отвечающих
ламинарному течению 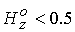 . Несмотря на то, что с ростом . Несмотря на то, что с ростом 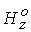 увеличивается значение
коэффициента увеличивается значение
коэффициента 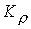 , большие значения продольного поля не представляют интереса,
поскольку в этом случае велика доля энергии, обусловленная вращением. При , большие значения продольного поля не представляют интереса,
поскольку в этом случае велика доля энергии, обусловленная вращением. При 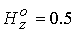 расчеты дают расчеты дают 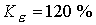 и и 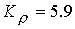 в то время, как для в то время, как для 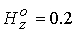 имеем имеем 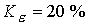 и и 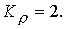
Существенные
изменения некоторых элементов картины течения связаны с дальнейшим ростом
концентрации плазмы на входе. В рассматриваемом случае равномерной подачи
плазмы и
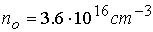 ( (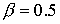 , , 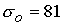 ) область с максимальными значениями продольного поля
перемещается к внутреннему электроду в наиболее узкой части канала ( ) область с максимальными значениями продольного поля
перемещается к внутреннему электроду в наиболее узкой части канала (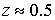 ) . Тем самым при больших ) . Тем самым при больших 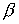 явным образом
проявляется то обстоятельство, что плазма по-прежнему “выталкивает” продольное
поле в область с меньшей концентрацией. Эта тенденция соответствует
распределению плотности, представленному на рис. 4б штриховыми линиями.
Максимум азимутальной скорости (штриховые кривые на рис. 4а) достигается на
выходе из канала в окрестности теперь уже внутреннего электрода, где плотность
имеет минимальные значения. Поэтому доля энергии, связанная с вращением, в
рассматриваемых течениях существенно меньше. В расчетах при явным образом
проявляется то обстоятельство, что плазма по-прежнему “выталкивает” продольное
поле в область с меньшей концентрацией. Эта тенденция соответствует
распределению плотности, представленному на рис. 4б штриховыми линиями.
Максимум азимутальной скорости (штриховые кривые на рис. 4а) достигается на
выходе из канала в окрестности теперь уже внутреннего электрода, где плотность
имеет минимальные значения. Поэтому доля энергии, связанная с вращением, в
рассматриваемых течениях существенно меньше. В расчетах при 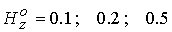 найдены соответственно
следующие значения коэффициента найдены соответственно
следующие значения коэффициента 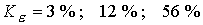 . Образование токовых
слоев и привязок тока не наблюдается. Таким образом, при больших значениях . Образование токовых
слоев и привязок тока не наблюдается. Таким образом, при больших значениях 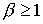 динамика
характеризуется качественно иной картиной распределения искомых величин. В этом
случае газодинамические факторы соизмеримы либо превалируют над
электромагнитными явлениями. динамика
характеризуется качественно иной картиной распределения искомых величин. В этом
случае газодинамические факторы соизмеримы либо превалируют над
электромагнитными явлениями.
Закономерности
происходящих процессов, их физическая интерпретация и возникающие течения
зависят от безразмерных параметров 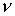 и и 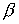 , участвующих в задаче. Эти параметры, в частности, могут
иметь одни и те же значения для различных комбинаций величин , участвующих в задаче. Эти параметры, в частности, могут
иметь одни и те же значения для различных комбинаций величин 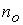 , , 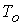 , , 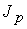 и и 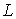 . Динамика плазмы в современных плазменных ускорителях
определяется малыми значениями . Динамика плазмы в современных плазменных ускорителях
определяется малыми значениями 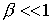 . .
3. Заключение
Разработана двумерная численная модель
для исследования динамики вращающихся осесимметричных потоков плазмы в канале
коаксиального плазменного ускорителя при наличии продольного магнитного поля.
В основе численных экспериментов лежат
МГД-уравнения в одножидкостном приближении. Верификация модели осуществлена с
помощью аналитических исследований двумерных течений, проведенных
ранее в рамках приближения плавного канала.
Установлено, что небольшое продольное
поле позволяет реализовать трансзвуковые течения в канале ускорителя при различных
условиях подачи плазмы на входе. При этом, на выходе доля энергии, обязанная
вращению, существенно меньше кинетической энергии направленного вдоль оси
потока плазмы. Продольное магнитное поле образует своеобразный дополнительный
канал для управления динамическими процессами в плазменном ускорителе и других
устройствах, принцип действия которых основан на использовании главным образом азимутальной компоненты магнитного поля.
Небольшое продольное магнитное поле,
действуя на протяжении всей длины канала, приводит к постепенно нарастающему
вращению плазмы. В результате наблюдается увеличение концентрации плазмы в
окрестности внешнего электрода. Данное обстоятельство указывает на возможность
преодоления или ослабления явления кризиса тока в каналах плазменных
ускорителей со сплошными электродами. В то же время при достаточно больших
значениях продольного поля в ряде случаев наблюдается формирование токовых
слоев в движущейся плазме и привязок тока на внешнем электроде.
Работа стимулирует дальнейшие теоретические,
численные и экспериментальные исследования, в частности, предполагается
разработка более сложных моделей, учитывающих эффект Холла и тензор
проводимости среды.
Литература
1. Морозов
А.И. Физические основы космических электрореактивных двигателей. М.: Атомиздат,
1978.
2. Энциклопедия
низкотемпературной плазмы. / Под ред. В.Е. Фортова. Т. III. М.: Наука, 2000. С. 407.
3. Морозов
А.И. Принципы коаксиальных
(квази)стационарных плазменных
ускорителей (КСПУ). //
Физика плазмы. 1990. Т.16, № 2. С. 131-146.
4. Белан В.Г.,
Золотарев С.П., Левашов В.Ф., Майнашев В.С., Морозов А.И., Подковыров В.Л.,
Скворцов Ю.В. Экспериментальное исследование квазистационарного плазменного
ускорителя, питаемого от индуктивного и емкостного накопителей . // Физика плазмы. 1990. Т.16, № 2. С.
176-185.
5. Tereshin V.I., Chebotarev V.V., Garkusha I.E., Makhlaj V.A., Mitina N.I., Morozov A.I., Solyakov D.G., Trubchaninov S.A., Tsarenko A.V., Wuerz H. Powerful
quasi-steady-state plasma accelerator for
fusion experiments. //
Brazilian Journal of Physics. 2002. V.
32, N 1. P.165-171.
6. Ананин
С.И., Асташинский В.М., Костюкевич Е.А., Маньковский А.А., Минько Л.Я. Интерферометрические исследования процессов в
квазистационарном сильноточном плазменном ускорителе. // Физика плазмы. 1998. Т.24, № 11. С. 1003-1009.
7. Alexandrov V.A., Dyakonov G.A., Popov G.A., Tikhonov
V.B., Tyutin V.K. Research of the influence of acceleration channel geometry
and external magnetic field on modes of plasma flow in quasistationary plasma
accelerator (QSPA) P-50A. // II-nd German-Russian conference on electric
propulsion engines and their technical applications. Moscow Aviation Institute,
1993. P.10.
8. Морозов
А.И., Соловьев Л.С. Стационарные течения плазмы в магнитном поле. // Вопросы теории плазмы. / Под ред.
М.А. Леонтовича. М.: Атомиздат,
1974. вып. 8. С. 3-87.
9. Брушлинский
К.В., Заборов А.М., Козлов А.Н., Морозов А.И., Савельев В.В. Численное
моделирование течений плазмы в КСПУ. // Физика плазмы. 1990.
Т. 16, № 2. С. 147-157.
10. Брушлинский К.В., Морозов
А.И. Расчет двумерных течений плазмы в каналах. // Вопросы теории плазмы. / Под
ред. М.А. Леонтовича. М.: Атомиздат,
1974. вып. 8. С. 88-163.
11. Козлов А.Н. Особенности
динамики плазмы в КСПУ в процессе установления течения. // Физика плазмы. 1992.
Т. 18, № 6. С.714-723.
12. Козлов А.
Н. Кинетика ионизации и рекомбинации в канале плазменного ускорителя. // Изв. РАН. МЖГ. 2000. № 5. С. 181-188.
13. Morozov A.I. and Savelyev V.V. Fundamentals of stationary plasma
thruster theory. // Reviews of plasma physics. / Edited by B.B.Kadomtsev
(deceased) and V.D.Shafranov.
Consultants Bureau, 2000. V. 21. P. 203-391.
14. Морозов А.И., Савельев В.В.
К теории пристеночной проводимости.
// Физика плазмы. 2001. Т. 27, № 6. С.607-613.
15. Козлов А.Н. Модель пристеночной
проводимости в окрестности макронеоднородной зеркально отражающей поверхности.
// Физика плазмы. 2002. Т. 28, № 2. С. 180-187.
16. Козлов А. Н. Влияние
продольного магнитного поля на эффект Холла в канале плазменного ускорителя.
// Изв. РАН. МЖГ. 2003. № 4. С. 165-175.
17. Брушлинский К.В., Жданова
Н.С. Стационарные МГД-течения в соплах с внешним продольным магнитным полем.
// Изв. РАН. МЖГ. 2004. № 3. С. 135-146.
18. Козлов А.Н. Численная модель
вращающихся осесимметричных потоков плазмы. Сопоставление с аналитической
моделью. Препринт № 48. М.:
ИПМ им. М.В. Келдыша РАН, 2004.
19. Kozlov A.N. Modeling of rotatory flows in the plasma accelerator channel
with longitudinal magnetic field. // Problems of Atomic Science and Technology.
Series: Plasma Physics (10). 2005. № 1. P. 104-106.
20. Козлов А.Н. Моделирование
осесимметричных вращающихся трансзвуковых потоков плазмы. // В сб. “Физика экстремальных состояний
вещества” под ред. Фортова В.Е. и др. Изд. ИПХМ РАН, Черноголовка. 2005. С.
226-227.
21. Брагинский С.И. Явление
переноса в плазме. // Вопросы теории плазмы.
/ Под ред. М.А. Леонтовича. М.:
Госатомиздат, 1963. вып. 1. С. 183-272.
22. Астрелин В.Т., Бурдаков
А.В., Поступаев В.В. Подавление теплопроводности и генерация ионно-звуковых
волн при нагреве плазмы электронным
пучком. // Физика плазмы. 1998. Т.
24, № 5. С. 450-462.
23. Бармин А.С., Успенский В.С.
Исследование нестационарного процесса распространения ионизуюшей ударной волны
в магнитном поле. // ПМТФ. 1989. № 3. С. 20-26.
24. Куликовский А.Г., Погорелов
Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических
систем уравнений. М.: Физматлит, 2001.
25. Волков Ю.А., Морозов
А.И. Структура приэлектродного
дрейфового слоя. Численная модель. //
Письма в ЖТФ. 1981. Т. 7, № 18. С. 1102-1106.
26. Морозов
А.И., Савельев В.В. Структура стационарных дебаевских слоев в разреженной
плазме вблизи диэлектрической поверхности. // Физика плазмы. 2004. Т. 30, № 4. С.330-338.
27. Landman I.S., Bazylev B.N., Garkusha I.E., Loarte A.,
Pestchanyi S.E., Safronov V.M. Simulation of tokamak armour erosion and plasma
contamination at intense transient heat fluxes in ITER. // Journ. Nucl. Mater.
2005. V. 761, P. 337-339.
28. Оран Э., Борис Д.П. Численное моделирование
реагирующих потоков. М.: Мир , 1990.
29. Радвогин Ю.Б. Квазимонотонные
многомерные разностные схемы второго порядка. Препринт № 19. М.: ИПМ им. М.В. Келдыша
АН СССР, 1991.
30. Дегтярев
Л.М., Фаворский А.П. Потоковый вариант
метода прогонки для разностных задач с сильно меняющимися коэффициентами. //
ЖВМ и МФ. 1969. Т. 9, N 1. С. 211-218.
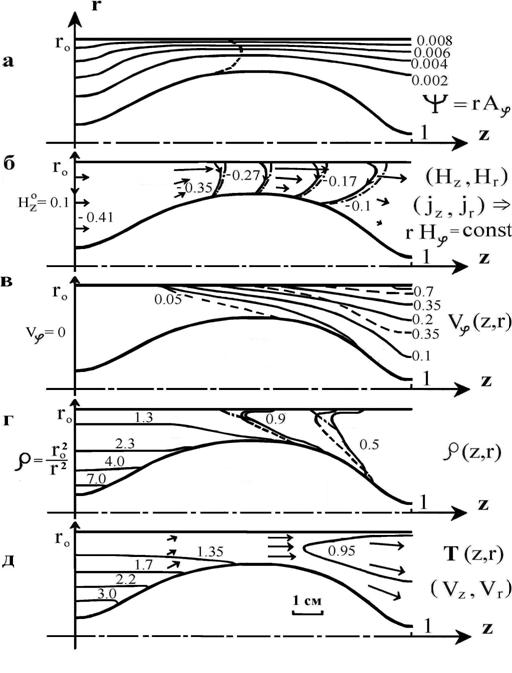
Рис. 1. Трансзвуковое течение плазмы в присутствии
продольного магнитного поля 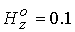 при неравномерной
подаче на входе : а – линии уровня функции при неравномерной
подаче на входе : а – линии уровня функции 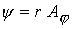 или магнитного потока
(сплошные кривые) и граница перехода через скорость быстрой магнитозвуковой
волны (штриховая линия); б –
векторное распределение магнитного поля
и электрический ток ( сплошные
линии уровня функции или магнитного потока
(сплошные кривые) и граница перехода через скорость быстрой магнитозвуковой
волны (штриховая линия); б –
векторное распределение магнитного поля
и электрический ток ( сплошные
линии уровня функции 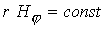 , штрих пунктирные
кривые - расчет при , штрих пунктирные
кривые - расчет при 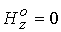 ) ; в – азимутальная скорость (сплошные
линии - расчет, штриховые кривые – аналитическая модель); г
– распределение плотности ( сплошные кривые - расчет, штриховые кривые –
аналитическая модель, штрих пунктирные кривые - расчет при ) ; в – азимутальная скорость (сплошные
линии - расчет, штриховые кривые – аналитическая модель); г
– распределение плотности ( сплошные кривые - расчет, штриховые кривые –
аналитическая модель, штрих пунктирные кривые - расчет при 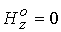 ); д – векторное поле скоростей и температура. ); д – векторное поле скоростей и температура.
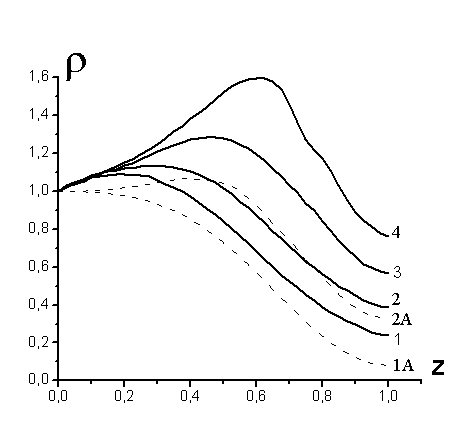
Рис.2. Распределение плотности вдоль внешнего
электрода: кривые 1 (1А) – расчет (аналитическая модель) при 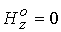 ; 2 (2А)
– расчет теория) при ; 2 (2А)
– расчет теория) при 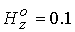 ; 3 – расчет при ; 3 – расчет при 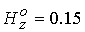 ; 4 - ; 4 - 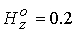
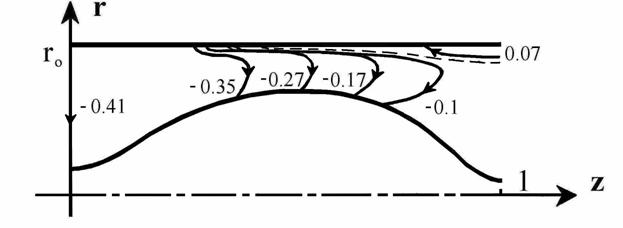
Рис. 3. Электрический ток при 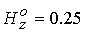
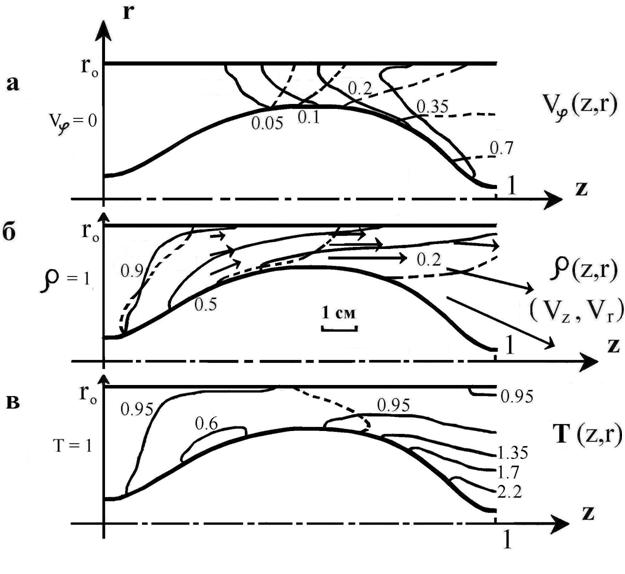
Рис. 4. Течение плазмы при наличии
продольного поля 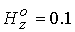 и равномерной подаче
на входе ( и равномерной подаче
на входе (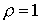 ): а – азимутальная скорость (на рис. а, б сплошные линии – расчет при ): а – азимутальная скорость (на рис. а, б сплошные линии – расчет при 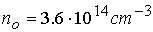 , штриховые кривые – , штриховые кривые –  ); б – векторное поле скоростей и распределение плотности; в
– температура и граница перехода через
скорость быстрой магнитозвуковой волны (штриховая линия). ); б – векторное поле скоростей и распределение плотности; в
– температура и граница перехода через
скорость быстрой магнитозвуковой волны (штриховая линия).
|

![]()

![]() и равномерной подаче
на входе (
и равномерной подаче
на входе (![]() ): а – азимутальная скорость (на рис. а, б сплошные линии – расчет при
): а – азимутальная скорость (на рис. а, б сплошные линии – расчет при ![]() , штриховые кривые –
, штриховые кривые – ![]() ); б – векторное поле скоростей и распределение плотности; в
– температура и граница перехода через
скорость быстрой магнитозвуковой волны (штриховая линия).
); б – векторное поле скоростей и распределение плотности; в
– температура и граница перехода через
скорость быстрой магнитозвуковой волны (штриховая линия). 
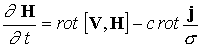
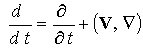
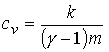
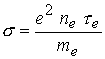
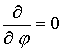 ). Действительно, в цилиндрической системе координат имеем
). Действительно, в цилиндрической системе координат имеем 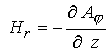
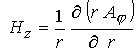
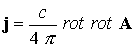 , что свидетельствует об адекватном описании процессов.
, что свидетельствует об адекватном описании процессов.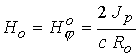
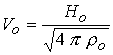
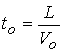
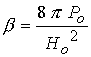
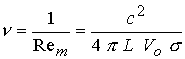
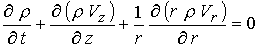
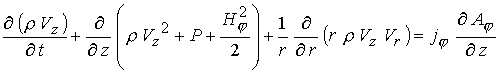
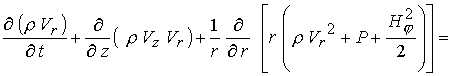
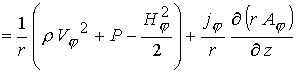
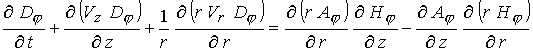
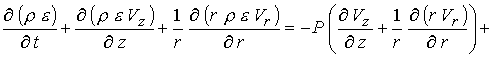
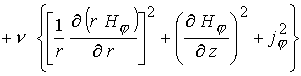
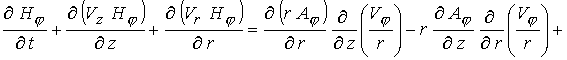
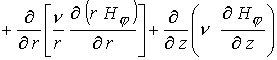
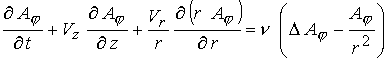
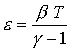
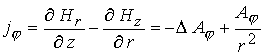
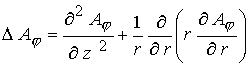 . В итоге имеем семь уравнений для переменных
. В итоге имеем семь уравнений для переменных 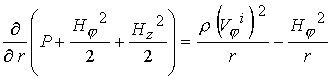
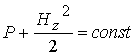
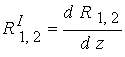
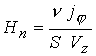 . Видно, что в случае идеально проводящей плазмы (магнитная
вязкость
. Видно, что в случае идеально проводящей плазмы (магнитная
вязкость 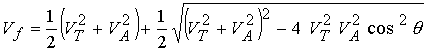 . Здесь
. Здесь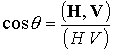 .
.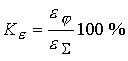
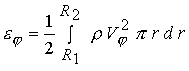 ,
,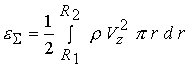 . В расчете
. В расчете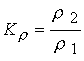 , при данном значении
, при данном значении 