Аннотация
В работе исследованы вынужденные колебания плазмы в круглой цилиндрической трубе под
действием периодически изменяющихся перепада давления плазмы вдоль оси трубы и полного тока.
Плазма предполагается квазинейтральной, несжимаемой, вязкой и электропроводной, в полном
объёме учитывается инерция электронов. В первой части работы представлено полное
математическое решение задачи о вынужденных колебаниях. Во второй – исследованы различные
предельные и частные случаи: приближение невязких электронов, МГД – предел,
электрон-позитронная плазма, низкочастотный и высокочастотный пределы и пр.
Abstract
In work the compelled fluctuations of plasma in a round cylindrical pipe under action of
periodically changing pressure difference of plasma along an axis of a pipe and a full
current are investigated. Plasma is supposed quasineutral, incompressible, viscous and
electro wire, inertia of electrons is in full considered. In the first part of work
the full mathematical decision of a problem on the compelled fluctuations is presented.
In the second - are investigated various limiting and and special cases: approach
nonviscous electrons, (МГД - a limit), electron-positronic plasma, low-frequency
and high-frequency limits and other.
Введение.
Задача о
нестационарном движении вязкой несжимаемой жидкости по цилиндрической трубе
круглого сечения с давних пор привлекала внимание исследователей. Этой задачей
занимались ещё Гельмгольц (H. Helmholtz, 1879г.) [1] и И.С.Громека (1882г.) [2]. Ёе частные случаи
были разобраны различными авторами [3,
4, 5]. В частности, в [5] рассмотрены вынужденные колебания вязкой несжимаемой
жидкости в цилиндрической трубе круглого сечения под действием гармонически
изменяющегося со временем перепада давления вдоль оси трубы (см. также [6]).
Представляет значительный интерес рассмотрение аналогичной задачи для
цилиндрической круглой трубы, заполненной плазмой. Однако вынужденные колебания
плазмы, в отличие от чисто гидродинамического случая, будут возбуждаться не
только гармонически изменяющимся по времени перепадом давления по оси трубы, но
и гармоническим по времени током, протекающим через трубу, причем частоты тока
(ω) и перепада давления (Ω) могут быть произвольными и различными.
Можно решить ещё более общую задачу, считая перепад давления по оси трубы и
полный ток произвольными периодическими по времени функциями с частотами Ω
и ω соответственно. Наконец, можно продвинуться ещё дальше, полагая
перепад давления и полный ток суммами конечного числа периодически зависящих от времени функций с
произвольными частотами.
Глубина
исследования вынужденных колебаний плазмы существенно зависит от принятой за
основу модели плазмы в трубе. В этой работе
будем считать плазму двухкомпонентной, полностью ионизованной,
несжимаемой, вязкой, электропроводной и квазинейтральной. Однако не будем
пренебрегать инерцией электронов и током смещения в уравнениях Максвелла, но
будем предполагать коэффициенты вязкости компонент плазмы и её
электропроводность константами, что существенно упрощает исследование.
Последнее допущено разумно, поскольку, как известно [7,8], в простейшем случае
коэффициенты вязкости электронов  , ионов , ионов 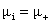 а также
электропроводность плазмы а также
электропроводность плазмы 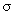 зависят только от
температуры. зависят только от
температуры.
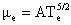 , , 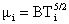 , , 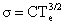 , ,
причем коэффициенты
пропорциональности 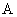 , , 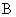 , , 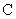 в гауссовской системе
единиц ( в гауссовской системе
единиц (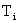 , , 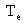 меряются меряются 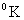 ) имеют экстремальные порядки: ) имеют экстремальные порядки: 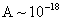 , , 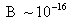 , , 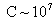 . Учитывая, что в уравнения динамики плазмы (см. ниже) входит
только . Учитывая, что в уравнения динамики плазмы (см. ниже) входит
только  , для существенного изменения , для существенного изменения 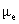 , , 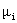 , ,  необходимо изменение необходимо изменение 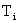 , , 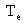 на несколько порядков.
Поэтому в широком диапазоне изменения температур на несколько порядков.
Поэтому в широком диапазоне изменения температур 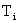 , , 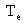 можно считать можно считать 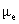 , , 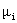 , ,  константами. константами.
В качестве
базовой модели динамики плазмы в трубе примем модель несжимаеамых жидкостей:
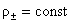 , , 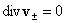 , ,
 , , 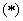
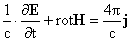 , ,
 , ,
где плотность тока 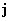 , тензоры напряжений , тензоры напряжений 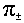 и вязких напряжений и вязких напряжений 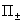 и силы трения и силы трения 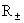 между компонентами
имеют вид: между компонентами
имеют вид:
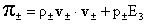 , , 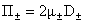 , ,
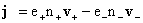 , , 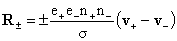 . .
Здесь 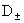 – тензор деформаций: – тензор деформаций:
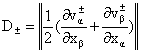 . .
Считается,
что 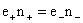  (условие квазинейтральности) и в начальный момент времени: (условие квазинейтральности) и в начальный момент времени:
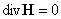 , , 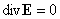 . .
Тогда в силу
уравнений системы  эти условия будут
выполнены и в любой другой момент времени. эти условия будут
выполнены и в любой другой момент времени.
Систему 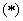 удобно редуцировать к
одножидкостной форме переходом к массовой скорости удобно редуцировать к
одножидкостной форме переходом к массовой скорости 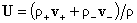 , , 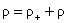 : :
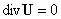 , ,
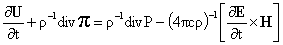 , ,
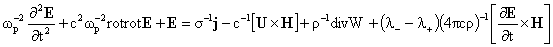 , , 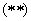
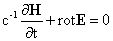 , ,
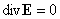 , ,
где 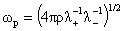 – плазменная частота, – плазменная частота, 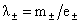 , , 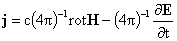 и в начальный момент
времени и в начальный момент
времени 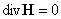 . Явные выражения для тензоров . Явные выражения для тензоров  вычислены ниже, см.
§1. Система вычислены ниже, см.
§1. Система  равносильна системе равносильна системе  и решается
относительно неизвестных функций и решается
относительно неизвестных функций 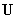 , , 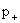 , , 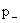 , , 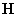 , , 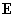 после чего скорости после чего скорости 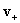 , , 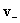 ищутся по явным
формулам: ищутся по явным
формулам:
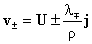 . .
§1. Уравнения динамики двухкомпонентной
несжимаемой плазмы.
Рассмотрим
поток вязкой несжимаемой гидродинамической электропроводной и квазинейтральной
двухкомпонентной плазмы. С учетом инерции как электронов, так и ионов динамика
потока подчиняется уравнениям:
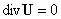 , ,
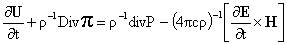 , ,
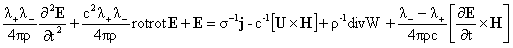 , (1) , (1)
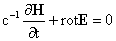 , ,
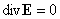 . .
В начальный момент 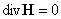 , и , и
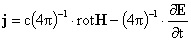 , , 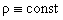 . (2) . (2)
Выражения для
тензоров 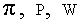 имеют вид: имеют вид:
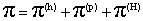 , ,  , (3) , (3)
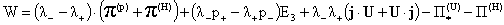 . .
Наконец,
тензоры  вычисляются по
формулам: вычисляются по
формулам:
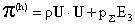 , , 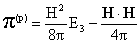 , , 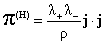 , (4) , (4)
где 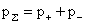 – суммарное
давление, а тензоры – суммарное
давление, а тензоры 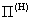 , , 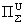 , , 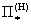 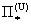 пропорциональны
тензорам деформаций пропорциональны
тензорам деформаций 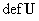 , , 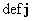 : :
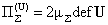 , , 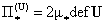 , , 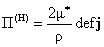 , , 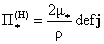 . (5) . (5)
Константы,
участвующие в предыдущих формулах, имеют вид:
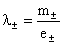 , ,  , , 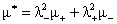 , , 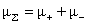 , (6) , (6)
где 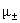 , , 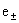 – массы и (абсолютные)
величины зарядов частиц плазменных компонент, – массы и (абсолютные)
величины зарядов частиц плазменных компонент,  , , 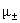 -
давления и гидродинамические вязкости компонент, -
давления и гидродинамические вязкости компонент, 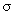 -
электропроводность плазмы. Если пренебречь зависимостью -
электропроводность плазмы. Если пренебречь зависимостью 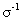 , , 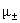 от температуры, то
соотношения от температуры, то
соотношения 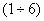 составляют замкнутую и определенную систему
уравнений для нахождения 11 скалярных неизвестных функций: компонент векторов составляют замкнутую и определенную систему
уравнений для нахождения 11 скалярных неизвестных функций: компонент векторов 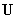 , , 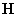 , , 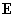 и давления и давления 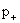 , , 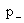 . Скорости . Скорости 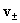 и плотности и плотности 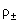 компонент плазмы
выражаются через решение системы компонент плазмы
выражаются через решение системы  по формулам: по формулам:
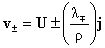 , , 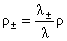 , , 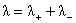 . (7) . (7)
С учетом
зависимости 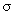 и и 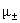 от температуры систему от температуры систему
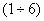 надо дополнить уравнениями для температур надо дополнить уравнениями для температур  плазменных компонент: плазменных компонент:
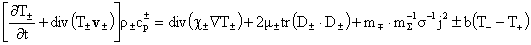 , (8) , (8)
где 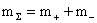 , , 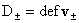 , , 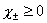 -
коэффициенты переноса, -
коэффициенты переноса, 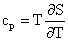 -
удельная теплоемкость при постоянном давлении ( -
удельная теплоемкость при постоянном давлении (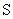 -
плотность энтропии). Для идеального газа -
плотность энтропии). Для идеального газа 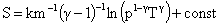 ( (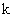 – постоянная Больцмана, – постоянная Больцмана, 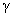 ‒
показатель адиабаты), ‒
показатель адиабаты),  . В итоге, система . В итоге, система 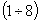 полностью описывает изменения скоростей, давлений, температур,
электрического и магнитного полей несжимаемой квазинейтральной вязкой
электропроводной плазмы. Она пригодна для исследования высокочастотных
процессов в плазме, равноправным образом учитывающих динамику обеих компонент,
в частности их взаимодействие, и в то же время является одножидкостной. Для
низко частотных процессов в системе полностью описывает изменения скоростей, давлений, температур,
электрического и магнитного полей несжимаемой квазинейтральной вязкой
электропроводной плазмы. Она пригодна для исследования высокочастотных
процессов в плазме, равноправным образом учитывающих динамику обеих компонент,
в частности их взаимодействие, и в то же время является одножидкостной. Для
низко частотных процессов в системе 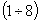 надо везде положить надо везде положить 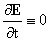 , , 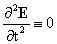 . Физически это равносильно игнорированию тока смещения.
Тогда снова получается замкнутая и определенная система уравнений для
нахождения величин . Физически это равносильно игнорированию тока смещения.
Тогда снова получается замкнутая и определенная система уравнений для
нахождения величин 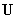 , , 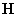 , , 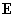 , , 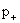 , , 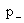 . .
§2. Задача о течении плазмы в цилиндрическом
канале.
Рассмотрим течение плазмы по цилиндрической трубе радиуса 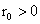 , ось которой совпадает с осью OZ. Будем считать , ось которой совпадает с осью OZ. Будем считать 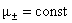 , , 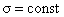 и предположим, что все
параметры течения, за исключением давлений, обладают цилиндрической симметрией и предположим, что все
параметры течения, за исключением давлений, обладают цилиндрической симметрией 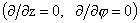 , а давления осесимметричны, , а давления осесимметричны, 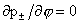 . Кроме того, считаем что отсутствуют особенности параметров
течения на оси OZ.
Тогда из условий . Кроме того, считаем что отсутствуют особенности параметров
течения на оси OZ.
Тогда из условий 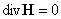 , , 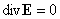 , , 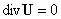 , следуют равенства , следуют равенства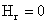 , , 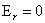 , , 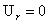 , а из равенства (2) тогда вытекает соотношение , а из равенства (2) тогда вытекает соотношение 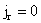 . В итоге система . В итоге система 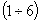 распадается на две
подсистемы: распадается на две
подсистемы:
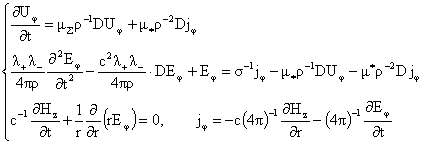 (I) (I)
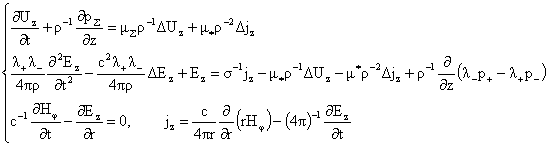 (II) (II)
где 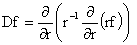 , , 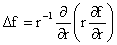 , и уравнения для нахождения давлений , и уравнения для нахождения давлений 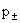 : :
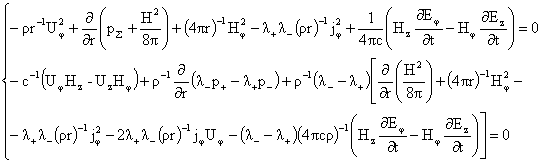 (III) (III)
Из уравнений (III) вытекает, что 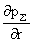 , , 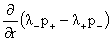 зависят только от t и r, но не от z. Отсюда следует, что зависят только от t и r, но не от z. Отсюда следует, что 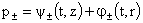 . Но тогда из первых двух уравнений системы (II) вытекает, что . Но тогда из первых двух уравнений системы (II) вытекает, что  . Откуда (присоединяя функции . Откуда (присоединяя функции 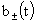 к к  ) получим: ) получим:
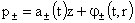 , , 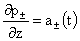 , , 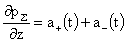 , ,
где функции 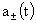 , определяющие перепад давлений вдоль оси Z в каждый момент времени, должны
задаваться, а функции , определяющие перепад давлений вдоль оси Z в каждый момент времени, должны
задаваться, а функции  ищутся из системы (III) после решения систем (I) и (II). Далее рассмотрим преимущественно
случай, когда ищутся из системы (III) после решения систем (I) и (II). Далее рассмотрим преимущественно
случай, когда 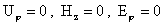 тогда и тогда и 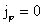 и система (I) удовлетворяется
тождественно. Для нахождения функций и система (I) удовлетворяется
тождественно. Для нахождения функций 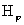 , , 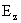 , , 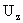 , , 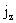 имеем систему (II), которую надо дополнить
начальными и граничными условиями. имеем систему (II), которую надо дополнить
начальными и граничными условиями.
Граничные
условия имеют вид:
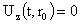 , , 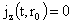 , (условие
“прилипания”), (9) , (условие
“прилипания”), (9)
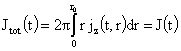 , (10) , (10)
где 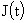 – заданная
функция, а – заданная
функция, а 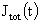 – полный ток,
протекающий в момент времени – полный ток,
протекающий в момент времени 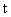 через сечение трубы.
Кроме того, к числу граничных условий относится ограниченность функций через сечение трубы.
Кроме того, к числу граничных условий относится ограниченность функций 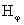 , , 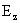 , , 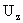 , , 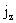 в окрестности в окрестности 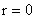 . .
Итак,
градиенты давлений 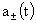 задают правые части
системы (II), а функция задают правые части
системы (II), а функция
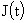 определяет
граничные условия. Далее будем рассматривать также и комплексные решения
системы (II). Поскольку
система (II) линейная с
вещественными коэффициентами, то, во-первых, для её решения верен принцип
суперпозиции и, во-вторых, вещественная и мнимая части комплексного решения
системы (II) являются
её вещественными решениями. определяет
граничные условия. Далее будем рассматривать также и комплексные решения
системы (II). Поскольку
система (II) линейная с
вещественными коэффициентами, то, во-первых, для её решения верен принцип
суперпозиции и, во-вторых, вещественная и мнимая части комплексного решения
системы (II) являются
её вещественными решениями.
Пусть теперь
правые части и граничные условия системы (II) меняются по гармоническому закону, т.е. имеют вид:
 , , 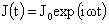 , , 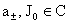 , (11) , (11)
Тогда
начальные условия теряют смысл и решение системы (II) ищется в виде:
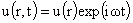 , , 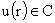 (12) (12)
где 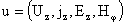 , а , а 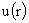 называется вектором комплексных амплитуд решения называется вектором комплексных амплитуд решения 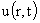 . Ниже, в §3, указан рецепт нахождения решения вида (12), в
частности, будет доказана его единственность. . Ниже, в §3, указан рецепт нахождения решения вида (12), в
частности, будет доказана его единственность.
Если правые
части и граничные условия имеют более общий вид:
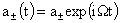 , , 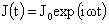 , , 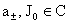 , ,
и, вообще говоря, 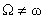 , то в силу принципа суперпозиции решение системы (II) является суммой
двух решений: , то в силу принципа суперпозиции решение системы (II) является суммой
двух решений:
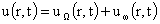 , ,
где решения  и и 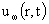 имеют вид имеют вид
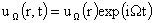 , , 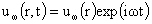
и определяются разными правыми
частями и граничными условиями. Для решения 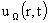 имеем имеем 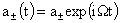 , , 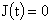 , а для решения , а для решения 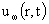 полагаем полагаем 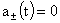 , , 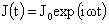 . Оба этих решения являются частными случаями решений системы
(II) вида (12) с
правыми частями и граничными условиями вида (11) и поэтому ищутся по методе §3.
Заметим, что принцип суперпозиции не
распространяется на радиальную часть давления, зависящую в каждый момент
времени только от r
(т.е. на функции . Оба этих решения являются частными случаями решений системы
(II) вида (12) с
правыми частями и граничными условиями вида (11) и поэтому ищутся по методе §3.
Заметим, что принцип суперпозиции не
распространяется на радиальную часть давления, зависящую в каждый момент
времени только от r
(т.е. на функции  ), поскольку хотя уравнения системы (III) относительно ), поскольку хотя уравнения системы (III) относительно  , ,  линейны по линейны по 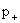 , , 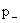 , но их правые части нелинейны по , но их правые части нелинейны по 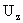 , , 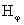 , , 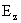 . В частности, . В частности, 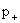 , , 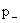 при при 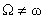 не являются
гармоническими по времени колебаниями, а при не являются
гармоническими по времени колебаниями, а при 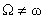 изменяются
гармонически по времени, но с частотой изменяются
гармонически по времени, но с частотой 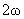 , а не , а не 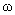 . Интересен вопрос, как соотношение частот . Интересен вопрос, как соотношение частот 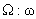 влияет на характер
решения влияет на характер
решения 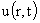 и радиальные части
давлений и радиальные части
давлений 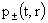 , в частности, могут ли быть резонансные явления? , в частности, могут ли быть резонансные явления?
Переход к
любым периодически изменяющимся во времени перепадам давлений и полным токам
очевиден. Пусть 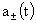 и и 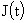 - периодические функции с периодами - периодические функции с периодами 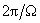 и и 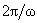 соответственно.
Разлагая эти функции в ряд Фурье, соответственно.
Разлагая эти функции в ряд Фурье,
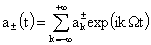 , , 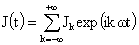
и пользуясь принципом
суперпозиции, получим формальное
решение системы (II)
для правой части 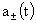 и граничного условия и граничного условия 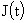 : :
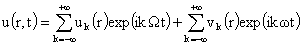 , ,
где 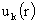 – вектор комплексных
амплитуд решения системы (II)
для частоты – вектор комплексных
амплитуд решения системы (II)
для частоты 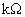 и и 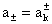 , , 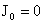 , а , а 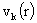 – вектор комплексных
амплитуд решения системы (II)
для частоты – вектор комплексных
амплитуд решения системы (II)
для частоты 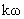 и и 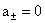 , , 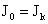 . .
Можно пойти
ещё дальше и, опираясь на принцип суперпозиции, указать формальное решение
системы (II) в случае,
когда перепады давлений вдоль оси трубы и полный ток есть сумма конечного числа
периодических колебаний с произвольными частотами. Однако детальный анализ всех
этих вопросов (включая исследование сходимости формальных рядов, задающих
решения) выходит за рамки настоящей работы.
§3. Общий случай вязкой плазмы
Рассмотрим
общий случай отличных от нуля вязкостей компонент плазмы, 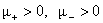 . Ищем решение системы (II) вида . Ищем решение системы (II) вида 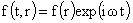 , для правых частей и граничных условий вида , для правых частей и граничных условий вида 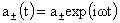 , , 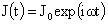 , , 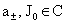 . Тогда для комплексных амплитуд получим следующую систему
уравнений: . Тогда для комплексных амплитуд получим следующую систему
уравнений:
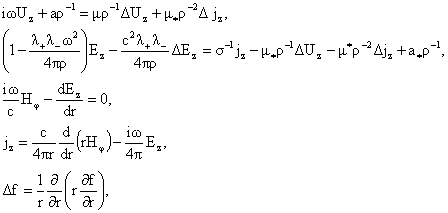 , (13) , (13)
где 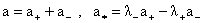 . Исключая посредством третьего уравнения полученной системы
из числа неизвестных . Исключая посредством третьего уравнения полученной системы
из числа неизвестных 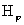 , получим неоднородную систему трех линейных обыкновенных
дифференциальных уравнений второго порядка относительно трёх функций , получим неоднородную систему трех линейных обыкновенных
дифференциальных уравнений второго порядка относительно трёх функций 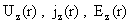 : :
 (14) (14)
Система (14) имеет
частное решение, состоящее из констант 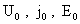 , являющихся решением линейной системы: , являющихся решением линейной системы:


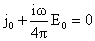
Откуда получим:
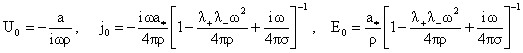 (15)
(15)
Общее решение
системы (14) есть сумма решения (15) и общего решения однородной системы (14).
При этом нас интересуют только решения, ограниченные в нуле. Относительно
дифференциального оператора 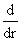 система (14) является
системой линейных уравнений с переменными
коэффициентами, а относительно дифференциального оператора система (14) является
системой линейных уравнений с переменными
коэффициентами, а относительно дифференциального оператора 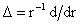 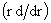 она является линейной
системой с постоянными
коэффициентами. Поэтому её решения можно искать по той же схеме, которая
используется для решения линейных обыкновенных дифференциальных уравнений с
постоянными коэффициентами. Так что ищем
решения однородной системы (14) в
виде линейной комбинации собственных функций оператора она является линейной
системой с постоянными
коэффициентами. Поэтому её решения можно искать по той же схеме, которая
используется для решения линейных обыкновенных дифференциальных уравнений с
постоянными коэффициентами. Так что ищем
решения однородной системы (14) в
виде линейной комбинации собственных функций оператора 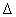 , ограниченных в нуле. , ограниченных в нуле.
Предварительно
найдем собственные функции оператора 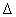 . Пусть . Пусть 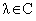 , , 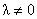 . Рассмотрим ограниченные в нуле решения уравнения . Рассмотрим ограниченные в нуле решения уравнения

(это и есть искомые собственные
функции). Последнее уравнение заменой независимой переменной 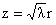 сводится к
модифицированному уравнению Бесселя порядка 0: сводится к
модифицированному уравнению Бесселя порядка 0:
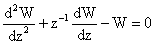 . .
Откуда
(учитывая ограниченность решения в нуле) 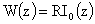 , ,  и значит собственные
функции оператора и значит собственные
функции оператора  , ограниченные в нуле, имеют вид: , ограниченные в нуле, имеют вид:
 , ,  , , 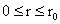 , ,
где 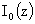 - функция Бесселя
мнимого аргумента индекса 0. Указанные собственные функции отвечают
собственному значению - функция Бесселя
мнимого аргумента индекса 0. Указанные собственные функции отвечают
собственному значению 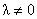 . .
Теперь,
подберем  так чтобы функции так чтобы функции 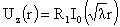 , , 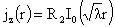 , , 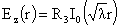 являлись решением
однородной системы (14). Подставляя указанные функции в однородную систему
(14), получим для нахождения являлись решением
однородной системы (14). Подставляя указанные функции в однородную систему
(14), получим для нахождения 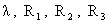 систему уравнений: систему уравнений:
 (16) (16)
Система (16),
линейная по 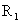 , , 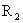 , , 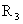 , имеет нетривиальное решение , имеет нетривиальное решение 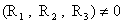 тогда и только тогда,
когда её определитель равен 0. Это дает кубическое уравнение для нахождения тогда и только тогда,
когда её определитель равен 0. Это дает кубическое уравнение для нахождения 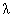 : :
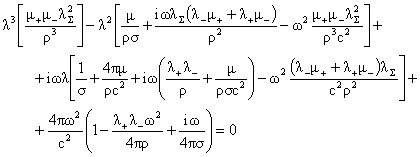 (17) (17)
Если 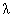 – корень кубического
уравнения (17), то вектор – корень кубического
уравнения (17), то вектор
 , , 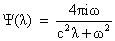 , , 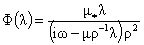 . .
лежит в пространстве решений
системы (16). Поэтому, если 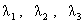 – попарно различные корни кубического уравнения (17), то
векторная функция – попарно различные корни кубического уравнения (17), то
векторная функция
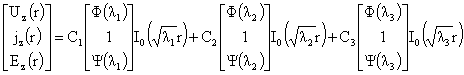
где 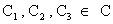 – произвольные
константы, является, очевидно, решением однородной системы (14),
удовлетворяющим условиям ограниченности в нуле. Значит общее решение
неоднородной системы (14), ограниченное в нуле, задается формулами: – произвольные
константы, является, очевидно, решением однородной системы (14),
удовлетворяющим условиям ограниченности в нуле. Значит общее решение
неоднородной системы (14), ограниченное в нуле, задается формулами:
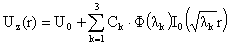 , ,
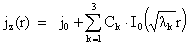 ,
(18) ,
(18)
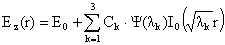 , ,
где 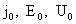 вычисляются по
формулам (15). Константы вычисляются по
формулам (15). Константы 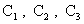 ищутся из граничных
условий прилипания (9) и заданного полного тока (10). Условия прилипания ищутся из граничных
условий прилипания (9) и заданного полного тока (10). Условия прилипания 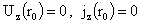 дают первые два
уравнения на три константы дают первые два
уравнения на три константы 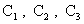 : :
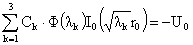 , , 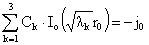 . (19) . (19)
Чтобы получить третье уравнение,
предварительно вычислим (с учётом тождества 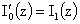 , см. [9]): , см. [9]):
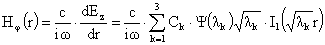
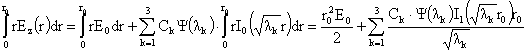
где 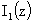 - функция Бесселя
мнимого аргумента индекса 1 и использовано тождество - функция Бесселя
мнимого аргумента индекса 1 и использовано тождество 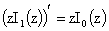 , см. [9]. Подставим эти выражения в четвертое уравнение
системы (II), проинтегрированное
от , см. [9]. Подставим эти выражения в четвертое уравнение
системы (II), проинтегрированное
от 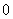 до до 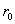 : :
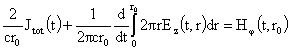 ,
(20) ,
(20)
где надо положить 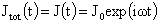 , , 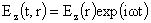 , , 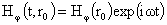 . Тем самым, в частности, задействовано граничное условие (10).
С учетом предварительного вычисления и выражения для . Тем самым, в частности, задействовано граничное условие (10).
С учетом предварительного вычисления и выражения для 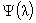 приходим к третьему
уравнению для нахождения приходим к третьему
уравнению для нахождения 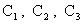 : :
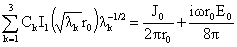 (21) (21)
Найдя из
системы (19), (21) трех линейных уравнений с тремя неизвестными константы 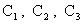 , получим, согласно
(18), искомое распределение тока. Вот явные формулы: , получим, согласно
(18), искомое распределение тока. Вот явные формулы:
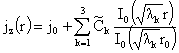 , , 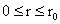 (22)
(22)
 , ,
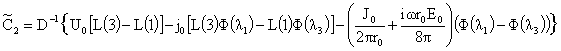 , ,
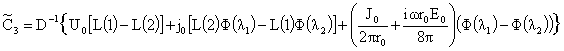 , ,
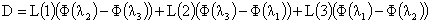 , ,
где введено обозначение 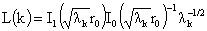 , , 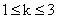 . .
Формула (22)
значительно упрощается в чисто электродинамическом случае, когда отсутствует
перепад гидродинамического давления по оси Z. Тогда 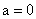 , , 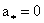 и значит, согласно
(15), и значит, согласно
(15), 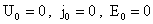 . Поэтому формула (22) приводит к такой формуле для
распределения тока: . Поэтому формула (22) приводит к такой формуле для
распределения тока:
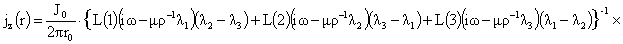 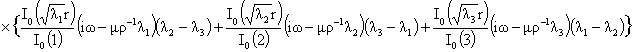 где где 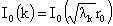 , , 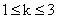 . Итак, получено решение поставленной задачи в случае, когда
все корни кубического уравнения (17) простые. . Итак, получено решение поставленной задачи в случае, когда
все корни кубического уравнения (17) простые.
§4. Общий случай вязкой плазмы: метод исключений
Если
кубическое уравнение (17) имеет кратные корни, то однородную систему (14)
нельзя решить изложенным выше способом. Применим в этом случае метод исключений. Исключая 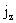 из однородной системы
(14) посредством третьего уравнения и из однородной системы
(14) посредством третьего уравнения и 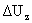 из второго уравнения
системы посредством первого уравнения. В результате получим следующие выражения
для из второго уравнения
системы посредством первого уравнения. В результате получим следующие выражения
для 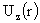 и и 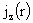 через через 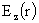 : :
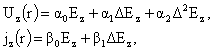 (24)
(24)
где
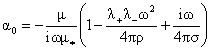 , , 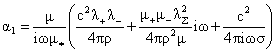 , ,
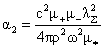 , ,  , , 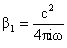 . .
Подставляя эти выражения во
второе уравнение однородной системы (14), получим следующее уравнение на
функцию 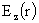 : :
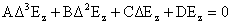 , ,
где 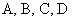 совпадают с коэффициентами при степенях совпадают с коэффициентами при степенях 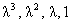 кубического многочлена
(17) соответственно. Поэтому, если кубического многочлена
(17) соответственно. Поэтому, если 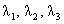 – корни (17) с учётом
кратности, то уравнение на – корни (17) с учётом
кратности, то уравнение на 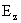 можно переписать в
оператором виде: можно переписать в
оператором виде:
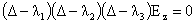 ,
(25) ,
(25)
причем операторные скобки
коммутируют друг с другом. В силу соотношений (24), поиск ограниченных в нуле
решений однородной системы (14) эквивалентен поиску решений уравнения (25),
удовлетворяющих условию ограниченности:
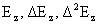 ограничены в нуле.
Практическое решение уравнения (25) основано на следующих результатах. ограничены в нуле.
Практическое решение уравнения (25) основано на следующих результатах.
Теорема 1. Пусть корни 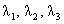 попарно различны.
Тогда: попарно различны.
Тогда:
1) шесть функций 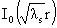 , , 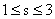 , ,  , , 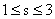 образуют базис в
пространстве решений уравнения (25), образуют базис в
пространстве решений уравнения (25),
2) три функции 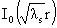 , , 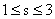 образуют базис в
подпространстве всех тех решений уравнения (25), которые удовлетворяют условию
ограниченности. образуют базис в
подпространстве всех тех решений уравнения (25), которые удовлетворяют условию
ограниченности.
Теорема 2. Пусть среди корней
(17) один корень двукратный, а один – простой: 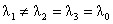 . Тогда: . Тогда:
1) шесть функций 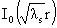 , , 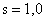 , , 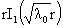 , ,  , ,  , , 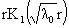 образуют базис в пространстве
решений уравнения (25), образуют базис в пространстве
решений уравнения (25),
2) три функции  , , 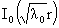 , , 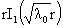 , образуют базис в подпространстве всех тех решений уравнения
(25), которые удовлетворяют условию ограниченности. , образуют базис в подпространстве всех тех решений уравнения
(25), которые удовлетворяют условию ограниченности.
Теорема 3. Пусть уравнение
(17) имеет один трёхкратный корень 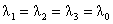 . Тогда: . Тогда:
1) шесть функций 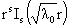 , , 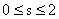 , , 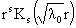 , , 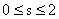 образуют базис в
пространстве решений уравнения (25), образуют базис в
пространстве решений уравнения (25),
2) три функции 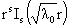 , , 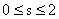 образуют базис в
подпространстве всех тех решений уравнения (25), которые удовлетворяют условию
ограниченности. образуют базис в
подпространстве всех тех решений уравнения (25), которые удовлетворяют условию
ограниченности.
В этих формулировках 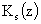 – функция Макдональда индекса – функция Макдональда индекса 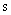 , а , а 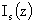 – функция Бесселя мнимого аргумента индекса – функция Бесселя мнимого аргумента индекса 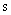 . Для нижеследующего важно, что функции . Для нижеследующего важно, что функции 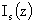 , ,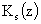 образуют базис в пространстве решений уравнения образуют базис в пространстве решений уравнения
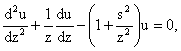
в частности, они линейно
независимы (см. [9]).
Теорема 1 даёт обоснование изложенному выше, в §3, способу решения системы (II) в случае простых корней. Теоремы 2 и 3 позволяют указать
практический способ нахождения решения системы (II) в случае кратных корней уравнения (17).
Разберем для примера подробно случай, когда кубический многочлен (17) имеет
один простой и один двукратный корни, обозначаемые 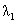 и и 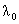 соответственно. Согласно Теореме 2, искомое решение уравнения (25) ищется в виде: соответственно. Согласно Теореме 2, искомое решение уравнения (25) ищется в виде:
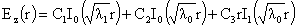 , ,  (26) (26)
Подставляя это выражение в (24), находим 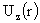 , , 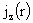 . Воспользуемся при
этом технической леммой. . Воспользуемся при
этом технической леммой.
Лемма 1. Пусть
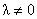 , , 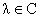 , тогда: , тогда:
1)
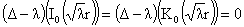 , ,
2)
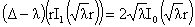 , , 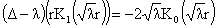 , ,
3)
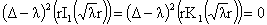
4)
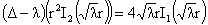 , , 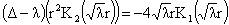 . .
Из леммы 1, в частности,
следуют формулы:
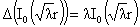 , , 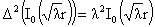 , ,
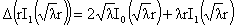 , , 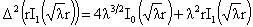 . .
Используя эти преобразования, находим:
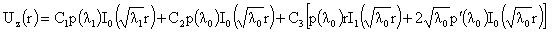 ,(27) ,(27)
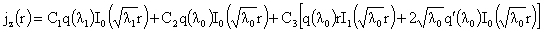 , ,
где
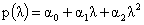 , ,  , ,
а коэффициенты 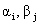 , ,  , , 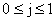 вычисляются так же как
и в формулах (24). Значит общее решение неоднородного уравнения (14) имеет вид: вычисляются так же как
и в формулах (24). Значит общее решение неоднородного уравнения (14) имеет вид:
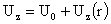 , , 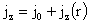 , , 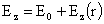 , (28) , (28)
где 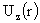 , , 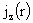 , , 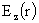 вычисляются по
формулам (26), (27), а константы вычисляются по
формулам (26), (27), а константы 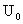 , , 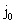 , , 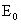 – по формулам (15).
Константы – по формулам (15).
Константы 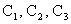 ищутся из граничных
условий. Условия прилипания (9) дают ищутся из граничных
условий. Условия прилипания (9) дают 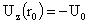 , , 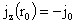 , откуда получаются два уравнения на искомые константы: , откуда получаются два уравнения на искомые константы:
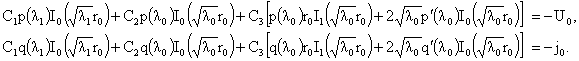 (29) (29)
Третье уравнение получается из граничного условия (20), которое даёт:
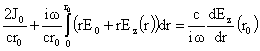
Подставляя сюда выражение (26) для 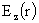 после несложных
преобразований приходим к третьему уравнению для после несложных
преобразований приходим к третьему уравнению для 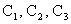 : :
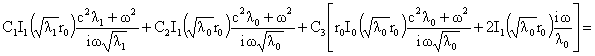 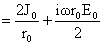 (30)
(30)
Находя из системы трёх линейных уравнений (29), (30) константы 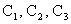 (скажем, по правилу
Крамера), по формулам (26), (27) – функции (скажем, по правилу
Крамера), по формулам (26), (27) – функции 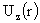 , , 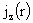 , , 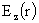 , получим по формулам (29) интересующее нас решение
неоднородного уравнения (14). Детали легко восстанавливаются. , получим по формулам (29) интересующее нас решение
неоднородного уравнения (14). Детали легко восстанавливаются.
Теоремы 1-3 доказываются единообразным способом.
Разберем для примера доказательство Теоремы
2. Заметим, что результаты этих теорем допускают следующее значительное
обобщение.
Теорема 4. Рассмотрим
однородное уравнение:
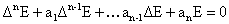 , , 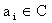 , , 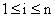 , , 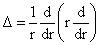
Пусть  – корни
характеристического многочлена – корни
характеристического многочлена
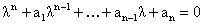
кратности  ( (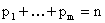 ) соответственно. Тогда: ) соответственно. Тогда:
1) 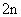 функций функций 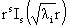 , ,  , , 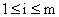 , , 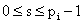 образуют базис в пространстве решений
однородного уравнения, образуют базис в пространстве решений
однородного уравнения,
2)
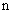 функций функций 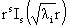 , , 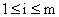 , , 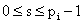 образуют базис в подпространстве всех тех
решений однородного уравнения, для которых функции образуют базис в подпространстве всех тех
решений однородного уравнения, для которых функции 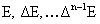 ограничены в нуле. ограничены в нуле.
Доказательство Теоремы 2.
1) Из Леммы 1 следует, что все
перечисленные в первой части теоремы функции являются решениями однородного
уравнения (25). Убедимся, что эти функции линейно независимы. Тогда из
размерностных соображений будет следовать, что они образуют базис в
пространстве всех решений уравнения (25) (уравнение (25) – обыкновенное
дифференциальное уравнение 6-го порядка, поэтому пространство его комплексных
решений имеет размерность 6, значит любые шесть линейно независимых функций
этого пространства образуют его базис).
Итак, пусть
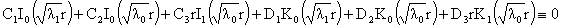 (*) (*)
Применяя к этому равенству оператор 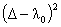 , с учётом Леммы 1,
получим: , с учётом Леммы 1,
получим:

Но 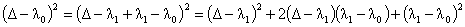 . Поэтому из Леммы 1
вытекает: . Поэтому из Леммы 1
вытекает:
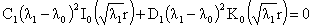
Поскольку 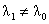 , а функции , а функции 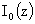 , , 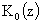 линейно независимы, отсюда вытекает линейно независимы, отсюда вытекает 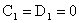 . Учитывая последние
равенства в (*) и применяя к (*) оператор . Учитывая последние
равенства в (*) и применяя к (*) оператор 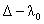 с учётом Леммы 1, получим: с учётом Леммы 1, получим:
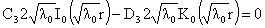
Из линейно независимости функций 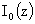 , , 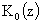 теперь следуют равенства теперь следуют равенства 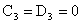 . Но тогда равенство
(*) сведётся к соотношению: . Но тогда равенство
(*) сведётся к соотношению:
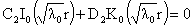
Ещё раз используя независимость функций 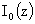 , , 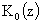 , заключаем , заключаем 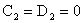 . Итак, все коэффициенты линейной комбинации (*) равны нулю.
Значит интересующие нас функции линейно независимы, ч.т.д. . Итак, все коэффициенты линейной комбинации (*) равны нулю.
Значит интересующие нас функции линейно независимы, ч.т.д.
2) Из предыдущего доказательства следует, что функции, перечисленные во
второй части теоремы, линейно независимы, а из Леммы 1 вытекает, что каждая из них (а значит и любая их линейная
комбинация) удовлетворяют условию ограниченности (свойства 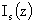 , , 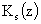 , см. в [9]).
Осталось проверить, что любое решение , см. в [9]).
Осталось проверить, что любое решение 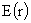 уравнения (25), удовлетворяющее условию
ограниченности, является их линейной комбинацией. Согласно предыдущему
доказательству, уравнения (25), удовлетворяющее условию
ограниченности, является их линейной комбинацией. Согласно предыдущему
доказательству, 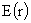 разлагается в сумму: разлагается в сумму:
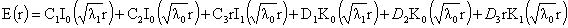
Поскольку 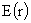 удовлетворяет
условию ограниченности, то функции удовлетворяет
условию ограниченности, то функции
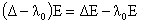 , ,
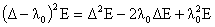
ограничены в нуле. Но по Лемме 1:

Т.к. 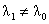 , то , то 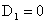 (ибо (ибо 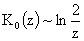 , , 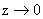 , см. [9] и значит при , см. [9] и значит при 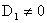 функция функция 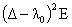 заведомо не ограничена
в нуле). Учитывая последнее равенство и применяя Лемму 1, получим: заведомо не ограничена
в нуле). Учитывая последнее равенство и применяя Лемму 1, получим:
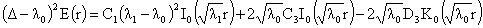
Теперь из ограниченности в нуле
функции 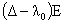 следует следует 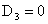 . Но тогда . Но тогда
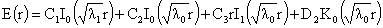
Из ограниченности 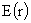 в нуле теперь
вытекает в нуле теперь
вытекает 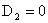 . Итак . Итак 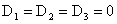 , откуда вытекает доказательство утверждения, ч.т.д. Теорема
доказана. , откуда вытекает доказательство утверждения, ч.т.д. Теорема
доказана.
Литература
1.
H.
Helmholtz, Uber electrishe Grenzschichten, Ann. d. Phys. u. Chem. 7, 1879,
337-382
2. И.
С. Громека, К теории движения жидкости в узких цилиндрических трубах, Ученые
записки Казанского ун-та, 1882. (Соб. соч. Изд. АНСССР, 1952, стр. 149-171)
3.
P.
Szymanski, Quelques solutions exactes des equations de l`hydrodynamique de
fluide visqueux dans un tube cylinderique, Journ. de Mathem. 11, 1932, 67-107
4. А.
И. Лурье, Операционное исчесление, ОНТИ, 1935, стр 205-209
5. П.
Лямбоси, Вынужденные колебания несжимаемой вязкой жидкости в жёстком
горизонтальной трубе, В сб. “Механика”, вып. 3, ИЛ, М., 1953, стр 67-77
6. Л.
Г. Лойцянский, Механика жидкости и газа, “Наука”, М., 1978, стр. 400-403
7. Брагинский
С. И., В сб. “Вопросы теории плазмы”. Под ред. М. А. Леонтовича. Вып. 1, М., Госатомиздат, 1963, с.
183
8. В.
С. Имшенник, Н. А. Боброва, Динамика столкновительной плазмы, Энергоатомиздат,
М., 1997., стр. 9 - 46 .
9. Н.
Н. Лебедев, Специальные функции и их приложения, ГИТТЛ, М., 1953, стр. 148-151
|