1 Введение

Объекты наномира слишком малы для непосредственного наблюдения и изучения, но слишком велики для того, чтобы изучать их поведение при помощи квантовомеханических моделей, построенных «из первых принципов». Характеристики наночастиц флуктуируют во времени и пространстве, а число объединяющихся в наносистемы частиц недостаточно велико, чтобы рассматривать эти системы в качестве статистических ансамблей [1].

Модели, которые строятся в настоящее время, обладают высокой сложностью, и их исследование требует значительных вычислительных мощностей. Например, для моделирования лазерного диода необходимо решение системы уравнений Шокли, уравнений Максвелла и уравнения Шредингера для квантовой ямы. Современные вычислительные системы не позволяют решать такие задачи, по крайней мере в трехмерном случае, а в нанотехнологии существуют и гораздо более сложные задачи [1].

В работе [2] приводится обзор классов моделей, которые применяются при моделировании объектов наномира:

·        Шредингеровские модели

·        Модели молекулярной динамики на первых принципах

·        Модели классической молекулярной динамики

·        Решеточные модели и алгоритмы вероятностных асинхронных клеточных автоматов

·        Модели типа реакция-диффузия

С точки зрения авторов сборника [1], «очевидная»  методология моделирования объектов наномира находится в очевидном тупике: прогресс достигается в основном за счет создания более мощных суперкомпьютеров, которые позволяют выполнить те расчеты, которые ранее не могли быть выполнены, а не за счет новых идей и теоретических представлений. Следует отметить, что продвижение по этому пути в перспективе сдерживается в том числе и технологическим пределом размеров элементов процессора, которые неуклонно движутся вниз по нанометровой шкале.

«Очевидная» методология состоит в следующем: для сложного объекта наномира, состоящего из большого числа атомов, молекул, электронов, связей и других составляющих, строится модель соответствующего уровня сложности, которая с точки зрения вычислителя представляет собой большую систему уравнений в частных производных, дифференциальных уравнений, интегро-дифференциальных уравнений. Сложность реальных моделей такова, что исследование динамики требует привлечения усилий коллективов исследователей, в том числе математиков, которые делают различные аналитические оценки и дают начальные данные для численного исследования, либо пытаются построить иерархию упрощенных моделей, специалистов по методам численного анализа, специалистов по программированию и распараллеливанию алгоритмов, и специалистов, которые интерпретируют  результаты расчетов в свете исходной задачи.

Как оказалось, простейшие дискретные модели могут обладать чрезвычайно сложным поведением. Достаточно вспомнить динамику простейшего логистического отображения (1), бифуркационная диаграмма для которого показана на рис. 1:

                                               (1)

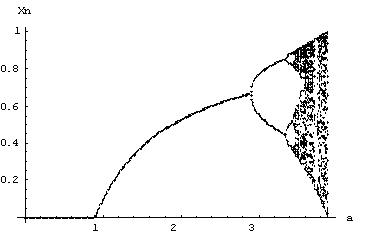
Рис. 1. Бифуркационная диаграмма для логистического отображения

         Введем небольшое усложнение в модель (1): пусть управляющий параметр а задается «внешней силой»: на каждом следующем шаге итерации выбирается из наперед заданной последовательности двух коэффициентов – b и с, например bcccba. Теперь рассмотрим квадрат на плоскости , каждая точка которого соответствует паре коэффициентов для логистического отображения с внешней силой. Для каждой такой точки квадрата D рассчитаем старший показатель Ляпунова, который определяет характер динамики системы. При сопоставлении показателям Ляпунова цветовой гаммы можем получить такую карту, как на рис. 2.

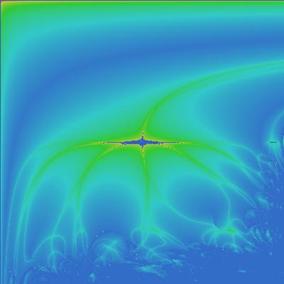
Рис. 2. Карта показателей Ляпунова для логистического уравнения с внешней силой

А теперь вообразим, что нам необходимо моделировать морфогенез трехмерной структуры подобной сложности при помощи «очевидного» подхода.

Дискретные модели удается использовать для моделирования сложного поведения во многих областях, например, в теории самоорганизованной критичности [3] или в теории искусственной жизни [4].

Из мыслей об очевидных трудностях в моделировании объектов наномира и о потенциале дискретных систем возникает задача данной работы – наметить новые подходы к моделированию объектов наномира на языке дискретных сред – клеточных автоматов, систем взаимодействующих тьюрмитов, «плиточных автоматов». На настоящий момент мы не имеем качественной теории этих объектов, мы имеем лишь примеры их успешного применения при решении конкретных задач моделирования.

Сегодня перед нанотехнологией стоят несколько задач, связанных со сборкой методом «снизу вверх»: это задачи построения алгоритмов самовоспроизведения, построения алгоритмов сборки необходимых конструкций из однородной среды, задачи формирования поверхностей заданной конфигурации, задачи проверки и восстановления целостности наноконструкций.

Как мы увидим ниже, существуют примеры того, как эти задачи решаются при помощи клеточных автоматов и тьюрмитов.

Моделирование самосборки наноконструкций методом «снизу вверх», на самом высоком уровне, основывается на следующем предположении: существует множество дискретных агентов, между которыми происходят локальные взаимодействия, которые определяют глобальную структуру. Отталкиваясь от такого представления, вполне естественно обратиться при моделировании к потенциалу дискретных систем.

2 Мир клеточных автоматов

Возраст теории клеточных автоматов невелик – около 50 лет. В основном мы имеем дело с периодом накопления фактов: каждый новый принцип построения автоматов, будь-то самовоспроизводящиеся автоматы Дж.фон Неймана, игра «Жизнь» Дж. Конуэя, модели теории самоорганизованной критичности или тьюрмиты вызывает глубокий интерес. Качественной теории подобных систем на данный момент не существует. Существует огромная работа С.Вольфрама по систематизации материала по дискретным системам [5].

Непосредственно к задачам нанотехнологии подходят работы по моделированию сложного поведения при помощи клеточных автоматов, моделированию отдельных аспектов эволюции при помощи систем взаимодействующих дискретных агентов в моделях теории искусственной жизни, моделированию биологических систем при помощи клеточных автоматов, в частности моделированию аспектов самовоспроизведения.

Наиболее простые клеточные автоматы состоят из клеток, расположенных вдоль одной линии, каждая клетка может находиться в одном из k состояний. Правила эволюции могут быть записаны в виде:

,

где - состояние i-й клетки в момент t. Автомат называется правильным, если . Если к тому же , то автомат называется суммирующим.

С. Вольфрам выделяет четыре класса правильных суммирующих автоматов:

1.     Вне зависимости от начальных данных за ограниченное количество шагов автомат переходит к однородному состоянию.

2.     Автомат переходит к локализованной стационарной конфигурации или циклу.

3.     Автоматы, для которых задание хаотических начальных данных приводит к хаотическому временному поведению.

4.     Автоматы, для которых не существует простого алгоритма, позволяющего предсказать эволюцию начальной конфигурации.

3 Игра «Жизнь» Дж. Конуэя

Что наша жизнь ….. игра.

         Клеточный автомат «Жизнь» был предложен в 1970г. английским математиком Дж. Конуэем. Рассматривается бесконечная плоская решетка квадратных клеток. Каждая клетка может находиться в одном из двух состояний – «живом» или «мертвом». Состояние клетки в момент времени t+1 определяется ее состояние в момент времени t и состоянием ее восьми соседних клеток в момент времени t. Если клетка мертва в момент времени t, то она оживает в момент t+1 только в том случае, если имеет три живые соседние клетки в момент времени t. Если клетка жива в момент времени t, то она погибает в момент времени t+1 только в том случае, если количество живых соседних клеток меньше двух или больше трех. В качестве примера на рис. 3 показана конфигурация, которая состоит из «планерного ружья», порождающего поток движущихся элементов – планеров, и пентадекатлона – конструкции, которая уничтожает планеры.

Рис. 3. Планерное ружье, поток планеров и пентадекатлон

         На данный момент получено огромное количество различных конфигураций: устойчивые конфигурации, циклические, передвигающиеся, порождающие бесконечный поток «элементарных частиц», конфигурации, которые уничтожают «элементарные частицы», аналог резонансного возбуждения.

         На основе правил клеточного автомата «Жизнь» построены несколько вариантов универсальной машины Тьюринга, таким образом, данный клеточный автомат может совершать любые алгоритмические вычисления.

         При помощи клеточного автомата «Жизнь» можно моделировать сам этот клеточный автомат – при этом клетки автомата более высокого уровня будет состоять из целый конфигураций более низкого уровня.

         Рассматривался вопрос о создании самовоспроизводящихся конфигураций. Дж. Конуэй считает, что такие конфигурации существуют, однако они до сих пор не найдены.

         Исследовались различные варианты автомата «Жизнь»: с треугольными ячейками, с гексагональными, одномерные варианты, варианты на обвертывающих поверхностях: цилиндрах, торах, листах Мебиуса, бутылках Клейна. Было получено множество интересных результатов, но по богатству комбинаций и разнообразию форм они не идут в сравнение с автоматом с простыми правилами.

4 Клеточные автоматы и самовоспроизведение

Один из аспектов биологических систем, важный в контексте нанотехнологических исследований – это способность к самовоспроизведению. Впервые принципиальная возможность создания клеточного автомата, способного воспроизводить себя была показана Дж. фон Нейманом [6].

В конце жизни Дж. фон Нейман работал над математическими и логическими проблемами самовоспроизведения. Исследовательская программа фон Неймана включала создание 5 моделей самовоспроизведения: кинематической, клеточной,  модели типа «возбуждение-порог-усталость», непрерывной и вероятностной модели. Автор успел изложить только первые две модели. Наиболее полно разработанной оказалась клеточная модель самовоспроизведения [6], которая представляет собой двумерное поле клеток, в каждой из которых находится конечный автомат с 29 состояниями, каждая клетка имеет 4 соседей, информация приходит с задержкой по крайней мере на 1 единицу времени. Из 29 состояний одно является невозбудимым (покой), 20 относятся к возбудимым, 8 – к чувствительным. На бесконечном поле задается исходный конечный набор клеток, имеющих не невозбудимое состояние. Затем клеточная система начинает работать по правилам переходов. Логическая структура бесконечного клеточного автомата такова, что через некоторый промежуток времени в некоторой области клеточного пространства, отличной от начального условия, появляется копия начального автомата. От дискретной клеточной модели самовоспроизведения фон Нейман собирался перейти к непрерывной модели, которая представляла бы систему дифференциальных уравнений в частных производных диффузионного типа. К сожалению, он не успел осуществить свой замысел.

Одним из направлений развития работы фон Неймана стали попытки конструирования более простых самовоспроизводящихся клеточных автоматов. Пример эволюции простого самовоспроизводящегося автомата (автомат Лэнгтона) показан на рис. 4 и рис.5 [7]. На рис. 4 изображено начальное состояние автомата, а на рис.5 – через некоторое время появляется копия начального состояния

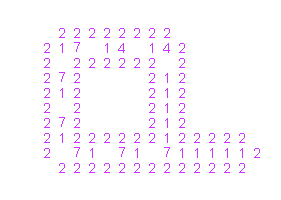
Рис. 4. Начальное состояние самовоспроизводящегося автомата

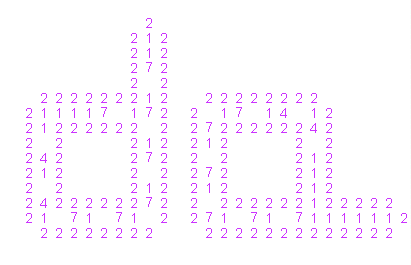
Рис. 5. Автомат порождает копии первоначального состояния

В автомате Лэнгтона клетка может находиться в одном из восьми возможных состояний (состоянию 0 на рис. 4 и 5 соответствует пустое место). Состояние клетки в следующий момент времени определяется состоянием в текущий момент и состоянием четырех соседей. Как видно из рис.4, автомат представляет собой сигнальную ленту, заключенную между двумя стенками. Сигнальная лента несет информацию, необходимую для создания копии автомата. Состояния 0,1,2 являются служебными состояниями, состояния 3,4,5,6,7 - сигнальными. Из клеток в состоянии 2 строятся «стенки» автомата. Состояние 1 является «несущей частотой», или скорее «несущей лентой» сигнала. Вслед за сигнальным состоянием должно идти состояние 0 – так задается направление распространения сигнала. Когда конца ленты достигает сигнал 70, то длина ленты увеличивается на 1. Когда в конец ленты приходят два сигнала 40, то лента делает поворот налево. Состояние 3 используется в качестве промежуточного состояния при повороте, состояния 5 и 6 используются при отделении дочернего автомата и для инициализации новой итерации самовоспроизведения. Копия исходного состояния получается через 151 такт времени после запуска автомата.

В статье [8] приводятся самовоспроизводящиеся автоматы, которые еще проще автоматов Лэнгтона, показанных на рис. 4 и 5. Оказалось, что можно сконструировать самовоспроизводящийся автомат всего лишь из 10 клеток, при этом каждая клетка автомата может находиться в одном из шести возможных состояний.

Остается открытым вопрос о том, можно ли сконструировать такие автоматы на молекулярном уровне.

Отличительной особенностью всех самовоспроизводящихся автоматов было то, что начальная конфигурация автомата совпадала с копией, которую он воспроизводил, и то, что каждый автомат работал только для какой-то одной заданной структуры.

Следующий шаг был предпринят в 1997г. H.H. Chou и J. Reggia построили такой автомат, который производит нужную структуру из начальной конфигурации, заданной случайным образом [9]. Более того, в модели [9] полученные самовоспроизводящиеся циклы, наподобие цикла Лэнгтона, взаимодействуют между собой, производят циклы более высокого размера (растут). На рис. 6 показано начальное состояние клеточного автомата (T=0), на последующих рисунках рис. 7 – рис. 10. показаны состояния автомата в моменты времени T=500, T = 1500, T=3500, T=5000 соответственно. Данные изображения получены при помощи симулятора JTrend авторов статьи [9].

Рис. 6. Начальное, случайно заданное состояние автомата

На рис. 7. видно, что образовались небольшие самовоспроизводящиеся циклы, которые вписываются в квадрат шириной 2 и 3 клетки. На рисунке циклы отмечены штриховкой. На рис. 8 мы видим уже самовоспроизводящиеся циклы размерностью 3 и 4. Далее размерность циклов снова растет (6 на рис. 9 и 7-8 на рис. 10). Так как поле автомата ограничено, то появление циклов слишком большой размерности приводит к их взаимной аннигиляции. При этом, в одних случаях автомат «вырождается», т.е. переходит в стационарное состояние, а в других – снова производит циклы небольшой размерности, как на рис. 7. – жизнь продолжается.

Рис. 7. Эволюция автомата в момент времени T=500

Рис. 8. Эволюция автомата в момент времени T=1500

Рис. 9. Эволюция автомата в момент времени T=3500

Рис. 10. Эволюция автомата в момент времени T=5000

Каждая клетка представляет собой переменную, хранящую 8 бит информации, которые разделены на 4 поля по функциональному признаку (рис. 11, таблица 1). Отсылая читателя за деталями работы этого автомата непосредственно к источнику [9], отметим, что, по-видимому, усложнение эволюционирующей системы, как и в природе, в случае самовоспроизводящихся автоматов, достигается при помощи усложнения клетки, а не правил взаимодействия между клетками. Может быть, поэтому не увенчались успехом попытки создания более сложных модификаций игры «Жизнь»: динамика автоматов с более сложными правилами оказалось более простой, чем исходного автомата «Жизнь».

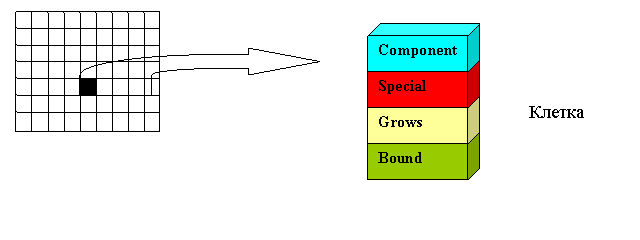
Рис. 11. Строение клетки

Таблица 1. Строение клетки

5 Диагностика и самовосстановление в природе

Одним из существенных аспектов самоорганизации живых организмов является их способность к поддержанию своей структуры путем своевременного определения неисправностей и самовосстановления. Например, молекулы ДНК в клетке постоянно подвергаются различным воздействиям: облучением, химическими агентами, нуклеазами, тепловым движением. В клетке существует репарирующая система, которая отслеживает эти повреждения и их исправляет. Эта работа выполняется ферментами различных типов: одни ферменты находят поврежденные места и помечают их, другие – вырезают поврежденную часть, третьи – наращивают молекулу в нужном месте.

Одной из важнейших задач нанотехнологии является разработка аналогичных механизмов на наноуровне – дискретных агентов, способных анализировать поверхность, по которой они двигаются, оставлять на ней различные пометки, или находить различные пометки и вносить необходимые изменения.

На роль аппарата для описания таких систем совершенно естественно претендуют тьюрмиты.

6 Тьюрмиты

Тьюрмит – это движущаяся по плоскости, размеченной клетками, машина Тьюринга, которая хранит свое внутреннее состояние, и, в зависимости от него и от цвета клетки, на которой она стоит, изменяет свое состояние, перекрашивает клетку в другой цвет и делает поворот влево или вправо. Программа для тьюрмита чрезвычайно проста (рис. 12), тем не менее, она позволяет формировать чрезвычайно сложные конструкции (рис. 13). Каждая строка программы записывается в следующем виде: <текущее состояние><цвет клетки под тьюрмитом><новый цвет клетки><смена направления><новое состояние>. Тьюрмиты можно программировать для решения достаточно сложных задач: например, один тьюрмит может анализировать размеченную поверхность и оставлять на ней пометки для другого, который будет вносить в нее изменения. При помощи всего лишь одного тьюрмита можно реализовать клеточный автомат «Жизнь»: тьюрмит обегает колонию и в соответствии с заданными правилами рисует следующее поколение.

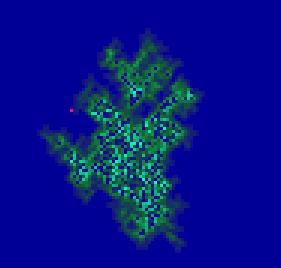
Рис. 12. Программа            Рис. 13. Поверхность, которую формирует тьюрмит

для тьюрмита

История исследования тьюрмитов начинается с 1950х годов, с ранних исследований по робототехнике, приведшим к задачам моделирования поведения мобильных черепах. В 1971г. Дж. Конуэй и М. Патерсон описали машину Тьюринга в двух измерениях, которая называлась «червем». Позже, машины Тьюринга в двух измерениях были переоткрыты несколько раз: в 1985г. К. Лэнгтоном под названием «vants», в 1987г. Р. Рукером под названием «тьюрмиты» и в 1987г. А. Брэди под названием «turning machines» (поворачивающиеся машины) [5].

В настоящее время тьюрмиты и системы взаимодействующих тьюрмитов чрезвычайно интересны, во-первых, с точки зрения проблемы формирования различных структур на наноуровне, и, во-вторых, с точки зрения теории вычислений, как модель особого параллельного вычислителя.

Тьюрмиты используются сегодня в основном как предмет математической забавы или как задание для реализации в курсе программирования. Для многих задач нанонауки, а именно - задач формирования структур на поверхности, задач доставки лекарств в нужную точку, задач восстановления различных структур необходимо целенаправленное развитие теории взаимодействующих тьюрмитов.

Необходимо создать принципы и алгоритмы синтеза тьюрмитов, которые создают поверхность нужной конфигурации, т.е. алгоритмы решения обратных задач: имеется структура, которую необходимо сформировать, структура переводится на язык состояний, и далее необходимо синтезировать алгоритм для одного тьюрмита или системы тьюрмитов, которые будут в состоянии реализовать заданную структуру.

Открытым остается вопрос о системах взаимодействующих тьюрмитов: какие возможности вычислений несут эти системы, каковы принципиальные возможности формирования структур на поверхности и в пространстве при помощи систем тьюрмитов, каковы ограничения этого подхода.

Остается открытым и вопрос о молекулярной реализации тьюрмитов: могут ли они, подобно конечным автоматам Шапиро, быть реализованы в лабораторном опыте, например при помощи ДНК-вычислений?

Очевидно, что теория систем взаимодействующих тьюрмитов должна развиваться путем создания качественного симулятора и накопления фактов, т.е. множества различных систем, которые выполняют различные функции, а затем – путем обобщения полученного опыта и создания методов решения обратных задач.

7 Плиточные тьюрмиты

При рассмотрении модели ДНК вычислений как вычислений плиточных, с одной стороны, и систем взаимодействующих тьюрмитов, с другой стороны, возникает мысль о следующем подходе к моделированию процессов создания наноструктур: задан набор плиток различной формы, которые могут взаимодействовать друг с другом. Правила взаимодействия определяются формами границ плиток. Каждая плитка обладает самостоятельным поведением: у нее есть своего рода «глаз», или встроенный тьюрмит, который и отвечает за движение и поворот плитки (рис.14). Задается начальный набор плиток нескольких типов, «правила поведения» для плитки каждого типа, и, в процессе взаимодействия плитки должны генерировать некоторую структуру. Правила поведения могут напоминать программу для тьюрмитов, с более гибким описанием поворотов.

Рис. 14. Плиточный тьюрмит с сенсором

         Вопрос исследования динамики подобных систем также остается открытым. Неясно, насколько сложные задачи можно решать таким способом.

         Вероятно, здесь, как и в плиточной модели ДНК-вычислений, мы сталкиваемся с совершенно новым типом вычислений, который еще только предстоит развить и которому только предстоит получить свое применение.

8 Заключение. Задел в ИПМ им. М.В.Келдыша РАН

Технический прогресс человечества вполне можно представить в виде слалома по шкале масштабов, с которыми оно оперирует: от преобразования механической энергии в метровых масштабах мы перешли к использованию внутренней энергии пара, затем к электричеству, затем к микроэлектронике. Каждый из этих переходов приводил к существенным изменениям и к новым возможностям. Сегодня на наших глазах осуществляется еще один переход – в шкалу наномасштабов, который будет не менее разительным, чем предыдущие.

Вероятно, мы станем свидетелями перемен в химическом синтезе, энергетике, науке о материалах, медицине, космических исследованиях и т.д.

В нашем Институте имеется большой задел, который может быть использован в исследованиях по нанобиологии и разработке вычислительных технологий на молекулярном уровне. Обратим внимание только на наиболее важные направления.

Исследования по анализу генетического кода с информационной точки зрения, моделирование пространственных конформаций биологических молекул (академик Т.М.Энеев, Н.Н.Козлов).

Нынешние модели ДНК-вычислений исходят из сверхупрощенных модельных представлений о молекуле ДНК, считая ее небольшим линейным фрагментом. Анализ трудностей и, вероятно, новых возможностей, связанных с ее сложной трехмерной структурой, в связи с ДНК-вычислениями впереди. Особенно важным в этом направлении представляется то, что в рассматриваемых в этом направлении задачах удается сформулировать принципы, позволяющие в ряде биологических задач выделить один или несколько вариантов из множества возможностей [10].

Анализ проблемы перекрываемости генетического кода [11] позволил установить его интересную особенность: оказывается, из множества альтернативных вариантов в реальности был реализован именно такой генетический код, который позволяет сформулировать правила запрета, решающие проблему перекрываемости, т.е., при наличии в последовательности аминокислот определенных в [11] пар перекрытие становится невозможным. Наиболее поразительным оказывается то, что правила запрета должны соответствовать линейной структуре молекул ДНК, с учетом комплементарности, т.е. генетический код выбран таким, чтобы обеспечивать это соответствие.

Синтез надежных систем из ненадежных элементов, анализ молекулярных систем с позиций дискретной математики (научная школа чл.-корр. РАН С.В.Яблонского, отдел академика О.Б.Лупанова).

В настоящее время актуальной является проблема создания вычислительных структур на наноуровне и молекулярных вычислительных машин [1]. При этом важно, чтобы сбои и повреждения отдельных элементов (неизбежные на молекулярном уровне, например, в связи с радиационным воздействием) не сделали итог работы молекулярной вычислительной системы бессмысленным. Вероятно, при выборе архитектуры молекулярных машин можно будет опираться на фундаментальные результаты синтеза логических схем и другие результаты дискретной математики [12].

В различных разделах компьютерных наук, в криптографии, возникают задачи большой вычислительной сложности (например, задача о дискретном логарифмировании, проблема изоморфизма графов, задача коммивояжера и т.д.) [13]. Именно эти задачи, лежащие за гранью возможностей современных вычислительных систем (либо способы их избегать, которыми, вероятно, пользуются живые системы), и являются естественной нишей для вычислительных машин наноуровня и для молекулярных вычислителей.

 Теория конечных автоматов и простейших моделей адаптивного целесообразного поведения (работы академика И.М.Гельфанда, проф. М.Л.Цетлина).

Теория конечных автоматов как классическая детально развитая теория была построена в 70-х годах XX века.  Она позволяла определить, какие автоматы «выигрывают» в среде со случайными свойствами, оценить оптимальную глубину памяти [14]. Закат этой теории был связан с тем, что не нашлось удачных материальных воплощений «конечноавтоматных моделей», а удешевление микропроцессоров свело на нет преимущества, которые давала поразительно простая структура.

С другой стороны, для описания живого на уровне организмов, органов, тканей и клетки эти системы слишком просты и схематичны. Нормой является выполнение биологической структурой такого уровня множества функций в разных ситуациях и на разных характерных временах.

Однако на молекулярном уровне и уже тем более на уровне наномасштабов ситуация радикально меняется. Простая структура становится громадным преимуществом, которое можно закладывать в структуру создаваемых объектов либо искать соответствующие аналоги среди существующих биологических объектов нанометрового диапазона. Поэтом можно ожидать второго пришествия теории конечных автоматов в молекулярном контексте.

Микророботы и молекулярные машины (работы сектора проф. А.К.Платонова).

В настоящее время робототехника представляет собой хорошо развитую область. Специалисты, которые работают в ней, представляют свои задачи на три века вперед [15]. При переходе на наномасштабы в настоящее время большое внимание уделяется наномашинам и наноразмерным датчикам.  Первые в перспективе будут использоваться для адресной доставки лекарств определенным органам, вторые – осуществлять эффективный мониторинг состояния организма. Кроме того, следует обратить особое внимание на обнаруженные внутри клетки естественные «молекулярные двигатели» - природные наномашины (в частности – F1 – АТФазу).

Нанобиотехнологии рассматриваются как один из главных приоритетов прикладной нанонауки в мире. Заметим, что на наноуровне ищутся решения и фундаментальных биологических проблем. В частности, в качестве одного из принципов развития нанобиотехнологий в США рассматривается следующий: «Тщательное изучение взаимодействия биомолекул с инертными материалами, что может иметь важное значение не только для решения чисто медицинских проблем, но и для понимания фундаментальных процессов зарождения и развития жизни на Земле» [1].

Робототехника позволяет, с одной стороны, строить наномашины, опираясь на фундаментальные результаты этой науки, а с другой – изучать и понимать принципы действия, структуры и функции природных наномашин.

Особенно интересным и перспективным предствляют и с точки зрения прикладных задач, и с точки зрения синергетики коллективные согласованные действия ансамбля микророботов, которым, очевидно, доступны задачи, далеко выходящие за пределы возможностей одной микромашины.

Квантовомеханические механизмы фундаментальных биологических процессов (П.В.Куракин)

Пафос книги Р. Пенроуза, стимулировавшей интерес к задачам нанобиологии, состоит в недостаточном понимании физики квантовомеханических явлений, в частности, для объяснения феномена сознания. Cвидетельством в пользу этого является бурное развитие квантовой информатики [16]. Классический парадокс Эйнштейна-Подольского-Розена стал основой для разработки квантовой криптографии, квантовой телепортации, парадигмы квантовых вычислений.

Поэтому особый интерес вызывают сейчас различные интерпретации и новые трактовки квантовой механики, а также возможные, предсказываемые этими вариантами проявления на физическом и биологическом уровне. Эти работы активно ведутся в Институте [17].

Гипотеза об объективной редукции волнового пакета, выдвинутая Р. Пенроузом, предполагает новый механизм самоорганизации на квантовом уровне. Но, очевидно, есть и другие возможности описания коллективных явлений на микро- и наномасштабах, связанных с квантовомеханическими эффектами, которые будут существенны для живых систем.

Исследования по теории диссипативных структур и динамическому хаосу (научная школа члена-корреспондента РАН С.П. Курдюмова, работы отдела проф. Г.Г. Малинецкого).

Принципиальное значение для биологических систем имеет гигантское усиление малых воздействий. Было исследовано несколько возможных механизмов такого усиления. Первый – в теории режимов с обострением, где рассматриваются системы с сильной положительной обратной связью [18]. Второй, характерный для динамических систем со странными аттракторами, где благодаря разбеганию близких траекторий в фазовом пространстве может генерироваться информация. И, наконец, в теории русел и джокеров, где в определенных областях фазового пространства (областях джокеров) информация создается, в то время как в других (так называемых руслах) используется [19]. Поскольку исследованные системные механизмы носят универсальный характер, интересно было бы увидеть, как они реализуются на наномасштабах в живых системах.

Классическим для синергетики было исследование диссипативных структур – пространственно неоднородных типов упорядоченности, возникающих в нелинейных диссипативных системах вдали от равновесия. При этом, как правило, рассматривался макромасштаб, где можно было оперировать с макропеременными – концентрациями, температурами, плотностями и т.д. Принципиально важный и для синергетики, и для нанобиологии вопрос состоит в том, как качественно меняются и типы самоорганизации, и свойства возникающих структур при уменьшении пространственных масштабов.

Создание иерархии математических моделей для описания химических процессов на микро- и наномасштабах (профессор Г.Г. Еленин).

Биологические системы часто трактуют как химические машины (в последнее время подчеркивая также принципиальную роль электромагнитных полей). Поэтому к нанобиологии естественно подойти и с «химической» стороны.

На определенной ступени развития параллельно и наряду с теоретической физикой возникла математическая физика. В последние 20 лет были вложены огромные усилия, чтобы опираясь на появившиеся возможности компьютерного анализа построить содержательную, эффективную иерархию математических моделей химии (математическую химию), которые могли бы быть исследованы в рамках уже созданных вычислительных технологий. Очень важным и ценным представляется перенос этого потенциала на проблемы нанонауки [2].

Описание нелинейных процессов и самоорганизации на языке клеточных автоматов (к. ф.-м. н. М.Е. Степанцов).

         Клеточные автоматы позволяют описывать те процессы, в которых сам объект может находиться в одном из конечного (обычно небольшого) набора состояний, в котором его поведение определяется только ближайшим окружением, в котором удовлетворительным приближением является дискретность временной и пространственных координат.

         С помощью клеточных автоматов, как показали работы последних десятилетий, можно описывать многие процессы в газовой динамике, в магнитной гидродинамике, а также во многих других областях, где традиционные модели представляют собой уравнения в частных производных – описание сплошной среды [5]. Однако еще более важно, что клеточные автоматы оказываются эффективны и полезны, когда таких уравнений нет [20].

         Очевидно, что чем меньше пространственные масштабы, тем более естественным будет описание на языке клеточных автоматов. Вполне вероятно, что и в нанобиологии, и в нанонауке такие модели в недалеком будущем займут ведущее место.

Распространение парадигмы параллельных вычислений на вычислительные системы наноуровня (к. ф.-м. н. В.Д.Левченко).

         Среди дискуссий о природе сознания и о сущности живого одно в настоящее время остается незыблемым. Переводя это утверждение на язык компьютерной метафоры, можно сказать, что и многие органеллы клетки, и сама клетка, и организм, и сознание являются системами с огромной степенью параллельности.

Одной из наиболее острых проблем в анализе параллельно протекающих процессов – это их организация, это способ, который позволяет организовать использование имеющегося ресурса так, чтобы одни подсистемы не простаивали подолгу, ожидая результатов деятельности остальных. Поэтому особый интерес и важность представляют те алгоритмы, задачи, принципы, которые позволяют организовывать вычисления с эффективностью использования ресурсов, близкой к 100%. Такие примеры есть [21]. Обратим внимание на то, что в упомянутой работе использован подход, опирающийся на представления теории клеточных автоматов.

         Естественно, в живом речь должна идти об эффективной самоорганизации параллельных процессов, однако удачные способы организации параллельных вычислений могут оказаться здесь полезной подсказкой.

Статистические методы химии полимеров (проф. С.И. Кучанов).

         Молекулы ДНК и множество других биологически важных молекул представляют собой полимеры. Динамика живых объектов представляет собой сочетание детерминированных алгоритмов (в последовательности ДНК многие буквы должны быть определены точно, чтобы организм был жизнеспособен, тут не место произволу) и статистических «программ» (их множество на разных уровнях, они-то зачастую и обеспечивают «грубость» и надежность функционирования). Поэтому, естественно было бы в нанобиологии использовать огромный потенциал, накопленный в статистической химии полимеров.

          С одной стороны, здесь интересна статистика возможных в нанобиологии объектов «в чистом виде». В самом деле, в парадигме ДНК-вычислений обычно предполагается синтез огромного числа молекул, одна из которых и является «ответом» (то есть на другой элементной базе реализуется метод Монте-Карло).

         С другой стороны, в химии полимеров во многих случаях удается получить «ключ» к созданию различных пространственных конфигураций на молекулярном уровне [22], что тоже может быть очень ценно. 

         Анализ и синтез нанобиологических систем и нанобиотехнологий с позиций теории искусственной жизни. (к. ф.-м. н. Бурцев М.С.).

         По существу, нанотехнологии проходят один и тот же путь, универсальный для всех технологий:

         -  создание предмета (молоток, молекула лекарства, самолет и т.д.)

         - создание адаптивного инструмента, способного учитывать изменения окружающей среды и корректировать свою программу действий (например, подготовленный специалист, огранизация и т.д.)

         - создание эволюционирующего объекта, способного видоизменять и корректировать свою структуру и функции в следующих поколениях (микроорганизмы, биосфера, цивилизации и т.д.).

         В настоящее время нанотехнологии находятся в большинстве своем на первом уровне (типичный пример: «есть наночастица», которая будучи добавлена к чему-то дает чудодейственный эффект).

         В этом тексте и в обозримой перспективе рассмотрен следующий уровень: (молекулярная машина оценивает ситуацию, вырабатывает решение и действует в соответствии с ним, но сама машина при этом не меняется).

         Однако можно пойти дальше, считая, что мы будем синтезировать или модифицировать нанообъекты, способные эволюционировать и решать свою задачу на протяжении многих поколений.

         В этом случае очень важными и интересными будут результаты недавно появившегося направления синергетики – искусственной жизни [4]. Это направление показывает, куда и при каких условиях может привести исходный процесс.

Моделирование элементов сознания, эволюционная биокибернетика

         В настоящее время внимание многих исследователей вновь оказалось приковано к проблемам возникновения жизни и к эволюционной теории [23].

         Возникает естественный вопрос, что мы будем считать критерием истинности реконструкции эволюционного процесса.

         Идеальной была бы прямая постановка эксперимента – организация и мониторинг искусственного эволюционного процесса. (На нашем нынешнем уровне знаний мы даже не знаем, может ли вообще так ставиться вопрос). Многие проблемы оказались бы решенными, если бы была найдена альтернативная форма жизни.

         В отсутствие этого различные научные дисциплины предлагают свои критерии верификации построенной картины. В палеонтологии таковым считается нахождение промежуточных форм организмов. Отсутствие таковых во многих случаях ставило под вопрос эволюционные теории.

         В молекулярной биологии таковым является правдоподобие сценария редактирования генома, согласующегося с данными о геномах известных организмов и «эволюционными часами», дающими вероятность возникновения мутаций.

         С точки зрения проблемы возникновения сознания и ряда задач нанобиологии, естественно было бы предлагать согласованную картину структур (материального носителя той или иной способности) и функций (программ действий структуры). В отношении последних большие успехи были достигнуты в эволюционной биокибернетике, где удалось на основе теории нейросетей показать естественное усложнение реакций в ходе эволюции от простейшей раздражимости до появления логического мышления, а также возникновение метапрограмм – программ следующего уровня [24, 25]. Возможно, это окажется важным для организации на молекулярном уровне тех или иных вычислительных процессов, например, аналоги генетических алгоритмов.

         Развитие парадигмы сложности и теории молекулярных фильтров (к.ф.-м.н. А.В. Подлазов).

         В рамках синергетики в настоящее время активно развивается парадигма сложности. В рамках этого подхода удается построить базовые модели редких катастрофических процессов (в частности, гигантских вымираний огромного количества семейств, десятки раз происходившие в ходе эволюции). Парадигма сложности дает свое объяснение гигантского усиления в сложных системах, находящихся на кромке хаоса [26]. Кроме того, она позволяет оперировать с такой категорией как ценность информации, моделировать распространение одного варианта выбора в ходе развития [27]. Возможно, развитие этого направления позволит предложить новые механизмы «вывода» результатов процессов на наноуровне на макроуровень, а также найти оригинальные способы решения нанотехнологических проблем.

         Кроме того, важным вопросом и в нанотехнологиях и в ДНК-вычислениях является выделение немногих нужных микрообъектов из огромного множества. Естественно, в решении этой задачи использовать и стандартные подходы, развитые в молекулярной биологии, и молекулярные фильтры, создаваемые на основе нанотехнологий. В этой области также имеется большой задел, который может быть использован.

ДНК-вычисления и новые молекулярные парадигмы (С.А. Науменко)

         В настоящее время активно развивается парадигма ДНК-вычислений. Традиционный подход ее разработки ведется с позиций информатики: теории алгоритмов, теории формальных языков [20]. Этот подход позволяет быстро пройти тот же путь, который был уже пройден классической парадигмой вычислений: разработка базовых элементов архитектуры вычислительной системы, составление простейших программ в машинных кодах для этой архитектуры, накопление решенных задач и алгоритмов, создание новых языков программирования с постепенным увеличением уровня абстракции и приближением к языку описания предметных областей, концентрация на вопросах методологии разработки сложных программных систем, вопросах, связанных с ограничениями, присущими парадигме. В этом случае, разрабатывая теорию молекулярного вычислителя, мы можем воспользоваться всей мощью существующей парадигмы, не забывая, однако, о совершенно специфических задачах, стоящих перед молекулярными вычислениями.

         С другой стороны, в начале развития нового научного направления появляется несколько альтернативных возможностей. По-видимому, целесообразно и в молекулярных вычислениях обратить внимание на них. При этом новые возможности могут быть найдены как синтез известных направлений. В частности, «плиточная» парадигма вычислений, которая обсуждается в этом тексте, может быть дополнена «автоматным подходом». При этом каждая плитка представляет собой клетку некоторого клеточного автомата, которая может иметь и ориентацию, и некоторое внутреннее состояние, и простую программу поведения. Это дает совершенно новые возможности для моделирования самоорганизации и вычислений в таких системах.

Литература

1. Нанотехнология в ближайшем десятилетии. Прогноз направления иссле-дований. /Под ред. М.К. Роко, Р.С. Уильямса и П. Аливисатоса. Пер. с англ. - М.: Мир, 2002 - 292с.

2. Еленин Г.Г. Нанотехнологии, наноматериалы, наноустройства. // Новое в синергетике: Взгляд в третье тысячелетие. – М.: Наука, 2002. – 478с.

3. Малинецкий Г.Г., Потапов А.Б. Современные проблемы нелинейной динамики. Изд.2-е, исправл. и доп. М.: Едиториал УРСС, 2002 - 360с.

4. Бурцев М.С. Исследование новый типов самоорганизации и возникновения поведенческих стратегий. Автореферат диссертации на соискание ученой степени кандидата физико-математических наук. М. 2005 - ИПМ им . М.В. Келдыша РАН

5. Wolfram S. A new kind of science. Wolfram media, 2002. - 1197 p.

6. Нейман Дж. фон. Теория самовоспроизводящихся автоматов. М.: Мир, 1971.

7. Langton С.G., Self-reproduction in cellular automata. Physica D, v.10 (1984), p.134-144.

8. Byl John. Self-reproduction in small cellular automata. Physica D, v. 34 (1989), p.295-299.

9. Chou, H.H., Reggia J.A.  Emergence of self-replicating structures in a cellular automata space. // Physica D 110 (1997) 252-276.

10. Козлов Н.Н., Кугушев Е.И., Энеев Т.М. Структурообразующие характеристики транскрипционного процесса // Математическое моделирование. 1998. Т. 10, № 6, с. 3-19.

11. Козлов Н.Н. Теорема для генетического кода. ДАН. 2002. Т. 382, № 5, с. 593-597.

12. Яблонский С.В. Введение в дискретную математику. М.: Наука, 1986, 384с.

13. Введение в криптографию. Под общей редакцией В.В. Ященко.М., МЦНМО, 2000г., 288с.

14. Цетлин М.Л. Исследования по теории автоматов и моделированию биологических систем. Главная редакция физико-математической литературы изд-ва "Наука", М., 1969, 316с.

15. Платонов А.К. Проблемы и перспективы робототехники. //Будущее прикладной математики. Лекции для молодых исследователей. М., УРСС, 2004, с.315-342.

16. Бауместер Д., Физика квантовой информации : Квантовая криптография. Квантовая телепортация. Квантовые вычисления. Постмаркет, 2002.,376с.

17. Куракин П.В.  Скрытые параметры и скрытое время в квантовой теории. Препринт ИПМ №33, Москва, 2004.

18. Режимы с обострением. Эволюция идеи: Законы коэволюции сложных систем. - (Кибернетика: неограниченные возможности и возможные ограничения).

М.: Наука, 1999, 254с.

19. Малинецкий Г.Г., Курдюмов С.П. Синергетика и прогноз. Настоящее и будущее. //В сборнике «Новое в синергетике: Взгляд в третье тысячелетие» - М.: Наука, 2002., с. 29-58.

20. Малинецкий Г. Г., Степанцов М. Е. Моделирование движения толпы при помощи клеточных автоматов. // Известия Высших учебных заведений. Прикладная нелинейная динамика, 1997, том 5, N 5, с.75-79.

21. В.Д. Левченко. Асинхронные параллельные алгоритмы как способ достижения 100 % эффективности вычислений. //Будущее прикладной математики. Лекции для молодых исследователей./Под ред. Г.Г.Малинецкого. – М.: Едиториал УРСС, 2005 – 512с.

22. Хохлов А.Р., Кучанов С.И., Лекции по физической химии полимеров. М.: Мир, 2000. – 192с.

23. Э.М. Галимов. Феномен жизни. Между равновесием и нелинейностью. Происхождение и принципы эволюции. М.: Едиториал УРСС, 2001. – 256с.

24.  В.Г. Редько. Эволюция, нейронные сети, интеллект: Модели и концепции эволюционной кибернетики. Серия «Синергетика: от прошлого к будущему», М.: Едиториал УРСС, 2005. – 224с.

25. В.Ф. Турчин. Феномен науки: Кибернетический подход к эволюции. Изд. 2-е. – М.: ЭТС. – 2000. – 368с.

26. Управление риском. Риск, устойчивое развитие, синергетика. Под ред. Г.Г. Малинецкого. М.: Наука, 2000г. http://risk.keldysh.ru.

27. Чернавский Д.С. Синергетика и информация (динамическая теория информации). Изд. 2-е, испр. и доп. - М.:Едиториал УРСС, 2004. - 288с.

28. Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений.: Пер. с англ. - М.: Мир, 2004. - 528 с.

29. Малинецкий Г.Г., Митин Н.А., Науменко С.А. Нанобиология и синергетика. Проблемы и идеи. Препринт ИПМ им. М.В.Келдыша РАН № 29 за 2005г.

30. Малинецкий Г.Г., Науменко С.А. Вычисления на ДНК. Эксперименты. Модели. Алгоритмы. Инструментальные средства. Препринт ИПМ им. М.В. Келдыша РАН №29.