Модификация метода Монте-Карло в задачах о трансформации ионизирующего излучения
|
 |
Оценка прошедшего сквозь объект ионизирующего излучения с помощью прямых испытаний методом Монте-Карло может оказаться неэффективной, когда лишь незначительная часть фотонных траекторий несет информацию о решении рассматриваемой задачи. Может оказаться, в особенности это характерно для сильно поглощающих сред, что очень малая доля первичных фотонов достигает детекторной плоскости.
Существуют
приемы увеличения эффективности расчетов методом Монте-Карло, которые так или иначе
связаны с увеличением информации, извлекаемой из отдельной траектории фотона. В
основном алгоритме реализованы две, помимо прямых испытаний, модификации метода
Монте-Карло, являющиеся результатом аналитических методов решения задачи,
позволяющих заменить одну из случайных величин
ее вероятным значением.
В
первой из этих модификаций вместо того, чтобы путем розыгрыша случайной величины
определять приведет ли данный акт взаимодействия к поглощению или к рассеянию фотона,
полагаем, что фотон всегда рассеивается с весом, равным вероятности
«выживания» ![]() . Этот вес имеет смысл средней доли фотонов в данной истории,
которые не поглотились в данном акте взаимодействия. Таким образом, в процессе
движения фотон в каждом столкновении выживает с соответствующим уменьшением
веса
. Этот вес имеет смысл средней доли фотонов в данной истории,
которые не поглотились в данном акте взаимодействия. Таким образом, в процессе
движения фотон в каждом столкновении выживает с соответствующим уменьшением
веса
![]() .
.
Таким
образом, при данном числе траекторий фотонов происходит формальное увеличение
количества источников фотонов по сравнению с проведением прямых испытаний, что
приводит к уменьшению дисперсии результата.
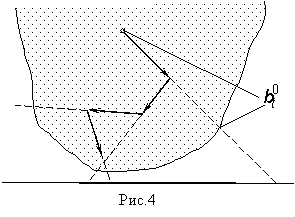 Другой
способ увеличения информационной ценности фотонных историй состоит в
следующем. Вместо того, чтобы рассматривать пересечение детекторной плоскости
фотоном как случайное событие, аналитически подсчитывается вероятность того, что
квант после очередного рассеяния достигнет детекторную плоскость без
последующих столкновений. В этом случае количество регистрируемого излучения
будет вычисляться как взвешенная сумма по всей совокупности звеньев
рассматриваемой траектории.
Другой
способ увеличения информационной ценности фотонных историй состоит в
следующем. Вместо того, чтобы рассматривать пересечение детекторной плоскости
фотоном как случайное событие, аналитически подсчитывается вероятность того, что
квант после очередного рассеяния достигнет детекторную плоскость без
последующих столкновений. В этом случае количество регистрируемого излучения
будет вычисляться как взвешенная сумма по всей совокупности звеньев
рассматриваемой траектории.
Вероятность
![]() того, что после
того, что после ![]() - го столкновения фотон попадет на детекторную плоскость,
равна (см. рис.4)
- го столкновения фотон попадет на детекторную плоскость,
равна (см. рис.4)
![]() , если луч вдоль направления движения пересекает эту
плоскость, и
, если луч вдоль направления движения пересекает эту
плоскость, и
![]() , в противном случае.
, в противном случае.
Вклад n-го звена в общий
результат будет иметь вид
![]() .
.
Такой
подсчет вклада траекторий ведет к уменьшению дисперсии результата, поскольку
подсчитывается парциальный вклад каждого звена, в отличие от метода прямых
испытаний, когда подсчитываются фотоны, действительно пересекшие детекторную
плоскость, что может случиться не более одного раза за всю траекторию.
Важным
моментом при использовании метода Монте-Карло является выбор генератора случайных
чисел, равномерно распределенных в интервале (0, 1). Современные стандартные
генераторы случайных чисел (например, входящие в стандартные библиотеки
фортрана) дают, как правило, хороший результат и требуют весьма скромных
вычислительных затрат. Однако, применение таких генераторов иногда бывает
ограничено версией установленного программного обеспечения, что вызывает
затруднения при переносе разрабатываемых программ с одного вычислительного
комплекса на другой. Поэтому в настоящей работе использовались генераторы, не
зависящие от операционной системы и комплектности стандартных библиотек. А
именно, применялся генератор [6] и так называемые ЛПt - последовательности [7].
Генератор
[6] по быстродействию и качеству случайных чисел вполне аналогичен стандартным,
в то время как применение ЛПt -
последовательностей с использованием экономичного способа их вычислений [8]
позволяет сэкономить во многих задачах более
20% расчетного времени при том же качестве результатов.
Приведем
описание тестирования разработанной методики расчета интенсивности проникающего
излучения.
Отметим,
во-первых, что использованная модификация метода Монте-Карло обеспечивает
практически точное вычисление интенсивности нерассеянного (первичного)
излучения согласно закону ослабления, так как при весовом способе подсчета
числа нерассеянных фотонов, достигших детекторной плоскости, статистическая
погрешность метода Монте-Карло слабо влияет на результат. Поэтому при
проведении расчетов с помощью статистических испытаний необходимым является
совпадение результатов вычисления параметров нерассеянного излучения с
аналогичными величинами, рассчитанными без использования метода Монте-Карло,
например, с помощью алгоритма [1].
Выбор
теста для проверки качества результатов расчета рассеянного излучения является
значительно более трудной задачей. Однако удается построить достаточно простое
аналитическое решение для однократно рассеянных фотонов от коллимированного
источника ионизирующего излучения падающего перпендикулярно на пластину
толщиной d вдоль оси z. А именно, зависимость интенсивности J
однократно рассеянного излучения (под интенсивностью излучения здесь
понимается количество зарегистрированных фотонов на единицу площади детектора)
от расстояния x от начала координат, расположенного на детекторной плоскости,
определяется формулой:
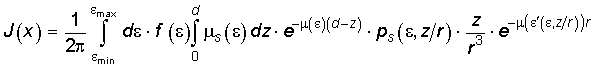 .
.
В
этой формуле ![]() ,
, ![]() - энергия
падающего фотона,
- энергия
падающего фотона, ![]() - энергия рассеянного фотона,
- энергия рассеянного фотона, ![]() - нормированный спектр
излучения,
- нормированный спектр
излучения, ![]() - коэффициент
рассеяния (когерентного или некогерентного),
- коэффициент
рассеяния (когерентного или некогерентного), ![]() - коэффициент ослабления
проникающего излучения,
- коэффициент ослабления
проникающего излучения, ![]() - плотность
вероятности рассеяния.
- плотность
вероятности рассеяния.
Результаты
расчетов, проведенных для различных материалов и различных характерных энергий
ионизирующего излучения, показали, что их отличие от тестовых значений находится
в пределах статистической погрешности вычисления рассеянного излучения. Описанный
выше алгоритм реализован в виде параллельного программного комплекса с
использованием интерфейса MPI,
ориентированного на многопроцессорные вычислительные системы. Расчеты
проводились на МВС-1000М.
§2. Модификации метода Монте – Карло при «ужесточении» энергетического
спектра
При получении
рентгеновского изображения объекта, находящегося под воздействием
рентгеновского излучения от полиэнергетического источника имеет место
трансформация энергетического спектра источника в энергетический спектр фотонов,
регистрируемых на детекторной плоскости. Поскольку низкоэнергетичные фотоны
имеют больший коэффициент ослабления, чем высокоэнергетичные, то они дают,
соответственно, меньший вклад в формирование рентгеновского изображения за
объектом. В связи с этим происходит смещение и локализация в области высоких
энергий энергетического спектра фотонов, регистрируемых на детекторной
плоскости. Чем больше оптическая толщина объекта, тем сильнее эта локализация,
которую будем называть «ужесточением» энергетического спектра.
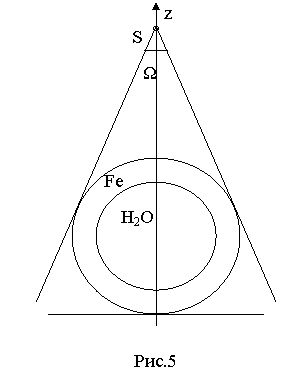 В качестве примера рассмотрим
следующий эксперимент (рис.5). Железная (Fe) труба,
заполненная водой (H2O), находится под воздействием
рентгеновского излуче-ния от точечного источника (S). Ось z проходит через источник и пересекает ось симметрии
трубы под прямым углом. Интенсивность прошедшего объект излучения
регистрируется на детекторной плоскости z = 0, которая касается внешней поверхности трубы. Ось y параллельна оси симметрии трубы. Источник расположен
в точке с координатой
В качестве примера рассмотрим
следующий эксперимент (рис.5). Железная (Fe) труба,
заполненная водой (H2O), находится под воздействием
рентгеновского излуче-ния от точечного источника (S). Ось z проходит через источник и пересекает ось симметрии
трубы под прямым углом. Интенсивность прошедшего объект излучения
регистрируется на детекторной плоскости z = 0, которая касается внешней поверхности трубы. Ось y параллельна оси симметрии трубы. Источник расположен
в точке с координатой ![]() см и излучает в телесный угол
см и излучает в телесный угол ![]() , ось симметрии которого совпадает с осью z. Внешний радиус трубы –
, ось симметрии которого совпадает с осью z. Внешний радиус трубы – ![]() см.; внутренний радиус трубы –
см.; внутренний радиус трубы – ![]() см.
см.
Прошедшее объект
излучение складывается из двух составляющих: нерассеянного и рассеянного
излучений. На детекторной плоскости можно выделить теневую область, в которой
регистрируется интенсивность нерассеянного излучения, прошедшего сквозь объект.
На рис.6 приведены графики отношения интенсивностей нерассеянного и рассеянного
излучений в теневой области на центральном срезе трубы (y = 0) к интенсивности источника.
Кривая, помеченная точками, относится к нерассеянному излучению. Интенсивность
источника на плоскости z =
0 описывается формулой:
![]() ,
,
где ![]() ,
, ![]() – количество фотонов,
выпущенных источником в элемент телесного угла
– количество фотонов,
выпущенных источником в элемент телесного угла ![]() . На рис.7 приведены аналогичные графики для меньшего
внутреннего радиуса трубы
. На рис.7 приведены аналогичные графики для меньшего
внутреннего радиуса трубы ![]() см. В этом случае объект имеет большую оптическую толщину,
поскольку труба толще, и коэффициент ослабления железа на порядок больше
коэффициента ослабления воды. Это обстоятельство приводит к тому, что значения
интенсивностей на рис.7 на два порядка меньше, чем на рис.6.
см. В этом случае объект имеет большую оптическую толщину,
поскольку труба толще, и коэффициент ослабления железа на порядок больше
коэффициента ослабления воды. Это обстоятельство приводит к тому, что значения
интенсивностей на рис.7 на два порядка меньше, чем на рис.6.
На рис.8 приведены
графики энергетического спектра источника и плотность распределения рассеянных
фотонов, зарегистрированных в детекторе ![]() , по их начальным энергиям (энергиям, которые они имели на
выходе из источника) для трубы с внутренним радиусом
, по их начальным энергиям (энергиям, которые они имели на
выходе из источника) для трубы с внутренним радиусом ![]() см., а на рис.9 приведены аналогичные графики для трубы с
внутренним радиусом
см., а на рис.9 приведены аналогичные графики для трубы с
внутренним радиусом ![]() см. На обоих рисунках кривая энергетического спектра
источника имеет один и тот же вид. Вторая кривая сильно отличается от
энергетического спектра источника и на рис.9 локализована в области высоких энергий сильнее, чем
на рис.8.
см. На обоих рисунках кривая энергетического спектра
источника имеет один и тот же вид. Вторая кривая сильно отличается от
энергетического спектра источника и на рис.9 локализована в области высоких энергий сильнее, чем
на рис.8.

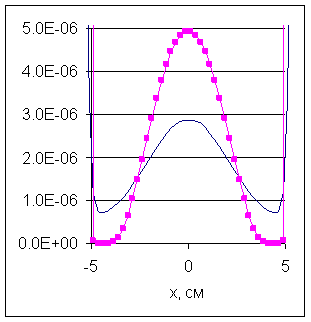
Рис.6 Рис.7
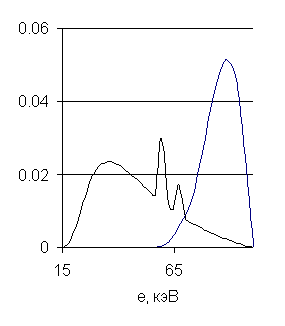
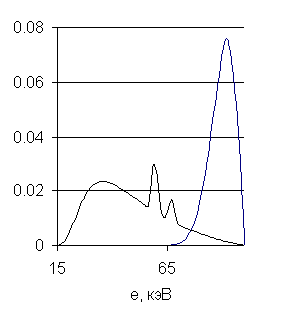
Рис.8 Рис.9
Априорную информацию об
«ужесточении» энергетического спектра полиэнергетических источников
целесообразно использовать для повышения эффективности расчётов методом Монте –
Карло. В прямых испытаниях методом Монте – Карло моделируются траектории
фотонов, имеющих энергетическое распределение источника. На рис.8,9 видно, что
основная доля этих фотонов имеет энергии от 20 кэВ в то время, как в детекторе
регистрируются, в основном, фотоны с более высокими энергиями от 65 кэВ. Это
обстоятельство наводит на мысль об изменении энергетического распределения
фотонов, моделируемых методом Монте – Карло, путём введения их начальных весов
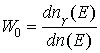 . (2)
. (2)
Здесь ![]() – доля фотонов в
источнике с энергией E,
– доля фотонов в
источнике с энергией E, ![]() – доля фотонов с
энергией E, моделируемых методом Монте – Карло.
Таким образом, плотность распределения
– доля фотонов с
энергией E, моделируемых методом Монте – Карло.
Таким образом, плотность распределения ![]() фотонов с весами (2)
отличается от энергетического спектра источника
фотонов с весами (2)
отличается от энергетического спектра источника ![]() и связана с ним
соотношением
и связана с ним
соотношением
![]() . (3)
. (3)
Из
формулы (3) следуют два простых частных случая.
1. Если ![]() , то
, то ![]() .
.
2. Если ![]() , то
, то ![]() .
.
В первом случае фотоны имеют
единичные начальные веса и распределены по энергии с плотностью ![]() . Во втором частном случае фотоны распределены равномерно по
соответствующему энергетическому диапазону
. Во втором частном случае фотоны распределены равномерно по
соответствующему энергетическому диапазону ![]() и имеют начальные
веса, распределённые по энергии прямо пропорционально энергетическому спектру
и имеют начальные
веса, распределённые по энергии прямо пропорционально энергетическому спектру ![]() используемого
полиэнергетического источника.
используемого
полиэнергетического источника.
В
табл.1 приведено сравнение статистической погрешности расчётов в указанных
частных случаях и при
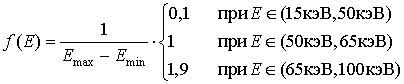 . (4)
. (4)
Первые три строчки таблицы
соответствуют внутреннему радиусу трубы ![]() см., последние три строчки –
см., последние три строчки – ![]() см. Статистическая погрешность рассчитана по формуле:
см. Статистическая погрешность рассчитана по формуле:
 , (5)
, (5)
где I –
интенсивность рассеянного излучения, D – оценка дисперсии интенсивности,
интегрирование ведётся по теневой области на детекторной плоскости. Оценка
дисперсии производится по следующей классической формуле:
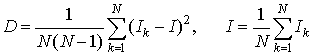 ,
,
где N –
количество вычислений, ![]() – результат k-го вычисления интенсивности рассеянного излучения при
фиксированном числе фотонов. Заметим, что детекторы на плоскости
– результат k-го вычисления интенсивности рассеянного излучения при
фиксированном числе фотонов. Заметим, что детекторы на плоскости ![]() имеют конечные размеры
(
имеют конечные размеры
(![]() см.,
см., ![]() см.), поэтому интегрирование в формуле (5) заменяется
суммированием по детекторам, расположенным в теневой области детекторной
плоскости.
см.), поэтому интегрирование в формуле (5) заменяется
суммированием по детекторам, расположенным в теневой области детекторной
плоскости.
Таблица 1
|
Внутр. радиус |
Начальный вес фотона |
Время
вычис-ий (мин.) |
Погрешность
d, % |
|
|
|
257 |
1,49 |
|
|
|
257 |
0,69 |
|
|
|
257 |
0,50 |
|
|
|
260 |
8,22 |
|
|
|
260 |
3,43 |
|
|
|
260 |
2,28 |
Из
результатов, приведённых в табл.1, следует, что наибольшая погрешность расчётов
имеет место в первом частном случае (![]() ). Во втором частном случае (
). Во втором частном случае (![]() ) погрешность в несколько раз меньше. Наименьшее значение
погрешности получено в последнем случае (3-я и 6-я строчки таблицы).
) погрешность в несколько раз меньше. Наименьшее значение
погрешности получено в последнем случае (3-я и 6-я строчки таблицы).
Таким
образом, для полиэнергетических источников имеет смысл использовать те
модификации метода Монте – Карло, в которых фотоны имеют начальные веса,
зависящие от энергии, и энергетическое распределение, отличающееся от
энергетического спектра используемого источника. В простейшем случае
целесообразно использовать равномерное распределение фотонов (второй частный
случай). Если необходимо, то можно провести дополнительный расчёт с учётом
энергетического спектра фотонов, регистрируемого на детекторной плоскости.
Такой способ оптимизации метода Монте – Карло относится к классу методов,
которые в литературе называют «выборкой по значимости». Выборка по значимости в
данном случае означает, что количество фотонов, направляемых алгоритмом в тот
или иной энергетический интервал, должно быть пропорционально некой функции
важности (4) этого интервала в формировании изображения объекта на детекторной
плоскости.
§3. Модификация метода Монте – Карло при большой оптической толщине
объекта
При
работе с объектами, оптическая толщина которых больше нескольких пробегов
фотона, подавляющее число фотонов застревает в слое, находящемся под облучаемой
поверхностью объекта, и, рассеиваясь, покидает объект через ту же облучаемую
поверхность. Однако вклад этих фотонов в изображение объекта на детекторной
плоскости, расположенной с противоположной стороны объекта, не столь велик. В
связи с этим представляется целесообразным изменить алгоритм Монте – Карло в
том месте, где разыгрывается длина звена траектории фотона до точки
взаимодействия.
Рассмотрим
движение фотонов в материале объекта в направлении оси z из заданной точки пространства ![]() (см. рис.1). Доля
фотонов, рассеянных в интервале
(см. рис.1). Доля
фотонов, рассеянных в интервале ![]() есть
есть
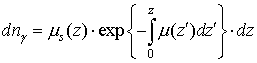 , (6)
, (6)
где ![]() – коэффициент
ослабления за счёт фотоэлектрического поглощения. Доля фотонов,
провзаимодействующих в интервале
– коэффициент
ослабления за счёт фотоэлектрического поглощения. Доля фотонов,
провзаимодействующих в интервале ![]() есть
есть
 . (7)
. (7)
В основном алгоритме Монте – Карло
(§1) длина пути фотона до точки взаимодействия z
разыгрывается в соответствии с плотностью распределения (7). При этом фотон
рассеивается с весом
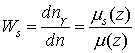 , (8)
, (8)
который трактуется как вероятность
«выживания» фотона в акте взаимодействия.
Из (8)
видно, что вес фотона равен, по определению, отношению двух величин ![]() и
и ![]() . Первая величина определена физической моделью рассеяния
(6). Вторая величина – плотность распределения фотонов, рассеиваемых в
алгоритме Монте – Карло по длине пути, может выбираться произвольным образом. В
частности, можно положить
. Первая величина определена физической моделью рассеяния
(6). Вторая величина – плотность распределения фотонов, рассеиваемых в
алгоритме Монте – Карло по длине пути, может выбираться произвольным образом. В
частности, можно положить
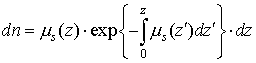 . (9)
. (9)
Тогда фотон будет рассеиваться с
весом
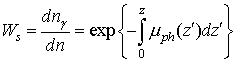 , (10)
, (10)
который можно трактовать как
вероятность «выживания» фотона на длине пути ![]() . При такой модификации метода Монте – Карло, при которой
длина звена траектории фотона разыгрывается в соответствии с плотностью
распределения (9), фотоны глубже проникают в объект, поскольку
. При такой модификации метода Монте – Карло, при которой
длина звена траектории фотона разыгрывается в соответствии с плотностью
распределения (9), фотоны глубже проникают в объект, поскольку ![]() (для железа и энергии
фотона меньше 100 кэВ выполнено неравенство
(для железа и энергии
фотона меньше 100 кэВ выполнено неравенство ![]() ).
).
Для
сравнения основного алгоритма Монте – Карло с его модификацией на основе формул
(9-10) рассмотрим эксперимент, описанный в предыдущем параграфе (см. рис.5). В
табл.1 приведены погрешности вычислений, проведённых с помощью основного
алгоритма (7-8). В табл.2 содержатся погрешности аналогичных вычислений,
проведённых с помощью модифицированного алгоритма (9-10).
Таблица 2
|
Внутр. радиус |
Начальный вес фотона |
Время
вычис-ий (мин.) |
Погрешность
d, % |
|
|
|
188 |
0,32 |
|
|
|
188 |
0,23 |
|
|
|
215 |
0,62 |
|
|
|
215 |
0,44 |
Кроме
погрешностей в таблицах указано время вычислений с использованием 1010
фотонов и 200 процессоров многопроцессорной системы МВС-5000М. Преимущество
модифицированного алгоритма (9-10) в рассматриваемом примере очевидно. Наряду с
существенным уменьшением погрешности наблюдается небольшой выигрыш во времени
вычислений, связанный с увеличением вероятности вылета фотона из объекта.
§4. Модификация метода Монте – Карло в задачах о формировании электронных
потоков
В
задачах, связанных с исследование электромагнитного воздействия проникающего
излучения, необходимо получать распределения потоков релятивистских электронов,
возникающих в результате взаимодействия ионизирующего излучения с материалами
объекта. Моделирование процесса рождения электронов и их регистрации на
детекторной плоскости можно осуществить с использованием основного метода Монте
– Карло, описанного в §1. Для этого достаточно процессы взаимодействия квантов
излучения с веществом сопровождать рождением электронов, и для каждого
рождённого электрона подсчитывать вероятность вылета из объекта согласно закону
ослабления:
 ,
,
где ![]() – коэффициент
ослабления электронного потока в материале объекта, r – длина
пути электрона в объекте, Е – энергия
электрона. Рождением электронов сопровождаются два типа рассматриваемых
взаимодействий: фотоэлектрическое поглощение и комптоновское рассеяние фотона.
– коэффициент
ослабления электронного потока в материале объекта, r – длина
пути электрона в объекте, Е – энергия
электрона. Рождением электронов сопровождаются два типа рассматриваемых
взаимодействий: фотоэлектрическое поглощение и комптоновское рассеяние фотона.
При
комптоновском рассеянии фотона рождается электрон со следующими параметрами.
– кинетическая энергия электрона: ![]() , где
, где ![]() и
и ![]() – энергии фотона до и
после рассеяния соответственно;
– энергии фотона до и
после рассеяния соответственно;
– полярный угол движения электрона в системе
координат, связанной с первоначальным движением фотона:
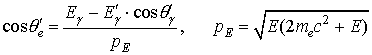 ,
,
где ![]() – косинус угла
рассеяния фотона;
– косинус угла
рассеяния фотона;
– азимутальный угол движения электрона: ![]() , где
, где ![]() – азимутальный угол
рассеяния фотона;
– азимутальный угол
рассеяния фотона;
– начальный вес электрона: ![]() , где
, где ![]() – вес фотона до
рассеяния,
– вес фотона до
рассеяния, ![]() – вероятность
комптоновского рассеяния в точке взаимодействия (см. стр.7).
– вероятность
комптоновского рассеяния в точке взаимодействия (см. стр.7).
При
фотоэлектрическом поглощении фотона рождается электрон со следующими
параметрами.
– кинетическая энергия электрона: ![]() , где
, где ![]() – энергия фотона
до поглощения,
– энергия фотона
до поглощения, ![]() – энергия связи
К-оболочки в атоме вещества;
– энергия связи
К-оболочки в атоме вещества;
– полярный угол движения электрона в системе
координат, связанной с первоначальным движением фотона, разыгрывается с
использованием углового распределения:
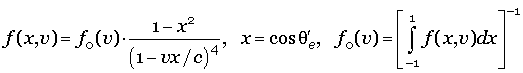 ,
,
где v – скорость
электрона с энергией E, с
– скорость света;
– азимутальный угол движения электрона
разыгрывается по формуле:
![]() ;
;
– начальный вес электрона: ![]() , где
, где ![]() – вес фотона до
поглощения,
– вес фотона до
поглощения, ![]() – вероятность
фотоэлектрического поглощения в точке взаимодействия (см. стр.7).
– вероятность
фотоэлектрического поглощения в точке взаимодействия (см. стр.7).
Таким
образом, в точке взаимодействия фотона с веществом объекта рождается два
электрона: комптоновский электрон и фотоэлектрон.
Указанный
способ моделирования процесса рождения электронов оказывается неработоспособным
в случае, когда толщина объекта во много раз превышает величину пробега
электрона в материале объекта. В этом случае лишь незначительная часть
электронов, рождённых в тонком приповерхностном слое объекта, даст
сколько-нибудь заметный вклад в формирование электронного потока на детекторной
плоскости. Поэтому необходимо модифицировать алгоритм Монте – Карло, изменив
статистику рождения электронов.
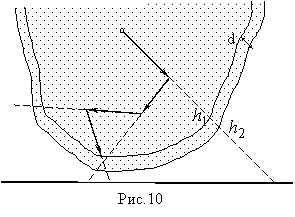 Естественным шагом в этом направлении
является выделение эффективного слоя у поверхности объекта (рис.10) толщиной d. При этом в алгоритме может понадобиться описать
дополнительную поверхность, ограничивающую указанный слой. Далее все процессы,
связанные с рождением электронов на каждом звене траектории фотона, можно
моделировать отдельно от процессов, связанных с рассеянием фотона. В частности,
точку рождения электрона можно разыгрывать на отрезке
Естественным шагом в этом направлении
является выделение эффективного слоя у поверхности объекта (рис.10) толщиной d. При этом в алгоритме может понадобиться описать
дополнительную поверхность, ограничивающую указанный слой. Далее все процессы,
связанные с рождением электронов на каждом звене траектории фотона, можно
моделировать отдельно от процессов, связанных с рассеянием фотона. В частности,
точку рождения электрона можно разыгрывать на отрезке ![]() (см. рис.10),
соединяющем точки пересечения соответствующего луча с границами эффективного
слоя. Для этого используется условная плотность распределения точек
взаимодействия кванта на этом отрезке:
(см. рис.10),
соединяющем точки пересечения соответствующего луча с границами эффективного
слоя. Для этого используется условная плотность распределения точек
взаимодействия кванта на этом отрезке:
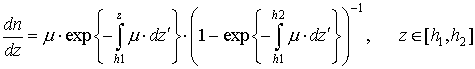 . (11)
. (11)
В (11) предполагается, что ![]() . Возможны другие ситуации. Если
. Возможны другие ситуации. Если ![]() , то начало луча лежит внутри эффективного слоя, и в (11)
следует положить
, то начало луча лежит внутри эффективного слоя, и в (11)
следует положить ![]() . Если
. Если ![]() , то луч пересекает только внутреннюю границу слоя, и в (11)
следует
, то луч пересекает только внутреннюю границу слоя, и в (11)
следует ![]() заменить на
заменить на ![]() и положить
и положить ![]() . Если
. Если ![]() , то луч не пересекает эффективный слой, и тогда рождения
электрона вообще не происходит. Возможно также, что луч несколько раз
пересекает эффективный слой. Тогда под отрезком
, то луч не пересекает эффективный слой, и тогда рождения
электрона вообще не происходит. Возможно также, что луч несколько раз
пересекает эффективный слой. Тогда под отрезком ![]() следует понимать ту
совокупность точек луча, которая принадлежит слою.
следует понимать ту
совокупность точек луча, которая принадлежит слою.
Заметим,
что доля фотоэлектронов, образованных в элементе ![]() фотоном с весом
фотоном с весом ![]() , определяется формулой:
, определяется формулой:
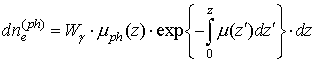 , (12)
, (12)
а доля комптоновских электронов,
образованных в элементе ![]() фотоном с весом
фотоном с весом ![]() , - формулой:
, - формулой:
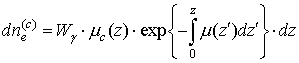 . (13)
. (13)
Поэтому начальные веса рождённых
электронов имеют вид:
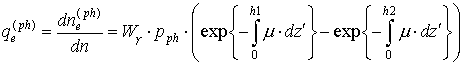 . (14)
. (14)
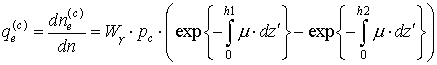 . (15)
. (15)
Разность экспоненциальных функций в
(14), (15) можно трактовать как вероятность взаимодействия фотона в эффективном
слое на отрезке ![]() .
.
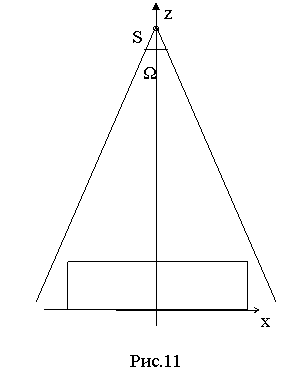 Для анализа эффективности
предлагаемого алгоритма были проведены расчёты электронных потоков, образующихся
при облучении квадратной железной (Fe) пластины
Для анализа эффективности
предлагаемого алгоритма были проведены расчёты электронных потоков, образующихся
при облучении квадратной железной (Fe) пластины ![]() (рис.11). В расчётах
использовался точечный полиэнергетический источник с энергетическим спектром,
описанным в §2 (см. рис.8,9). Источник был расположен в точке с координатой
(рис.11). В расчётах
использовался точечный полиэнергетический источник с энергетическим спектром,
описанным в §2 (см. рис.8,9). Источник был расположен в точке с координатой ![]() см и излучал в телесный угол
см и излучал в телесный угол ![]() . Вычислялись отношения декартовых компонент вектора
плотности потока электронов к мощности источника (количеству излучаемых фотонов
в единицу времени) в теневой области
. Вычислялись отношения декартовых компонент вектора
плотности потока электронов к мощности источника (количеству излучаемых фотонов
в единицу времени) в теневой области ![]() на детекторной
плоскости
на детекторной
плоскости ![]() . Результаты расчётов в сечении
. Результаты расчётов в сечении ![]() приведены на рис.12.
приведены на рис.12.
 Сплошная линия соответствует z-компоненте вектора плотности потока электронов,
пунктирная линия – x-компоненте. Третья компонента равна
0 в указанном сечении. Отметим, что свойства симметрии полученных результатов
соответствуют свойствам симметрии задачи.
Сплошная линия соответствует z-компоненте вектора плотности потока электронов,
пунктирная линия – x-компоненте. Третья компонента равна
0 в указанном сечении. Отметим, что свойства симметрии полученных результатов
соответствуют свойствам симметрии задачи.
Простая
геометрия численного эксперимента позволила аналитически указать в алгоритме толщину
эффективного плоского слоя у поверхности объекта ![]() (рис.13) как функцию энергии и направления
движения электрона:
(рис.13) как функцию энергии и направления
движения электрона:
Рис.12
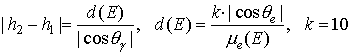 , (16)
, (16)
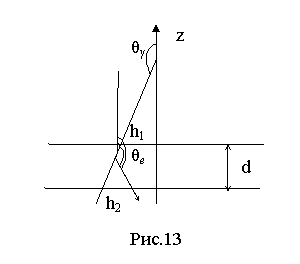
![]() – коэффициент
ослабления электронного потока в железе. Таким образом, определение толщины d эффективного слоя и розыгрыш точки рождения
производились для каждого электрона после определения его энергии E и направления движения (полярного
– коэффициент
ослабления электронного потока в железе. Таким образом, определение толщины d эффективного слоя и розыгрыш точки рождения
производились для каждого электрона после определения его энергии E и направления движения (полярного ![]() и азимутального
и азимутального ![]() углов).
углов).
Кроме
плотности распределения (11) для розыгрыша точки рождения электрона в алгоритме
использовалось и другое распределение:
![]() , (17)
, (17)
где 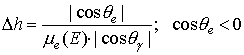 ;
; ![]() ;
; ![]() , если
, если ![]() . В пределе при
. В пределе при 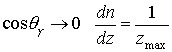 . Начальные веса рождённых электронов имеют вид, вытекающий
из их определения
. Начальные веса рождённых электронов имеют вид, вытекающий
из их определения

и соотношений (12), (13) и (17).
В
следующей таблице указаны время вычислений с использованием 233
фотонов и 64 процессоров многопроцессорной системы МВС-5000М, а также
погрешность расчёта z-компоненты вектора плотности потока
электронов.
|
№ |
Время
вычис-ий (мин.) |
Погрешность
d, % |
|
1. |
18 |
0,18 |
|
2. |
18 |
0,14 |
Погрешность вычислялась по формуле,
аналогичной (5). Первая строка таблицы соответствует использованию плотности
распределения (11), (16) для розыгрыша точки рождения электрона, вторая строка
таблицы соответствует использованию плотности распределения (17). Приведённые результаты
позволяют сделать вывод о достаточно высокой эффективности предложенного
алгоритма, позволяющего рассчитывать электронные потоки с достаточной точностью
при приемлемых вычислительных затратах на современной многопроцессорной
технике.
Литература.
1. V.P. Zagonov, S. V. Podolyako, G.-R. Tillack, C. Bellon. Fast 3D ray tracer algorithm for cone beam radiography. 3-я международная конференция
«Компьютерные методы и обратные задачи в неразрушающем контроле и диагностике»,
Москва 2002, с.102
2. В.П.Загонов и др. Применение поверхностно ориентированного
описания объектов для моделирования трансформации ионизирующего излучения в
задачах вычислительной диагностики // Матеем. моделирование, т.16, №5,
2004, с.103-116
3.
C. Cercignani: The Boltzmann Equation and its Applications. Springer, New York,
1988.
4. G.-R.
Tillack, V. M. Artemiev, and A. O. Naumov: Transport
Equations for Photon Flow Exploiting the Theory of Markov Processes with Random
Structure Part 1: Derivation of Basic Equations. Journal of Nondestructive
Evaluation 20 4 (2001) 153-161
5. У.Фано, Л.Спенсер, М.Бергер. Перенос гамма-излучения. Госатомиздат,
Москва, 1963.
6.
G. Marsaglia and A. Zaman: A new class of random number generators.
Annals of Applied Probability 1
(1991) 462-480.
7. И.М.Соболь, Ю.Л.Левитан. Получение точек, равномерно расположенных в
многомерном кубе. Препринт ИПМ им. М.В.Келдыша РАН, 1976, №40.
8. И.А.Антонов, В.М.Салеев. Экономичный способ вычисления ЛПt - последовательностей. ЖВМ и МФ, 1979, т.19, №1, с.243-245.
 , где
, где 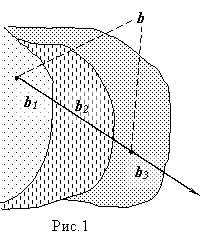
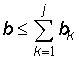 (на рис.1 -
(на рис.1 -  , а соответствующая координата конца звена определяется по
формуле:
, а соответствующая координата конца звена определяется по
формуле: 
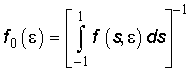 .
.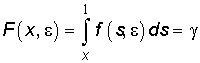 ,
,