Содержание

1. Введение

В последнее время растет интерес к Formation Flying - групповым полетам спутников - образований из нескольких спутников, летящих на сравнительно близком взаимном расстоянии от несколько десятков метров до сотни километров. Обычно такие спутники работают вместе над выполнением одной и той же задачи. Групповые полёты позволяют частично снизить стоимость проекта и привнести качественно новые возможности в научную и технологическую программу полета. Основным отличием групповых полетов (Formation Flying) от созвездий (Constellation) заключается в том, что в системах первого типа управление осуществляется с учетом взаимного положения спутников, движущихся по весьма близким орбитам, то есть реализуется управление относительным движением, а в системах второго типа (Constellation) осуществляется индивидуальное управление каждым объектом.

Структура Formation Flying дает возможность сохранить работоспособность формации в случае выхода из строя одного из её элементов. В этом случае работа системы может быть продолжена, но, быть может, с меньшей производительностью. Существует ряд проблем для реализации таких проектов, в том числе и с точки зрения динамики входящих в нее спутников. Первая проблема - это определение и формирование пространственных спутниковых конфигураций. Вторая проблемы - их поддержание во времени. Для решения второй проблемы целесообразно сначала изучить механизмы, способствующие разрушению формации. Рассмотрению отдельных причин, способствующих разрушению формации на коротких интервалах времени, и посвящена настоящая работа. Приведен пример использования полученных результатов для анализа относительного движения Международной космической станции и первого российского наноспутника ТНС-0, выведенного на орбиту с ее борта 28-го марта 2005 года российским космонавтом С.Шариповым, который, стоя на внешней стороне МКС, оттолкнул спутник рукой.

В работе рассмотрено относительное движение двух близколетящих спутников. Сначала описывается невозмущённое движение. Один спутник движется по круговой, а второй - по эллиптической орбите. Для описания относительного движения используются уравнения Хилла. Далее рассматривается эволюция относительного движения в случае слабой эллиптической орбиты, а также в случае наличия солнечного давления и сопротивления атмосферы.

В работе не учитывается влияние несферичности Земли на относительное движение спутников. Так делается потому, что действие рассмотренных в работе факторов преобладает в течение первых витков над эффектом от сжатия Земли.

Если посмотреть работы, посвящённые данной тематике, то можно увидеть, что в большинстве из них рассматриваются вопросы, связанные с реконфигурацией и поддержанием формаций. Так, например, авторы работы [1] рассматривают проблемы оптимального перехода от одной формации к другой. В случае перехода от формации лидер-последователь (группа спутников летящих по одной орбите, различающихся только средней аномалией) к эллиптической формации оптимальным будет переход с помощью трёх импульсов, направленных по касательной к траектории. Аналогична ситуация перехода от эллиптической формации к подобной только меньшего или большего размера. Первый и третий импульсы равны по величине и направлению, а второе – в два раза больше по величине и противоположен по направлению. Импульсы следует прикладывать с интервалом в полвитка. При увеличении же расстояния между спутниками, в случае формации лидер-последователь, оптимальным будет использование двух импульсов, направленных вдоль траектории, и чем больше будет временной интервал между ними, тем меньше топлива потребуется для выполнения манёвра. Работа [2] касается более глубокого изучения проблем реконфигурации и оптимального управления.

Существует ряд работ, посвященных конкретным проектам, которые осуществляются с помощью Formation Flying. Так в [3] рассмотрен интерферометрический телескоп, сформированный с помощью трёх микроспутников, движущихся по орбитам с одинаковым наклонением, эксцентриситетом, аргументом перигея и величиной большой полуоси. Долгота восходящего узла для каждого из спутников выбирается таким образом, чтобы горизонтальные поперечные смещения соответствовали рассматриваемой эффективной базовой линии интерферометрического телескопа. В связи с этим возникает проблема точного управления группой.

Существуют также работы, касающиеся построения моделей, описывающих относительное движение. Однако большая часть из них затрагивается лишь создание численных моделей. В [4] рассматривается построение аналитической модели относительного движения спутников, летящих на низких орбитах. В работе описывается движение в нецентральном поле тяжести Земли. Получена достаточно точная модель относительного движения с учётом не только второй гармоники геопотенциала Земли, но и членов его разложения более высокого порядка.

Слабые возмущения, рассмотренные в настоящей работе, уже были изучены в [5]. Однако там они касались только абсолютного движения одного спутника. Здесь же рассматривается относительное движение двух спутников. С учётом специфики такого движения, появляются качественно новые эффекты.

2. Уравнения Хилла

Для начала рассмотрим уравнение Хилла [6]. Оно описывает невозмущенное относительное движение, и в векторной форме выглядит следующим образом:

.

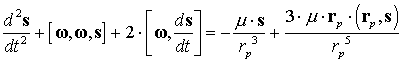Здесь  - угловая скорость вращения спутника вокруг Земли, - радиус-вектор, направленный от одного спутника (назовем его основным или материнским спутником) к другому, а - радиус орбиты основного спутника. Другой спутник будем называть вторым или дочерним. В координатной форме уравнение Хилла будет выглядеть так:

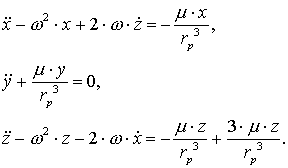
Перепишем эти уравнения с учётом обозначения

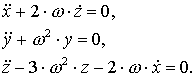
Решение этой системы, как известно [6], при имеет вид

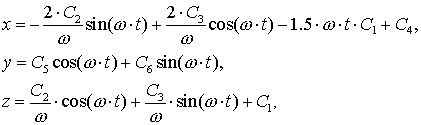
где - постоянные интегрирования. Этим исчерпывается невозмущенная задача Хилла. Как видно, она имеет решение в квадратурах и при этом легко интегрируется. Теперь усложним задачу. Учтём возмущения от эллиптичности орбиты основного спутника, давления солнечной радиации и сопротивления атмосферы, действующие на дочерний спутник.

3. Слабая эллиптичность орбиты основного спутника

Считаем, что основное тело движется по слабой эллиптической орбите. Запишем уравнение относительного движения в векторной форме

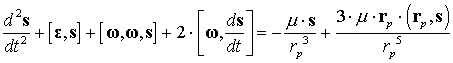.            (3.1)

Как можно заметить, теперь в уравнение входит ещё член, содержащий угловое ускорение (скобка  в уравнении (3.1)). Стоит также отметить, что радиус орбиты основного спутника определяется формулой , где p – параметр орбиты,  - истинная аномалия,  - эксцентриситет орбиты основного спутника. Перепишем это уравнение в координатной форме

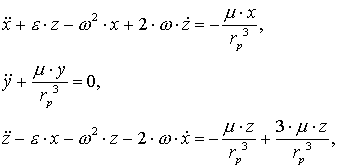                   (3.2)

где точкой обозначены производные по времени, а , , . Что для малых  имеет вид , . Тогда, с учётом этих формул и малости , система (3.2) примет вид

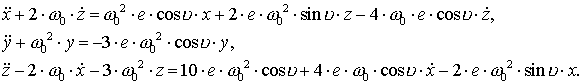              (3.3)

Здесь сохранены члены степени не выше первой по  Используя формулы

, ,

, ,

, ,

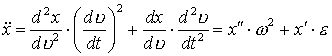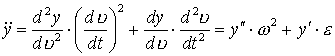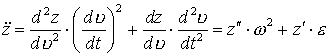перейдём в первом уравнении (3.3) от производных по времени к производным по истинной аномалии. Штрихами обозначены производные по истинной аномалии.

.

Преобразовав это выражение с учётом , и сохранив члены степени не выше первой по , получим

.

Аналогично преобразуем остальные уравнения системы (3.3) и запишем конечный результат

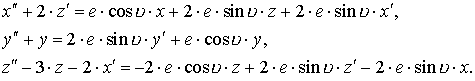        (3.4)

Решим систему (3.4). Сначала рассмотрим первое и третье уравнения системы

Как показано во втором разделе, решением однородного уравнения является следующая пара выражений:

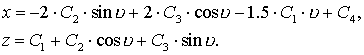,                  (3.5)

Здесь , , ,  - некоторые произвольные постоянные.

Используем метод вариации постоянных для решения первого и третьего уравнения системы (3.4). Найдем производные выражений (3.5)

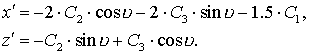                             (3.6)

С другой стороны, с учётом того, что , , ,  уже зависят от истинной аномалии, получим следующие равенства:

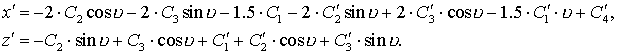(3.7)

Дифференцируя (3.7) по  и учитывая, что , , ,  не являются постоянными, получим вторые производные переменных x и z

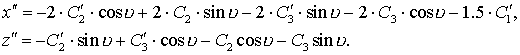
Подставляя выражения для первых и вторых производных x и z в систему (3.4), а также с учётом равенства соответствующих уравнений систем (3.6) и (3.7), получим уравнения

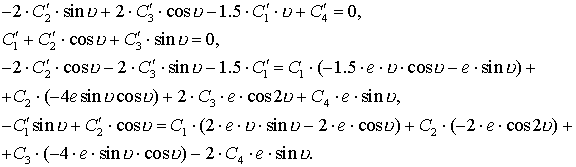
Разрешая эту систему относительно производных, мы находим выражения для производных , , ,

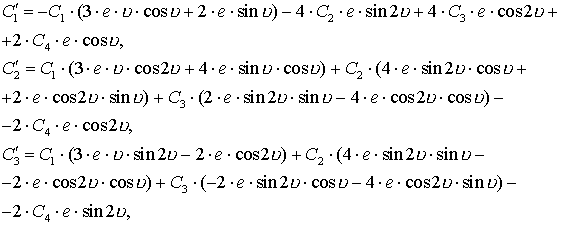(3.8)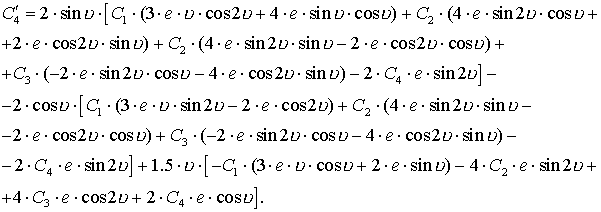

Решить эти уравнения в квадратурах не удаётся. Так как эксцентриситет мал, поэтому скорость изменения переменных , ,  и , пропорциональная  тоже мала. Тогда проведём усреднение правых частей уравнений (3.8) по истинной аномалии за период обращения спутника по орбите, считая , ,   при осреднении постоянными. В результате получим

, , , .

Отсюда, после интегрирования по истинной аномалии следует, что

, , , ,

где , ,   - постоянные интегрирования. Подставив эти выражения в решение (3.5) однородной системы, получим уравнения усреднённого движения

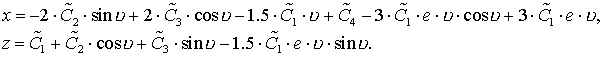
Рассмотрим теперь второе уравнение системы (3.3). Используем метод Ван-дер-Поля для нахождения его приближенного решения. Решением соответствующего ему однородного уравнения будет . Здесь  - амплитуда, а  - фаза, и тогда . С другой стороны . Из равенства этих выражений между собой получаем

                                  (3.9).

Вторая производная от y определяется выражением . Подставляя это выражение и выражение для первой производной во второе уравнение системы, получим

 .

Объединяя это уравнение и уравнение (3.9), получаем систему

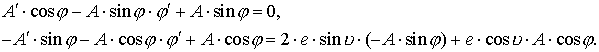
Отсюда можно найти значения производных  и . Запишем эти значения

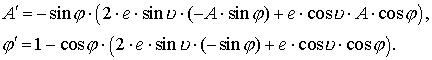                   (3.10)

Здесь мы имеем две быстрые переменные – это фаза  и истинная аномалия . Периоды правых частей этих уравнений по ним соответственно равны  и . Сделаем замену , тогда . После этого система примет вид

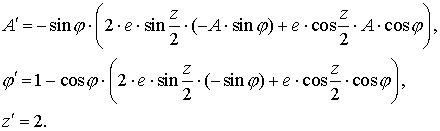             (3.11)

Теперь мы имеем две быстрые переменные  и . С точностью до  имеет место резонанс 1:2 по переменным  и . Следуя стандартной процедуре [7], введём новую переменную . С учётом этого выражения вычтем в системе (3.11) третье уравнение из второго, тогда получим следующие выражения:

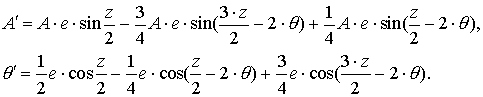
После усреднения обоих уравнений этой системы по  получим

Решением этой системы будет следующая пара выражений:

где  и  - постоянные интегрирования. Подставим выражения для и  в  и учтём, что  и , тогда получим

.

Сведём полученные уравнения в одну систему

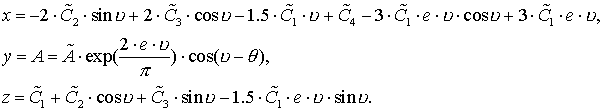(3.12)

Таким образом, мы рассмотрели относительное движение двух спутников, причём основной спутник движется по слабой эллиптической орбите, и получили их усреднённое движение. Выражения (3.12), описывающее это движения, говорят нам о том, что при наличии эксцентриситета расстояние между спутниками будет увеличиваться, так как в уравнениях присутствуют вековые члены. Однако стоит отметить, что все эти слагаемые зависят от постоянной  для первого и третьего уравнений и от  для второго. Значит, при определённых начальных условиях её можно сделать равной нулю и, таким образом, избежать расхождения спутников.

4. Влияние солнечного давления на относительное движение спутников

Следующим шагом будет рассмотрение случая, когда на второй спутник действует сила солнечного давления. Второй спутник считается значительно более лёгким, поэтому сила солнечного давления, действующая на него существенна. Здесь мы считаем, что движение основного спутника происходит по круговой орбите. В этом случае уравнения Хилла запишутся следующим образом:

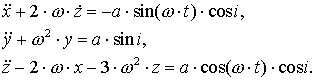                     (4.1)

Здесь , где  - некоторая эффективная площадь спутника, - масса второго спутника и  - солнечная постоянная, характеризующая величину солнечного давления, - наклонение орбиты. Решая эту систему методом вариации постоянных, получаем

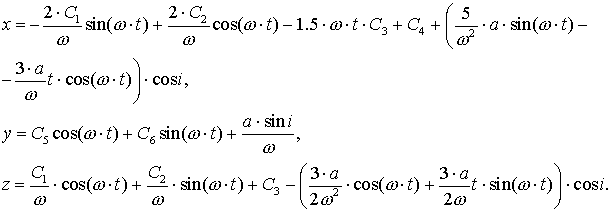
Это справедливо, когда сила солнечного давления действует постоянно, то есть орбита не затеняется Землей.

Рассмотрим теперь случай, когда имеет место вхождения спутника в тень Земли. Тогда система (4.1) запишется в виде

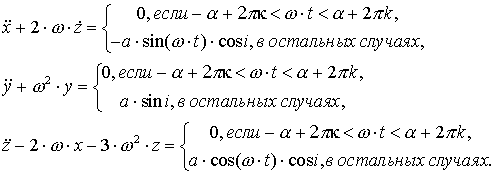 (4.2)

Здесь  - угол между направлением на Солнце и радиус-вектором основного спутника, при котором спутник находится в тени. Сначала решим первое и третье уравнение этой системы. Используем метод вариации постоянных. Выражения для производных , , ,  будут следующим:

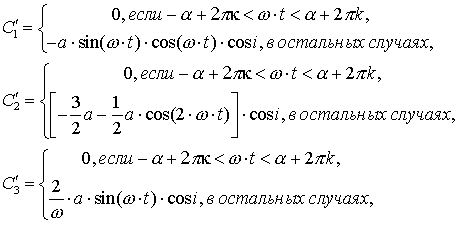
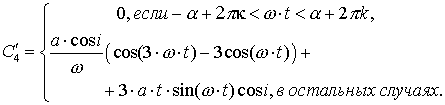
Получим усреднённые по времени за период выражения для производных , , ,

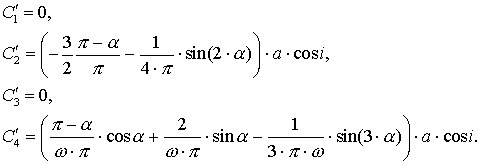
Решаем эту систему уравнений и находим

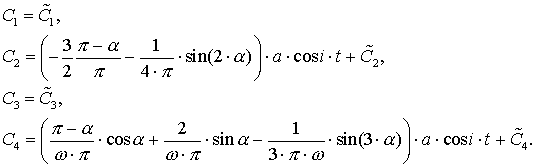
Теперь рассмотрим второе уравнение системы (4.2). Выражения для производных будут выглядеть следующим образом:

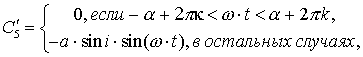
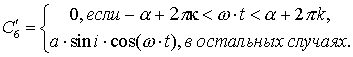
Произведя усреднение по времени за период, получим

,

.

Тогда , .

Запишем теперь выражения для усреднённого движения

   (4.4)

Видно что, как в случае постоянно действующей силы солнечного давления, так и в случае вхождения в тень, имеет место резонанс, а, следовательно, появляются вековые члены, которые способствуют разлёту спутников. Ситуация отличается от слабой эллиптичности тем, что здесь в вековые члены не входят постоянные и выбором начальных условий не удаётся их сделать равными нулю. В данном случае не учитывается годовое движения Земли, и, соответственно, нет изменения направления на Солнце, так как за интервал времени порядка нескольких витков оно меняется на малую величину.

Приведём пример относительного движения с нулевыми начальными условиями. Графики, изображённые на рис.4.1, получены для орбиты с нулевым наклонением и высотой 360 км. Масса спутника – 5.5 кг, радиус его сферического корпуса – 0.17 м. Подсчёт даёт величину . На рис.4.1 пунктиром обозначено движение с нулевыми начальными относительными скоростями и отклонениями в задаче Хилла, сплошная линия – при наличии солнечного давления.

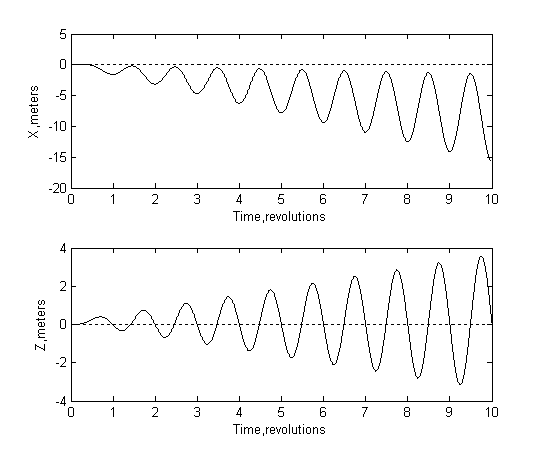
Рис.4.1. Относительное движение при наличии солнечного давления. Нулевые начальные относительные скорости и отклонения. Пунктирная линия – движение в задаче Хилла с нулевыми начальными условиями, сплошная – при наличии солнечного давления

Как и следовало ожидать, имеем движение с нарастающей амплитудой.

5. Влияние сопротивления атмосферы

Рассмотрим теперь влияние сопротивления атмосферы. Сила сопротивления записывается в виде , где - баллистический коэффициент, S – сечение, c_x - коэффициент лобового сопротивления, r - плотность атмосферы, - скорость основного тела. Силы, действующие на разные спутники, будут разные, так как спутники имеют различные скорости и баллистические коэффициенты. При расчетах берется некоторое осредненное по орбитальному и угловому движениям значение коэффициентов лобового сопротивления.

Пусть основной спутник движется по круговой орбите, тогда в орбитальной системе координат его скорость запишется следующим образом: . Скорость второго тела можно представить в виде ,,. Тогда

.

Отсюда

,

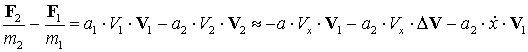где . Считая, что угловое ускорение связанной с основным спутником системы координат мало, пренебрегаем слагаемым, содержащим это ускорение. Тогда уравнение движения второго спутника относительно основного выглядит следующим образом:

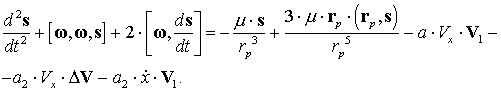
В координатной форме это уравнение запишется так:

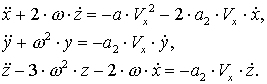                               (5.1)

Найдем решение (5.1) подобно тому, как это делалось в предыдущих разделах. Опять же рассмотрим сначала первое и третье уравнения системы (5.1). В результате получим выражения для производных , , ,  в виде

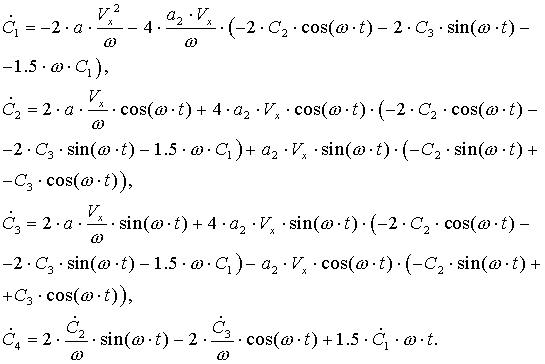
После усреднения правых частей по времени за период, получим

Решением этой системы будут выражения

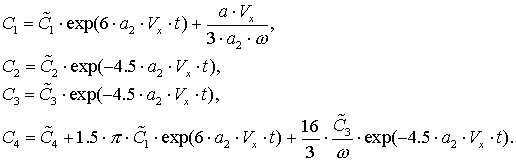
Здесь , ,   - постоянные интегрирования.

Теперь рассмотрим второе уравнение системы (5.1). Это однородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решение будет следующим:

.

Здесь  и - некоторые постоянные. Запишем теперь конечные выражения для усреднённого движения

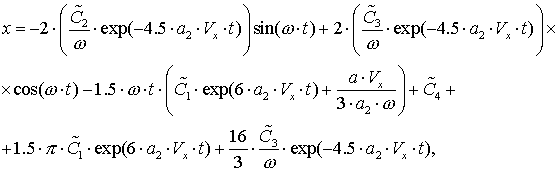
                                                          (5.2)

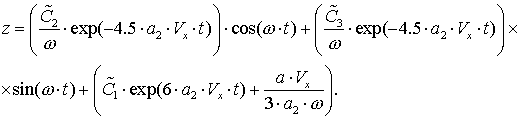
Итак, мы видим, что появляются вековые члены в первом уравнении, один из которых можно сделать равным нулю путём выбора подходящих начальных условий, а второй обратить в нуль не удается.

6. Набор двустрочных элементов системы NORAD

Сравним теперь движение, полученное в предыдущем разделе, с реальным движением на примере конкретным объектов. Для этого воспользуемся набором двустрочных элементов системы NORAD [9]. Сначала рассмотрим как использовать эти данные (далее для примера представлены данные по Международной космической станции). Они имеют следующий вид:

Здесь, в первой строке нам будет нужно число 05168.18002262 (год – 2005 и время 168.18002262 в днях) и число 13543-3 (что означает ). Последнее является коэффициентом аэродинамического сопротивления, его размерность (радиус Земли)^-1. Во второй строке - 051.6453 наклонение орбиты в градусах, 260.9417 – долгота восходящего узла в градусах, .0004123 эксцентриситет, 265.7312 – аргумент перицентра в градусах, 175.6907 – средняя аномалия в градусах, 15.72912223 – среднее число оборотов за день. Далее, используя модель SGP4, разработанной К.Кренфордом [9], пересчитываем набор двустрочных элементов в координаты и скорости в системе отсчёта, центром которой является Земля, для нужных моментов времени.

После этого перейдём в систему отсчёта связанную с основным спутником. Сделаем переход в систему координат , с началом в притягивающем центре. Ось  системы совпадает с направлением на перицентр орбиты, плоскость  совпадает с плоскостью орбиты. Этот переход осуществляется с помощью матрицы [5]

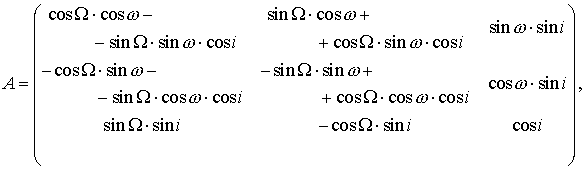
а затем повернём систему таким образом, чтобы радиус-вектор основного спутника совпадал с осью OZ новой системы координат, а ось OX была бы направлена по касательной к траектории материнского спутника. Матрица этого перехода запишется следующим образом:

Здесь .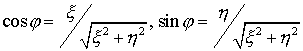

Таким образом, мы получили движение второго спутника относительно первого.

7. Технологический наноспутник ТНС-0

Теперь, для иллюстрации полученных результатов рассмотрим движение наноспутника ТНС-0 [8] (рис.7.1), выведенного на орбиту космонавтом С.Шариповым с борта Международной космической станции 28 марта 2005 года (рис.7.2).

Рис.7.1. Наноспутник ТНС-0 (летный образец, фото РНИИ КП)

Для начала проведём оценку изменения расстояния между спутниками на протяжении первых витков, которое появляется за счёт несферичности Земли. Изменение расстояния между спутниками будет иметь порядок

    (7.1)

Здесь . Формула (7.1) справедлива для круговых и слабо эллиптических орбит. Тогда, подставляя данные для МКС и ТНС-0 , полученные с по измерениям системы NORAD, имеем  за виток. В течение нескольких оборотов станции и спутника по орбите вокруг Земли, по-видимому, можно пренебречь влиянием сжатия Земли на их относительное движение.

Рис.7.2. Вывод наноспутника ТНС-0 космонавтом С.Шариповым с борта Международной космической станции (фото с экрана ТВ)

Во время отделения ТНС-0 станция двигалась по круговой орбите, высота которой примерно 360 км. Тогда для спутника , а для станции . Проведём оценку их относительного смещения за несколько витков.

Для демонстрации влияния аэродинамического сопротивления на относительное движение спутника и МКС приведём результаты расчетов при нулевых начальных относительных скоростях и отклонениях. Тогда, находя соответствующие константы и подставляя их в уравнения (5.2), получим графики, изображенные на рис.7.3.

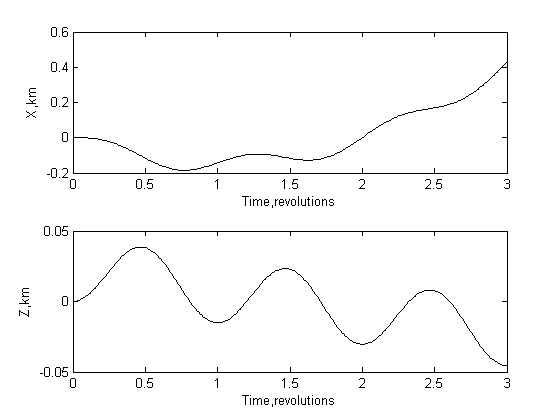
Рис.7.3. Изменение относительного расстояния спутников при нулевых начальных условиях движения. На рисунках ось Z направлена по радиус-вектору, а ось X по касательной к траектории МКС

Или, если рассмотреть больший интервал времени, то получим движение изображенное на рис.7.4.

Как видно, по оси Х наблюдается вначале небольшое движение назад, а затем второй спутник обгоняет основной. Движение назад следует из того, что коэффициент аэродинамического сопротивления у ТНС-0 больше, чем у МКС. А обгон – это, так называемый, парадокс спутника [5]. По оси Z видно движение, похожее на периодическое, но с постепенной потерей высоты относительно Земли. Как видно, это смещение намного больше смещения, которое является следствием несферичности Земли. По оси Y, направленной перпендикулярно плоскости орбиты, при нулевых начальных условиях не будет.

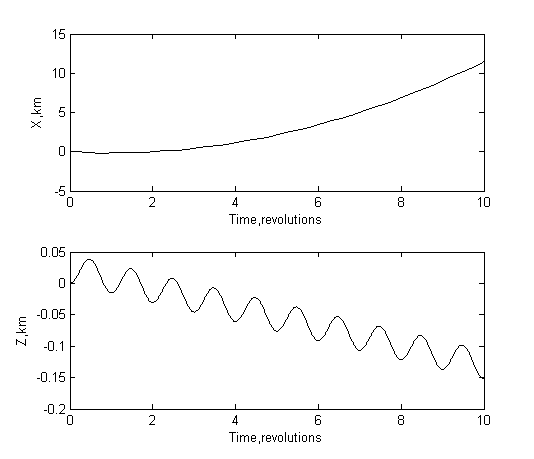
Рис.7.4. Изменение относительного расстояния спутников при нулевых начальных условиях движения. На рисунках ось Z направлена по радиус-вектору, а ось X по касательной к траектории

На самом деле, спутник запускался с ненулевыми начальными условиями. Они точно нам не известны, но их можно попытаться определить с помощью данных, полученных системой NORAD. Сделаем это следующим способом. Сначала воспользуемся данными для ТНС-0 и МКС на 28 марта 2005 [9]:

МКС

ТНС-0

Затем проведём расчеты, описанные в разделе 6, с шагом по времени, равным одной минуте. После этого, используя метод наименьших квадратов, найдём начальные условия, которым соответствует наименьшее отклонение реальной траектории от аналитической, полученной с помощью (5.2). Таким образом, получаем следующие начальные условия:

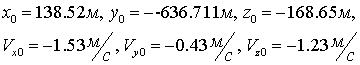.             (7.2)

На рис.7.5 изображен график движения ТНС-0 относительно МКС построенного по формулам (5.2) с начальными условиями (7.2).

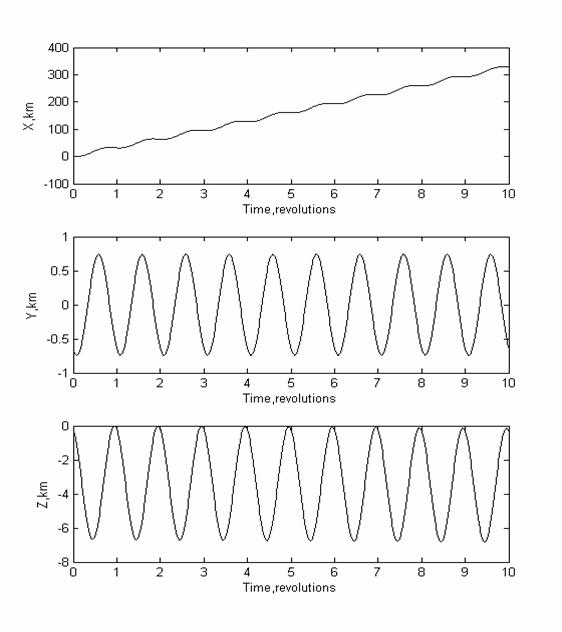
Рис.7.5. Изменение относительного расстояния ТНС-0 и МКС с учётом сопротивления атмосферы, найденного по (5.2) и с начальными условиями (7.2). На рисунках ось Z направлена по радиус-вектору, ось X по касательной к траектории, а ось Y – перпендикулярно плоскости орбиты

Ясно, что начальные отклонения не соответствуют действительности, это связано с тем, что данные, полученные с помощью системы NORAD, не обеспечивают нужной точности измерения. Начальные скорости же получились достаточно правдоподобными вследствие того, что они получены с помощью статистической обработки NORAD’oвских данных, что позволило несколько повысить точность определения скорости.

Видно, что по оси Z амплитуда колебаний увеличилась в несколько раз, что говорит о превалирующей роли начальных условий движения. На рис.7.6 изображено относительное движение станции и спутника, в этом случае представленное в плоскости OXZ.

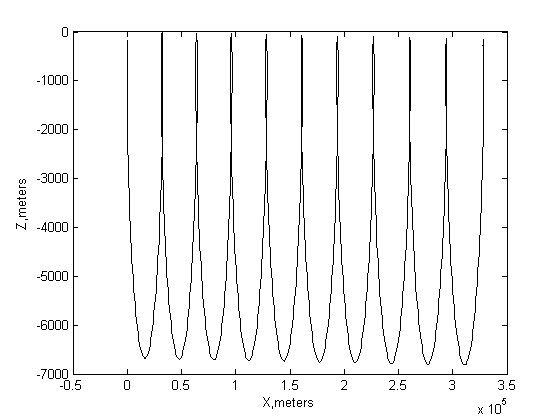
Рис.7.6. График относительного движения ТНС-0 и МКС в плоскости орбиты

Если рассмотреть движение ТНС-0 в этой системе координат, то это будет именно то движение, какое рассматривалось выше (рис 7.3-7.5). Построим график этого движения. На рис. 7.7 сплошная линия – реальное движение, а пунктирная – движение, полученное аналитически.

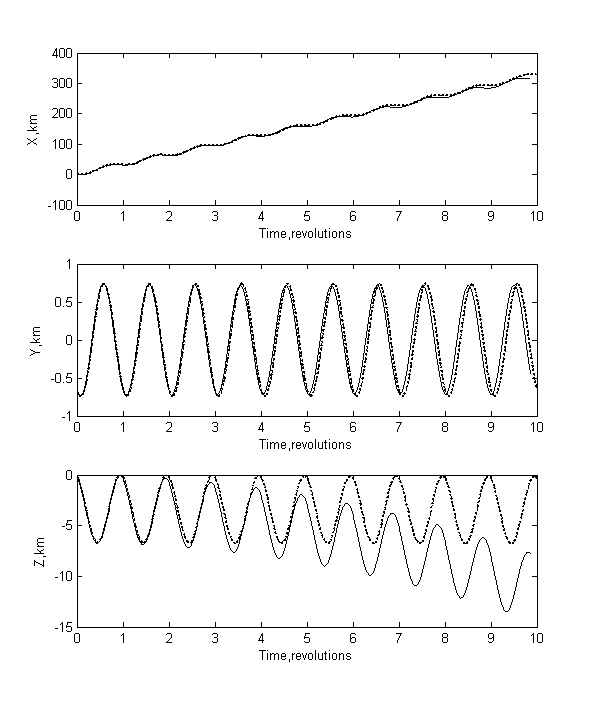
Рис.7.7. График зависимости относительного расстояния ТНС-0 и МКС по оси X, по оси Z и по оси Y по данным системы NORAD. Пунктирная линия – реальное движение, а сплошная – движение, полученное аналитически

Как и предполагалось, на первых витках основную роль играют начальные условия. Далее за счёт несферичности Земли наблюдается отклонение от движения, полученного аналитически. На рис.7.8 изображены графики, характеризующие разницу аналитического и реального движений.

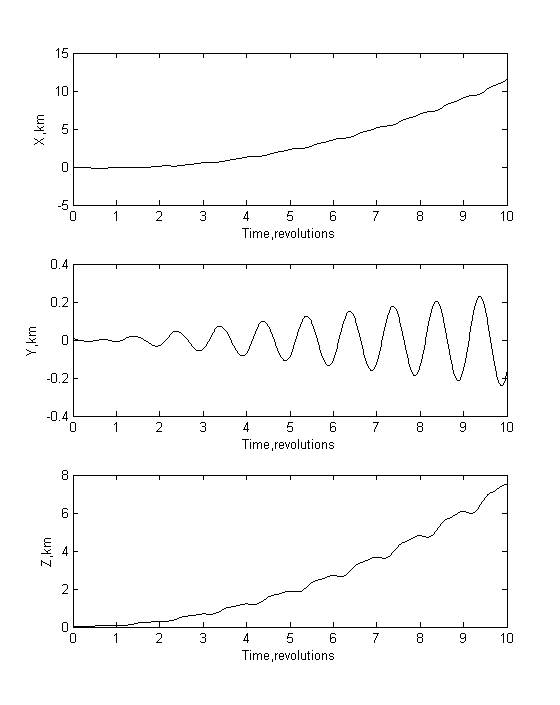
Рис.7.8. Отличие графика, построенного по (5.2), от графика, полученного с помощью данных NORAD

В заключение рассмотрим график относительного движения, который мы получим, используя уравнения Хилла без учёта аэродинамического сопротивления (рис.7.9). На этом графике видно большое сходство

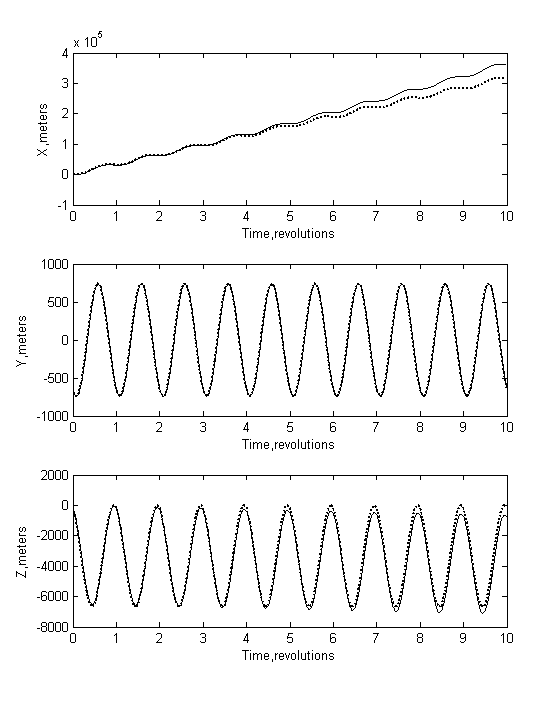
Рис.7.9. Относительное движение без учёта аэродинамического сопротивления пунктирная линия, с учётом - сплошная

движений при наличии аэродинамического сопротивления и при его отсутствии (начальными условиями в обоих случаях являются условия (7.2)) на начальном этапе движения.

8. Благодарности

Работа поддержана РФФИ (грант 03-01-00652) и Программой поддержки Ведущих научных школ России (проект НШ-2003.2003.1).

9. Заключение

В работе рассмотрен ряд задач, направленных на изучение механизмов, разрушающих формации. В частности, были рассмотрены: слабая эллиптичность орбиты основного спутника, действие солнечного давления на второй спутник и влияние атмосферного сопротивления. Получены уравнения усреднённого движения в этих случаях. Оказалось, что во всех трёх случаях наблюдается разрушение формации, причём, в случае эллиптичности орбиты вековые члены зависят от постоянных, а в остальных двух случаях – нет. Было рассмотрено относительное движение ТНС-0 и МКС, которое на первых витках оказалось весьма близким к движению, полученному с использованием приближенных формул.

Литература

[1] C.A.Mclaughlin, K.T.Alfriend, T.A.Lovell, Analysis reconfiguration algorithms for formation flying experiments. International Symposium on Formation Flying Missions and Technologies, Toulouse, France, 29-31 October, 2002.

[2] R.Armellin, M.Massari, A.Finzi, Optimal formation flying reconfiguration and station keeping maneuvers using low trust propulsion. The 18th International Symposium on Space Flight Dynamics, Munich, Germany, 11-15 October 2004.

[3] H.Fiedler, G.Krieger, Close formation flight of passive receiving micro-satellites. The 18th International Symposium on Space Flight Dynamics, Munich, Germany, 11-15 October 2004.

[4] T.Kormos, Dr.P.Palmer, High accuracy modeling of relative orbits of formation flying spacecraft in LEO. International Symposium on Formation Flying Missions & Technologies, Toulouse, France, 29-31 October, 2002.

[5] П.Е.Эльясберг. Введение в теорию полёта искусственных спутников Земли. М.:Наука, 1965.

[6] W.H.Clohessy and R.S.Wiltshire, Terminal guidance system for satellite rendezvous. Journal of Aerospace Science, 1960, Vol.27. Sept., pp.653-658.

[7] Н.Н.Моисеев. Асимптотические методы нелинейной механики. М.: Наука, 1981.

[8] Н.В.Куприянова, М.Ю.Овчинников, В.И.Пеньков, А.С.Селиванов. Пассивная система ориентации первого российского наноспутника ТНС-0. Препринт Института прикладной математики им.М.В.Келдыша РАН, 2005г., №46.

[9] www.celestrak.com