Расчет токовых катушек для управления макетом спутника в лабораторных условиях
|
|
|
|
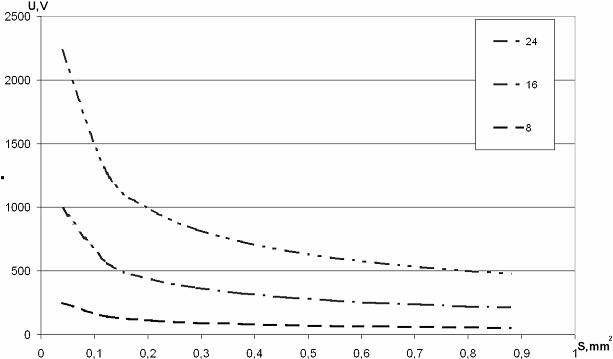
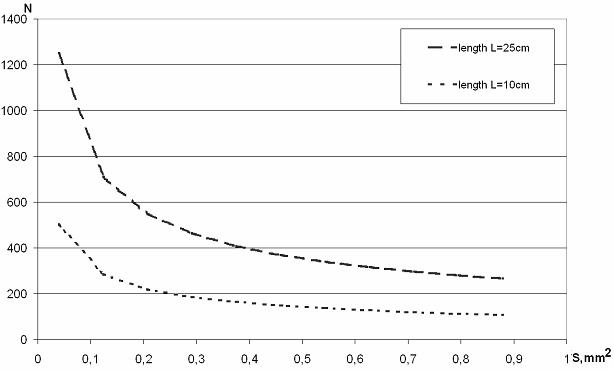
Рис.1. Напряжение источника в зависимости от площади обмотки при длине катушки L=0.25м при различных значениях диаметра катушки (мм). Значения диаметра катушки указаны на врезке в порядке следования графиков |
|
|
|
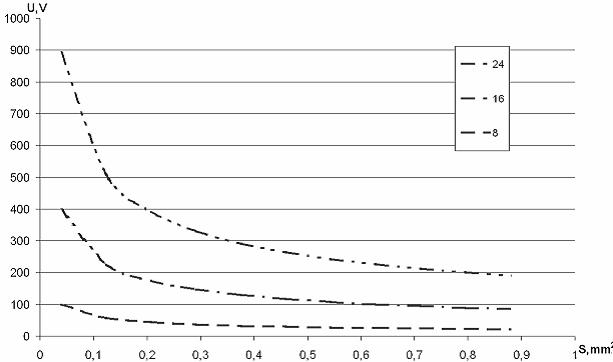
Рис.2. Напряжение источника в зависимости от площади обмотки при длине катушки L=0.1 м при различных значениях диаметра катушки (мм). Значения диаметра катушки указаны на врезке в порядке следования графиков |
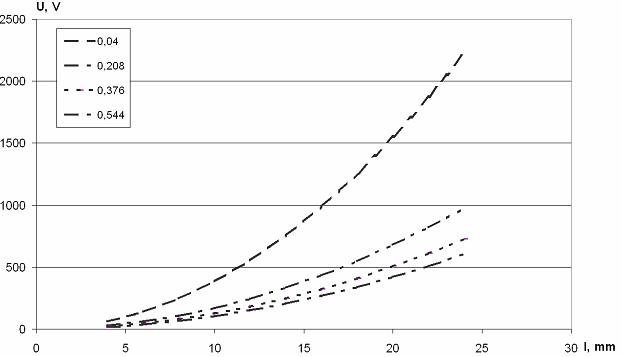
На рис.3 и
рис.4 показана зависимость напряжения источника от диаметра катушки при
различных длинах катушки для фиксированных значений площади сечения обмотки.
|
|
|
Рис.3. Зависимость напряжения источника от диаметра катушки при длине
катушки L=0.25м для различных значений сечений обмотки
(в |
|
|
|
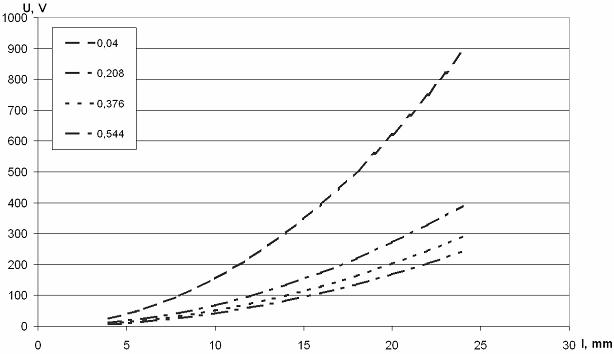
Рис.4. Зависимость напряжения источника от диаметра катушки при длине
катушки L=0.1 м
для различных значений сечений обмотки (в |
На рис.5
проиллюстрирована обратная зависимость количества витков катушки от площади
сечения обмотки при фиксированных значениях длины катушки.
|
|
|
Рис.5. Зависимость количество витков катушки от площади сечения обмотки для двух значений длины катушки |
Теперь
запишем формулы для случая квадратного сечения катушек. В результате
подстановки преобразованных соответствующим образом выражений для площади
сечения и диаметра проволоки формулы для напряжения, массы и мощности запишутся
следующим образом:
![]() ,
,
![]() ,
,
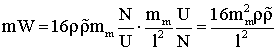 ,
,
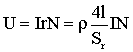 .
.
Видим, что полученные
формулы незначительно отличаются (множителем ![]() ) от соответствующих формул (2.6, 2.9, 2.10, 2.11) для
круглого сечения. Поэтому в случае использования квадратного каркаса не
обязательно пересчитывать численные значения, если уже произведен расчет для
круглого каркаса, достаточно учесть поправку на 20% на увеличение мощности в
случае круглого каркаса и увеличение массы в случае квадратного. Произведение
же величин массы и мощности остается постоянным.
) от соответствующих формул (2.6, 2.9, 2.10, 2.11) для
круглого сечения. Поэтому в случае использования квадратного каркаса не
обязательно пересчитывать численные значения, если уже произведен расчет для
круглого каркаса, достаточно учесть поправку на 20% на увеличение мощности в
случае круглого каркаса и увеличение массы в случае квадратного. Произведение
же величин массы и мощности остается постоянным.
Далее
посмотрим, как повлияет наличие сердечника. В качестве материала сердечника
рассмотрим пермаллой 79НМ. Будем считать, что его магнитная проницаемость равна
50000, так как табличная величина проницаемости изменяется от 20000 до
70000 – 150000. Для простоты проведем все выкладки для случая
квадратного каркаса.
Считаем, что
дипольный момент от сердечника и самой катушки складывается
![]() .
.
После
несложных преобразований получаем выражение для площади сечения обмотки
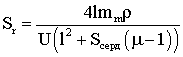 .
(2.12)
.
(2.12)
Масса катушки равна сумме
масс обмотки и магнита
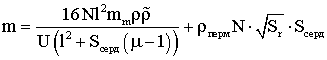 .
(2.13)
.
(2.13)
Потребляемая мощность равна
![]() .
(2.14)
.
(2.14)
Тогда произведение массы
катушки на потребляемую мощность равно
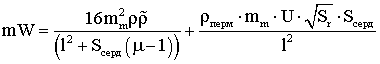 .
.
Подставим
численные значения в формулу (2.12). Все расчеты будем проводить при заданном
дипольном моменте в ![]() . Выпишем основные заданные величины:
. Выпишем основные заданные величины:
-
площадь сечения сердечника, а значит и диаметр, равны соответственно ![]() ;
;
-
магнитная проницаемость пермаллоя: ![]() ;
;
-
плотность пермаллоя: ![]() .
.
После
подстановки значений получаем площадь сечения обмотки ![]() . Тогда диаметр сечения равен
. Тогда диаметр сечения равен ![]() . Получили слишком малое значение диаметра проволоки для
создания тонкой длинной катушки с заданными ограничениями. Уменьшение
дипольного момента еще больше уменьшит значение диаметра.
. Получили слишком малое значение диаметра проволоки для
создания тонкой длинной катушки с заданными ограничениями. Уменьшение
дипольного момента еще больше уменьшит значение диаметра.
Пусть весь
дипольный момент дает сердечник (можно оценить соотношение между моментом,
создаваемым магнитом, и моментом от обмотки катушки, и показать, что такое
предположение непротиворечиво), проведем в этом случае исследования уравнений
для площади обмотки. Значение сопротивления на одном витке в таком случае равно
![]() , а после преобразования формулы для расчета сопротивления
получаем, что соотношение общей длины проволоки к ее площади сечения равно
, а после преобразования формулы для расчета сопротивления
получаем, что соотношение общей длины проволоки к ее площади сечения равно ![]() . Среди рассмотренных образцов проволоки не удалось подобрать
такие значения диаметра катушки и площади обмотки, чтобы выполнялось это
соотношение.
. Среди рассмотренных образцов проволоки не удалось подобрать
такие значения диаметра катушки и площади обмотки, чтобы выполнялось это
соотношение.
Рассмотрим
графики зависимости площади сечения материала обмотки от диаметра катушки
(рис.6). Видим, что площадь сечения проволоки для приемлимых значений диаметра
катушки слишком мала.
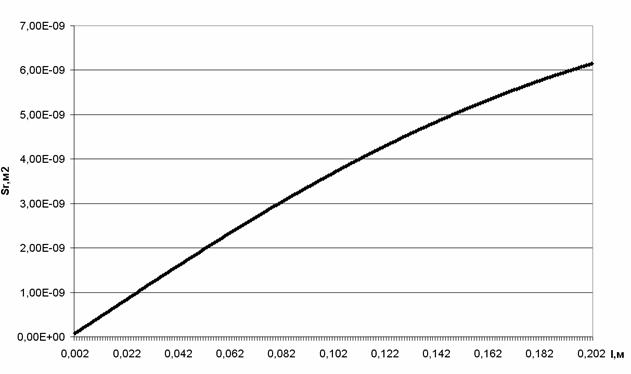
Рис.6. График зависимости площади сечения обмотки от характерного размера витка катушки
3.
Расчет катушек для макета
В настоящем
разделе проведем расчеты катушки непосредственно для макета спутника с учетом
всех наложенных сверху ограничений.
Исходные данные:
- максимальное напряжение источника – 14.4В,
-
общая потребляемая мощность - менее 1 Вт,
-
требуемый момент - порядка 0.2 ![]() ,
,
-
общая масса трех катушек - не более 0.25 – 0.3 кг,
-
длина ребра макета спутника - 0.14 м.
Ограничения:
-
![]() ‑ магнитный
момент катушки,
‑ магнитный
момент катушки,
-
![]() ‑ джоулева
мощность на одной катушке (то есть в сумме это составляет менее 1 Вт
на трех катушках),
‑ джоулева
мощность на одной катушке (то есть в сумме это составляет менее 1 Вт
на трех катушках),
-
![]() ‑ масса одной
катушки.
‑ масса одной
катушки.
Ограничение
на требуемый дипольный момент возникло в п.2 в результате введенного
ограничения на характерное время осцилляций макета спутника.
Характеристики
меди
![]() – плотность меди,
– плотность меди,
![]() – удельное сопротивление меди.
– удельное сопротивление меди.
Из формул (2.9) и (2.10)
получаем
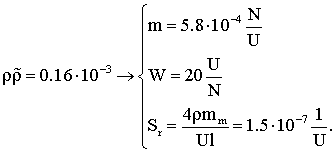 (3.1)
(3.1)
Добавив начальные
ограничения, получим следующие условия на массу и мощность:
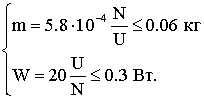
Далее, преобразовав эти
условия, получим следующие ограничения на количество витков катушки: ![]() . Откуда при заданном значении максимального напряжения
следуют неравенства
. Откуда при заданном значении максимального напряжения
следуют неравенства ![]() . Получили совместное условие на количество витков. Выбор
количества витков зависит от того, какую величину нам желательнее уменьшить -
массу или энергопотребление.
. Получили совместное условие на количество витков. Выбор
количества витков зависит от того, какую величину нам желательнее уменьшить -
массу или энергопотребление.
Таким образом,
мы приходим к следующим выводам:
- материалом катушки следует брать медь,
- диаметр витка l=0.135м (так как задано ограничение сверху),
- площадь сечения материала обмотки должна
быть равна ![]() ,
,
- напряжение на катушке равно 14.4В,
- количество витков берем равным 965,
- длина катушки (в случае однослойной
намотки) ![]() .
.
Если же
намотку делать не однослойную, то, соответственно, во сколько раз хотим
уменьшить высоту катушки, таким и будет количество слоев намотки. Например,
если хотим свести к L=10 мм, то слоев должно быть 10, в каждом слое
98 ‑ 100 витков (намотка плотная), и высота намотки, то есть
увеличение диаметра катушки, в случае плотной намотки будет порядка 5мм. Для учета изоляции достаточно
прибавить еще по 5мм.
- масса намотки катушки будет равна ![]() .
.
Вычислим ток в катушке, используя формулу (2.1).
Получаем ![]() .
.
Увеличивать
площадь сечения обмотки для увеличения создаваемого момента не получится, так
как при таком увеличении площади сечения быстро растет масса катушек, - как
квадрат дипольного момента, так как площадь сечения прямо пропорциональна
дипольному моменту
![]() .
.
Приведем
листинг численных результатов, полученный с помощью программы «katushka2»[1]:
Введи маг. момент катушки (![]() ): 0.29
): 0.29
Введи потребляемую мощность (вт):
0.3
Введи
напряжение на концах катушки (в): 14.4
Введи
диаметр катушки (м): 0.135
========================================
М Е Д Ь
Удельная масса меди ![]() , удельное сопротивление
, удельное сопротивление ![]()
Масса провода
0.038331 [кг]
Объем провода
4.3069 10-6![]()
Площадь поперечного сечения провода 0,010442 ![]()
Диаметр провода
0,11531 мм
Длина провода
412,4444 м
Число витков
972,4825
Длина однослойной
катушки из провода без
изоляции 0,11213 м
Сопротивление провода 691,2
ом
Ток в катушке
0,020833 а
Плотность тока
1,9951 ![]()
Видим
достаточно хорошее согласование результатов программы с результатами,
полученными нами. Относительные погрешности расчетов:
-
массы провода 4%;
-
площади поперечного сечения 4%;
-
число витков 1%;
-
длина однослойной катушки 12%;
-
ток в катушке 4% .
Уменьшать
количество витков за счет уменьшения дипольного момента нельзя, так как при
этом уменьшится и площадь сечения обмотки. Посмотрим, как изменятся результаты,
если бы диаметр проволоки был равен ![]() , тогда площадь поперечного сечения будет равна
, тогда площадь поперечного сечения будет равна ![]() . Во Введении было показано, что значение дипольного момента
около
. Во Введении было показано, что значение дипольного момента
около ![]() дает период колебаний меньше 10 минут. Площадь сечения
проволоки:
дает период колебаний меньше 10 минут. Площадь сечения
проволоки: ![]() . Считая, что диаметр катушки l=0.135м, найдем момент, который можем получить на такой системе, -
. Считая, что диаметр катушки l=0.135м, найдем момент, который можем получить на такой системе, - ![]() . Значение дипольного момента достаточно для того, чтобы
период колебаний макета был порядка 5 минут.
. Значение дипольного момента достаточно для того, чтобы
период колебаний макета был порядка 5 минут.
Вычислим
потребляемую такой системой мощность по формуле (2.6) - ![]() . Из требований ограничения по мощности найдем минимальное
число витков в обмотке - так как
. Из требований ограничения по мощности найдем минимальное
число витков в обмотке - так как ![]() , то, следовательно,
, то, следовательно, ![]() . Длина катушки в случае однослойной намотки
. Длина катушки в случае однослойной намотки ![]() . Если же тзготавливать не однослойную катушку, то,
соответственно, во сколько раз требуется уменьшить высоту катушки, столько
слоев необходимо намотать. Масса катушки будет равна
. Если же тзготавливать не однослойную катушку, то,
соответственно, во сколько раз требуется уменьшить высоту катушки, столько
слоев необходимо намотать. Масса катушки будет равна ![]() . Вычислим ток в катушке -
. Вычислим ток в катушке - ![]() . Длина провода, необходимого на обмотку одной катушки, -
142 м. На три катушки, соответственно, требуется 426 м.
. Длина провода, необходимого на обмотку одной катушки, -
142 м. На три катушки, соответственно, требуется 426 м.
Численные
результаты: листинг программы расчета параметров токовых катушек:
Введи маг. момент катушки (![]() ): 0.1
): 0.1
Введи потребляемую мощность (вт): 0.3
Введи напряжение на концах катушки (в) : 14.4
Введи диаметр
катушки (м) : 0.135
========================================
М Е Д Ь
Удельная масса меди ![]() , удельное сопротивление
, удельное сопротивление
![]()
Масса провода
0.0045578 [кг]
Объем провода
0.5121 10-6![]()
Площадь поперечного сечения провода 0.0036008 ![]()
Диаметр провода 0.06771 мм
Длина провода
142.2222 м
Число витков
335.3388
Длина однослойной
катушки из провода без
изоляции 0.022706 м
Сопротивление провода 691.2 ом
Ток в катушке
0.020833 а
Плотность тока
5.7857 ![]()
Сравним
результаты расчетов программы с нашими расчетами. Относительные погрешности
расчета основных параметров катушек:
-
масса проволоки 1%;
-
площадь поперечного сечения проволоки <1%;
-
длина проволоки <1%;
-
число витков <1%;
-
длина однослойной катушки 13%;
-
ток в катушке 4%;
Видим относительно
хорошее совпадение результатов, полученных с использованием приближенных
формул, с результатами расчетов с использованием программы.
4. Результаты
В качестве
материала для каркаса катушек используется эбонит (его плотность - 1150 – 1680 кг/м3).
Каркас выточен из пластины толщиной 8 мм, поэтому и высота катушки равна
8 мм, а ширина обмотки составляет 6 мм. Внутренний диаметр каркаса
равен 0.125м, отступы на «щечки» -
5 мм. Отход от планируемого значения 0.135м возник из-за необходимости укладывать проволоку
в ограниченный размер по высоте катушки. Общая масса такой конструкции каркаса
и обмотки по расчетам будет достигать величины порядка 0.07 – 0.08 кг.
Диаметр
проволоки, используемой для намотки катушек, равен 0.1 мм. Сопротивление
всей катушки 1550Ом. Тогда удельное
сопротивление равно 1.7 Oм![]() м. Используя формулы (2.4) и (2.6), получим значения
количества витков и создаваемый дипольный момент. Дипольный момент от каждой
катушки равен 0.21
м. Используя формулы (2.4) и (2.6), получим значения
количества витков и создаваемый дипольный момент. Дипольный момент от каждой
катушки равен 0.21![]() , количество витков равно 823.
, количество витков равно 823.
Расположение
трех катушек на макете спутника и отдельная катушка показаны на рис.7 и рис.8
соответственно.

Рис.7. Макет спутника с установленными во взаимно перпендикулярных плоскостях тремя катушками

Рис.8. Катушка для макета спутника
Сравним
расчетные электрические характеристики катушки с измеренными величинами после
намотки катушки. Расчетное сопротивление катушки можно получить, зная общее
сопротивление исходного мотка проволоки и его длину, воспользовавшись тем, что
сопротивление проволоки прямо пропорционально ее длине. Начальная длина
проволоки равна 715 м, ее сопротивление равно 1550 Ом.
Расчетная длина намотки на одну катушку равна ![]() , где D – диаметр катушки (в
среднем 0.13 м), расчетное количество витков для достижения
необходимого дипольного момента порядка 823. Тогда расчетная длина намотки
примерно равна 336 м. Из соотношения пропорции получаем, что
сопротивление одной намотанной катушки порядка
, где D – диаметр катушки (в
среднем 0.13 м), расчетное количество витков для достижения
необходимого дипольного момента порядка 823. Тогда расчетная длина намотки
примерно равна 336 м. Из соотношения пропорции получаем, что
сопротивление одной намотанной катушки порядка ![]() , что примерно равно 730 Ом. Измеренное значение сопротивления намотанной
катушки примерно равно 750 Ом. То есть отклонение
измеренного сопротивления от расчетного составляет около 3%. Измеренная масса
катушки равна 0.084 кг, то есть суммарная масса трех катушек равна
0.252 кг, что достаточно хорошо согласуется с ограничениями на массу
катушек.
, что примерно равно 730 Ом. Измеренное значение сопротивления намотанной
катушки примерно равно 750 Ом. То есть отклонение
измеренного сопротивления от расчетного составляет около 3%. Измеренная масса
катушки равна 0.084 кг, то есть суммарная масса трех катушек равна
0.252 кг, что достаточно хорошо согласуется с ограничениями на массу
катушек.
5. Заключение
В работе
приведены различные параметры магнитных катушек и установлены зависимости между
ними. Показана возможность подбора параметров массы и мощности по возможности
близких к их требуемым оптимальным значениям. Проведены расчеты катушек для
макета спутника. Итог расчетов:
- Для намотки катушек выбрана проволока
диаметром 0.1мм, катушка плоская, многослойная, количество слоев -
20 – 25.
- Внутренний диаметр катушки – 125 мм без учета
многослойности, намотка слоев и учет изоляции дает еще около
3 – 7 мм. Тем самым, края каркаса выступают на 4 мм с
каждой стороны.
- Высота катушки зависит от количества
намотанных слоев, но не может превышать 10 мм за счет ограничений со
стороны каркаса, и составляет 6 мм.
- Количество витков - не менее 823.
- Масса обмотки для каждой катушки будет в
таком случае около 0.025 кг. Суммарная масса одной катушки -
0.084 кг.
- Мощность, потребляемая каждой катушкой,
ограничена величиной 0.3Вт при
напряжении 14.4 В.
- Создаваемый катушкой дипольный момент -
0.21![]() .
.
-
Длина проволоки для обмотки одной катушки - не более 340 м.
На намотку всех трех катушек затрачено около 1100 м проволоки.
-
Расчетное сопротивление каждой катушки - 730 Ом;
-
Измеренное сопротивление катушек - около 750 Ом.
Благодарности
Работа
выполнена при поддержке РФФИ (грант N 03-01-00652) и Программы Президента
РФ по поддержке Ведущих научных школ (проект НШ.2003.2003.1).
Отдельная
благодарность Пенькову В.И. за предоставленную программу для вычисления
параметров токовых катушек и полезные обсуждения.
Литература
1.
www.asri.org.au/ASRI/research/
satellite/australis/19acs.doc
2.
Ovchinnikov
M.Yu., Small Satellites in Russia and in the World: Current State, Journal for
Space Communications, 1995, V.13, N 1, pp.45-50.
3.
www.aoe.vt.edu/~cdhall/papers/aas01-311.pdf
4.
microsat.sm.bmstu.ru/e-library/
Algorithms/CommonDesign/dtu_torsten.pdf
5.
http://www.dtusat.dtu.dk
6.
www.acfr.usyd.edu.au/projects/
development/aerospace/CASsat/AD&C/
7.
www.particle.kth.se/~fmi/hugin/publ/HUGIN11.html
8. Овчинников М.Ю.,
Цветков Е.А., Проектирование имитатора геомагнитного поля в составе
лабораторного стенда для отработки способов управления ориентацией
микроспутников, Препринт ИПМ им.М.В.Келдыша РАН №55, Москва, 2005
9. Сивухин Д.В.,
Общий курс физики том 3 Электричество //М.: Физматлит МФТИ, 2002
10. Калашников С.Г.,
Электричество, "Наука", 1970
11. Коваленко А.П.,
Магнитные системы управления космическими летательными аппаратами, М.:
Машиностроение, 1975
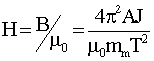 .
.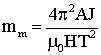 .
.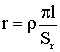 ,
, .
. .
. .
.