Тестирование и калибровка прототипа миниатюрного солнечного датчика, разработанного на основе APS-технологии

( Laboratory Testing and Calibration of the APS-based Miniature Sun Sensor Prototype
Preprint, Inst. Appl. Math., the Russian Academy of Science)

СОДЕРЖАНИЕ

1. ВВЕДЕНИЕ

Современные достижения и тенденции будущего развития микро-инженерии и микроэлектроники доказывают, что микро- и нано-технологии будут играть доминирующую роль при разработке космической техники [1]. Разработка микро-акселерометров, микро-гироскопов и электронно-оптических навигационных сенсоров является многообещающим и интересным направлением внедрения новых технологий в космическую технику. Одним из основных требований, предъявляемых к современным космическим аппаратам, является надежная автономная работа их систем навигации. Данное требование может быть выполнено путем размещения на борту аппарата датчиков различного типа. Современные микро- и нано-технологии позволяют сделать такие системы компактными, обладающими малой массы и низким энергопотреблением, что в конечном итоге приведет к снижению стоимости всего проекта.

Миниатюрные электронно-оптические датчики ориентации и навигации на основе APS (Active Pixel Sensor) технологии играют доминирующую роль  в связи с их принципиальными особенностями [2,3,4]. Физические принципы работы и устройство активно-пиксельных сенсоров, разработанных на базе CMOS (Complementary Metal Oxide Semiconductor) технологий, а так же структура датчика в целом рассматриваются в обзоре [5]. Чувствительные элементы на основе CMOS-технологии имеют большой ряд преимуществ по сравнению с аналогичными устройствами на основе CCD-технологии. Среди основных достоинств CMOS-сенсоров можно выделить следующие: высокая радиационная устойчивость; низкое энергопотребление; широкий динамический диапазон; малые масса и размер (вся система формирования изображения, включая массив светочувствительных элементов и управляющие схемы, интегрированы на одном кристалле кремния); существует возможность локального считывания данных с некоторых частей всего массива светочувствительных элементов; существует возможность гибкой настройки как всего массива фотодетекторов, так и отдельных групп пикселей и т.д.

В препринте описывается устройство прототипа цифрового солнечного датчика на основе APS детектора и испытательного лабораторного оборудования для его тестирования и калибровки, разработанных исследовательской группой университета Неаполя. Предложено несколько методов построения калибровочных функций. Рассмотрены возможности использования различных интерполяционных и аппроксимационных методов, а так же, возможность применения нейронных сетей.

2. УСТРОЙСТВО ЛАБОРАТОРНОГО СТЕНДА

На рис.1 схематически представлено устройство лабораторного стенда, предназначенного для тестирования и калибровки разрабатываемого прототипа солнечного датчика. Условно стенд можно разделить на две основные части. Первая часть – это симулятор солнечного излучения, задача которого - максимально правдоподобное воссоздание реальных условий солнечного излучения. Вторая часть – прототип солнечного датчика, закрепленный на поворотном механизме, имеющем две степени свободы  и обеспечивающем микропозиционирование датчика относительно источника Солнца. На рис.2 представлены фотографии основных элементов лабораторного стенда.

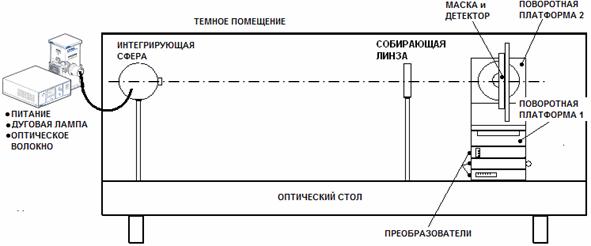
Рис.1: Схема устройства лабораторного стенда

Рис.2: Основные элементы стенда

Детальное описание всех элементов стенда и обоснование выбора их технических характеристик описаны в работах [2,3,6].

2.1. СИСТЕМА МОДЕЛИРОВАНИЯ СОЛНЕЧНОГО ИЗЛУЧЕНИЯ (СМСИ)

Основная задача СМСИ это воссоздание в лабораторных условиях реального солнечного излучения с максимальной точностью. При создании этой системы ставились следующие задачи:

·        основная часть спектра излучения источника должна находится в видимом  диапазоне,

·        должно симулироваться условие удаленности источника излучения от датчика “на бесконечность”,

·        должен симулироваться реальный угловой размер источника (0.52⁰), наблюдаемый с орбиты Земли.

На рис.3 представлена схема функционирования СМСИ.

Рис.3: Схема работы СМСИ

В качестве излучателя используется ксеноновая дуговая лампа мощностью 1000 Вт, запитанная от стабилизированного источника, мощность которого 1200 Вт. Излучение лампы воспроизводит спектр Солнца в диапазоне от 250 до 2500 нм с пиком в 290 нм. Лампа находится в специальном кожухе, оснащенным зеркальным отражателем, который собирает весь поток излучения в пучок диаметром 48 мм. Водяной фильтр вырезает участок инфракрасного спектра выше 1200 нм (сенсоры на основе APS не чувствительны к данному типу излучения). Полученный поток излучения через специальный адаптер передается в интегрирующую сферу по кварцевому оптическому волокну диаметром 3.2 мм. В сфере поток излучения подвергается многократным переотражениям так, что на выходе получается поток рассеянного света. Радиус выходного отверстия интегрирующей сферы R равен 6.82 мм. Для симуляции бесконечной удаленности источника используется собирающая линза с фокусным расстоянием f =1500 мм. После прохождения линзы получается практически параллельный пучок, а угловой размер источника может быть вычислен по формуле

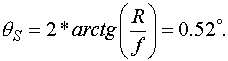
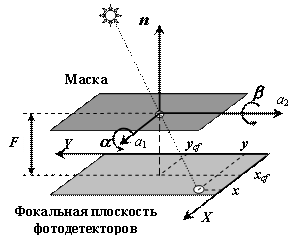
2.2. УСТРОЙСТВО И ПРИНЦИП РАБОТЫ ПРОТОТИПА СОЛНЕЧНОГО ДАТЧИКА

         Основная часть прототипа солнечного датчика - это радиационно устойчивый APS детектор (на базе Ibis 4), закрытый непрозрачной маской с одним (или несколькими равноудаленными) крошечным отверстием диаметром 0.2 мм, которая существенно ограничивает поступающий на детектор поток солнечного излучения. Прототип датчика закреплен на поворотной платформе, имеющей две степени свободы и обеспечивающей двухосную ориентацию сенсора относительно источника излучения (точнее - относительно оптической оси собирающей линзы). Основные параметры используемого APS детектора приведены в таблице1.          Принцип работы прототипа солнечного датчика представлен на рис. 4.

Солнечный свет, проходя через отверстие в маске, формирует на плоскости фотодетекторов некоторое изображение источника. Положение центра масс изображения дает возможность определить ориентацию прибора относительно направления на источник. Углы ориентации сенсора a и b могут быть определены из простейших геометрических соображений, согласно формулам

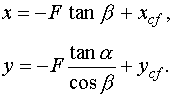                                                                                 (1)

Здесь  - положение центра масс изображения в системе координат OXY, связанной с плоскостью фотодетекторов, F – расстояние от маски до плоскости фотодетекторов,  - координаты центра масс изображения в случае, когда источник находится в зените (фактически - это расчетные значения проекции центра отверстия маски на плоскость фотодетекторов).

В работе исследованы возможности применения масок различных конфигураций. Первая рассмотренная конфигурация характеризуется наличием одного единственного отверстия, во втором случае рассмотрена маска, имеющая сто одинаковых отверстий. Использование многодырочной структуры позволяет улучшить точность определения ориентации, вследствие усреднения большого числа одновременных измерений [2].

3. АЛГОРИТМЫ ОПРЕДЕЛЕНИЯ «ЦЕНТРА МАСС» ИЗОБРАЖЕНИЯ

В работе рассматривались два различных алгоритма поиска координат «центра масс» изображения. Первый из этих алгоритмов описан в работе [4]. Его основная идея состоит в следующем.

·        Загружается растровое изображение источника.

·        Вычисляется среднее значение интенсивности пикселов (Im), находящихся в двух граничных столбцах и строках матрицы размерностью 1024 x 1280 пикселов. Пороговая граница шума определяется как 3*Im.

·        Сканируется матрица размерностью 1022x1278. Определяется пиксел, интенсивность которого выше, чем выбранный порог. Далее сканируется область 5 x 5, центром которого является данный пиксел (размеры области могут варьироваться). Если количество пикселов, интенсивность которых больше порогового значения, внутри выбранного окна 5x5 менее 18, то полагается, что это не пятно и сканирование продолжается.

·        В случае, когда подходящий пиксел найден, определяется «Интересная Область» (ИО) размером 130 x 130, центром которой он является. ИО приблизительно в 2.5 раз больше, чем размер пятна.

·        Определяется новый шумовой порог путем усреднения значений интенсивности пикселов, находящихся в двух граничных строках и столбцах ИО.

·        Сканируется область размерностью 128x128 с целью выявления пикселов, интенсивность которых ниже порогового уровня. Если интенсивность пиксела меньше либо равна порогового значения, она устанавливается равной нулю, если больше, то пересчитывается, как «интенсивность-порог».

·        После того как вся область 128x128 просканирована, координаты ее центра масс вычисляются в системе координат (X,Y) по формулам

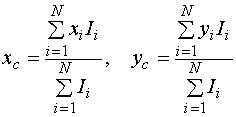               ,                                                             (2)

где N – общее количество пикселов в рассматриваемой области  – x-координата i-го пикселя,  – y-координата i-го, – интенсивность i-го пикселя.

Данный метод имеет ряд недостатков, одним из которых является недостаточная точность определения размеров и расположения окна, в котором вычисляется центр масс источника. Был предложен другой алгоритм поиска центра масс изображения, структурное описание которого представлено на рис.5.

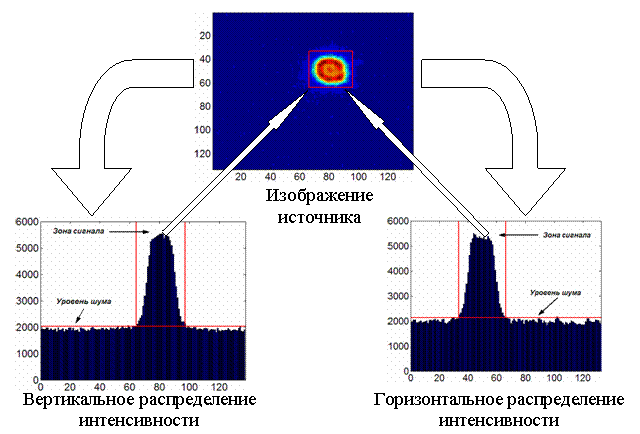
Рис.5: Определение центра масс изображения по функциям распределения интенсивности

Этот метод базируется на анализе функций распределения интенсивности по двум координатам (i-ый элемент функции вертикального распределения это сумма интенсивностей всех пикселов i-го столбца, а j-ый элемент функции горизонтального распределения – сумма интенсивностей всех пикселов j-ой строки). После того, как функции распределения интенсивностей построены, легко определить интегральный уровень шума и найти границы зоны сигнала. Пересечение зон сигналов вертикального и горизонтального распределения интенсивности определяет в плоскости OXY окно, которое жестко привязано к геометрическим особенностям изображения. Далее координаты центр масс пятна вычисляются по формулам (2) внутри построенного окна.

4. МЕТОДЫ ПОСТРОЕНИЯ КАЛИБРОВОЧНЫХ ФУНКЦИЙ

4.1. ГЕОМЕТРИЧЕСКИЕ МОДЕЛИ

Простейший способ определения ориентации сенсора базируется на геометрической модели (1). Однако точность определения углов ориентации в этом случае довольно низка. Подход оперирует с априори заданными параметрами и предполагает абсолютную идеальность как отдельных компонент сенсора, так и их взаимное расположение относительно друг друга (рис.6). Можно выделить ряд факторов, которые объясняют значительные ошибки, возникающие при использовании простой геометрической модели (1):

·        расстояние между маской и фокальной плоскостью отлично от номинального (расчетного) значения;

·        плоскость маски и фокальная плоскость непараллельны, то есть  и  на самом деле не являются координатами центра изображения при нулевой ориентации.

Рис.6

При учете этих факторов геометрическая модель может быть записана в виде

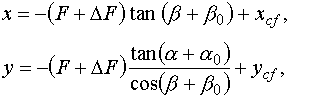                                                                              (3)

где - погрешность установки маски относительно плоскости фотодетекторов,  - погрешности установки датчика на поворотной платформе. Измеряемые значения углов ориентации в этом случае могут быть представлены в виде

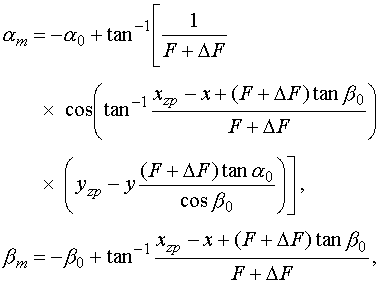                                                          (4)

где  - координаты центра масс изображения при нулевой ориентации поворотной платформы (рис.6).

Решение оптимизационной задачи

         ,

где  ориентация датчика согласно модели (4),  реальная ориентация датчика (согласно показаниям поворотной платформы), N – число рассматриваемых ориентаций, дало возможность определить оптимальные значения параметров модели . Подробно проблема построения оптимизированной геометрической модели рассмотрена в [3].

4.2. ПОСТРОЕНИЕ ВЫСОКОТОЧНЫХ КАЛИБРОВОЧНЫХ ФУНКЦИЙ

При построении геометрической модели с оптимизированными параметрами была предпринята попытка учета и компенсации основных факторов, которые влияют на точность определения ориентации прототипа сенсора. Конечно, при таком подходе невозможно учесть абсолютно все факторы, влияющие на точность определения ориентации. Для повышения точности необходимо разработать методы, которые строят соответствие между координатами центра масс изображения и углами ориентации сенсора

и не требуют никаких априорных знаний и предположений о начальных ошибках, которые требуется компенсировать.

Были предложены следующие подходы для построения функций  и :

·        применение теории нейронных сетей;

·        полиномиальная аппроксимация калибровочных функций (определение порядка аппроксимации и матрицы коэффициентов полинома);

·        построение калибровочной таблицы и линейная (и кубическая интерполяция калибровочных функций).

4.2.1. МЕТОД НЕЙРОННЫХ СЕТЕЙ

Калибровочные функции были построены посредством применения двух нейронных сетей - по одной для каждого угла (рис.7). Обе сети имеют одинаковую структуру, представленную на рис.8.

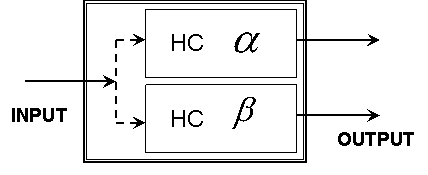
Рис.7

Рассматривается сеть с механизмом прогнозирования событий с двумя уровнями нейронов [7,8]. Скрытый уровень состоит из n нейронов (число нейронов подбиралось эмпирически), имеющих гиперболический тангенс в качестве передаточной функции, а уровень выхода состоит из одного единственного нейрона с линейной передаточной функцией. Это классическая структура нейронной сети, характерная для аппроксимации сложных функций. При обучении сетей рассматривались четыре стратегии, характеризующиеся различным набором входных и выходных параметров представленных в табл.2.

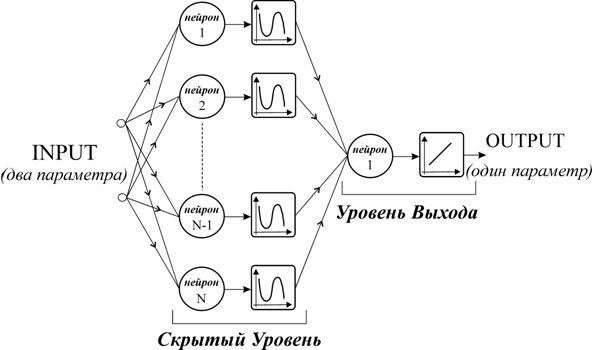
Рис.8: Схема используемой нейронной сети

Табл.2: Входные и выходные параметры, использующиеся при обучении сети

4.2.2. ПОЛИНОМИАЛЬНАЯ АППРОКСИМАЦИЯ

Основная идея этого метода – построение функциональной зависимости между углами ориентации и координатами центра масс изображения, то есть построение функций вида . Функции  могут быть представлены в виде полиномиального разложения Тейлора

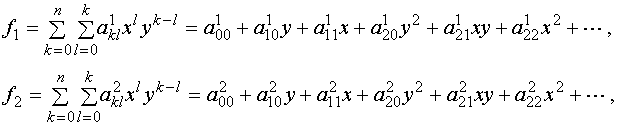
где n – порядок аппроксимации. Рассматриваемую функциональную зависимость можно записать в векторном виде

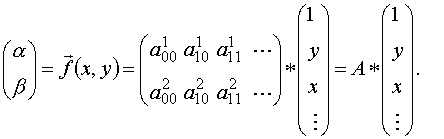
Для определения матрицы A коэффициентов полиномов необходимо решить следующую оптимизационную задачу:

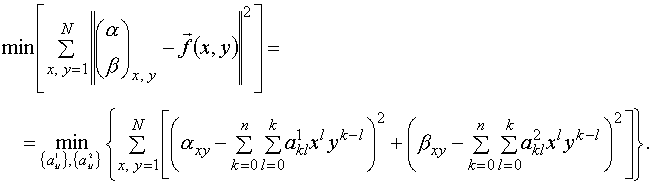
Также рассматривалась возможность тригонометрического разложения функций , однако полученные результаты были намного хуже, чем при использовании полиномиального разложения.

5. СХЕМА ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТОВ И СРАВНЕНИЕ РЕЗУЛЬТАТОВ В СЛУЧАЕ ПРИМЕНЕНИЯ ОДНОДЫРОЧНОЙ МАСКИ

Калибровка прототипа солнечного датчика, оборудованного однодырочной маской, проводилась с целью проверки работы сенсора и лабораторного оборудования, а так же с целью сравнения различных подходов построения и использования калибровочных функций. Так как основной задачей являлось проверка работоспособности системы в целом, основное внимание было уделено рассмотрению части всего поля зрения прибора, ограниченной следующими углами ориентации . Были проведены три серии экспериментов по захвату изображений источника излучения.

·        Данные первого эксперимента (I) использовались для построения калибровочных функций (при использовании модели (2), при построении НС и при определении коэффициентов аппроксимационных функций (3)) и для построения калибровачной интерполяционной сетки.

·        Данные второго эксперимента (II) использовались для контроля степени обучения НС и для выбора оптимального значения порядка аппроксимационной функции (3), кроме того данные этого эксперемента могут дополнять данные эксперемента (I) в случае построения аппроксимационных и интерполяционных калибровочных функций.

• Данные третьего эксперимента (III) использовались для анализа качества работы и сравнения рассматриваемых методов калибровки.

Для каждой рассматриваемой ориентации было проведено 8 съемок источника излучения. Каждый из экспериментов характеризовался свом набором рассматриваемых ориентаций сенсора, которые приведены в таблице 3.

Табл.3: Рассматриваемые ориентации прибора для трех эксперементов

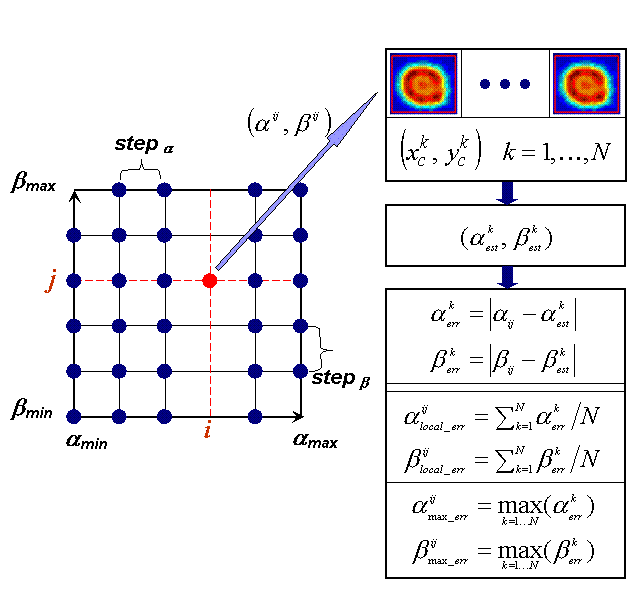
Рис. 9: Схема проведения экспериментов

Общая схема тестирования работы различных калибровочных функций, представленая на рис. 9, состоит из следующих этапов.

·        Для каждой ориентации сенсора  из эксперимента (III) захватывается 8 изображений источника.

·        Определяются координаты центра масс  каждого захваченного изображения.

·        Вычисляется ориентация сенсора  как результат применения калибровочной функции.

·        Вычисляются ошибки определения ориентации  как модуль разности измеренной и вычисленной ориентаций.

·        Для каждой ориентации сенсора  вычисляются значения локальных ошибок для каждого угла  и максимальных ошибок .

На рис.10 представлены результаты применеия полиномиальной аппроксимации в терминах локальной статистики для всего рассматриваемого поля зрения сенсора.

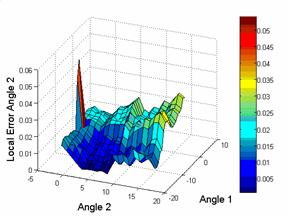
Рис. 10: Полученные результаты в терминах локальной статистики при

полиномиальной аппроксимации калибровочных функций

Полученные результаты были интерпретированы в терминах глобальной статистики. Были выбраны следующие параметры для глобальной оценки качества работы калибровочных функций:

·         - среднее значение локальных ошибок по всему рассматриваемому полю зрения сенсора,

·         - среднеквадратичное отклонение локальных ошибок,

·        M - среднее значение максимальных ошибок по всему рассматриваемому полю зрения сенсора,

·        - среднеквадратичное отклонение максимальных ошибок.

В табл.4 представлены статистические параметры ошибок определения ориентации по всей рассматриваемой части поля зрения прибора (глобальная статистика) для различных методов калибровки.

Табл.4: Полученные результаты в терминах глобальной статистики

Для достоверной оценки результатов экспериментов необходимо ответить на следующие вопросы. Что же такое точность прибора? Каким образом можно сравнивать качество работы того или иного алгоритма калибровки? В начале работы над проектом солнечного датчика была поставлена задача достижения точности определения ориентации порядка 0.01 градуса. Точность определения ориентации в данном случае нужно характеризовать двумя параметрами  и . Однако сравнение методов калибровки только по этим параметрам не совсем корректно. Ошибка определения ориентации - это случайная величина, функция распределения которой аппроксимируется нормальным распределением, и при сравнении полученных результатов необходимо учитывать все возможные реализации этой случайной величины, включая наихудшие. Именно поэтому в рассмотрение была введена вторая пара глобальных параметров  и . Все возможные реализации ошибки определения ориентации (по каждому из углов) распределены в интервале . Пример такого распределения ошибки определения ориентации по углу  в случае использования полиномиальной аппроксимации показан на рис.11.

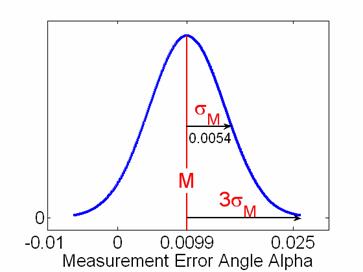
Рис. 11: Распределение ошибки определения ориентации

На рис.12 результаты использования различных калибровочных функций представлены в виде прямоугольников, ребрами которых являются интервалы всех возможных реализаций ошибок определения ориентаций. Сравнение результатов при использовании того или иного калибровочного метода - это сравнение площадей соответствующих прямоугольников. Лучшие результаты достигнуты в случае применения полиномиальной аппроксимации и подхода, базирующегося на использовании нейронных сетей, когда по координатам центра масс изображения вычисляется ошибка определения ориентации при использовании модели (1) (п.4, табл.2). Кроме того, видно, что точность определения второго угла ориентации всегда хуже, чем точность определения первого угла. Данная тенденция характерна для любого из рассматриваемых калибровочных методов, что указывает на то, что разная точность определения ориентации связана с некоторыми особенностями (ошибками) работы поворотного устройства.

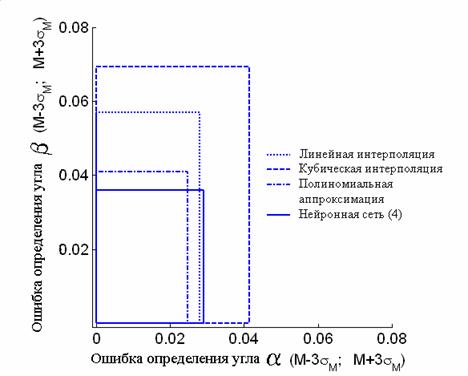
Рис.12: Сравнение методов калибровки

6. ИСПОЛЬЗОВАНИЕ МНОГОДЫРОЧНОЙ СТРУКТУРЫ

В работе рассматривалась другая конфигурация прототипа солнечного датчика, когда плоскость фотодетекторов закрыта непроницаемой маской, имеющей 100 равноудаленных друг от друга крошечных отверстий. Типичное изображение, получаемое с помощью такой маски, представлено на рис.13.

Рис.13: Изображение 100-дырочной маски

Из теоретических соображения ясно, что использование многодырочной структуры позволяет улучшить точность определения ориентации, путем усреднения большого числа одновременных измерений [2]. Обоснование этого улучшения можно суммировать следующим образом.

·        Есть некоторая случайная величина, имеющая нормальное распределение с параметрами  и .

·        Есть 100 одновременных реализаций этой случайной величины.

·        Оценка дисперсии случайной величины, полученная усреднением по 100 реализациям, может быть записана в виде

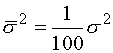.                                                                                                 (5)

Таким образом, теоретическое улучшение среднеквадратичного отклонения локальных ошибок составляет один порядок.

         Однако, формула (5) верна только в том случае, когда мы имеет дело с независимыми реализациями случайной величины, т.е. когда отсутствует какая-либо корреляция. Отсутствие корреляции между различными реализациями в данном случае - спорное утверждение, так как отверстия в маске имеют одинаковый диаметр, равноудалены друг от друга и т.д. Кроме того, использование многодырочной структуры имеет еще один недостаток, проиллюстрированный на рис.14. Изображения, получаемые через некоторые отверстия, сильно искажены, что является следствием производственного брака (изготовление таких масок довольно сложный процесс), либо следствием засорения этих отверстий микрочастицами пыли. Существует большая вероятность того, что подобные «бракованные» отверстия будут вносить значительный негативный вклад в общую картину.

Проведенные эксперименты не подтвердили теоретически ожидаемый результат.

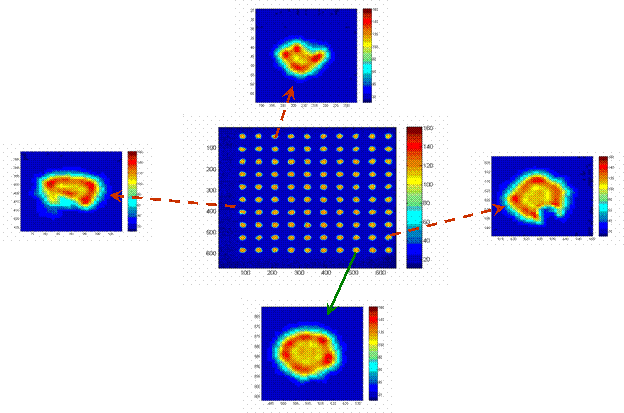
Рис.14: Искажение изображений некоторых отверстий

6.1. ОПИСАНИЕ ЭКСПЕРИМЕНТА И АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

При работе с многодырочной структурой рассматривалась только полиномиальная аппроксимация калибровочных функций. Условия проведения экспериментов аналогичны условиям, описанным в табл.3. Были предложены две различные стратегии.

В первом случае вычисляется геометрический центр всех ста изображений

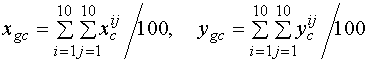
и эти данные используются для построения калибровочных функций и их тестирования, то есть считается

Второй метод базируется на идее построения калибровочных функций для каждого из 100 отверстий. В этом случае каждую ориентацию можно аппроксимировать 100 раз и далее усреднить полученные результаты по формулам

.

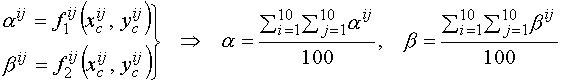Основные полученные результаты в терминах глобальной статистики приведены в табл.5. Кроме того, в этой таблице для сравнения продублированы результаты, полученные при использовании маски с одним отверстием в случае полиномиальной аппроксимации калибровочных функций.

Табл.5: Глобальные статистические параметры результатов

Геометрическая интерпретация результатов в терминах областей, описывающих все возможные реализации случайной величины, представлена на рис.15. Обе предложенные стратегии использования 100-дырочной маски показали практически идентичные результаты, так что данный рисунок иллюстрирует сравнение полученных результатов при использовании маски с одним отверстием и многодырочной маски.

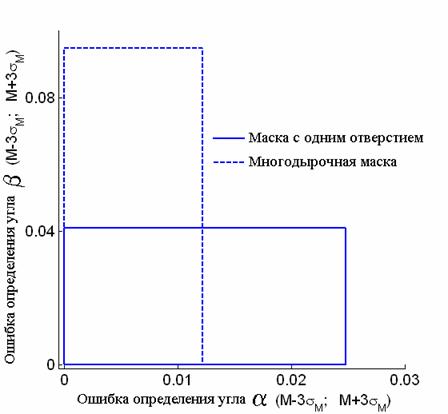
Рис.15: Сравнение результатов при использовании масок различного типа

Из табл.5 и рис.15 видно, что в случае применения многодырочной маски получено улучшение точности определения первого угла ориентации, хотя это улучшение значительно ниже, чем теоретически ожидаемое. Однако точность определения второго угла ориентации в этом случае несравнимо хуже, чем в случае применения однодырочной маски. Это может быть связано как с нарушением «чистоты» эксперимента (некачественная установка новой маски перед фотодетекторами), так и с некорректной работой поворотного устройства (эта проблема обсуждалась ранее в рамках обсуждения результатов, полученных при использовании однодырочной маски).

         Выводы, которые можно сделать, базируясь на полученных результатах, следующие.

·        Использование многодырочной структуры может повысить точность определения ориентации сенсора.

·        Полученное улучшение ниже, чем теоретически ожидаемое.

·        Необходимо рассмотреть возможность использования многодырочной маски, которая максимально снижает корреляцию между получаемыми изображениями. Например, использование маски с хаотически расположенными отверстиями разного диаметра.

·        Необходимо понять и устранить проблему работы механизма ориентации прототипа датчика, которая приводит к ухудшению точности определения второго угла ориентации по сравнению с первым.

7. ЗАКЛЮЧЕНИЕ

Цель рассматриваемого проекта – создание недорогих сенсоров, имеющих малую массу и низкое энергопотребление. Разработан прототип солнечного датчика на основе APS-технологии и лабораторное оборудование для его тестирования и калибровки. Предложен новый алгоритм определения центра масс изображения, получаемого на фокальной плоскости прибора. Рассмотрены различные методы построения калибровочных функций. Наилучшие результаты были получены при использовании теории нейронных сетей и при полиномиальном разложении калибровочных функций. Достигнутая точность определения ориентации при использовании однодырочной маски составила порядка 0.01°. Замена однодырочной маски на маску, имеющую 100 отверстий привело к улучшению точности определения первого угла ориентации, но значительно ухудшило точность определения второго угла.

Работа поддержана ISA, а также РФФИ (грант 03-01-00652) и Российским Агенством по науке и инновациям (контракт 02.700.12.050).

СПИСОК ЛИТЕРАТУРЫ

1.     Dreischer T., “Advanced miniature optical terminals for inter-satellite links in spacecraft constellations”, Proc. оf the 2^nd Round Table on Micro/Nanotechnology for Space, ESTEC, The Netherlands, 15-17 Oct 1997, ESA WPP-132.

2.     Buonocore M., Grassi M., and Rufino G., “APS-based Miniature Sun Sensor for Earth Observation Nanosatellites”, Proc. of the 4^th IAA Symp. On Small Satellites for Earth Observation, Berlin, Germany, 2003, paper IAA-B4-0703, 7pp.

3.     Rufino G., Perrotta A., and Grassi M., “Laboratory Test of an APS-Based Sun Sensor Prototype”, Proc. of the 5^th ICSO, Toulouse, France, 2004.

4.     Pratt, W. K., Digital Image Processing, New York, John Wiley and Sons, 1991.

5.     А.М. Овчинников, А.А. Ильин, М.Ю. Овчинников, “Принцип работы и устройство активно-пиксельных датчиков”, препринт ИПМ им.М.В. Келдыша РАН, № 85, 2003г.

6.     Rufino G., Grassi M., and Perrotta A., “Development and Validation of a Modern CMOS Digital Sun Sensor at UniNa”, Proc. of the 6^th International Conf. on Dynamics and Control of Systems and Structures in Space, Riomaggiore, Italy, 18 - 22 July 2004.

7.     H. Demuth and M. Beale. “Neural Network Toolbox for Use with MATLAB, vers. 4”, The MathWorks, Natick (MA), USA, 2001.

8.     M. T. Hagan and M. B. Menhaj, “Training feedforward networks with the Marquardt algorithm,” IEEE Trans. on Neural Networks, Vol. 5, No. 6, 1994, pp. 989 – 993.