Некоторые аспекты интерпретирующей навигации мобильного робота
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
СОДЕРЖАНИЕ |
|
|
|
стр. |
|
Введение
…………………………………………………………. |
3 |
|
1. Некоторые аспекты теории
интерпретирующей навигации…..………….. |
3 |
|
1.1. Используемые
модели ……………………………...…………….. |
3 |
|
1.2. Относительные и
абсолютные описания ………………………............ |
4 |
|
2. Особенности моделирования
алгоритма интерпретирующей навигации в искусственных средах
…………………………………... |
5 |
|
2.1. Формат универсальной
команды интерпретирующей навигации.….. |
6 |
|
2.2. Метод магистралей
………….……………………………….......... |
6 |
|
2.3. Модель представления
здания ..………..………………………… |
9 |
|
3. Получение оценок объёма
передаваемой информации при интерпретирующей навигации
………………………………………... |
9 |
|
4. Алгоритм аварийного
возврата …………………………………...... |
10 |
|
Заключение
…………………………………………………………………….. |
11 |
|
Литература……………………………………………………………………… |
12 |
|
Рисунки
………………………………………………………………..... |
12 |
Введение
Традиционная
навигация состоит в представлении положения робота в некоторой абсолютной
системе координат. Альтернативой ей служит интерпретирующая навигация (ИН) - представление положения робота в
некоторой глобальной модели специального типа на основе анализа полученных при
помощи соответствующей информационной системы описаний видимой части среды.
Первый подход требует наличия системы счисления пути, второй - ее "аналога" - системы информационного слежения, позволяющей
адекватно интерпретировать как наблюдаемую ситуацию, так и положение робота в
глобальной модели. [3]
При
построении корректных алгоритмов интерпретирующей навигации встают три
проблемы:
§
несвязность областей среда, где
используемое локальное относительное (т.е. вычислимое информационной системой)
описание принимает фиксированное значение, так как любая локальная ситуация
может повториться на любом уровне относительного описания;
§
"самоналожимость" локальных относительных
описаний, т.е. разные объекты имеют одинаковые относительные признаки;
§
один и тот же ориентир (выделенный объект
среды) может восприниматься по разному (иметь различные относительные признаки)
в зависимости от "точки зрения" -
местонахождения робота;
БЛАГОДАРНОСТИ
Автор
выражает признательность А.К.Платонову, С.М.Соколову и А.А.Кирильченко за
поддержку исследований и плодотворные творческие дискуссии.
1. Некоторые
аспекты теории интерпретирующей навигации
1.1 Используемые модели.
Пусть
робот может двигаться по области плоскости, ограниченной препятствиями - замкнутыми самонепересекающимися многоугольниками
с углами в 90 и 270 градусов. Примем следующие обозначения:
![]() - множество доступных роботу точек,
- множество доступных роботу точек,
![]() - множество граничных точек препятствий,
- множество граничных точек препятствий,
![]() - множество вершин
препятствий.
- множество вершин
препятствий.
Последнее
множество будем полагать всегда состоящим из конечного числа элементов. Будем
также полагать: ![]() (то есть робот -
точка, лишенная размеров, которая может находиться на препятствии).
(то есть робот -
точка, лишенная размеров, которая может находиться на препятствии).
Мы
будем полагать ![]() ограниченным некоторой прямоугольной рамкой.
Далее везде под понятием "местность" подразумевается конечносвязное
ограниченное множество
ограниченным некоторой прямоугольной рамкой.
Далее везде под понятием "местность" подразумевается конечносвязное
ограниченное множество ![]() . Под роботом будем понимать в общем случае ориентированную
точку, способную перемещаться по местности. Скорость движения робота по
местности будем полагать ограниченной значением
. Под роботом будем понимать в общем случае ориентированную
точку, способную перемещаться по местности. Скорость движения робота по
местности будем полагать ограниченной значением ![]() . Предполагается, что робот снабжен информационной системой.
. Предполагается, что робот снабжен информационной системой.
Введем
на множестве ![]() отношение видимости:
отношение видимости: ![]() , если
, если ![]()
(при этом может
быть ![]() ). Отношение видимости
есть отношение толерантности, заданное
на бесконечном (по числу элементов) множестве V.
). Отношение видимости
есть отношение толерантности, заданное
на бесконечном (по числу элементов) множестве V.
Пусть
![]() - множество точек. Через
- множество точек. Через ![]() будем обозначать подмножество
точек
будем обозначать подмножество
точек ![]() , видимых из точки
, видимых из точки ![]() , а через
, а через ![]() - множество
точек местности, видимых хотя бы из одной точки
- множество
точек местности, видимых хотя бы из одной точки ![]() .
.
Отношение
видимости или видимости в пределах заданного расстояния (радиуса действия
информационной системы) продуцирует понятие локальности или локального
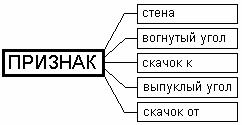
описания. Введем классификацию видимых из ![]() вершин (рис. 1). Классификационный
признак, принимающий значения 1-5, будем
считать локально вычислимым на основе информационной системы (например, использующей
дальномер в качестве измерителя).
вершин (рис. 1). Классификационный
признак, принимающий значения 1-5, будем
считать локально вычислимым на основе информационной системы (например, использующей
дальномер в качестве измерителя).
1.2.
Абсолютные и относительные локальные описания.
При
помощи информационной системы робота можно вычислить локальные признаки видимых
вершин. Выделенные на основе подобной обработки, эти признаки могут быть упорядочены
в кольцевую структуру (по углу ![]() ). Описания в виде
кольца признаков будут служить основой для анализа роботом среды в нашей
постановке. В общем виде описание в виде кольца признаков представляет собой
некоторые признаки или наборы признаков, причем в последнем случае некоторые из
признаков в наборе могут отсутствовать. Каждый набор соответствует видимой из
данного местонахождения робота и локально выделимой точке местности - ориентиру (вершине).
). Описания в виде
кольца признаков будут служить основой для анализа роботом среды в нашей
постановке. В общем виде описание в виде кольца признаков представляет собой
некоторые признаки или наборы признаков, причем в последнем случае некоторые из
признаков в наборе могут отсутствовать. Каждый набор соответствует видимой из
данного местонахождения робота и локально выделимой точке местности - ориентиру (вершине).
В
состав каждого набора признаков могут, в частности, входить:
1) угол наблюдения ориентира ![]() ;
;
2) координаты ориентира в собственной
системе координат измерителя ![]() ;
;
эти
признаки не являются устойчивыми (меняются при смене положения робота);
3) Классификационный признак видимой вершины
![]() ; при этом значения признака являются локально устойчивыми - в окрестности
; при этом значения признака являются локально устойчивыми - в окрестности ![]() существуют области
ненулевой площади, где значение локального признака не изменяется.
существуют области
ненулевой площади, где значение локального признака не изменяется.
Все
указанные выше признаки являются локально вычислимыми. Такие признаки мы будем
называть также относительными, но для
каждого ориентира (вершины) существует еще абсолютный
признак, отличающий эту точку от других точек местности в глобальной модели,
например - координаты этой точки в
некоторой абсолютной системе координат или абсолютный номер, "имя" и
т.д. Абсолютный признак не является локально вычислимым: одинаковым относительным
признакам могут соответствовать разные абсолютные, так как локальная ситуация
(на всех уровнях) в местности может повториться.
Будем
полагать, что абсолютный признак у всех используемых ориентиров различен.
Будем
рассматривать также такие кольца, в состав наборов признаков видимых ориентиров
которых входит и абсолютный признак. Такие описания будем называть абсолютными локальными описаниями в
отличие от относительных локальных описаний, которые получаются на основе
локально вычислимых признаков. При помощи измерителя робот может вычислять
только относительные локальные описания.
Абсолютный
признак и абсолютное описание следует понимать как "ключи" к возможности
использования имеющейся у робота глобальной модели местности того или иного
типа, гарантирующие правильную интерпретацию его положения по отношению к
среде в глобальном смысле.
Под
структурным (дополнительным) признаком данного элемента кольца (набора
признаков) будем понимать упорядоченную последовательность признаков (или
наборов признаков), начиная от данного элемента и кончая предыдущим по кольцу.
В связи с тем, что нас будет интересовать лишь факт совпадения или несовпадения структурных признаков
элемента кольца, каждый структурный признак данного описания можно
"свернуть" в одно число.
Если
структурные признаки хотя бы у двух элементов кольца совпадают, то кольцо
называется самоналожимым. Очевидно,
что абсолютное кольцо самоналожимым быть не может. В случае относительного
кольца структурный признак может способствовать разделению ориентиров, имеющих одинаковые начальные наборы
признаков. Например, после проведения измерения было выявлено 5 каких-либо
относительных признаков. Пусть мы имеем два признака одного типа (обозначим А),
два признака другого типа (обозначим В) и один признак третьего типа (обозначим
С). Предположим, что мы имеем кольцо, составленное из этих признаков: ABABC. Возникает вопрос: как
отличать друг от друга признаки В или А. Ответом служат структурные признаки. У
первого признака В структурный признак: АВСА. У второго признака В – САВА.
Кольцо
АВАВ является самоналожимым.
Сеансом
будем называть построение информационной системой робота локального
относительного описания в некоторой точке местности. Время сеанса будем считать
пренебрежимо малым.
2. ОСОБЕННОСТИ МОДЕЛИРОВАНИЯ
АЛГОРИТМА ИНТЕРПРЕТИРУЮЩЕЙ НАВИГАЦИИ В ИСКУССТВЕННЫХ СРЕДАХ
Навигационная система
мобильного робота должна решать две задачи:
1) задача «Где» - определение
текущего положения МР;
2) задача «Куда» - определение
текущих подцелей движения МР.
Для решения первой задачи служат алгоритмы ИН.
Разработан формат универсальной команды ИН, который показан в 2.1.
Для решения второй обычно применяется теория графов,
в частности метод магистралей – 2.2.
2.1. Формат универсальной команды
интерпретирующей навигации
В результате исследований был выделен универсальной формат команды ИН.
Затем, для сокращения объёмов передаваемой информации, из этой команды была
создана минимальная команда ИН.
На рис. 2 представлен формат универсальной команды ИН. Минимальная команда
получается из неё, отбрасыванием последних 3-х блоков .
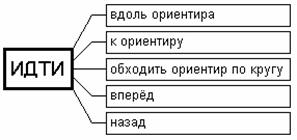
Первый блок определяет тип признака.
Второй блок определяет тип движения: вдоль
ориентира означает движение вдоль указанного ориентира, к ориентиру означает движение по направлению
к ориентиру, при движении обходить
ориентир по кругу МР движется по окружности, центром которой является
ориентир, значения двух оставшихся пунктов (вперёд
и назад) не связанны с ориентиром.
Третий блок определяет, на каком расстоянии от ориентира необходимо двигаться
МР.
Четвёртый блок указывает интервал времени, в течении которого роботу
разрешено двигаться. По истечении этого интервала выполнение данной команды
завершается.
Пятый блок определяет длину пути, который необходимо пройти.
Шестой блок указывает расстояние, на которое необходимо приблизиться к ориентиру
(используется только тогда, когда выбран тип движения к ориентиру).
Седьмой блок задаёт пару колец признаков (относительных и абсолютных) в
начальный момент движения.
В восьмом блоке указываются событие, до наступления которого роботу необходимо
двигаться (основное событие), и
события, в группе с которыми должно появиться основное событие (сопутствующие события).
В девятом блоке роботу задаётся пара колец признаков (относительных и
абсолютных), при появлении которых следует завершить выполнение программы.
Выигрыш в информации при передачи минимальной команды ИН в зависимости от ![]() показан на рис.3.
показан на рис.3.
2.2. Метод магистралей
Метод магистралей
предполагает, что транспортный граф (граф, состоящий из вершин, которые
являются областями, в которых может находится МР и дуг их соединяющих) покрыт специальными путями – магистралями - ![]() , причем если
, причем если ![]() ,
, ![]() , то трасса между
, то трасса между ![]() и
и ![]() входит в
входит в ![]() ; если
; если ![]() ,
, ![]() , то трасса содержится в
, то трасса содержится в ![]() , т.е. может быть получена поэтапным соединением участков
магистралей между собой. Хорошим примером подобной магистральной организации
служит метро или магистральная сеть города. Вообще говоря, необязательно, чтобы
сеть магистралей покрывала весь транспортный граф. Если, например,
, т.е. может быть получена поэтапным соединением участков
магистралей между собой. Хорошим примером подобной магистральной организации
служит метро или магистральная сеть города. Вообще говоря, необязательно, чтобы
сеть магистралей покрывала весь транспортный граф. Если, например,![]() , то можно воспользоваться любым пошаговым алгоритмом, чтобы
построить трассу от
, то можно воспользоваться любым пошаговым алгоритмом, чтобы
построить трассу от ![]() до ближайшей магистральной
вершины. Аналогичным образом можно поступить, если целевая вершина
до ближайшей магистральной
вершины. Аналогичным образом можно поступить, если целевая вершина ![]() не находится на магистрали.
Затем оставшуюся часть трассы можно получить магистральной трассировкой (прокладкой
пути на магистральном покрытии).
не находится на магистрали.
Затем оставшуюся часть трассы можно получить магистральной трассировкой (прокладкой
пути на магистральном покрытии).
Для описания структуры метода магистралей
вводятся некоторые обозначения. Через ![]() обозначается оптимальный путь из
обозначается оптимальный путь из ![]() в, через
в, через ![]() -
длина оптимального пути из
-
длина оптимального пути из ![]() в у. Вершина
в у. Вершина ![]() называется магистральной проекцией вершины
называется магистральной проекцией вершины ![]() , если
, если ![]() . Если
. Если ![]() и
и ![]() - два пути, то запись
- два пути, то запись ![]() означает, что путь
означает, что путь ![]() содержится в
содержится в ![]() , а запись
, а запись ![]() означает, что путь
означает, что путь ![]() cодержится в
объединении путей
cодержится в
объединении путей ![]() , т.е. все вершины и
ребра пути в левой части выражения входят в множества вершин и ребер в правой
части. Запись
, т.е. все вершины и
ребра пути в левой части выражения входят в множества вершин и ребер в правой
части. Запись ![]() , где
, где ![]() - вершина, а
- вершина, а ![]() - путь (или объединение путей), означает,
что вершина
- путь (или объединение путей), означает,
что вершина ![]() входит в путь
входит в путь ![]() .
.
Пусть на графе ![]() выделены магистрали
выделены магистрали ![]() . Они образуют магистральное
покрытие графа, если выполнены следующие условия:
. Они образуют магистральное
покрытие графа, если выполнены следующие условия:
1. Если ![]() ,
то
,
то ![]() .
.
2. Если
одна из вершин задачи, например, не входит в магистральное покрытие (![]() ), то для вершины
), то для вершины ![]() , являющейся
магистральной проекцией вершины
, являющейся
магистральной проекцией вершины ![]() , справедливо следующее соотношение
, справедливо следующее соотношение
![]() ,
,
где
через • обозначена операция конкатенации
путей.
Задача прокладки маршрута с помощью метода
магистралей решается следующим образом.
1°
Определяются магистральные проекции начальной и целевой вершин задачи ![]() и
и ![]() (магистральная
проекция может совпадать с самой вершиной). Этот этап называется этапом проектирования задачи на магистраль.
(магистральная
проекция может совпадать с самой вершиной). Этот этап называется этапом проектирования задачи на магистраль.
2°
Строится трасса ![]() . Этот этап называется магистральной трассировкой.
Магистральная трассировка определяет последовательность магистральных вершин
. Этот этап называется магистральной трассировкой.
Магистральная трассировка определяет последовательность магистральных вершин ![]() таких, что
таких, что ![]() и
и
а)
для любых соседних членов последовательности ![]()
![]() ;
;
б)
![]() принадлежит
по крайней мере двум магистралям (т.е. является вершиной магистрального
перехода). Такие вершины называются "станциями
пересадки" по аналогии с сетью линий метро. При этом если
принадлежит
по крайней мере двум магистралям (т.е. является вершиной магистрального
перехода). Такие вершины называются "станциями
пересадки" по аналогии с сетью линий метро. При этом если ![]() , то
, то ![]() .
.
3°
Строится трасса ![]()
![]() . В случае совпадения магистральной проекции вершины с самой
вершиной первый и последний члены правой части отсутствуют. Этап 3° называется
составлением результирующей трассы.
. В случае совпадения магистральной проекции вершины с самой
вершиной первый и последний члены правой части отсутствуют. Этап 3° называется
составлением результирующей трассы.
Этапа 1° - проектирование задачи на магистраль (в
случае, если хотя бы одна из вершин задачи не является магистральной)
осуществляется с использованием известных пошаговых алгоритмов (алгоритм поиска
в «глубину» и в «ширину», алгоритмы равных цен, алгоритмы упорядоченного
поиска).
На этапе магистральной трассировки (этап 2°)
используется структура данных, представленная на рис. 4. В массиве ссылок ![]() для каждой вершины
хранится величина, принимающая следующие значения:
для каждой вершины
хранится величина, принимающая следующие значения:
- 0, если вершина находится не на магистрали;
-
номер магистрали ![]() , если через вершину
проходит одна магистраль;
, если через вершину
проходит одна магистраль;
- ссылку в массив ![]() , являющийся графом пересадок, если
через вершину проходит более одной магистрали.
, являющийся графом пересадок, если
через вершину проходит более одной магистрали.
Поиск
при магистральной трассировке осуществляется через граф пересадок, к которому
добавляются начальная и целевая магистральные проекции (в случае, если они не
являются станциями пересадок). Это требует изменения массивов ![]() и
и ![]() для этих вершин с последующим их
восстановлением по окончании поиска. Поэтому связи станции пересадок с другими
такими же станциями описываются традиционным списком. Каждая такая связь
включает в свое описание в общем случае вершину
- станцию пересадок, куда она ведет, цену связи, а также номер
магистрали, по которой она осуществляется.
для этих вершин с последующим их
восстановлением по окончании поиска. Поэтому связи станции пересадок с другими
такими же станциями описываются традиционным списком. Каждая такая связь
включает в свое описание в общем случае вершину
- станцию пересадок, куда она ведет, цену связи, а также номер
магистрали, по которой она осуществляется.
"Подстыковка"
к графу пересадок магистральных проекций задачи осуществляется с
использованием массивов ![]() и
и ![]() . Входом в массив
. Входом в массив ![]() является номер
магистрали
является номер
магистрали ![]() , а выходом - адрес в массиве описания магистралей
, а выходом - адрес в массиве описания магистралей ![]() . Каждое описание магистрали включает в себя заголовок, куда
входят число вершин, признак, определяющий, разрешено ли движение по магистрали
в обоих направлениях, и признак, является ли магистраль закольцованной. При
этом каждой станции может соответствовать ориентирное описание, а переходу от
станции к станции – команда движения на языке ИН.
. Каждое описание магистрали включает в себя заголовок, куда
входят число вершин, признак, определяющий, разрешено ли движение по магистрали
в обоих направлениях, и признак, является ли магистраль закольцованной. При
этом каждой станции может соответствовать ориентирное описание, а переходу от
станции к станции – команда движения на языке ИН.
На этап 3° с помощью тех же массивов реализуется
этап составления результирующей трассы: части магистралей, находящиеся между
станциями пересадок, переписываются в выходной массив.
Преимущество метода магистралей заключается в том, что затраты на вычисление
оптимального маршрута значительно снижаются на этапе 2°, т.к. продвижение по
магистралям ведется "большими" шагами между станциями пересадок. [4]
2.3. Модель представления здания
В данной работе использовался вариант представления местности в виде
клетчатого информационного поля. В соответствии с этим вся местность покрывается
регулярной сеткой. Препятствия в такой модели аппроксимируются фигурами,
составленными из клеток сетки. В данной работе, необходима информация ещё и о
высоте препятствия (дальномер робота расположен на какой-то высоте от земли),
поэтому используется 2,5D – мерная система. Это означает, что любой трёхмерный объект задаётся значениями
![]() ,
,![]() и
и ![]() , причём значения
, причём значения ![]() не может изменяться в
пределах объекта, и, кроме того, движение происходит по базовой плоскости.
не может изменяться в
пределах объекта, и, кроме того, движение происходит по базовой плоскости.
Полная модель среды, представленная на рис. 5, состоит из:
1) ППЗ – полное представление здания в виде
информационного поля и графа смежности районов. Вершинами этого графа являются
комнаты, лестничные клетки, станции пересадок с магистрали на магистраль. Дуги
графа – это переходы между вершинами;
2) МаГ – магистральный граф. Вершинами этого графа
являются станции пересадок между магистралями, а рёбрами – магистрали;
3) ССО – система статических объектов. Объекты,
положение которых не меняется в течение всего времени моделирования (стол, шкаф
и т.д.);
4) СДО – система динамических объектов. Объекты,
положение которых может меняется в течение времени моделирования (стул и т.д.);
5) Процедура абсолютной инвентаризации – процедура
присвоения каждому ориентиру порядкового номера. Эту процедуру проводит
оператор.
3. ПОЛУЧЕНИЕ ОЦЕНОК ОБЪЁМА ПЕРЕДАВАЕМОЙ ИНФОРМАЦИИ ПРИ
ИНТЕРПРЕТИРУЮЩЕЙ НАВИГАЦИИ
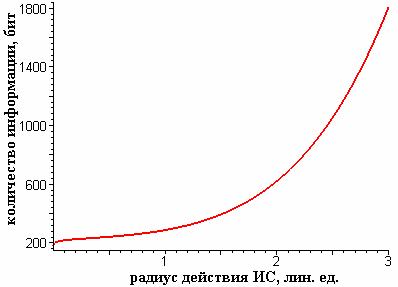
Рассмотрим вначале количество информации,
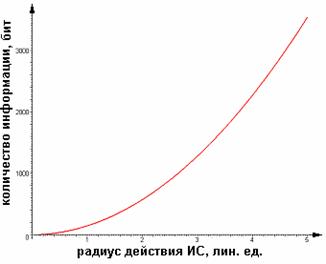
передаваемое от робота оператору. Введём
в рассмотрение следующие величины. Максимально возможное количество видимых из
точки ориентиров:  , где
, где ![]() - это радиус измерения,
- это радиус измерения, ![]() - единичный размер препятствия. Количество информации (в
битах) необходимое для передачи числа
- единичный размер препятствия. Количество информации (в
битах) необходимое для передачи числа ![]() равняется
равняется ![]() . Для передачи относительного признака выделим 5 битов, для
передачи абсолютного – 10 битов. Итак, для передачи оператору двух колец (относительного
и абсолютного) потребуется:
. Для передачи относительного признака выделим 5 битов, для
передачи абсолютного – 10 битов. Итак, для передачи оператору двух колец (относительного
и абсолютного) потребуется: ![]() битов. Подставляя в
битов. Подставляя в ![]() выражение для
выражение для ![]() получим функцию от
получим функцию от ![]() . Построим график этой функции при
. Построим график этой функции при ![]() (рис. 6).
(рис. 6).
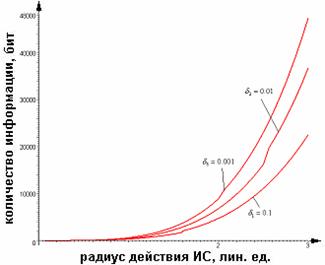
Введём ещё два понятия. Первое – матрица
расстояний – матрица, элементами которой являются расстояния между признаками,
т.е. на пересечении столбца стоит расстояние между ![]() и
и ![]() признаком. Второе –
погрешность измерения дальномера
признаком. Второе –
погрешность измерения дальномера ![]() . Понятно, что точнее этого значения передавать расстояние не
имеет смысла. Теперь, для передачи двух колец и матрицы расстояний требуется:
. Понятно, что точнее этого значения передавать расстояние не
имеет смысла. Теперь, для передачи двух колец и матрицы расстояний требуется: ![]() бит. Подставляя в
бит. Подставляя в ![]() выражение для
выражение для ![]() , получаем функцию от
, получаем функцию от ![]() (рис. 7).
(рис. 7).
Итак, мы получили некоторые оценки
для количества информации, передаваемого от робота оператору, но это оценки
сверху, так как мы предполагали, что препятсвия расположены вплотную друг у
другу (см. выражение для ![]() ).
).
Получим теперь средние значения величин ![]() и
и ![]() . Для этого представим
. Для этого представим![]() как
как ![]() , где
, где ![]() - характерное
расстояние между препятствиями, а
- характерное
расстояние между препятствиями, а ![]() - характерный размер препятствия
- характерный размер препятствия ![]() и
и ![]() распределены по
нормальному закону:
распределены по
нормальному закону: ![]() , т.е. среднее значение
, т.е. среднее значение ![]() равняется
равняется ![]() и
и ![]() для
для ![]() (рис. 8 и рис. 9).
(рис. 8 и рис. 9).
Займёмся теперь информацией,
передаваемой от оператора к роботу. Как говорилось выше, существует минимальная
команда ИН. Подсчитаем количество информации, передаваемое при использовании
приведённого выше формата.
1-ый блок – 5 бит, 2-ой блок – 5 бит, 3-ий блок - ![]() бит, 4-ый блок – 10
бит, 5-ый блок -
бит, 4-ый блок – 10
бит, 5-ый блок - ![]() бит, 6-ой блок -
бит, 6-ой блок - ![]() бит. В итоге имеем:
бит. В итоге имеем:
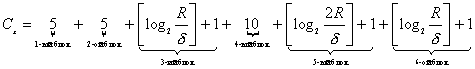
Приводя подобные и подставляя в ![]() выражение для
выражение для ![]() , получаем функцию от
, получаем функцию от ![]() . Построим также графики следующих функций:
. Построим также графики следующих функций: ![]() при
при ![]() (рис. 10 и рис.
11).
(рис. 10 и рис.
11).
2. АЛГОРИТМ АВАРИЙНОГО ВОЗВРАТА
МОБИЛЬНОГО РОБОТА
Современные системы навигации должны уметь возвращать
МР в исходное положение без помощи диспетчера. Эта необходимо для того, чтобы в случа непредвиденного разрыва связи
с диспетчером МР мог самостоятельно вернуться назад. В свете алгоритмов ИН
возникает вопрос о построении алгоритма
аварийного возврата МР. В нижеследующей таблице приведено правило перетрансляции
признаков, а утверждение 1 определяет общее правило перетрансляции прямого пути
в обратный.
Таблица 1. Преобразование локальных относительных
признаков ориентира
|
Прямой путь |
Обратный путь |
|
|
Для
выполнения следующей команды в прямом пути произошёл: |
||
|
поворот МР направо или
поворота не произошло |
поворот МР налево |
|
|
СКАЧОК “К” СКАЧОК “ОТ” ВЫПУКЛЫЙ УГОЛ ВОГНУТЫЙ УГОЛ |
ВЫПУКЛЫЙ УГОЛ СКАЧОК “К” СКАЧОК “ОТ” ВОГНУТЫЙ УГОЛ |
СКАЧОК “ОТ” ВЫПУКЛЫЙ УГОЛ СКАЧОК “ОТ” ВОГНУТЫЙ УГОЛ |
Утверждение 1. Для перетрансляции
прямого пути в обратный необходимо каждую команду прямого пути перевести
в соответствующую команду обратного пути по следующим правилам:
-
Информационно-двигательное
действие остаётся такое же как и в соответствующей команде прямого пути;
-
Признак берётся
из предыдущей команды прямого пути;
-
Признак «справа» меняется на признак «слева» и наоборот.
Подтвердим
сформулированное утверждение несколькими примерами.
ЗАКЛЮЧЕНИЕ
В работе получены следующие
результаты:
1) разработана система команд
на основе интерпретирующей навигации для движения мобильного робота в здании (с
использованием метода магистралей);
2) разработан интерфейс для
задания структуры внешней среды в виде здания;
3) исследовано поведения оценки
сверху для объёма передачи данных при движения мобильного робота на основании интерпретирующей
навигации;
4) разработан алгоритм
трансляции аварийного возврата по пройденному пути.
На основании полученных
результатов можно сделать следующие выводы:
1) существующий канал передачи
данных заведомо обеспечивает работу системы в диапазоне заданных структурных
параметров среды;
2) проведенные эксперименты
показали, что для организации передвижения в рамках 11 команд интерпретирующей
навигации для типичной лабораторной обстановки достаточно передачи данных на
сеансе в объеме 300 бит.
3) для алгоритма трансляции
аварийного возврата по пройденному пути показана его адекватность для случая
полной интерпретации ориентиров и выделены
проблемы для разработки такого алгоритма в случае ограниченной интерпретации
ориентиров.
ЛИТЕРАТУРА
1. Петров А.А. Активное
формирование моделей среды очувствлёнными роботами. М.: ИППИ РАН, 1997.
2. Э. Хант. Искусственный
интеллект. М.: Мир, 1978 – 560 с.
3. Кирильченко А.А.
Интерпретация локальных относительных описаний среды подвижным роботом //
Препринт ИПМ им. М.В. Келдыша РАН СССР, 1983, №149
4.
Барбашова
Т.Ф., Кирильченко А.А., Павловский В.Е. Исследование и выбор эффективных
алгоритмов маршрутизации // Препринт ИПМ им. М.В. Келдыша РАН, 1987, №4, 32 с.
5. Кирильченко А.А., Платонов
А.К., Соколов С.М. Теоретические аспекты организации интерпретирующей навигации
мобильного робота. // Препринт Ин-та прикл. матем. им.М.В.Келдыша РАН, 2002, №5
40с.
РИСУНКИ
1. Классификация видимых из точки ![]() вершин: 1 – стена; 2 –
вогнутый угол; 3 – скачок “к”; 4 - выпуклый угол; 5 – скачок “от”
вершин: 1 – стена; 2 –
вогнутый угол; 3 – скачок “к”; 4 - выпуклый угол; 5 – скачок “от”

2.
Формат универсальной команды ИН
|
1. |
+ |
2. |
+ |
|
+ |
3.
НА РАССТОЯНИИ d |
+ |
4. НЕ БОЛЕЕ ВРЕМЕНИ Т |
+ |
|
+ |
5. ПРОЙТИ НЕ БОЛЕЕ L |
+ |
6. ДО ПРИБЛИЖЕНИЯ К ОРИЕНТИРУ
НА РАССТОЯНИЕ |
= |
3. Выигрыш в информации при передачи минимальной
команды ИН в зависимости от ![]()
4. Базовая структура данных магистрального
алгоритма: ![]() - массив указателей
для вершин графа;
- массив указателей
для вершин графа; ![]() - массив станций
пересадок;
- массив станций
пересадок; ![]() - массив указателей для магистралей;
- массив указателей для магистралей; ![]() - массив описания магистралей;
- массив описания магистралей; ![]() - цена связи.
- цена связи.
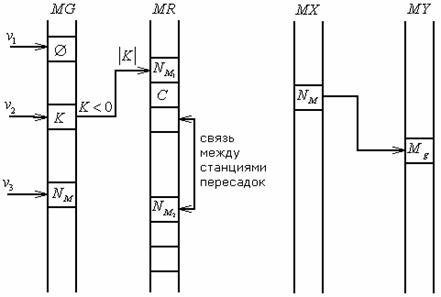
5. Общая схема используемой
модели
6.
Количество информации при передаче двух колец признаков при ![]()
7.
Количество информации при передаче двух колец признаков и матрицы расстояний
для ![]()
8.
Количество информации при передаче двух колец признаков при ![]()

9.
Количество информации при передаче двух колец признаков и матрицы расстояний
для ![]()
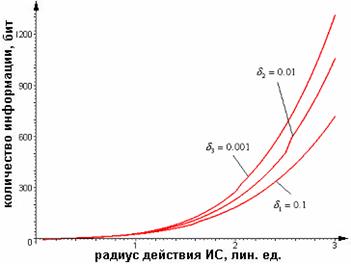
10.
Количество информации при передаче 1,3,5 и 10 универсальных команды ИН для ![]()
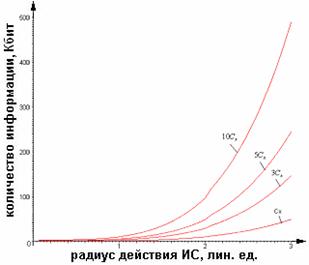
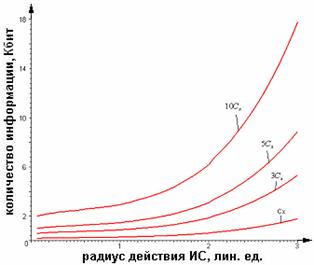
11.
Количество информации при передаче 1,3,5 и 10 универсальных команды ИН для ![]()
12. Пример работы алгоритма
аварийного возврата
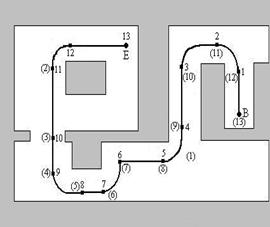
Прямой путь:
0. Фиксация вогнутого угла справа; 1. Идти до появления скачка к слева; 2. Обходить скачок
к на расстояние e; 3. Обходить скачок
к на расстояние e; 4. Идти до появления скачка от справа; 5. Обходить скачок
от на расстояние e; 6. Идти до появления скачка от слева; 7. Обходить скачок
от на расстояние e; 8. Идти до появления скачка от слева; 9. Обходить скачок
от на расстояние e; 10. Идти до
появления скачка от справа; 11. Идти до
появления скачка от справа; 12. Обходить скачок от на расстояние e; 13. Идти до появления вогнутого угла слева |
Обратный путь: 1. Идти до появления скачка к; 2. Обходить скачок
к на расстояние e; 3. Идти до появления выпуклого угла слева; 4. Идти до появления скачка к слева; 5. Обходить скачок
к на расстояние e; 6. Идти до появления скачка к слева; 7. Обходить скачок
к на расстояние e; 8. Идти до появления скачка к слева; 9. Обходить скачок
к на расстояние e; 10. Идти до
появления скачка от справа; 11. Обходить скачок от на расстояние e; 12. Обходить скачок от на расстояния e; 13. Идти до
появления вогнутого угла слева; |