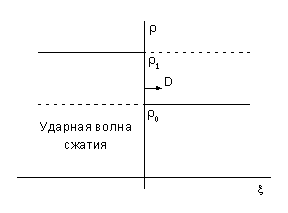
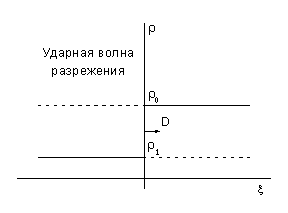
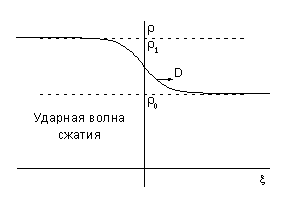
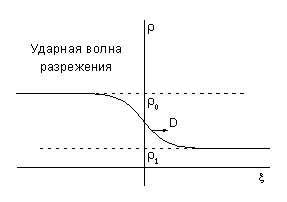
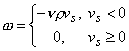Об ударных волнах разрежения в вычислительной газовой динамике
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
рис. 1 |
|
Модифицируя схему (2.4), увеличивая степень ее неявности и
повышая запас устойчивости, можно добиться возможности расчета задачи с
крупными шагами по времени (![]() ):
):
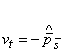 ,
, ![]() ,
,
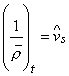 ,
,
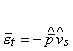 ,
, 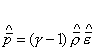 . (2.6)
. (2.6)
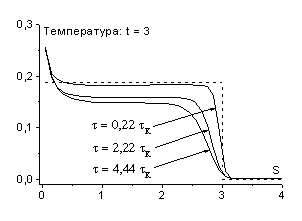
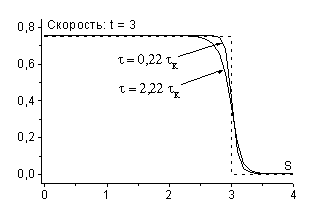
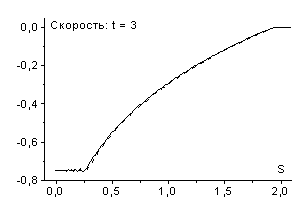
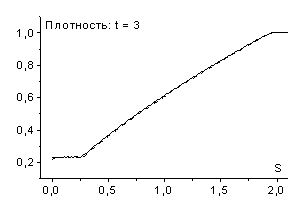
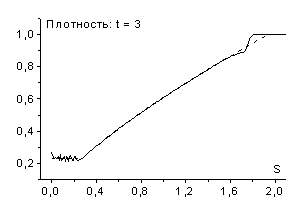
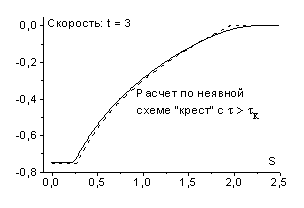
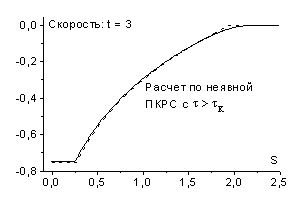
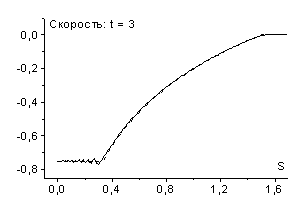
На рис. 2 представлены результаты соответствующих расчетов
(в этой работе для решения неявных схем применялся метод Ньютона) на момент
времени ![]() с шагами по времени
с шагами по времени ![]() (
(![]() ),
), ![]() (
(![]() ) и
) и ![]() (
(![]() ). Как видно, при малых шагах по времени (
). Как видно, при малых шагах по времени (![]() ,
, ![]() ) численное решение достаточно хорошо соответствует точному.
В случае схемы (2.6) возможно использование и больших
) численное решение достаточно хорошо соответствует точному.
В случае схемы (2.6) возможно использование и больших ![]() (
(![]() ); параметры течения газа за фронтом волны, полученные в
результате расчетов, заметно отличаются от точного решения (для температуры при
); параметры течения газа за фронтом волны, полученные в
результате расчетов, заметно отличаются от точного решения (для температуры при
![]() примерно на 25%),
ширина фронта волны возрастает и скорость его движения меньше единицы. Отметим,
что отклонения температуры за фронтом волны от точного решения в схемах (2.4) и
(2.6) – противоположны по знаку. Аналогичны отличия в скорости фронта ударной
волны.
примерно на 25%),
ширина фронта волны возрастает и скорость его движения меньше единицы. Отметим,
что отклонения температуры за фронтом волны от точного решения в схемах (2.4) и
(2.6) – противоположны по знаку. Аналогичны отличия в скорости фронта ударной
волны.
|
|
|
|
рис. 2 |
|
Иследуем, с чем связаны недостатки схем (2.4) и (2.6).
В дифференциальном случае уравнения газовой динамики могут быть записаны в различных формах. Например, уравнение энергии можно представить в дивергентной форме, непосредственно выражающей закон сохранения энергии:
![]() , (2.7)
, (2.7)
В разностном случае для схемы “крест” (2.4) уравнение энергии приводится к виду (в этой и всех последующих формулах черта над сеточными функциями плотности, давления и внутренней энергии, означающая, что значение функции относится к полуцелой точке, опущена):
![]() , где
, где ![]() ,
,
для схемы (2.6) к виду:
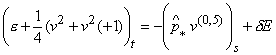 , где
, где ![]() .
.
Легко видеть, что в схемах (2.4) и (2.6) разностный аналог закона сохранения энергии не выполнен, а, значит, не выполняются и соотношения Гюгонио, выражающие законы сохранения на разрывных решениях. Сказанное объясняет недостатки численных решений задачи о вдвигаемом в газ поршне, полученных по схемам (2.4) и (2.6).
Естественно требовать, чтобы в схеме выполнялись разностные аналоги законов сохранения, то есть разностная схема была консервативной [2,3].
2.2. Консервативные и полностью консервативные разностные схемы
Рассмотрим семейство консервативных схем газовой динамики [3]:
![]() ,
, ![]() ,
, 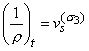 ,
,
![]() , (2.8)
, (2.8)
![]() .
.
Для схем этого семейства при любых ![]() ,
, ![]() выполнены разностные аналоги основных законов
сохранения: массы, импульса и энергии. Расчеты, проведенные по таким схемам, демонстрируют
их эффективность во многих задачах, в том числе в задаче о вдвигаемом поршне.
выполнены разностные аналоги основных законов
сохранения: массы, импульса и энергии. Расчеты, проведенные по таким схемам, демонстрируют
их эффективность во многих задачах, в том числе в задаче о вдвигаемом поршне.
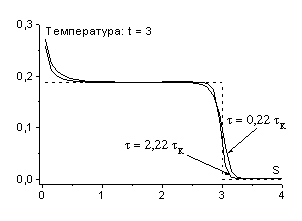
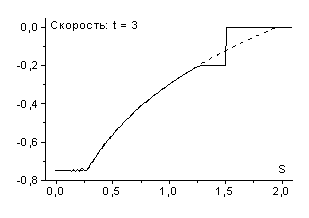
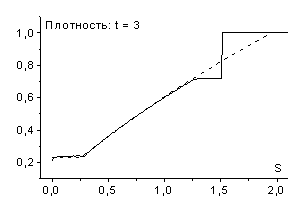
На рис. 3 представлены результаты расчетов задачи о
вдвигаемом поршне по одной из схем семейства (2.8): ![]() ,
, ![]() . Начальные данные, граничные условия и шаг сетки по
пространству были взяты теми же, что и в предыдущих расчетах. Расчеты проводились
с шагами по времени
. Начальные данные, граничные условия и шаг сетки по
пространству были взяты теми же, что и в предыдущих расчетах. Расчеты проводились
с шагами по времени ![]() (
(![]() ) и
) и ![]() (
(![]() ). Легко видеть, что решение в обоих расчетах передается
хорошо. Фронт волны размазан на 3-4 интервала сетки; с увеличением
). Легко видеть, что решение в обоих расчетах передается
хорошо. Фронт волны размазан на 3-4 интервала сетки; с увеличением ![]() ширина фронта
возрастает.
ширина фронта
возрастает.
Однако и у консервативных схем есть недостатки. Связаны они с тем, что в реальной газодинамической среде выполняются не только законы сохранения, но и другие важные соотношения. Так, уравнение неразрывности (второе уравнение в (2.1)), используя уравнение для траектории частицы газа (2.3), можно записать в виде:
![]() . (2.9)
. (2.9)
|
|
|
|
рис. 3 |
|
Это соотношение называют “законом сохранения объема” [3]. Уравнение энергии помимо дивергентной может быть записано в энтропийной и в недивергентной формах:
![]() , (2.10)
, (2.10)
![]() . (2.11)
. (2.11)
Рассматривая семейство консервативных схем, легко придти к следующим результатам:
![]() , где
, где ![]() , (2.12)
, (2.12)
![]() , где
, где ![]() , (2.13)
, (2.13)
![]() , где
, где ![]() . (2.14)
. (2.14)
Требуя, чтобы дисбалансы ![]() ,
, ![]() ,
, ![]() тождественно
обращались в нуль, получим условия [3]
тождественно
обращались в нуль, получим условия [3]
![]() ,
, ![]() , (2.15)
, (2.15)
которые выделяют из семейства консервативных схем (2.8) однопараметрическое семейство. Построенные схемы обычно называют полностью консервативными схемами газовой динамики [2].
Отметим, что дисбаланс внутренней энергии ![]() для
консервативных схем имеет дивергентный вид. Следовательно, фиктивные источники
энергии работают лишь в граничных узлах сетки, а внутрь области возмущения,
возникающие за счет их действия, распространяются в виде своеобразного потока
фиктивной энергии. В рассмотренной задаче о поршне граничные условия
практически постоянны во времени, поэтому в граничных точках дисбалансы
для
консервативных схем имеет дивергентный вид. Следовательно, фиктивные источники
энергии работают лишь в граничных узлах сетки, а внутрь области возмущения,
возникающие за счет их действия, распространяются в виде своеобразного потока
фиктивной энергии. В рассмотренной задаче о поршне граничные условия
практически постоянны во времени, поэтому в граничных точках дисбалансы ![]() близки к нулю. Поэтому
консервативные и полностью консервативные схемы следует сравнивать на задачах с
переменными во времени граничными условиями. К таковым относится, например,
задача об ускоряющемся поршне.
близки к нулю. Поэтому
консервативные и полностью консервативные схемы следует сравнивать на задачах с
переменными во времени граничными условиями. К таковым относится, например,
задача об ускоряющемся поршне.
Пусть в холодный газ (![]() ) вдвигается поршень с нарастающей скоростью
) вдвигается поршень с нарастающей скоростью ![]() . Начальные данные и граничные условия выберем следующим
образом:
. Начальные данные и граничные условия выберем следующим
образом:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Эта задача допускает автомодельное решение. В качестве автомодельной переменной удобно взять
![]() .
.
Автомодельность сохранится, если ввести вязкость следующего вида:
![]() ,
,
для расчетов положим ![]() . Решение будет иметь вид:
. Решение будет иметь вид:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
(2.16)
,
(2.16)
где автомодельные функции ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() легко найти из системы
обыкновенных дифференциальных уравнений [8].
легко найти из системы
обыкновенных дифференциальных уравнений [8].
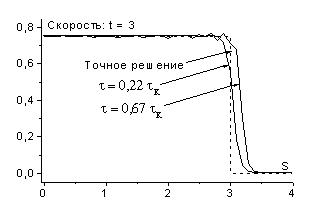
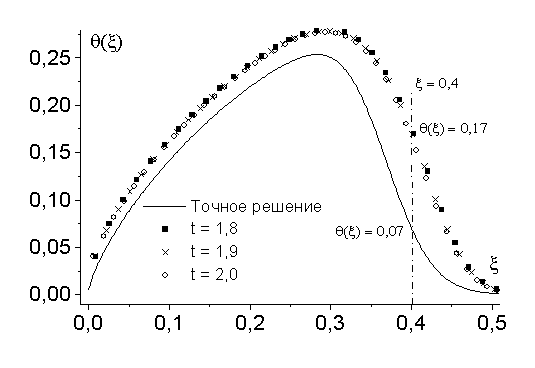
Выберем равномерную разностную сетку с шагом ![]() по массе, и
по массе, и ![]() по времени. На рис. 4
в автомодельной переменной даны результаты расчетов поставленной задачи по
консервативной схеме с весами
по времени. На рис. 4
в автомодельной переменной даны результаты расчетов поставленной задачи по
консервативной схеме с весами ![]() ,
, ![]() на три момента
времени:
на три момента
времени: ![]() ,
, ![]() ,
, ![]() . Значения
. Значения ![]() накладываются примерно
на одну линию, что свидетельствует о автомодельности численного решения; однако
эта линия не совпадает с точным решением. Причем, отличия от точного решения в
некоторых точек составляют более 100% (см.
накладываются примерно
на одну линию, что свидетельствует о автомодельности численного решения; однако
эта линия не совпадает с точным решением. Причем, отличия от точного решения в
некоторых точек составляют более 100% (см. ![]() ).
).
Таким образом, рассмотренная консервативная схема дает существенно искаженное решение задачи.
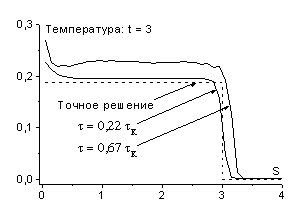
На рис. 5 показаны результаты расчетов этой же задачи по
полностью консервативной схеме (![]() ). Легко видеть, что использование полностью консервативной
схемы приводит к хорошему результату; численное решение автомодельно, значения
). Легко видеть, что использование полностью консервативной
схемы приводит к хорошему результату; численное решение автомодельно, значения ![]() накладываются на
точное решение.
накладываются на
точное решение.
Следовательно, полностью консервативные разностные схемы дают определенные количественные преимущества по сравнению с консервативными схемами того же порядка аппроксимации. Эти преимущества проявляются при расчете быстропеременных во времени и пространстве течений на грубых временных сетках.
Таким образом, в этом пункте проведен краткий обзор результатов исследования разностных схем газовой динамики. Отметим, что сопоставление свойств различных схем и демонстрация преимуществ полностью консервативных схем здесь проводилась на примере классической задачи о поршне, вдвигаемом в газ, где в результате рождается ударная волна.
|
|
|
рис. 4 |
|
|
|
рис. 5 |
Для завершения настоящего обзора результатов, приведем необходимые и достаточные условия устойчивости семейства схем газовой динамики (2.8) в акустическом приближении [7]:
![]() , (2.17)
, (2.17)
![]() . (2.18)
. (2.18)
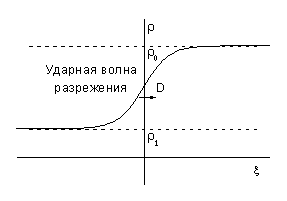
3. Ударные волны разрежения в численных решениях
Задача о поршне, вдвигаемом в газ, является классическим тестом, на котором проходили и проходят апробацию практически все вычислительные методы газовой динамики. Задача о поршне, выдвигаемом из газа, реже используется для тестирования методов расчета и сопоставления их свойств.
3.1. Адиабатический случай
Рассмотрим задачу о поршне, выдвигаемом из газа с постоянной
скоростью ![]() . В этом случае по газу от поршня будет распространяться
волна разрежения; решение может быть получено в автомодельном виде [8]:
. В этом случае по газу от поршня будет распространяться
волна разрежения; решение может быть получено в автомодельном виде [8]:
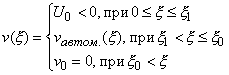 ,
,  и т.д.,
и т.д.,
где ![]() ,
, ![]() - скорость звука,
- скорость звука,
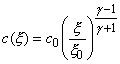 ,
, 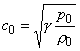 ,
,
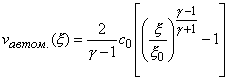 ,
,
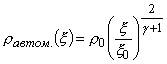 ,
,
![]() ,
, ![]() ,
,
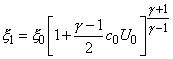 . (3.1)
. (3.1)
В лагранжевых массовых переменных это решение для любого ![]() “подобно”
автомодельному, только ширина волны разрежения
“подобно”
автомодельному, только ширина волны разрежения ![]() линейно растет со временем.
При этом передний фронт волны движется со скоростью звука на “фоне”
линейно растет со временем.
При этом передний фронт волны движется со скоростью звука на “фоне” ![]() , а задний со скоростью, вычисляемой по параметрам в зоне,
примыкающей к поршню:
, а задний со скоростью, вычисляемой по параметрам в зоне,
примыкающей к поршню: ![]() (см. рис. 6).
(см. рис. 6).
Выберем для расчета следующие начальные данные:
![]() ,
, ![]() ,
, ![]() (
(![]() ),
),
и граничные условия:
![]() - левое граничное
условие,
- левое граничное
условие,
![]() - правое граничное
условие.
- правое граничное
условие.
Для численного решения воспользуемся схемой “крест” (2.4) без искусственной вязкости.
|
|
|
рис.
6 |
По пространству введем равномерную сетку с шагом ![]() . Шаги по времени будем варьировать и сравнивать с шагом
Куранта, который для выбранных начальных данных составляет на фоне
. Шаги по времени будем варьировать и сравнивать с шагом
Куранта, который для выбранных начальных данных составляет на фоне
![]() , где
, где 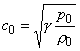 - скорость звука.
- скорость звука.
Расчеты, проведенные с шагом по времени равным ![]() ,
, ![]() , показывают, что схема хорошо передает решение задачи (см.
рис. 7).
, показывают, что схема хорошо передает решение задачи (см.
рис. 7).
|
|
|
рис.
7 |
|
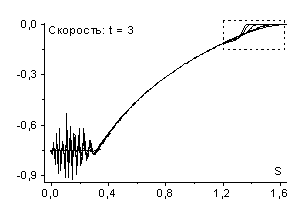
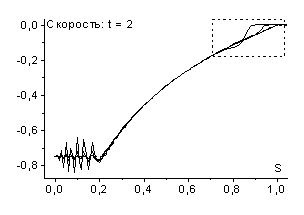
Однако при расчете по той
же схеме, например, с шагом ![]() ,
, ![]() в численном решении
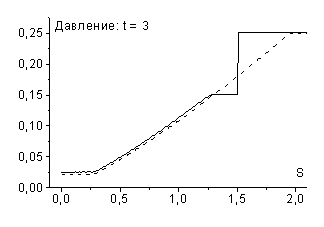
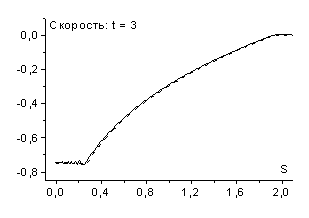
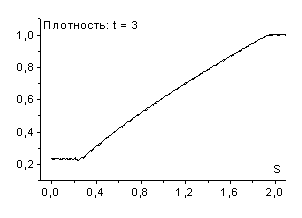
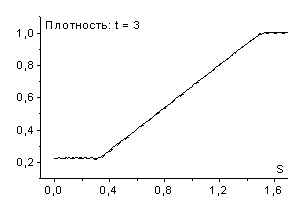
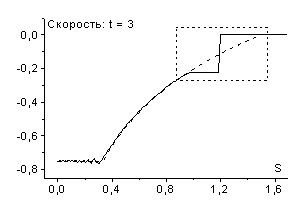
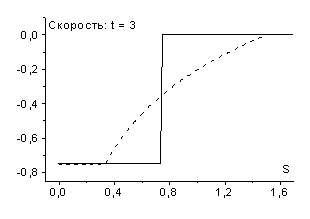
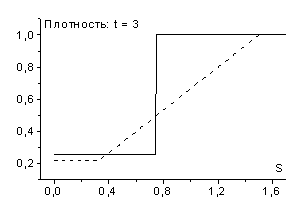
возникает разрыв - ударная волна разрежения (рис. 8 и рис. 9).
в численном решении
возникает разрыв - ударная волна разрежения (рис. 8 и рис. 9).
В дифференциальном случае возникновение ударных волн разрежения запрещает теорема Цемплена [6], однако дискретные среды обладают иными свойствами, в частности, в них могут возникать такие нефизичные эффекты как ударные волны разрежения. Пример такой среды дает рассмотренная схема “крест”. Следует отметить, что ударные волны разрежения наблюдаются при расчетах не только по схемам рассматриваемого семейства, но и по другим используемым в настоящее время схемам, например по схеме Роу [9].
|
|
|
|
рис.
8 |
|
|
|
|
|
рис.
9 |
|
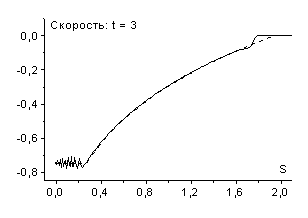
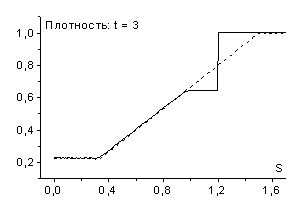
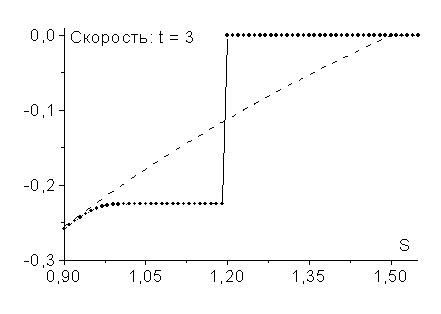
Эффект возникновения ударных волн разрежения присущ не только
схеме “крест”, но и другим схемам семейства (2.8). Например, этим же свойством
обладает явная полностью консервативная схема (![]() ). На рис. 10 и рис. 11 приведены результаты
соответствующих расчетов с шагами по времени
). На рис. 10 и рис. 11 приведены результаты
соответствующих расчетов с шагами по времени ![]() ,
, ![]() (рис. 10) и
(рис. 10) и ![]() ,
, ![]() (рис. 11). Обратим
внимание, что в явной полностью консервативной схеме ударная волна разрежения
возникает при других величинах шагов сетки по времени, чем в схеме “крест”.
Так, в “кресте” она наблюдается лишь при
(рис. 11). Обратим
внимание, что в явной полностью консервативной схеме ударная волна разрежения
возникает при других величинах шагов сетки по времени, чем в схеме “крест”.
Так, в “кресте” она наблюдается лишь при ![]() , а в явной полностью консервативной схеме уже при
, а в явной полностью консервативной схеме уже при ![]() (см. рис. 11).
(см. рис. 11).
|
|
|
рис.
10 |
|
|
|
|
|
рис.
11 |
|
Однако не для всех схем семейства (2.8) в численных решениях
задачи о выдвигаемом поршне возникают ударные волны разрежения. Например, для
схемы (2.6) – неявного “креста” и для неявной полностью консервативной схемы (![]() ) этот эффект отсутствует при любых
) этот эффект отсутствует при любых ![]() . Соответствующие результаты расчетов приведены на рис. 12. В
обоих случаях расчеты проводились при
. Соответствующие результаты расчетов приведены на рис. 12. В
обоих случаях расчеты проводились при ![]() ,
, ![]() . Легко видеть, что решение задачи заметно размазано. Это
объясняется наличием в схемах сильных внутренних диссипативных и дисперсионных
свойств. При увеличение
. Легко видеть, что решение задачи заметно размазано. Это
объясняется наличием в схемах сильных внутренних диссипативных и дисперсионных
свойств. При увеличение ![]() схемная диссипация
усиливается, решение размазывается на большее число интервалов сетки.
схемная диссипация
усиливается, решение размазывается на большее число интервалов сетки.
|
|
|
рис. 12 |
|
3.2. Изотермический случай
Выше были рассмотрены схемы адиабатической газовой динамики.
Однако ударные волны разрежения возникают и при расчете задачи о поршне для
изотермического случая (![]() ), анализом которого мы далее ограничимся.
), анализом которого мы далее ограничимся.
Схема (2.8) в этом случае принимает вид:
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (3.2)
, (3.2)
![]() - скорость звука. Начальные
данные и граничные условия выберем следующим образом:
- скорость звука. Начальные
данные и граничные условия выберем следующим образом:
![]() ,
, ![]() ,
, ![]() (
(![]() ) - начальные данные,
) - начальные данные,
![]() - левое граничное
условие,
- левое граничное
условие, ![]() - правое граничное
условие,
- правое граничное
условие, ![]() -
изотермическая скорость звука.
-
изотермическая скорость звука.
Рассмотрим аналог схемы “крест” для изотермического случая: ![]() , и проведем для нее подробный анализ численного
решения задачи о выдвигаемом поршне при различных шагах по времени. Шаги по
времени будем сравнивать с шагом Куранта
, и проведем для нее подробный анализ численного
решения задачи о выдвигаемом поршне при различных шагах по времени. Шаги по
времени будем сравнивать с шагом Куранта![]() .
.
При ![]() получаем решение,
хорошо согласующееся с точным. Результаты соответствующего расчета для
получаем решение,
хорошо согласующееся с точным. Результаты соответствующего расчета для ![]() (
(![]() ) представлены на рис. 13.
) представлены на рис. 13.
|
|
|
|
рис. 13 |
|
При ![]() , где
, где ![]() - экспериментально
найденное значение для данного расчета, получаются решения, показанные на рис.
14 для
- экспериментально
найденное значение для данного расчета, получаются решения, показанные на рис.
14 для ![]() (
(![]() ). Возникает ударная волна разрежения, распространяющаяся по
газу. Особенностью ударной волны разрежения в решении по схеме “крест”, как и в
адиабатическом случае, является практически неразмазанный скачок параметров
газа на фронте волны (см. рис. 15, где окрестность ударной волны разрежения
дана в укрупненном виде).
). Возникает ударная волна разрежения, распространяющаяся по
газу. Особенностью ударной волны разрежения в решении по схеме “крест”, как и в
адиабатическом случае, является практически неразмазанный скачок параметров
газа на фронте волны (см. рис. 15, где окрестность ударной волны разрежения
дана в укрупненном виде).
|
|
|
|
рис. 14 |
|
|
|
|
|
рис. 15 |
|
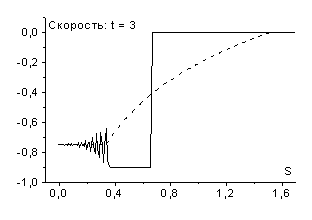
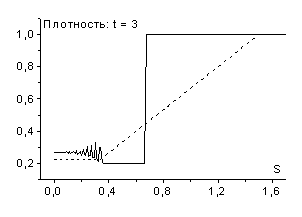
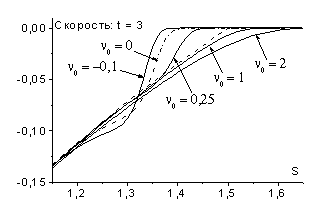
При увеличении шага по времени амплитуда ударной волны разрежения
возрастает и, наконец, при ![]() (
(![]() ) получается решение показанное на рис. 16.
) получается решение показанное на рис. 16.
При ![]() (
(![]() ) решение помимо ударной волны разрежения содержит ударную
волну сжатия (см. рис. 17). Осцилляции за ее фронтом происходят в силу
отсутствия в схеме искусственной вязкости.
) решение помимо ударной волны разрежения содержит ударную
волну сжатия (см. рис. 17). Осцилляции за ее фронтом происходят в силу
отсутствия в схеме искусственной вязкости.
Проверим, выполняются ли условия Гюгонио - соотношения, выражающие законы сохранения массы и импульса - на ударной волне разрежения. В случае лагранжевых массовых переменных они могут быть записаны в виде:
![]() - следствие закона
сохранения массы, (3.3)
- следствие закона
сохранения массы, (3.3)
![]() - закон сохранения
импульса. (3.4)
- закон сохранения
импульса. (3.4)
где индексом 0 обозначены значения параметров газа слева от разрыва,
а индексом 1 – справа. В таблице приведены полученные в расчете для ![]() (см. рис. 14) значения
параметров среды.
(см. рис. 14) значения
параметров среды.
|
|
Параметры газа слева от разрыва |
Параметры газа справа от разрыва |
|
|
-0,225 |
0,0 |
|
|
0,64 |
1,0 |
|
|
0,16 |
0,25 |
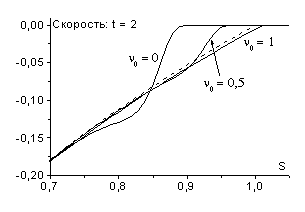
Для определения скорости фронта ударной волны воспользуемся
соотношением: ![]() , где
, где ![]() - массовый путь,
пройденный фронтом волны за время
- массовый путь,
пройденный фронтом волны за время ![]() . Для данного расчета эта формула дает
. Для данного расчета эта формула дает ![]() .
.
Подставляя далее найденное значение ![]() в (3.3) и (3.4),
убеждаемся в выполнении соотношений Гюгонио для ударной волны разрежения.
в (3.3) и (3.4),
убеждаемся в выполнении соотношений Гюгонио для ударной волны разрежения.
Легко также проверить, что для ударной волны разрежения
выполняются неравенства для скорости фронта ударной волны: ![]() . В нашем случае:
. В нашем случае: ![]() ,
, ![]() ,
, ![]() .
.
|
|
|
|
рис. 16 |
|
|
|
|
|
рис. 17 |
|
4. Дифференциальное приближение
Проведем исследование возможных причин возникновения описанных выше ударных волн разрежения при решении задачи о поршне. Для анализа схем используем метод дифференциального приближения [5,11]. Проиллюстрируем идею метода на простом примере [3,11].
4.1. Модельный пример
Рассмотрим линейное уравнение переноса:
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (4.1)
. (4.1)
Аппроксимируем это уравнение на равномерной сетке с помощью следующей разностной схемы:
![]() ,
, ![]() ,
, ![]() , (4.2)
, (4.2)
или в индексной форме:
![]() .
.
Как известно, необходимым и достаточным условием ее устойчивости
является условие Куранта ![]() .
.
Возьмем достаточно гладкую функцию ![]() и разложим ее
по формуле Тейлора с центром в узле
и разложим ее
по формуле Тейлора с центром в узле ![]() . Подставим полученное разложение в схему (4.2) и, отбрасывая
члены выше первого порядка малости по
. Подставим полученное разложение в схему (4.2) и, отбрасывая
члены выше первого порядка малости по ![]() и
и ![]() , получим соотношение, записанное в узле
, получим соотношение, записанное в узле ![]() :
:
![]() . (4.3)
. (4.3)
Будем предполагать, что это соотношение выполнено всюду в области ![]() . В этом случае (4.3) представляет собой так
называемую Г-форму первого дифференциального приближения схемы (4.2).
. В этом случае (4.3) представляет собой так
называемую Г-форму первого дифференциального приближения схемы (4.2).
Используя (4.3) легко перейти к П-форме дифференциального приближения схемы:
![]() ,
, ![]() . (4.4)
. (4.4)
Итак, уравнение (4.4) является первым дифференциальным
приближением разностной схемы (4.2), записанным в П-форме. Правую часть можно
трактовать при ![]() как присутствие
в схеме некоторой диссипации типа линейной вязкости. Она имеет разностную
природу, то есть это – схемная вязкость.
как присутствие
в схеме некоторой диссипации типа линейной вязкости. Она имеет разностную
природу, то есть это – схемная вязкость.
Заметим, что при нарушении условия Куранта, то есть при
![]() , (4.5)
, (4.5)
коэффициент схемной вязкости становится отрицательным. В этом случае можно формально рассматривать (4.4) как уравнение теплопроводности с отрицательным коэффициентом теплопроводности. Как известно, задача Коши для такого уравнения является некорректной, что свидетельствует о дефектах рассматриваемой схемы, которые проявляются в виде ее неустойчивости.
4.2. Дифференциальное приближение для изотермического случая
Рассмотрим теперь общее семейство изотермических схем
газовой динамики, с учетом искусственной линейной вязкости ![]() :
:
![]() , (4.6.a)
, (4.6.a)
![]() , (4.6.b)
, (4.6.b)
![]() ,
, ![]() ,
, ![]() . (4.6.c)
. (4.6.c)
Преобразуем последние три уравнения в одно, тогда схема примет вид:
![]() , (4.7.a)
, (4.7.a)
![]() , (4.7.b)
, (4.7.b)
![]() , (4.7.c)
, (4.7.c)
где обозначено ![]() .
.
Напомним, что функции плотности и давления относятся к
полуцелым узлам сетки ![]() , а функция скорости – к целым
, а функция скорости – к целым ![]() . Разложим функции по формуле Тейлора с центром в узле
. Разложим функции по формуле Тейлора с центром в узле ![]() до членов второго
порядка малости
до членов второго
порядка малости ![]() включительно.
Предположим, что коэффициент искусственной вязкости выбран так, что
включительно.
Предположим, что коэффициент искусственной вязкости выбран так, что ![]() [3].
[3].
В итоге получим Г-форму дифференциального приближения [11] разностной схемы (4.7):
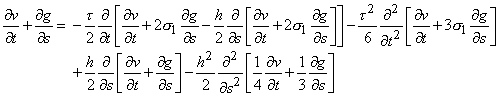 , (4.8.a)
, (4.8.a)
![]() , (4.8.b)
, (4.8.b)
![]() . (4.8.c)
. (4.8.c)
Перейдем к П-форме дифференциального приближения. Пользуясь
уравнениями (4.8.a) и
(4.8.b), подставим в их
правые части производные по времени ![]() и
и ![]() . Приводя подобные члены, получим Г-форму в ином виде:
. Приводя подобные члены, получим Г-форму в ином виде:
![]() , (4.9.a)
, (4.9.a)
![]() , (4.9.b)
, (4.9.b)
![]() . (4.9.c)
. (4.9.c)
Необходимо отметить, что полученные уравнения имеют
одинаковую структуру. При этом члены с ![]() , отличающие уравнение (4.8.a) от (4.8.b), возникли за счет того, что
разностное уравнение (4.7.a)
записано симметрично для узла
, отличающие уравнение (4.8.a) от (4.8.b), возникли за счет того, что
разностное уравнение (4.7.a)
записано симметрично для узла ![]() , а (4.7.b)
для
, а (4.7.b)
для ![]() . Поскольку разложение в ряд Тейлора было произведено в узле
. Поскольку разложение в ряд Тейлора было произведено в узле ![]() , в разложение функций из (4.7.a) вошли дополнительные члены с
, в разложение функций из (4.7.a) вошли дополнительные члены с ![]() . Однако дальнейший переход к (4.9) привел к взаимному
уничтожению этих членов.
. Однако дальнейший переход к (4.9) привел к взаимному
уничтожению этих членов.
Подставим далее ![]() в первое уравнение
(4.8) и вновь выразим
в первое уравнение
(4.8) и вновь выразим ![]() и
и ![]() . Окончательно, получим П-форму дифференциального
приближения:
. Окончательно, получим П-форму дифференциального
приближения:
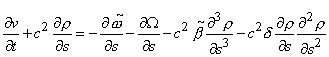 , (4.10.a)
, (4.10.a)
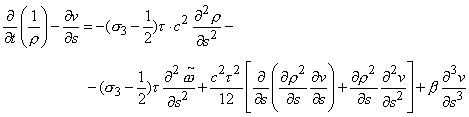 (4.10.b)
(4.10.b)
![]() , где
, где ![]() ,
, ![]() , (4.11)
, (4.11)
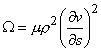 , где
, где ![]() , (4.12)
, (4.12)
![]() ,
, ![]() , (4.13)
, (4.13)
![]() . (4.14)
. (4.14)
Из вида дифференциального приближения следует, что помимо
явно введенной искусственной линейной вязкости с коэффициентом ![]() , схема обладает собственной линейной вязкостью с
коэффициентом
, схема обладает собственной линейной вязкостью с
коэффициентом ![]() , а также собственной квадратичной вязкостью
, а также собственной квадратичной вязкостью ![]() с коэффициентом
с коэффициентом ![]() . Коэффициенты достигают минимальных значений при
. Коэффициенты достигают минимальных значений при ![]() :
: ![]() ,
, ![]() . Видно также, что при увеличении степени неявности схемы
внутренние диссипативные свойства схемы усиливаются.
. Видно также, что при увеличении степени неявности схемы
внутренние диссипативные свойства схемы усиливаются.
В дифференциальном приближении присутствуют также члены,
содержащие третьи производные ![]() ,
, ![]() , которые, как показано в [12], характеризуют дисперсионные
свойства схемы.
, которые, как показано в [12], характеризуют дисперсионные
свойства схемы.
5. Анализ дифференциального приближения
1. Уравнение структуры фронта ударной волны в вязкой среде
Рассмотрим первое дифференциальное приближение семейства схем (4.6):
![]() ,
, ![]() ,
, ![]() , (5.1.a)
, (5.1.a)
![]() , (5.1.b)
, (5.1.b)
![]() , где
, где ![]() ,
, ![]() , (5.2)
, (5.2)
![]() . (5.3)
. (5.3)
Будем трактовать уравнения (5.1) – (5.3) как математическую
модель некоторой гипотетической среды. Очевидно, при ![]() и
и ![]() она близка к обычной
изотермической газодинамике. При конечных шагах сетки эта среда обладает
некоторыми своеобразными диссипативными свойствами, роль которых необходимо
оценить. Построим для системы уравнений (5.1) – (5.3) автомодельное решение
типа “бегущей волны” [8], которое используется для получения структуры фронта
ударной волны в обычных газодинамических средах.
она близка к обычной
изотермической газодинамике. При конечных шагах сетки эта среда обладает
некоторыми своеобразными диссипативными свойствами, роль которых необходимо
оценить. Построим для системы уравнений (5.1) – (5.3) автомодельное решение
типа “бегущей волны” [8], которое используется для получения структуры фронта
ударной волны в обычных газодинамических средах.
Будем искать решение в виде
![]() ,
, ![]() . (5.4)
. (5.4)
Решение рассматривается в неограниченной области ![]() , при
, при ![]() , при этом
, при этом ![]() . Роль правого граничного условия при
. Роль правого граничного условия при ![]() играет “фон”
играет “фон” ![]() ; будем считать, что при
; будем считать, что при ![]() решение “выходит” на
постоянные значения
решение “выходит” на
постоянные значения ![]() , которые неизвестны. Также считаем, что
, которые неизвестны. Также считаем, что
![]() . (5.5)
. (5.5)
Таким образом, мы ищем установившееся решение,
перемещающееся по массовой координате с постоянной скоростью ![]() .
.
Функция ![]() дает профиль параметра
дает профиль параметра
![]() по переменной
по переменной ![]() в фиксированный момент
времени (
в фиксированный момент
времени (![]() ) либо закон изменения со временем этого параметра в
фиксированной частице среды (
) либо закон изменения со временем этого параметра в
фиксированной частице среды (![]() ).
).
Замена переменных (5.4) эквивалентна переходу в систему
координат, связанную с волной, где профили всех параметров стационарны. Эта
замена позволяет выразить производные по ![]() и
и ![]() через производную по
через производную по ![]()
![]() ,
,
и тем самым свести систему уравнений в частных производных (5.1) к системе обыкновенных дифференциальных уравнений:
![]() , (5.6.a)
, (5.6.a)
![]() . (5.6.b)
. (5.6.b)
Равенство (5.5), играющее роль граничных условий, преобразуется к виду
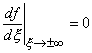 . (5.7)
. (5.7)
Проинтегрируем уравнения (5.6) по ![]() от фона
от фона ![]() до некоторого
текущего значения:
до некоторого
текущего значения:
![]() , (5.8.a)
, (5.8.a)
![]() . (5.8.b)
. (5.8.b)
Отсюда легко получить
![]() ,
,
или для случая идеального газа
![]() , (5.9)
, (5.9)
где  - значение полученное из
классических соотношений Гюгонио.
- значение полученное из
классических соотношений Гюгонио.
Заметим, что обе части этого равенства обращаются в нуль на
фоне при ![]() (
(![]() ) в полном соответствии с (5.7). Аналогично левая, а,
следовательно, и правая части должны обратиться в нуль и при
) в полном соответствии с (5.7). Аналогично левая, а,
следовательно, и правая части должны обратиться в нуль и при ![]() . Поэтому значение плотности, которое устанавливается при
. Поэтому значение плотности, которое устанавливается при ![]() , должно быть равно
, должно быть равно ![]() .
.
Отметим также, что формально возможно существование либо
ударной волны сжатия (![]() , при этом
, при этом ![]() ), либо ударной волны разрежения (
), либо ударной волны разрежения (![]() ,
,![]() ). Далее будут найдены условия, при которых в среде возникают
ударные волны разрежения.
). Далее будут найдены условия, при которых в среде возникают
ударные волны разрежения.
Вернемся к уравнению (5.9) и подставим в него формулы (5.2) и (5.3). Имеем:
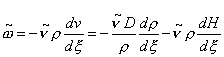 ,
,
![]() .
.
Поскольку мы ограничились рассмотрением первого дифференциального
приближения и считаем, что ![]() , то можно пренебречь членами второго порядка малости по
, то можно пренебречь членами второго порядка малости по ![]() и
и ![]() . Тогда
. Тогда
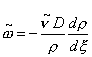
и уравнение (5.10) может быть преобразовано к виду:
![]() . (5.10)
. (5.10)
Таким образом, получено уравнение (5.10) описывающее
структуру фронта ударной волны в вязкой среде. Отметим, что это уравнение при ![]() переходит в уравнение
для структуры фронта изотермической ударной волны.
переходит в уравнение
для структуры фронта изотермической ударной волны.
2. Случай ![]()
Рассмотрим решения, которые дает уравнение (5.10) при
отсутствии искусственной вязкости (![]() ). В этом случае уравнение (5.10) имеет вид
). В этом случае уравнение (5.10) имеет вид
![]() (5.11)
(5.11)
Если ![]() (это условие
выполнено, например, для схемы “крест”), то уравнение (5.11) не является
дифференциальным и с точки зрения структуры фронта необходимо учитывать члены
второго порядка малости. Из (5.11) получим:
(это условие
выполнено, например, для схемы “крест”), то уравнение (5.11) не является
дифференциальным и с точки зрения структуры фронта необходимо учитывать члены
второго порядка малости. Из (5.11) получим:
![]() . (5.12)
. (5.12)
Возможные решения данного уравнения приведены на рис. 18 (соответствует ударной волне сжатия) и рис. 19 (соответствует ударной волне разрежения).
Отметим, что решение уравнения (5.12) имеет разрыв. Это соответствует расчетам по схеме “крест” задачи о выдвигаемом поршне, в которой возникало практически разрывное решение - ударная волна разрежения (см. пункт 3).
Если ![]() , то уравнение (5.11) – дифференциальное. Оно легко
интегрируется:
, то уравнение (5.11) – дифференциальное. Оно легко
интегрируется:
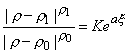 , где
, где ![]() ,
, ![]() .
.
|
|
|
|
рис. 18 |
рис. 19 |
Однако решение удобнее анализировать, рассматривая само уравнение (5.11), дающее знак производной плотности:
![]() . (5.13)
. (5.13)
Рассмотрим случай, когда ![]() . Если
. Если ![]() (при
(при ![]() ), то уравнение (5.13) имеет решение, представляющее собой
ударную волну сжатия; оно показано на рис. 20. Для
), то уравнение (5.13) имеет решение, представляющее собой
ударную волну сжатия; оно показано на рис. 20. Для ![]() решение есть ударная
волна разрежения, как показано на рис. 21. Таким образом, мы построили два формально
возможных решения задачи.
решение есть ударная
волна разрежения, как показано на рис. 21. Таким образом, мы построили два формально
возможных решения задачи.
|
|
|
|
рис. 20 |
рис. 21 |
Учитывая, что, при ![]() плотность
должна “выходить” на “фоновое” значение
плотность
должна “выходить” на “фоновое” значение ![]() , можно выбрать единственно допустимое решение задачи (см.
[15]). В данном случае в среде существует ударная волна сжатия (рис. 20), а
ударная волна разрежения существовать не может. Математически последнее
означает, что при
, можно выбрать единственно допустимое решение задачи (см.
[15]). В данном случае в среде существует ударная волна сжатия (рис. 20), а
ударная волна разрежения существовать не может. Математически последнее
означает, что при ![]() (
(![]() ) решения задачи типа “бегущей волны” нет, и его следует
искать в ином виде. Для обычной газовой динамики такое решение есть римановская
волна разрежения, являющееся автомодельным (
) решения задачи типа “бегущей волны” нет, и его следует
искать в ином виде. Для обычной газовой динамики такое решение есть римановская
волна разрежения, являющееся автомодельным (![]() ).
).
Аналогично строится решение при ![]() - см. рис. 22. В среде
возникает ударная волна разрежения с
- см. рис. 22. В среде
возникает ударная волна разрежения с ![]() , при этом
, при этом 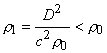 ,
, ![]() .
.
|
|
|
рис. 22 |
Таким образом, при ![]() в среде будет
существовать ударная волна сжатия, а при
в среде будет
существовать ударная волна сжатия, а при ![]() - ударная волна
разрежения. Отметим, что условие возникновения ударной волны сжатия совпадает с
условием (2.17) устойчивости разностной схемы в акустическом приближении.
- ударная волна
разрежения. Отметим, что условие возникновения ударной волны сжатия совпадает с
условием (2.17) устойчивости разностной схемы в акустическом приближении.
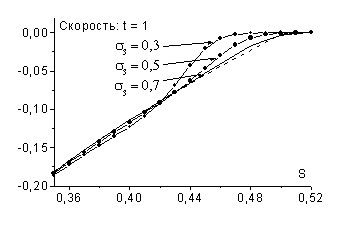
Проведем расчеты задачи о выдвигаемом поршне по схемам (4.6)
со следующими весами: ![]() ,
, ![]() . Легко видеть, что для этих схем выполнено условие
. Легко видеть, что для этих схем выполнено условие ![]() , а значит, в решении может содержаться ударная волна
разрежения.
, а значит, в решении может содержаться ударная волна
разрежения.
Выберем следующие начальные данные для расчета:
![]() ,
, ![]() ,
, ![]() (
(![]() ),
),
пусть скорость поршня равна ![]() ; значение изотермической скорости звука
; значение изотермической скорости звука ![]() . Выберем значения шагов по пространству и времени:
. Выберем значения шагов по пространству и времени: ![]() ,
, ![]() .
.
|
|
|
рис. 23 |
На рис. 23 приведены результаты расчетов для трех схем ![]() ,
, ![]() ,
, ![]() . Действительно, в решениях присутствует ударная волна
разрежения, размазанная схемной вязкостью, действие которой увеличивается с
ростом
. Действительно, в решениях присутствует ударная волна
разрежения, размазанная схемной вязкостью, действие которой увеличивается с
ростом ![]() . Отметим, что с увеличением
. Отметим, что с увеличением ![]() ударная волна
разрежения становится все более “размазанной” и при
ударная волна
разрежения становится все более “размазанной” и при ![]() практически пропадает.
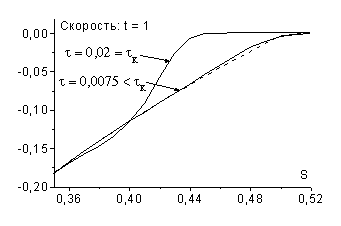
На рис. 24 приведены результаты расчетов по схеме
практически пропадает.
На рис. 24 приведены результаты расчетов по схеме ![]() с двумя шагами по
времени:
с двумя шагами по
времени: ![]() и
и ![]() . Легко видеть, что с увеличением шага
. Легко видеть, что с увеличением шага ![]() ширина размазывания фронта
ударной волны возрастает. Это связано с увеличением коэффициента схемной
вязкости
ширина размазывания фронта
ударной волны возрастает. Это связано с увеличением коэффициента схемной
вязкости ![]() . Как показывают результаты расчетов (см. пункт 3), для схемы
“крест” она появляется при
. Как показывают результаты расчетов (см. пункт 3), для схемы
“крест” она появляется при ![]() ; для схем
; для схем ![]() ,
, ![]() при
при ![]() , причем
, причем ![]() .
.
|
|
|
рис. 24 |
3. Случай ![]()
Оценим теперь влияние искусственной вязкости на решение
задачи о выдвигаемом поршне. Проведем расчеты с различными коэффициентами ![]() : без вязкости (
: без вязкости (![]() ,
, ![]() ) и с вязкостью (
) и с вязкостью (![]() ,
, ![]() ), при этом потребуем выполнение следующего соотношения (см.
(5.10)):
), при этом потребуем выполнение следующего соотношения (см.
(5.10)):
![]() .
.
И, следовательно,
![]() . (5.14)
. (5.14)
|
|
|
|
рис. 25 |
|
Выберем ![]() ,
, ![]() ,
, ![]() (при этом значении
шага
(при этом значении
шага ![]() в численных решениях
присутствуют ударные волны разрежения). На рис. 25 представлены результаты
соответствующих расчетов. Для сравнения на том же рисунке нанесены точное решение
(пунктир) и численное решение с
в численных решениях
присутствуют ударные волны разрежения). На рис. 25 представлены результаты
соответствующих расчетов. Для сравнения на том же рисунке нанесены точное решение
(пунктир) и численное решение с ![]() без вязкости. Легко
видеть, что введение в схему с весом
без вязкости. Легко
видеть, что введение в схему с весом ![]() искусственной вязкости
(5.14) приводит к изменению амплитуды ударной волны и ширины ее фронта
(штрихпунктирная линия), в результате, численное решение задачи с
искусственной вязкости
(5.14) приводит к изменению амплитуды ударной волны и ширины ее фронта
(штрихпунктирная линия), в результате, численное решение задачи с ![]() становится близко к
решению задачи по схеме с весом
становится близко к
решению задачи по схеме с весом ![]() . Отметим, что коэффициент вязкости (5.14) нелинеен. Если его
задать постоянным:
. Отметим, что коэффициент вязкости (5.14) нелинеен. Если его
задать постоянным: ![]() , то различие между численными решениями немного
увеличивается (см. рис. 25).
, то различие между численными решениями немного
увеличивается (см. рис. 25).
3. Случай нелинейной искусственной вязкости
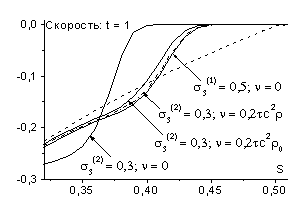
Пусть в схему введена искусственная вязкость (![]() ) следующего специального вида:
) следующего специального вида:
![]() . (5.15)
. (5.15)
Ограничимся рассмотрением случая ![]() . Преобразуем уравнение (5.10)
. Преобразуем уравнение (5.10)
![]() . (5.16)
. (5.16)
Анализ возможных интегральных кривых приводит к следующим результатам.
Если ![]() , то при
, то при ![]() в среде возникает
ударная волна сжатия, а при
в среде возникает
ударная волна сжатия, а при ![]() ударная волна
разрежения.
ударная волна
разрежения.
Если ![]() , то при
, то при ![]() в среде возникает
ударная волна разрежения, а при
в среде возникает
ударная волна разрежения, а при ![]() ударная волна сжатия.
ударная волна сжатия.
Как и в предыдущем пункте рассмотрим схемы семейства (4.6) с
весами ![]() ,
, ![]() , для которых выполнено условие
, для которых выполнено условие ![]() .
.
Выберем следующие начальные данные для расчета:
![]() ,
, ![]() ,
, ![]() (
(![]() ),
),
пусть скорость поршня равна ![]() ; значение изотермической скорости звука
; значение изотермической скорости звука ![]() .
.
В схемы введена линейная вязкость
![]() ,
,
коэффициент вязкости положим равным
![]() . (5.17)
. (5.17)
Отметим, что переход от нелинейного коэффициента вязкости
(5.15) к линейному коэффициенту вида (5.17) оправдан в силу того, что
рассматриваемая ниже ударная волна разрежения имеет малую амплитуду; на волне
будет выполнено условие ![]()
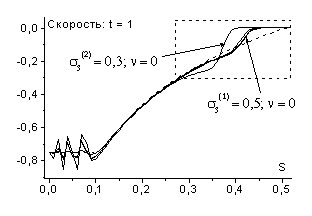
На рис. 26 показано влияние данной вязкости на решение,
полученное по схеме с ![]() и шагами
и шагами ![]() ,
, ![]() (для выбранных
параметров
(для выбранных
параметров ![]() ).
).
Для того же коэффициента вязкости на рис. 27 приведены
результаты расчетов по схеме с другими параметрами ![]() и шагами
и шагами ![]() ,
, ![]() .
.
Приведенные расчеты показывают влияние вязкости с
коэффициентом (5.17) на решение задачи о выдвигаемом поршне. Они подтверждают
сделанные аналитически выводы о том, что при ![]() и
и ![]() возникает ударная
волна разрежения, а при
возникает ударная
волна разрежения, а при ![]() волна сжатия.
волна сжатия.
Таким образом, в настоящем параграфе проведено исследование первого дифференциального приближения семейства схем (4.6) изотермической газовой динамики, в ходе которого найдены условия возникновения в численных решениях модельных задач ударных волн разрежения. Показано, что эти волны возникают за счет внутренних диссипативных свойств разностных схем (подобные схемы обладают отрицательной схемной вязкостью).
|
|
|
|
рис. 26 |
|
|
|
|
|
рис. 27 |
|
6. Заключение
В работе показано, что при использовании разностных схем газовой динамики, неустойчивых в акустическом приближении, возникают ударные волны разрежения. Их возникновение может быть объяснено спецификой диссипативных свойств схем. С помощью дифференциального приближения получены условия, связывающие весовые коэффициенты разностных схем и шаги сетки, при которых возникают указанные ударные волны разрежения.
В работе также изучено влияние искусственной вязкости и шага по времени на возникновение в решении задачи о выдвигаемом поршне ударной волны разрежения. Показано, что соответствующим выбором весовых коэффициентов разностных схем, шагов сетки, а также коэффициента искусственной вязкости можно исключить появление ударной волны разрежения. Отметим, что неявные схемы, обладающие большим запасом устойчивости, этого дефекта не имеют.
Литература
1. Самарский А.А. Теория разностных схем. – М.: Наука, 1989.
2. Попов Ю.П., Самарский А.А. Полностью консервативные разностные схемы - ЖВМ и МФ, 1969, Т. 9, № 4, С. 953-958.
3. Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. – М.: Наука, 1992.
4. Тихонов А.Н., Самарский А.А. Об однородных разностных схемах - ЖВМ и МФ, 1961, Т. 1, № 1, С. 5-63.
5. Давыдов Ю.М. Применение метода дифференциального приближения для исследования и построения нелинейных разностных схем. – ЧМ МСС, Новосибирск: 1980, Т. 11, № 4, С. 41-59.
6. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. – М.: Наука, 1988.
7. Арделян Н.В., Гулин А.В. К обоснованию устойчивости разностных схем для уравнений акустики. – Препринт/ИПМ АН СССР. – М., 1978. - №96.
8. Седов Л.И. Методы подобия и размерности в механике. – М.: Физматгиз, 1962.
9. Кузнецов О.А. Численное исследование схемы Роу с модификацией Эйнфельдта для уравнений газовой динамики. – Препринт/ИПМ АН СССР. – М., 1998.
10. Трощиев В.Е. О дивергентности схемы “крест” численного решения уравнений газовой динамики // Численные методы механики сплошной среды. – Новосибирск: Наука. – 1970.
11. Шокин Ю.И. Метод дифференциального приближения, Новосибирск: Наука, 1979.
12. Мухин С.И., Попов С.Б., Попов Ю.П. О разностных схемах с искусственной дисперсией // ЖВМ и МФ. - Т. 23, №6.
13. Рождественский Б. Л., Яненко Н. Н. Системы квазилинейных уравнений. – М.: Наука, 1978.
14. Von Neumann J., Richtmyer R. D. A method for numerical calculation of hydrodynamics shocks // J. Appl. Phys. – 1949. V. 21.
15. Гельфанд И.М. Некоторые задачи теории квазилинейных уравнений. – УМН, 1959, Т. XIV, вып.2(86), С. 87-158.
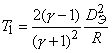 .
.