Труды Совещания “Управление движением малогабаритных спутников”

( Digest of the Workshop “Small Satellite Motion Control”
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Содержание

О работах в ИПМ им.М.В.Келдыша РАН по анализу динамики, разработке и реализации

систем ориентации малогабаритных спутников

М.Ю.Овчинников

Институт прикладной математики им.М.В.Келдыша РАН

Начиная с объекта “Д” – первого искусственного спутника Земли, в Институте прикладной математики (в то время именовавшемся ОПМ МИАНа) разрабатывались схемы управления ориентацией и проводились расчеты углового движения проектируемых спутников. В 1954 году Д.Е.Охоцимским была предложена оригинальная схема гравитационной ориентации спутника, которая в дальнейшем легла в основу многих пассивных и полупассивных систем ориентации малых спутников, использующих гравитационное поле Земли для создания восстанавливающего момента. В дальнейшем была построена подробная теория гравитационной ориентации, определяющий вклад в создание которой внесли В.В.Белецкий и В.А.Сарычев, а в дальнейшем теория и приложения гравитационных, аэродинамических, магнитных, гироскопических систем ориентации получили свое развитие в работах их коллег и многочисленных учеников. Были разработану методики определения фактического углового движения спутников по измерениям параметров внешних среды, которые в дальнейшем легли в основу алгоритмов определения ориентации многих реализованных космических аппаратов.

На заре космической эры технологическое развитие космических аппаратов ассоциировалось с увеличением им массы, размеров, энергетики. На рубеже 21-го века технологические достижения стали связываться, наоборот, с микроминиатюризацией - уменьшением массы, размеров, потребляемой энергии. В начале 90-х годов прошлого столетия в связи с появлением новой миниатюрной и экономичной элементной базы, изменением приоритетов, связанных с изменением финансовых и экономических возможностей стран - лидеров в освоении космического пространства, сформировался новый класс космических аппаратов, названных малыми (или микро-) спутниками. Говоря о микроспутниках, следует упомянуть связанные с ними основные понятия и признаки. Первым и наиболее очевидным формальным признаком микроспутника можно считать его относительно небольшые массу, размеры и ограниченные энергетические возможности. Существует некая условная классификация спутников по массе: до килограмма – это пикоспутники, от одного килограмма до 10 килограмм – наноспутники, от 10 до 100 килограмм – микроспутники, от 100 до 500 килограмм – малые спутники, позволяющая по столь формальному признаку отнести его к тому или иному семейству малых аппаратов.

Другой признак микроспутников скорее относится не к формальным, а к идеологическим понятиям и его парадигма звучит так: “cheaper, faster, better”. Низкая стоимость достигается, например, использованием доступных коммерческих компонент (Components-Off-The-Shelf), привлекаемой к работам недорогой рабочей силой, попутного или иного, но по цене ниже рыночной, вывода на орбиту, нестандартных средств управления; при создании группировок целенаправлено снижается срок гарантированного существования спутников, ее составляющих, специально, имея ввиду своевременную оперативную замену спутников на более современные, что опять же приводит к снижению стоимости аппаратов. Но какой бы принцип не был положен в основу идеологии создания микроспутника, проблема обеспечения его ориентации остается актуальной.

         Один из первых микроспутников с пассивной гравитационной системой ориентации, включающей сферический магнитный демпфер, динамика которого была исследована в Институте прикладной математики, был Искра-5, разработанный в Московском авиационном институте и выведенный на орбиту в 1982 году. Исследования динамики проведены для малого спутника Старт-1 с аналогичной системой ориентации разработки Московского института теплотехники (спутник выведен на орбиту в 1992 году). Для микроспутника МАК-А разработки НИИ прикладной механики и электродинамики была предложена концепция пассивной аэродинамической системы ориентации с гистерезисными стержнями, проведен анализ динамики и изготовлены элементы системы ориентации, проведены лабораторные испытания демпфирующих свойств системы ориентации. Летный образец спутника был построен и были проведены его наземные испытания. В начале 90-х был выполнен цикл работ по анализу динамики микроспутника УМКП-1 разработки ВНИИ электромеханики с пассивной гравитационной системой ориентации, снабженной системой предварительной магнитной ориентации на сферическом магнитном демпфере. Аналогичная схема была использована и в проекте малого СПС-спутника, разработки КБ им.Макеева. Его система ориентации разрабатывалась также во ВНИИЭМ. Институт прикладной математики выполнил цикл исследований по выбору схемы функционирования и анализу динамики СПС-спутника.

В конце 90-х годов Институт принял участие в формировании облика ряда международных наноспутников. В результате этих работ, выполнявшихся в рамках соглашений и договоров Института с зарубежными и отечественными организациями, в 2000-ом году был выведен на орбиту шведский наноспутника Munin с пассивной магнитной системой ориентации разработки Института прикладной математики. Из-за ограниченности измерительной информации была предложена и реализована схема определения ориентации по измерениям токосъема с шести панелей солнечных батарей. В результате удалось подтвердить работоспособность системы ориентации. В 2001-ом году был успешно выведен на орбиту российско - американский наноспутник REFLECTOR с пассивной гравитационной системой ориентации, содержащей гистерезисные стержни. Спутник разработан НИИ прецизионного приборостроения, система ориентации - Институтом прикладной математики. Из служебной и полезной нагрузки на спутнике установлены лишь лазерные ретрорефлекторы, с помощью которых можно измерить расстояние до каждого видимого рефлектора, а путем вычислений определить расстояние от каждого видимого рефлектора до картинной плоскости. Эта информация позволяет определить отдельные параметры углового движения спутника. Одновременно с наноспутником REFLECTOR был выведен на орбиту пакистанский микроспутник BADR-B. Для этого спутника в Институте были предложены методики управления и определения его фактического углового движения.

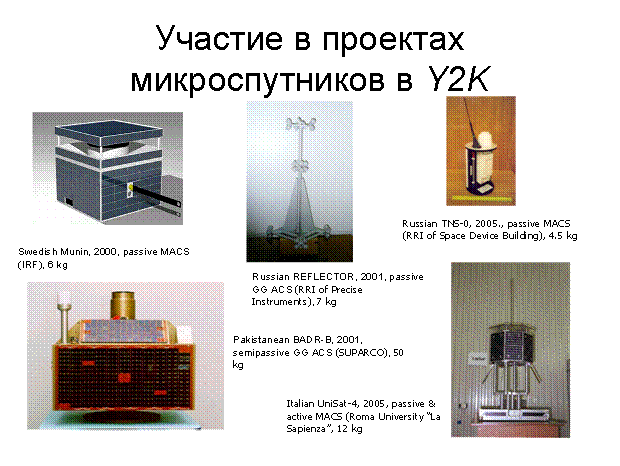
В марте 2005 года был успешно выведен на орбиту первый российский наноспутник ТНС-0 разработки РНИИ космического приборостроения. Институт прикладной математики предложил пассивную магнитную систему ориентации, выполнил расчеты ее параметров и провел анализ динамики и обработку результатов летных испытаний этого спутника. Одновременно предложена схема активного управления угловым движением другого российского наноспутника ТНС-1 и выполнен анализ его динамики. В настоящее время Институт совместно с МФТИ и ZARM (Бремен, Германия) разработывает систему управления совместным российско-немецким студенческим наноспутником GRESat, а также принимает участие в анализе динамики cтуденческих итальянских микроспутников UniSat и PalaMede.

Для отработки элементов систем ориентации, алгоритмов управления и определения углового движения малоразмерных аппаратов в Институте разрабатывается лабораторный стенд, позволяющий имитировать угловое движение аппарата, внешнее магнитное поле и еще ряд внешних факторов.

Работы выполняются при поддержке РАН, РФФИ, Роснауки, Минобрнауки, организаций промышленности, зарубежных партнеров и фондов.

Об участии МГУ им.М.В.Ломоносова в создании первых советских спутников

В.В.Александров

Московский государственный университет им.М.В.Ломоносова

Известно, что первые девять результатов по космонавтике, зафиксированных в книге рекордов Гиннеса, принадлежат СССР (рис.1). Остановимся на вкладе ученых Московского университета в получение этих и других результатов в космонавтике.

В 1933-34 годах в соответствии с Постановлением Совета Министров СССР в ведущих университетах страны были созданы механико-математические факультеты. Благодаря этому появилась уникальная возможность впервые в истории организации научных исследований создать научные школы по применению математических методов  для решения физических проблем, в том числе и для познания космоса. И такие школы были созданы в МГУ.

Рис.1. Из книги рекордов Гиннеса

         Работы по изучению движения искусственных спутников Земли были начаты в Московском университете в 50-е годы на механико-математическом факультете. Коллектив ученых, сплотившихся вокруг определенного круга научных проблем во главе с Д.Е.Охоцимским, начал формироваться еще в конце 40-х годов. Он получил интенсивное развитие после 1953 года, когда в созданном во главе с академиком М.В.Келдышем Институте прикладной математики Академии наук СССР был сформирован отдел, который возглавил Д.Е.Охоцимский. С 1962 г. он возглавляет кафедру теоретической механики МГУ. Основным содержание работы с самого начала были исследования по динамике полета ракет и космических аппаратов и управление их движением. Работы проводились в тесном контакте с промышленностью (ОКБ-1 С.П.Королева и ряд других).

Университетские учёные во главе с академиком С.Н.Верновым из НИИЯФ МГУ долгое время занимались исследованием космических лучей с помощью наземных и аэростатных методов. В 1953 г. по инициативе С.Н.Вернова в МГУ был построен специальный лабораторный корпус для детекторов электронов и адронов. Поэтому естественной была их инициатива о продолжении этих экспериментов в космосе. В 1956г было  принято Решение АН СССР о подготовке проектов экспериментов для первых ИСЗ. В 1957г. по инициативе С.Н.Вернова в НИИЯФ МГУ начала создаваться научная аппаратура для исследования космических лучей для второго советского ИСЗ, который был выведен на орбиту 3 ноября 1957 года.

Вслед за ним, 15 мая 1958 года, на орбиту был выведен третий советский ИСЗ. На нём также была установлена университетская научная аппаратура для исследований космических лучей. Но это были уже более сложные приборы. С помощью детекторов заряженных частиц, установленных на втором и третьем советских ИСЗ, была зарегистрированы мощные потоки радиации вблизи Земли. Это стало большим научным открытием. Оказалось, что Земля окружена стабильными потоками радиации, захваченными в магнитное поле Земли. Это, так называемые, радиационные пояса Земли. Их исследования на многие годы вперёд определили направления и фундаментальных и прикладных исследований околоземного космического пространства. Радиация в космосе воздействует как на биологические структуры, так и на элементы и конструкции самих космических аппаратов. Так зародилось направление космического материаловедения в Московском университете. Авторами открытия радиационных поясов стали сотрудники МГУ академик С.Н.Вернов, академик А.Е,Чудаков, д.ф.-м.н. П.В.Вакулов, д.ф.-м.н..  Ю.И.Логачёв, д.ф.-м.н. Е.В.Горчаков.

Зная возможности ГАИШ (Государственный астрономический институт МГУ) С.П.Королев 22 марта 1958г. посетил институт. Главный конструктор поставил задачу наблюдения лунных космических аппаратов. Для решения этой задачи заведующий отделом радиоастрономии И.С.Шкловский предложил использовать метод «искусственной кометы» - испарения натрия на трассе полета к Луне. ГАИШ также разработал средства наблюдения, а ОКБ-1 установил испаритель натрия на разгонном блоке ракеты. После успеха «искусственной кометы» все сотрудники отдела получили личные подарки от С.П.Королева. И.С.Шкловский был удостоен звания лауреата Ленинской премии в 1960 году. Длинноволновые радиотелескопы, разработанные в ГАИШ, были установлены и успешно работали на КА Луна-11, Луна-12 в 1966г. и Луна-22 в 1974 году. В 1961-1996 годах сотрудники НИИЯФ и ГАИШ принимали участие в экспериментах на борту 19 автоматических межпланетных станций (АМС) «Венера» и 11 АМС серии «МАРС». Основные результаты, полученные на АМС следующие. Открытие солнечного ветра и динамических процессов, связанных с ним и установление факта отсутствия радиационных поясов у Венеры и Марса. Ученые МГУ в 1968-1997 годах принимали участие в экспериментах на сорока ИСЗ серии «Космос». Всего университетское оборудование было установлено более чем на четырехстах спутниках.

Определение параметров вращательного движения первого российского наноспутника ТНС-0 по результатам летных испытаний

А.А.Ильин¹, Н.В.Куприянова², М.Ю.Овчинников¹, В.И.Пеньков³, А.С.Селиванов⁴

¹Институт прикладной математики им. М.В.Келдыша РАН

²Московский физико-технический институт

³Московский авиационный институт

⁴Российский научно-исследовательский институт космического приборостроения

По своей конструкции и функциональному назначению ТНС–0 относится к классу простых аппаратов (рис.1). Цель запуска – проведение экспериментов по проверке возможности управления космическими аппаратами через глобальную систему связи GLOBALSTAR, использованию радиомаяка системы КОСПАС-САРСАТ для определения местонахождения спутника на орбите, отработке элементов системы ориентации, способа вывода спутника на орбиту. При использовании GLOBALSTAR спутник становится абонентом системы, что дает возможность передавать на спутник и получать со спутника телеметрическую и иную информацию, используя стандартное оборудование для глобальной связи.

Рис.1. Внешний вид наноспутника ТНС-0 без внешней термовакуумной изоляции (фото РНИИ КП)

Спутник оснащен пассивной магнитной системой ориентации, состоящей из сильного постоянного магнита и набора гистерезисных стержней. Система ориентации препятствует хаотическому вращению с неконтролируемыми скоростями и обеспечивает ориентацию продольной оси спутника вдоль местного вектора напряженности геомагнитного поля. Рассчитываются магнитные и геометрические параметры магнита и гистерезисных стержней, место и способ их размещения. Анализируется влияние поля постоянного магнита на гистерезисные стержни и взаимное влияние стержней. Приводятся примеры переходных процессов и установившегося предельного движения спутника относительно центра масс.

Наноспутник ТНС-0 был успешно выведен на орбиту 28-го марта 2005 года с борта Международной космической станции. Для получения информации о вращательном движении на спутнике установлено несколько простейших солнечных датчиков и датчик горизонта. За время функционирования через систему GLOBALSTAR было произведено несколько сеансов обмена информацией со спутником. Для определения ориентации использовались показания трех солнечных датчиков-фотодиодов. Измерения могли проводиться в режиме реального времени и передаваться в те моменты, когда возможна связь со спутником или же можно было задавать другую программу проведения измерений, позволяющую накапливать показания датчиков в течение витка (не более 1000 точек), и затем получить их во время следующего сеанса связи. В докладе рассматриваются результаты определения параметров вращательного движения спутника по имеющимся показаниям солнечных датчиков. Проведен анализ эволюции величины кинетического момента спутника. В качестве примера обработки данных, полученных со спутника, на рис.2 приводятся зависимости косинусов углов между направлением на Солнце и нормалью к плоскости соответствующего фотодиода от времени (время измеряется в секундах, начальная точка соответствует началу измерений).

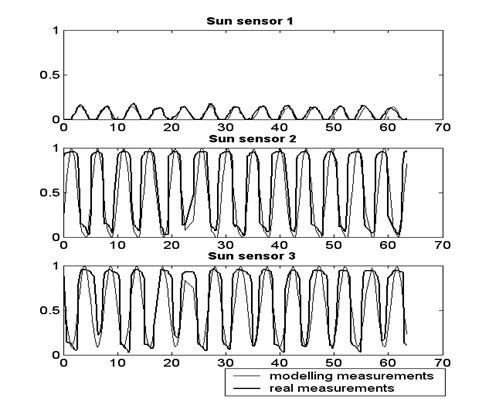
Рис. 2. Данные от 28.03.05, 09:42 и результаты моделирования

Алгоритмы управления ориентацией микроспутников

С.О.Карпенко

Институт прикладной математики им.М.В.Келдыша РАН

К настоящему времени микроспутники все шире эксплуатируются разными странами для решения научных и образовательных задач. Несмотря на имеющийся в проектировании таких спутников опыт, актуальной остается проблема создания недорогой, надежной и дешевой системы управления ориентацией этих аппаратов. Проблема заключается в выборе датчиков ориентации, достаточно надежных и дающих нужную точность; выборе исполнительных элементов, достаточно малогабаритных, надежных и потребляющих минимальное количество энергии; а также выборе и исследовании алгоритмов управления всей системой ориентации в целом.

Что касается датчиков определения ориентации, в докладе рассматриваются достоинства и недостатки магнитометров, солнечных датчиков, звездных камер, датчиков горизонта, инерциальных измерительных систем, а также приводятся математические модели по определению ориентации КА с использованием информации с этих датчиков.

Предлагается описание вариантов комплектации исполнительных элементов систем стабилизации, оцениваются их достоинства и недостатки, приводятся примеры реализации подобных систем на практике.

Рассматриваются системы ориентации двух типов. Первая тип – это магнитные пассивные и активные системы стабилизации, содержащие постоянные магниты или токовые катушки. Приводится обзор реализуемых на борту простых алгоритмов гашения угловой скорости и ориентации аппарата: вдоль силовых линий магнитного поля Земли; стабилизации КА по трем осям как при наличии гравитационной штанги, так и без нее. Второй тип систем – это системы стабилизации, использующие маховики и токовые катушки. Рассматриваются возможность и особенности применения одного или трех маховиков на борту КА, алгоритмы их разгрузки, проблемы, связанные с включением и выключением маховиков на борту КА.

Рассматривается общая циклограмма работы бортовой системы управления ориентацией на примере реально проектируемого микроспутника.

Реализация маховичной системы ориентации и стабилизации углового движения малых спутников

В.В.Черемисин

Московский государственный университет им. М.В.Ломоносова

В зависимости от поставленных задач применяют различные системы ориентации и стабилизации спутников, которые принято классифицировать на пассивные (стабилизация вращением, гравитационная стабилизация, аэродинамическая и т.д.), активные (маховичная система, система ориентации и стабилизации с помощью ракетных двигателей) и комбинированные [1]. На малых спутниках, как правило, используют более простые, а, следовательно, более дешевые пассивные системы, не требующие бортовых источников энергии. Существует целый ряд задач, в которых более целесообразным видится применение активных, в частности, маховичных систем. При этом возникают характерные отличия от аналогичных для массивных спутников отличий, связанные с ограничениями на размеры, массу, мощность бортовых источников энергии.

Рассматривается спутник, центр масс которого движется по круговой орбите. На спутнике установлены три гиростабилизированных маховика. На движущийся по орбите спутник действуют возмущающие моменты различной природы: магнитные, аэродинамические, моменты сил солнечного давления. Особенно пагубно влияние паразитных моментов при рассмотрении класса малых спутников, так как при этом управляющие моменты становятся если не сравнимы с паразитными, то, по крайней мере, значительно приближаются к ним по сравнению с управляющими моментами на массивных спутниках. Поэтому прежде чем давать ответ на вопрос о возможности реализации того или иного теоретического алгоритма управления для малых спутников, следует тщательно изучить характер влияния паразитных моментов на его дееспособность.

Рассмотрим идеальный случай в предположении отсутствия внешних моментов за исключением гравитационного момента. Кинематические уравнения получаются проецированием абсолютной угловой скорости спутника  на оси системы Oxyz, жестко связанной со спутником:

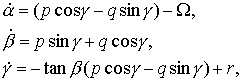
где углами α, β, γ задается ориентация системы координат Oxyz относительно орбитальной системы координат, а Ω – величина абсолютной угловой скорости орбитальной системы координат.

Динамические уравнения получаются проецированием теоремы об изменении полного кинетического момента системы на оси системы Oxyz:

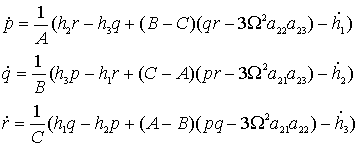
где A,B,C – главные моменты инерции системы спутник-маховики, h₁,h₂,h₃ – абсолютные значения кинетических моментов маховиков относительно осей вращения (которые совпадают с осями Oxyz).

Управление системой осуществляется изменением кинетических моментов маховиков путем приложения внутренних моментов к осям вращения маховиков:

Получаемые уравнения схожи с уравнениями для массивных спутников, однако имеются различия в порядке входящих в уравнения членов. Так, например, допущение о малости кинетических моментов маховиков относительно осей вращение по сравнению с моментами инерции спутника, делаемое в некоторых теоретических работах для больших спутников [2], уже не является правомерным.

Изучим возможность стабилизации углового движения спутника относительно некоторого выбранного положения равновесия. Поиску и исследованию устойчивости положений равновесия спутников посвящено множество работ, например, [3]. Ограничимся рассмотрением одного из них, при котором оси системы, жестко связанной с телом совпадают с осями орбитальной системы координат. Движение будем считать происходящим в некоторой заданной окрестности положения равновесия.

Как и для массивных спутников, в первом приближении система разделяется на две подсистемы – по α,p,h₁ и по β,γ,q,r,h₂,h₃. Первая система не является вполне управляемой, что следовало ожидать, так как проекция внешних моментов на соответствующую ось равна нулю, а, следовательно, полный кинетический момент системы вдоль данной оси сохраняется. Таким образом, мы можем лишь перераспределять кинетический момент между корпусом спутника и маховиком. Для второй системы наличие гравитационного момента делает ее вполне управляемой, то есть гравитационный момент способен “сбрасывать” накопленный в маховиках кинетический момент. Однако, поскольку по величине гравитационный момент мал, система оказывается слабо управляемой.

Вышесказанное наглядно иллюстрируется на приведенных ниже графиках, где представлены результаты численного моделирования линейного алгоритма стабилизации:

где K – выбранная матрица коэффициентов. В качестве численных данных используются характеристики некоторых западных и отечественных микроспутников.

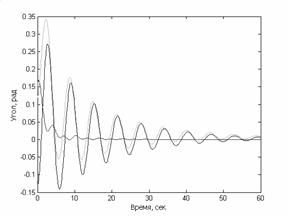
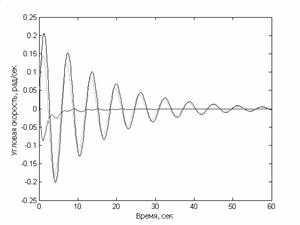
	Рис.1. Графики изменения углов ориентации от времени		Рис.2. Графики изменения угловых скоростей от времени

 

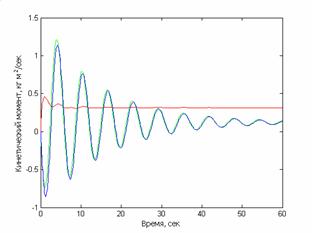
Рис.3. Графики изменения кинетических моментов маховиков от времени

 

Как видно, вращение спутника удается погасить за счет перераспределения кинетического момента между корпусом спутника и маховиками. Может возникнуть критическая ситуация, когда один или несколько маховиков обладают максимально возможным кинетическим моментом, что делает невозможной работу алгоритма. Для этого случая требуется предусмотреть системы разгрузки маховиков, которые должны включаться по достижении маховиками  максимальных значений кинетического момента.

Дальнейшая работа заключается в нахождении алгоритма управления, оптимального с точки зрения некоторого выбранного критерия (в случае малых спутников таким критерием видится критерий оптимальности энергетических затрат) и исследование характера влияния различных возмущений на работу данного алгоритма.

Работа ведется при финансовой поддержке РФФИ (гранты № 04-01-00379, № 05-08-50148a) и программы “Университеты России”.

1. М.Ю.Овчинников. “Системы ориентации спутников: от Лагранжа до Королева”, Соросовский образовательный журнал, 1999, N12, стр. 91-96.

2. Б.В.Раушенбах, Е.Н.Токарь “Управление ориентацией космических аппаратов”, М., Наука, 1974.

3. В.А.Сарычев, С.А. Мирер, А.А. Дегтярев. “Равновесия и устойчивость спутника-гиростата с вектором гиростатического момента, параллельным главной оси инерции спутника”. Препринт ИПМ им.М.В.Келдыша РАН, М., 2004.

Лабораторный стенд для отработки способов управления ориентацией малых КА

И.Е.Зараменских¹, С.О.Карпенко², А.М.Овчинников³, А.С.Середницкий³, С.В.Фокин ³, Е.А.Цветков ¹

¹ Московский физико-технический институт

² Институт прикладной математики им. М.В.Келдыша РАН

³Московский авиационный институт им.Серго Орджоникидже

В настоящее время в ИПИ им.М.В.Келдыша РАН ведутся работы по созданию лабораторного стенда, предназначенного для моделирования динамики движения КА вокруг центра масс во внешнем магнитном поле (рис.1). Задачи, которые можно предполагается с его помощью:

- моделирование изменения внешнего магнитного поля (МПЗ) вдоль орбиты КА,

- моделирование солнца, звездного неба на орбите КА,

- полунатурное моделирование алгоритмов магнитной стабилизации с использованием как постоянных магнитов, так и токовых катушек;

- исследование алгоритмов определения ориентации КА с использованием магнитометров, звездного датчика, солнечных датчиков;

- отработка комбинированных систем стабилизации, использующих в качестве элементов управления магнитные катушки и маховики,

- наземная отработка бортовых программных алгоритмов управления ориентацией малого КА

В состав стенда входят:

- катушки Гельмгольца, предназначенные для моделирования внешнего магнитного поля (МПЗ), с собственной системой управления;

- макет космического аппарата, подвешенный на струне (нити) и помещенный внутри поля, создаваемого катушками.

Основа стенда – шесть попарно соединенных магнитных катушек, имитирующих внешнее по отношению к макету КА магнитное поле. Система управления катушками состоит из обычного ПК, моделирующего заданный закон изменения магнитного момента катушек, и устройства, преобразующего управляющее воздействие в ток для каждой из катушек.

Макет также снабжен тремя катушками, управляемыми бортовым компьютером по заданному алгоритму. Благодаря взаимодействию магнитных полей внешних катушек и макета создается механический момент, вращающий спутник вокруг центра масс. Исследование этого движения и представляет интерес в первую очередь.

Определение ориентации макета в пространстве ведется с использованием датчиков положения. В самом простом случае это магнитометр, а при условии имитации солнечной засветки и звездного неба – солнечным датчиком и звездной камерой.

В настоящее время собраны, управляются и готовы к эксплуатации магнитные катушки и управляющее программное обеспечение (ПО) для них. Ведется разработка макета КА и ПО для управления бортовыми магнитными катушками.

Рис.1. Лабораторный стенд для моделирования углового управляемого движения макета наноспутника

Тестирование точности магнитной стабилизации малых спутников

А.Ю.Андреев, С.С.Лемак, Э.МореноАльварез

Московский государственный университет им.М.В.Ломоносова

При разработке новых спутниковых систем часто встречается ситуация, когда стоимость работ по стендовым испытаниям (тестированию) системы управления спутником сравнима со стоимостью самого спутника. Особенно это характерно для малых спутников, которые в последнее время получают все большее распространение. В некоторой мере с данной проблемой можно справиться с помощью компьютерной системы тестирования. Тестирование основано на решении ряда экстремальных задач и позволяет получить оценку качества алгоритмов стабилизации без использования дорогих стендовых испытаний. Стратегия тестирования сводится к поиску наихудшей точки на прямом произведении множества начальных возмущений и множества постоянно действующих возмущений (гравитационных, магнитных, аэродинамических и т.п.) в результате решения дифференциальной игры с дискриминацией одного из игроков [1,2]. Дискриминация состоит в том, что система тестирования обладает информацией о действиях тестируемой системы стабилизации (но система не знает, по каким правилам и алгоритмам формируются эти действия). В этом случае, как было показано Н.Н.Красовским [3], существует седловая точка дифференциальной игры.

Процедура тестирования состоит из трех этапов. На первом, предварительном этапе находятся оптимальные стратегия, контрстратегия и цена дифференциальной игры. На втором, основном этапе реализуется тестирование, при котором на текущие действия тестируемой системы управления имитаторы внутренней и внешней среды вырабатывают контрстратегию, что позволяет вычислить результат тестирования. На третьем, заключительном этапе этот результат сравнивается с ценой игры, которая представляет результат оптимального поведения тестируемого управления.

Рассмотрим решение задачи первого этапа тестирования в классе программных стратегий. Оценку качества управления будем проводить на основе анализа поведения линейной системы уравнений линейной системы в отклонениях управляемого объекта, которую запишем в виде

                  u(×)ÎU = {u(×) L₂(0,¥)Π| u(t)ΠW Ì R^s};   pΠP Ì R^r;                        (1)  

     q(×)ÎV={q(×)ÎKC | q(t)ÎQ Ì R^m},  x(t₀) Î R₀ Ì Rⁿ.

Здесь x(t) — n-мерный вектор отклонений от заданной траектории, p — r-мерная вектор-функция параметрических возмущений, u(×)ÎL₂(0,¥) — s-мерная вектор-функция стабилизирующих управлений, q(t) — постоянно действующие возмущения, x(t₀)ÎR₀ — множество начальных отклонений.

Точность стабилизации определим  функционалом

                                                                                               (2)

где матрица  постоянна, симметрична и положительно полуопределена.  Моменты времени ,  фиксированы.

Тестирование качества работы некоторого автоматического (либо полуавтоматического) алгоритма стабилизации  заключается в сравнение показателя (функционала) точности стабилизации (вычисленного при работе тестируемого алгоритма  и некоторой "оптимальной" контрстратегии w⁰ поведения возмущений) с нижней оценкой показателя точности , полученной в результате решения максиминной задачи

                                                                                     (3)

где w={x₀, p, q} — совокупность начальных возмущений, параметрических возмущений и постоянно дейcтвующих возмущений q(t), а W=R₀´P´V. Пусть S=S³0 — диагональная матрица с одной, двумя или k£n единицами на диагонали. Будем рассматривать случай, когда в дифференциальной игре имеет место седловая точка [3] и существует цена игры. Предлагаемый алгоритм поиска седловой точки использует эквивалентность исходной динамической игры и некоторой геометрической игры на множествах достижимости системы (1). Необходимые и достаточные условия существования седловой точки в геометрической игре получены в работе [4].

Рассмотрим решение задачи на примере тестирования  тангажных колебаний  малого спутника с активной магнитной системой стабилизации, движущегося по круговой орбите. Магнитное поле Земли задано косым диполем,  направленным под углом  к оси вращения Земли. Обозначим  - проекции единичного вектора, задающего это направление в орбитальной системе  координат. Проекции полного вектора магнитной индукции  на оси  равны

                                 ,

где  - возмущения магнитного поля Земли. Обозначим  - безразмерное время, - круговая частота, -  -главные моменты инерции, - угловая скорость вращения Земли, . Будем считать, что на спутнике установлена одна рамка с током, магнитный момент которой составляет с осью с осью  связанной системы  угол . Вектор магнитного момента ,- магнитный параметр. В безразмерном виде уравнения тангажных колебаний имеют вид

                           ,                       (4)

где , , , , , . Для спутника "Satex" , , "Университетский" , . Обозначив , , , уравнение (4) перепишем в виде (1), где u={1,0,-1}. Рассмотрим структуру алгоритма стабилизации , который будет протестирован. Синтез системы стабилизации осуществим в результате решения задачи быстрейшего перевода  системы (4) в начало координат:

Закон управления можно реализовать, если известна информация о . Ее можно построить по измерениям магнитного поля Земли. Пусть на борту имеется трехкомпонентный датчик магнитного поля, оси чувствительности которого параллельны осям . Следовательно, измеряются величины  , i=1,2,3 где  - вектор инструментальных погрешностей. Для простоты будем считать его белым шумом с матрицей интенсивности . Немоделируемые компоненты магнитного поля  тоже будем считать белым шумом  с матрицей интенсивности . Пусть на борту имеется информация о положении центра масс. Тогда можно для системы (4) построить вектор измерений

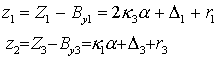                                                                             (5)

где  — белый шум.

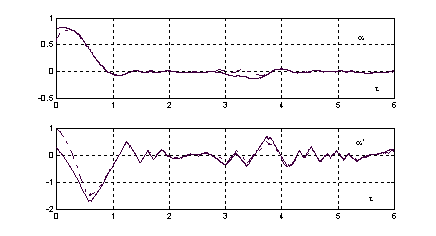
Рис. 1

Если в момент времени  поступило измерение, с помощью дискретного фильтра Калмана можно осуществить коррекцию оценки и ее прогноз  на отрезке . Управление  строится по оценке, т.е. . На рис.1 представлены результаты математического моделирования процесса стабилизации для спутника «Университетский» при интенсивности относительных возмущения магнитного поля  , инструментальных погрешностей магнитометра . Прерывистыми линиями показаны оценки угла тангажа и его производной. На рис.2  представлены множества достижимости  системы по управлению (5) и  для системы по возмущению (4) в момент времени

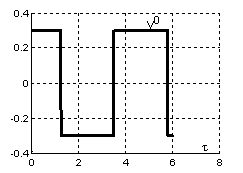
                         Рис. 2                                                  Рис. 3

Показана работа алгоритма поиска седловой точки. Пара (M,N) составляет седловую точку  игровой задачи первого этапа тестирования. Максимальная величина возмущения  составляет 30% от величины магнитного моля Земли, а начальные условия системы (4)  На рис. 3 изображено наихудшее поведение возмущения , использующееся для тестирования алгоритмов стабилизации на втором этапе.

Работа ведется при финансовой поддержке РФФИ (гранты № 04-01-00379, № 05-08-50148a) и программы “Университеты России”

1.     В.В.Александров и др. Оптимизация динамики управляемых систем. Изд-во МГУ, 2000, 304с.

2.     Александров В.В., Воронин Л.И., Лемак С.С. и др. Тестирование качества визуальной стабилизации космических объектов на динамическом стенде с трехуровневой системой управления. // Теоретические основы кибернетики, вып.10. – М.: Физматлит, 2001.

3.     Красовский Н.Н. Управление динамической системой. – М.: Наука, 1985

4.     Александров В.В., В.В.,Блаженнова-Микулич Л.Ю. и др. Максиминное тестирование точности стабилизации и седловые точки в геометрии-ческих играх // Вестник МГУ, сер.: мат. и мех., 2004, № 4.

Определение ориентации космических аппаратов,
оборудованных лазерными ретрорефлекторами,
 по результатам внешнетраекторных измерений

Р.Б.Немучинский

Институт прикладной математики им.М.В.Келдыша РАН

Одним из возможных подходов к решению актуальной задача определения ориентации космического аппарата по результатам внешнетраекторных измерений является установка на КА лазерных ретрорефлекторов. При движении КА по орбите ретрорефлекторы подсвечиваются лазером со станции слежения, и по времени прохождения луча в обе стороны определяется расстояние от станции слежения до рефлектора. Зная заранее определенную орбиту КА, можно вычислить разность расстояний от станции слежения до центра масс и от станции до рефлектора[1]. То есть, учитывая малость угла между этими направлениями, фактически вычисляется проекция радиус-вектора рефлектора относительно центра масс КА на направление на станцию слежения. Определим ориентацию КА, исходя из этих данных.

Введем связанную с Землей систему координат O_aY₁Y₂Y₃. O_a — центр масс Земли, плоскость O_aY₁Y₂ совпадает с плоскостью орбиты КА, а в плоскости O_aY₁Y₃ лежит станция слежения. OX₁X₂X₃ — орбитальная система координат. O — центр масс КА, ось OX₃ направлена вдоль местной вертикали, OX₁ совпадает с трансверсалью, OX₂ — с нормалью к плоскости орбиты. Ox₁x₂x₃ — произвольная связанная с КА система координат (рис. 1).

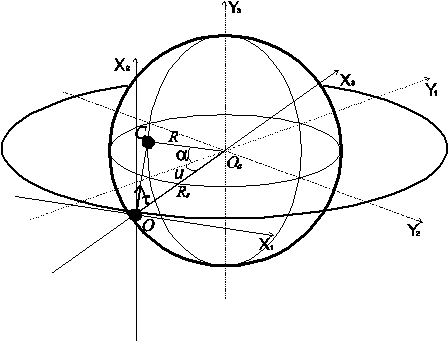
Рис. 1: Системы координат

Вычислим выражения для результатов внешнетраекторных измерений. Пусть a — угол между плоскостью орбиты и направлением от центра масс Земли на станцию слежения, u — аргумент широты КА, отсчитываемый от отрицательного направления оси O_aY₁ (рис.1). Тогда матрица перехода от O_aY₁Y₂Y₃ к OX₁X₂X₃ определяется выражением

_,

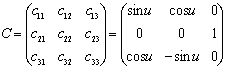а матрица перехода от OX₁X₂X₃ к Ox₁x₂x₃ —

_,

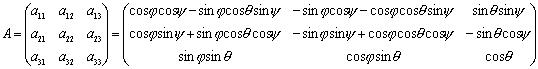где j, q, y — углы Эйлера (прецессии, нутации и собственного вращения соответственно).

В результате измерения получаем значение выражений (t,r_i), где r — единичный вектор, направленный от КА к станции слежения, а r _i(i=1,2,...,n) — радиус-векторы ретрорефлекторов относительно центра масс КА,

^t

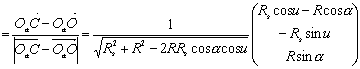
В последнем выражении R — радиус Земли, R_s — расстояние от КА до центра масс Земли, а C — точка, в которой находится станция слежения. Вектор t задан в системе координат O_aY₁Y₂Y₃. В случае если векторы r_i выражены в наиболее естественной для них связанной системе координат, то указанные выражения для измерений будут иметь вид (t,r_i)= r_i^TAC t = r_i^Tt_x=d_i, где t_x — вектор t в системе координат Ox₁x₂x₃, d_i — полученный результат измерения для i-ого рефлектора.

Таким образом, для определения ориентации имеем набор линейных уравнений

r_i^Tt_x=d_i.                                                                                                                (1)

Если на КА установлено три ретрорефлектора так, что их радиус-векторы относительно центра масс не компланарны, то можно решить уравнения (1) и найти t_x, что даст возможность определить ориентацию с точностью до поворота вокруг вектора t. Если же есть дополнительные измерения, например, рефлекторы возвращают поляризованный свет и можно определить его поляризацию или КА наблюдается одновременно с двух станций слежения, то ориентация определяется однозначно. Отсюда становится понятно, что установленные сверх трех рефлекторы не дают никакой дополнительной информации, а напротив только запутывают общую картину наблюдений, в особенности в том случае, когда отражения, полученные от разных рефлекторов, неразличимы между собой.

Точно так же в качестве r_i можно брать радиус-векторы не относительно центра масс, а относительно любой другой точки — например, относительно четвертого рефлектора, если он не лежит в одной плоскости с тремя другими. В этом случае не надо вычислять орбиту и положение центра масс КА.

Обратимся к произвольному случаю. В результате единичного измерения получаем проекцию вектора, принадлежащего некоторому заданному векторному полю (в данном случае полю направлений на станцию слежения) на некоторое направление, заданное в связанной системе координат. Исследователи уделяли внимание этой задаче для случая, когда векторное поле является магнитным полем Земли, а в качестве измерителей используются магнитометры. В случае же, когда не известно соответствие между d_i и r_i,, решение задачи требует перебора соответствий и выбора наиболее подходящего из них.

Малые космические аппараты для решения научных и образовательных радиофизических задач

В.М.Шахпаронов

Московский государственный университет им.М.В.Ломоносова

Рассматриваются задачи космической радиофизики и применение к ним малых космических аппаратов, которое не только стало возможным, но и непрерывно расширяется в связи с совершенствованием микрорадиоэлектронной и микроэлектромеханической элементной базы.

1.     Введение

Быстро развивающиеся микроэлектроника и микроэлектромеханика создают условия для миниатюризации элементной базы, что в свою очередь позволяет создавать малогабаритную радиоэлектронную аппаратуру для размещения на борту малых и сверхмалых космических аппаратов. Производством на сегодняшний день успешно осваивается уже 0,09-микронная технология. Для таких устройств характерны не только малые масса и габариты, но и  весьма невысокое энергопотребление при низких питающих напряжениях, при этом коэффициент полезного действия достаточно высок. Таким образом, возрастают возможности малых космических аппаратов в целом и для проведения радиофизических исследований в частности.

2.     Основные направления

В радиофизике рассматриваются задачи связанные с физическими основами радиотехники и электроники. В свою очередь, радиотехника решает задачи передачи и приёма информации при помощи радиоволн и связанные с этим вопросы, а в электронике, в частности, разрабатываются устройства, предназначенные для генерации, формирования и преобразования электрических сигналов.  Вполне очевидно, что приведённая классификация более чем условна. Тем не менее, совершенно очевидно, что при разработке, изготовлении и эксплуатации космических аппаратов значительное внимание приходится уделять решению радиофизических задач.

Радиофизические задачи, опять же условно, можно разделить на два направления: исследования, направленные на применение радиофизических методов и аппаратуры для космического пространства, Земли из космоса, а также других планет, и исследования, направленные на совершенствование и развитие собственно самих радиофизических методов и аппаратуры.

В первом случае речь идёт, например, о задачах, связанных с изучением распространения радиоволн различных диапазонов на трассе Земля-спутник и спутник-спутник и получении информации о процессах в космическом пространстве или о том, как процессы, происходящие внутри или на поверхности планеты, могут быть зарегистрированы с орбиты космического аппарата. На самом деле круг задач, решаемых космической радиофизикой в этом направлении достаточно широк, от излучения радиоизлучения Солнца и других космических объектов, до приёма информации, поступающей с космических аппаратов и передачи управляющих сигналов на борт КА. Для решения всех этих задач специально предусмотрены и распределены соответствующие полосы частот в каждом диапазоне ультракоротких радиоволн.

Во втором случае исследуются собственно процессы передачи и приёма информации, её преобразования, хранения и отображения. Здесь рассмотрение затрагивает собственно процессы управления спектром сигнала и элементную базу бортовой и наземной аппаратуры. Цель этих исследований разработка и создание методов надёжного переноса информации по радиоканалу, повышение скорости информационного обмена, уменьшение массогабаритных показателей элементной базы, а следовательно, и самой аппаратуры, улучшение экономических показателей.

3.     Применение малых космических аппаратов

Малые КА (масса не превышает сотни килограмм) разрабатывались и строились, начиная с самых первых запусков искусственных спутников Земли. Однако, элементная база радиоэлектроники 60-80-х годов сдерживала развитие этого направления. В настоящее время число запусков малых космических аппаратов учебного и учебно-научного назначения в год превысило полтора десятка и тенденции к его сокращению не предвидится. Совершенно очевидно, что здесь не последнюю роль играют экономические показатели: значительно меньший расход материалов на конструкцию самого КА, снижение и в некоторых случаях даже весьма ощутимое трудозатрат на разработку, изготовление и транспортировку к месту запуска. Существенно меньшая стоимость запуска таких КА, так как запуск производится попутным или групповым способом и не требует специальных носителей.

Безусловно, весь круг задач, решаемых в космосе, переложить на малые КА по вполне понятным причинам невозможно, да и нет необходимости, однако, задачи учебно-научного направления совместно с отработкой значительного количества частных исследовательских задач успешно решаются малыми КА. Развитие космических навигационных методов и методов решения баллистических задач, а также создание малогабаритной навигационной аппаратуры позволяют определить местоположение, скорость, характеристики орбиты для малых космических аппаратов, а это, в свою очередь, позволяет решать радиофизические задачи по исследованию Земли и космического пространства: распространение радиоволн по трассе спутник-Земля и спутник-спутник, исследование процессов, происходящих в ионосфере методами радоспектроскопии, исследование атмосферы, поверхности Земли, планет и глубинных процессов в них в радиодиапазоне. С другой стороны, развитие микроэлектромеханики совместно с микроэлектроникой, конечно, позволило значительно снизить массогабаритные характеристики как датчиков (микрогироскопов, микроакселерометров, солнечных и звёздных датчиков, ИК-горизонтов), так и исполнительных устройств (например, управляющих двигателей-маховиков), и обеспечивающих их взаимодействие бортовых вычислителей для систем точной ориентации и стабилизации малых КА.

Высокоточные системы ориентации и стабилизации малых КА позволяют, в свою очередь, воспользоваться узконаправленными антеннами и перейти в гигагерцовый диапазон как для организации высокоскоростных каналов передачи информации, так и для мониторинга Земли, атмосферы, космического пространства и Солнца в диапазоне СВЧ.

4.     Элементная база

Современная твердотельная микроэлектронная технология позволяет разместить на подложке площадью порядка одного квадратного сантиметра несколько миллионов транзисторов, работающих на частотах в единицы гигагерц. Лабораторные образцы усилителей на биполярных и полевых кремниевых транзисторах успешно работают на частотах превышающих сотню гигагерц. Успешно осваивается терагерцовый диапазон. Современные интегральные технологии позволяют объединять радиосхемы, схемы аналоговой и цифровой электроники в корпусе одного устройства, что переводит возможности аппаратуры на качественно иной, более высокий уровень.

Вопрос радиационной стойкости радоэлектронных и микромеханических компонент по прежнему актуален. Это обусловлено прежде всего тем, что для бортовой аппаратуры малых КА особенно научно-учебного назначения применяются широко распространённые, легко доступные электрорадиоизделия в обычном промышленном исполнении. Для проведения исследований в этой области малые космические аппараты используются достаточно широко. Здесь важно совмещение измерения радиационной обстановки на борту КА и исследования устойчивости работы бортовых систем, их элементной базы и деградационных процессов в них, вызванных влиянием космической среды и времени.

5.     Выводы

Малые космические аппараты волне пригодны для решения задач космической радиофизики и в первую очередь научно-учебных задач. Сравнительно невысокие затраты на производство и запуск делают малые КА доступными для ВУЗов, а микроэлектронная и микроэлектромеханическая элементная база позволяет решать широкий спектр исследовательских радиофизических задач и непосредственно примыкающих к ним образовательных задач.

Использование данных системы NORAD для определения относительного движения МКС и наноспутника ТНС-0

С.С.Ткачев

Московский физико-технический институт

Получить информацию о местоположении спутника можно различными способами. Один из них заключается в использовании данных системы NORAD, представляющих собой наборы двустрочных элементов по различным спутникам. Эти данные доступны пользователям через Интернете (www.space-track.org). Здесь можно найти информацию по запущенным спутникам, начиная с 1957 года. Эти данные, например для Международной космической станции (МКС), выглядят следующим образом:

Параметры, включенные в эту таблицу, являются средними по определенному интервалу времени и получены с помощью исключения различных периодических отклонений особым образом. Именно поэтому для построения движения по этим данным следует пользоваться специальными моделями, например, SGP4 (Simplified General Perturbations 4). Описание этой модели можно также найти на сайте www.space-track.org. Все объекты классифицируются NORAD’ом как околоземные (с периодом меньше 225 минут) или как дальние космические объекты (с периодом больше 225 минут). В зависимости от этого используются различные модели (SGP4 используется для околоземных объектов).

Кроме движения в абсолютном пространстве, необходимо бывает получать так же и относительное движение аппаратов. Такого рода задачи могут возникать при определении точности аналитических моделей относительного движения, например, для Formation Flying. В настоящей работе рассмотрено относительное движение МКС и первого российского наноспутника ТНС-0, выведенного на орбиту с ее борта 28-го марта 2005 года российским космонавтом С.Шариповым, который, стоя на внешней стороне МКС, оттолкнул спутник рукой.

Движение рассматривается в системе координат, связанной с МКС. В работе описывается методика построения такого движения и производится сравнение полученного ранее аналитически при наличии аэродинамического сопротивления относительного движения ТНС-0 и МКС с этим движением. С помощью статистической обработки данных получены относительные начальные условия, с которыми был запущен спутник, и которые не представляется возможным измерить при запуске. На рис.1 изображено относительно движение с этими начальными условиями. Сплошной линией обозначено движение, вычисленное по данным системы NORAD, а пунктирной движение, полученное аналитически. Ось ОХ направлена по вектору скорости станции, OY – перпендикулярно плоскости орбиты, а OZ – по радиус-вектору МКС.

Работа поддержана РФФИ и Роснаукой (Гос.контракт N 02.434.11.7061), а также Программой поддержки ведущих научных школ России.

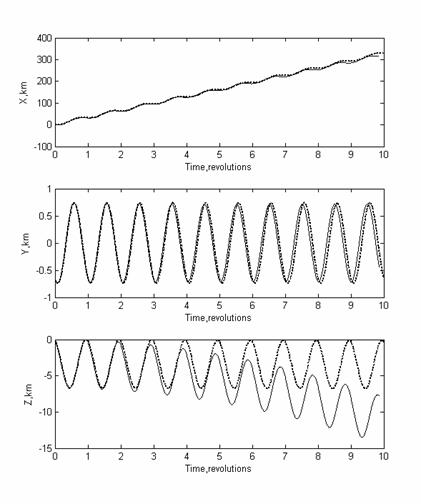
Рис.1. График зависимости относительного расстояния ТНС-0 и МКС по оси X, по оси Z и по оси Y по данным системы NORAD. Сплошная линия – реальное движение, а пунктирная – движение, полученное аналитически

Система дистанционного гиперспектрального зондирования Земли на базе микроспутника

А.М.Овчинников

Институт прикладной математики им.М.В.Келдыша РАН, Москва

Одним из наиболее перспективных направлений для предсказания различного вида катастроф, разведки природных ископаемых и других задач, решаемых в рамках систем дистанционного зондирования Земли, являются гиперспектральные системы.

Для работы системы дистанционного зондирования Земли в настоящее время используют спутники, которые трудно назвать малыми. Достаточно вспомнить «Ресурс-О1» (Россия); «NOAA», «Hyperion» и спутники серии «LandSat» (США), серию французских «SPOT». Это спутники - размером в несколько метров, массой в сотни килограмм и энергетическим потенциалом в несколько киловатт. Разработка, производство и вывод на орбиту подобных аппаратов доступна только крупным конгломератам компаний, обладающих крупными финансовыми, людскими и политическими потенциалами. Разработка же микроспутника в настоящее время доступна небольшим компаниям и университетам.

В Институте прикладной математики им.М.В.Келдыша РАН создается лабораторный макет гиперспектральной системы. В дальнейшем предполагается адаптировать его к экспериментальному микроспутнику. Принципиальным отличием этой системы от уже созданных и успешно работающих, является то, что эта система создается не из специализированных и высокопрецизионных компонентов, а из относительно недорогих коммерческих компонент (COTS – Components-Off-The-Shelf). Ставка делается на уменьшение не только цены, но и габаритов, массы и энергопотребления.

Разрабатываемая для определения очагов возгораний и распознавания горящих веществ система состоит из трех каналов: инфракрасного, гиперспектрального и видеоканала. Инфракрасный канал, представленный инфракрасной камерой служит для определения очага пожара. Гиперспектральная камера разработана для получения спектральной характеристики горящего вещества, что позволяет определить и предсказать возможный район распространения огня, выбрать технологию и средства для тушения пожара, а также при сопоставлении данных инфракрасной и гиперспектральной камер, предсказать зону возможного возникновения пожара. Видеокамера предназначена для «привязки» зоны съемки к карте местности при обработке данных. Данные со всех трех каналов поступают в бортовую вычислительную систему, где проводится обработка информации и подготовка для передачи на Землю.

Движение быстро вращающегося спутника с постоянным магнитом

А.А.Ильин

Институт прикладной математики им.М.В.Келдыша РАН

Рассматриваемая в работе задача возникла из задачи определения вращательного движения и анализа динамики спутника ТНС-0 по результатам летных испытаний. Первый российский наноспутник ТНС-0 был успешно запущен в марте 2005 года с борта Международной космической станции. Цель запуска спутника — проведение экспериментов по проверке технологии управления космическими аппаратами через глобальную систему связи GLOBALSTAR или ей подобную.

Спутник ТНС-0 был оснащен пассивной магнитной системой ориентации, состоящей из сильного постоянного магнита и набора гистерезисных стержней. С помощью такой системы предполагалось обеспечить отслеживание осью симметрии спутника вектора индукции магнитного поля. Однако когда спутник выводили на орбиту, ему предали большой вращательный момент. Так, вопреки ожиданиям спутник ТНС-0 оказался быстровращающимся телом, взаимодействующим с геомагнитным полем.

Для получения информации о вращательном движении на спутнике было установлено несколько простейших солнечных датчиков и датчик горизонта. Первоначально в каждый сеанс связи спутник передавал измерения датчиков за несколько минут. Анализ измерений показал, что скорость вращения спутника уменьшается согласно тому, как и должно затухать вращение спутника, оснащенного гистерезисными стержнями. После нескольких таких сеансов спутник был «усыплен» на длительное время, чтобы не тратить энергию батарей.

Когда спутник был «разбужен», то ему были переданы команды на изменение режима проведения измерений. Это позволило получить измерения датчиков за один виток. Как показал анализ этих измерений, спутник возможно вышел следующий режим, когда при достаточно быстром вращении спутника осредненное по периоду нутации направление магнита в среднем отслеживает вектор индукции геомагнитного поля. При этом угол между вектором индукции магнитного поля и осью симметрии составляет примерно 45 градусов.

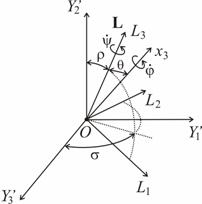
Было проведено аналитическое исследование такого режима. Для описания динамики спутника использовались уравнения вращательного движения в переменных Белецкого-Черноусько. Это следующие переменные: величина кинетического момента , углы  и , задающие направление вектора кинетического момента в инерциальном пространстве (в системе координат ) и углы Эйлера ,  и , задающие ориентацию связанной со спутником системы координат  относительно системы координат, связанной с направлением кинетического момента , как это изображено на рис.1.

Кратко охарактеризуем математическую модель рассматриваемого в работе спутника. Спутник ТНС-0 является осесимметричным твердым телом. По оси симметрии спутника расположен сильный постоянный магнит. В экваториальной плоскости магнита расположены гистерезисные стержни по двум взаимо ортогональным направлениям.

В работе будем использовать осредненную модель геомагнитного поля. Согласно этой модели вектор индукции магнитного поля заметает круговой конус с углом при вершине 2, оставаясь постоянным по величине. Угол  определяется наклонением орбиты спутника. Для начала рассмотрим движение спутника только с постоянным магнитом.

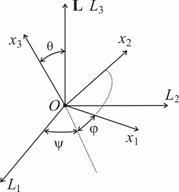
(а)                                                                     (б)

Рис.1. Задание ориентации связанной со спутником системы координат  с использованием переменных Белецкого-Черноусько. (а) ‑ углы  и , задающие направление вектора кинетического момента спутника в инерциальном пространстве и связанная с ним система координат ; (б) ‑ углы Эйлера ,  и , задающие ориентацию связанной со спутником системы координат  относительно

В безразмерных уравнениях переменные, описывающие вращение спутника, можно разделить на быстрые и медленные. Быстрой переменной является угол . Медленными переменными являлись:  (безразмерный кинетический момент), , , . Осредненные по быстрой переменной уравнения движения принимают вид

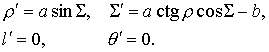                                    (1)

где ,  ‑ угол определяющий положение вектора индукции  на соответствующем конусе,  и  ‑ коэффициенты:

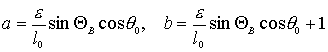.                            (2)

 ‑ безразмерный параметр. Такая система допускает интеграл движения

,

который используется в этой работе для построения функций Ляпунова при доказательстве устойчивости решений.

Уравнения (1) имеют две стационарные точки. Первая стационарная точка  соответствует тому, что кинетический момент отслеживает вектор магнитной индукции . Вторая стационарная точка   соответствует тому, что кинетический момент отслеживает вектор . Обе стационарные точки являются устойчивыми, но не асимптотически, так как в системе отсутствует демпфирование. Поскольку угол  в данном случае может быть любым, то осредненный по прецессионному вращению дипольный момент спутника устойчиво может отслеживать как вектор , так и вектор . Заметим, что это отслеживание не точное. Существует отличный от нуля угол между вектором  (или ). Чем медленней скорость изменения магнитного поля, тем меньше этот угол. Если же считать магнитное поле постоянным, то в стационарных точках кинетический момент выставлен точно по вектору магнитной индукции  или противоположен ему.

Далее, чтобы получить асимптотическую устойчивость стационарных точек введем в систему гистерезисное демпфирование. Поскольку при этом получаются довольно громоздкие формулы, то для простоты рассмотрим систему с постоянным магнитным полем.

Следует сказать несколько слов о используемой в работе модели гистерезиса. Предположим, что дипольный момент спутника от гистерезисных стержней определяется выражением

,

где  ‑ проекция индукции магнитного поля на экваториальную плоскость спутника с запаздыванием на время Dt . Предполагая, что задержка  Dt мала, а дипольный момент постоянного магнита намного сильнее наведенного момента от гистерезисных стержней, получаем действующий на спутник механический момент в связанной системе координат как

.                                                   (4)

Исследуем на асимптотическую устойчивость стационарные точки при неизменном магнитном поле. При фиксированном угле  (если его выбрать из определенной области) существуют два асимптотически устойчивых положения кинетического момента по B и –B. Для доказательства устойчивости каждой из стационарных точек используются в качестве функций Ляпунова следующие функции (для каждой стационарной точки своя функция):

.

Рассмотрим динамику угла q  при фиксированном направлении вектора кинетического момента, которое выбирается коллинеарным вектору индукции магнитного поля. Пусть вектор кинетического момента сонаправлен вектору индукции магнитного поля. Тогда дифференциальное уравнение для угла  будет выглядеть следующим образом

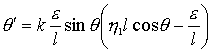.                                              (5)

Асимптотически устойчивая стационарная точка уравнения (5) будет 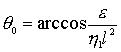. Далее пусть вектор кинетического момента направлен противоположно вектору индукции магнитного поля. Тогда дифференциальное уравнение для угла

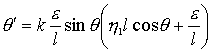.                                               (6)

Асимптотически устойчивая стационарная точка: 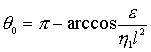. Полученные стационарные точки говорят о том, что в случае гистерезисного демпфирования существует только одно значение угла , при котором возможно стационарное вращение. Осредненный по прецессионному вращению дипольный момент спутника теперь может отслеживать только вектор , а не вектор , как это было ранее.

Анализ уравнений показывает, что при таком режиме отсутствует уменьшение кинетического момента, даже при наличии на спутнике гистерезисных стержней, Это происходит из-за того, что спутник в таком режиме вращается так, что не происходит перемагничивание гистерезисных стержней. Наличие же на спутнике гистерезисных стержней делает этот режим асимптотически устойчивым.

Работа поддержана РФФИ , Роснаукой (Гос.контракт N 02.434.11.7061) и Программой поддержки ведущих научных школ России.