Разработка и реализация алгоритмов трехмерной триангуляции сложных пространственных областей:
итерационные методы
|
|
|
|
|
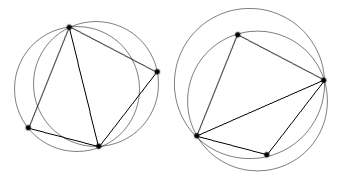
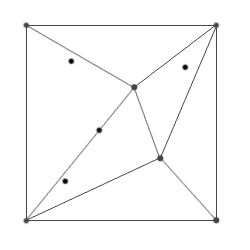
а) Заданный набор точек |
б) Постройка суперструктуры (квадрат), один
из заданных узлов используется как вершина квадрата |
|
|
|
|
в) Постройка исходной триангуляции Делоне.
Т.к. квадрат является правильным многоугольником, для этого можно
использовать любой из заданных узлов |
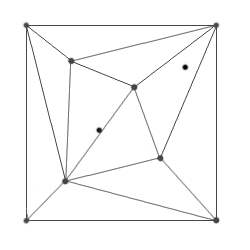
г) Выбор нового (произвольного) узла и
удаление всех треугольников, для которых выбранный узел лежит внутри
описанной окружности |
|
|
|
|
д) Соединение ребрами новой вершины с
углами образовавшегося многоугольника |
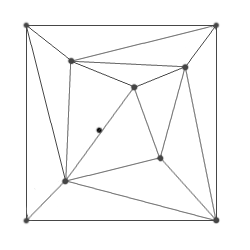
е) Выбор следующего узла и дальнейшее
повторение процедуры, пока не останется неиспользованных заданных узлов |
|
|
|
|
ж) Обработка еще одной точки |
з) Еще одной |
|
|
|
|
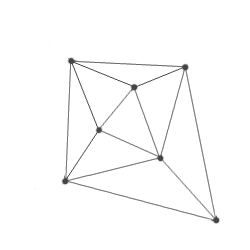
и) Сетка построена |
к) Удаление из сетки всех треугольников,
среди вершин которых были вспомогательные узлы суперструктуры |
Рис. 8. Двумерный вариант алгоритма на основе
критерия Делоне
Описанный алгоритм
позволяет гарантированно строить триангуляцию Делоне для произвольного набора
точек, причем граница сетки будет представлять собой (в общем случае
невыпуклый) многогранник с треугольными гранями, опирающимися на наиболее
удаленные от центра триангуляции узлы. К сожалению, на практике приходится
иметь дело с областями, представляют собой более сложные геометрические формы.
В принципе, описанный
алгоритм можно использовать для любой области, если в качестве входных данных
передавать не только набор точек, но и некую грубую начальную триангуляцию
Делоне заданной области (то есть сразу перейти к п. 5). С другой стороны, если
такая триангуляция уже есть, то проще получить итоговую сетку методами
дробления - измельчив имеющиеся тетраэдры до нужных размеров, что будет гораздо
быстрее и с учетом последующей минимальной оптимизации обеспечит примерно такое
же качество. Поэтому такой вариант может быть использован, только если
необходимо обеспечить локальное сгущение сетки в нужных местах области (т.к.
сетки, полученные методами дробления, являются равномерными). При этом остается
вопрос о построении начальной грубой сетки, что само по себе является отдельной
задачей. Именно поэтому куда большее значение имеет задача построения
триангуляции Делоне с ограничениями
3.2. Триангуляции Делоне с
ограничениями
Триангуляцией Делоне с ограничениями в виде поверхностей называют такую сетку, для которой
внутрь сферы, описанной вокруг любого тетраэдра этой сетки, не попадают никакие
другие видимые вершинам этого
тетраэдра узлы сетки (считается, что точка а видима точке b (и
наоборот), если отрезок [a,b] не пересекает никаких поверхностей
ограничений). Что такое триангуляция Делоне с ограничениями, если ограничения
представлены в том числе и отрезками, до сих пор общепринятого определения нет.
В двумерном случае
проблема построения триангуляции Делоне с ограничениями давно и успешно решена,
причем самыми разными способами [3]. Что касается трех измерений, то к
настоящему времени разработано лишь несколько алгоритмов, и все они базируются
на одном и том же принципе. Их идея заключается в том, чтобы сначала в заданной
области построить триангуляцию Делоне без
ограничений, а затем восстановить поверхности и линии ограничений путем
локальной перестройки сетки. Различие между алгоритмами состоит как раз в том,
как именно осуществляется эта перестройка [5, 6, 24, 25].
Рассмотрим один из
вариантов такого алгоритма, основанный на идее
К. Хэзлвуд (Carol Hazlewood). В своей работе [21] она доказала, что возможно построить
триангуляцию Делоне с ограничениями, ретриангулируя (только) те тетраэдры,
которые пересекаются поверхностями ограничений. В статье Хэзлвуд этот факт
доказывается для случая пересечения тетраэдра произвольным выпуклым
многогранником. Для ясности упростим алгоритм, введя дополнительные несложные
требования к входным данным. А именно, потребуем, чтобы поверхности ограничения
были представлены либо плоскостями, либо слабо изогнутыми (радиус кривизны
много больше линейных размеров элементов) сплайнами, а также, чтобы все угловые
точки поверхностей ограничения использовались на первом этапе для построения
триангуляции Делоне. В результате все тетраэдры построенной триангуляции могут
пересекаться только либо "ребрами" поверхностей ограничений, либо
самими поверхностями. Поскольку вариантов таких пересечений немного, для
каждого из них можно использовать заранее подготовленный шаблон ретриангуляции.
Процесс можно упростить еще больше, если предварительно добиться, чтобы все
ребра ограничений были аппроксимированы цепочкой ребер триангуляции. Тогда
тетраэдры смогут быть пересечены только плоскостями (сплайнами), а возможных вариантов
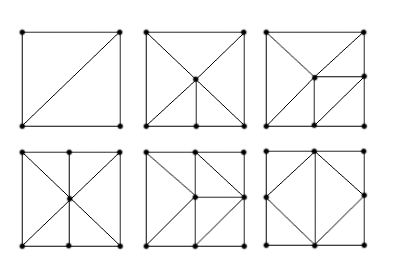
такого пересечения всего ТРИ (рис. 9).
Таким образом, алгоритм
можно разбить на четыре этапа:
1) построение
триангуляции Делоне без ограничений;
2) восстановление
"ребер" ограничений ("edge recovery");
3) восстановление
поверхностей ограничений ("face recovery");
4) отсечение
"лишних" тетраэдров, оказавшихся вне границы заданной области ("trimming").

Рис. 9. Три возможных варианта пересечения тетраэдра
плоскостью и соответствующие способы разбиения образующихся частей на
тетраэдры: а) плоскость не пересекает вершины; б) плоскость пересекает две
вершины; в) плоскость пересекает только одну вершину.
Подробнее остановимся на
каждом этапе.
Этап 1. Несмотря на
кажущуюся простоту, этот этап имеет несколько важных нюансов. Во-первых, как
уже было сказано, все "углы" поверхностей ограничения (включая концы
"незакрепленных" "ребер"), должны в обязательном порядке
войти в набор узлов, по которым строится триангуляция. Во-вторых, поскольку
многогранник, получающийся при использовании описанного выше алгоритма, не
обязательно будет выпуклым, вполне возможна ситуация, при которой некоторые
участки поверхностей ограничений окажутся вне этого многогранника. Чтобы не
допустить этого, можно использовать слой дополнительных узлов, окружающий
заданную область. На 4 этапе все тетраэдры, образованные с этими узлами,
удаляются наряду с остальными тетраэдрами, оказавшимися "по ту сторону
границы".
Этап 2. Восстановление
"ребер" производится с помощью дополнительных узлов[4].
Заметим, что если в двумерном случае всегда возможно построить триангуляцию
Делоне с ограничениями без использования дополнительных узлов, то в трехмерном
случае это, как правило, невозможно.
Дополнительные узлы
вставляются в точки пересечений "ребер" ограничений с гранями и
ребрами тетраэдров. Заметим, что вариантов пересечения "ребра" с
тетраэдром всего шесть (рис. 10). Соответственно, для каждого варианта
используется свой шаблон разбиения тетраэдра. При этом встает вопрос
согласования триангуляции на гранях соседних тетраэдров, поскольку некоторые
случаи (рис. 10. в) допускают различные способы разбиения граней. Это проблема
решается установкой следующих двух правил: 1) из всех вариантов всегда
выбирается самое короткое ребро; 2) если ребра равны, проводится ребро от узла
с самым меньшим глобальным номером (например).
Вспомним, что тетраэдр
может пересекаться не одним "ребром", а сразу несколькими. Чтобы
избежать ввода дополнительных шаблонов (поскольку, теоретически,
"ребер", пересекающих тетраэдр, может быть неограниченно много),
достаточно обрабатывать каждое "ребро" отдельно, по очереди. При
обработке каждого "ребра" остальные, еще не обработанные, не
учитываются, а после обработки "ребро" уже аппроксимировано цепочкой
ребер триангуляции и естественным образом входит в сетку, поэтому указанная
проблема исчезает.
Этап 3. На предыдущем
этапе все "ребра" ограничений были аппроксимированы цепочками ребер
сетки. Теперь нужно добиться того, чтобы все поверхности ограничений были
представлены множеством смежных граней. Это также осуществляется вставкой
дополнительных вершин - в точках пересечения поверхностей ограничения с ребрами
сетки (см. рис. 9). Опять встает вопрос об однозначности разбиения граней, но
теперь он несколько сложнее. В случае, если поверхность пересекает 3 ребра
тетраэдра (рис. 9. а), то возможен такой вариант проведения ребер, при котором
нижняя часть элемента - пятигранник (усеченный тетраэдр) - не разбивается на
тетраэдры. Разрешить эту ситуацию можно с помощью дополнительного узла,
вставляемого внутрь пятигранника. Тогда согласование ребер можно осуществлять
по правилам, изложенным выше.
Этап 4. Удаление лишних
тетраэдров, лежащих вне границы заданной области, не представляет какой-либо
проблемы. Зато можно сказать, что после их удаления граница области будет
полностью аппроксимирована гранями и ребрами построенной триангуляции. То же
самое относится и к внутренним ребрам и поверхностям ограничений, если таковые
были.

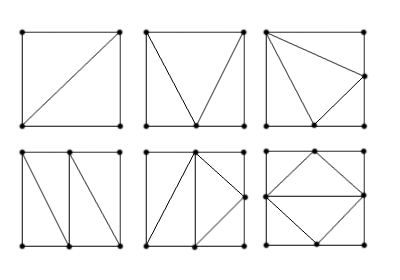
Рис. 10. Возможные варианты пересечения "ребра"ограничения с тетраэдром и соответствующие способы разбиения тетраэдра на части: а) вершина - ребро; б) вершина - грань; в) ребро - ребро; г) ребро - грань; д) ребро - вырожденный случай; е) грань - грань.
На рис. 11 представлен
результат триангуляции с помощью описанного алгоритма области, являющей собой
объединение икосаэдра и додекаэдра[5].

Рис. 11. Триангуляция области, представляющей собой объединение додекаэдра и икосаэдра (триангуляция Делоне с ограничениями)
Качество сеток,
построенных данным методом, находится на среднем уровне (тетраэдры у границ
могут иметь очень плохую форму), поэтому обычно дополнительно прибегают к
одному из методов оптимизации.
В работах Б. Джо [23, 24] предложены другие варианты алгоритма, не использующие дополнительных точек и полностью основанные на локальных трансформациях, аналогичных "трейду".
3.3. Особенности технической
реализации алгоритмов на основе критерия Делоне
Общий недостаток всех
методов на основе критерия Делоне - крайне высокая чувствительность к точности
машинных вычислений. Многие вычислительные процедуры, используемые в этих методах
(нахождение центра и радиуса описанной окружности, проверка компланарности и
коллинеарности векторов и т.п.) представляют собой плохо обусловленные задачи,
а их неизбежное интенсивное использование столь же неизбежно влечет к
накоплению ошибок округления, что в итоге может привести к ошибкам в структуре
сетки или зацикливанию алгоритма.
Типичная ошибка,
допускаемая в реализации этого класса алгоритмов, заключается в использовании
приближенных вычислений и операций, например, использование для сравнения не
нуля (x>0.0), а заданной точности (x>EPS или x>-EPS). Такой подход вполне оправдан и
верен во многих других случаях, но только не в методах на основе критерия
Делоне.
К сожалению, простое
увеличение точности не дает существенных результатов. Использование числовых
типов с удвоенной точностью перестает работать уже на задачах средней сложности
(сетки с несколькими тысячами узлов). Частичным решением этой проблемы может
быть использование числовых типов с фиксированной запятой. За счет отдельного
хранения в 24-байтной структуре целой и десятичной частей числа (в виде целых
чисел), на указанных выше плохо обусловленных задачах можно добиться точности
вплоть до 10 знака, что является уже более-менее допустимым результатом [11].
Также возможно
использование так называемой "точной арифметики", модули для
реализации которой уже разработаны для многих популярных прикладных языков
программирования (С++, Фортран и др.). В точной арифметике все иррациональные
числа представляются как набор предикатов (арифметических и алгебраических
операторов) от рациональных/целых чисел и установленных констант (таких, как ![]() ,
, ![]() и т.п.). То есть,
например, в точной арифметике
и т.п.). То есть,
например, в точной арифметике ![]() - это действительно
- это действительно
![]() , а не 1,73205080756887729...
, а не 1,73205080756887729...
Недостатком обоих
подходов является (весьма существенное) снижение скорости вычислений, так как
ни точная арифметика, ни числа с фиксированной запятой пока аппаратно не
поддерживаются процессорами современных персональных компьютеров. Поэтому все
эти операции приходится реализовывать на уровне подпрограмм, что приводит к
дополнительным затратам ресурсов.
Иной путь улучшения
ситуации - оптимизация процедур вычисления. Так, например, сотрудники
исследовательского центра IBM Павло Кавальканти и Улисс Мелло сумели создать
устойчивый алгоритм построения триангуляции Делоне, сведя все геометрические
операции к двум предикатам: проверке условия "пустой сферы" и
нахождению положения точки относительно заданной плоскости [10].
Впервые идея метода
исчерпывания была предложена Рейнальдом Лонером (R. Lohner), а его трехмерный вариант
разработал профессор Гонконгского университета С.Х. Ло. Алгоритм Ло вот уже
многие годы успешно используется в программном комплексе ANSYS для дискретизации произвольных
объемных областей.
Общая идея этого класса
методов заключается в последовательном изымании из заданной области фрагментов
тетраэдрической формы до тех пор, пока вся область не окажется
"исчерпана". Впрочем, этот легко представимый в воображении процесс
на самом деле имеет мало общего с практической реализацией. Английское название
"advancing front" (что можно перевести как "продвижение
фронта"), пожалуй, лучше отражает сущность алгоритмов.
Отправной точкой всех
алгоритмов этого класса является некая триангуляция границы заданной области,
причем не грубая, а наиболее полно соответствующая требованиям разработчика,
поскольку в дальнейшем никаких изменений этой триангуляции не будет. Заметим,
что подобное требование к начальным данным может быть как положительной
стороной метода, так и отрицательной. Если никаких ограничений на границу
области не накладывается, то это приводит к необходимости ее отдельной
триангуляции, что само по себе является самостоятельной задачей. С другой
стороны, если необходимо обеспечить согласование триангуляции в сложной
области, либо же триангуляция поверхности задана изначально, то использование
метода исчерпывания будет самым удачным выбором.
Триангуляции границы
является тем самым "фронтом", упоминаемым в названии. Используя
какой-либо треугольник из фронта, можно на его основе построить тетраэдр,
причем четвертой вершиной тетраэдра может быть либо другая вершина фронта, либо
дополнительный узел, помещаемый внутрь заданной области. При изъятии
полученного тетраэдра из фронта может быть удалено от 1 (случай вставки
дополнительного узла) до 4 граней и одновременно добавлено от 1 до 3 новых
граней. Таким образом, текущий фронт дискретизации постепенно продвигается в
пространстве - откуда и само название "advancing front". Обновив данные о фронте,
можно вновь изъять тетраэдр, снова обновить фронт и так далее, пока вся область
не окажется "исчерпана".
Заметим, что процесс
исчерпывания применим как для дискретизации внутренности области, так и для
внешности (например, для дискретизации пространства вокруг модели самолета в
задаче аэродинамики, рис. 12).
Несмотря на кажущуюся
простоту идеи, реализация алгоритма исчерпывания таит в себе ряд тонкостей
(заметим, что реализация алгоритмов исчерпывания в двумерном случае намного
проще). Самый сложный момент любого алгоритма исчерпывания заключается в
проверке правильности построенного тетраэдра, ведь необходимо удостовериться,
что этот новый тетраэдр не пересекается ни с какими уже существующими. Причем
на каждой итерации алгоритма эта процедура с различными параметрами может
вызываться от 5 до 20 раз (иногда и больше). От того, каким образом реализована
эта проверка, главным образом и зависит производительность алгоритма.
Второй сложный момент является
краеугольной проблемой трехмерной дискретизации. Нередка ситуация, когда в
результате работы алгоритма образуются области, которые невозможно
дискретизировать, не используя дополнительных внутренних узлов (в плоском
случае любой многоугольник можно разбить на треугольники одними только
внутренними ребрами).
Стоит также помнить, что
во время работы алгоритма фронт может разбиться на несвязанные фрагменты.
Четвертой особенностью
алгоритмов исчерпывания является необходимость контроля над объемом и/или
линейными размерами получающихся тетраэдров. В отличие от методов на основе
критерия Делоне, в которых линейные размеры тетраэдров фактически определяются
плотностью предварительно размещаемых узлов, в методах исчерпывания размеры
тетраэдров могут значительно колебаться. Появление близко расположенных
тетраэдров с сильно различными размерами влечет дальнейшее расхождение размеров
новых тетраэдров, в результате чего обычно появляются тетраэдры плохой формы (и
низкого качества) - сильно вытянутые, приплюснутые и т.п. Чтобы не допустить
этой нежелательной тенденции, обычно используют специальную контрольную функцию
![]() , которая обозначает желаемый объем тетраэдра в данной точке
пространства (для равномерных сеток это будет константа). При этом из всех
возможных вариантов нового тетраэдра выбирается тот, чей объем ближе всех к
значению этой функции в центре тетраэдра.
, которая обозначает желаемый объем тетраэдра в данной точке
пространства (для равномерных сеток это будет константа). При этом из всех
возможных вариантов нового тетраэдра выбирается тот, чей объем ближе всех к
значению этой функции в центре тетраэдра.
Наконец, еще одна
сложность связана с выбором текущей грани фронта для построения тетраэдра. Дело
в том, что для этого весьма желательно использовать грань, вершинами которой
являются узлы с наименьшими значениями внутренних телесных углов. В то время
как вычисление планарных и двугранных углов тривиально, вычисление телесных углов представляет собой куда
более трудоемкую задачу (особенно если учесть, что каждый телесный угол в
данном случае может быть сформирован различным числом граней) [27, 28, 29, 30,
34].
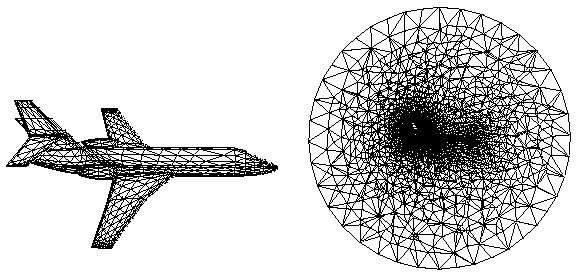
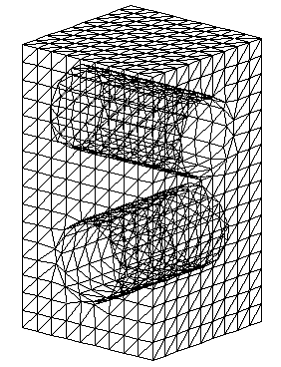
Рис. 12. Триангуляция пространства вокруг
модели самолета для решения задачи аэродинамики[6]
4.1. Пример алгоритма исчерпывания
Рассмотрим алгоритм
исчерпывания, разработанный вторым автором данной работы и предназначенный для
построения равномерных сеток в произвольных областях.
Пусть необходимо
построить сетку с желаемой средней длиной ребра, равной h (эту величину часто называют шагом триангуляции). В качестве исходных данных алгоритм требует
два массива данных: массив, описывающий триангуляцию границы (фактически,
начальный фронт; представляется в виде списка треугольников-граней) и массив
вспомогательных точек F. Этот массив формируется так:
заданная область помещается в супер-область (параллелепипед), которая
равномерно заполняется вспомогательными точками F с шагом ![]() (то есть плотность их
размещения должна быть на порядок больше плотности размещения узлов
триангуляции.) Заметим, что, поскольку координаты этих узлов можно легко
вычислять (
(то есть плотность их
размещения должна быть на порядок больше плотности размещения узлов
триангуляции.) Заметим, что, поскольку координаты этих узлов можно легко
вычислять (![]() ), под этот массив не
потребуется много памяти. Фактически, множество F будет
описываться трехмерным массивом 1-битных булевых переменных (TRUE = точка существует, FALSE = точка удалена). Таким образом,
хранение 8 миллионов элементов F потребует около мегабайта
оперативной памяти. После формирования множества F из него
удаляются все точки, лежащие вне заданной области. Оставшиеся точки будут
представлять своего рода объемное растровое изображение заданной области.
Именно с помощью множества F в этом алгоритме и решаются многие
проблемы, указанные выше.
), под этот массив не
потребуется много памяти. Фактически, множество F будет
описываться трехмерным массивом 1-битных булевых переменных (TRUE = точка существует, FALSE = точка удалена). Таким образом,
хранение 8 миллионов элементов F потребует около мегабайта
оперативной памяти. После формирования множества F из него
удаляются все точки, лежащие вне заданной области. Оставшиеся точки будут
представлять своего рода объемное растровое изображение заданной области.
Именно с помощью множества F в этом алгоритме и решаются многие
проблемы, указанные выше.
Поскольку алгоритм
рассчитан на построение равномерных сеток, контрольная функция ![]() считается константой,
равной
считается константой,
равной ![]() (объем правильного
тетраэдра с ребром h плюс допуск 25%).
(объем правильного
тетраэдра с ребром h плюс допуск 25%).
Далее производятся
следующие действия:
1. Формируется множество
узлов G, состоящее из вершин фронта (т.е.
изначально в него входят все существующие узлы сетки); для каждого узла G проводится оценка
телесного угла. Эта оценка сводится к нахождению числа существующих (т.е., неудаленных) точек F,
находящихся от данного узла на расстоянии не более чем ![]() (что требует
существенно меньших затрат ресурсов, чем прямое вычисление телесных углов).
(что требует
существенно меньших затрат ресурсов, чем прямое вычисление телесных углов).
2. Находится вершина ![]() с наименьшим оценочным
значением величины телесного угла и выбирается такая грань (
с наименьшим оценочным
значением величины телесного угла и выбирается такая грань (![]() ) фронта, для которой сумма оценок величин телесных углов для
) фронта, для которой сумма оценок величин телесных углов для
![]() минимальна.
минимальна.
3. Формируется множество ![]() узлов G, находящихся от каждой из вершин выбранной грани на
расстоянии не более
узлов G, находящихся от каждой из вершин выбранной грани на
расстоянии не более ![]() (это множество может
оказаться и пустым). Для каждого узла
(это множество может
оказаться и пустым). Для каждого узла ![]() из
из ![]() рассматривается
тетраэдр (
рассматривается
тетраэдр (![]() ), причем тетраэдр отбрасывается, если не выполняется хотя бы одно из следующих условий:
), причем тетраэдр отбрасывается, если не выполняется хотя бы одно из следующих условий:
1) строго внутри этого
тетраэдра нет ни одной удаленной точки F
(существование таких точек на гранях допускается);
2) внутри этого тетраэдра
нет других существующих узлов сетки, за исключением самих вершин этого
тетраэдра;
3) тетраэдр не пересекается
никаким существующим ребром сетки (считается, что тетраэдр пересекается ребром,
не являющимся ребром этого тетраэдра, если у него с этим ребром есть хотя бы
одна общая точка, не являющаяся вершиной этого тетраэдра.)[7];
4) объем тетраэдра не
больше максимально допустимого (![]() ).
).
Из всех тетраэдров (![]() ) выбирается тетраэдр наилучшего качества [45] и производится
переход к п. 5; если же тетраэдров, удовлетворяющих указанным условиям, не
оказалось, то осуществляется переход к п. 4.
) выбирается тетраэдр наилучшего качества [45] и производится
переход к п. 5; если же тетраэдров, удовлетворяющих указанным условиям, не
оказалось, то осуществляется переход к п. 4.
4. Находится такая точка ![]() внутри еще
неисчерпанной области, что:
внутри еще
неисчерпанной области, что:
1) тетраэдр (![]() ) удовлетворяет всем условиям п. 3;
) удовлетворяет всем условиям п. 3;
2) в шаре ![]() нет ни одной удаленной точки F (это предотвращает размещение узла p слишком близко от граней и вершин
существующих тетраэдров).
нет ни одной удаленной точки F (это предотвращает размещение узла p слишком близко от граней и вершин
существующих тетраэдров).
Вариант алгоритма поиска
узла p рассмотрен ниже.
5. Удаляются все вершины F, попавшие внутрь (и на границы) сформированного
тетраэдра. Затем фронт обновляется по следующей схеме: рассматривается каждая
грань сформированного тетраэдра и
1) если грань является
гранью фронта, то она удаляется из фронта;
2) если грань НЕ является
гранью фронта, она добавляется во фронт.
6. Если еще остались
неудаленные точки F или (что эквивалентно) фронт не пуст
(то есть область еще не исчерпана полностью), осуществляется переход к п. 1,
иначе процесс окончен.
Таким образом, массив F используется сразу для нескольких
целей: для оценки величины телесного угла, для контроля правильности построения
и для контроля размещения новых узлов. Также массив F удобно использовать для индикации
процесса выполнения. Отношение числа удаленных во время работы алгоритма точек F к начальному числу существующих
точек F фактически показывает, какая часть области уже исчерпана.
Вернемся к вопросу
нахождения координат нового узла для построения тетраэдра (п. 4 описанного
алгоритма). Пусть заданы три узла - ![]() .
.
1. На
первом шаге находятся ![]() - центр масс
треугольника (как среднее арифметическое координат его узлов) и единичная
нормаль
- центр масс
треугольника (как среднее арифметическое координат его узлов) и единичная
нормаль ![]() к плоскости грани
(через нормированное векторное произведение).
к плоскости грани
(через нормированное векторное произведение).
2. Далее определяется
первое приближение для расстояния от ![]() до искомой точки p (H), исходя из
максимального объема тетраэдра:
до искомой точки p (H), исходя из
максимального объема тетраэдра: ![]() . Заметим, что площадь грани S фактически найдена на предыдущем
шаге (результат векторного произведения двух ребер равен удвоенной площади
грани), а максимальный объем обусловлен значением контрольной функции.
. Заметим, что площадь грани S фактически найдена на предыдущем
шаге (результат векторного произведения двух ребер равен удвоенной площади
грани), а максимальный объем обусловлен значением контрольной функции.
3. Проверяется точка ![]() . Если
тетраэдр (
. Если
тетраэдр (![]() ) удовлетворяет всем требованиям, происходит переход к п. 6,
иначе - к п. 4.
) удовлетворяет всем требованиям, происходит переход к п. 6,
иначе - к п. 4.
4. Проверяется точка ![]() . Если
тетраэдр (
. Если
тетраэдр (![]() ) удовлетворяет всем требованиям, происходит переход к п. 6,
иначе - к п. 5.
) удовлетворяет всем требованиям, происходит переход к п. 6,
иначе - к п. 5.
5. Полагают ![]() и переходят к п. 3.
и переходят к п. 3.
6. Искомый узел найден.
Заметим, что в 99%
случаев искомая точка находится на 1 или 2 итерации данного алгоритма.
В описанном выше
алгоритме исчерпывания на каждом шаге из области изымается один тетраэдр.
Сотрудник НАСА Ш. Пирзаде (Shahyar Pirzadeh) предложил другой вариант алгоритма,
в котором за один раз из области изымается сразу целый слой тетраэдров (то есть
на каждой итерации тетраэдры строятся сразу для всех граней текущего фронта)
[32]. Вопреки ожиданию, этот вариант не позволяет сколько-нибудь существенно
ускорить процесс построения (т.к. все новые тетраэдры все равно необходимо
проверять на корректность), однако он избавляет от необходимости искать
наиболее подходящую для построения тетраэдра грань. Это, однако, скорее минус,
чем плюс, так как из-за этой особенности вариант Пирзаде менее надежен и может
дать сбой на геометрически сложных областях. Вместе с тем на сравнительно
простых областях он показывает неплохие результаты.
Сетки, построенные
методами исчерпывания, как правило, обладают неплохим качеством, а последующая
оптимизация положения узлов дает дополнительную прибавку к качеству. Подводя
итог, заметим, что методы исчерпывания наиболее эффективны, если изначально
задана триангуляция границы области. В этом и состоит их основное отличие от
методов на основе критерия Делоне, для которых ситуация прямо обратная.
Список литературы
1.
Шайдуров В.В. Многосеточные методы конечных элементов. - М., Наука,
1989. - 288с.
2.
Скворцов А.В. Обзор алгоритмов построения триангуляции Делоне // Вычислительные методы и программирование,
2002, №3, c. 14-39.
3.
Скворцов А.В. Алгоритмы построения триангуляции с ограничениями // Вычислительные методы и программирование,
2002, №3, c. 82-92.
4.
I.Babushka, W.C. Rheinboldt.
A-posteriori Error Estimates for Finite Element Method // Int. J. Numer. Meth. Eng., Vol.
12, p.p. 1597-1615, 1978.
5.
T.J. Baker. Automatic Mesh
Generation for Complex Three-Dimensional Regions Using a Constrained Delaunay
Triangulation // Engineering With
Computers, Springer-Verlag, № 5, p.p. 161-175, 1989.
6.
M. Bern, D. Eppstein. Mesh
Generation and Optimal Triangulation // Computing
in Euclidean Geometry, World Scientific Publishing Co., p.p. 23-90, 1995.
7.
D.K. Blandford, G. Blelloch,
D. Cardoze, C. Kadow. Compact Representations of Simplicial Meshes In Two and
Three Dimensions // Proceedings of 12th
International Meshing Roundtable, Sandia National Laboratories,
p.p.135-146, Sept. 2003.
8.
H. Borouchaki, S.H. Lo. Fast
Delaunay Triangulation In Three Dimensions // Computer Methods In Applied Mechanics And Engineering, Elsevier,
Vol. 128, p.p. 153-167, 1995.
9.
E.K. Buratynski. A
Three-Dimensional Unstructured Mesh Generator for Arbitrary Internal Boundaries
// Numerical Grid Generation in
Computational Fluid Mechanics, Pineridge Press, p.p. 621-631, 1988.
10.
P.R. Cavalcanti, U.T. Mello.
Three-Dimensional Constrained Delaunay
Triangulation: A Minimalist Approach // Proceedings
of the 8th International Meshing Roundtable, p.p. 119-129, 1999.
11.
Dey, K. Tamal, K. Sugihara,
C.L. Bajaj. Delaunay Triangulations In Three Dimensions With Finite Precision
Arithmetic // Computer Aided Geometric
Design, North-Holland, № 9, p.p. 457-470, 1992.
12. H.N. Djidjev. Force-Directed Methods For Smoothing Unstructured
Triangular And Tetrahedral Meshes // Proceedings
of 9th International Meshing Roundtable, Sandia National Laboratories, p.p.
395-406, October 2000.
13.
L. Durbeck. Evaporation: A Technique For Visualizing Mesh
Quality // Proceedings of 8th
International Meshing Roundtable, South Lake Tahoe, CA, U.S.A., p.p.
259-265, October 1999.
14. D.A. Field. Laplacian Smoothing And Delaunay Triangulations // Communications
in Applied Numerical Methods, vol. 4, p.p. 709-712, 1988.
15. P.J. Frey, H. Borouchaki, P.-L. George. Delaunay Tetrahedralization
Using an Advancing-Front Approach // Proceedings
of 5th International Meshing Roundtable, Sandia National Laboratories, p.p.
31-46, October 1996.
16. L.A. Freitag, C. Ollivier-Gooch. A Comparison of Tetrahedral Mesh
Improvement Techniques // Proceedings of
5th International Meshing Roundtable, Sandia National Laboratories, p.p.
87-106, October 1996.
17. L.A. Freitag, C. Ollivier-Gooch.
Tetrahedral Mesh Improvement Using Swapping and Smoothing // International
Journal for Numerical Methods in Engineering, vol. 40, p.p. 3979-4002,
1995.
18. L.A. Freitag, C. Ollivier-Gooch. The Effect Of Mesh Quality On Solution
Efficiency // Proceedings of 6th
International Meshing Roundtable, Sandia National Laboratories, p.p.249,
October 1997.
19. P.L. George. TET MESHING: Construction, Optimization and Adaptation // Proceedings
of 8th International Meshing
Roundtable, p.p.133-141, 1999.
20.
N.A. Golias, T.D. Tsiboukis.
An Approach to Refining Three-Dimensional Tetrahedral Meshes Based on Delaunay
Transformations // International Journal
for Numerical Methods in Engineering, John Wiley, № 37, p.p.793-812, 1994.
21. C. Hazlewood. Approximating Constrained Tetrahedralizations // Computer
Aided Geometric Design, vol. 10, p.p. 67–87, 1993.
22. B. Joe. Delaunay Triangular Meshes in Convex polygons, SIAM J. Sci.
Stat. Comput., Vol. 7, p.p. 514-539, 1986.
23.
B. Joe. Construction Of
Three-Dimensional Delaunay Triangulations Using Local Transformations // Computer Aided Geometric Design, Vol. 8,
p.p. 123-142, 1991.
24. B. Joe. Construction of Three-Dimensional Improved-Quality
Triangulations Using Local Transformations // Siam J. Sci. Comput., vol.
16, p.p. 1292-1307, 1995.
25.
R.W. Lewis, Yao Zheng, D.T.
Gethin. Three-Dimensional Unstructured Mesh Generation: Part 3. Volume Meshes
// Computer Methods In Applied Mechanics
And Engineering, Elsevier, Vol 134, p.p.285-310, 1996.
26. A.Liu, B. Joe. On The Shape Of Tetrahedra From Bisection // Mathematics
of Computation, vol. 63, №207, 141–154, 1994.
27.
S.H. Lo. Volume
Discretization into Tetrahedra-I. Verification and Orientation of Boundary
Surfaces // Computers and Structures,
Pergamon Press, Vol. 39, № 5, p.p. 493-500, 1991.
28.
S.H. Lo. Volume
Discretization into Tetrahedra - II. 3D Triangulation by Advancing Front
Approach // Computers and Structures,
Pergamon, Vol. 39, № 5, p.p. 501-511, 1991.
29. R. Lohner. Generation Of Three-Dimensional Unstructured Grids By The
Advancing Front Method //Proceedings of the 26th AIAA Aerospace Sciences
Meeting, Reno, Nevada, 1988.
30.
S.J. Owen. A Survey of
Unstructured Mesh Generation Technology // Proceedings
of 7th International Meshing Roundtable, p.p. 239-269, Dearborn, MI, 1998.
31.
V.N. Parthasarathy, C.M.
Graichen, A.F. Hathaway. A Comparison of Tetrahedron Quality Measures // Finite Elements in Analysis and Design,
Elsevier, №. 15, p.p. 255-261, 1993.
32. S. Pirzadeh. Unstructured Viscous Grid Generation by Advancing-Layers
Method // AIAA-93-3453-CP, AIAA, p.p. 420-434, 1993.
33.
V.T. Rajan. Optimality of
Delaunay Triangulation in ![]() // Proc. 7th ACM Symp.
Comp. Geometry, p.p. 357-363, 1991.
// Proc. 7th ACM Symp.
Comp. Geometry, p.p. 357-363, 1991.
34.
A.Rassineux. Generation and
Optimization of Tetrahedral Meshes by Advancing Front Technique // International Journal for Numerical Methods
in Engineering, Wiley, Vol. 41, p.p. 651-674, 1998.
35. S. Rebay. Efficient Unstructured Mesh Generation by Means of Delaunay
Triangulation and Bowyer-Watson Algorithm // Journal Of Computational
Physics, vol. 106, p.p. 125-138, 1993.
36. M.-C. Rivara. Selective Refinement/Derefinement Algorithms For Sequences
Of Nested Triangulations // International
Journal for Numerical Methods in Engineering, №28, p.p. 2889-2906, 1998.
37. M.-C. Rivara, C. Levin. A 3D Refinement Algorithm Suitable For Adaptive
And Multigrid Techniques // Communications
in Applied Numerical Methods, № 8, p.p. 281-290, 1998.
38. J. Ruppert. A Delaunay refinement algorithm for quality 2-dimensional
mesh generation // Journal of Algorithms,
№18, p.p. 548-585, 1995.
39. M.S. Shephard, M.K. Georges. Three-Dimensional Mesh Generation by Finite
Octree Technique // International Journal for Numerical Methods in
Engineering, vol. 32, p.p. 709-749, 1991.
40. M.S. Shephard, F. Guerinoni, J.E. Flaherty, R.A. Ludwig, P.L. Baehmann.
Finite octree mesh generation for automated adaptive 3D Flow Analysis // Numerical grid generation in computational
Fluid mechanics, Miami, 1988
41. K. Shimada, D.C. Gossard. Bubble Mesh: Automated Triangular Meshing of
Non-manifold Geometry by Sphere Packing // Proceedings
of 3rd Symposium on Solid Modeling and
Applications, p.p. 409-419, 1995.
42. K. Shimada, A. Yamada, T. Itoh. Anisotropic Triangular Meshing of
Parametric Surfaces via Close Packing of Ellipsoidal Bubbles // Proceedings
of 6th International Meshing Roundtable, p.p. 375-390, 1997.
43. D.F. Watson. Computing the Delaunay Tessellation with Application to
Voronoi Polytopes // The Computer Journal, Vol. 24(2), p.p. 167-172,
1981.
44. M.A. Yerry, M.S. Shephard. Three-Dimensional Mesh Generation by Modified
Octree Technique // International Journal
for Numerical Methods in Engineering, Vol. 20, p.p. 1965-1990, 1984.
45.
Галанин М.П., Щеглов И.А. Разработка и реализация алгоритмов трехмерной
триангуляции сложных пространственных областей: прямые методы. Препринт ИПМ им.
М.В. Келдыша РАН, 2006, в печати.
[1] "Сплайнами" в данном случае называются фрагменты поверхностей
[2] Следует отметить, что свойство минимизации радиусов описанных сфер сохраняется; более того, как показывает работа сотрудника исследовательского центра IBM В.Т. Раджана (V.T. Rajan), это справедливо и для n-мерного случая [33]
[3] В англоязычной литературе также часто называется "2-to-3 flip"
[4] Это т.н. Steiner points, т.е. узлы Штейнера - дополнительные узлы, не входившие в изначальный набор
[5] П. Кавальканти, У. Мелло [10]
[6] из
архива
Dassault-Aviation
[7] Может показаться, что из условия 3 следует условие 2, но на самом деле это не так. Например, существующий тетраэдр может целиком оказаться внутри проверяемого тетраэдра.