Компьютерный практикум по небесной механике.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
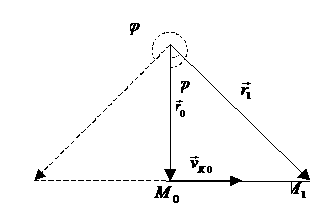
Рис.2.
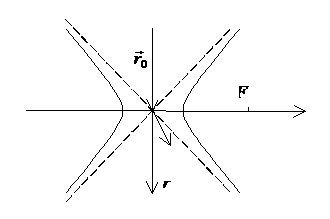
Области допустимых скоростей. |
|
При перелете на внешнюю орбиту ![]() допустимые скорости
перелета лежат вне эллипса
допустимые скорости
перелета лежат вне эллипса
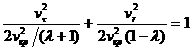 .
.
Описание программы.
Программа в окрестности
данной точки ![]() строит и изображает на
экране по заданному
строит и изображает на
экране по заданному ![]() границу области
достижимости для конца вектора
границу области
достижимости для конца вектора ![]() . Программа используется как непосредственно, так и для
проверки результатов работы учащихся.
. Программа используется как непосредственно, так и для
проверки результатов работы учащихся.
Некоторые задачи одноимпульсного маневрирования.
Задача оптимальной
достижимости.
Задача оптимальной достижимости заключается в нахождении траектории,
проходящей через данную точку ![]() и сферу радиуса
и сферу радиуса ![]() и удовлетворяющей
дополнительным условиям оптимальности. В качестве условий оптимальности может
выступать минимизация начального импульса.
и удовлетворяющей
дополнительным условиям оптимальности. В качестве условий оптимальности может
выступать минимизация начального импульса.
Оптимальное достижение заданной круговой орбиты.
Рассматривается
движение по круговой орбите ![]() со скоростью
со скоростью ![]() . Требуется найти минимальный импульс - модуль
приращения скорости, который позволяет осуществить перелет к орбите радиуса
. Требуется найти минимальный импульс - модуль
приращения скорости, который позволяет осуществить перелет к орбите радиуса ![]() . Положим
. Положим ![]() , тогда скорости, необходимые для достижения орбиты радиуса
, тогда скорости, необходимые для достижения орбиты радиуса ![]() , удовлетворяют неравенству (см. выше)
, удовлетворяют неравенству (см. выше)
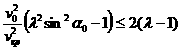 .
.
|
|
|
|
|
|
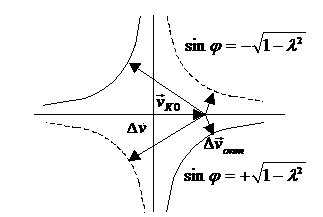
Рис.3.
Оптимальные импульсы скоростей.
Введем систему
координат ![]() с центром в точке
старта, ось
с центром в точке
старта, ось ![]() направлена по радиус-вектору
направлена по радиус-вектору
![]() , ось
, ось ![]() – по направлению движения. При перелете на внутреннюю орбиту
– по направлению движения. При перелете на внутреннюю орбиту ![]() допустимые скорости
перелета лежат внутри гиперболы
допустимые скорости
перелета лежат внутри гиперболы
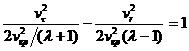 или
или ![]() ,
, ![]() ,
, ![]() .
.
При перелете на внешнюю орбиту ![]() допустимые скорости
перелета лежат вне эллипса
допустимые скорости
перелета лежат вне эллипса
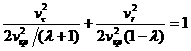 , или
, или ![]() ,
, ![]() ,
, ![]() .
.
Утверждение. В обоих случаях для ![]() и
и ![]() верно
верно ![]() .
.
Доказательство. Пусть координаты ![]() вектора
вектора ![]() удовлетворяют
уравнению
удовлетворяют
уравнению
![]()
![]()
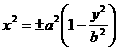 , где
, где
![]() ,
, ![]() ,
, ![]() .
.
Найдём 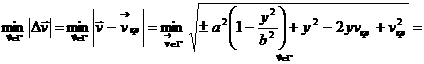
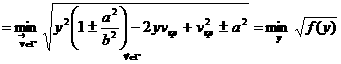
Вершина параболы, задаваемой функцией ![]() , находится в точке
, находится в точке ![]() ,
,
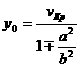 .
.
Для эллипса ![]() ,
,
![]()
![]()
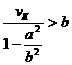
![]()
![]()
![]()
![]() .
.
Последнее неравенство выполняется для любого ![]() , такого что
, такого что ![]() , так как
, так как
![]() ,
, ![]()
![]()
![]() .
.
Таким образом, так как для эллипса ![]() ,
, ![]() , то минимум достигается при
, то минимум достигается при ![]() .
.
Аналогично для гиперболы ![]() ,
,
![]()
![]()
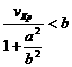
![]()
![]()
![]()
![]() .
.
Последнее неравенство выполняется для
любого ![]() , так как
, так как
![]() ,
, ![]()
![]()
![]() .
.
Таким образом, так как для
соответствующей ветви гиперболы ![]() ,
, ![]() , то минимум достигается при
, то минимум достигается при ![]() . Следовательно, при перелете на внутреннюю орбиту
оптимальный импульс направлен против движения
. Следовательно, при перелете на внутреннюю орбиту
оптимальный импульс направлен против движения
![]() ,
, 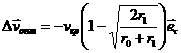 ,
, 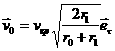 ,
,
при перелете на внешнюю орбиту
оптимальный импульс направлен по направлению движения
![]() ,
, 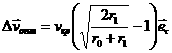 ,
, 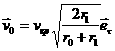 .
.
Описание программы.
Программа находит оптимальный импульс, строит
соответствующую траекторию и изображает её на экране. Приложение используется
как непосредственно, так и для оценки результатов работы учащихся.
Оптимальное
попадание с круговой орбиты в заданную точку.
Движение происходит по круговой орбите радиуса ![]() с круговой
скоростью
с круговой
скоростью ![]() . Требуется найти минимальный по модулю импульс
. Требуется найти минимальный по модулю импульс ![]() , обеспечивающий попадание в заданную точку
, обеспечивающий попадание в заданную точку ![]() .
.

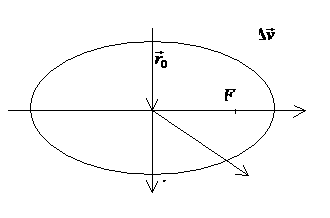
Рис.4. Оптимальное попадание в точку.
Пусть угловая
дальность перелета ![]() , а начальная скорость
, а начальная скорость ![]() составляет с
радиус-вектором
составляет с
радиус-вектором ![]() угол
угол ![]() . В плоскости скоростей рассмотрим гиперболу, которой
принадлежат концы векторов скоростей, обеспечивающих попадание в заданную
точку. Воспользуемся полученной ранее зависимостью
. В плоскости скоростей рассмотрим гиперболу, которой
принадлежат концы векторов скоростей, обеспечивающих попадание в заданную
точку. Воспользуемся полученной ранее зависимостью
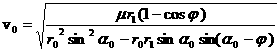
![]()
и найдём явный вид уравнения гиперболы.
Введем в точке старта декартовы координаты ![]()
![]() ,
, ![]() ,
, ![]() .
.
Преобразуем ![]() к виду
к виду
![]() ,
, ![]() .
.
Возможны два случая а) ![]() и б)
и б) ![]() .
.
|
|
|
|
|
|
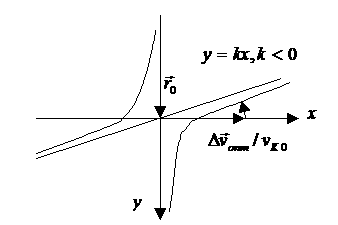
Рис.5.
Допустимые скорости перелета.
а) В первом случае условие ![]() означает, что точка
означает, что точка ![]() оказалась на одной
линии с начальной скоростью
оказалась на одной
линии с начальной скоростью ![]() («по курсу» или строго
«позади»). Уравнение кривой
(«по курсу» или строго
«позади»). Уравнение кривой ![]() принимает вид
принимает вид
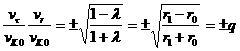
![]()
![]() .
.
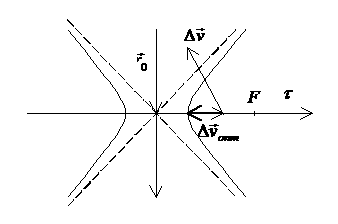
Найдем минимальный импульс, для этого
рассмотрим гиперболу ![]() . Допустим, вектор
. Допустим, вектор ![]() соответствует импульсу
соответствует импульсу
![]() . Исходя из того, что оптимальный импульс должен быть направлен
по нормали к гиперболе, получим
. Исходя из того, что оптимальный импульс должен быть направлен
по нормали к гиперболе, получим
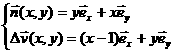 ,
, 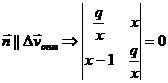
![]()
![]() .
.
Данное уравнение имеет единственный
положительный корень ![]() . Для него оптимальный импульс
. Для него оптимальный импульс ![]() .
.
б) В случае, когда ![]() уравнение
уравнение ![]() преобразуется к виду
преобразуется к виду
![]()
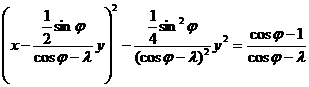 .
.
Это гипербола, асимптотами которой служат прямые
![]() ,
,![]() ,
, ![]() .
.
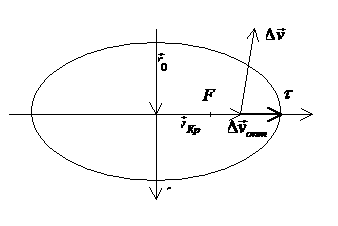
В случае, когда ![]() , получим следующую картину
, получим следующую картину
|
|
|
|
|
|
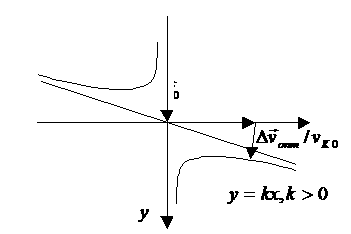
Рис.6.
Оптимальный импульс скорости.
Оптимальный
импульс находится итерациями из условия ![]() , где
, где ![]() – нормаль к гиперболе. В качестве начального
приближения берется импульс, перпендикулярный асимптоте. Аналогичным образом
можно рассмотреть случай, когда
– нормаль к гиперболе. В качестве начального
приближения берется импульс, перпендикулярный асимптоте. Аналогичным образом
можно рассмотреть случай, когда ![]() . В частности, пусть
. В частности, пусть ![]() , тогда
, тогда
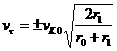 ,
, ![]() – любое.
– любое.
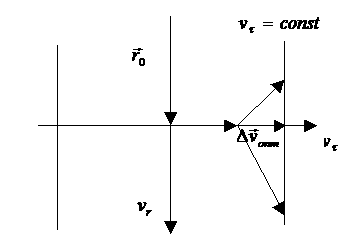
Рис.7.
Оптимальный импульс скорости в случае ![]() .
.
При перелете к
внешней орбите оптимальный импульс должен быть приложен по направлению
движения, при перелете к внутренней – против. В обоих случаях, как и следовало
ожидать, получаем хомановский эллипс
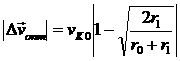 .
.
Описание программы.
Программа находит оптимальный импульс, строит
соответствующую траекторию и изображает её на экране. Приложение используется
как непосредственно, так и для оценки результатов работы учащихся.
Задача попадания в данную движущуюся планету.
Пусть КА движется в центральном гравитационном поле по
круговой орбите. Задача заключается в том, чтобы выбрать начальные данные
(положение КА и импульс скорости в момент старта) таким образом, чтобы КА
встретился с планетой, движущейся по круговой орбите заданного радиуса.
Эта задача решается только экспериментально. Пользователь
задает точку в области достижимости и проводит эксперимент. Основываясь на
результатах, начальные данные корректируются и эксперимент повторяется до тех
пор, пока не будут выполнены условия встречи с планетой с заданной точностью.
В данной задаче область достижимости двумерная. Программа
использует другие приложения и изображает по выбору пользователя одномерные
подмножества, соответствующее дополнительным условиям (например, фиксировано
время перелета, энергетические затраты – ![]() и т.п.) На этих
подмножествах поиск попадающей траектории значительно облегчается.
и т.п.) На этих
подмножествах поиск попадающей траектории значительно облегчается.
3.3. Иллюстрирующие программы.
Иллюстрирующие программы предназначены для демонстрации учащимся основных понятий и явлений, изучаемых в курсе небесной механики. Пользователь может изменять параметры моделей, проводить эксперименты, обращаться к справочному разделу.
Программы Конические сечения, Эллипс по двум параметрам, Траектории задачи Кеплера, Скорость и ускорение в кеплеровом движении, Классификация орбит по начальной скорости и др. демонстрируют базовые понятия курса [11].
Далее приведены примеры иллюстрирующих программ, реализованных в рамках практикума по небесной механике.
Эллипс безопасности.
Рассмотрим на плоскости эллиптические орбиты, исходящие из
одной и той же точки, с постоянной по модулю скоростью ![]() . Для всех этих орбит значение большой полуоси одинаково
. Для всех этих орбит значение большой полуоси одинаково
![]() .
.
Все траектории семейства будут лежать в области, ограниченной огибающей – эллипсом безопасности, его фокусы совпадают с центром притяжения и точкой старта. Параметры эллипса безопасности имеют следующие значения [17]
![]() ,
, ![]() ,
, ![]() ,
,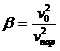 .
.
Программа предназначена для демонстрации свойств эллипса безопасности. В начальный момент фиксируется положение старта и энергия. После установки значений параметров программа изображает эллипс безопасности. Пользователь может изменять направление вектора начальной скорости. Задавая различное направление вылета, можно убедиться в том, что получающиеся траектории полностью лежат внутри соответствующего эллипса безопасности.
Максимальная дальность на
сфере.
Рассмотрим всевозможные
траектории, начинающиеся на поверхности сферы радиуса ![]() с фиксированной по
модулю начальной скоростью
с фиксированной по
модулю начальной скоростью ![]() . Обозначим
. Обозначим ![]() – угол между
вертикалью и вектором начальной скорости,
– угол между
вертикалью и вектором начальной скорости, ![]() – угловая дальность,
– угловая дальность, ![]() – истинная аномалия точки старта,
– истинная аномалия точки старта, ![]() – вектор Лапласа.
Определим максимальную возможную угловую дальность
– вектор Лапласа.
Определим максимальную возможную угловую дальность ![]() на сфере.
на сфере.
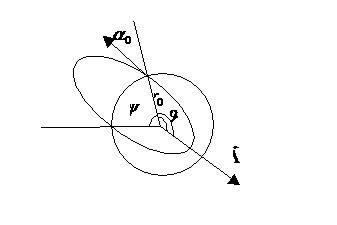
Рис.8.
Максимальная дальность на сфере.
Учитывая,
что
![]() ,
,
Получаем,
что ![]()
и
![]()
достигаются
одновременно. Дифференцируя
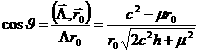
по ![]() , получим
, получим
![]()
![]()
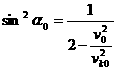 .
.
Отсюда следует, что
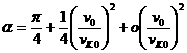 и
и ![]() ,
, 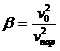 .
.
Программа
моделирует движение между двумя точками сферической поверхности. По выбору
пользователя программа строит траекторию, доставляющую максимальную дальность
на сфере. Пользователь имеет возможность, изменяя графически угол ![]() , сравнивать произвольные траектории с оптимальной.
, сравнивать произвольные траектории с оптимальной.
Хомановский эллипс.
Рассмотрим
траекторию, представляющую собой эллипс, который в перицентре и апоцентре
касается двух окружностей радиусов ![]() – эллипс Хомана [10].
– эллипс Хомана [10].

Рис.9. Хомановский эллипс.
Найдем значения скоростей в точках касания. Так как
![]() ,
, ![]() ,
,
то
![]() ,
, ![]() .
.
Используя эти соотношения, получим значение скорости в перицентре
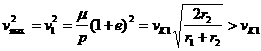 ,
,
аналогично в апоцентре
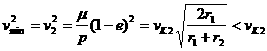 .
.
Приложение позволяет менять радиусы круговых орбит, при этом на экране отображаются значения параметров эллипса и скоростей в точках касания.
Карта
Земли с орбиты.
Приложение
моделирует движение по кеплеровской траектории вокруг Земли. Пользователь может
наблюдать вид Земли с борта виртуального космического аппарата. Параметры
траектории КА задаются пользователем. Модель Земли представляет собой сферу с
наложенной текстурой – картой поверхности Земли. Движение происходит в
трехмерном пространстве. Пользователь может изменять как точку наблюдения, так
и масштаб изображения.
Сравнение
методов расчета траекторий.
В системе Земля-Луна программа строит траектории движения, рассчитанные методом сфер действия и одновременно траекторию ограниченной задачи трех тел с одинаковыми начальными данными, задаваемыми пользователем. Например, программа позволяет сравнивать траектории, параметры движения (скорости выхода из сферы действия Луны) в задаче о приземлении ИСЗ с использованием гравитационного поля Луны.
3.4. Справочная информация.
Справочная информация,
необходимая пользователю при работе с практикумом, содержится в справочном
разделе. Доступ к вспомогательному материалу контролируется преподавателем.
Например, при демонстрации новых явлений целесообразно использовать
вспомогательный материал для улучшения усвоения материала. С другой стороны, на
первом этапе учебной программы, когда учащийся самостоятельно решает
контрольную задачу, доступ к справочной информации ограничивается.
В настоящее время справочник
содержит следующие статьи Закон тяготения
Ньютона, Силовая функция, Притяжение материальных тел, Притяжение точки шаром,
Притяжение точки эллипсоидом, Законы Кеплера, Задача Кеплера, Энергетическая
классификация орбит, Классификация орбит по скоростям, Скорость и ускорение в
кеплеровом движении, Время на кеплеровой траектории, Решение уравнения Кеплера и др.
Далее приведены некоторые примеры теоретической составляющей практикума в виде определений, теорем, формул с выводами или указаниями, а также даны числовые значения основных параметров стандартных сред.
Основные параметры планет и их орбит [2, 16, 18].
В таблице 1 обозначено:
![]() – масса планеты;
– масса планеты; ![]() – масса Солнца;
– масса Солнца;
![]() – большая полуось
орбиты;
– большая полуось
орбиты;
![]() – радиус
планеты;
– радиус
планеты; ![]() – радиус сферы
тяготения;
– радиус сферы
тяготения;![]() – радиус сферы действия;
– радиус сферы действия; ![]() – сидерический
период обращения;
– сидерический
период обращения;
![]() –
эксцентриситет (1950.0);
–
эксцентриситет (1950.0);
![]() – наклонение к
эклиптике (1950.0).
– наклонение к
эклиптике (1950.0).
Таблица
1.
|
планета |
|
млн км |
км |
млн км |
млн км |
|
|
троп. год |
|
град |
|
Меркурий |
0,17 |
57,909 |
2424 |
0,32 |
0,112 |
0,001934 |
0,021643 |
0,240 |
0,206 |
7,004 |
|
Венера |
2,45 |
108,209 |
6100 |
1,45 |
0,615 |
0,005683 |
0,009919 |
0,615 |
0,007 |
3,394 |
|
Земля |
3,04 |
149,598 |
6378 |
2,16 |
0,925 |
0,006183 |
0,006895 |
1,000 |
0,017 |
– |
|
Марс |
0,32 |
227,941 |
3412 |
1,56 |
0,579 |
0,002540 |
0,005893 |
1,880 |
0,093 |
1,850 |
|
Юпитер |
954,79 |
778,328 |
71420 |
75,0 |
48,1 |
0,061799 |
0,001485 |
11,862 |
0,048 |
1,306 |
|
Сатурн |
285,58 |
1426,99 |
60440 |
93,0 |
54,6 |
0,038262 |
0,001107 |
29,4578 |
0,056 |
2,491 |
|
Уран |
43,73 |
2870,93 |
24860 |
100,0 |
52,0 |
0,018113 |
0,000478 |
84,015 |
0,047 |
0,773 |
|
Нептун |
51,78 |
4498,51 |
26500 |
166,0 |
86,9 |
0,019318 |
0,000305 |
164,788 |
0,009 |
1,774 |
|
Плутон |
2,78 |
5911,77 |
1150 |
83,0 |
34,0 |
0,005751 |
0,00003 |
247,696 |
0,247 |
17,144 |
Задача двух неподвижных
центров.
Большое значение имеет в небесной механике задача о
движении точки в ньютоновском поле притяжения двух неподвижных центров. Силовая
функция двух точек с массами ![]() и
и ![]() имеет вид [1, 4, 19]
имеет вид [1, 4, 19]
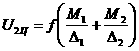 ,
,
где ![]() – расстояние от точки
– расстояние от точки ![]() до точки
до точки ![]() . Предположим, что точки
. Предположим, что точки ![]() и
и ![]() находятся на оси
находятся на оси ![]() неподвижной декартовой
системы координат
неподвижной декартовой
системы координат ![]() в точках с
координатами
в точках с
координатами ![]() и
и ![]() соответственно, так
что
соответственно, так
что ![]() их центр масс, то есть
их центр масс, то есть
![]() , тогда в этих координатах получим
, тогда в этих координатах получим
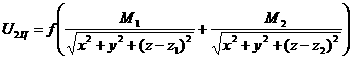 .
.
Положив в этой формуле ![]() ,
, ![]() , где
, где ![]() – комплексное число –
мнимая единица, а
– комплексное число –
мнимая единица, а ![]() и
и ![]() – действительные
положительные числа, получим вещественную функцию вещественных переменных
– действительные
положительные числа, получим вещественную функцию вещественных переменных ![]()
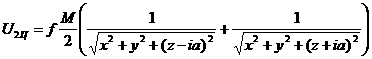 ,
,
которую называют силовой функцией обобщенной задачи
двух неподвижных центров. Потенциал обобщенной задачи двух неподвижных центров
аппроксимирует потенциал тяготения осесимметричной планеты, что дает в
квадратурах решение задачи о движении спутника сфероидальной планеты.
Формула Ламберта.
Допустим, спутник совершает
перелет по известной орбите с большой полуосью ![]() и эксцентриситетом
и эксцентриситетом ![]() . Если известны расстояния от концов дуги орбиты и длина
хорды, соединяющей эти концы, то можно вычислить, сколько времени займет
перелет спутника по этой дуге. Связь между двумя заданными положениями
. Если известны расстояния от концов дуги орбиты и длина
хорды, соединяющей эти концы, то можно вычислить, сколько времени займет
перелет спутника по этой дуге. Связь между двумя заданными положениями ![]() ,
, ![]() и временем перелета
и временем перелета ![]() задается так
называемой формулой Ламберта [4].
задается так
называемой формулой Ламберта [4].
1) Эллиптическая орбита.
Время ![]() перелета по дуге
кеплеровской эллиптической орбиты, определяется формулой
перелета по дуге
кеплеровской эллиптической орбиты, определяется формулой
![]() .
.
Здесь
![]() и
и ![]() – корни уравнений
– корни уравнений
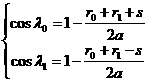 ,
,
где ![]() – хорда, соединяющая
– хорда, соединяющая ![]() и
и ![]() ,
, ![]() – большая полуось
орбиты. Выбор корней происходит следующим образом. Пусть корни
– большая полуось
орбиты. Выбор корней происходит следующим образом. Пусть корни ![]() ,
, ![]() – часть внутренности
эллипса, заключенная между дугой
– часть внутренности
эллипса, заключенная между дугой ![]() и стягивающей ее
хордой,
и стягивающей ее
хордой, ![]() – притягивающий центр,
– притягивающий центр,
![]() – "пустой"
фокус орбиты. Тогда
– "пустой"
фокус орбиты. Тогда
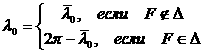 ,
,  .
.
2)
Гиперболическая орбита.
Время
перелета по дуге гиперболической орбиты, вычисляется по формуле
![]() ,
,
причем
числа ![]() и
и ![]() находятся из уравнений
находятся из уравнений
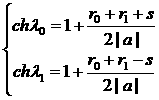 .
.
Здесь
![]() – действительная
полуось орбиты. Если движение происходит после прохождения через перицентр, то
– действительная
полуось орбиты. Если движение происходит после прохождения через перицентр, то ![]() ,
, ![]() .
.
3)
Параболическая орбита.
Время перелета по параболической дуге
определяется согласно формуле Эйлера
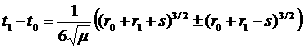 ,
, 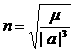 .
.
Знак "![]() " берется тогда, когда разность истинных аномалий
" берется тогда, когда разность истинных аномалий ![]() , знак "–" в противном случае.
, знак "–" в противном случае.
Задача n тел.
Пусть имеется ![]() материальных точек с
массами
материальных точек с
массами ![]() . Задача
. Задача ![]() тел состоит в изучении
движений данной системы материальных точек, притягивающихся к друг другу в
соответствии с законом тяготения Ньютона.
тел состоит в изучении
движений данной системы материальных точек, притягивающихся к друг другу в
соответствии с законом тяготения Ньютона.
Обозначим через ![]() радиус-векторы точек в
некоторой абсолютной системе координат с началом в произвольно выбранной точке
и с неизменными направлениями осей,
радиус-векторы точек в
некоторой абсолютной системе координат с началом в произвольно выбранной точке
и с неизменными направлениями осей, ![]() – расстояние между
точками
– расстояние между
точками ![]() и
и ![]() , тогда уравнения движения системы [8] имеют вид
, тогда уравнения движения системы [8] имеют вид
![]() ,
, ![]() ,
, 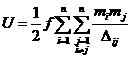
или
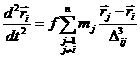 ,
, ![]() .
.
Относительное движение в задаче n тел.
Рассмотрим движение системы относительно одной из
точек, например, точки ![]() , то есть примем точку
, то есть примем точку ![]() за центральное тело в
системе. Введем систему координат с центром в выбранной точке, тогда уравнения
движения [8] имеют вид
за центральное тело в
системе. Введем систему координат с центром в выбранной точке, тогда уравнения
движения [8] имеют вид
![]() ,
, ![]() ,
, 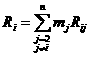 ,
, ![]() ,
,
где
![]() – возмущающие или пертурбационные
функции. В явном виде
– возмущающие или пертурбационные
функции. В явном виде
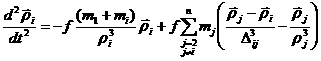 ,
, ![]() .
.
Сфера
действия.
Предположим, что система
состоит из трёх тел и что одним притягивающим телом ![]() является планета,
другим
является планета,
другим ![]() – Солнце, а третьим –
точка
– Солнце, а третьим –
точка ![]() с малой массой,
например, космический аппарат.
с малой массой,
например, космический аппарат.
Пусть ![]() – ускорение,
сообщаемое КА планетой
– ускорение,
сообщаемое КА планетой ![]() , когда планета принимается за центральное тело, а
, когда планета принимается за центральное тело, а ![]() – возмущающее
ускорение, вызываемое притяжением Солнца
– возмущающее
ускорение, вызываемое притяжением Солнца ![]() . Пусть, далее,
. Пусть, далее, ![]() – ускорение,
сообщаемое КА Солнцем, когда последнее принимается за центральное тело,
– ускорение,
сообщаемое КА Солнцем, когда последнее принимается за центральное тело, ![]() – возмущающее
ускорение, вызываемое притяжением планеты
– возмущающее
ускорение, вызываемое притяжением планеты ![]() (см. выше).
(см. выше).
Сферой действия планеты ![]() называется область
пространства, в которой
называется область
пространства, в которой
![]() , где
, где ![]() ,
, ![]() .
.
Граница сферы действия ![]() планеты
планеты ![]() определяется
уравнением
определяется
уравнением
![]() .
.
Утверждение. Приближенное значение радиуса сферы действия
планеты определяется по формуле [2,4,13]
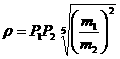
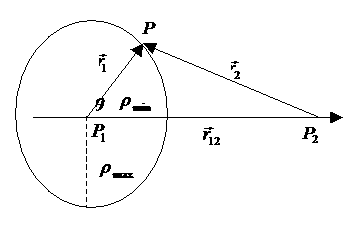
Рис.10. Сфера действия.
Более точно граница сферы действия - это поверхность вращения вокруг оси ![]() кривой, уравнение
которой в полярных координатах
кривой, уравнение
которой в полярных координатах ![]() приближенно имеет вид
приближенно имеет вид
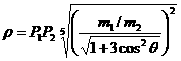
Доказательство. Движение спутника ![]() относительно
относительно ![]() описывается уравнением
описывается уравнением
![]() ,
, ![]() ,
, 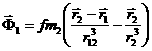 .
.
Аналогично
уравнение движения спутника ![]() относительно
относительно ![]() имеет вид
имеет вид
![]() ,
, ![]() ,
, 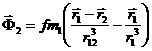 .
.
На
границе сферы действия ![]() , то есть
, то есть
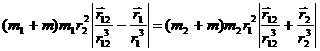 .
.
Из
этого уравнения и условия ![]() следует, что внутри
сферы действия
следует, что внутри
сферы действия ![]() . Положим
. Положим ![]() , перепишем уравнение границы СД в виде
, перепишем уравнение границы СД в виде
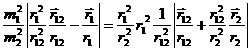
и разложим обе части равенства по степеням малого
параметра ![]() . Заметим, что, учитывая
. Заметим, что, учитывая
![]() ,
, ![]() ,
,
мы
можем получить следующие разложения
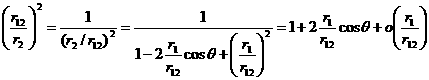 ,
,
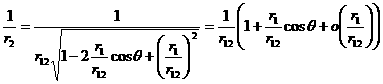 .
.
Используя это, преобразуем выражение в правой части
уравнения
 .
.
Раскрыв
скобки, получим
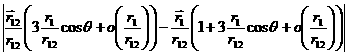 =
= ,
,
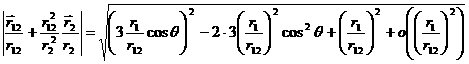

Преобразуем левую часть равенства
![]()
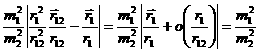 .
.
Так
как
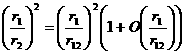 ,
,
то
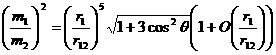 ,
,
что и требовалось.
Сфера тяготения.
В небесной механике, кроме
сферы действия, рассматриваются также другие гравитационные сферы, в том числе
сферы тяготения [4]. При движении объекта в пределах Солнечной системы по
гелиоцентрической орбите главной силой, определяющей движение, является сила
тяготения Солнца. При сближении с планетой рассматриваемый объект попадает в
область притяжения этой планеты, в каждой точке которой планета притягивает
сильнее Солнца. Эта область называется сферой тяготения. Границей сферы
тяготения является сфера радиуса ![]() . Получим для него формулу.
. Получим для него формулу.
Предположим, что одним
притягивающим телом ![]() является планета с
массой
является планета с
массой ![]() , другим
, другим ![]() – Солнце с массой
– Солнце с массой ![]() , так что
, так что ![]() , а точка
, а точка ![]() с малой массой
с малой массой ![]() – некоторое притягиваемое тело, например, космический
аппарат. Пусть
– некоторое притягиваемое тело, например, космический
аппарат. Пусть ![]() – сила, с которой
планета
– сила, с которой
планета ![]() притягивает КА, а
притягивает КА, а ![]() – сила, с которой КА
притягивается Солнцем
– сила, с которой КА
притягивается Солнцем ![]() . Тогда на границе сферы тяготения
. Тогда на границе сферы тяготения
![]()
![]()
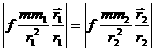
![]()
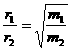 .
.
Как известно из курса
элементарной геометрии геометрическим местом точек, для которых отношение
расстояний до двух данных точек постоянно, является "сфера
Аполлония", центр которой всегда лежит вне отрезка ![]() , причем
, причем
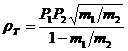 ,
, ![]() ,
,
где
![]() – расстояние от центра
сферы до планеты
– расстояние от центра
сферы до планеты ![]() .
.
Максимальный угол поворота вектора скорости.
Рассмотрим облет планеты по
гиперболической траектории [15]. При движении по гиперболе вектор скорости
поворачивается на угол ![]() , причем
, причем
![]() ,
, ![]() ,
, ![]() .
.

Рис.11. Максимальный угол
поворота вектора скорости.
Рассмотрим облет
планеты ненулевого радиуса ![]() при фиксированной по
модулю скорости на бесконечности
при фиксированной по
модулю скорости на бесконечности ![]() . Найдём максимальный угол поворота вектора скорости. Исходя
из того, что во время движения для скорости выполняется равенство
. Найдём максимальный угол поворота вектора скорости. Исходя
из того, что во время движения для скорости выполняется равенство
![]() ,
,
следующее
из уравнения траектории и интеграла энергии, получим
![]()
![]()
![]() .
.
Во время движения
![]() ,
, ![]() .
.
Подставив
сюда выражение для ![]() , найдём
, найдём
![]() .
.
Следовательно, учитывая
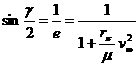 ,
,
получим,
что для максимального угла поворота выполняется равенство
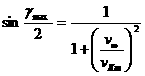 ,
, 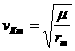 .
.
Гравитационные маневры в поле двух центральных сил.
В основе космической навигации лежит осуществление маневров в поле
нескольких центральных сил. При исследовании возможных траекторий полета к Луне
и планетам Солнечной системы нашел применение простой расчетный способ,
основанный на приближении траектории искусственного небесного тела
последовательностью дуг кеплеровских орбит. Траектория разбивается на участки,
для каждого из которых движение тела предполагается происходящим под действием
только одного притягивающего центра (Земли, Луны, Солнца, планеты). На границах
участков производится соответствующее преобразование координат и скоростей,
учитывающее взаимное движение притягивающих центров [4,7,9,13].
Ошибка такого приближенного расчета зависит от принятого способа
разбиения траектории на участки. Наибольшее распространение получил способ, при
котором переход от одного притягивающего центра к другому производится на
границе соответствующей сферы действия – Луны относительно Земли, Земли
относительно Солнца и т.п.
Рассмотрим полет КА от Земли к другой планете через гелиоцентрическое
поле притяжения с возможным облетом промежуточной планеты. Эффективным способом
исследования траекторий в ограниченной круговой задаче трех тел является метод гравитационных сфер. Данный метод
основан на том, что возмущение гелиоцентрического движения вне СД планеты
невелико, а также мало сказывается и возмущение планетоцентрического движения
полем притяжения Солнца внутри СД планеты. Поэтому всюду возмущениями по
сравнению с притяжением центрального тела в приближенных расчетах можно
пренебрегать. Таким образом, при движении внутри сферы действия планеты
учитывается только влияние поля притяжения планеты, вне СД траектория
определяется только притяжением Солнца.
Будем считать, что Земля движется по круговой орбите радиуса ![]() со скоростью
со скоростью ![]() . Космический аппарат находится на геоцентрической орбите
радиуса
. Космический аппарат находится на геоцентрической орбите
радиуса ![]() и движется со
скоростью
и движется со
скоростью ![]() . В результате приложения импульса скорости
. В результате приложения импульса скорости ![]() КА начинает движение с
гиперболической геоцентрической скоростью
КА начинает движение с
гиперболической геоцентрической скоростью ![]() . Внутри сферы действия Земли будем учитывать только влияние
гравитационного поля планеты. Движение будет определяется с помощью интегралов
энергии и площадей. На границе СД Земли движение будет происходить практически
по асимптоте гиперболы со скоростью
. Внутри сферы действия Земли будем учитывать только влияние
гравитационного поля планеты. Движение будет определяется с помощью интегралов
энергии и площадей. На границе СД Земли движение будет происходить практически
по асимптоте гиперболы со скоростью ![]() , причем
, причем
![]() ,
, ![]() ,
,
где ![]() - угол между вектором
скорости и геоцентрическим радиус-вектором в момент приложения импульса,
- угол между вектором
скорости и геоцентрическим радиус-вектором в момент приложения импульса, ![]() - радиус сферы
действия Земли, p - прицельная дальность - расстояние от центра планеты до асимптоты,
из уравнения гиперболы следует, что прицельная дальность равна длине ее мнимой
полуоси. После выхода из СД Земли КА начнет движение в поле притяжения Солнца
по траектории с начальной скоростью
- радиус сферы
действия Земли, p - прицельная дальность - расстояние от центра планеты до асимптоты,
из уравнения гиперболы следует, что прицельная дальность равна длине ее мнимой
полуоси. После выхода из СД Земли КА начнет движение в поле притяжения Солнца
по траектории с начальной скоростью
![]() .
.
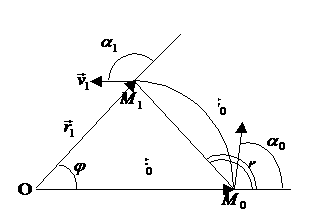
Гравитационный маневр.
Допустим, траектория КА пересекает сферу действия планеты в точке с
гелиоцентрическими радиус-вектором ![]() и скоростью
и скоростью ![]() , причем
, причем
![]() .
.
Планета движется по круговой орбите со скоростью ![]() , где
, где ![]() . Внутри сферы действия планеты при расчете траектории КА
будем учитывать только притяжение планеты. Относительно планеты движение будет
происходить между двумя точками сферы действия. Аппарат входит в СД и выходит
из нее с одной и той же по величине гиперболической скоростью
. Внутри сферы действия планеты при расчете траектории КА
будем учитывать только притяжение планеты. Относительно планеты движение будет
происходить между двумя точками сферы действия. Аппарат входит в СД и выходит
из нее с одной и той же по величине гиперболической скоростью ![]() , которую мы будем считать гиперболической относительно
планетоцентрической системы координат, при этом
, которую мы будем считать гиперболической относительно
планетоцентрической системы координат, при этом
![]() .
.
В результате изменения направления планетоцентрического вектора
скорости движения аппарата происходит изменение гелиоцентрической скорости.
Благодаря гравитационному маневру можно изменять как направление так и модуль
гелиоцентрической скорости. Степень изменения скорости аппарата характеризуется
искривлением его траектории, т. е. углом между асимптотами гиперболической
траектории, который в свою очередь зависит от прицельной дальности ![]() и относительной
скорости входа
и относительной
скорости входа ![]() в СД планеты.
в СД планеты.
|
|
|
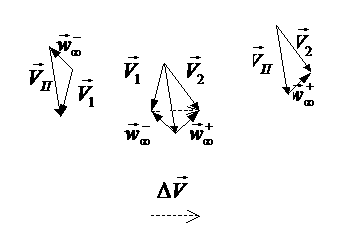
Рис.12.
Диаграммы изменения скорости.
Процесс изменения скорости представлен на векторных
диаграммах. Величину приращения скорости ![]() можно найти с помощью очевидной формулы [7,15]
можно найти с помощью очевидной формулы [7,15]
![]() .
.
Поскольку ![]() зависит от прицельной
дальности
зависит от прицельной
дальности ![]() , то, изменяя её, можно изменять величину приращения скорости
, то, изменяя её, можно изменять величину приращения скорости
![]() . Если допустить, что на границе СД движение происходит
практически по асимптоте гиперболы, то можно отметить, что теоретический предел
приращения скорости
. Если допустить, что на границе СД движение происходит
практически по асимптоте гиперболы, то можно отметить, что теоретический предел
приращения скорости ![]() достигается при
достигается при ![]() , т.е.
, т.е. ![]() . В этом случае планетоцентрическая скорость входа аппарата в
СД
. В этом случае планетоцентрическая скорость входа аппарата в
СД ![]() почти противоположно
направлена скорости выхода
почти противоположно
направлена скорости выхода ![]() . В действительности стремление
. В действительности стремление ![]() ограничено размерами
планеты, поэтому прицельную дальность невозможно сделать меньше радиуса планеты
ограничено размерами
планеты, поэтому прицельную дальность невозможно сделать меньше радиуса планеты
![]() (см. задачу о максимальном угле поворота).
(см. задачу о максимальном угле поворота).
В
результате гравитационного маневра КА покидает СД планеты в точке ![]() с гелиоцентрической скоростью
с гелиоцентрической скоростью
![]() .
.
Далее движение происходит с учетом влияния только
притяжения Солнца. При пересечении траектории КА и СД некоторой планеты для
расчета траектории гиперболической встречи можно воспользоваться изложенными
ранее формулами. В случае, если планета является конечной целью перелета,
следует приложить соответствующий импульс скорости, чтобы выйти на круговую
орбиту планеты.
Допустим, что КА входит в СД планеты-цели с гелиоцентрической
скоростью ![]()
![]() .
.
Планета-цель движется по круговой орбите с
гелиоцентрической скоростью ![]() . Для относительной скорости входа в СД планеты
. Для относительной скорости входа в СД планеты ![]() имеем
имеем
![]() .
.
В момент, когда КА находится на заданном расстоянии ![]() до центра планеты, для
выхода на круговую орбиту необходимо придать импульс скорости
до центра планеты, для
выхода на круговую орбиту необходимо придать импульс скорости
![]() ,
,
где ![]() – скорость КА в момент
пересечения конечной круговой орбиты,
– скорость КА в момент
пересечения конечной круговой орбиты, ![]() – скорость на
планетоцентрической круговой орбите радиуса
– скорость на
планетоцентрической круговой орбите радиуса ![]() , причем
, причем ![]() .
.
Изложенный метод гравитационных
сфер является эффективным методом приближенного анализа межпланетных
траекторий. Упрощенным вариантом метода ГС является метод точечной сферы
действия (ТСД). Данный метод основан на дополнительных предположениях о том,
что размером СД и временем пребывания внутри СД планеты можно пренебречь, то
есть считается, что маневр совершается мгновенно в точке, совпадающей с центром
притяжения планеты маневра. Основанием для такого предположения служат данные
таблицы (см. выше).
Импульсное маневрирование.
Для исследования перелетов КА с двигателями большой тяги
будем использовать импульсную модель движения [5]. Разобьем траекторию на
активный и пассивный участки. На активном участке движение центра масс
космического аппарата подчиняется уравнению Мещерского для точки переменной
массы
![]() ,
,
где ![]() – масса КА,
– масса КА, ![]() скорость точки в
выбранной инерциальной системе координат,
скорость точки в
выбранной инерциальной системе координат, ![]() – главный вектор
внешних сил, приложенных к КА,
– главный вектор
внешних сил, приложенных к КА, ![]() – абсолютная скорость
отбрасываемых частиц.
– абсолютная скорость
отбрасываемых частиц.
Обозначим через ![]() импульс (изменение)
скорости при движении на активном участке в течение времени
импульс (изменение)
скорости при движении на активном участке в течение времени ![]()
![]() .
.
Если движение на активном участке
считать прямолинейным, то при отсутствии внешних сил уравнение Мещерского
приводит к формуле Циолковского
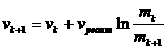 ,
, ![]() .
.
Здесь индекс k отвечает значению величины до маневра,
k+1 – после
![]() ,
, ![]() .
.
Полагая реактивную силу ![]() одинаковой для каждого
маневра, просуммировав равенства, при наличии
одинаковой для каждого
маневра, просуммировав равенства, при наличии ![]() активных участков
получим
активных участков
получим
![]() ,
,
или
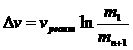 ,
, ![]() .
.
Таким образом, задача о минимизации
запаса топлива сводится к минимизации суммарной величины изменений скорости ![]() , которую будем считать мерой энергетических затрат. При этом
, которую будем считать мерой энергетических затрат. При этом
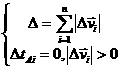 .
.
Не смотря на значительные упрощения, импульсная модель движения позволяет получать важные качественные результаты в задачах небесной механики.
Заключение.
В работе рассмотрены
особенности реализации компьютерного практикума по небесной механике. Приведены
математический аппарат и сценарии работы реализованных задач по небесной
механике. Рассмотрена организация работы программы в рамках виртуальной среды.
В работе представлены
экспериментальные и учебные среды, на основе которых формируется практикум по
небесной механике. Приведены примеры их наполнения и дано краткое описание
сценария работы организующих и контролирующих программ. Предложена
классификация экспериментальных сред. Представлено подробное решение
реализованных задач, используемых организующей программой для контроля усвоения
материала. Даны примеры иллюстрирующих программ. Приведено подробное описание
теоретической составляющей практикума.
Литература.
1.
Актуальные
проблемы классической и небесной механики: Межведомственный сборник научных
трудов. М., "Эльф", 1998.
2.
В.К. Абалкин
и др. Справочное руководство по небесной механике и астродинамике. Под ред.
В.Г. Демина. М., Наука, 1975.
3.
Е.П. Аксенов
Специальные функции в небесной механике. М., Наука, 1986.
4.
М.Б. Балк
Элементы динамики космического полета. М., Наука, 1965.
5.
М.Б. Балк,
В.Г. Демин, А.Л. Куницын Сборник задач по небесной механике и космодинамике.
М., Наука, 1972.
6.
Н. Бахвалов,
Н. Жидков, Г. Кобельков Численные методы. М., Спб., Физматлит, 2000.
7.
Г.А. Гурзадян
Теория межпланетных перелетов, Изд-во Академии Наук Армении, 1991.
8.
Г.Н. Дубошин
Небесная механика. Основные задачи и методы. М., Наука, 1975.
9.
В.А. Егоров,
Л.И. Гусев Динамика перелетов между Землей и Луной. М., Наука, 1980.
10. В.В. Ивашкин Оптимизация космических маневров при
ограничениях на расстояния до планет, М., Наука, 1975.
11. Т.А. Игнатюк, В.А. Прошкин, В.Е. Павловский
Компьютерный практикум по небесной механике. Концепция и структура. Препринт
№73. М., Институт прикладной математики им. М.В. Келдыша, 2002.
12. В.А. Ильин, Э.Г. Позняк Аналитическая геометрия.
М., Наука. Физматлит, 1999.
13. М.Д. Кислик Сферы влияния больших планет и Луны. Космические исследования. Т. I I, Вып. 6, 1964.
14. В. Себехей Теория орбит: ограниченная задача трех
тел. М., Наука, 1982.
15. С. Херрик Астродинамика. М., Мир, 1976
16. Г.А. Чеботарев Аналитические и численные методы
небесной механики. М., АН СССР, 1965.
17. Н.Г. Четаев Теоретическая механика. М., Наука,
1987
18. Основы теории полета космических аппаратов. Под
ред.Г.С. Нариманова. М., Машиностроение, 1972.
19. В.Г. Демин Движение спутника в нецентральном поле
тяготения. М., Наука, 1968.
 ,
, ,
, 
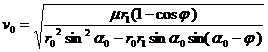 .
.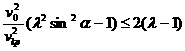 ,
,