Аннотация
Работа посвящена исследованию динамики модульных колесных аппаратов с высокой адаптацией,
синтезу управления ими, анализу и улучшению качества управления. В работе получены уравнения
движения колесных роботов с различными схемами расположения колес и геометрией корпуса.
Проведено моделирование и исследование сложных движений четырехколесного робота. Построены
и исследованы модели многоопорных колесно-шагающих роботов при движении по поверхности с
препятствиями с помощью программного комплекса «Универсальный механизм».
Abstract
This paper is deals with the dynamics analysis of the modular wheeled machines with high
adaptability, with synthesis of the control by them, with analysis of quality of the control
system. There are dynamic equations of the wheeled robots motion with the different
wheels-schemes and geometry of the body obtained. The simulation and analysis of complicated
motions for the four-wheeled robot is shown as well. There are made multisupporting
wheeled-walking robots modeling motion along surface with obstacles with using program
system “Universal mechanism”.
СОДЕРЖАНИЕ
Введение
……………………………………………………………………….. 3
1. «Универсальная» модель колесного аппарата
с изменяемой геометрией
корпуса................................................................................................ 5
2. Полная система уравнений 4-х колесного аппарата и обратная задача
движения. «Вальс на прямой». «Вальс на
окружности»..................... 10
3. Моделирование движения «Вальс»....................................................... 17
4. Моделирование движения модульных
колесно-шагающих аппаратов в
программном комплексе «Универсальный
механизм»........................ 23
Заключение................................................................................................. 27
Литература................................................................................................. 27
Введение.
В настоящее время большое внимание уделяется разработке мобильных
машин с высокой приспособляемостью к движению по сложным траекториям и сложным
поверхностям. Во всем мире в различных отраслях промышленности и сельского
хозяйства, для исследования космоса, мирового океана и труднодоступных областей
ведутся разработки подобных аппаратов для реализации задач, с которыми не
справляются существующие мобильные машины. В этих разработках наибольшее внимание
исследователей привлекают машины, использующие гибридный способ передвижения -
колесно-шагающий. Известно, что основным преимуществом таких аппаратов является
сочетание высоких адаптационных возможностей шагающих машин и высокая скорость
и устойчивость, а также простота управления, колесных шасси, когда аппарат
перемещается по плоской или ровной с малыми неровностями поверхности. Как
следствие можно обоснованно считать, что роботы с колесно-шагающими шасси могут
найти, например, эффективное применение в задачах экстремальной робототехники.
 
 
Рис.1.
Примеры гибридных мобильных роботов.
Zanthic и WorkPartner
В работах [6]-[11] описаны
такие системы различных механических схем. На Рис.1 представлены некоторые
примеры высокоадаптивных гибридных машин из этих работ.
На
верхних фотографиях изображен колесно–шагающий робот компании Zanthic
Technologies Inc. Его несомненными достоинствами в отношении мобильности
являются его относительно небольшие размеры по высоте и способность поднимать
колесо выше его вертикальных размеров. Сотрудники компании утверждают, что этот
робот может балансировать на трех колесах с одним поднятым, что позволяет
называть эту машину именно шагающей. Сочлененный корпус аппарата придает ему
большую свободу при прохождении крутых поворотов. Независимые приводы на колеса
повышают проходимость. Можно сделать вывод, что этот робот был разработан для
реализации определенных задач, связанных с передвижением в местах с небольшим
зазором по высоте с неровностями на поверхности движения, по пересеченной
местности.
На нижних фотографиях рис.1
изображен робот WorkPartner. Гибридная система передвижения позволяет роботу использовать
одновременно и колеса, и ноги. Робот может передвигаться только на ногах,
только на колесах, или одновременно используя и колеса, и ноги. Механическая
часть робота была разработана и изготовлена Rover Company Ltd, Санкт-Петербург,
Россия. Одинаковые части робота идентичны друг другу: одинаковы колеса, ноги,
одинакова конструкция "мускулов" и моторов для них. Это действительно
высокоадаптивный модульный колесно-шагающий аппарат.
 
 
Рис.2. Примеры гибридных мобильных роботов.
Hylos.
На рис.2 изображен еще один колесно-шагающий робот, передвигающийся
по такому же принципу, что и WorkPartner.
Эта машина называется Hylos (разработчики Laboratoire de Robotique de
Paris - Universit´e de
Paris 6). Hylos
значительно меньше по размеру, чем WorkPartner, и изготовлен не для промышленной эксплуатации. Это
дает преимущество для проведения экспериментов по методам управления и
отработки автономного передвижения по пересеченной местности. В работах [12] -
[15] подробно описаны алгоритмы управления этим роботом. На рис.3
проиллюстрирован процесс моделирования движения Hylos по пересеченной местности ([15]).
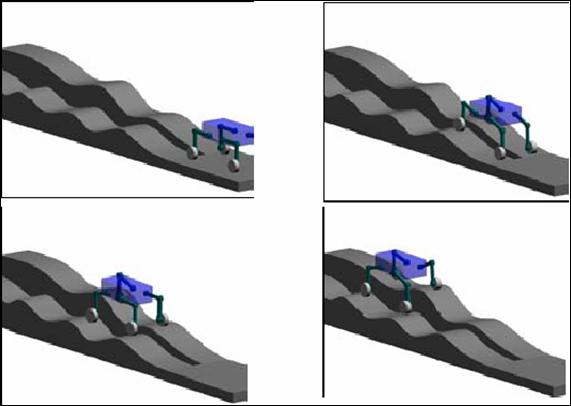
Рис.3. Моделирование движения Hylos по пересеченной местности
Основным преимуществом таких аппаратов является сочетание высоких
адаптационных возможностей шагающих машин и высокая скорость и устойчивость, а
также простота управления, колесных шасси, когда аппарат перемещается по
плоской или ровной с малыми неровностями поверхности. Как следствие можно
обоснованно считать, что роботы с колесно-шагающими шасси могут найти,
например, эффективное применение в задачах экстремальной робототехники.
Принципиальным является тот факт, что движение таких машин и
управление ими являются весьма сложными процессами. Поэтому и решение
соответствующих задач возможно только путем их создания как роботов, с
использованием накопленного робототехникой опыта. Технически создание
адекватных систем управления стало возможным только в последнее время - на
основе того прогресса в микроэлектронике и микромеханике, который мы сейчас наблюдаем.
Несомненным является тот факт, что до создания сложного аппарата со многими
степенями свободы необходим предварительный расчет и анализ динамики системы,
которая в последующем будет реализована на роботе.
Даная работа посвящена исследованию динамики движения модульных
колесно-шагающих аппаратов и синтезу управления ими.
1. «Универсальная» модель колесного
аппарата с изменяемой геометрией корпуса.
Рассмотрим четырехколесный
экипаж, у которого все колеса, невесомые плоские диски, могут поворачиваться
относительно его корпуса в шарнирах B1B2,B3,B4. Корпус экипажа состоит из двух весомых частей NAB1B2 и NA'B3B4 с центрами тяжести в
точках O и O', которые находятся на
прямых NA и NA'. Весомые части
корпуса соединены шарнирно в точке N, причем ось вращения этого шарнира, как и у четырех других,
будем считать вертикальной. Рассматриваемый аппарат схематично изображен на
Рис.1.1. Введем следующие обозначения: B1B2=2b, B3B4=2b', NA=l, NA'=l'', NO=a, NO'=a'', радиусы колес для номеров 1 и 2
- r, а для номеров
3 и 4 - r',
проекции NA' и NO' на горизонтальную
плоскость, в которой лежит отрезок NA, обозначим через l' и a'
соответственно, отрезки выноса колес обозначим c для колес 1 и 2, c' – для 3 и 4.
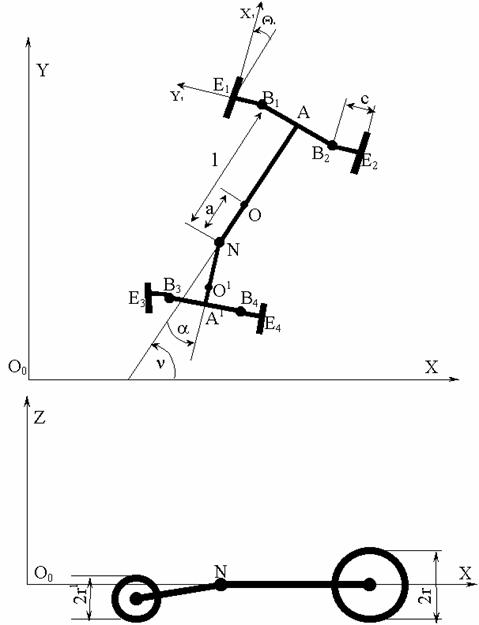
Рис. 1.1.
Универсальная четырехколесная модель аппарата
с
изменяемой геометрией корпуса.
Будем считать, что аппарат движется по ровной горизонтальной
плоскости без проскальзывания. Контакт колес с плоскостью точечный (в точках K1, K2, K3, K4
соответственно). Центры колес (плоских дисков) обозначим точками E1, E2, E3, E4, как это
показано на рисунке. Тогда B1E1=B2E2=c и B3E3=B4E4=c'.
Введем неподвижную систему координат O0XYZ такую, что плоскость O0XY параллельна плоскости, по которой
происходит движение, ось Z
направлена по вертикали и составляет с ними правую тройку. Также введем
трехгранники EiXiYiZi,
жестко связанные с поворотными вилками колес (i=1,…,4) таким образом, что оси Xi, Zi расположены в
плоскости колеса, Zi
коллинеарна Z, и
образует с Xi
и Yi правую тройку. 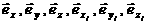 - единичные векторы осей X, Y, Z, Xi,Yi и
Zi соответственно (i=1,…,4). - единичные векторы осей X, Y, Z, Xi,Yi и
Zi соответственно (i=1,…,4).
Введем обобщенные координаты: x, y,
ν, α, Θi, ψi (i=1,…,4), где (x, y,0) - координаты точки O, ν - угол
поворота прямой NA
относительно оси O0X, или курсовой угол, α
- угол поворота прямой NA'
относительно прямой NA
(как показано на рисунке-схеме). Будем называть луч NA курсом.
Тогда углы, составляющие с курсом оси Xi обозначим
через Θi
соответственно. (Здесь и дальше i=1,…,4) Углы поворота колес относительно
осей Yi обозначим через ψi.
Пользуясь формулой Эйлера и общими теоремами динамики при условии
отсутствия бокового и продольного проскальзывания колес в точках касания с
плоскостью (неголономная система) и введя силы и моменты, действующие в системе
и на нее со стороны поверхности, получим уравнения движения для описанной
модели.
[1.1] 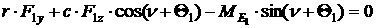
[1.2] 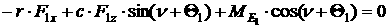
[1.3] 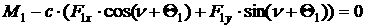
[1.4] 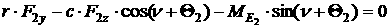
[1.5] 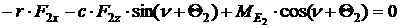
[1.6] 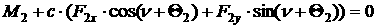
[1.7] 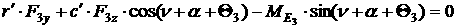
[1.8] 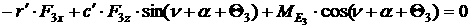
[1.9] 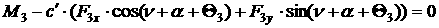
[1.10] 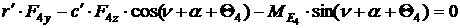
[1.11] 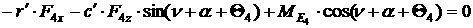
[1.12] 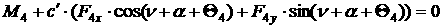
[1.13] 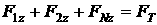
[1.14] 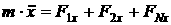
[1.15] 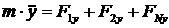
[1.16] 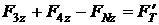
[1.17] 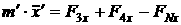
[1.18] 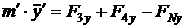
[1.19] 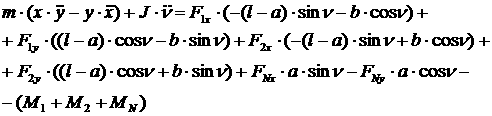
[1.20] 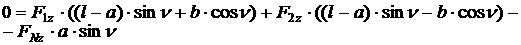
[1.21] 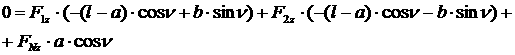
[1.22] 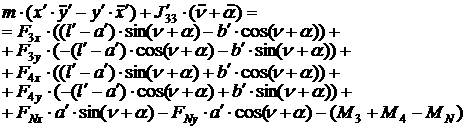
[1.23] 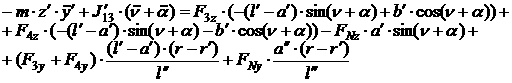
[1.24] 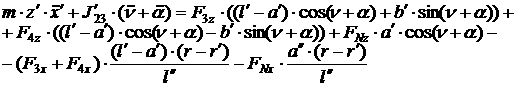
Так получены 24 скалярных уравнения, 16 из которых алгебраические,
а 8 – дифференциальные, относительно следующих 32 неизвестных: 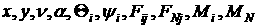 , где j=x,y,z. Замыкание этой системы выполняется присоединением кинематических
уравнений связей. , где j=x,y,z. Замыкание этой системы выполняется присоединением кинематических
уравнений связей.
[1.25] 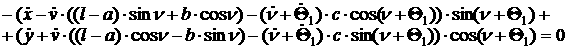
[1.26]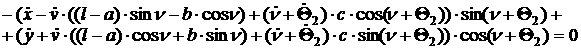
[1.27]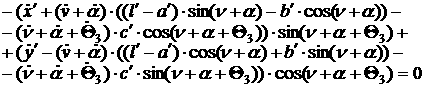
[1.28] 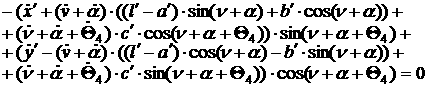
[1.29] 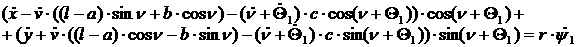
[1.30] 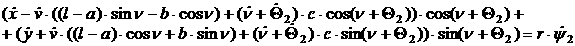
[1.31] 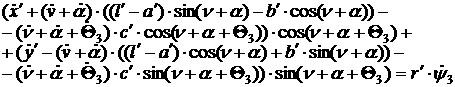
[1.32] 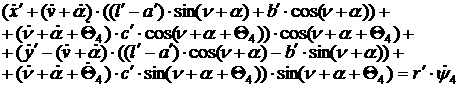
Из рассмотренной «универсальной» схемы получены уравнения движения
для четырехколесной схемы с жестким корпусом (которая изображена на Рис.1.2)
следующим образом:
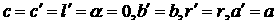
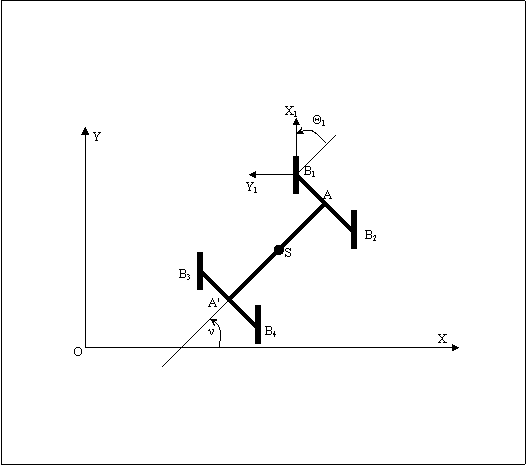
Рис. 1.2. Четырехколесный аппарат с жестким корпусом
Так же аналогичные уравнения получены и для трехколесного экипажа с одним «рояльным»
колесом. Они совпадают с уравнениями, полученными и исследованными в работе
[2], что позволило дополнительно верифицировать модель.
2. Полная система уравнений 4-х колесного аппарата и обратная задача
движения. «Вальс на прямой». «Вальс на окружности».
Рассмотрим четырехколесный
экипаж, у которого все колеса - весомые плоские диски - могут поворачиваться
относительно его корпуса в шарнирах B1B2,B3,B4. Пусть центр масс расположен в геометрическом
центре корпуса S. Введем следующие обозначения: B1B2= B3B4=2b, AA'=2a, радиусы колес – r (схема приведена на Рис.
1.2.)
Будем считать, что тележка
движется по ровной горизонтальной плоскости без проскальзывания. Контакт колес
с плоскостью точечный (в точках K1, K2, K3, K4 соответственно). Центры колес (плоских дисков)
находятся в точках B1B2,B3,B4 (Рис. 1.2).
Введем неподвижную систему
координат OXYZ такую, что плоскость OXY параллельна плоскости, по которой происходит
движение, ось Z направлена по вертикали и
составляет с осями OX
и OY правую тройку. Также
введем трехгранники BiXiYiZi, жестко связанные с
поворотными вилками колес (i=1,…,4) таким образом, что оси Xi, Zi расположены в плоскости колеса, Zi коллинеарна Z, и образует с Xi и Yi правую тройку. 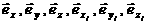 - единичные векторы осей X, Y, Z, Xi,Yi и Zi соответственно (i=1,…,4). - единичные векторы осей X, Y, Z, Xi,Yi и Zi соответственно (i=1,…,4).
Введем
обобщенные координаты: x, y,
ν, Θi,
ψi
(i=1,…,4),
где (x, y,0)
- координаты
точки S, ν - угол поворота прямой A'A относительно оси OX, или курсовой угол. Будем
называть луч A'A курсом. Тогда углы, составляющие с курсом оси Xi, обозначим через Θi соответственно. (Здесь и
дальше i=1,…,4) Углы поворота колес относительно осей Yi обозначим через ψi.
При отсутствии продольного
и поперечного проскальзывания колес пользуясь формулой Эйлера получим уравнения
связей для каждого из колес. В абсолютной системе координат кинематические
уравнения связей будут иметь вид:
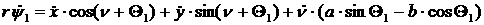
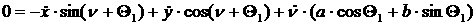
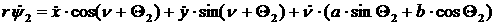
[2.1] 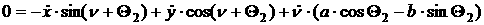
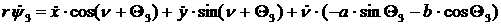
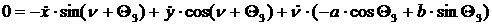
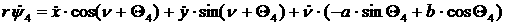
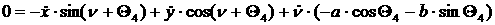
Пусть тележка движется с
постоянными линейной скоростью центра масс и угловой скоростью корпуса 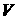 и и  соответственно и соответственно и 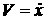 , , 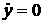 , , 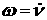 . Назовем такое движение «Вальсом на прямой». Преобразуем
уравнения для каждого из колес и выразим зависимость . Назовем такое движение «Вальсом на прямой». Преобразуем
уравнения для каждого из колес и выразим зависимость 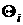 и и 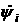 от этих параметров: от этих параметров:
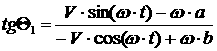
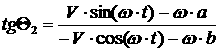
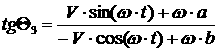
[2.2] 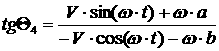
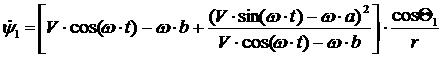
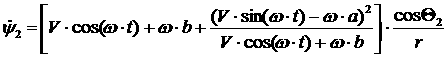
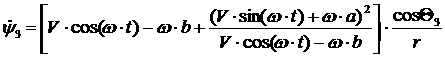
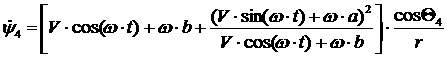
Получим динамические
уравнения рассматриваемой системы. При этом
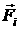 - силы, с которыми
действуют колеса на корпус в точках крепления, - силы, с которыми
действуют колеса на корпус в точках крепления, 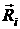 - силы реакции
поверхности, действующие на колеса, - силы реакции
поверхности, действующие на колеса, 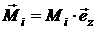 - моменты относительно
вертикальной оси, действующие на колеса со стороны корпуса в точках крепления
колес и - моменты относительно
вертикальной оси, действующие на колеса со стороны корпуса в точках крепления
колес и 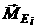 - осевые управляющие
моменты относительно осей вращения колес, действующие на колеса в точках
крепления. - осевые управляющие
моменты относительно осей вращения колес, действующие на колеса в точках
крепления.
Запишем выражения для
импульса и его момента относительно начала координат абсолютной системы
координат для системы (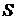 -центр корпуса): -центр корпуса):
[2.3] 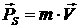
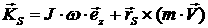 . .
Здесь 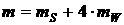 - масса всей системы, - масса всей системы,  - момент инерции
системы относительно вертикальной оси, проходящей через центр корпуса. - момент инерции
системы относительно вертикальной оси, проходящей через центр корпуса.
Теперь выражения для
импульса и его момента относительно начала координат абсолютной системы
координат для каждого из колес:
[2.4] 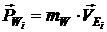
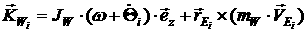 , ,
где 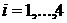 , , 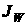 - момент инерции
колеса относительно вертикальной оси, проходящей через центр диска колеса, - момент инерции
колеса относительно вертикальной оси, проходящей через центр диска колеса, 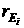 - радиус вектор центра колеса в абсолютной системе координат. - радиус вектор центра колеса в абсолютной системе координат.
Запишем уравнения движения
для корпуса и каждого из колес, пользуясь теоремами об изменении импульса и
кинетического момента.
Для корпуса:
[2.5] 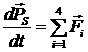
[2.6] 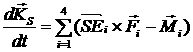 ; ;
для каждого из колес (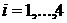 ): ):
[2.7] 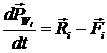
[2.8] 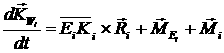 . .
Поскольку 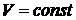 и и 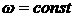 , ,
[2.9] 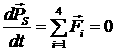
[2.10] 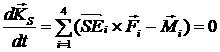 . .
Отсюда получим:
[2.11] 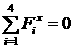
[2.12] 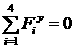
[2.13] 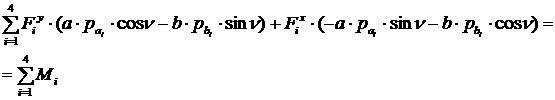
(здесь 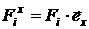 , , 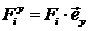 , , 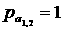 , , 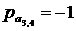 , , 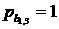 , , 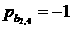 ). ).
Далее, для колес:
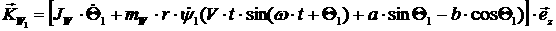
[2.14] 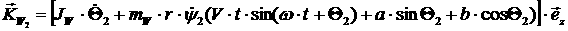
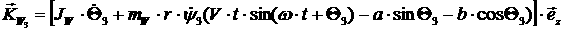
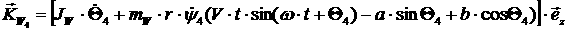
откуда:
[2.15] 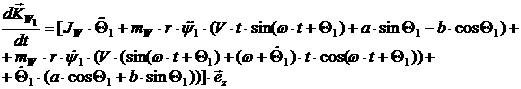
[2.16] 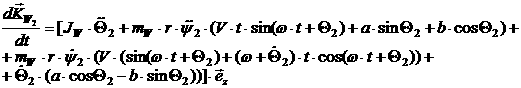
[2.17] 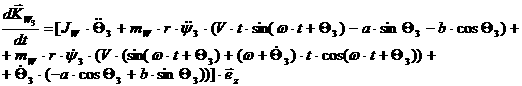
[2.18] 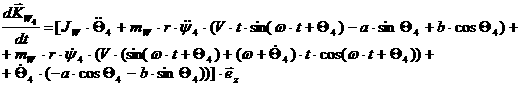
Импульсы (по-прежнему
пользуемся условием отсутствия проскальзывания колес в точках контакта с
поверхностью):
[2.19] 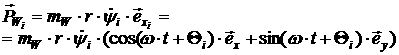
для 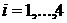 . .
Отсюда следует:
[2.20] 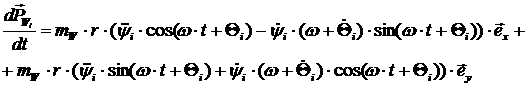
Подставим в [2.7] и [2.8] выражения левых частей и
разложим по осям координат. Получим:
[2.20] 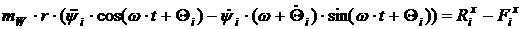
[2.21] 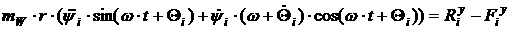
[2.22] 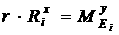
[2.23] 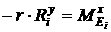
[2.24] 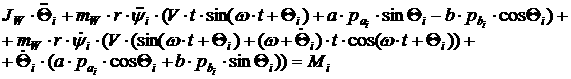
Последнее равенство дает выражение
для каждого из моментов 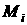 . .
Положим 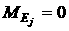 для для 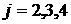 . .
Тогда
получим:
[2.25] 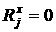
[2.26] 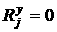
[2.27] 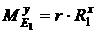
[2.28] 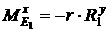
[2.29] 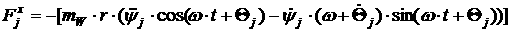
[2.30] 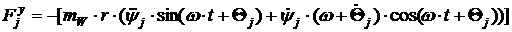
[2.31] 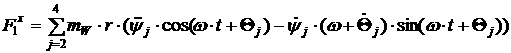
[2.32] 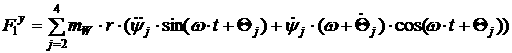
Отсюда:
[2.33] 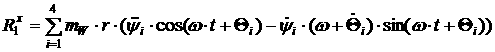
[2.34] 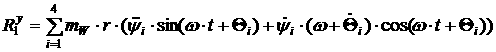
Тогда
получим выражения для управляющих моментов в проекциях на неподвижные оси
координат:
[2.35] 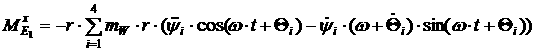
[2.36]  . .
Таким образом, мы решили обратную задачу. То есть по заданному
движению, в данном случае движению с постоянными скоростями линейной и угловой,
мы восстановили управляющие моменты на колесах: осевые и вертикальные
диаметральные.
Далее, из [2.19] следует:
[2.36] 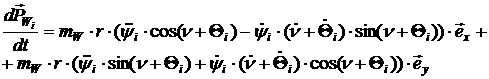
Из [2.14] получим:
[2.37] 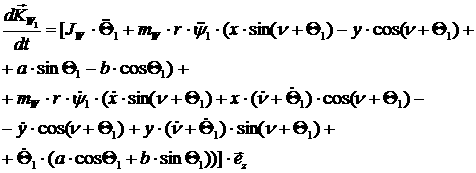
[2.38] 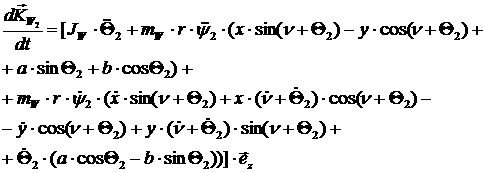
[2.39] 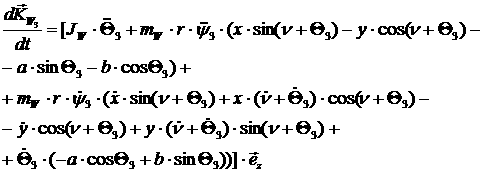
[2.40] 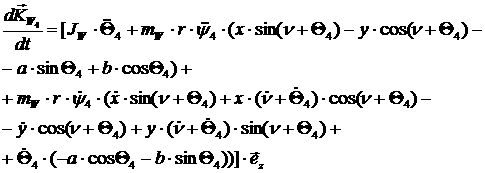
После преобразований [2.9] и [2.10] получим:
[2.41] 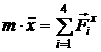
[2.42] 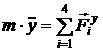
[2.43] 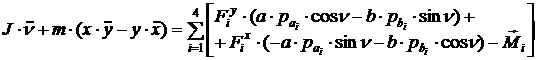 . .
Из уравнений движения для колес выразим 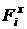 , , 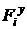 , и , и 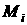 , и подставим их в уравнения [2.41]- [2.43]. , и подставим их в уравнения [2.41]- [2.43].
[2.44] 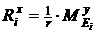
[2.45] 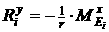
[2.46] 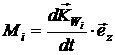
Определим функции 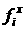 и и 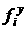 следующим образом: следующим образом:
[2.47] 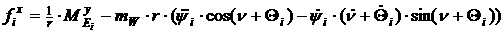
[2.48] 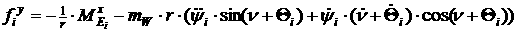
Тогда:
[2.49] 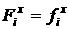
[2.50] 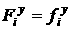
Подставляя эти выражения в уравнения движения корпуса, получим
равенства, которые в совокупности с кинематическими уравнениями связи дают
полную систему уравнений движения описанной четырехколесной модели ([2.51]- [2.59]).
При этом моменты 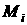 задаются выражениями [2.15]- [2.18] и [2.46]. задаются выражениями [2.15]- [2.18] и [2.46].
[2.51] 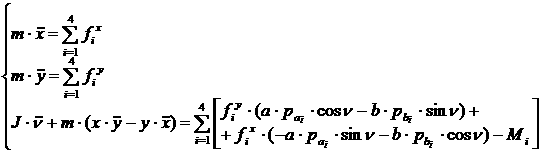
[2.52] 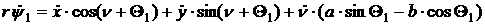
[2.53] 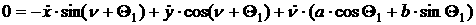
[2.54] 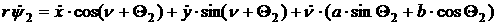
[2.55] 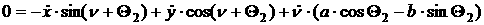
[2.56] 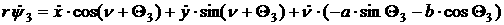
[2.57] 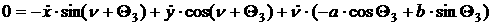
[2.58] 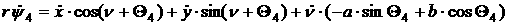
[2.59] 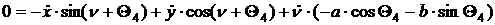 . .
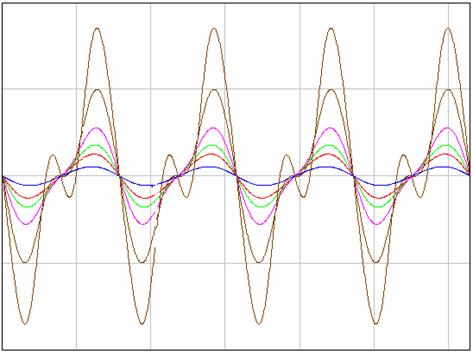
Рис.2.1. Семейство графиков суммы управляющих моментов
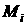
для движения «Вальс на прямой»
На Рис.2.1.1 изображено семейство графиков суммы управляющих
моментов 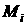 для движения «Вальс на
прямой» для различных значений линейной скорости центра корпуса V и постоянного значения
угловой скорости корпуса. Ось ординат – это значения суммы моментов для движения «Вальс на
прямой» для различных значений линейной скорости центра корпуса V и постоянного значения
угловой скорости корпуса. Ось ординат – это значения суммы моментов 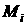 , а ось абсцисс – время. Рассмотренный отрезок времени
соответствует двум полным оборотам робота вокруг вертикальной оси, проходящей
через центр корпуса, во время движения по базовой прямой. , а ось абсцисс – время. Рассмотренный отрезок времени
соответствует двум полным оборотам робота вокруг вертикальной оси, проходящей
через центр корпуса, во время движения по базовой прямой.
Теперь рассмотрим такое движение, при котором тележка двигается с
постоянной линейной скоростью 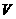 и постоянной угловой
скоростью и постоянной угловой
скоростью 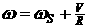 , где , где 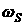 - угловая скорость
корпуса относительно вертикальной оси, связанной с его центром S, а R – радиус окружности, по которой
происходит движение ( - угловая скорость
корпуса относительно вертикальной оси, связанной с его центром S, а R – радиус окружности, по которой
происходит движение (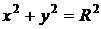 ). Назовем это движение «Вальс на окружности». Тогда ). Назовем это движение «Вальс на окружности». Тогда
[2.60] 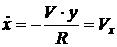
[2.61] 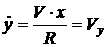
и
[2.62] 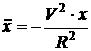
[2.63] 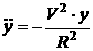 . .
Тогда при одном ведущем колесе получим выражения для проекций
управляющего момента:
[2.64] 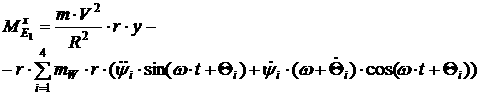
[2.65] 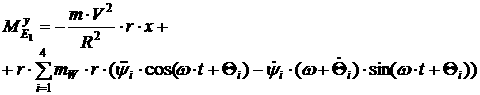
где
[2.66] 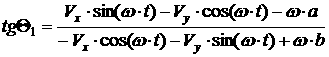
[2.67] 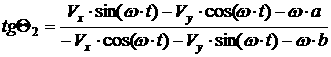
[2.68] 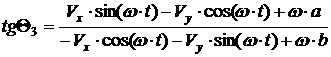
[2.69] 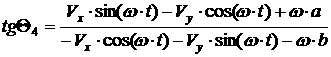
3. Моделирование движения «Вальс».
Для проверки корректности полученных уравнений движения и выражений
для управляющих моментов воспользуемся программным продуктом MathCad 2001. Для этого полученные
выражения для моментов подставим в правые части уравнений движения и решим
систему дифференциальных уравнений движения при помощи численного
интегрирования методом Рунге-Кутта с шагом фиксированной длины. В MathCad для этого есть
специальная функция rkfixed().
Удобство такой проверки заключается в том, что MathCad принимает уравнения в таком
виде, в котором мы их получили аналитически, лишь с незначительными изменениями
для соблюдения синтаксиса, предусмотренного программой. Результатами
интегрирования являются графики изменения величин, задающих движение 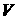 и и  , в зависимости от времени. Интегрирование показало, что
уравнения верны, так как полученные графики – это прямые, параллельные оси
времени. То есть , в зависимости от времени. Интегрирование показало, что
уравнения верны, так как полученные графики – это прямые, параллельные оси
времени. То есть 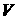 и и  - константы. - константы.
Для движения «Вальс на окружности» таких графиков недостаточно. Для
анализа реализации такого движения еще необходимо видеть, что центр корпуса
движется по окружности заданного радиуса. Поэтому для проверки этого построен
еще один график в абсолютной системе координат Y(X).В результате интегрирования получен график координат центра
корпуса исследуемого аппарата в горизонтальной плоскости y от x. Это окружность, радиуса заданного
R.
Для моделирования движения использовался программный комплекс
«Универсальный механизм» (UM), предназначенный для моделирования динамики и
кинематики механических систем, плоских и пространственных механизмов.
Исследуемая модель – четырехколесный аппарат с весомыми колесами.
Дерево-структура описания модели и внешний вид объекта в «Универсальном
механизме» изображены на Рис.3.1.
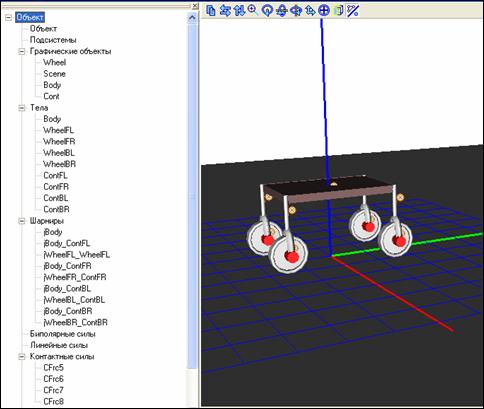
Рис.3.1. Модель четырехколесного аппарата в
«Универсальном механизме»
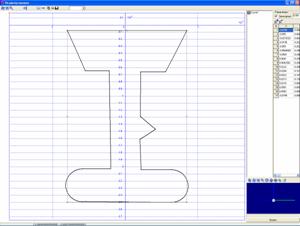 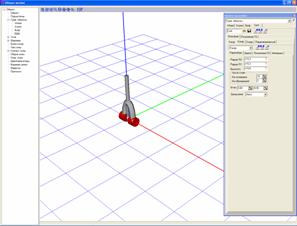
Рис.3.2. Профиль колеса Рис.3.3.
Объект «вилка колеса»
Робот состоит из девяти тел, представленных тремя графическими объектами
(ГО). Помимо ГО, описывающих тележку, введен ГО для поверхности, по которой
происходит движение. Итак, тела:
Body –
корпус робота – ГО Body
WheelFL –
переднее левое колесо – ГО Wheel
WheelFR –
переднее правое колесо – ГО Wheel
WheelBL –
заднее левое колесо – ГО Wheel
WheelBR –
заднее правое колесо – ГО Wheel
ContFL –
вилка переднего левого колеса – ГО Cont
ContFR –
вилка переднего правого колеса – ГО Cont
ContBL –
вилка заднего левого колеса – ГО Cont
ContBR –
вилка заднего правого колеса – ГО Cont.
Поверхности, по которой происходит движение, сопоставлен
графический объект Scene.
Геометрические параметры графических объектов следующие:
На Рис.3.2 изображен профиль половины колеса ГО Wheel. Для изображения вилки колеса
выбран графический образ, изображенный на Рис.3.3.
ГО корпуса – прямоугольный параллелепипед. Динамические параметры
тел требуют определения следующих значений:
Body –
корпус робота
mc – масса
корпуса;
icx –
элемент диагонального тензора инерции корпуса, соответствующий оси X;
icy – элемент
диагонального тензора инерции корпуса, соответствующий оси Y;
icz –
элемент диагонального тензора инерции корпуса, соответствующий оси Z;
WheelFL, WheelFR, WheelBL, WheelBR – колеса робота
mw – масса
колеса;
iwx –
элемент диагонального тензора инерции колеса, соответствующий оси X;
iwy –
элемент диагонального тензора инерции колеса, соответствующий оси Y;
iwz –
элемент диагонального тензора инерции колеса, соответствующий оси Z;
ContFL, ContFR, ContBL, ContBR – вилки колес робота
инерционные параметры вычисляются автоматически из расчета того,
что вилки (с заданной геометрией) сделаны из стали заданной плотности.
Описание шарниров объекта:
jBody –
шарнир, определяющий подвижность корпуса
относительно поверхности, по которой происходит движение. Состоит из
шести степеней свободы относительно неподвижной системы координат (трех
поступательных и трех вращательных)
jBody_ContFL, jBody_ContFR, jBody_ContBL, jBody_ContBR – шарниры между корпусом робота и вилками колес. Составные
части шарниров следующие:
TVz –
поступательная степень свободы вдоль оси Z с наложенным ограничением в виде силы 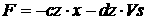 , где , где 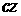 и и 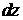 - коэффициенты
жесткости и демпфирования - коэффициенты
жесткости и демпфирования
TC –
постоянный сдвиг по осям,
RTz –
вращательная функция времени относительно оси Z, заданная параметром alfaFL, alfaFR, alfaBL, alfaBR соответственно, который
определяется в файле управления.
jWheelFL_ContFL, jWheelFR_ContFR, jWheelBL_ContBL, jWheelBR_ContBR – шарниры между вилками колес и
самими колесами. Эти шарниры заданы как вращательные степени свободы
относительно осей вращения колес. Для одного из шарниров при этом задан
управляющий момент torq4,
рассчитываемый и задаваемый в файле управления на каждом шаге интегрирования
при моделировании движения.
Для описания контактных сил между колесами и поверхностью, по
которой происходит движение, выбран типовой вариант контакта «Сфера – Z-поверхность». В простейшем
случае Z-поверхность –
это плоскость.
Отметим, что в созданной модели только на одном колесе установлен
управляющий момент относительно оси вращения колеса. Выражение для него при
реализации движения «Вальс на прямой» задаются равенствами [2.35] и [2.36]. Для движения «Вальс на окружности» -
это равенства [2.64] и [2.65].
Пользуясь этими выражениями и кинематическими уравнениями движения,
модернизируем файл управления таким образом, чтобы при его выполнении
вычислялся управляющий момент на каждом шаге интегрирования. Надо отметить, что
модель, построенная в «Универсальном механизме» несколько отличается от
математической идеализированной модели аппарата, использованной при решении
обратной задачи для движения «Вальс». Так, например, контакт колес с
поверхностью, по которой происходит движение, в «Универсальном механизме»
выбран контакт с трением, а при аналитическом исследовании использовался
контакт с условием отсутствия проскальзывания. Поэтому выражения для
управляющих моментов, перенесенные в чистом виде в файл управления, не
обеспечат реализации заданного движения на большом участке времени.
Для решения этой проблемы, для стабилизации движения модели,
приближенной к реальной, около заданного движения «Вальс» предлагается в
выражения для управляющих моментов добавить линейный стабилизирующий член,
зависящий от отклонений реальных значений параметров, задающих движение.
Тогда для движения «Вальс на прямой» выражение для управляющего
момента будет выглядеть так:
[3.1] 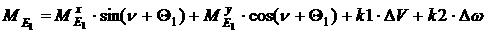
где k1
и k2 –
константы.
Исследования показали, что наибольший вклад в стабилизацию движения
«Вальс на прямой» вносит член с коэффициентом k2. На рисунках Рис. 3.4 и Рис. 3.5
изображены графики изменений реальных величин угловой скорости корпуса робота ( ), проекции линейной скорости центра корпуса на
неподвижную ось X ( ), проекции линейной скорости центра корпуса на
неподвижную ось X (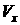 ) и ось Y
( ) и ось Y
( ) при значениях коэффициента k2=10 и k2=1000 соответственно. ) при значениях коэффициента k2=10 и k2=1000 соответственно.
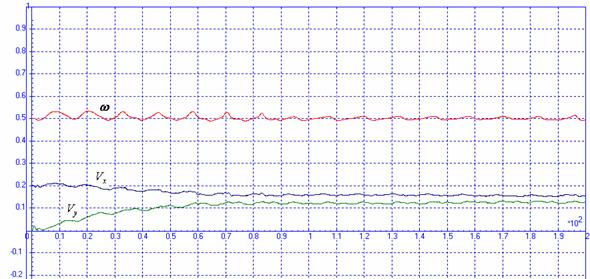
Рис. 3.4. Графики отклонений от заданного движения. k2=10
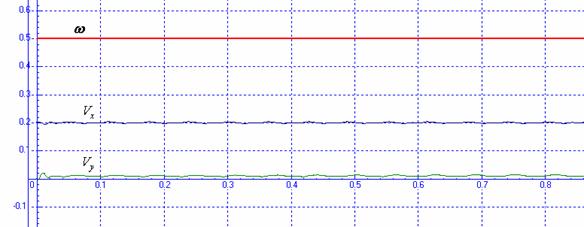
Рис. 3.5. Графики отклонений от заданного движения. k2=1000
Конечно, необходимо заранее знать значение
k2, при котором
уравнения обеспечат заданное движение аппарата с определенной точностью. Для
этого предлагается построить графики зависимости минимальных значений
коэффициента k2,
от величин, задающих движение для различных ограничений. Приведем два примера
таких графиков.
Первый график (Рис.3.6 вверху) построен при следующих значениях
параметров: период модельного времени – 400 секунд, максимальное отклонение
линейной скорости по оси Y
(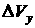 ) – 0.02, угловая скорость корпуса робота относительно
вертикальной оси ( ) – 0.02, угловая скорость корпуса робота относительно
вертикальной оси ( ) – 0.5. По оси абсцисс – значения проекции линейной
скорости центра корпуса аппарата на ось X ( ) – 0.5. По оси абсцисс – значения проекции линейной
скорости центра корпуса аппарата на ось X (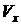 ), а по оси ординат – значения коэффициента k2. ), а по оси ординат – значения коэффициента k2.
При этом надо отметить, что значения коэффициента, лежащие выше
графика, подходят для всех значений скоростей из рассматриваемого диапазона.
Для сравнения приведем еще один график такой зависимости. Для него
выбрано значение угловой скорости ( ) 0.8 при прочих равных параметрах (Рис.3.6 снизу).
Видно, что график на правой части рисунка более круто поднимается по тем же
значениям линейных скоростей (масштабы правого и левого рисунков совпадают). ) 0.8 при прочих равных параметрах (Рис.3.6 снизу).
Видно, что график на правой части рисунка более круто поднимается по тем же
значениям линейных скоростей (масштабы правого и левого рисунков совпадают).
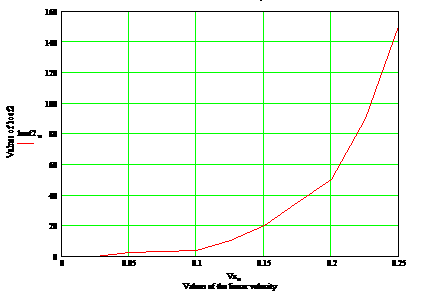 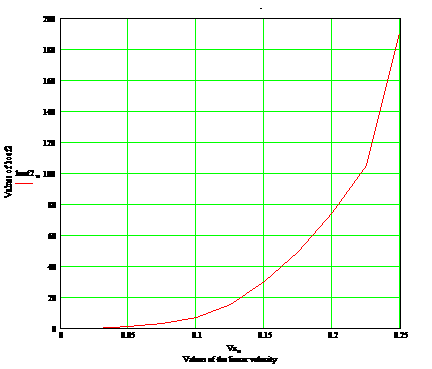
Рис. 3.6. Графики минимальных значений k2
обеспечивающих заданную точность
Аналогичное исследование проведено и для движения «Вальс на
окружности».
Выражение для управляющего момента будет иметь вид:
[3.2] 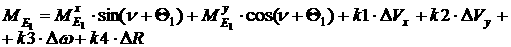
В правую часть добавлено еще одно
слагаемое 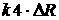 . Для движения «Вальс на окружности» - это главный
стабилизирующий член. . Для движения «Вальс на окружности» - это главный
стабилизирующий член.
4. Моделирование движения модульных
колесно-шагающих аппаратов в программном комплексе «Универсальный механизм».
Рассмотрим модели модульных колесных
аппаратов, аналогичные той, что рассматривалась в параграфе 3 при моделировании
движения «Вальс» в «Универсальном механизме».
Только теперь рассмотрим не четыре
колесных модуля, а шесть. Возможны различные схемы расположения колес. Например
«продольно-симметричная 3х3» (Рис. 4.1) или «ромбовидная» (Рис. 4.2).
Преимущества шестиколесного аппарата
перед четырехколесным при движении по поверхности с препятствиями очевидны.
Рассмотрим некоторые элементы движения (Рис. 4.3) при преодолении препятствия
«брус» шестиколесным роботом со схемой расположения колес
«продольно-симметричной 3х3» (Рис. 4.1).
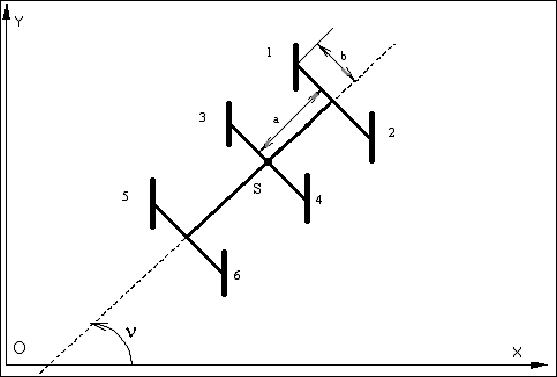
Рис 4.1. Шестиколесный аппарат с
«продольно-симметричной 3х3»
схемой расположения колес
Рис 4.2. Шестиколесный аппарат с «ромбовидной»
схемой расположения колес
Исследование
движения шестиколесного аппарата в режиме совместного качения и шагания при
преодолении препятствий на примере «бруса» на горизонтальной плоскости
количественно подтвердило преимущество режима движения с точки зрения динамических
характеристик комфортабельности движения и силовых нагрузок в опорах аппарата.
А режим шагания невозможен для четырехколесного робота.
 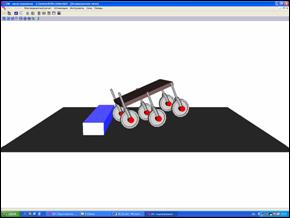
Рис. 4.3. Шестиколесный аппарат с
«продольно-симметричной 3х3»
схемой расположения колес при преодолении препятствия.
Также
виден недостаток «продольно-симметричной 3х3» схемы расположения колес
(Рис. 4.3 справа). При резком поднятии передней или задней пары колес возникает
значительный момент относительно средней пары, который заставляет аппарат
склониться (завалиться) в сторону поднятой пары, что ликвидирует преимущества
колесно-шагающего робота перед колесной машиной с пассивной подвеской.
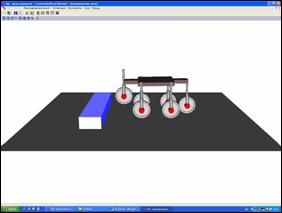
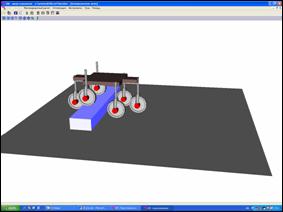
Рис. 4.4. Шестиколесный аппарат с «ромбовидной»
схемой расположения колес при преодолении препятствия
Решением проблемы «заваливания»
становится «ромбовидная» схема расположения колес (Рис. 4.2 и Рис. 4.4).
При исследовании движения модели такого
аппарата в модели с помощью «Универсального механизма» был разработан и
реализован алгоритм преодоления препятствия «брус» в автоматическом режиме с
полной информацией о его (препятствия) местонахождении при гибридном режиме
движения качения и шагания. Поскольку поднятие колес над землей происходит при
этом во время движения, и оно не мгновенно, то необходимо обеспечить заблаговременное
начало движения колесных модулей вверх для обеспечения максимально-допустимой
высоты центра колеса в момент его (центра) прохождения над ближним ребром
бруса.
Эта задача решается обеспечением
движения центра поднимающегося колеса (колес) по ребру трапеции с большим
основанием, лежащим в плоскости, по которой происходит движение, и меньшим на
высоте равной высоте бруса плюс R (радиус колеса), либо на максимальной высоте поднятия
колес.
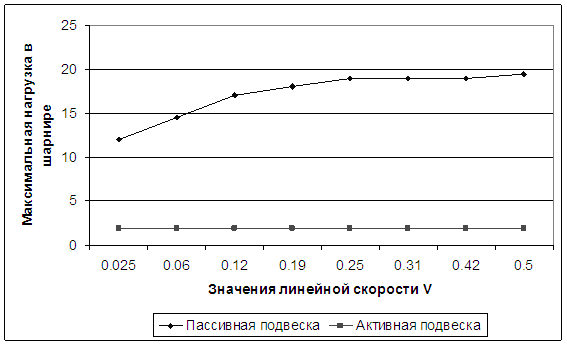
Рис.4.5. Зависимости максимальной нагрузки в шарнире передней вилки
На
Рис.4.5 приведены относительные графики зависимости максимальной нагрузки в
шарнире передней вилки при наезде на брус от линейной скорости. Исследование
проведено при движении с пассивной подвеской и с активной при прочих одинаковых
параметрах.
Аналогично решена задача движения по
синусоидальной поверхности с активной подвеской. Если уравнение профиля
поверхности z = sin(y), то траектория,
которую должен описывать центр колеса с координатами (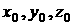 ) при движении аппарата по этому профилю, то графически эта
траектория точками изображена на рис. 4.6 справа. ) при движении аппарата по этому профилю, то графически эта
траектория точками изображена на рис. 4.6 справа.
А аппарат с активной подвеской при
движении по такой поверхности будет выглядеть так, как показано на Рис. 4.6
слева.
При моделировании решена задача
преодоления препятствия «брус» с частичной информацией о его местонахождении.
Допустим на робот поступила информация о направлении, в котором находится брус,
но нет информации о точном расстоянии до него и о его точной высоте. Конечно,
предполагается, что высота бруса не превосходит максимально-допустимую, которую
может преодолеть робот. Также, пусть на аппарате установлен гиродатчик, который
показывает углы отклонения корпуса робота от горизонтальной плоскости.
Алгоритм обнаружения и преодоления препятствия в таком случае сводится
к следующему. Передним колесом надо совершать шагающие движения до тех пор,
пока нормаль к поверхности корпуса не отклонится на критический угол (Рис.
4.7). Критический угол может быть выбран экспериментально с учетом используемых
ускорений робота и величин неровностей поверхности, по которой происходит
движение.
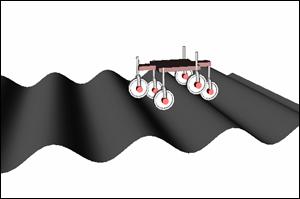 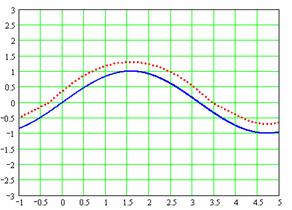
Рис. 4.6. Шестиколесный аппарат с активной подвеской
на поверхности с синусоидальным профилем.
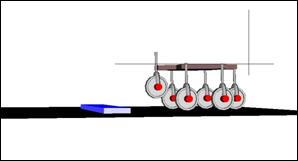 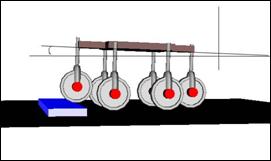
Рис. 4.7. Робот во время обнаружения препятствия.
Заключение.
Работа показала эффективность
созданных методов исследования динамики модульных колесных аппаратов,
рассмотренные в работе модели позволяют охватить широкий спектр вариантов
геометрии колесных систем и их кинематических и динамических характеристик.
Проведено исследование движения шестиколесного аппарата в режиме
совместного качения и шагания при преодолении препятствий на примере «бруса» на
горизонтальной плоскости. Выполнено сравнение динамических характеристик
комфортабельности движения и силовых нагрузок в опорах аппарата для случаев
пассивной и активной подвесок опор к корпусу. Показано существенное
преимущество активной системы: в рассмотренных примерах в 10 раз для
комфортабельности и в 1.5 раза для вертикальных силовых нагрузок в шарнирах.
Для рассмотренной модели реализован алгоритм обнаружения препятствия активными
опорами аппарата при заданном направлении движения.
Литература.
[1]
Лобас Л.Г.
«Неголономные модели колесных экипажей»
[2]
Девянин Е.А. «О
движении колесных роботов»
[3]
Голубев Ю.Ф.
«Основы теоретической механики»
[4]
Мусарский Р.А.,
Фуфаев Н.А. «Концепция твердого тела в теории движения колесных экипажей»
[5]
Лобас Л.Г.,
Вербицкий В.Г. «Качественные и аналитические методы в динамике колесных машин»
[6]
Endo G.
and Hirose S., Study on Roller-Walker (Multi-mode Steering
Control and Self-contained Locomotion). // International Conference on Robotics
and Automation (ICRA'2000), USA, San
Francisco, 2000.
[7]
Benamar F., Bidaud Ph., Plumet F., Andrade G. and
Budanov V. A high-mobility redundantly actuated mini-rover for self adaptation
to terrain characteristics. // Proc. CLAWAR'2000, Spain, Madrid, 2000.
[8]
ZANTIC robots WEB-site: http://www.zanthic.com
[9]
Halme A., Leppanen I., Salmi S. and Ylonen S. Hybrid
locomotion of a wheel-legged machine. //
Proc. CLAWAR'2000, Spain, Madrid 2000.
[10]
Halme A., Leppanen I., Montonen M. and Ylonen S. Robot motion by simultaneously wheel and leg
propulsion. // Proc. CLAWAR'2001, Germany, Karlsruhe 2001.
[11]
Lauria M., Piguet Y., R. Siegwart. Octopus - an
autonomous wheeled climbing robot. // Proc. CLAWAR'2002, France, Paris, 2002,
pp.315-322.
[12]
Benamar F., Bidaud Ph., Plumet F., Andrade G. and
Budanov V. A high-mobility redundantly actuated mini-rover for self adaptation
to terrain characteristics. // Proc. CLAWAR'2000, Spain, Madrid, 2000,
pp.105-112.
[13]
Ch.Grand, F.Ben Amar, F.Plumet, Ph.Bidaud. Stability
control of a wheel-legged mini-rover. // Proc. of 5-th Int. Conf. on Climbing
and Walking Robots CLAWAR'2002. Paris, France, September 2002, pp.323-331.
[14]
G.Andrade, F.BenAmar, Ph.Bidaud, and R.Chatila.
Modeling wheel-sand interaction for optimization of a rolling-peristaltic
motion of a marsokhod robot. // Proc. IROS's International Conference on
Intelligent Robots and Systems, 1998, pp.576-581.
[15]
Ch.Grand, F.BenAmar, F.Plumet, Ph.Bidaud. Decoupled
control of posture and trajectory of the hybrid wheel-legged robot Hylos. //
Proc. of the 2004 IEEE International Conference on Robotics & Automation,
New Orleans, LA, April 2004, pp.5111-5116.
|