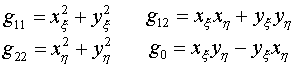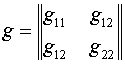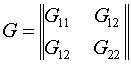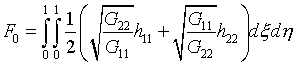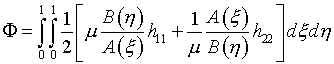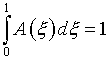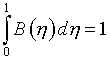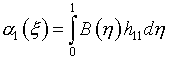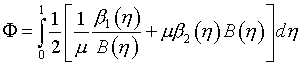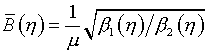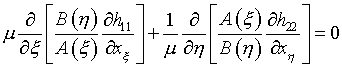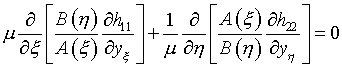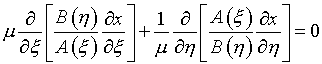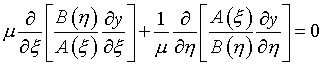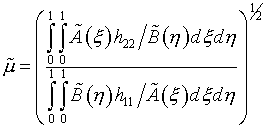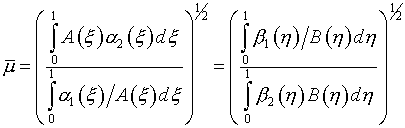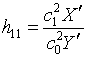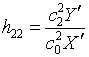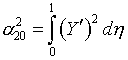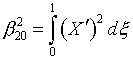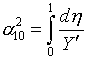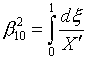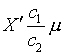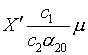Содержание

                                                                                                                стр.

Введение …………………………………………………………..        3

§ 1. Одномерные управляющие функции и их назначение…….        4

§ 2. Неравномерные прямоугольные «сетки» …………………..        8

§ 3. Неравномерные полярные «сетки»………………………….       11

§ 4. Дискретная реализация управления функционалом……….       14

§ 5. Некоторые замечания о расчете двумерных сеток…………       16

§ 6. Выбор функционала для трехмерных сеток и назначение

       одномерных  управляющих функций……………………….       21

§ 7. Модельные примеры для пространственного случая.

       Функционал без якобиана для трехмерных сеток………….       25

§ 8. О дискретизации пространственного функционала………..       26

Заключение  ………………………………………………………….   30  

Список литературы ………………………………………………..     31                              

Введение

         Дискретные аналоги вариационных функционалов широко используются, как один из возможных путей, при конструировании алгоритмов расчета двумерных сеток, необходимых для численного решения разнообразных задач математической физики. Существенной частью такой работы является автоматизация назначения коэффициентов функционалов. При решении нестационарных задач для их назначения могут использоваться метрические параметры сетки, полученной на предыдущем шаге расчета, с некоторой корректировкой для обеспечения удовлетворительных свойств сетки.

         В этом отношении в особом положении находится получение начальной сетки, для которого «предыдущего» шага нет. Некоторым аспектам возможных путей автоматизации назначения параметров функционала посвящена настоящая работа.

         Результаты, достигнутые при использовании вариационного подхода для двумерных сеток, создали уверенность в возможности их обобщения на случай пространственных (трехмерных) сеток. Проблема их построения была актуальной всегда, поскольку позволяет решать задачи для реальных объектов без той идеализации приближенного подхода, который неизбежно порождается рассмотрением двумерных задач.

         Существенно выросшая производительность вычислительной техники и растущие запросы практики потребность в надежных алгоритмах построения трехмерных сеток сделали особенно острой. Поэтому в настоящей работе будут рассматриваться и вопросы обобщения упомянутых выше алгоритмов на пространственный случай.

§ 1. Одномерные управляющие функции и их назначение.

1.1. Как обычно, при построении регулярной сетки в отдельной односвязной области W на плоскости переменных (х,у) будем считать ее четырехугольником с криволинейными границами. Тогда задачу можно трактовать как дискретную реализацию невырожденного отображения квадрата Q: (0£x, h£1) на область W .

В работах автора [1]-[3] для этой цели привлекаются вариационные функционалы вида:

(1.1)            ,          

(1.2)           ,              

Входящие в них величины представляют метрические параметры отображения:

(1.3)              

Ввиду очевидного тождества

(1.4)              

невырожденность отображения  взаимосвязана с положительной определенностью симметричной матрицы g и коэффициентов G:

  (1.5)        ,        

Функционалы (1.1) или (1.2) минимизируются на классе функций ,  , являющихся гладким продолжением внутрь квадрата Q заданных на его границе функций . Эти последние осуществляют  взаимно-однозначное отображение границы квадрата Q на границу области W, в которой должна быть построена сетка.

         Функционалы (1.1) и (1.2) различаются только отсутствием или наличием в знаменателе якобиана отображения g₀. Для краткости и наглядности условимся называть (1.1) функционалом без якобиана (ФБЯ), а (1.2) – функционалом с якобианом (ФЯ).

1.2. Если назначить в качестве коэффициентов

(1.6)               ,           ,           ,

оба функционала (1.1) и (1.2) достигают абсолютного минимума. Для второ-го из них , а для первого величина  равна площади области W..

         Следовательно, при назначении (1.6) оба функционала воспроизводят любое заданное невырожденное  отображение квадрата Q на область W. Их дискретные аналоги можно считать универсальными генераторами сеток.

         При расчете нестационарных задач с подвижными границами можно использовать сетку, полученную на предыдущем шаге по времени, и условия (1.6) для расчета сетки на новом шаге. По соображениям, обсуждавшимся, например, в [3]  на стр. 18-19, возникающие функционалы, названные опорными, нуждаются в некоторой корректировке посредством других функционалов для обеспечения удовлетворительных и желательных свойств сетки.

         Если этого не сделать, то, образно говоря, опорный функционал штампует очередную сетку по образу и подобию предыдущей, «не задумываясь», хороша она или плоха.

         В особом положении находится получение начальной сетки на исходный момент расчета, для которого «предыдущего» шага нет. Аналогичной является ситуация для задач, в которых сетка остается неподвижной в процессе нестационарного расчета или вообще речь идет о стационарной задаче.

1.3. Назначение коэффициентов матрицы G становится первоочередной заботой для таких ситуаций. В [3] были высказаны соображения о целесообразности использования (в качестве одного из вариантов решения этой проблемы) двух одномерных функций аргументов x,и h. Рассмотрением такой возможности мы и займемся.

         Назначим коэффициент . Это можно трактовать как стремление к получению «квазиортогональных» сеток.

Тогда функционалы (1.1) и (1.2) принимают вид:

(1.7)                 ,

(1.8)                ,                   в случае ФБЯ (1.1)

(1.9)                ,     в случае ФЯ (1.2)

         Введем в рассмотрение функционал вида:

(1.10)         

Здесь А(x), В(h) – некоторые управляющие функции. Как видно из (1.10), умножение их на одинаковый произвольный множитель не изменяет функционала. Чтобы обеспечить их детерминированность, использован прием из работы [4] .

         Будем считать обе функции А(x), В(h) нормированными:

(1.11)                 ,    ,

«компенсировав» эти ограничения дополнительным свободным параметром m, который должен быть подобран в процессе минимизации.

1.4. Пусть задано некоторое начальное состояние управляющих функций А(x), В(h) и отображения , , представляющего непрерывный аналог искомой сетки. Для краткости будем и его называть «сеткой» (отмечая это кавычками).

         Вычислим ее метрические параметры (1.3) и назначим функции ,  в соответствии с формулами (1.8) или (1.9).

         Как выяснится позже, с практической точки зрения представляется естественным в качестве исходного состояния функций А(x), В(h) использовать производные усредненных законов расстановки узлов сетки на противоположных границах области. Условия нормировки (1.11) при этом будут выполнены.

         Далее «заморозим»  В(h) и вычислим функции

(1.12)      ,      

Тогда для (1.10) получим выражение:

Очевидно, что его минимизация достигается при задании вместо А(x) управляющей функции

(1.13)                  

Аналогично,  «замораживая» А(x), вычислим функции:

(1.14)            ,         

Тогда для (1.10) получается выражение:

Его минимизация достигается назначением вместо В(h) управляющей  функции

(1.15)          

Для обеспечения нормировки (1.11) в качестве новых функций полагаем:

(1.16)            ,        

                     ,        

1.5. Отметим, что из формул (1.13) и (1.15) величину m можно убрать ввиду последующей нормировки (1.16).

         Однако параметр m будет играть весьма существенную роль при пересчете сетки. Напомним, что, как известно из курсов вариационного исчисления, уравнения Эйлера-Лагранжа, которым должна удовлетворять «сетка» , , обеспечивающая минимум вариационного функционала (1.10), имеют вид:

(1.17)                  

В случае ФБЯ (1.1) это линейные уравнения:

(1.18)                   

         В случае ФЯ (1.2) уравнения нелинейные и имеют существенно более громоздкий вид, который неоднократно обсуждался (см., напр., [3], стр.8). Мы их выписывать не будем.

         Параметр m определяется требованием минимизации функционала (1.10). Следовало бы воспользоваться полученными новыми функциями , что привело бы к формуле:

(1.19)                   

Однако, в целях экономии вычислительных затрат, разумно и, по-видимому, вполне допустимо, учитывая интегральный характер параметра m, совмещать его расчет с расчетом . Причем воспользоваться не просто вычислениями , а результатами (1.12) или (1.14) в таком виде:

(1.20)          

         Новое обозначение введено в (1.20) потому, что, вообще говоря,  в формуле (1.19).

1.6. После реализации формул (1.12)-(1.16), а затем (1.19) или (1.20), возникает альтернатива: либо сразу принять ,  (или ) в качестве управляющих, либо продолжить процесс их вычисления, приняв их в качестве нового приближения и повторяя еще раз описанную процедуру при зафиксированной «сетке» , , т.е. для прежних функций , . К обсуждению вопроса о целесообразности такого гипотетического итерационного процесса вернемся позже.

         Пока же отметим, что в случае, если в формулах (1.16) отменить нормировку посредством величин А₀, В₀ и упразднить параметр m, то результат будет аналогичным. Проблема состоит в том, не приведет ли это к неконтролируемому росту погрешностей вычислений при использовании такой упрощенной процедуры на огромном числе временных шагов нестационарного процесса. Поэтому мы предпочитаем описанный, несколько более обременительный в плане вычислительных затрат, но более надежный вариант.

Ввиду того, что назначение управляющих параметров приобретает итерационный характер, стоит обратить внимание на возможность использования меры предосторожности в виде коэффициента «запаса», чтобы демпфировать возможные колебательные процессы. Этот прием настолько традиционен, что мы ограничимся этим замечанием.

§ 2. Неравномерные прямоугольные «сетки».

         2.1. В качестве методического примера, иллюстрирующего предлагаемый алгоритм выбора одномерных управляющих функций, рассмотрим неравномерные прямоугольные «сетки». Они задаются формулами:

(2.1)                

Естественно предполагать, что , .

         Здесь и далее подразумевается, что

(2.2)         ,        ,

т.е. дифференцирование делается по своему аргументу.

         Без ограничения общности можно предполагать, что

(2.3)          ,            .

Для упрощения дальнейших формул введем величины:

(2.4)      ,            ,          

Величины с₁, с₂ представляют длины сторон области Ω , занимаемой отображением квадрата Q, которая является параллелограммом.

         Если  , то область Ω – прямоугольник.

Вычислим производные отображения (2.1):

         ,         ,         ,      

         В силу условий нормировки (2.3) функции ,  представляют законы расстановки узлов «сетки» на границах области.

         Метрические параметры «сетки» определяются формулами:

(2.5)                  

В соответствии с (1.8) и (1.9) будем иметь:

(2.6)        ,          в случае ФБЯ (1.1)

                ,                в случае ФЯ (1.2)

2.2. Рассмотрим по два варианта исходного задания управляющих функций:

первый -  ,  ;

второй  -  .

Результаты, получаемые по формулам (1.12)-(1.16), дополним значениями параметра , получаемыми по формулам (1.20). Значение  для всех этих вариантов. Результаты представлены в таблице 1.

Возникшие по ходу дела постоянные определяются так:

(2.7)                         

                                                Таблица 1.

         2.3. Прокомментируем полученные результаты.

1⁰. Во всех рассмотренных вариантах этого простейшего примера получаются или подтверждаются правильные значения управляющих функций

(2.8)          ,         .

В случае прямоугольной области площади прямоугольника.

Легко проверить, что в случае (2.8) получаются значения функционала:

                          для ФЯ (1.2),                для ФБЯ (1.1).

          Следовательно, (2.8) обеспечивают абсолютную минимизацию обоих функционалов (1.8)-(1.10). Ожидаемая произвольная неравномерная прямоугольная  «сетка» (2.1) является оптимальной с точки зрения этих функционалов при правильном задании (2.8). Естественно, что она, как легко видеть, удовлетворяет уравнениям Эйлера-Лагранжа (1.18) для ФБЯ (1.1). Можно проверить, что так будет и для упомянутых выше более громоздких уравнений (1.17) для ФЯ (1.2).

          2⁰. При назначении управляющих функций

(2.9)                ,             

уравнения (1.18) не выполнены, за исключением простейшего случая равномерной сетки . Последний попадает в сферу действия (2.8). Следовательно, при назначении (2.9) неравномерная «сетка» (2.1) функционалами (1.8)-(1.10) воспроизводиться не будет, т.е. будет нарушена при решении уравнений (1.18).

          Для рассматриваемого примера оказалось достаточно одной итерации, чтобы получить «правильные» управляющие функции , .

          2.4. Заслуживает специального внимания пример простейшей неортогональной сетки, задаваемой формулами (2.1) в случае, если . Легко проверить, что при управляющих функциях (2.8) она удовлетворяет уравнениям (1.18), т.е. является стационарной точкой функционалов (1.8)-(1.10). При этом получаются значения функционала:

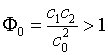                    в случае ФЯ (1.2),

                  , т.е. больше площади области, в случае ФБЯ (1.1).

          Возникает интересная альтернатива.

          Либо значение  при минимизации ФБЯ (1.1) с G₁₂=0 уменьшено быть не может, и тогда обсуждаемая параллелограммная «сетка» (2.1) является оптимальной для него и единственным решением задачи.

          Либо при зафиксированных граничных узлах существует отличная от (2.1) «сетка» («квазиортогональная»), для которой значение функционала при тех же (2.8) окажется меньше  . Тогда мы оказываемся в ситуации неединственности решения, которая уже неоднократно обсуждалась (см., напр., [5], с.25).

          Очевидно, что аналогичная ситуация имеет место и для ФЯ (1.2). Заметим, что «сетки», на которых гипотетически достигается реальный минимум функционала (1.10), вообще говоря, могут быть различными для (1.8) и (1.9).

§ 3. Неравномерные полярные «сетки»

3.1. В качестве второго, более содержательного методического примера рассмотрим неравномерную полярную «сетку», описываемую формулами:

(3.1)        ,          .

         По некоторым соображениям по сравнению со стр.18 работы [3] изменены обозначения с тем, чтобы привести их в соответствие с общепринятыми (см., напр.,[6], с.217) при рассмотрении пространственного случая (см. ниже §7).

         Будем предполагать, что , .

Для производных (3.1) имеем:

(3.2)            ,          

                   ,           

Метрические параметры описываются формулами:

(3.3)       ,          ,          ,        

В соответствии с (1.8)-(1.9) будем иметь:

(3.4)       ,           в случае ФБЯ (1.1)

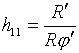                ,              в случае ФЯ (1.2)

Поскольку при назначении (1.6) имеем

                            ,

естественно было бы задавать управляющие функции формулами:

(3.5)            ,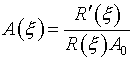        

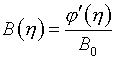
         Числовые параметры А₀, В₀ предназначены для обеспечения условий нормировки (1.11). Поэтому

(3.6)           ,           .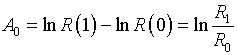

         Нетрудно проверить, что при задании (3.5) в качестве управляющих функций формулы (1.12)-(1.16) приведут к их воспроизведению, т.е. , . В этом случае сетка (3.1) обеспечивает абсолютный минимум обоих из функционалов (1.8)-(1.10) и, следовательно, является оптимальной для них.

         Формулы (1.19) и (1.20) дают одинаковые результаты .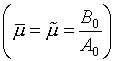

3.2. Более интересным представляется анализ варианта с заданием в качестве управляющих функций

(3.7)               ,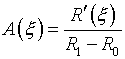        

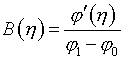
на основе законов расстановки узлов на границах.

Рассмотрим этот вариант сначала для ФБЯ (1.1). Тогда формулы (1.12)-(1.16) приводят к следующему.

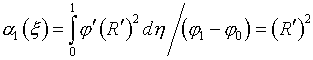
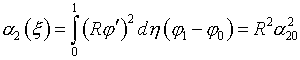
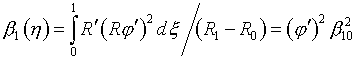
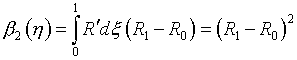
Очевидно, что после нормировки (1.16) получим

(3.8)               ,           ,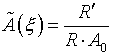

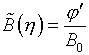что совпадает с (3.5).

Конкретные значения a₂₀, b₁₀ скажутся при вычислении . Результат мы  не приводим, чтобы не загромождать изложения.

Проведем аналогичный расчет для ФЯ (1.2). По формулам (1.12)-(1.16) получаем:

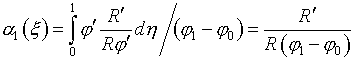
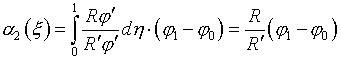
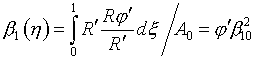
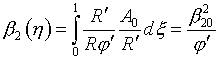
со своими числовыми параметрами.

После нормировки (1.16) получаем тот же результат (3.8) для управляющих  , , что и в случае ФБЯ (1.1). А вот параметр , вообще говоря, будет другим.

         3.3. Полученные результаты, в основном, аналогичны описанным в §2, и мы не будем повторяться. Из новых фактов заслуживают внимания следующие.

1⁰. Неравномерная полярная «сетка» (3.1) является оптимальной для обоих функционалов (1.8)-(1.10) при назначении управляющих функций формулами (3.5). При этом достигается абсолютная их минимизация.

2⁰. При отличном от (3.5) задании управляющих функций формулами (3.7), привлекающими законы расстановки на границах, удается за одну итерацию (если использовать полярную сетку) получить правильные нормированные управляющие (3.5) для обоих функционалов.

3⁰. Значения параметра  при этом расчете получаются различными для функционала с якобианом и без якобиана. Поскольку параметр m существенно работает в уравнениях Эйлера-Лагранжа (1.17)-(1.18), естественно, что расчет самой сетки для этих функционалов  с «неправильным» m пойдет разными путями.

4⁰. Очевидно, если в описанной ситуации сделать при зафиксированной сетке (3.1) еще одну итерацию, то для обоих функционалов будут получены одинаковые значения параметра m. Этот факт стоит иметь в виду, если обратить внимание на очень широкий диапазон изменения параметра m в зависимости не только от геометрических характеристик области, но и от конкретных законов расстановки R(x), j(h). А, следовательно, серьезное влияние параметра m на решение уравнений Эйлера-Лагранжа для расчета сетки при выбранных управляющих функциях.

5⁰. Из формул (1.7)-(1.10) естественно предположить, что аналогичные результаты могут быть получены для произвольной «сетки», метрические параметры которой удовлетворяют условиям:

(3.9)                 ,         .

§ 4. Дискретная реализация управления функционалом.

         4.1. Следующим шагом должно быть рассмотрение дискретной реализации алгоритма расчета управляющих параметров, изложенного в §1. Как обычно, это естественно сделать для регулярной сетки, упорядоченной по двум индексам:

(4.1)         

         При описании расчетных формул для наглядности широко используются так называемые полуцелые индексы , . Это усиливает громоздкость формул. Чтобы этого избежать, сохраняя наглядность, воспользуемся практическим приемом, описанным, например, в [1] на стр.17. Вместо индекса  используется , вместо  - индекс  (аналогично для m ).

         В частности, для реализации управляющих функций ,               в дискретной модели вводятся числовые последовательности

(4.2)           ,    

         Вариационный функционал моделируется интегральной суммой

(4.3)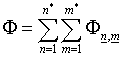                           

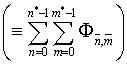
«Вклад» отдельной ячейки сетки для вариационного функционала (1.10) имеет вид:

(4.4)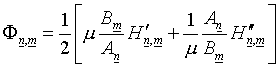             

         4.2. Для вычисления входящих в него величин  в литературе описаны разнообразные варианты формул и их практической реализации на ЭВМ. В частности, в целях реализации так называемого барьерного метода четырехугольная ячейка разрезается на две пары треугольников, получаемых после проведения ее диагонали. Расчетные формулы одни и те же для всех четырех треугольников (но работают со своей информацией). При реализации функционалов (1.1) и (1.2) ситуация упрощается благодаря тому, что они инвариантны относительно преобразования координат и можно не «следить» за тем, с какой из переменных, x или h, происходит работа. Автор считает нужным обратить внимание, что при работе с функционалом (4.3)-(4.4) это не так и за этим нужно старательно «следить».

         Один из возможных вариантов формул для  описан в двух уже упоминавшихся работах [2]-[3], и, во избежание утомительных повторов, мы не будем на этом останавливаться.

         Дискретизация формул (1.12)-(1.16) носит достаточно формальный характер, и мы ее приводим скорее для полноты сводки расчетных формул без всяких комментариев.

(4.5)          ,           ;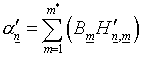      

                 ,           ;      

                        ,          

                       ,         

                      ,                       

                        ,            ,          

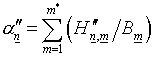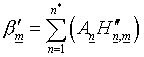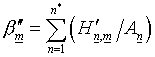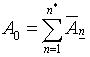
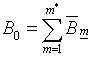
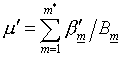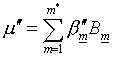Для вычисления параметра m избрана  дискретизация второго варианта (1.20).

4.3. При написании формул (4.5) молчаливо предполагается, что шаги по параметрическим переменным . Если заботиться о связи разностного и непрерывного вариантов расчетных формул (например, для понимания и сопоставления в целях контроля результатов расчетов), то следовало бы назначать , . Это изменение привело бы к появлению в формулах (4.5) некоторых коэффициентов (своих для каждого из типов величин), однако не влияет на значения результирующих величин, которые будут использоваться в дальнейшем расчете. Поэтому и избран упомянутый простейший вариант формул.

         Автор считает нужным отметить, что в методическом плане настоящая работа имеет много общего с давней работой [4], выполненной под руководством С.К.Годунова. В частности, в ней представлено несколько специальных примеров иллюстративного характера (см. [4], с.1045-1048), которые являются таковыми и для настоящей работы.

         Можно было бы на примере полярных сеток провести исследования, аналогичные описанным в §3, например, с точки зрения возможности их точного воспроизведения в разностной форме. При этом обнаруживается, например, зависимость параметра m еще и от конкретного числа узлов разностной сетки. Однако это слишком громоздко и мало полезно с практической точки зрения. Поэтому мы не сочли целесообразным этого делать.

§ 5. Некоторые замечания о расчете двумерных сеток.

         Вопрос об управляющих параметрах при расчете регулярных двумерных сеток интересен в нескольких аспектах.

5.1. Широкое распространение получили так называемые гармонические сетки, которые получаются, если в функционалах (1.1) или (1.2) задать коэффициенты простейшим способом:

                                   ,           .

Зачастую и расстановка узлов сетки на границах при этом выбирается (или предполагается) равномерной. И даже такой максимально упрощенный вариант функционалов оказывался приемлемым для решения интересных задач. Тем более этого можно ожидать от функционала (1.10), который располагает гораздо более широкими возможностями.

5.2. Управляющие параметры, появляющиеся в результате процедуры (4.5), становятся естественной альтернативой тем возможностям, которые достигаются использованием неравномерных расстановок граничных узлов сетки. Такие возможности особенно необходимы, например, для конструирования сеток, ориентированных на расчет пограничных слоев. Законы расстановки граничных узлов в определенной степени позволяют решать такую задачу, но их возможности ограничены из-за того, что сеточные уравнения «забывают» эти законы расстановки по мере удаления от границ.

         Управляющие параметры должны способствовать достижению лучших результатов, хотя бы потому, что расстановка граничных узлов зачастую определяется локальными и иногда вынужденными интересами (например, для передачи каких-либо мелких особенностей граничного контура). Описанные управляющие параметры, во-первых, носят интегральный характер и, следовательно, более взвешенно реагируют на такие особенности, а, во-вторых, по исходному замыслу подбираются, по возможности, наилучшим образом (с точки зрения некоторого функционала).

         Обратим еще раз особое внимание на параметр m,  играющий очень существенную роль при решении уравнений Эйлера-Лагранжа (1.17),(1.18), и на то, что он может изменяться в весьма широких пределах.

5.3. Естественно, что следует использовать управляющие параметры вместо законов распределения узлов  при конструировании корректирующего функционала, описанного в [3] на стр.22-23, полагая

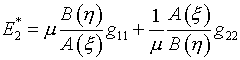
вместо формулы

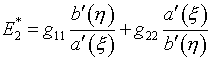
К сожалению, по небрежности автора эта последняя формула была приведена в [3] на стр.22 с ошибкой: в формуле (4.7) знаки квадратного корня следует убрать, так же как и в следующих формулах (4.8)-(4.9). Напротив, в формулах (5.11) на стр.27 в левых частях не хватает показателя 2.  Следовало бы и специально обратить внимание на неинвариантный характер функционала с плотностью энергии , что требует внимательно «следить» за переменными x,h, как отмечалось выше в §4.  Автор пользуется случаем указать на эти ошибки и приносит извинения возможным пользователям.

5.4. Вопрос о назначении параметров интересовал автора и с точки зрения возможности автоматизации их расчета.

         Как уже отмечалось, функционалы (1.1) и (1.2) носят универсальный характер, позволяя получить любую невырожденную сетку при соответствующем задании коэффициентов. Этот путь используется многими авторами, однако основная трудность состоит как раз в практической реализации таких целенаправленных усилий. В работе [7] на стр.902 есть прямое признание: «Способ  устранения недостатка, связанный с заданием некоторой управляющей функции во всех ячейках сетки, оказался неэффективным, так как для каждой новой задачи подбор такой управляющей функции требует значительных усилий, увеличивающихся вместе с увеличением числа узлов сетки».

         Возможность автоматизированного подбора управляющих параметров является несомненным достоинством предлагаемого алгоритма.

         Сетка является оптимальной (если таковой получается) с точки зрения некоторого функционала, привлеченного для решения практической задачи построения регулярной сетки в заданной области. Эта задача сама по себе бывает достаточно трудной из-за сложной формы области, да еще деформирующейся в процессе решения нестационарной задачи.

         Однако получение такой сетки – не самоцель, а лишь инструмент для решения некоторой конкретной задачи математической физики. И для этой задачи оптимальной (или просто хорошей) вполне может быть совсем другая сетка. И на такие случаи нужны другие алгоритмы.

         Именно эта цель ставится привлечением адаптивных сеток, которым посвящен весьма широкий круг публикаций различных авторов.

         Интересные возможности в этом плане представляет использование так называемых мониторных метрик (см., напр., [8]). Но их рассмотрение выходит за рамки настоящей работы.

5.5. Мы подошли к вопросу – нужно или нет выполнять несколько итераций по предложенному алгоритму (4.5) при зафиксированной сетке?

         При расчете нестационарных задач (например, газодинамических), особенно с малым шагом по времени, представляется вполне достаточным расчет таких управляющих параметров один раз на шаге по времени и основывать его на сетке, полученной на предыдущем шаге.

         Если при этом привлекается и состояние управляющих параметров от предыдущего шага, то, вероятнее всего, достаточно одной описываемой (4.5) итерации для уточнения их состояния.

         Если хранение такой дополнительной информации нежелательно (например, в случае уже сложившихся программных комплексов), то можно попробовать обойтись и без этого. Как уже отмечалось в §1, в качестве исходного состояния управляющих параметров можно привлекать усредненные законы расстановки узлов на противоположных границах (их необходимо иметь или рассчитывать для реализации интерполяционных формул при получении начального приближения сетки очередного шага). Далее следует выполнить, по-видимому, не более 1-3 итераций по  расчету управляющих параметров на зафиксированной сетке предыдущего шага. Это желательно сделать для того, чтобы в описанной в [2]-[3] методике иметь не слишком плохие невязки разностных уравнений для сетки, получаемые за счет корректирующих функционалов. (Хотя они могут регулироваться и напрямую путем уменьшения коэффициентов их «подключения», нежелательно чтобы эти последние были слишком малы).

5.6. Более содержательный характер вопрос, поставленный в начале раздела 5.5.,  приобретает при расчете сетки исходного шага. Основная трудность связана с тем, что необходимо гарантированно получить невырожденную сетку, а желательно – сетку из выпуклых ячеек (обычно оговаривается исключение для четырех угловых ячеек, если вынуждает форма расчетной области). Этому вопросу издавна уделялось специальное внимание и придумывались модификации алгоритмов (например, связанные с наличием якобиана в знаменателе и возможным обращением его в нуль), позволяющие достигать цели. Любопытно сейчас обратиться к давним публикациям. В качестве примера возьмем [9]-[10], которые были «первопроходцами» методов барьерного типа. Приведенные в них иллюстрации «перевывернутых» начальных сеток и сведения о затратах машинного времени (тогда это были БЭСМ-6) буквально приводят в изумление. Возможно, это делалось целенаправленно для демонстрации «могущества» предлагавшихся модификаций.

         Конечно, для достижения цели все способы, если не хороши, то имеют право на существование. Но с точки зрения надежности и практической целесообразности не имеет смысла сначала создавать трудности, а потом их мучительно преодолевать. А трудности эти возникают не случайно. Ведь при реализации барьерного метода для узла, попавшего «за барьер», очень трудно преодолеть его, чтобы попасть обратно, на «правильную» сторону. Трудно, даже если ему «помогают» (например, модификацией якобиана). Да и полной гарантии, что это произойдет, в общем-то, нет, несмотря на теоретический факт существования «хорошего» решения. Не этим ли объясняются упомянутые выше «изумляющие» иллюстрации?

5.7. Именно эту цель имеет предложение получить сетку с выпуклыми ячейками на исходном шаге и далее не допускать появления невыпуклых ячеек, постоянно оставаясь во множестве «хороших» сеток.

         Для получения исходной сетки на начальном шаге наиболее рациональным представляется использование такого пути. Допустим область представляет «водоем» (условно) с причудливой береговой линией. Вместо нее берется в качестве исходной более простая область, для которой построение приемлемой сетки не вызывает сомнений. А затем эта область постепенно деформируется в нужную, причем процесс деформации сочетается с итерационным процессом по пересчету сетки. Заметим, что в газодинамических комплексах программ обычно содержится тип границ, имеющих заранее заданное положение или движущихся по заданному закону и никак не влияющих на среду, через них протекающую. Эти границы получили название эйлеровых.

         Автор отнюдь не претендует на приоритет. Такой прием рассматривался, например, в [11]. Изложение подробностей можно найти в [12], наиболее «привязанной» к рассматриваемому вариационному подходу.

         Заметим, что в качестве подходящей «хорошей» области может быть использована или окаймляющая, или внутренняя по отношению к ней, или вообще область с «облагороженной настоящей» границей. (Если использовать «водную» аналогию, то условно речь может идти об области, которая заполняется во время весеннего половодья. А «настоящая» область с изрезанной береговой линией – та, которая образуется в результате летнего высыхания водоема.)  При современных возможностях диалогового режима реализовать такое предложение не так уж и трудно (речь идет только о начальном шаге или о моментах, когда изменяется структура сетки).

         Что касается самой «настоящей» границы, то сам подход с использованием выделенных подвижных границ ставит цель не допускать искажения формы реальных объектов и объектов, возникающих в ходе расчетов. Однако заметим, что уже факт замены реального пространственного процесса его двумерным аналогом несет в себе элемент идеализации (не говоря уж об эмпирическом характере некоторых коэффициентов и т.п.). Так всегда ли целесообразно «цепляться» за передачу слишком мелких деталей границ?

5.8. В [3] на стр.29 автор писал о целесообразности использования полезного опыта других исследователей для конструирования корректирующих функционалов. В этом плане представляет интерес уже упоминавшаяся работа [7] по следующим моментам.

         Во-первых, «квазиодномерный» функционал легко включается в множество рассматриваемых. Например, если заменить (1.10) на

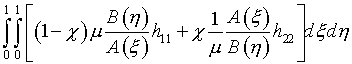
с числовым параметром c, то при c=0 реализуется функционал «квазиодномерных» сеток одного семейства, при c=1 – второго, при c=0.5 – прежний (1.10). Возможность в случаях c=0 и c=1 использовать специальные методы решения (типа прогонок для векторов размерности 2), рекомендуемая в [7] со ссылкой на более раннюю публикацию, конечно, может способствовать сокращению вычислительных затрат. Рассмотрение такого рода возможностей представляет интерес как альтернатива методу простой итерации при решении разностных уравнений для сетки. Возможность ускорения сходимости, конечно же, практически весьма важна.

5.9. Заслуживает внимания и описанная в [7] на с.904 идея модификации разностной формы функционала посредством введения «условной длины, используя интерполяцию соответствующих длин на граничных линиях». Аналогичное по содержанию предложение делалось и в [1] на стр.22. К сожалению, оно не слишком универсально, что можно легко понять на примере области в форме «песочных часов».

         Заметим, что предлагаемый в настоящей работе алгоритм подбора управляющих параметров является одним из вариантов автоматизированной реализации именно этой идеи. В качестве «условной длины» при этом будут выступать просуммированные вдоль границы значения управляющих параметров.

5.10. Работа [7] заслуживает упоминания еще и потому, что содержит интересные результаты, иллюстрирующие методы на примере задач, связанных с исследованием неустойчивости границы раздела сред. Они свидетельствуют, что приемлемые сетки можно получать в очень трудных ситуациях типа заполнения узлами регулярной сетки «языков» весьма причудливой формы или тонкой «перемычки». На стр. 905 есть даже упоминание о расчетах, когда происходит отрыв «языка». Такой расчет влечет за собой необходимость изменения в ходе его структуры сетки и, как пишут авторы [7], «хотя и громоздок, но в принципе возможен».

         5.11. Есть еще один серьезный вопрос: зачем автору понадобилось вести изложение для двух функционалов (1.8)-(1.10)? Ответ на него уже излагался на стр.29-30 работы [2], и мы его не будем повторять. Вернемся к нему в  §8 после обсуждения возможностей использования предложенного варианта вариационного подхода в пространственном случае, к которому и переходим.

§ 6. Выбор функционала для трехмерных сеток и назначение

                 одномерных  управляющих функций.

         6.1. Результаты, достигнутые при вариационном подходе к расчету двумерных сеток, создали уверенность в возможности обобщения такого подхода на случай пространственных (трехмерных) сеток. Для создания надежных методов их построения представляется естественным привлечение вариационных функционалов барьерного типа. Оказалось, что для этого обнаруживается гораздо больше различных возможностей, чем  в двумерном случае. По этому поводу имеется достаточно обширная литература, но мы сразу обратимся к только что опубликованной работе [13], в которой предлагаемый алгоритм доведен до расчетных формул, их практической реализации и проиллюстрирован примерами. В [13] можно найти и краткий обзор соответствующей литературы и аргументы в пользу выбора конкретного функционала.

         Функционал, используемый в работе [13], имеет вид

(6.1)                ,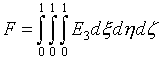

где Е₃ – плотность энергии отображения единичного куба Q₃:  на заданную пространственную область W₃, в которой должна быть построена сетка. Она назначается формулами:

(6.2)         ,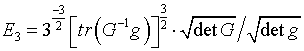

(6.3)       

         В точке с координатами  элементы метрического тензора g задаются соотношениями

(6.4)           ,             ,           

                   ,     ,  

    - элементы матрицы, обратной аналогичной матрице G коэффициентов функционала.

          В интересах обобщения алгоритма расчета управляющих функций, который был описан выше для двумерного случая, вместо (6.1) будет рассматриваться функционал с плотностью

(6.5)                

Возможность выбора такой функции  аргументирована в [13] на стр. 46-47. Для двумерных сеток аналогичное предложение обсуждалось в [1] на стр. 31.

          По аналогии с двумерным случаем назначим

(6.6)                            .

          Тогда формула для E₃₀ приобретает вид:

(6.7)            

          6.2. Далее, по аналогии с двумерным случаем, введем одномерные управляющие функции А(x), В(h), С(z) и рассмотрим функционал с плотностью

(6.8)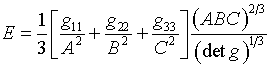              

          К своему удовольствию, в статье [14] на стр.848 автор обнаружил предложение определять качество ячейки сетки именно такой величиной. Проще было бы ввести обозначения А, В, С вместо А², В², С² , но автор сделал выбор, исходя (как выяснится в §7) из интересов наглядности и пространственного функционала без якобиана, который будет определен формулой (7.9).

          6.3. Алгоритм назначения управляющих функций естественно обобщается так.

          При «замороженных» А(x), В(h), С(z) вычисляются следующие функции:

(6.9)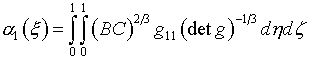                

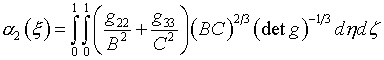
(6.10)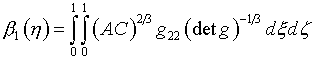            

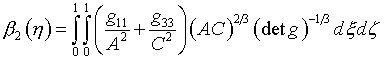
(6.11)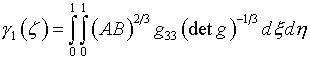             

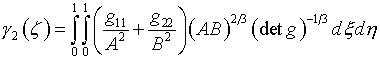
Назначение А(x) определяется из условия минимума интегрального выражения

(6.12)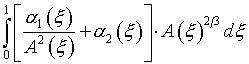                    

Минимум функции

(6.13)              ,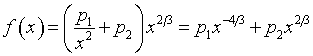

для которой производная определяется формулой:

(6.14)             ,

достигается при . Сомножитель 2 можно убрать (ввиду последующей нормировки) и для дальнейшего это целесообразно сделать. Поэтому из (6.12) определяем

(6.15)            

Аналогично на основе формул (6.10) и (6.11) получаем:

(6.16)              ,         

Они и определяют назначение управляющих функций (точнее, очередное приближение для их назначения).

6.4. Следуя изложенному в §1, эти функции следует нормировать. Например, так:

(6.17)              ,         

                       ,         

                       ,         

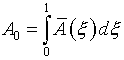
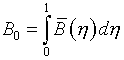
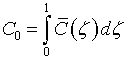
Формула (6.8) записывается в виде:

(6.18)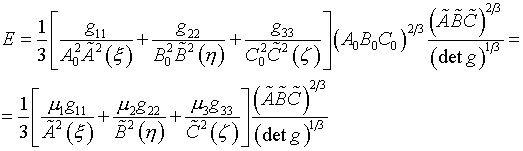      

Входящие в нее параметры:

(6.19)          ,      ,      ,    

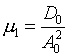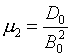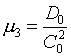будут играть ту же роль, что и коэффициенты m, 1/m в двумерном случае (1.10). Заметим, что    m₁ m₂ m₃ =1   аналогично     m× 1/m=1.

6.5. При сравнении формул (6.9)-(6.16) с аналогичными формулами (1.12)-(1.15) для двумерного случая обнаруживается следующее. В двумерном случае параметр m не играл никакой роли при определении нормированных функций  ,   . В пространственном случае это не так: в формулах для a₂(x), b₂(h), g₂(z) происходит «смешение» двух функций с фактически неизвестными весовыми коэффициентами (это особенно существенно для первой «итерации»).

         В определенной степени этот недостаток можно устранить следующим приемом. Полагаем, что исходные функции А(x), В(h), С(z) являются нормированными. (На их роль наиболее естественно претендуют усредненные законы расстановки узлов на граничных ребрах).

         Вместо a₂(x) вычислим две вспомогательных функции:

(6.20)             

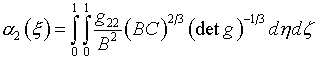
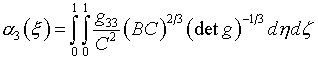
Тогда формулу (6.15) для  можно, исходя из (6.20), записать в виде:

(6.21)              

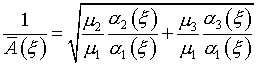
Аналогично производится расчет пар функций b₂(h),b₃(h) вместо b₂(h) и функций g₂(z),g₃(z) вместо g₂(z), а затем выписываются формулы для , аналогичные (6.21).

         Однако расчет  по полученным формулам будет завершен только после того, как будут назначены величины m₁, m₂, m₃ . В свою очередь, формулы для этих величин определяются тоже требованием минимизации функционала с плотностью энергии (6.18).

         При условии нормировки m₁ m₂ m₃=1 минимум формы

(6.22)                   

достигается для значений параметров

(6.23)         ,        ,        ,       

Очевидные, но громоздкие формулы для величин F₁, F₂, F₃ мы опускаем.

§ 7. Модельные примеры для пространственного случая.

       Функционал без якобиана для трехмерных сеток.

         7.1. В качестве первого примера рассмотрим простейшие прямоугольные «сетки», ориентированные по осям координат:

(7.1)        ,      ,   

Естественно, предполагается, что  ,  , .

Для них метрические параметры

(7.2)            ,            ,         

Плотность (6.8) энергии этого отображения принимает вид:

(7.3)           

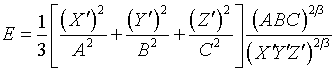
Ее абсолютное минимальное значение Е=1 достигается, если

(7.4)               ,            ,         

(Мы сознательно опускаем подробности, связанные с нормировкой этих функций, чтобы не загромождать изложение.)

         Следовательно, произвольная прямоугольная «сетка» является оптимальной для функционала (6.8) при назначении в качестве управляющих функций (7.4).

         7.2. В качестве второго модельного примера рассмотрим сферическую (полярную) «сетку»:

(7.5)              

Ее метрические параметры

(7.6)                 ,             ,         

                        ,       

Плотность (6.8) энергии отображения (7.5) принимает вид:

(7.7)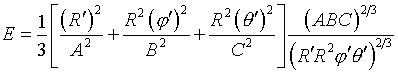        

Ее абсолютное минимальное значение Е=1 достигается, если

(7.8)              ,           ,       

         Следовательно, произвольная сферическая «сетка» (7.5) является оптимальной для функционала (6.8) при назначении в качестве управляющих функций (7.8).

         7.3. В двумерном случае рассматривались два функционала, один из которых для наглядности назывался функционалом без якобиана, а другой – функционалом с якобианом.

         В трехмерном случае аналогом функционала с якобианом является (6.1) с плотностью энергии (6.8) или (6.18), а в качестве аналога функционала без якобиана следует рассматривать (6.1) с плотностью

(7.9)                

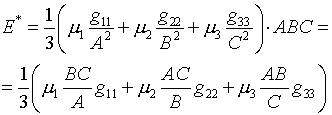
         Обратим внимание, сравнивая (7.9) с (6.18), что, кроме отсутствия якобиана, изменяется еще и показатель 2/3 на 1. Естественно, что соответственно должны быть изменены и формулы (6.9)-(6.16) для назначения управляющих функций. Эти изменения столь очевидны, что мы не будем выписывать получающиеся формулы.

         Заметим, что минимизация функции  достигается при . Поэтому формулы (6.15) и (6.16) остаются в силе.

Уравнения Эйлера-Лагранжа, которым должно удовлетворять отображение, обеспечивающее минимум функционала (6.1) с плотностью (7.9), имеют вид:

(7.10)           

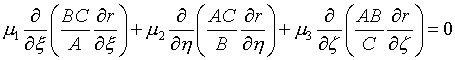
для каждой из трех компонент радиус-вектора r=(x,y,z). Они линейны и, как и в двумерном случае, это существенно упрощает алгоритмы их численного решения.

         Очевидно, что в этих уравнениях важную роль играют коэффициенты . Они аналогичны (6.19) для функционала с плотностью (6.18).

7.4. Нетрудно проверить, что описанные выше результаты для модельных примеров прямоугольных неравномерных и сферических (полярных) «сеток» полностью переносятся и на функционал без якобиана, т.е. с плотностью энергии (7.9). Это подтверждается и непосредственной подстановкой в уравнения (7.10).

         Можно было бы аналитически исследовать варианты задания управляющих функций, аналогичные описанным для двумерного случая, но это громоздко и заняло бы слишком много места. Поэтому мы этого делать не будем.

§ 8. О дискретизации пространственного функционала.

         8.1. Для реализации численного алгоритма построения пространственных сеток вариационный функционал (6.1) с плотностью энергии отображения (6.18) моделируем интегральной суммой

(8.1)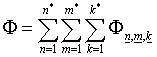              

«Вклад» отдельной трехмерной ячейки имеет вид:

(8.2)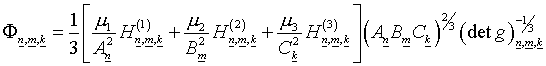      

         При заданной сетке  вычисление управляющих параметров  осуществляется по формулам, представляющим дискретные аналоги (6.9)-(6.16), и их возможной модификацией по (6.20)-(6.21). Они столь очевидны, что мы не будем их приводить.

8.2. Основная проблема дискретизации связана с величинами

и оказалась далеко не простой.

         В двумерном случае введение билинейного отображения единичного квадрата Q: (0£x,h£1) на четырехугольник, имеющий заданные координаты вершин ячейки, позволило успешно решить проблему обеспечения невырожденности и выпуклости ячеек сетки. Как уже описывалось, это достигается посредством разрезания ячейки на две пары треугольников проведением ее диагоналей и формулируется в виде требования положительности (неотрицательности)  площадей этих треугольников.

         Естественно для пространственного случая искать путь решения аналогичной проблемы посредством введения трилинейного отображения единичного куба Q₃: (0£x,h,z£1) на шестигранную ячейку с заданными координатами ее 8 вершин. (Вместо термина «шестигранная» ячейка используются также «гексаэдральная» или «линейчатая»). Однако до настоящего времени не получено условий, являющихся одновременно необходимыми и достаточными, которые обеспечивали бы невырожденность упомянутого выше трилинейного отображения.

         Этому вопросу посвящено достаточно много работ, из которых в первую очередь заслуживают быть упомянутыми [15]-[16], в которых он исследован наиболее полно. В них можно найти ссылки и на другие работы.

8.3. Что касается практической реализации такого подхода, то представляет интерес вариант, избранный в [13]. При его реализации вместо линейчатой ячейки рассматриваются два двенадцатигранника. Они имеют те же вершины и получаются проведением одной дополнительной диагонали в каждой грани ячейки.

         Заметим, что в пространственном случае четыре вершины, определяющие грань ячейки, как правило, не лежат в одной плоскости. Чтобы конкретизировать форму грани ячейки, нужно строить криволинейную поверхность, проходящую через эти четыре вершины. Задача решается, например, привлечением в качестве такой поверхности однополостного гиперболоида (см., напр., [6], с.228).  Однако это слишком обременительно и недостаточно надежно в вычислительном плане (часто придется «балансировать» на грани вырождения поверхности гиперболоида в плоскость).

         Проведение диагонали ячейки позволяет более просто решить проблему, заменяя грань двумя плоскими треугольниками. Заметим, что они не лежат (как правило) в одной плоскости, как и два другие, получающиеся проведением другой диагонали в грани ячейки. А эти две диагонали, как правило, представляют отрезки скрещивающихся прямых.

         Как описано в [13], для практической реализации каждый из двух упомянутых выше двенадцатигранников разрезается на пять тетраэдров: четыре угловых и один внутренний. Упомянутое выше единое для ячейки трилинейное отображение заменяется на набор линейных отображений базовых тетраэдров из пространства (x,h,z), на которые разбивается единичный куб Q₃, в соответствующие тетраэдры, из которых составлены два двенадцатигранника. Базовые тетраэдры – это 8 угловых при вершинах куба и 2 внутренних.

         Условие невырожденности ячейки подменяется требованием положительности (неотрицательности) объема каждого из этих 10 тетраэдров. Это позволяет конструировать интегральную сумму для минимизируемого функционала, которую можно трактовать как реализацию барьерного метода для пространственного случая.

8.4. Как уже отмечалось в §6, автору [13] удалось осуществить описанное для функционала (6.1)-(6.4), довести алгоритм до расчетных формул (достаточно «трудоемких» с точки зрения вычислительных затрат) и их практической реализации, проиллюстрированной примерами.

         Заметим, что сделано это в «стационарном» варианте – с целью расчета сетки в пространственной области с фиксированными границами.

         Нас же интересует алгоритм применительно к нестационарной задаче. Представляется совершенно естественным обобщение для этой цели технологии построения сеток, изложенной в [2]-[3], на пространственный случай. Речь идет, прежде всего, об использовании соответствующих универсальных функционалов с плотностью энергии отображения в форме (6.5). Коэффициенты функционала вычисляются как метрические параметры сетки, полученной на предыдущем шаге по времени. Это – то, что называется опорным функционалом. Он корректируется посредством функционала, содержащего одномерные управляющие функции, описанные выше в §6. Главной ценностью его мы полагаем получение параметров (6.18) m₁, m₂, m₃ и их использование при решении уравнений Эйлера-Лагранжа для пространственной сетки. Получаемые одновременно с ними управляющие функции А(x), В(h), С(z) позволяют сетке правильно «реагировать», в том числе, и на неравномерные расстановки узлов на границах, как проиллюстрировано на модельных примерах прямоугольных и полярных сеток.

         8.5. А вот теперь вернемся к вопросу о двух функционалах (1.8)-(1.9), рассматривавшихся в двумерном случае. В своих воспоминаниях [17] на стр.21 С.К.Годунов писал: «Мы опасались чрезвычайных затрат времени. Было решено сначала использовать вариационный подход в каких-либо стационарных задачах… Только после успеха, достигнутого в решении стационарных задач, мы решились строить сетки на каждом шагу путем решения эллиптических уравнений».

         Несмотря на неизмеримо выросшее быстродействие вычислительной техники, представляется определенное сходство нынешней создавшейся ситуации с упомянутой.

         Если в процессе расчета нестационарной задачи придется на каждом шаге иметь дело с реализацией вариационного подхода, при котором ячейка будет разбиваться на 10 тетраэдров и т.д., не приведет ли это к чрезмерным, недопустимым вычислительным затратам?

         Эти затраты безусловно существенно снижаются, если, по аналогии с двумерным случаем, вместо функционала с якобианом, для которого плотность энергии задается формулой (6.18), использовать функционал без якобиана с плотностью, определенной формулой (7.9) . Это означает, что в формуле для его плотности убирается сомножитель  и показатель 2/3 заменяется на 1 (что тоже снижает вычислительные затраты). Естественно, что это делается и во всех последующих формулах. Для вычисления же метрических параметров g₁₁, g₂₂, g₃₃ совсем не обязательно «резать» ячейку на тетраэдры и не нужно заботиться о положительности (необращении в нуль) знаменателя. Упрощения, которые вносит линейный характер уравнений Эйлера-Лагранжа (7.10) в случае функционала без якобиана, для двумерного случая уже описывались в [2]-[3].

         Как мы уже упоминали, аргументы для такого решения при рассмотрении двумерного случая были изложены в [2] на с.30. Кратко повторим их суть.

         1⁰. Если достигается абсолютная минимизация функционала, то это происходит на одной и той же сетке для функционала с якобианом и без якобиана.

         2⁰. Избрав опорный функционал, слабо возмущенный корректирующими функционалами, мы «работаем» именно в окрестности абсолютного минимума.

         3⁰. Минимизируя функционал с якобианом, мы обязаны работать с множеством невырожденных (выпуклых) сеток. Что мешает нам делать это и при работе с функционалом без якобиана, не допуская возникновения вырожденной  (невыпуклой) сетки? (Вопрос, как это наиболее просто контролировать, остается. Однако нужны не столько «хитроумные» критерии, сколько относительно легко проверяемые достаточные условия).

         На стр.30 в [2] высказана мысль о целесообразности иметь в арсенале алгоритмов построения сеток оба функционала, но прибегать к использованию функционала с якобианом только после того, как исчерпаны возможности функционала без якобиана.

8.6. Считаем необходимым специально остановиться на вопросе о расчете начальной сетки. Получение «хорошей» сетки в случае области сложной формы могло бы осложниться из-за отказа от работы с якобианом. Предложение использовать «улучшенную» исходную область (с последующей деформацией в нужную) снимает такое осложнение: «хорошая» сетка для соответственно «улучшенной» области должна быть гарантированно получена с помощью интерполяционных формул или используемого функционала без якобиана.

Как подтверждение правильности предлагаемого подхода, мы рассматриваем и сделанное на стр.35 работы [13] сообщение, что для одного из вариантов модификации якобиана, эффективно работавшего в двумерном случае, «трехмерный аналог не позволяет получать невырожденную сетку даже в простой кубической области с первоначально «испорченной» (т.е. вырожденной) сеткой».

Заключение

         Предложенный в настоящей работе автоматизированный вариант назначения управляющих параметров должен увеличить возможности традиционного вариационного подхода к расчету как двумерных, так и пространственных сеток.

         Как показывает модельный пример полярных «сеток» с произвольной расстановкой узлов по радиальному и угловым направлениям, предлагаемые управляющие параметры позволяют воспроизводить такие сетки, препятствуя «забыванию» законов расстановки традиционно используемыми вариационными уравнениями.

         Резкое возрастание вычислительных затрат при реализации вариационного подхода, особенно в пространственном случае, вызывает необходимость настоятельной заботы об их уменьшении. По мнению автора, с этой точки зрения представляет несомненный интерес использование «функционалов без якобиана».

         Сложилось так, что уже во время завершения настоящей работы автор ознакомился со статьей [18], посвященной построению двумерных нерегулярных сеток. Она произвела очень приятное впечатление, особенно иллюстративными примерами по части построения сеток в областях типа «песочных часов», с «языками», многосвязных и др. Высказанное в ней мнение, что на базе такой методики можно «создать геометрически безавостную методику на подвижных сетках», принципиальных возражений не вызывает. Однако именно «геометрически». Реализация, например, методов «типа Годунова» (каждый смотрит со своей «колокольни») вызовет определенные трудности из-за необходимости перехода (на каждом шаге) с одной нерегулярной сетки на другую нерегулярную, которая может отличаться от нее структурой. Неизвестно и каковы будут последствия таких постоянных переходов с точки зрения численного решения уравнений газовой динамики. Если трудности удастся успешно преодолеть и, особенно, если описанную в [18] методику удастся обобщить на пространственный случай, то нерегулярные сетки – безусловно великолепная альтернатива регулярным. По-видимому, способная существенно потеснить последние, представляющие надежный и удобный инструмент до тех пор, пока есть условия для их использования. Тем более это очевидно для задач с неизменной, неподвижной сеткой.

         Автор выражает искреннюю благодарность М.С.Гавреевой за помощь в оформлении работы.

Список литературы

1.        Прокопов Г.П. Универсальные вариационные функционалы для построения двумерных сеток. //М., Препринт ИПМ им.М.В.Келдыша РАН, 2001, №1, 36 стр.

2.        Прокопов Г.П. Вариационные методы расчета двумерных сеток при решении нестационарных задач. //М., Препринт ИПМ им.М.В.Келдыша РАН, 2003, №4, 32 стр.

3.        Прокопов Г.П. Реализация вариационного подхода к расчету двумерных сеток в нестационарных задачах. //М., Препринт ИПМ им.М.В.Келдыша РАН, 2005, №116, 36 стр.

4.        Годунов С.К., Прокопов Г.П. О расчетах конформных отображений и построении разностных сеток.// ЖВМ и МФ, 1967, т.7, №5,сс.1031-1059.

5.        Прокопов Г.П. О расчете разностных сеток, близких к ортогональным, в областях с криволинейными границами. //М., Препринт ИПМ АН СССР, 1974, №17.

6.        Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов.// М., Гос.издательство тех.-теор.лит., 1953, 608с.

7.        Грынь В.И., Фролова А.А., Чарахчьян А.А. Сеточный генератор барьерного типа и его применение для расчета течений с подвижными границами.// ЖВМ и МФ, 2003, т.43, №6, сс.902-908.

8.        Шокин Ю.И., Лисейкин В.Д., Лебедев А.С., Данаев Н.Т., Китаева (Васева) И.А. Методы римановой геометрии в задачах построения разностных сеток.// Новосибирск, Издательство «Наука», 2005.

9.        Иваненко С.А., Чарахчьян А.А. Криволинейные сетки из выпуклых четырехугольников.// ЖВМ и МФ, 1988, т.28, №4, сс.503-514.

10.   Иваненко С.А. Построение невырожденных сеток.//ЖВМ и МФ, 1988, т.28, №10, сс.1498-1506.

11.   Сидоров А.Ф., Шабашова Т.И. Об одном методе расчета оптимальных разностных сеток для многомерных областей.// Числ. методы мех.сплош.среды, 1981, т.12, №5, сс.106-124.

12.   Антонова Р.Н., Прокопов Г.П., Софронова О.И. Расчет подвижных сеток и проблема начального приближения для сетки в сложной области.// ВАНТ, сер.: Матем. моделир. физ.процессов, 1996, вып.1-2, сс.84-90.

13.   Азаренок Б.Н. Об одном вариационном методе построения пространственных сеток. Сообщения по вычислительной математике.// М., Вычисл. Центр РАН им.А.А.Дородницына, 2006, 51 стр.

14.   Delanaye M., Hirsch Ch., Kovalev K. Untangling  and optimization of Unstructured hexahedral meshes.// ЖВМ и МФ, 2003, т.43, №6, сс.845-853.

15.   Ушакова О.В. Условия невырожденности трехмерных ячеек. Формула для объема ячеек.//ЖВМ и МФ, 2001, т.41, №6, сс.881-894.

16.   Ушакова О.В. О невырожденности трехмерных сеток.// Труды Ин-та Математики и Механики УРО РАН, 2004, т,10, №1, сс.78-100.

17.   Годунов С.К. Воспоминания о разностных схемах. Доклад на Международном симпозиуме «Метод Годунова в газовой динамике». Мичиганский университет (США). Май, 1997.// Новосибирск, Научная Книга, 1997, 40 стр.

18.   Сковпень А.В. Реализация фронтального алгоритма построения нерегулярных четырехугольных сеток.// ВАНТ, сер.: Матем. моделир. физ.процессов, 2005, вып.1, сс.9-30.