Аннотация
Описаны метод и результаты определения тензора инерции геостационарного спутника “Ямал” по
телеметрической информации о его вращательном движении и суммарном кинетическом моменте
маховиков. Информация о движении спутника представляет собой значения кватерниона
ориентации и угловой скорости в дискретные моменты времени. По этим значениям, относящимся
к некоторому временному интервалу, с помощью сглаживания сплайнами строится аппроксимация
фактического движения спутника относительно центра масс, которая затем используется в линейной
системе дифференциальных уравнений, описывающих изменение на том же интервале суммарного
кинетического момента маховиков. Указанная линейная система выражает теорему об изменении
полного кинетического момента спутника и маховиков и записана с учетом действия на спутник
гравитационного момента и момента, создаваемого световым давлением. Решение указанной системы
уравнений линейно зависит от компонент тензора инерции спутника и параметров, характеризующих
момент светового давления. Оценки этих величин находятся методом наименьших квадратов из
условия наилучшей аппроксимации телеметрических значений суммарного кинетического момента
маховиков решениями указанной линейной системы. Приведены примеры обработки реальной
измерительной информации. Погрешность определения диагональных (преобладающих) компонент
тензора инерции в этих примерах составила 5 – 17% при обработке телеметрической информации
об освещенном Солнцем участке орбиты и 4 – 8% при обработке теневого участка (на нем
отсутствует момент светового давления).
Abstract
The paper presents the method and the results of estimating the inertia tensor of the satellite
Yamal on the base of the telemetry information about its attitude motion and the total angular
momentum of flywheel. The information about an attitude motion is time sequences of the
quaternion of the satellite attitude with respect to an inertial coordinate system and the
satellite angular rate. Basing on the information, we reconstruct the satellite motion using
splines. Such an approximation is used in the linear differential equations, which describe
the variation of the total angular momentum of flywheels during the motion. Solutions of the
equations depend linearly upon inertia tensor components and satellite geometric parameters.
We find estimations of these quantities from the condition of the best approximation of angular
momentum measurement data by those solutions using the least squares method. The method was
applied for processing real telemetry data. The errors of estimating the diagonal (the most
large) inertia tensor components were in limits of 5 –-17% if the telemetry data were referred
to sunny part of the orbit and 4 – 8% if the data were refereed to the shady part.
1. Введение. В
настоящее время на геостационарной орбите функционируют спутники связи серии
«Ямал» [1, 2]. Их создание и ввод в эксплуатацию явились важным этапом в
развитии отечественных спутниковых систем связи.
При
математическом моделировании вращательного движения геостационарного спутника
(ГСС) для нужд управления полетом и целевого использования необходимо достаточно
точно знать его динамические характеристики. Математическое моделирование
является основой успешного создания сложных КА и выполнения на них целевых
задач и экспериментов [3, 4], а в процессе построения и применения
математических моделей необходимо знание истинных характеристик моделируемых
объектов – космических кораблей и орбитальных станций. Задача уточнения
динамических и ряда других характеристик КА в полете решалась ранее для
орбитальных станций «Салют», «Мир», МКС. Для отработки методик решения подобных
задач были организованы и проводились технические эксперименты «Тензор»,
«Изгиб»», «Искажение», «Среда» и др. [4 – 6]. Обработка результатов, полученных
в рамках данных экспериментов, позволила определить и уточнить ряд
характеристик орбитальных станций. Полученные данные использовались при
управлении орбитальными станциями и выполнении на них целевых программ
исследований. Отработанные на орбитальных станциях методы и технологии
целесообразно использовать также для других аппаратов, в том числе
исследовательских и прикладных спутников. Это позволит, в частности, проводить
в полете юстировочные работы для целевой аппаратуры, уточнять динамические и
другие характеристики спутников. Уточнение динамических характеристик
геостационарого КА даст возможность построить адекватную модель вращательного
движения спутника относительно центра масс (для орбитальных станций эта задача
осложняется необходимостью учета возмущений за счет действия атмосферы). Наличие
адекватной модели вращательного движения позволит, в частности, построить алгоритмы
управления ориентацией без использования датчиков угловых скоростей и непрерывного
включения датчиков ориентации, что повысит надежность и долговечность системы
ориентации КА.
В данной работе рассмотрим задачу уточнения тензора
инерции ГСС «Ямал» по телеметрической информации. Со временем, по мере
выработки рабочего тела, тензор инерции меняется и его новое значение
определить расчетным путем не всегда возможно. Уточнение тензора проводилось
еще для станции "Мир". Применялись два способа. Первый использовал
определение неуправляемого вращательного движения станции по данным измерений
бортовых датчиков или по телеметрической информации об ее ориентации. Определение
движения сводилось к построению функций, аппроксимирующих данные измерений или
телеметрическую информацию и рассчитываемых вдоль решений полной системы
уравнений вращательного движения станции. В результате обработки уточнялись начальные
условия движения и некоторые параметры математической модели, в том числе 5
параметров, характеризующих тензор инерции станции – три угла, задающих
направления главных центральных осей инерции в строительной системе координат и
две безразмерных комбинации главных центральных моментов инерции. Приемлемые по
точности оценки получались только в результате обработки показаний оптического
звездного датчика и значений кватерниона, задающего ориентацию станции [7 –
10].
Второй способ заключался в использовании данных
измерений суммарного кинетического момента гиродинов, полученных при
поддержании неизменной ориентации станции в абсолютном пространстве. Как
оказалось, при обработке измерений, выполненных на интервале поддержания одной
ориентации, можно оценить только четыре специально выбранные линейные комбинации
шести компонент тензора инерции. В частности, если кинетический момент
гиродинов измеряется в системе главных центральных осей инерции станции, то
можно оценить разности ее главных моментов инерции. При совместной обработке
измерений, выполненных на нескольких временных интервалах при разных ориентациях
станции, можно оценить недиагональные компоненты тензора инерции и разности его
диагональных компонент. Оценки, найденные при обработке двух интервалов,
достаточно точно совпадали с оценками, полученными расчетным путем [9, 10].
Указанные способы применялись и для оценивания
тензора инерции МКС [11]. При выборе способа оценивания учитывался тип
вращательного движения станции и вид имеющейся телеметрической информации. В
настоящее время первый способ модифицирован так, что его можно использовать и в
случае управляемых движений (неуправляемые движения станции практически
отсутствуют). При этом необходимо располагать информацией об ориентации
станции, например, в виде значений кватерниона ориентации, о суммарном кинетическом
моменте гиродинов и о работе двигателей ориентации. Этот способ в настоящее
время опробован, и полученным в его рамках результатам будет посвящена
отдельная работа. Модифицированный первый способ требует особого рассмотрения,
поскольку самой трудоемкой его составляющей является сбор и учет информации о
работе реактивных двигателей ориентации станции.
Первый способ был существенно упрощен. Ограничились
рассмотрением интервалов, на которых двигатели ориентации не были задействованы.
В этом случае в рамках первого способа задача оценивания тензора инерции может
решаться примерно так же, как в случае неуправляемого движения станции. Однако,
при таком подходе, информации о кинетическом моменте гиродинов приписывается
существенно больший вес, чем информации об ориентации станции. Это отнюдь не
так, и хотя применение первого способа в описываемой ситуации представляет
большой методический интерес, второй способ здесь является более
предпочтительным – в рамках второго способа наибольший вес приписывается
информации об ориентации станции. Для его использования выбраны отрезки движения
станции без срабатывания двигателей ориентации. На этих отрезках движение станции
было близко к покою в абсолютном пространстве, но не сводилось к полному покою.
Благодаря этому обстоятельству удалось выйти из ограничений подхода,
использованного в [9, 10], и получить оценки всех компонент тензора инерции
[11].
Аналогичный подход был реализован при оценке тензора
инерции ГСС “Ямал”, ориентация которого стабилизирована в орбитальной системе
координат (ОСК). Точность ориентации спутников не хуже 0.10. Наличие
небольших колебаний ориентации ГСС в ОСК позволило оценить все компоненты
тензора инерции.
2. Изменение кинетического момента маховиков.
Как и в случае решения задачи для МКС ГСС
будем считать гиростатом. Центр масс спутника движется по геостационарной
орбите. Элементы этого движения находятся по данным радиоконтроля орбиты. В качестве
исполнительных органов, используемых на ГСС для управления ориентацией, применяются
маховики. Для записи уравнений изменения собственного кинетического момента
системы маховиков введем две правые декартовы системы координат. Начала обеих
систем поместим в центр масс – точку  . .
В
качестве базовой системы координат примем систему  , плоскость , плоскость  которой параллельна
среднему земному экватору эпохи 2000.0. Ось которой параллельна
среднему земному экватору эпохи 2000.0. Ось  направлена в точку
весеннего равноденствия указанной эпохи, ось направлена в точку
весеннего равноденствия указанной эпохи, ось  направлена в
соответствующий северный полюс мира. Под ориентацией спутника будем понимать
ориентацию жестко связанной с его корпусом строительной системы координат направлена в
соответствующий северный полюс мира. Под ориентацией спутника будем понимать
ориентацию жестко связанной с его корпусом строительной системы координат  . В режиме поддержания штатной ориентации ГСС ось . В режиме поддержания штатной ориентации ГСС ось  направлена по текущему
радиус-вектору, ось направлена по текущему
радиус-вектору, ось  – по текущему вектору
линейной скорости. – по текущему вектору
линейной скорости.
Положение
системы  относительно системы относительно системы  задается с помощью
нормированного кватерниона задается с помощью
нормированного кватерниона  , ,  [12]. Матрицу перехода
от системы Oy1y2y3 к системе OY1Y2Y3
обозначим [12]. Матрицу перехода
от системы Oy1y2y3 к системе OY1Y2Y3
обозначим 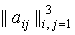 , где , где  – косинус угла между
осями – косинус угла между
осями  и и  . Элементы этой матрицы выражаются через компоненты . Элементы этой матрицы выражаются через компоненты  с помощью известных формул с помощью известных формул
 и т. п. Ниже компоненты векторов и
координаты точек указываются в системе и т. п. Ниже компоненты векторов и
координаты точек указываются в системе  . .
Оценка
тензора инерции спутника выполнялась на освещенных Солнцем интервалах орбиты и
при движении ГСС в тени Земли. В первом случае из моментов внешних сил,
приложенных к спутнику, учитывались гравитационный и момент от силы светового
давления. Во втором случае, считая, что собственный магнитный момент спутника
равен нулю, учитывался только гравитационный момент.
Компоненты
гравитационного момента задавались формулами

Здесь  - компоненты геоцентрического радиуса-вектора центра масс
станции, - компоненты геоцентрического радиуса-вектора центра масс
станции,  – компоненты тензора инерции
станции в строительной системе координат, – компоненты тензора инерции
станции в строительной системе координат,   , ,  – гравитационный параметр Земли.
Момент от силы светового давления аппроксимируется выражениями – гравитационный параметр Земли.
Момент от силы светового давления аппроксимируется выражениями

Здесь  , ,  – скорость света, – скорость света,  – средний радиус
орбиты Земли; – средний радиус
орбиты Земли;  – расстояние от КА до
Солнца; – расстояние от КА до
Солнца;  – постоянные
коэффициенты; – постоянные
коэффициенты;  - компоненты орта направления ГСС – Солнце. При выводе этих
выражений предполагалось, что на интервалах оценки площадь поверхности ГСС, на
которую воздействует набегающий световой поток, неизменна и отражающие свойства
поверхности спутника во всех его точках одинаковы. Высокая точность оценки возмущающих
моментов, действующих на ГСС, выполненная на таких временных интервалах,
позволяет сделать выводы, что принятые допущения вполне оправданы и не окажут
существенного негативного влияния на расчетные оценки компонент тензора инерции. - компоненты орта направления ГСС – Солнце. При выводе этих
выражений предполагалось, что на интервалах оценки площадь поверхности ГСС, на
которую воздействует набегающий световой поток, неизменна и отражающие свойства
поверхности спутника во всех его точках одинаковы. Высокая точность оценки возмущающих
моментов, действующих на ГСС, выполненная на таких временных интервалах,
позволяет сделать выводы, что принятые допущения вполне оправданы и не окажут
существенного негативного влияния на расчетные оценки компонент тензора инерции.
Компоненты
кинетического момента спутника в его движении относительно центра масс имеют
вид
 , ,
где  и и  – компоненты
собственного кинетического момента системы маховиков и угловой скорости ГСС.
Теорема об изменении кинетического момента ГСС под действием указанных выше
внешних моментов выражается соотношениями – компоненты
собственного кинетического момента системы маховиков и угловой скорости ГСС.
Теорема об изменении кинетического момента ГСС под действием указанных выше
внешних моментов выражается соотношениями

Здесь точкой обозначено
дифференцирование по времени  . Подставив в эти соотношения выписанные выше выражения для
величин . Подставив в эти соотношения выписанные выше выражения для
величин  , ,  и и  , получим уравнения , получим уравнения

 (1) (1)

С
помощью соотношений  из этих уравнений исключены компоненты тензора инерции из этих уравнений исключены компоненты тензора инерции  при при  . .
Ниже
выписанные уравнения будем использовать следующим образом. На некотором отрезке
времени длиной не более нескольких часов по телеметрической информации
восстановим фактическое движение спутника относительно центра масс, в том
числе, его угловую скорость и угловое ускорение. В результате уравнения (1)
станут замкнутой системой относительно переменных   . В этой системе величины . В этой системе величины  , ,  будем рассматривать
как параметры. Общее решение этих уравнений, указав явно его зависимость от параметров
и начальных условий, представим следующим образом будем рассматривать
как параметры. Общее решение этих уравнений, указав явно его зависимость от параметров
и начальных условий, представим следующим образом
 (2) (2)
где  – начальные условия, – начальные условия,  – заданный момент времени, – заданный момент времени,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  . Функции . Функции  определяются начальными
задачами, для линейных дифференциальных уравнений, не содержащих параметров. определяются начальными
задачами, для линейных дифференциальных уравнений, не содержащих параметров.
Математическое
обеспечение системы маховиков позволяет в некоторые моменты времени   измерять значения измерять значения  компонент ее
собственного кинетического момента. Точность определения кинетического момента
маховиков КА “Ямал-200” составляет 0.1Нмс. Результаты измерений этих величин
обозначим, соответственно компонент ее
собственного кинетического момента. Точность определения кинетического момента
маховиков КА “Ямал-200” составляет 0.1Нмс. Результаты измерений этих величин
обозначим, соответственно  . Если указанные измерения приходятся на отрезок времени, для
которого имеются значения кватерниона ориентации, то с помощью соотношений (2)
их можно обработать каким-либо статистическим методом и определить вектор . Если указанные измерения приходятся на отрезок времени, для
которого имеются значения кватерниона ориентации, то с помощью соотношений (2)
их можно обработать каким-либо статистическим методом и определить вектор  . Поскольку вычисляемые по формулам (2) величины . Поскольку вычисляемые по формулам (2) величины  зависят от зависят от  линейно, наиболее
подходящим в данном случае методом обработки является метод наименьших
квадратов. В рамках этого метода оценкой вектора линейно, наиболее
подходящим в данном случае методом обработки является метод наименьших
квадратов. В рамках этого метода оценкой вектора  служит его значение,
минимизирующее функцию служит его значение,
минимизирующее функцию
 . .
Это значение определяется так
называемыми нормальными уравнениями, которые в данном случае имеют вид
 , (3) , (3)

Если ошибки в измерениях величин  независимы и имеют одинаковое
нормальное распределение с нулевым средним значением и стандартным отклонением независимы и имеют одинаковое
нормальное распределение с нулевым средним значением и стандартным отклонением  , то оценка , то оценка  вектора вектора  , определяемая системой (3), является несмещенной с ковариационной
матрицей , определяемая системой (3), является несмещенной с ковариационной
матрицей  , где , где  – матрица системы (3).
Поскольку значение – матрица системы (3).
Поскольку значение  неизвестно, его
квадрат– дисперсию ошибок измерений– при расчете ковариационной матрицы можно
заменить оценкой неизвестно, его
квадрат– дисперсию ошибок измерений– при расчете ковариационной матрицы можно
заменить оценкой

Чтобы реализовать описанный подход к оцениванию тензора
инерции спутника, необходимо располагать методом восстановления его
фактического движения по телеметрической информации. Ниже используется метод,
основанный на аппроксимации вращательного движения спутника сплайнами.
3. Аппроксимация вращательного движения спутника. Телеметрическая информация собирается на временном
интервале не более часа, содержит последовательность моментов времени,
кватернионов и угловых скоростей
 (4) (4)
Здесь  , ,  – значение
кватерниона – значение
кватерниона  , вычисленное на момент времени , вычисленное на момент времени  , ,  – значение
угловой скорости, определенное на этот же момент времени. Как правило, – значение
угловой скорости, определенное на этот же момент времени. Как правило,  2 с. Кватернион,
задающий ориентацию спутника, определен с точностью до знака. Знаки 2 с. Кватернион,
задающий ориентацию спутника, определен с точностью до знака. Знаки  и момент и момент  в (2) выбираются из
условия в (2) выбираются из
условия
 . .
Сглаживание
последовательности кватернионов (4) выполняется покомпонентно с использованием
решения следующей задачи. Пусть для моментов времени   , ,  , известны приближенные
значения , известны приближенные
значения  некоторой гладкой
функции некоторой гладкой
функции  . Требуется восстановить эту функцию на отрезке . Требуется восстановить эту функцию на отрезке  . .
В [13]
отыскание  в предположении, что
эта функция дважды непрерывно дифференцируема, сводится к решению вариационной
задачи в предположении, что
эта функция дважды непрерывно дифференцируема, сводится к решению вариационной
задачи
 (5)
(5)
Здесь S - заданное положительное
число. Решением задачи (5) является кубический сплайн. В [13] приведена программа
на алголе-60 вычисления коэффициентов этого сплайна по величинам  , ,  , ,   . Эта программа, переписанная на турбо-паскаль, применялась
для аппроксимации движения станции. . Эта программа, переписанная на турбо-паскаль, применялась
для аппроксимации движения станции.
Норма
кватерниона, который образован сплайнами, сглаживающими компоненты кватернионов
(4), уже не равна единице, но мало отличается от нее. Полученная кватернионная
функция нормируется на единицу и служит аппроксимацией вращения системы  относительно системы относительно системы  на отрезке на отрезке  . .
Для
уменьшения случайных ошибок при определении значений угловой скорости спутника
использовался процесс сглаживания, основанный на применении метода наименьших
квадратов. Предполагалось, что измеренные значения угловой скорости имеют
одинаковую точность и функция 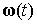 на участке измерений
может быть достаточно хорошо приближена многочленом третьей степени. В
результате по наблюденным значениям функции в точках измерений методом
наименьших квадратов построен многочлен третьей степени, приближающий функцию на участке измерений
может быть достаточно хорошо приближена многочленом третьей степени. В
результате по наблюденным значениям функции в точках измерений методом
наименьших квадратов построен многочлен третьей степени, приближающий функцию  и за значения этой
функции принимались значения и за значения этой
функции принимались значения  полученного многочлена
в точках tm.
Вычисление выполнялось по четырем точкам с использованием следующего выражения полученного многочлена
в точках tm.
Вычисление выполнялось по четырем точкам с использованием следующего выражения
 . (6) . (6)
Такое
определение угловой скорости спутника позволило уменьшить влияние ошибок
измерений при последующей аппроксимации функции  , которая выполнялась для получения значений угловой скорости
в требуемые моменты времени. Методика аппроксимация та же, что и для
кватернионов. Аналогичный подход использовался при вычислении значений
кинетического момента маховиков. , которая выполнялась для получения значений угловой скорости
в требуемые моменты времени. Методика аппроксимация та же, что и для
кватернионов. Аналогичный подход использовался при вычислении значений
кинетического момента маховиков.
Примеры
аппроксимации вращательного движения ГСС описанным способом приведены на рис. 1
– 4. Эти рисунки иллюстрируют стабилизацию спутника в орбитальной системе
координат при движении ГСС по освещенной Солнцем части орбиты. На рис. 1a – 4a
маркеры указывают точки  , отвечающие телеметрическим данным (4), а кривые
изображают сглаживающие эти данные сплайны. , отвечающие телеметрическим данным (4), а кривые
изображают сглаживающие эти данные сплайны.
Детали
движения спутника на соответствующих временных интервалах представлены на рис.
1б – 4б. Здесь точками представлены измеренные значения кинетического момента и
угловой скорости, а сплошные линии – результат аппроксимации.
В
приведенных примерах ориентация спутника поддерживалась одними лишь маховиками.
Реактивные двигатели системы управления движением ГСС не включались. Это
обстоятельство позволило использовать полученные на соответствующих временных интервалах
данные измерений кинетического момента маховиков для оценивания тензора инерции
спутника. В таблице приведены результаты оценивания этого тензора, а также параметров
светового давления ГСС при движении по освещенной Солнцем части орбиты на
четырех таких интервалах (инт.1 – 4). В таблице указаны номер интервала, дата и
время, на которые этот интервал приходится, оценка  стандартного
отклонения ошибок в данных измерений кинетического момента маховиков, оценки
параметров стандартного
отклонения ошибок в данных измерений кинетического момента маховиков, оценки
параметров  и и  , а также стандартные отклонения этих оценок , а также стандартные отклонения этих оценок  и и  . В нижней строке таблицы указаны расчетные значения
компонент тензора инерции спутника. . В нижней строке таблицы указаны расчетные значения
компонент тензора инерции спутника.
Результаты оценок тензора инерции спутника при его
движении в тени Земли представлены в таблице (инт. 5 – 7). На рисунках 5 – 7 приведены примеры аппроксимации
вращательного движения ГСС на этих участках орбиты.
Анализ полученных результатов свидетельствует о
возможности применения описанных моделей и получаемых с их помощью оценок
моментов инерции спутника для нужд управления полетом. Полученные результаты
расчетов, выполненных при использовании телеметрической информации (ТМИ) на теневых
участках орбиты и на освещенных Солнцем, довольно близки. Величины полученных
оценок параметров момента от силы светового давления и стандартные отклонения
этих оценок свидетельствуют о том, что при выполнении расчетов на временных
интервалах ~40 минут влиянием момента от силы светового давления можно
пренебречь. При решении задачи оценки тензора инерции с использованием ТМИ
теневого участка оценки недиагональных компонент тензора инерции и соответствующие
им стандартные отклонения меньше, чем те же оценки, полученные при обработке
ТМИ освещенного Солнцем участка орбиты. Объясняется это, видимо, выбранным
способом оценки параметров момента от силы светового давления. Повышение точности
оценок компонент тензора инерции может идти по пути более точного моделирования
момента от силы светового давления, действующего на спутник.
Дальнейшая разработка адекватной математической
модели вращательного движения связана с построением модели возмущений от сил
светового давления, а также моделей закона изменения суммарного кинетического момента
КА и закона изменения кинетического момента маховиков.
Литература
[1] Севастьянов Н.Н. Спутники
связи «Ямал». Аэрокосмический курьер, 2000, №1.
[2] Севастьянов Н.Н. Система
спутниковой связи «Ямал»: состояние и перспективы развития. Аэрокосмический
курьер, 2002, №3.
[3] Брюханов Н.А., Беляев М.Ю.
Математическое моделирование при создании и эксплуатации орбитальных
комплексов. Полет, 2005, №8, с. 3-9.
[4] Беляев М.Ю. Научные
эксперименты на космических кораблях и орбитальных станциях. М.:
Машиностроение, 1984.
[5] Бабкин Е.В., Беляев М.Ю.,
Ефимов Н.И. и др. Измерение и моделирование микроускорений на МКС. Труды 37-х
Чтений К.Э. Циолковского. Секция «Проблемы ракетной и космической техники»,
Казань, УНИПРЕСС, 2002.
[6] Беляев М.Ю., Банит Ю.Р.,
Завалишин Д.А. и др. Эксперимент «Тензор» по определению динамических
характеристик МКС. Труды 38-х Чтений К.Э. Циолковского. Секция «Проблемы
ракетной и космической техники», Казань, КГУ, 2004.
[7] Беляев М.Ю., Ефимов Н.И.,
Сазонов В.В. Определение ориентации орбитального комплекса «Мир» по показаниям
оптического звездного датчика. Космические исследования, 1995, т. 33, №4, с.
395-402.
[8] Бабкин Е.В., Беляев М.Ю.,
Ефимов Н.И. и др. Неуправляемое вращательное движение орбитальной станции Мир.
Космические исследования, 2001, т. 39, №1, С. 27-42.
[9] Сазонов В.В., Беляев
М.Ю., Зыков С.Г. Исследование задачи
оценивания тензора инерции орбитальной станции «Мир» по данным измерений кинетического
момента гиродинов . Космические исследования 1994, т. 32, №3. с. 3-16.
[10] Сарычев В.А., Сазонов В.В., Беляев М.Ю. и др. Оценивание тензора
инерции орбитальной станции «Мир» по данным измерений кинетического момента
гиродинов. Космические исследования, 1994, т. 32, №4-5, с. 22-42.
[11] Банит Ю.Р., Беляев М.Ю., Добринская Т.А. и др. Определение
тензора инерции Международной
космической станции по телеметрической информации. Космические исследования,
2005, т. 43, №2, с. 135-146.
[12] Бранец В.Н., Шмыглевский И.П. Применение кватернионов в задачах ориентации
твердого тела. М., Наука, 1973.
[13] Reinsch
C.H. Smoothing by spline functions. Numerische mathematik, 1975, B. 24, H. 5,
S. 383-393.
Таблица
|
Инт.
|
Дата
|

|

|

|

|

|
|
1
|
31.12.04
22:43:29–23:23:30
|
0.001
|
6884.3
|
203.5
|
–7.4
|
9.5
|
|
2
|
01.01.05
12:13:27–12:55:02
|
0.001
|
7049.2
|
98.2
|
–84.9
|
14.9
|
|
3
|
01.01.05
8:28:17–9:02:39
|
0.001
|
6975.9
|
163.6
|
38.7
|
34.8
|
|
4
|
01.01.05
13:43:01–14:24:15
|
0.001
|
6987.6
|
88.7
|
0.1
|
7.4
|
|
5
|
23.09.05
23:05:29–23:31:14
|
0.001
|
7008.8
|
88.851
|
–3.7
|
2.6
|
|
6
|
13.09.05
23:08:43–23:50:29
|
0.001
|
6949.8
|
144.4
|
0.3
|
1.5
|
|
7
|
13.03.05
23:21:59-23:53:37
|
0.0008
|
6909.8
|
25.9
|
–1.5
|
0.2
|
|
|
|
|
6719.5
|
|
–5.7
|
|
|
Инт.
|

|

|

|

|

|

|

|

|
|
1
|
35.9
|
44.1
|
6866.7
|
95.0
|
–64.9
|
29.9
|
917.9
|
303.5
|
|
2
|
–146.6
|
34.2
|
6822.4
|
153.3
|
1.1
|
24.4
|
1128.9
|
278.3
|
|
3
|
–65.7
|
37.8
|
6844.0
|
96.3
|
–71.3
|
19.9
|
1016.8
|
241.5
|
|
4
|
–52.9
|
18.8
|
6843.1
|
118.7
|
16.4
|
16.2
|
1186.7
|
122.5
|
|
5
|
–11.7
|
4.9
|
6693.2
|
97.9
|
0.7
|
3.6
|
1076.9
|
190.2
|
|
6
|
1.6
|
3.4
|
6837.9
|
66.2
|
–16.0
|
3.1
|
1020.9
|
157.2
|
|
7
|
–2.7
|
0.9
|
6849.2
|
27.6
|
–2.3
|
0.4
|
1091.9
|
128.4
|
|
|
17.0
|
|
6503.4
|
|
–17.7
|
|
1014.9
|
|
|
Инт.
|

|

|

|

|

|

|
|
1
|
13.6
|
7183.7
|
–3.8
|
5069.2
|
–22.0
|
4330.1
|
|
2
|
21.1
|
5606.1
|
–22.9
|
7098.2
|
40.5
|
2616.7
|
|
3
|
–28.6
|
4267.9
|
–10.8
|
4403.2
|
–23.9
|
4132.0
|
|
4
|
78.8
|
4275.4
|
20.4
|
5198.1
|
17.9
|
1699.7
|
|
5
|
0
|
–
|
0
|
–
|
0
|
–
|
|
6
|
0
|
–
|
0
|
–
|
0
|
–
|
|
7
|
0
|
–
|
0
|
–
|
0
|
–
|
Рисунки
|

 ,
,





 ,
,















