1. ВВЕДЕНИЕ

                 Геостационарные спутники, практически неподвижно «висящие» над соответствующими точками Земли, важны для обеспечения линий космической связи и наблюдения за Землей. В рамках центрального ньютоновского гравитационного поля такой спутник, как известно, должен двигаться по т.н. геостационарной орбите – круговой геоэкваториальной орбите радиуса R»42164 км, с звездно-суточным периодом обращения. С точки зрения прикладной небесной механики для обеспечения функционирования таких спутников надо решить ряд задач, в частности, задачу выведения космического аппарата с Земли на ГСО и задачу удаления КА с ГСО [1]. Относительно выведения КА на ГСО с использованием двигателя большой тяги анализ показал [2-4], что при достаточно большой широте точки старта, свыше ~ 28° (это выполняется для Российских космодромов Байконур и Плисецк), энергетически выгоднее использовать не «прямую» схему полета, а «обходную», с предварительным подлетом к Луне. При этом выполняется лунный гравитационный маневр с пассивным изменением наклонения и перигейного расстояния и затем осуществляется подлет к ГСО, см. рис. 1 [2-4]. В силу важности этого результата данное исследование позднее было повторено европейскими учеными [5].

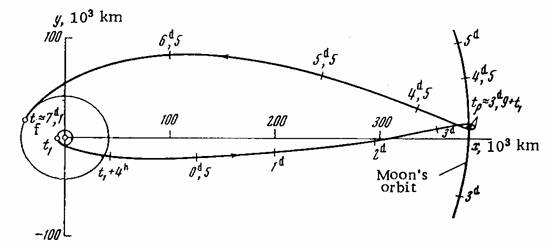
Рис. 1. Траектория выведения КА на геостационарную орбиту с гравитационным маневром у Луны.

На рис. 2 приведена зависимость характеристической скорости выведения на ГСО от начального наклонения - для двух схем полета [2-4]. Здесь кривая w_к^I соответствует двух- и трехимпульсному полету в поле притяжения Земли, а кривая w_к^II – полету с маневром у Луны. Последняя схема выведения, основанная на идеях А. Штернфельда об «обходных» перелетах [6-7] и идеях Ф.А. Цандера о гравитационных маневрах [8], была реализована на практике космонавтики для выведения спутника ASIASAT 3/HGS-1 [9, 10], и это было названо «наиболее впечатляющим» событием космонавтики в 1998 г. [9]; на рис. 3 приведена траектория этого полета [9].

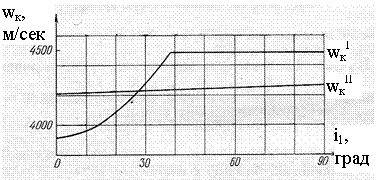
Рис. 2. Энергетика выведения на ГСО для двух схем полета.

Рис. 3. Траектория выведения КА ASIA SAT 3/HGS-1 на ГСО.

                 Вторая задача – задача увода КА с ГСО, являющаяся предметом нашего анализа, возникает, в первую очередь, ввиду того, что места на ГСО очень дефицитны. Так, уже сейчас на ГСО работает ~ 350 КА. Поэтому, чтобы не создавать «космического мусора» на ГСО, КА после окончания своего функционирования должен быть уведен с этой орбиты. Сейчас этот увод осуществляется поднятием высоты его орбиты на несколько сотен километров. Однако это представляется временной мерой, и в будущем скоро должен встать вопрос о кардинальном решении данной задачи.

                 Таким решением является, например, возвращение КА с ГСО к Земле. При этом будет происходить сгорание и разрушение КА в атмосфере или посадка его на поверхность Земли. Последний вариант может быть необходим, в частности (и это вторая причина постановки данной задачи), для возвращения на Землю ценного оборудования, результатов научных исследований или многоразового аппарата обслуживания объектов на ГСО [11]. В настоящей работе изложены основные результаты численного и аналитического исследования данной задачи при использовании двигателя большой тяги. Показано, что «обходные» траектории, использующие предварительный подлет к Луне для выполнения специального лунного гравитационного маневра торможения и последующий полет к Земле, энергетически всегда выгоднее обычных «прямых» траекторий возврата к Земле. Выявлены условия реализуемости «обходной» схемы возвращения с ГСО. Построено семейство таких траекторий, выполнен анализ их характеристик [1, 12].

2. «ПРЯМОЙ» СПУСК КА С ГСО К ЗЕМЛЕ

В случае «прямого» возвращения космическому аппарату на ГСО сообщается тормозной импульс скорости DV^(I),  см. рис. 4,  уменьшающий скорость КА с начальной скорости V₁ (» 3,075 км/с) до некоторой скорости V_a2 (<V₁) и переводящий КА на эллиптическую экваториальную орбиту подлета к Земле.

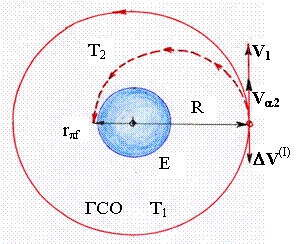
Рис. 4. Схема «прямого» спуска КА с ГСО на Землю.

Апогейное расстояние орбиты Т₂ равно R, геоцентрическое расстояние в условном перигее r_pf должно обеспечить спуск КА, это варьируемый параметр задачи:

0£ r_pf £ r_{pf max} » 6421 км.                                              (1)

На рис. 5 кривая DV^(I) дает изменение величины этого импульса скорости как функцию от конечного расстояния r_pf, DV^(I) » (1,49-3,075) км/с.

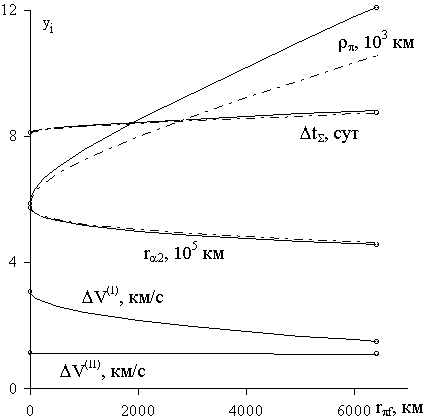
Рис. 5. Зависимость характеристик возвращения КА с ГСО на Землю от конечного расстояния в условном перигее.

3. «ОБХОДНЫЕ» ПЕРЕЛЕТЫ ГСО-ЗЕМЛЯ С ОБЛЕТОМ ЛУНЫ. ЧИСЛЕННЫЙ АНАЛИЗ

Если учесть результаты анализа задачи выведения КА на ГСО, то естественно предположить, что и для задачи спуска энергетически оптимальной может быть «обходная» схема полета с гравитационным маневром у Луны. На основе качественного анализа проблемы, который рассмотрим далее, и с учетом опыта построения и исследования траекторий Земля-ГСО [2-4], а также обходных перелетов между Землей и Луной [13-14] разработан численный алгоритм, с помощью которого построено семейство «обходных» траекторий полета к Земле с ГСО. При этом траектории КА определяются интегрированием уравнений движения точки в невращающейся геоэкваториальной геоцентрической прямоугольной системе координат OXYZ. Используется метод интегрирования [15], разработанный в ИПМ им. Келдыша для расчета траекторий КА. Учтено поле притяжения Земли (вместе с ее главной гармоникой с₂₀), Луны и Солнца. Координаты Луны и Солнца вычисляются по JPL–эфемеридам DE403. Определяется также движение точки в селеноцентрической системе координат MXYZ.

                 На Рис. 6, 7 приведены характеристики одной типичной «обходной» траектории возвращения с ГСО к Земле [16-18].

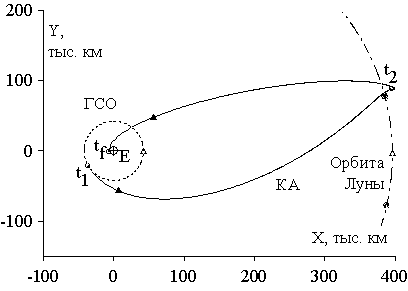
Рис. 6. Геоцентрическая траектория "обходного" типа для спуска КА с ГСО на Землю при использовании Лунного гравитационного маневра, в проекции XY.

                 Здесь E – Земля, M – Луна. На рис. 6 сплошная кривая дает геоцентрическое движение КА, штрих-пунктир - орбиту Луны, пунктир – орбиту ГСО. В начальный момент t₁ (29 декабря 2000 г.) КА, после увеличения его скорости на ~1100 м/с, отлетает с ГСО к Луне по орбите с апоцентическим расстоянием r_a2 »490 тыс. км. Все дальнейшее движение точки – пассивное (без учета возможной коррекции). Через ~ 3,8 суток полета, в момент t₂ (2 января 2001 г.) КА пролетает на минимальном расстоянии от Луны r_p (~13 тыс. км). При этом Луна находится вблизи восходящего узла ее орбиты относительно экватора Земли.

                 На рис. 7 представлено движение КА относительно Луны на участке ее облета. Здесь дана также схема изменения скорости КА в результате облета Луны. Под влиянием ее гравитации происходит поворот вектора селеноцентрической скорости «на бесконечности» на некоторый угол d (от V_¥^- к V_¥⁺). Новая селеноцентрическая скорость V_¥⁺ направлена практически противоположно скорости Луны V_M, т.е. происходит торможение геоцентрической скорости КА (от V₂ к V₃), уменьшение перигейного расстояния его орбиты с R » 42164 км до r_pf » 6421 км. После этого КА летит к Земле, достигая ее в момент t_f (8 января 2001 г.), через Dt_S » 9,4 суток полета, имея высоту условного перигея H_p » 50 км.

Рис. 7. Селеноцентрическое движение КА вблизи Луны и схема изменения скорости КА при облете Луны.

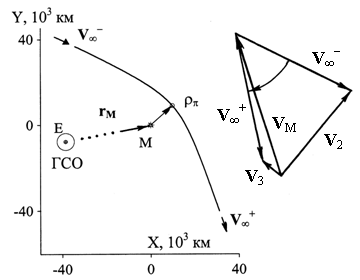
4. КАЧЕСТВЕННЫЙ АНАЛИЗ «ОБХОДНЫХ» ПЕРЕЛЕТОВ ГСО-ЗЕМЛЯ

Для более глубокого исследования характеристик «обходной» схемы полета с ГСО к Земле дадим качественный анализ этой схемы. При этом применим модель точечной сферы действия Луны, эффективность которой для данного класса задач показана при анализе перелета с Земли на ГСО [2-4]. В соответствии с этим методом сфера действия Луны стягивается в точку, так что геоцентрическая траектория КА для полета с начальной орбиты T₁ (ГСО) к Земле представляется двумя дугами кеплеровских орбит T₂ и T₃, соединенных в центре Луны при ее облете в момент t₂. Здесь геоцентрическая скорость КА меняется скачком с V₂ до V₃ в соответствии с поворотом на некоторый угол d вектора селеноцентрической скорости КА «на бесконечности» от V_¥^- к V_¥⁺ (см. рис. 8).

            В рамках данной модели примем следующую расчетную схему «обходной» траектории. В некоторой точке начальной орбиты T₁ (ГСО) космическому аппарату сообщается вдоль его скорости ускоряющий импульс скорости DV^(II), увеличивающий скорость КА от начальной V₁ до скорости V_p2 (V_p2 >V₁) и переводящий КА на вытянутую эллиптическую экваториальную орбиту Т₂ для полета к Луне. Перигейное расстояние орбиты Т₂ равно R, ее апогейное расстояние r_a2 есть второй варьируемый параметр задачи. Чтобы, двигаясь по орбите Т₂, КА встретился с Луной, Луна при встрече должна находится в плоскости Земного экватора, т.е. в узле ее орбиты относительно экватора Земли.

Рис. 8. Схема полета в модели точечной сферы действия Луны.

Пусть выбран некоторый момент t_M прохождения Луной узла ее орбиты при облете КА, ему соответствуют параметры движения центра Луны: радиус-вектор r_M и вектор скорости V_M. Это задает время t₂ и радиус-вектор r₂ КА при сближении с Луной:

t₂ = t_M; r₂ = r_M; z₂ = z_M (t_M)=0;                                            (2)

здесь z – координата по оси OZ, перпендикулярной плоскости экватора Земли. Тем самым определяется момент отлета с ГСО t₁ и положение орбиты Т₂ в пространстве, в частности, геоцентрическая скорость КА при подлете к Луне V₂ . Это позволяет найти вектор селеноцентрической скорости КА «на бесконечности» при подлете к Луне:

V_¥^- = V₂ - V_М; | V_¥^-| = V_¥.                                                  (3)

После его поворота на некоторый угол d, определяемый расстоянием до Луны в периселении орбиты, получаем селеноцентрическую скорость КА «на бесконечности» при отлете от Луны и, тем самым, геоцентрическую скорость КА полета к Земле V₃ (рис. 8):

V₃ = V_М + V_¥⁺; |V_¥⁺| = V_¥;                                                  (4)

cos d=(V_¥^-,V_¥⁺)/V_¥²;                                                         (5)

r_p= a (1/sin(d/2)-1); a = m_M/V_¥²;                                           (6)

где m_M (»4902,8 км³/с²) – гравитационная константа Луны, r_p - расстояние до Луны в периселении, a – действительная полуось гиперболы, селеноцентрической орбиты КА.

Условие (4) показывает, что в пространстве скоростей V конец вектора скорости V₃ лежит на сфере S с центром в конце вектора скорости Луны V_M и радиусом V_¥ , см. рис. 9:

S:                        (7)

где V_r, V_m, V_b – компоненты скорости по радиусу, трансверсали и бинормали орбиты Т₂ в момент t_M (т.е. оси V_r, V_m лежит в плоскости экватора Земли, ось V_b направлена по оси вращения Земли OZ); V_Mr, V_Mm, V_Mb – аналогичные компоненты вектора скорости Луны.

Вектор (t_M, r_M, V₃) задает геоцентрическую орбиту T₃ движения КА к Земле после облета Луны. Ее перигейное расстояние r_p3 должно быть равно заданному значению r_pf (1):

                                                                       (8)

Это условие геометрически задает в пространстве V гиперболоид вращения H, которому должен принадлежать конец вектора скорости V₃, см. рис. 9:

H:                (9)

здесь m_E (»398600,45 км³/с²) – гравитационная константа Земли, r=r_M, r_p= r_pf.

Рис. 9. Схема определения геоцентрической скорости и траектории полета к Земле;

а) Вид с оси V_t на множество решений A=H∩S.

            Пересечение сферы S (4) и гиперболоида H (9) задает в пространстве V множество A решений задачи, см. рис. 9. Здесь начало пространства скоростей V помещено в центр Луны M, ось V_t направлена по трансверсальной скорости Луны V_Mt, поэтому плоскость (V_r, V_t) есть плоскость орбиты Луны, в ней лежит скорость Луны V_M и, следовательно, центр O_S сферы S и ось симметрии гиперболоида H. Она является поэтому плоскостью симметрии множества решений A=H∩S. На рис. 9 справа приведен вид на это множество A с оси V_t для приведенного варианта пересечения поверхностей H и S. Здесь V_n – компонента скорости по нормали к плоскости орбиты Луны.

В общем случае, если d – наименьшее расстояние от центра сферы до гиперболоида, то решение задачи существует, когда

V_¥ ³ V_{¥ min}=d.                                                                 (10)

При этом для реализуемости маневра должно быть также выполнено условие на расстояние до Луны в периселении орбиты (6):

r_p ³ r_{p min} º R_M+DR,                                                       (11)

где R_M (=1838 км) – средний радиус Луны, DR (~ 100 км) – допуск на ошибки системы управления движением КА.

            Замечание. Аналитическая запись условия (10) несложна, но в общем случае довольно громоздка. Однако в данной задаче, когда гиперболоид очень близок к круговому цилиндру  = , и, кроме того, V_¥/t_p<<1, ½V_Mr½/t_p<<1 (ибо s_p/t_p<<1, s_p »0,2 км/с, t_p »11 км/с, V_¥ »1 км/с, ½V_Mr½»0,05 км/с, здесь V_Mr - радиальная скорость Луны), это условие довольно хорошо (с относительной точностью ~ 2×10^-6) записывается в виде:

                                                         (12)

где

                                                      (13)

трансверсальная компонента скорости Луны.

            Так как функция  монотонна, то из условия (10, 12) следует ограничение:

                                                          (14)

где V_¥ (r_{a2 min})=V_{¥ min}.

            При V_¥ = V_{¥ min}, r_a2 = r_{a2 min} имеем касание поверхностей S, H и единственное решение задачи. На рис. 5 сплошная кривая r_a2 (r_pf) дает минимальное расстояние

r_{a2 min} как функцию конечного перигейного расстояния r_pf : r_{a2 min} » (450-570)×10³ км. Другие сплошные кривые на рис. 5 дают минимальное расстояние от Луны r_p, время полета Dt_S, величину импульса скорости DV^(II) при разгоне с ГСО – для данного оптимального варианта, при r_a2=r_{a2 min}. Для всех этих решений выполняется с большим запасом условие (11) нестолкновения КА с поверхностью Луны. Величина импульса скорости «обходной» схемы DV^(II) существенно меньше импульса DV^(I) для случая «прямого» спуска, DV^(II) » 1,1 км/с, DV^(I) - DV^(II) ~ (0,4-1,9) км/с.

            Если V_¥ > V_{¥ min}, то множество решений A в пространстве V образует одну или две замкнутых кривых. За параметр на этом множестве решений взята радиальная компонента V_3r скорости V₃ (это третий параметр задачи), для одной кривой:

V_Mr - V_¥ <V_{3r min} (r_pf, V_¥) £ V_3r £ V_{3r max} (r_pf, V_¥) < V_Mr+V_¥,             (15)

причем для каждого значения V_3r внутри (15) имеется два решения, см. рис. 9а, где представлено множество A для варианта, когда это множество есть одна кривая, причем V_3r = V_{3r min} в точке A₁ и V_3r = V_{3r max} в точке A₂. Точки пересечения сферы S (7) и гиперболоида H (9) можно определить, рассматривая, например, их сечения плоскостью V_r=V_3r=const:

С_H:                                             (16a)

С_S:                                    (16b)

Здесь взяты оси V_r,V_t, V_n . Из этих уравнений получим (опуская для краткости индекс 3) координаты  двух точек пересечения этих окружностей:

                                              (17a)

    (17b)

Координаты V_m(i), V_b(i):

V_m(i) =V_t(i) cos i_M –V_n(i) sin i_M ; V_b(i)=V_t(i) sin i_M + V_n(i) cos i_M;                 (18)

где i_M  есть наклонение плоскости лунной орбиты к земному экватору:

sin i_M=V_Mr/V_Mt; cos i_M=V_Mm/V_Mt.                                                 (19)

            На рис. 10 при фиксированных типичных значениях r_pf (=6421 км) и r_a2 (=490 000 км > r_{a2 min}) для всего множества решений (являющегося здесь замкнутой кривой в V) приведены зависимости основных характеристик «обходной» траектории - наклонения i₃ орбиты T₃, угла поворота d скорости на «бесконечности», расстояния r_p, времени полета Dt_S - от скорости V_3r.

Рис. 10. Изменение основных характеристик траектории возврата с ГСО к Земле при фиксированном конечном расстоянии в условном перигее r_pf =6421 км и апогейном расстоянии r_a2 =490 тыс. км.

            Внизу на рисунке указана штриховая прямая r_{p min} = 2000 км. Все «обходные» решения реализуемы, выполняется условие (11).

            Видна также однозначность функции Dt_S (V_3r). В этом проявляется более общее интересное свойство орбиты T₃. Справедлива

            Теорема. Для орбиты T₃ полета от Луны к Земле при задании перигейного расстояния, скорости на «бесконечности» и радиальной компоненты скорости отлета от Луны оба решения задачи имеют одинаковые параметры в плоскости орбиты (большую полуось, истинную аномалию, время перелета) и отличаются лишь ориентацией орбиты в пространстве.

            Действительно, при V_3r=const сечение гиперболоида H в пространстве скоростей V есть окружность =с, поэтому оба решения имеют одинаковую скорость и, следовательно, при заданности расстояния (2), одинаковую константу энергии и большую полуось орбиты. Далее, в силу заданности перигейного расстояния (8) для обоих решений получим одни и те же значения эксцентриситета и апогейного расстояния. Из этого и из равенства радиальной скорости следует равенство истинной аномалии при t=t₂ и полное совпадение параметров в плоскости орбиты для обоих решений. Конечно, различными будут наклонения орбит i₃, как и параметры селеноцентрического движения (например, d, r_p).

            Штриховые кривые на рис. 5 также соответствуют случаю, когда V_¥ > V_{¥ min}, причем для определенности здесь взято V_¥ (r_pf) = V_{¥ min}+0,1 s_p, скорость V_3r принята равной радиальной скорости Луны: V_3r=V_Mr, а из двух решений задачи взято решение с бóльшим углом наклона орбиты T₃ к экватору Земли. Импульс скорости DV^(II) здесь практически тот же, что в оптимальном случае V_¥ = V_{¥ min}, DV^(II)<DV^(I).

ЗАМЕЧАНИЯ

1. Выше рассмотрен переход с орбиты. При переходе из начальной точки ГСО следует или сначала выполнить «дрейф» КА из этой начальной точки в точку, соответствующую «обходному» спуску с орбиты, или подбором начального времени обеспечить дополнительное условие на долготу начальной точки. Последнее можно сделать, например, введением пассивного витка на участке разгона КА с ГСО. Это выгодно также для уменьшения гравитационных потерь и расхода топлива при разгоне.

2. Из-за ошибок работы двигателя при разгоне КА с ГСО фактическая орбита будет отличаться от расчетной, и может потребоваться коррекция траектории, чтобы обеспечить вхождение КА в допустимую «трубку» подлета к Земле, с допустимым отклонением от заданного конечного расстояния в условном перигее.

3. При необходимости обеспечить в конце полета, кроме перигейного расстояния, некоторое дополнительное условие, например наклонение орбиты, можем для этого использовать параметр на множестве решений, например, радиальную скорость V_3r, см. рис. 10.

5. ВЫВОДЫ

            Суммируя результаты анализа задачи, можем сделать вывод, что использование гравитационного поля Луны позволяет осуществить «обходные» слабоэнергетические траектории возвращения с ГСО к Земле с пассивным уменьшением перигейного расстояния орбиты КА. Это дает возможность реализовать полет с ГСО к Земле заметно более экономично, при мéньшем расходе топлива, хотя и приводит к бóльшему времени полета и требует более точной системы управления, чем для обычных, «прямых» перелетов КА.

Данное исследование выполнено при поддержке Российского Фонда Фундаментальных исследований (Гранты 06-01-00531а, НШ-2003.2003.1).

6.      СПИСОК ЛИТЕРАТУРЫ

1.      Ивашкин В.В. О траекториях возвращения космического аппарата с геостационарной орбиты к Земле при использовании гравитационного поля Луны. // Актуальные проблемы космонавтики: Труды XXX Академических чтений по космонавтике. Москва, январь 2006 г. / Под общей редакцией А.К. Медведевой. М.: Комиссия по разработке научного наследия пионеров освоения космического пространства, 2006. С. 80-81.

2.      Ивашкин В.В., Тупицын Н.Н. Об использовании гравитационного поля Луны для выведения космического аппарата на стационарную орбиту спутника Земли. // Препринт, Институт прикладной математики Академии наук СССР, Москва, 1970. 32 с.

3.      Ивашкин В.В., Тупицын Н.Н. Об использовании гравитационного поля Луны для выведения космического аппарата на стационарную орбиту спутника Земли. // Космические исследования. 1971, т. IX, вып. 2, c. 163-172.

4.      Ивашкин В.В. Оптимизация космических маневров при ограничениях на расстояния до планет. М.: Наука, 1975, 392 с.

5.      Graziani F., Gastronuovo M.M. and Teofilatto P. Geostationary obits from mid-latitude launch sites via lunar gravity assist. // American Astronautical Society Publications, Advances in Astronautical Sciences. V. 84. 1993. AAS 93-289. P. 561-572.

6.      Sternfeld A. Sur les trajectoires permettant d'approcher d'un corps attractifs central à partir d'une orbite Keplérienne donnée. // Comptes rendus de l’Académie des Sciences (Paris), 1934, vol. 198. Р. 711— 713.

7.      Штернфельд А.А. Введение в космонавтику. а) 1937, М.- Л.: ОНТИ, 318 с. б) Изд. 2-е, М: Наука, 1975, 240 с.

8.      Цандер Ф.А. Перелеты на другие планеты (Теория межпланетных путешествий). // В кн.: Пионеры ракетной техники: Кибальчич. Циолковский. Цандер. Кондратюк. Избранные труды, М.: Наука, 1964. С. 277-359.

9.      Riebe T., and Schweitzer M. Space operations and support. // AEROSPACE AMERICA, Dec. 1998, p. 83.

10. Ivashkin V.V. Lunar space projects. // American Astronautical Society Publications, Science and Technology Series, Vol. 108, 2004. Proceedings of the International Lunar Conference 2003, November 16-22, 2003, Hawaii Island, USA. Eds: Steve M. Durst, et al. AAS 03-763. P. 481-499.

11. Ивашкин В.В., Райкунов Г.Г. Оптимальное обслуживание системы ИСЗ. // Известия Академии Наук. Техническая кибернетика. 1993. N 1. С. 111–120.

12. Ивашкин В.В. О траекториях возвращения космического аппарата с геостационарной орбиты к Земле с использованием гравитационного маневра у Луны. // Доклады Академии наук, 2006. В печати.

13. Ивашкин В.В. О траекториях полета точки к Луне с временным захватом ее Луной. // Доклады Академии наук, 2002, том 387, N 2, с. 196-199.

14. Ивашкин В.В. О траекториях полета точки от Луны к Земле с гравитационным освобождением от лунного притяжения. // Доклады Академии Наук, 2004, том 398, N 3, с. 340-342.

15. Степаньянц В.А., Львов Д.В. Эффективный алгоритм решения системы дифференциальных уравнений движения. // Математическое моделирование. 2000, т. 12, вып. 6, с. 9-14.

16. Ивашкин В.В. Ари Штернфельд и космонавтика. // Препринт, ИПМ им. Келдыша РАН, 2005, N 20. 32 с. http://www.keldysh.ru/papers/2005/source/prep2005_20.pdf.

17. Ивашкин В.В. Научное наследие А.А.Штернфельда. // Сборник: Штернфельд А.А. «Меня считали неизлечимым фантастом…» М.: Политехнический музей. 2005. С. 8-27.

18. Ивашкин В.В. Лунные траектории нового типа и роль гравитационных возмущений в их формировании. // Международный симпозиум «Астрономия 2005 – современное состояние и перспективы», 1–6 июня 2005 года, Россия, Москва. а) Труды ГАИШ МГУ, т. 78, М., 2005, с.10.

б) http://www/keldysh/ru/paper/2005/source/article/IAS-05/pdf .