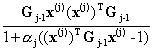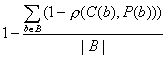Развитие метода полиномиальной регрессии и его практическое применение в задачах распознавания

( Development of Polynomial Regression in recognition of printed and hand-printed letters
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Введение

В настоящей работе рассмотрены теоретические основы и аспекты  практического применения метода [1] распознавания образов печатаных и рукопечатных символов, основанного на полиномиальной регрессии. Приведены характеристики качества программной реализации метода, определенные на базах графических образов символов с известными границами. Выполнено сопоставление с характеристиками  таких алгоритмов распознавания символов, таких как нейронные сети и алгоритм сравнения с эталонными образами.

Работы осуществлялись в ИПМ им. М.В.Келдыша РАН и ИСА РАН при финансовой поддержке ЗАО «Интеллектуальные Технологии».

1. Математическая постановка  задач обучения и распознавания согласно методу полиномиальной регрессии

            Краткая история вопроса.                 Первые работы по распознаванию образов с использованием метода полиномиальной регрессии относятся к середине прошлого столетия [2,3]. Для получения более обширной информации по данному вопросу можно, в частности, обратиться к трудам Шурмана (Jürgen Schürmann) [4,5]. В работе [6] излагается рекурсивный метод вычисления матрицы распознавания на этапе обучения. В [7] рассматривается проблема отделения от обучающего множества изображений некоторого подмножества трудных для распознавания изображений. Расширению структуры вектора, который строится по растру изображения, т.е. переходу от полиномиальной к структурной регрессии, посвящены работы [8,9].

Дальнейшее изложение теоретических основ метода полиномиальной регрессии соответствует аналогичному материалу, содержащемуся в [5], но является более компактным и представляет самостоятельный интерес.      

Математическая постановка задачи.     Задача распознавания символов состоит в разработке алгоритма, позволяющего по предъявляемому растру изображения определить, какому символу из некоторого конечного множества с K элементами  он соответствует.  Представлением символа является растр, состоящий из N=N1´N2 серых или черно-белых пикселей. Перенумеровав все пиксели растра, запоминаем в i-ой компоненте (1£i£N) вектора vÎR^N состояние i-го пикселя, а именно, 0 или 1 в случае черно-белого растра и значение на отрезке [0,1] для серого растра. Пусть V={v} – совокупность всевозможных растров. Очевидно, VÍR^N, причем если пиксели черно-белые, то V={0,1}^N –  конечное множество, элементами которого являются последовательности из нулей и единиц длины N. Если пиксели серые, то V=[0,1]^N – N-мерный единичный куб в R^N.

            Математическая постановка задачи распознавания состоит в следующем. Пусть для некоторого предъявляемого растра vÎV можно найти p_k(v) – вероятность того, что растр изображает символ с порядковым номером k, 1£k£K. Тогда результатом распознавания считается символ с порядковым номером k_o, где

p_ko(v)=max p_k(v),  1£k£K

Для решения задачи следует вычислить вектор вероятностей (p₁(v), p₂(v),…, p_K(v)). Он может быть найден на основе метода наименьших квадратов.

Метод наименьших квадратов.  Отождествим k-й символ с базисным вектором e_k=(0…1…0)  (1 на k-м месте, 1£k£K) из R^K, причем Y={e₁,…,e_K}. Пусть p(v,y) – вероятность наступления события (v,y), vÎV, yÎY (если V континуально, то плотность вероятности). Наступление события (v,y) означает, что выпадает растр v, и этот растр изображает символ y. Тогда вероятность p_k(v) – это условная вероятность p_k(v)=p(e_k|v)=p(v,e_k)/. С другой стороны, имеет место следующий результат [5,16]:

Теорема 1.     Экстремальная задача

E{||d(v)-y||²}min                                                   (1)

достигает минимума на векторе d(v)=(p₁(v),…,p_K(v)), причем min берется по всем непрерывным d: V® R^K.

            В Теореме 1 ||×|| - евклидова норма в R^K и для любой функции f: V´Y® R через E{f(v,y)} обозначено математическое ожидание случайной величины f:

                                   E{f(v,y)}

(в случае конечного V или Y интегрирование по соответствующей переменной заменяется на сумму). Итак, требуемый вектор вероятностей (p₁(v),…,p_K(v)) ищется как решение экстремальной задачи (1). Приближенное решение задачи (1) может быть найдено методом полиномиальной регрессии.

Метод полиномиальной регрессии.         Приближенные значения компонент вектора (p₁(v),…,p_K(v)) будем искать в виде многочленов от координат v=(v₁,…,v_N):

            p₁(v) @ c+ ++…

p₂(v) @ c+ ++…                                                           (2)

………………………………………….

p_K(v) @ c+ ++…         

Суммы в правых частях равенств (2) конечные и определяются выбором базисных мономов (например, (11) и (12)). А именно, если

x(v)=(1,v₁, … ,v_N, … )^T

конечный вектор размерности L из выбранных и приведенных в (2) базисных мономов, упорядоченных определенным образом, то в векторном виде соотношения (2) можно записать так:

            p(v) = (p₁(v),…,p_K(v)) @ A^Tx(v)                                                                    (2’)

где A – матрица размера L´K, столбцами которой являются векторы а⁽¹⁾,…, а^(K). Каждый такой вектор составлен из коэффициентов при мономах соответствующей строки (2) (с совпадающим верхним индексом), упорядоченных так же, как в векторе x(v).  Следовательно, приближенный поиск вектора вероятностей p(v) сводится к нахождению матрицы A. Учитывая результат Теоремы 1, следует понимать, что матрица А является решением следующей экстремальной задачи:

 E{||А^Тx(v)-y||²}min                                                (3)

где min берется по всевозможным матрицам А размера L´K.

            Имеет место следующий результат [5].

Теорема 2.     Матрица А размера L´K доставляет решение экстремальной задаче (3) тогда и только тогда, когда А является решением матричного уравнения

E{x(v) x(v)^Т}А = E{x(v) y^Т}                                                  (4)

Итак, согласно методу полиномиальной регрессии

            p(v) @ А^Тx(v),             А = E{x(v) x(v)^Т}^-1 E{x(v) y^Т}  

Заметим, что если x(v)=(1,v₁, … ,v_N)^T, то метод полиномиальной регрессии называется методом линейной регрессии [15].

Вычисление матриц E{x(v) x(v)^Т}, E{x(v) y^Т} основано на следующем результате математической статистики. Пусть имеется датчик случайных векторов, распределенных по неизвестному нам закону p(v,y):

[v⁽¹⁾,y ⁽¹⁾], [v⁽²⁾,y ⁽²⁾],…

Тогда математическое ожидание любой случайной величины f(v,y) может быть вычислено из предельного равенства:

            E{ f(v,y) } =

Если J достаточно большое, то верно приближенное равенство:

            E{ f(v,y) } @                                  (5)

Практически набор [v⁽¹⁾,y ⁽¹⁾],…, [v^(J),y ^(J)] реализуется некоторой базой данных, а вычисления по формуле (5) называются обучением. В данном случае f(v,y) = x_i(v)x_j(v) или f(v,y) = x_i(v)y_k и по определению

E{x(v) x(v)^Т} = [E{x_i(v)x_j(v)}]_1£i,j£L = []_1£i,j£L

            E{x(v) y^Т} = [E{x_i(v)y_k}]_{1£i£L, 1£k£K} = []_{1£i£L, 1£k£K}=

                                                                    = []_{1£i£L, 1£k£K}

А согласно формуле (5), получим выражение для практического вычисления:

E{x(v) x(v)^Т}@,         E{x(v) y^Т}@                            (6)

где  x^(j) = x(v^(j)), 1£j£J

         Практическое нахождение матрицы А.                       Согласно (4) и (6) имеем следующее приближенное значение для А:

            А @ ()^-1()                                                         (7)

В [5] показано, что правую часть (7) можно вычислить по следующей рекуррентной процедуре:

            A_j = A_j-1-a_jG_jx^(j)[Ax^(j)-y^(j)]^T,    a_j = 1/J                                                        (8)

            G_j = [G_j-1-a_j]              1£j£J                              (9)

где А₀ и G₀ заданы.

Введение вспомогательной матрицы G_j размера L´L  помогает избежать процедуры обращения матрицы в (7). Реально выбор параметров a_j  производится экспериментально.

2. Метод полиномов и его практическая реализация

            В методе полиномов [1], базирующемся на методе полиномиальной регрессии, используется следующая упрощенная модификация процедуры (8):

            G_jº D^-1, D = diag ( E{x}, E{x},…, E{x})                                  (10)

где x₁, x₂,…,x_L  - компоненты вектора x(v). В этом случае были получены приемлемые практические результаты. Рассматривались серые растры размера N=256=16´16. Масштабирование  образов до размера 16х16 сохраняет особенности геометрии исходных символов (рис.1).

Рис. 1. Образы 16х16 печатных и рукопечатных образов

Построение вектора x. Приведенная выше математическая постановка  задач обучения и распознавания согласно методу полиномиальной регрессии не является полной, поскольку не определен вектор базисных мономов x(v). «Ноу-хау» метода полиномов [1] является конкретный вид этого вектора, полученный  еще в 1999г. Структура вектора х была оптимизирована  по суммарной оценке качества распознавания всех символов обучающей выборки на базах графических образов (175 тыс. для рукопечатных цифр, 1 млн. символов для печатных букв и цифр). В настоящей работе используются два варианта  вектора  x из [1]: короткий и длинный. Для более длинного вектора больше размеры таблицы (матрицы) распознавания, медленнее осуществляется обучение и распознавание,  но при этом качество распознавания выше. Длинный вектор строится следующим образом:

x =(1, {v_i}, {v_i²}, {(dv_i)_r}, {(dv_i)_r²}, {(dv_i)_y}, {(dv_i)_y²},

{(dv_i)_r⁴}, {(dv_i)_y⁴}, {(dv_i)_r(dv_i)_y}, {(dv_i)_r²(dv_i)_y²}, {(dv_i)_r⁴(dv_i)_y⁴},

{(dv_i)_r((dv_i)_r)_L}, {(dv_i)_y((dv_i)_y)_L}, {(dv_i)_r((dv_i)_y)_L},                                                   (11)

{(dv_i)_y((dv_i)_r)_L}, {(dv_i)_r((dv_i)_r)_D}, {(dv_i)_y((dv_i)_y)_D},

{(dv_i)_r((dv_i)_y)_D}, {(dv_i)_y((dv_i)_r)_D})

Короткий вектор составлен из элементов длинного вектора, записанных в первой строке (11):

х =(1, {v_i}, {v_i²}, {(dv_i)_r}, {(dv_i)_r²}, {(dv_i)_y}, {(dv_i)_y²})                                           (12)  

В (11) и (12) выражения в фигурных скобках соответствуют цепочкам элементов вектора, вычисляемым по всем пикселям растра (за исключением указанных ниже случаев). Через (dv_i)_r  и (dv_i)_y обозначены конечные центральные разности величин v_i по ортогональным направлениям ориентации растра – нижние индексы r и y соответственно. Если имеется нижний индекс L  (left) или D (down), то это  означает, что соответствующие величины относятся к пикселю слева или снизу от рассматриваемого. Компоненты вектора x, не имеющие индекса L или D, вычисляются для всех пикселей растра; с индексом L – кроме левых граничных, с индексом D – кроме нижних граничных пикселей. Вне растра считаем, что v_i=0 (используется при вычислении конечных разностей на границе растра). Для длинного вектора x к  перечисленному в (11) добавляются компоненты, являющиеся средним арифметическим значений v_i (по восьми пикселям, окружающим данный), а также квадраты этих компонент.

Практическая реализация. При обучении элементы матрицы D (10) вычисляются следующим образом. Для каждого j-го элемента базы символов последовательно, начиная с первого и заканчивая J-м (последним), строится вектор xсогласно (11) или (12). Попутно рассчитываются значения компонент вспомогательного вектора mпо рекуррентной формуле:

m = (1-β) m+ β (x),         j=1,…,J ,         p=1,…,L                     (13)

β=1/j

По окончании этой процедуры для последнего элемента имеем согласно (10):

            G_J º D^-1 = diag (1/m,1/m,…,1/m)                                                          (14)

После того, как завершено вычисление G_J, элементы матрицы A_j  (8) рассчитываются следующим образом. Выполняется еще один проход по базе и для каждого j-го элемента базы символов, начиная с первого и заканчивая J-м, строится вектор x^j согласно (11) или (12). Попутно вычисляется A_j:

            a = a- α_j x(ax- y)/m,             α_j = 1/J                                (15)  

            A = [a],    j = 1,…,J         j=1,…,J,    p = 1,…,L ,    k = 1,…,K

На этом этап обучения закончен: матрица A=A_J  получена.

Распознавание осуществляется следующим образом. Для серого изображения размером 16х16 пикселей строится вектор x согласно (11) или (12). После этого по формуле (2’), используя A=A_J (15), вычисляются оценки, соответствующие каждому из возможных символов. Затем выбирается символ с максимальной оценкой.

Получаемые оценки могут выходить за рамки отрезка [0,1] из-за того, что используемый метод является приближенным. Проблема коррекции оценок является важной, в работе [5] этому вопросу уделяется большое внимание. Мы искусственно обнуляли отрицательные значения и делали равными 1 те, которые были больше этой величины. Практика распознавания показала приемлемость такого довольно грубого способа коррекции оценок.

3. Характеристики метода полиномов

Объектом анализа для нас будет служить реализация метода полиномов в виде программной компоненты, обучающейся с помощью образов и распознающей образы из графической базы данных, содержащей как изображения, так и коды символов. Результатом обучения служит матрица A. Результатом распознавания образа является код символа и его целочисленная оценка, лежащая в диапазоне [1,16] (оценка 16 является наилучшей). Эта новая оценка получается следующим образом: в результате умножения оценки на 16  старый диапазон оценок [0,1] переходит в новый [0,16], после чего проводится дискретизация, а именно, [0,1]→1, (1,2]→2,…, (15,16]→16.   Мы будем манипулировать следующими характеристиками качества методов распознавания символов: точностью, монотонностью оценок и быстродействием, подробно описанными в [10]. Определения этих характеристик таковы.

Точностью распознавания по базе B называется величина

где       b          – элементы тестовой базы образов B,

            | B |      – число образов в базе B,

            C(b)     – код символа, известный для каждого образа из тестовой базы,

            P(b)     – код символа, полученный в результате распознавания, 

   ρ(s,t)   – расстояние между известным и распознанным кодами символа, в качестве такого расстояния берется функция сравнения, равная 1, если s и t неразличимы, и равная 0 в противоположном случае. Различимость символов учитывает особенности представления образа, то есть собственно полинома, использующего нормализованный до размера 16х16 образ. То есть коды прописных и строчных символов, обладающих одинаковым начертанием, не различаются, например, группы букв кириллицы и цифр оО0 зЗ3 нН.

Ниже используются следующие обозначения:

-         N_E(W) – количество неправильно распознанных символов с оценкой, равной W;

-         N(W)   – количество символов, распознанных с оценкой W;

-         v_E(W)  – частота ошибочного распознавания с оценкой, равной W;

-         v(W)   – частота распознавания с оценкой, равной W.

Монотонность оценок – это свойство оценок характеризовать надежность распознавания символа. Пусть производится вычислительный эксперимент, состоящий в распознавании тестовой последовательности образов известных символов, для каждого тестового символа фиксируется факт безошибочности  и оценка распознавания. Для каждой оценки распознавания W определяется частота ее ошибочного распознавания v_E, равная отношению N_E(W), количества символов, распознанных неверно с оценкой W, к N(W), общему числу тестовых символов, распознанных с оценкой W. Если количество символов, распознанных с оценкой W равно 0, то такие частоты не рассматриваем. Рассмотрим совокупность  частот   {v_E(W_MIN), … , v_E(W_MAX)} появления ошибок распознавания. Монотонность графика частот появления ошибок распознавания назовем монотонностью оценок метода. Очевидно, что нас интересуют методы с монотонным убыванием графика частот.

Распределением оценок метода назовем совокупность  частот { v(W_MIN), … , v(W_MAX) } появления оценок, получаемых при распознавании, равных отношению N(W), количества символов, распознанных с оценкой W, к общему числу тестовых символов. Здесь учитывается сам факт распознавания с данной оценкой при произвольном результате – случаи правильного и ошибочного распознавания с конкретной оценкой суммируются. Этот частотный ряд интересен для методов с монотонными оценками. В самом деле, если большие оценки характеризуются большей надежностью распознавания, то желательно, чтобы метод чаще распознавал образы с большими оценками.

Быстродействием назовем количество распознанных в единицу времени  образов в процессе обработки тестовой последовательности. Быстродействие учитывает только время работы программной реализации метода распознавания и не учитывает накладные расхода на чтение из хранилища образов. Эта характеристика зависит как от особенностей реализации метода, так и от платформы. В нашем случае во всех рассмотренных ниже вариантах распознавание проводилось на платформе Pentium IV – 1500Мц – SDRAM, Windows2000 с помощью разработанной в среде Microsoft Developer Studio 6.0 библиотеки, скомпилированной в режиме максимальной скорости исполнения и использующей возможности SSE процессора Pentium IV, и оптимизированной с помощью Intel VTune 5.0 .

На всех приведенных далее рисунках гистограммой обозначено распределение v_E(W), а графиком – распределение v(W).

Печатные прямые буквы и цифры. Обучение и распознавание проводилось как на длинном векторе х (11), так и на коротком (12). Ниже для удобства изложения короткий вектор будем обозначать х_1. Получено, что повторное обучение на одной и той же базе (в 1 млн. символов) приводит к улучшению распознавания. Этот итерационный процесс имеет характер затухания по мере увеличения числа проходов по базе. Так на одной и той же базе после первоначального обучения распознавание давало точность 0,9855, а после третьей итерации – 0,9905. Время однократного обучения для длинного вектора х составило около 9 часов, включая чтение из базы графических образов и другие затраты времени, не входящие в алгоритм обучения. Аналогичные времена были зафиксированы и для других сеансов обучения методом полиномов, приводимых ниже.

В тестовой последовательности было 9787 образов.

Для длинного вектора х точность составила 0,9846, а быстродействие -  1100 символов/сек. Распределения оценок и ошибок представлены в таблице 1 и на  рисунке 2.

Таблица 1. Распределения оценок и ошибок распознавания прямых печатных

 букв и цифр на длинном векторе

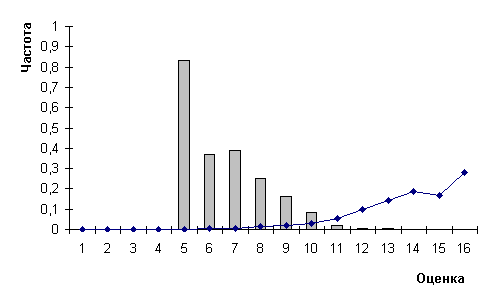
Рис.2. Распределения частот ошибок (гистограмма) и оценок (график) для прямых печатных букв и цифр на длинном векторе

Для короткого вектора х₁ точность составила 0,9681, а быстродействие -  2650 символов/сек. Распределения оценок и ошибок представлены в таблице 2 и на  рисунке 3.

Таблица 2. Распределения оценок и ошибок распознавания прямых печатных

 букв и цифр на коротком векторе

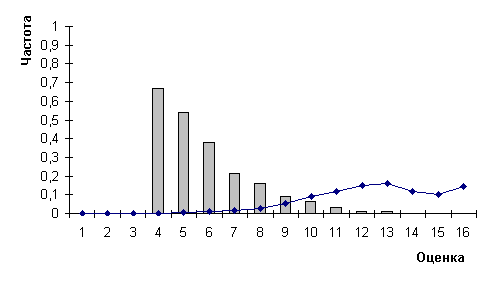
Рис.3. Распределения частот ошибок (гистограмма) и оценок (график) для прямых печатных букв и цифр на коротком векторе

Обратим внимание на две особенности полученных статистик обоих типов векторов:

-         ошибки с максимальной оценкой 16  отсутствуют, доля этой оценки по отношению к общему числу распознанных образов составляет около 0,14;

-         частота ошибок со старшими оценками (то есть равными 14, 15 и 16) составляет 0,0002, доля этих оценок составляет около 0,63.

То есть на тестовых базах метод порождает оценки, отвечающие критериям монотонности. Некоторое нарушение монотонности в области низких оценок не  представляется важным. Использование короткого вектора позволяет повысить быстродействие примерно в 2 раза, при этом почти в 2 раза увеличивается количество ошибок распознавания.

Печатные прямые и курсивные цифры.  Обучение проводилось на базе в 95 тыс. элементов с коротким вектором х₁. При обучении и распознавании между прямыми и курсивными символами не делалось различий. Точность на обучающей последовательности составляет 0,9946 при однократном обучении, а после третьего прохода по базе – 0,9966. 

Тестовая последовательность содержала 129822 образов.

Полученная точность равняется 0,9812, а быстродействие -  11500 символов/сек. Распределения оценок и ошибок представлены в таблице 3 и на  рисунке 4.

Таблица 3. Распределения оценок и ошибок распознавания прямых и

курсивных печатных цифр

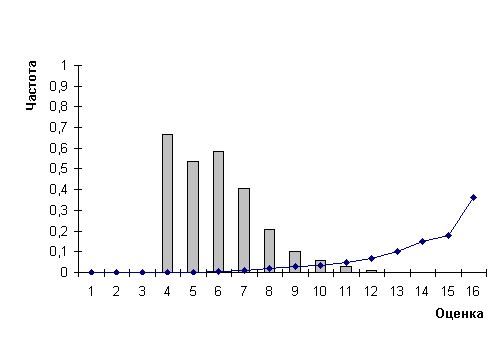
Рис.4. Распределения частот ошибок (гистограмма) и оценок (график) для прямых и курсивных печатных цифр

Для этого класса образов отметим, что распознавание  полиномами дало сходную точность по отношению к распознаванию прямых печатных букв и цифр и очень высокое быстродействие. Обратим внимание, что алфавит обучения и распознавания содержал 20 символов (10 прямых и 10 курсивных цифр). Отметим, что частота ошибок со старшими оценками  составляет 0,0001, доля этих оценок составляет около 0,69.

            Рукопечатные цифры.      После обучения по базе в 175 тыс. элементов для длинного вектора х  полученная матрица на той же базе обеспечивает распознавание 98.33% элементов, а после четвертой итерации качество распознавания возрастает до 98.81%. Также производилось обучение на коротком векторе х₁ (12).

Тестовая последовательность содержала 8416 образов.

Для длинного вектора х полученная точность равняется 0,9846, а быстродействие -  4000 символов/сек. Распределения оценок и ошибок представлены в таблице 4 и на    рисунке 5.

Таблица 4. Распределения оценок и ошибок распознавания рукопечатных

 цифр с помощью длинного вектора

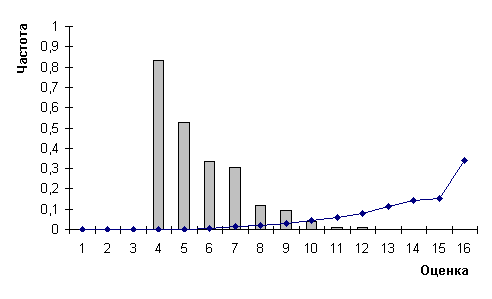
Рис.5. Распределения частот ошибок (гистограмма) и оценок (график) для распознавания рукопечатных цифр с помощью длинного вектора

Для короткого вектора х₁ полученная точность равняется 0,9703, а быстродействие -  9500 символов/сек. Распределения оценок и ошибок представлены в таблице 5 и на  рисунке 6.

Таблица 5. Распределения оценок и ошибок распознавания рукопечатных

 цифр с помощью короткого вектора

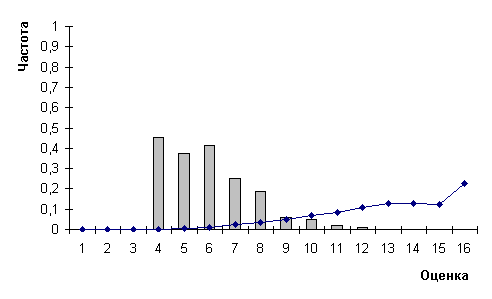
Рис.6. Распределения частот ошибок (гистограмма) и оценок (график) для распознавания рукопечатных цифр с помощью короткого вектора

Распознавание  методом полиномов (с длинным и коротким векторами) класса образов рукопечатных цифр дало сходные характеристики точности и быстродействия по отношению к распознаванию прямых печатных букв и цифр. Кривые распределений, характеризующие монотонность, также аналогичны кривым для прямых печатных букв и цифр (см. рис. 2,3).

На основании приведенных результатов численных экспериментов можно сделать вывод о том, что реализация метода полиномов показала высокие характеристики точности, быстродействия и, в особенности, монотонности оценок.

4.      Обсуждение результатов

В заключении попробуем ответить на вопрос: зачем нужен еще один метод распознавания символов, в то время как их описано немалое множество?

Обратимся к схеме алгоритмов в программах распознавания текстов (OCR) [10] и в системах массового ввода структурированных документов [11], включающей в себя:

-         алгоритмы бинаризации;

-         предварительное распознавание текста;

-         сегментацию страницы на блоки с текстом, таблицами, иллюстрациями, поля с рукопечатным текстом, разделительные линии и т.п. объекты;

-         распознавание строк (полей) символов с неизвестными границами;

-         адаптацию к особенностям страницы и использованным шрифтам для многопроходного распознавания;

-         словарную коррекцию и дораспознавание;

-         финальную сегментацию (форматирование в известные форматы).

Перечисленные этапы могут повторяться в соответствии с логикой адаптивного распознавания страницы документа. Любой из этих этапов может использовать методы распознавания символов для решения следующих задач:

-         классификация (отнесение к одному из известных символов) образа;

-         отделение символов от «несимволов» - образов, не входящих в алфавит распознавания;

-         оценка принадлежности образа к одному из известных классов.

Легко видеть, что основной характеристикой для двух последних задач служит монотонность оценок, а не точность распознавания. Учитывая повторяемость этапов распознавания и сложность переборных алгоритмов сегментации, следует обращать внимание на быстродействие методов распознавания символов.  Ответ на вопрос о необходимости создания новых методов распознавания таков: новые методы представляют интерес с точки зрения характеристик качества, превосходящих свойства известных методов.

Сопоставим характеристики метода полиномов и двух известных методов:

-         нейронные сети, описанные в [12] и обладающие высочайшей характеристикой точности;

-         метод сравнения с эталоном [13,14], обладающий высочайшим быстродействием (как обучения, так и распознавания) и высокой монотонностью оценок.

В качестве тестовой последовательности возьмем базу графических образов, содержащую  8416 рукопечатных цифр. Особенности процессов обучения методов сравнения с эталонами и нейронной сети рассматривать не будем.

Таблица 6. Распределения оценок и ошибок распознавания методом

 сравнения с эталонами 3х5

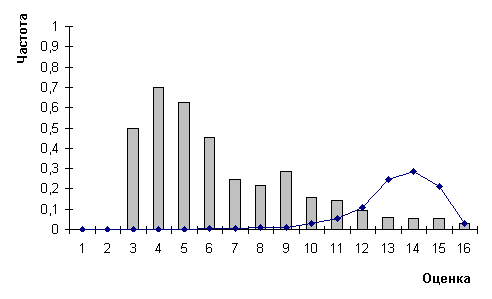
Рис.7. Распределения частот ошибок (гистограмма) и оценок (график) для распознавания методом сравнения с эталонами 3х5

Для метода сравнения с эталонами размера 3х5 [12] полученная точность равняется 0,9259, а быстродействие -  8000 символов/сек. Распределения оценок и ошибок представлены в таблице 6 и на  рисунке 7.

Таблица 7. Распределения оценок и ошибок распознавания нейронной сетью

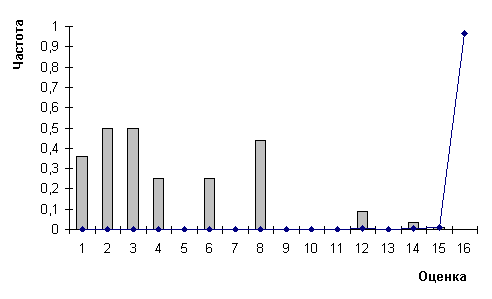
Рис.8. Распределения частот ошибок (гистограмма) и оценок (график) для распознавания нейронной сетью

Для нейронной сети размера 16х16 [12] полученная точность равняется 0,9976, а быстродействие -  4500 символов/сек. Распределения оценок и ошибок представлены в таблице 7 и на  рисунке 8.

Вначале сопоставим характеристики нейронной сети и полиномов. Мы видим неоспоримое превосходство нейронной сети над полиномами в точности распознавания (0,9976 против 0,9846) и в распределении оценок (нейронная сеть порождает 95,79% случаев распознаваний с максимальной оценкой 16, полиномы же – всего 22,7%). В то же время количество ошибок с максимальной оценкой 16 для нейронной сети составляет 1 случай, а для полиномов 0. И это не является случайностью, поскольку во всех приведенных выше результатах для полиномов ошибки с максимальной оценкой отсутствуют. Быстродействие методов сходно.

Метод сравнения с эталонами находится вне конкуренции с полиномами (также как и с указанной нейронной сетью) из-за возможности быстрого дообучения, не превосходящего нескольких секунд. При этом оценки метода сравнения с эталонами также монотонны, что можно видеть в таблице 6 и на рис. 7. Однако, на графике рис. 7 заметно сильное уменьшение доли старших оценок (0,0303 против 0,227 у полиномов для максимальной оценки). Ухудшение монотонности оценок по отношению к монотонности оценок метода полиномов очевидно также в численном выражении частот ошибок для старших оценок (для сравнения см. таблицы 6 и 4).

Сравнительные результаты распознавания рукопечатных цифр сведены в таблицу 8, которая содержит характеристики качества и распределения для старших оценок для трех методов: полиномов с коротким вектором, нейронной сети и сравнения с эталонами.

Таблица 8. Сводные характеристики методов полиномов, нейронной сети

 и  сравнения с эталонами.

Таким образом, сравнение характеристик метода полиномов с алгоритмами распознавания символов другой природы показывает его конкурентоспособность в области генерации монотонных оценок и быстродействия, что делает возможным его использование в комбинированных алгоритмах распознавания символов.

5.      Литература

[1]       Гавриков М.Б., Пестрякова Н.В. Метод полиномиальной регрессии в задачах распознавания печатных и рукопечатных символов. Препринт ИПМ им. М.В.Келдыша РАН, 2004, №22.

[2]        Sebestyen G.S. Decision Making Processes in Pattern Recognition, MacMillan, New York, 1962.

[3]       Nilson  N. J. Learning Machines, McGraw-Hill, New York, 1965.

[4]       Schürmann J. Polynomklassifikatoren, Oldenbourg, München, 1977.

[5]       Schürmann J. Pattern Сlassification,  John Wiley&Sons, Inc., 1996.

[6]        Albert A.E. and Gardner L.A. Stochastic Approximation and Nonlinear Regression // Research Monograph 42. MIT Press, Cambridge, MA, 1966.

[7]        Becker D. and Schürmann J. Zur verstärkten Berucksichtigung schlecht erkennbarer Zeichen in der Lernstichprobe // Wissenschaftliche Berichte AEG-Telefunken 45, 1972, pp. 97 – 105.

[8]        Pao Y.-H.        The Functional Link Net: Basis for an Integrated Neural-Net Computing Environment // in Yoh-Han Pao (ed.) Adaptive Pattern Recognition and Neural Networks, Addisson-Wesley, Reading, MA, 1989, pp. 197-222.

[9]        Franke J. On the Functional Classifier, in Association Francaise pour la Cybernetique Economique et Technique (AFCET), Paris // Proceedings of the First International Conference on Document Analysis and Recognition, St. Malo, 1991, pp.481-489.

[10]      Арлазаров В.Л., Логинов А.С., Славин О.А. Характеристики программ оптического распознавания текста // Программирование № 3, 2002, с. 45 – 63

[11]     Арлазаров В.В., Постников В.В., Шоломов Д.Л. Cognitive Forms – система массового ввода структурированных документов // Сборник трудов ИСА РАН «Управление информационными потоками», 2001, с. 35-46

[12]     Мисюрев А.В. Использование искусственных нейронных сетей
для распознавания рукопечатных символов // Сборник трудов ИСА РАН «Интеллектуальные технологии ввода и обработки информации»,  1998, с. 122-127

[13]     Cлавин О.А., Корольков Г.В., Болотин П.В. Методы распознавания грубых объектов // Сборник трудов ИСА РАН «Развитие безбумажных технологий в организациях», 1999, с.  290-311

[14]     Barroso J., Bulas-Cruz J., Rafael J., Dagless E. L. Identificação Automática de Placas de Matrícula Automóveis // 4.as Jornadas Luso-Espanholas de Engenharia Electrotécnica, Porto, Portugal, Julho (1995), ISBN 972-752-004-9.

[15]     Дж.Себер. Линейный регрессионный анализ. М.:”Мир”, 1980.

[16]   Ю.В.Линник. Метод наименьших квадратов и основы математико - статистической теории обработки наблюдений. М.:”Физматлит”, 1958.