Аннотация
Трехмерная компьютерная модель была применена для численного расчета разряда в высокочастотном
поле. Двухкомпонентная модель учитывает плазмодинамику газа, ионизацию, диссоциацию,
диффузию электронов, химическую кинетику и т.д.
Abstract
A three-dimensional computer code has been developed for numerical calculation
of the discharge in UHF fields. The two-component model takes into account
plasma - gas dynamics, ionization, dissociation, electron diffusion, chemical kinetics etc.
Содержание
Введение............................................................................................. 3
§1 Постановка
задачи......................................................................... 3
§2 Результаты
расчета........................................................................ 5
§3
Заключение………………………………………………………….10
Литература.................................................................................... …11
Введение
Настоящая работа посвящена описанию результатов
численного моделирования процесса
микроволнового разряда стримерного типа и является продолжением и уточнением
наших работ [1]-[7], в которых используются физические модели, предложенные К.В. Ходатаевым.
Объект расчетов - находящаяся в высокочастотном поле
двухтемпературная двухкомпонентная частично ионизованная плазма. Исследуются
последствия возникновения в газе небольшой проводящей каверны, вытягивание ее
вдоль направления внешнего линейно - поляризованного электромагнитного поля,
образование и развитие разряда стримерного типа.
Модель учитывает множество физических
эффектов - процессы ионизации,
рекомбинации, диффузии, диссоциации, радиационных потерь, физико-химической
кинетики и т.д.
Мы не
описываем здесь численный алгоритм. Он не содержит каких-либо принципиальных
новшеств и является комбинацией известных
конечно-разностных схем.
§1
Постановка задачи
Взаимодействие электромагнитного поля
заданной частоты с проводящим частично ионизованным газом описывается системой Максвелла для комплексных
амплитуд поля E, H
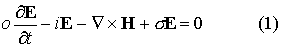
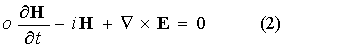
совместно
с уравнениями двухтемпературной плазмодинамики
 (3) (3)
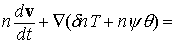 oq oq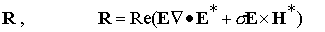 (4) (4)
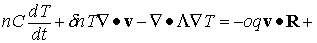 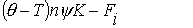 (5) (5)
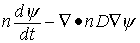  (6) (6)
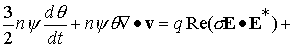 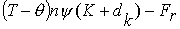 (7) (7)
Здесь
n, v, T - это плотность числа частиц, скорость и температура
газа, соответственно, ψ –
относительная концентрация электронов,
θ – их температура.
Используемые единицы измерения и выражения
для всех коэффициентов, проводимости
σ, диссоциации δ, теплоемкости C, теплопроводности
L, диффузии D, ионизации νi,
рекомбинации νr,
теплообмена K и т.д.
приведены ниже.
При
выборе единиц измерения
[*] используем фиксированные
значения частоты внешнего поля ω=2.2 ·1010 сек-1,
массы молекулы газа М=3.3·10-24
г и положим
[x]=c/ω=1.36 см,
[σ]=ω/4π=1.75·109 сек-1
[n]=2.4 ·1019 см-3,
[θ]=[T]=4.1 ·10-14
эрг,
[H]= [E]=36 г1/2
см-1/2 сек -1,
[v]=([T]/M)1/2 =1.11· 105
см/сек,
[t] =[x]/[v]=1.22· 10-5
сек.
Для
энергии системы, силы тока и количества электронов используются единицы:
[W]=[Q]=[n][T][x]3=2.5
·106 эрг,
[J]= [σ][E][x]2=1.2· 1011 г1/2 см3/2 сек
-2,
[S]= [n][x]3=6·1019
.
При этом
константы и функции, входящие в систему уравнений (1)-(7), имеют следующий вид:
o=1/ω[t]
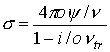 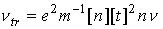 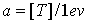
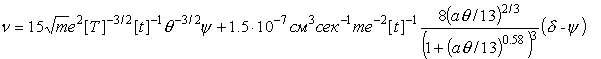
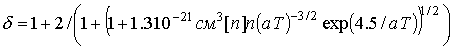
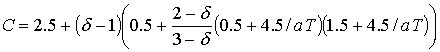
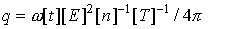 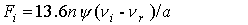
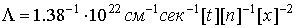
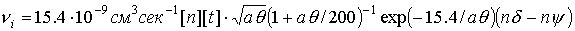
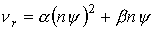 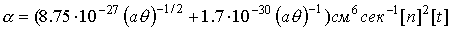
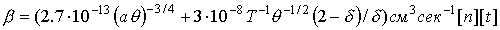
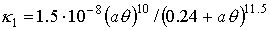 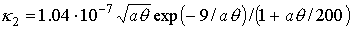
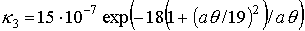 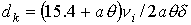
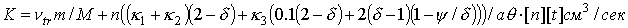 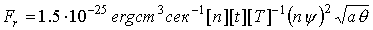 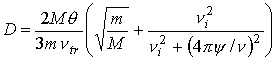 , , 
где
m и e - масса и заряд электрона.
Ввиду малости коэффициента (o ~10-6) при производных по времени в уравнениях (1), (2), пренебрегаем этими
членами и решаем полученную систему
Гельмгольца как стационарную, при каждом
t , с условиями Зоммерфельда на бесконечности для возмущения поля. Внешнее, первичное, поле - линейно
поляризованная плоская волна, распространяющаяся в направлении оси x, с
отличными от нуля компонентами Ez =-Hy =E0eix.
Кроме E0
параметрами задачи являются начальные значения: n = n0 , T = T0,
v = ψ = 0, причем
последняя имеет малое локальное возмущение ψ0, развитие
которого и является предметом расчета.
Хорошо известно, что среди решений
уравнения типа (6) имеются неустойчивые. Благодаря этому и возможно
образование стримера. Но это же – причина трудностей при конструировании и
реализации вычислительного алгоритма.
§2 Результаты расчета
Основной
вариант определяется значениями параметров n0=T0 =E0=1 и возмущением
ψ0 <10-5 внутри сферы радиуса ~ 0.03 с
центром в начале координат. Сама величина
ψ0
сколько-нибудь существенной
роли не играет, влияя лишь на масштаб времени
из-за экспоненциальности нарастания ψ на начальном этапе.
Задача
симметрична по z, и численный алгоритм хорошо эту симметрию
сохраняет. Поэтому мы всюду приводим распределения только для z>0.
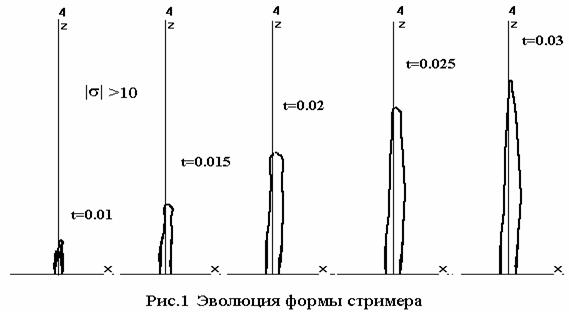
Общее представление о развитии стримера
дает рис.1, демонстрирующий эволюцию его
формы и размера. На нем изображены (в сечении плоскостью y=0) области, где проводимость |σ|>10, с
указанием моментов времени. В начальный
момент эта область - точка в начале координат. После t=0.01
скорость роста стримера V=dZ/dt достигает
нескольких сотен - всего на три порядка меньше скорости света. Как видно,
имеются незначительные отклонения стримера в направлении распространения
внешней волны. Отклонения в поперечном направлении ( по у ) отсутствуют и
симметрия сохраняется.
На серии рисунков 2а - 2f показаны
распределения поля |E|, проводимости
|σ|, тока Jz= ∫∫σEzdxdy, электронной
температуры θ и концентрации
ψ, температуры газа T вдоль оси стримера на момент t=
0.02.
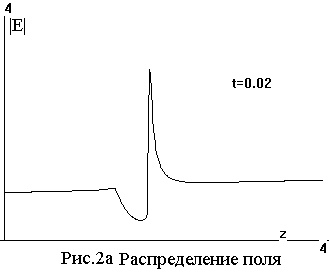
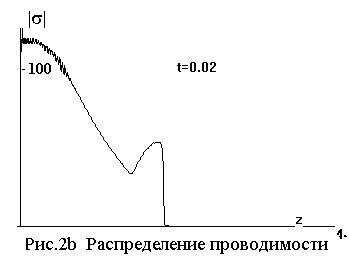
Отметим, что поле |E| и электронная температура θ имеют чрезвычайно острые
максимумы на конце стримера, где
концентрация электронов ψ еще
ничтожна, а вместе с ней и
проводимость σ с током J. С
ростом их, при отступлении от конца, поле резко падает.
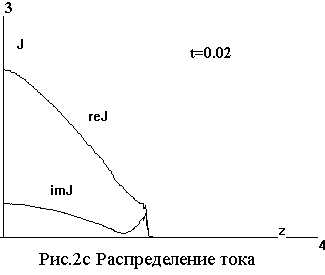
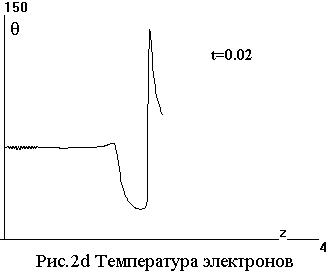
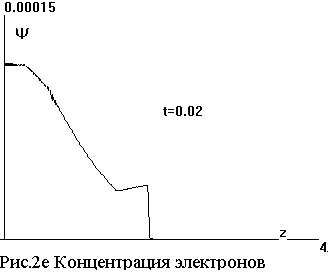
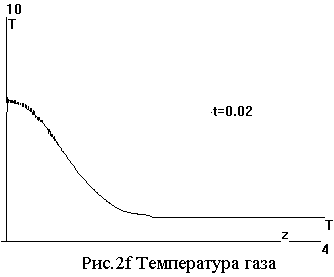
За столь короткое время гидродинамические процессы не успевают проявиться. Плотность газа практически не меняется, скорости малы.
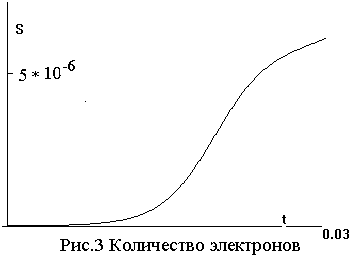
Темп ионизации и накопление электронной
массы демонстрирует рис.3, где дана зависимость от времени величины S(t) = ∫∫∫nψdxdydz - количества электронов. При этом начальное
значение S(0) ~10-9. Видны стадии процесса
разряда: экспоненциальное накопление, интенсивный линейный рост и некоторое замедление.
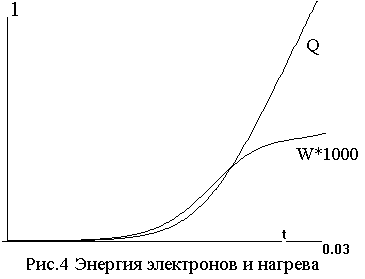
Подобная
картина и на рис.4, где показаны энергии электронов W(t)=1.5∫∫∫nψΘdxdydz и джоулева нагрева Q(t)= ∫dt∫∫∫qRe(σEE*)dxdydz. Заметим, что первая на три порядка меньше второй. Практически всю
получаемую энергию электроны передают газу.
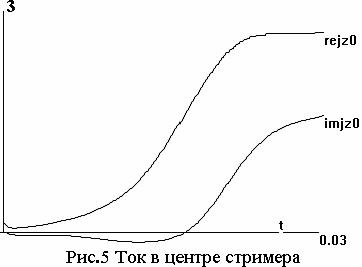
Зависимость от времени действительной и мнимой части тока Jz=
∫∫σEzdxdy в центре стримера показана на рис.5. Мнимая
часть меняет знак в начале активной стадии процесса. Максимальное значение
тока |Jz| =3 достигается в конце этой
стадии.
Некоторое представление об интенсивности
излучения и поглощения электромагнитной
энергии в области стримера дает рис.6. Здесь изображена х - компонента вектора Пойнтинга F=Re [E H*] - ее распределения вдоль осей х и z на тот же момент t=0.02., что
и рис.2. H*] - ее распределения вдоль осей х и z на тот же момент t=0.02., что
и рис.2.
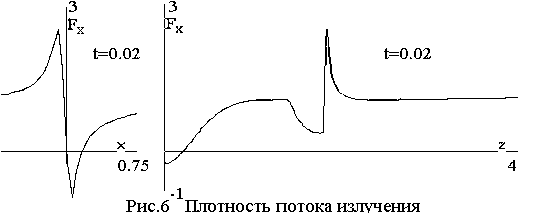
Максимальные значения поля |E| =3 и электронной температуры θ=130 достигаются на фронте ионизации в активный
период 0.015< t<0.02.
При этом, по причине остроты этих
максимумов, численный алгоритм, очевидно, занижает их. Остальные функции имеют
максимум в центре стримера. К моменту t=0.03 эти величины
|σ| = 200, ψ = 0.0002, T=20 и продолжают расти. Плотность газа упала в
центре до n =0.9.
Не приводя подробно результатов расчетов
других вариантов, отметим лишь основные отличия.
Изменение величины внешнего первичного
поля существенно сказывается на характере процесса. При уменьшении Е0 на 50% стример не развивается,
возмущение затухает. Увеличение же Е0 на 50% приводит к
резкому ускорению роста стримера.
Увеличение в десять раз начальной
плотности (и давления) газа n0 влечет за собой такое же увеличение критического
значения поля, необходимого для развития стримера. Кроме десятикратного
ускорения процесса никаких новых эффектов не возникает. Значения поля, тока,
количества и энергии электронов возрастают на порядок. В то же время
относительная концентрация и
температура электронов, проводимость и температура газа меняются мало.
В нижеследующей таблице приведены значения
некоторых характерных величин,
полученных в трех упомянутых вариантах.
n0 E0 |E|max θmax Vmax |J|max
1 1
3 130 200
3
1 1.5
4.5 170 800
7
10
10 35 150
2500 30
§3
Заключение.
Подводя
итог заметим, прежде всего, что последняя модель стримера, рассмотренная в
данной работе, дает существенно другие и, по-видимому, более разумные
результаты, по сравнению с использовавшимися нами ранее упрощенными
моделями, описанными в [1]-[4]. Она работоспособна и может эффективно использоваться для оценки
различных характеристик процесса
разряда.
Обобщая
сами результаты расчета, следует отметить: чрезвычайно малую степень ионизации
( ψ<0.001 ), небольшую
температуру электронов (θ ~100) и слабый нагрев газа. Из-за большой скорости протекания процесса гидродинамические
явления проявиться не успевают. Но, возможно, мы рассмотрели только начальную
стадию.
С точки
зрения разработки и реализации численного алгоритма главные трудности возникают
из-за "сложности" задачи, порождаемой, в основном, тонкой структурой
фронта ионизации и отмеченным выше наличием неустойчивых решений. К тому же
задача - на грани возможностей компьютера, что не позволяет добиться высокой
точности результатов расчета.
Литература
[1]
О.И. Воскобойникова, С.Л. Гинзбург, В.Ф. Дьяченко, К.В. Ходатаев. Инициация
микроволнового стримерного разряда в газе. // Препринт ИПМ им. М.В. Келдыша РАН, 2001, № 13.
[2]
О.И. Воскобойникова, С.Л. Гинзбург, В.Ф. Дьяченко, К.В. Ходатаев. Численное
исследование подкритического микроволнового разряда в газе высокого давления.
// ЖТФ, 2002, Т. 72, Вып. 8, С. 21-26.
[3]
О.И. Воскобойникова, С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик, К.В. Ходатаев. Расчеты микроволнового
стримерного разряда в газе.
// Препринт ИПМ им. М.В. Келдыша РАН,
2002, № 35.
[4]
О.И. Воскобойникова, С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик. Расчеты
микроволнового разряда в газе. // Препринт ИПМ им. М.В. Келдыша РАН, 2003, №
30.
[5]
С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик, К.В. Ходатаев Модель микроволнового разряда в газе. //
Препринт ИПМ им. М.В. Келдыша РАН, 2004, № 16.
[6]
С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик, К.В. Ходатаев 2-D модель микроволнового разряда в газе. // Препринт
ИПМ им. М.В. Келдыша РАН, 2005, № 1.
[7]
С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик, К.В. Ходатаев 3-D модель микроволнового разряда в газе. // Препринт
ИПМ им. М.В. Келдыша РАН, 2005, № 58.
|